Mixing with herringbone-inspired microstructures: overcoming the diffusion limit in co-laminar microfluidic devices

Abstract

Enhancing mixing is of uttermost importance in many laminar microfluidic devices, aiming at overcoming the severe performance limitation of species transport by diffusion alone. Here we focus on the significant category of microscale co-laminar flows encountered in membraneless redox flow cells for power delivery. The grand challenge is to achieve simultaneously convective mixing within each individual reactant, to thin the reaction depletion boundary layers, while maintaining separation of the co-flowing reactants, despite the absence of a membrane. The concept presented here achieves this goal with the help of optimized herringbone flow promoting microstructures with an integrated separation zone. Our electrochemical experiments using a model redox couple show that symmetric flow promoter designs exhibit laminar to turbulent flow behavior, the latter at elevated flow rates. This change in flow regime is accompanied by a significant change in scaling of the Sherwood number with respect to the Reynolds number from Sh ~ Re^0.29 to Sh ~ Re^0.58. The stabilized continuous laminar flow zone along the centerline of the channel allows operation in a co-laminar flow regime up to Re ~325 as we demonstrate by micro laser-induced fluorescence (μLIF) measurements. Micro particle image velocimetry (μPIV) proves the maintenance of a stratified flow along the centerline, mitigating reactant cross-over effectively. The present work paves the way toward improved performance in membraneless microfluidic flow cells for electrochemical energy conversion.

---

Introduction

The operating regime of microfluidic devices is typically characterized by laminar flows and low Reynolds numbers, where the viscous forces play an important role. The importance of viscosity in microchannels is due to the encountered high surface-to-volume ratios.¹ The laminar nature of such flows is in stark contrast to macroscale devices in which often chaotic flow patterns and turbulence are readily triggered.² Many types of microscale devices such as membraneless fuel cells,^3,4 micro total analysis systems,⁵ or drug discovery devices⁶ exploit the laminarity of the flow. For example, in membraneless redox flow cells the membrane can only be excluded due to the low Reynolds number operating conditions. In this kind of device two reactant streams flow side-by-side and transversal cross-over at the interface progresses only due to interdiffusion of the two reactant flows (cf. Fig. S1†).^3,4 At the same time, this laminarity has a serious negative effect, since it poses a diffusion limit to the transfer of each reactant (i.e. anolyte and catholyte) to the reactive surfaces (i.e. to the anode and cathode) at the walls of the microchannel. Further downscaling and better performance (in terms of harvested power per unit area) can be achieved if the mass transport to reactive boundaries is intensified.⁷

The above necessitates overcoming the serious challenge of maintaining no transversal cross-over flow at the membraneless interface of the co-flowing reactants, while promoting convective mixing in each reactant region on both sides of this interface in order to improve mass transfer to the reactive boundaries.⁸ The latter is directly related to controlling the thickness of the depletion boundary layer above the reactive surface (cf. Fig. S1†),^9,10 which is the result of reactant consumption at the reactive site and leads to concentration gradients, hindering the supply of reactants. Flow-through electrodes effectively reduce the overall mass transfer limitations due to higher available surface area and confinement of the flow in micron or sub-micron sized pores, but devices with the flow-through electrode configuration are limited by ohmic resistance.^11–14 For devices with planar electrodes the most straight-forward solution is to increase the flow velocity and thereby decrease the thickness of the boundary layer to mitigate mass transfer limitations.¹⁰ Another approach is to segment the electrode in order to inhibit the continuous growth of the depletion boundary layer.^15,16 Although the average current can be increased to a degree with such solutions, the device is still in a diffusion-limited operating regime.

Mitigating and thinning the depletion boundary layers in microfluidic devices using strategies to mix the individual reactants is promising, because it overcomes the limitations of pressure-driven laminar channel flow by inducing secondary flow patterns superposed on the main basic flow.¹⁷ Strategies to induce mixing in microfluidic devices by both active and passive means have been proposed.¹⁸ In the category of passive mixing the herringbone mixer consisting of herringbone-shaped grooves or ridges on the walls of microchannels has drawn significant attention.¹⁹ However, for co-laminar devices mixing strategies have to take into account the compulsory avoidance of advective cross-over between the two flowing streams.²⁰ Here we aim toward achieving these two goals simultaneously: enhanced mass transfer to the reactive boundaries and a stable co-laminar flow profile with minimal cross-over at the interface of the two reactants.²¹

To achieve such a state of individual reactant mixing without intermixing, only mixer designs which are symmetric with respect to the centerline of the microchannel are viable. Mixing strategies have already been successfully applied in work related to microfluidic redox flow cells. Yoon et al. studied the conversion efficiency of a model redox system in microchannels with and without herringbone ridges. They found that the induced secondary flow patterns increased the conversion efficiency by up to 40%.²² Da Mota et al. integrated herringbone grooves within the channel of a membraneless fuel cell. Their data shows that the maximum power density doubled when integrating passive mixers consisting of grooves in a herringbone pattern.²³ Recently, Ha and Ahn presented a microfluidic fuel cell in which ridges were patterned on the electrode surfaces. The results of their simulations revealed that flow promoters cause increased cross-over even though the design was still symmetric to the centerline along the main flow direction.²⁴ These contributions prove that flow promotion is in general possible in co-laminar devices. However, the microfluidic community can benefit from a deeper understanding of how flow promoters need to be designed to optimize the intrinsic mixing of the reactants while suppressing transversal cross-over.

In the present paper, we systematically evaluate herringbone-inspired symmetric flow promoting structures to meet the goal of both effective mixing and low cross-over in co-laminar devices. We analyze the mass transfer for a surface-bound model redox reaction and transversal cross-over for Reynolds numbers spanning three orders of magnitude from Re = 6 to Re = 600. We increase the current response of the model redox system by inducing secondary flow patterns in the microchannel. Our electrochemical measurements reveal that such secondary flow patterns are only evoked efficiently if the Re number is sufficiently high. In fact, we find evidence that the scaling regime changes from a purely laminar regime to an entrance region turbulent regime with increasing Reynolds numbers. Moreover, our results provide general insight into the rational design of an important category of flow promoting structures which enhance mass transfer to the electrodes through rigorous mixing of each reactant to overcome the diffusion limitation, while simultaneously restricting cross-over at the co-laminar flow reactant interface.

Experimental

Device fabrication

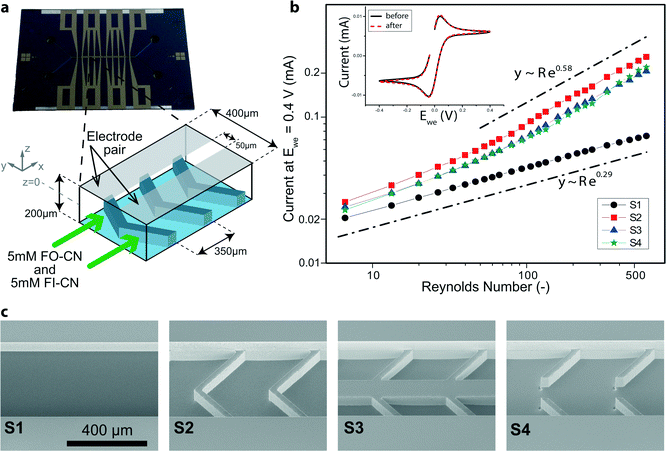
Test devices (see Fig. 1a, c) were fabricated by a series of microelectromechanical systems (MEMS) and integrated circuit (IC) standard fabrication processes in a class 100/1000 cleanroom. In detail, a 1000 nm SiO₂ layer was deposited by plasma-enhanced chemical vapor deposition (PECVD, Oxford Plasmalab System 100) on a 100 mm, <100>-oriented, single-side polished n-type silicon test wafer. 400 μm wide channels including Y-shaped in- and outlets were patterned in this layer of SiO₂ with a positive-tone photoresist mask by buffered HF solution. The photoresist was then removed and the wafer thoroughly cleaned. On top of the patterned SiO₂ hard mask a soft mask (positive-tone photoresist) with the design of the flow promoters was patterned. Herringbone grooves were thus fabricated with pitch and width of 350 μm and 300 μm, respectively, and an angle of 45° (see Fig. 1a). Subsequently, the flow promoters were dry-etched by deep reactive ion etching (DRIE, Alcatel AMS 200). The depth of the grooves was 100 μm. Then the soft mask was stripped and the wafer was thoroughly cleaned to remove post-etch residues, before the channels were etched in a second DRIE step. During this second etching step the channel with a depth of 100 μm was obtained and the pre-etched flow promoters at the channel bottom were simultaneously lowered to fabricate multilevel silicon structures.²⁵ The etching depths were checked with a stylus profilometer. In a third DRIE step, backside-aligned mm-sized holes for fluidic and electric world-to-chip interfacing were fully opened. Lastly, the SiO₂ hard mask was removed in buffered HF and a layer of 300 nm SiO₂ deposited by PECVD for chemical inertness and electrical insulation on both wafer sides. The channel was covered by a glass wafer (Borofloat 33) and sealed by anodic bonding at 450 °C and 600 V (Suess MicroTech SB8e in combination with Suess MicroTech MA8/BA8 for alignment). Prior to anodic bonding the two wafers were thoroughly cleaned using megasonic and piranha (SSE Optiwet ST30). For electrochemical testing, electrodes were added on the glass wafer. Working, counter and reference electrodes were all made of platinum. For this, slots for the electrodes were first etched by reactive-ion etching (RIE, Oxford Plasmalab 80 Plus) and then Cr/Pt (10/150 nm) was deposited by electron-beam evaporation (Evatec BAK501). The same negative-tone soft-mask was used both for the RIE step and the metal deposition. The final patterning was eventually achieved by lift-off in acetone. Planarity of the electrodes with the surrounding surface was checked with a stylus profilometer (Bruker DektakXT). Fluidic world-to-chip interfaces²⁶ were given by either a custom-made polyphenylene sulfide holder with O-rings as intermediate elements or NanoPorts (Upchurch Scientific). Tubing was from chemically inert perfluoroether (Upchurch Scientific). Electrically, the chip was accessed with a conductive elastomeric connector in between the chip and a custom-made printed-circuit board.

Fig. 1 Mass transfer enhancement by passive mixing in devices with flow promoters. (a) A photograph of the silicon-based test device including microchannel and thin film Pt electrodes. The illustration depicts the microchannel and the position of the flow promoters opposite to the Pt electrodes. In equimolar experiments, both inlets are fed with the same solution containing both 5 mM FO-CN and 5 mM FI-CN. (b) Measured current at E_we = 0.4 V versus an on-chip platinum quasi-reference electrode for different flow promoting structures. The double logarithmic plot includes two lines with indicated slope for guidance. The inset shows typical cyclic voltammograms at 50 mV s⁻¹ taken both before and after the actual flow experiments in stagnant flow conditions in a three-electrode configuration (on-chip). (c) Scanning electron microscopy (SEM) images of the 4 different geometries without and with flow promoting structures. S1 is a plain microchannel, S2 is a symmetric herringbone design, whereas S3 and S4 include an additional solid or vacant zone, respectively, along the centerline of the channel.

Chemicals

Experiments were performed with 18 MΩ Millipore water. Chemicals were purchased from Sigma-Aldrich. Purity of chemicals for electrochemical testing was at least 98.5%.

Electrochemical testing

Electrochemical tests were performed using a potentiostat (BioLogic SP-300). The chosen model redox reaction was the ferrocyanide/ferricyanide reaction with a standard reduction potential of E⁰ = 0.36 V vs. SHE:

[Fe(CN)₆]⁴⁻ ⇔ [Fe(CN)₆]³⁻ + e⁻ (1)

All solutions for electrochemical testing used 0.5 M potassium sulfate as supporting electrolyte. An equimolar model redox pair solution was prepared with 5 mM potassium hexacyanoferrate(III) (potassium ferricyanide, FI-CN) and 5 mM potassium hexacyanoferrate(II) trihydrate (potassium ferrocyanide, FO-CN). In addition, two biased solutions were prepared, each containing only one of the two aforementioned species at a concentration of 5 mM. Solutions were stored in amber glass bottles to prolong stability.²⁷ For the flow experiments employing the equimolar solution, both inlets were fed with the same solution. In flow experiments employing the biased solutions, one chip inlet was fed with 5 mM FI-CN while the other chip inlet was fed with 5 mM FO-CN. The volume flow of the electrolytes was controlled with a syringe pump (cetoni neMESYS) equipped with two glass syringes (SGE Analytical Science). The Pt working and counter electrode were of the same size (5200 × 175 μm²) and faced each other with a gap of 50 μm as illustrated in Fig. 1a. A Pt quasi-reference was located in situ upstream of this pair of working and counter electrode.²⁸Ex situ cyclic voltammograms in a plate cell (evaporated Pt film on Si as working electrode, platinum wire as counter electrode, and Hg/Hg₂SO₄/K₂SO₄ (sat.) reference electrode) were consistent with in situ electrochemical measurements. Ex situ we measured E_1/2 = −0.16 V vs. Hg/Hg₂SO₄/K₂SO₄ (sat.) in the same electrolyte as used in the flow experiments. The Pt working electrodes were preconditioned by cycling three times at 50 mV s⁻¹ between a working electrode potential of E_we = 0.4 V and E_we = −1 V vs. Pt quasi-reference electrode. At E_we = −1 V no evidence of hydrogen evolution was observed preserving the physical integrity of the electrodes. The electrode activities were then checked by running 20 cycles at 50 mV s⁻¹ with limits of +0.4/−0.4 V vs. Pt both before and after actual flow experiments to verify that no changes to electrode activity occurred during the flow experiment. In the actual flow experiments, the voltage was cycled between 0 and +0.4 V vs. Pt at 50 mV s⁻¹ and the current at +0.4 V vs. Pt was taken as reference value for comparison of different flow promoter structures (cf. Fig. S4†).

Concentration and flow field measurements

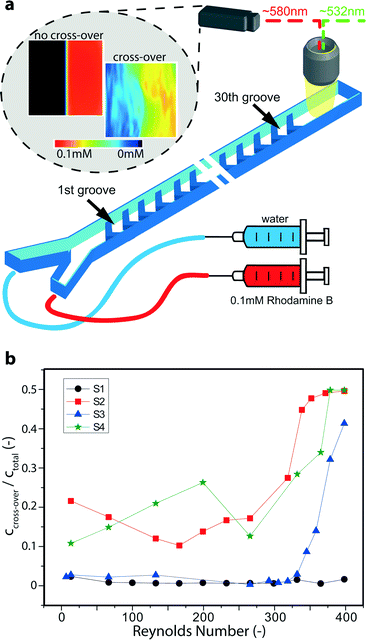
Concentration and flow field measurements were performed by micro laser-induced fluorescence (μLIF) and micro particle image velocimetry (μPIV), respectively, using deionized water as working fluid. The set-up consisted of an epi-fluorescence microscope system including a 3D stage system (LaVision FlowMaster Mitas) in combination with a 532 nm Nd:YAG laser (New Wave, Solo II-15) and a 2048 × 2048 pixel CCD camera (LaVision Imager ProX 4 M). Images were acquired with a 20×/NA = 0.4 microscope objective and data post-processing was performed in the commercial software package Davis 7 (LaVision). The volume flow of fluids was controlled with a syringe pump (Harvard Apparatus PHD Ultra) equipped with two glass syringes (Hamilton Company). For μLIF concentration measurements the fluid at one inlet was dyed with 0.1 mM Rhodamine B and the cross-over was studied after passing 30 rows of flow promoters. After performing the standard LIF procedure for concentration calibration,²⁹ experimental images were taken for each flow condition (trigger rate 8 Hz), processed and time-averaged. The average concentration images were calculated over a sufficiently large number of experimental images (>30) depending on the steadiness of the flow conditions. μPIV measurements were performed by seeding the flow with 1 μm fluorescent particles (Invitrogen nile red FluoSpheres) and two-frame experimental images were acquired at a trigger rate of 4 Hz for each flow condition (20 images at 1 ml min⁻¹, >200 images at 6 ml min⁻¹). The cross-correlation technique was used for analysis.³⁰ The final interrogation window of 128 × 128 pixels overlapped by 75%, the corresponding vector spacing was 7.8 μm. The depth of correlation was calculated for the given conditions as suggested by Olsen and Adrian to be about 17.7 μm.³¹ After processing, images were time-averaged. Further details on the experimental set-up can be found in earlier reports.^32–34 Particle sticking to the wall was mitigated by stabilizing the pH to ~9 with sodium hydroxide and adding 0.5 g L⁻¹ Triton X-100 as a surfactant.³⁵ In combination with the SiO₂ surface coating of the devices, very few particles stuck to the channel walls during the experiments. To clean the channels toluene was used which dissolved the polystyrene particles.³⁶

Results and discussion

Microfluidic devices with integrated flow promoter structures

Symmetric (with respect to the centerline) herringbone designs consisting of grooves patterned at an angle of 45° at the bottom of a microchannel (see Fig. 1a) are known to induce secondary flow patterns.²² Our experiments relied on microfabricated devices with three different designs of flow promoting structures (samples S2–S4 in Fig. 1c) and one device without flow promoters as a reference (S1, see Fig. 1c). The plain channel is 100 μm deep and for devices S2–S4 with flow promoters the grooves are an additional 100 μm deep (see Fig. 1a). The dimensions were chosen to optimize the interaction of the flow with the electrodes located at the channel top inner surface (Fig. 1a). Forbes et al.³⁷ recently developed a framework according to which we dimensioned the groove width and groove pitch (300 and 350 μm, see Fig. 1a and cf. S3†). Their guidelines rely on the hydraulic resistance of a single groove in comparison to the resistance of the effective channel above. During this process of dimensioning we fixed the width of the ridges to 50 μm for structural reasons. In order to simultaneously suppress transverse mixing of the two flows, the test geometries S3 and S4 additionally feature a 100 μm wide separation zone at the center of the 400 μm wide channel (see Fig. 1c). In S3, a solid ridge separates the grooves from each side of the centerline, while S4 incorporates a continuous groove along the centerline in the main flow direction.

The flow direction (with respect to the flow promoters), indicated in Fig. 1a, performed in preliminary tests better than the reverse direction, both in terms of enhancing mass transfer to the electrodes and maintaining reactant separation. In this flow direction, the grooves tend to direct the flow toward the side walls and then upwards. Thereby, the grooves guide the two fluids toward the respective electrodes which are located side-by-side on the top channel wall over the flow promoter structures (see Fig. 1a).

The dependency of mass transfer enhancement on Reynolds number using flow promoters

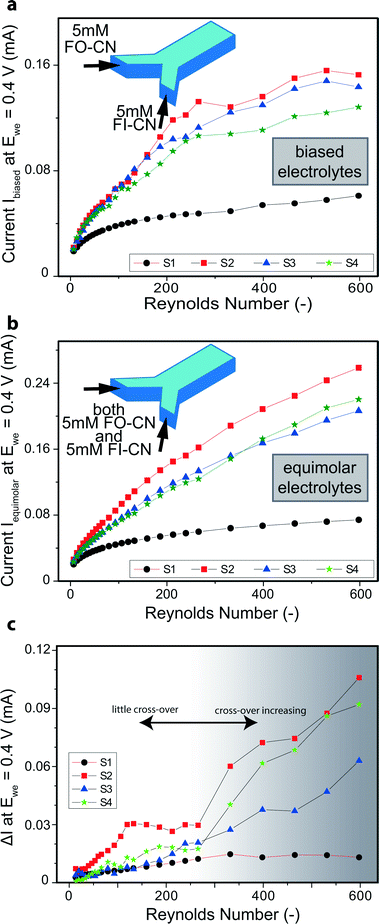
For devices S1–S4, the current at E_we = 0.4 V vs. Pt quasi-reference electrode was compared for various flow rates to investigate the effect of flow promotion on mass transfer enhancement (cf. Fig. S4†). The inset in Fig. 1b presents the two steady state voltammograms in stagnant equimolar electrolyte both before and after flow experiments. These two voltammograms show minimal change, therefore the activity of the thin film Pt working electrode is indeed maintained throughout the experiment. Moreover, at E_we = 0.4 V vs. Pt, the overpotential for the FO-CN oxidation reaction was found to be sufficiently high for the reaction rate to be limited by diffusive mass transfer to the electrode (and not by the kinetics of the electrochemical reaction).³⁸

In the flow experiments employing identical equimolar solutions at each inlet, cross-over of redox reactants does not change the net distribution of species in the channel. Therefore the oxidation current at E_we = 0.4 V vs. Pt is unaffected by any cross-over between the two flows. We observe a monotonic increase in the current at E_we = 0.4 V vs. Pt with Reynolds number for all channel designs (see Fig. 1b), with the Reynolds number being defined with respect to the plain channel rectangular cross-section to ensure best comparability among the four different samples:

where V̇ is the total volumetric flow rate, W and H are the channel width and height, respectively (W = 400 μm, H = 100 μm), and ν denotes the kinematic viscosity with a numerical value ν = 10⁻⁶ m² s⁻¹ for the aqueous solution used herein.²⁷ As the unobstructed cross-section in devices S1, S2 and S3 is constant (100 × 400 μm² above the flow promoting grooves) the superficial velocity remains comparable for any given Reynolds number. Only device S4 has an additional unobstructed area of 100 × 100 μm², i.e. the superficial velocity decreases slightly in this case.

The devices containing flow promoting structures (S2, S3, S4) perform better in comparison to the plain reference channel (S1), showing higher current values for the same Reynolds number due to increased mixing and therefore thinner depletion boundary layers. Interestingly, the scaling behavior of current with Reynolds number is remarkably different for the devices with flow promoters (S2, S3, S4) compared to the plain channel (S1). The current for the plain channel (S1) scales with Re^0.29 as indicated in Fig. 1b. For the devices including flow promoters, the scaling behavior changes substantially over the plotted range of Reynolds numbers and approaches Re^0.58. This change in scaling behavior with increasing Reynolds number is an important observation as it proves that the employed flow promoters require a much smaller volume flow rate to operate effectively (i.e. in the regime of Re^0.58 scaling).

The scaling of Re^0.29 for the plain channel is in close agreement with theory and therefore affirms the methodology applied in this work.³⁸ According to Newman, the following correlation between the Sherwood number (Sh = h_mL_ch/D, where h_m is the mass transfer coefficient, L_ch the characteristic length, and D the diffusivity, i.e. Sherwood number represents the ratio of convective to diffusive mass transport) and the Reynolds number holds in laminar flow between two parallel electrodes in a slit:³⁹

Sh_avg ~ Re^1/3L_e^−1/3, (3)

where L_e denotes the electrode length. The Sherwood number is directly proportional to the current measured in our experiments.³⁸ The slight mismatch of the scaling of Re^0.29 in our experiment versus Re^1/3 in eqn (3) is due to the different channel geometry considered, that is a nominally 400 μm wide microchannel compared to a slit of infinite width for eqn (3). Although the rates of mass transfer vary across the width of the electrode in a microchannel,⁴⁰ the effect of the walls is small.⁴¹Eqn (3) thus adequately correlates the two important dimensionless numbers (Sherwood and Reynolds number) in our experiments with device S1 (no flow promoters). Furthermore, the close agreement of the experimental data for device S1 with eqn (3) confirms the operation in a regime limited by mass transfer only.⁴²

For the devices including flow promoters, with increasing Reynolds numbers the limiting current scales with Re^0.58 for all flow promoting geometries S2, S3, and S4. This scaling is comparable to the scaling of Re^2/3 reported by Da Mota et al. in a room-temperature fuel cell.²³ Interestingly, a scaling to the power of 0.58 is also encountered in the mass transfer entry region in macroscopic turbulent flows. In this entry region the average Sherwood number correlates with the Reynolds number as:³⁹

Sh_avg ~ Re^0.58L_e^−1/3 (4)

Although the Reynolds numbers considered in this study are certainly below the threshold to turbulent flow, the flow promoters seem to induce fluctuations in the flow characteristic of a transition to an entry region turbulent flow regime. This flow regime results in a thinner depletion boundary layer at the electrodes and thereby enhances convective mass transfer. The finding that our flow promoters induce a similar scaling behavior of Re^0.58 as in the entrance region of turbulence and not as in fully developed turbulent flow (where Sh_avg ~ Re^0.8)³⁹ is discussed in the remainder of this section.

First, we answer the question whether the test section in our experiments is longer than the expected hydrodynamic entry length L_entry. This length scale correlates with Re as:⁴³

where C and n are fitting constants and D_h is the hydraulic diameter of the microchannel. Even with a conservative estimate for an upper bound of the entry length (C = 4.4, n = 1/6)⁴³ this length scale remains small with L_entry/D_h < 13 (L_entry < 2.1 mm) at Re = 600 in comparison to the overall length of the electrode (5.2 mm). Therefore, we expect to be in a fully developed regime for more than half of the electrode length, however we only observe a scaling with Re^0.58 of the current, which is similar to the scaling in entry region flows.

According to the theory of the energy cascade of turbulence, eddies of various sizes contain the energy of turbulent flows and viscous dissipation occurs only on the smallest scales. This smallest length scale in turbulent flows is the Kolmogorov length η.⁴⁴ In microfluidic flows the length scale of the channel constrains the size of the largest eddies. In fact, our microfluidic channel is not much larger than the Kolmogorov microscale. For this reason, any energy contained in turbulence is rapidly dissipated. This reasoning is supported by estimations of the Kolmogorov length scale in microfluidic flow situations reported by Liu and Garimella.⁴⁵ They determined the length scale η = (ν³/ε)^1/4, where ν is the kinematic viscosity, by calculating the rate of kinetic energy dissipation ε from the mean flow field. Their approximations show that depending on the channel dimensions and mean flow field, the Kolmogorov scale can be of similar size as the channel dimensions.⁴⁵ From our experimental observations that in flow promoting devices (i.e. S2–S4) the scaling of Sherwood number correlates with Re^0.58 (and not with Re^0.8 as expected in fully developed turbulent flow) up to Re = 600, we deduce that the evoked eddies in this work are barely (if at all) in the energy-containing range, but instead more probably in a range of sizes close to the Kolmogorov length scale. According to the theory of the energy cascade of turbulence, viscosity would have little effect in the energy-containing range. Instead, our data indicates that the largest eddies already start in a size regime which transfers turbulent energy rapidly to the dissipation range. A classical cascade of turbulence is not generated because the integral scale of turbulence is not much larger than the Kolmogorov microscale, i.e. the creation and destruction of turbulence occurs on similar length scales.⁴⁶ Any turbulent energy created by passing the flow over the flow promoters is quickly dissipated again by viscous effects and the eddies induced by the flow promoting structures are not sustained. For this reason we observe entry region scaling at higher Re numbers (Sh ~ Re^0.58 and not Sh ~ Re^0.8 as expected in fully developed turbulent flow). In this mass transfer entry region scaling regime eddies are created by the individual rows of flow promoters, yet also immediately dissipated again by viscosity. Therefore, the correlation in eqn (4) is successfully applied to describe the scaling behavior observed in our experiments.

How Reynolds number influences cross-over

Besides enhancing mass transfer in the reaction zones, it is important for co-laminar devices to minimize the cross-over of reactants. Such cross-over becomes apparent in experiments carried out with biased electrolytes, in which the two species FO-CN and FI-CN are separately fed into each inlet. In this case, any cross-over will result in a dilution of the reactant species which is expected to reduce the diffusion-limited current at E_we = 0.4 V. For the reference case of the plain channel (S1) our experimental results with biased electrolytes (see Fig. 2a) are similar to those obtained with equimolar electrolytes (see Fig. 2b) over the entire range of considered Reynolds numbers. In a microfluidic channel without flow promoters, transverse inter-mixing occurs by diffusion only.⁴⁷ The inevitable extent of cross-over in a pressure-driven laminar flow can be assessed by estimating the width of the mixing zone,⁴⁸where D is the diffusion coefficient of the considered species, H the channel height, u the average downstream flow velocity, and x the downstream coordinate. The scaling law of eqn (6) reveals that especially at low Reynolds numbers transverse mixing by diffusion becomes important. However, from our experiments with equimolar and biased electrolytes (see Fig. 2a, b) we observe for S1 that the electrodes have an adequate spacing (50 μm, see Fig. 1a) in order to effectively suppress the adverse effects of transverse diffusive mixing.

Fig. 2 Flow promotion induced cross over. (a) Current at E_we = 0.4 V in biased experiments (two separate solutions of 5 mM FO-CN and 5 mM FI-CN are fed into the inlets, see inset). (b) Current at E_we = 0.4 V in equimolar experiments (identical solutions of both 5 mM FO-CN and 5 mM FI-CN are fed into the inlets, see inset). Same data as in Fig. 1b but on linear scale for better comparability of experiments with equimolar and biased electrolytes. (b) Difference of the measured currents of both equimolar and biased electrolyte experiments, i.e. ΔI = (I_equimolar − I_biased). The background shading indicates the two operational regimes.

A different observation was made for the designs including flow promoters. Although the concentrations of the reactants were unchanged, the measured currents in the experiments with biased electrolytes remained distinctly lower than in the equimolar experiments for increased Reynolds numbers (see Fig. 2a, b). This is attributed to cross-over which effectively lowers the concentration of reactants in the case of biased electrolytes and thus reduces the current. In fact, the current finally levels off and approaches a plateau (Fig. 2a). For total intermixing of the two co-laminar flows, the effective concentration of each species (i.e. FO-CN and FI-CN) reduces to one half (2.5 mM) of the concentration at the respective inlet (5 mM). Therefore, the maximal current for high Re numbers in the biased electrolyte experiments (see Fig. 2a) levels off at values which equal about half the values reached previously in the equimolar electrolyte experiments (see Fig. 2b).

The Reynolds number at which the current saturates is a critical value because it represents the onset where cross-over by advection becomes more important than by diffusion. The penalty in reaction yield for the FO-CN oxidation due to cross-over can be quantified by simple subtraction of the oxidation current with cross-over effects, I_biased (Fig. 2a), from the oxidation current without cross-over effects, I_equimolar (Fig. 2b), i.e. ΔI = I_equimolar − I_biased. This difference is plotted in Fig. 2c. For the plain channel (S1) this difference remains relatively low, indicating that the cross-over is diffusion limited and does not significantly affect the reaction yield at the working electrode. On the other hand, for the flow promoter designs S2 and S4 convective cross-over dominates from Re ≈ 275 onward as can be seen from the sudden increase in ΔI. For S3, the rise is less sudden, which indicates that this geometry is less prone to cross-over due to transverse advective fluid motion. Interestingly, for S2 the difference ΔI exhibits a plateau at Reynolds numbers between ~100 and ~275 and shows the highest cross-over in this region in comparison to the other designs. Samples S3 and S4 differ from S2 by the presence of a continuous separation zone. For S3 this separation zone seems to be beneficial, whereas S4 shows a similar cross-over behavior as S2 at Reynolds numbers above 275. The aforementioned plateau for S2 from Re ≈ 100 to about 275 is attributed to imperfections stemming from the fabrication, e.g. a slight asymmetry due to misalignment errors, and flow pulsations introduced by the pump. Therefore, a design without a flow separation zone like S2 is most vulnerable to cross-over even at relatively low Reynolds numbers. We speculate that for similar reasons previous studies of co-laminar microfluidic fuel cells including flow promoting designs akin to our samples S2 and S4 were typically only operated in Reynolds number ranges well below Re = 100 where cross-over remained low.^23,24

The above results from the electrochemical experiments are further supported by micro laser-induced fluorescence (μLIF) measurements, which were conducted separately from the electrochemical experiments. Using plain water at both inlets the solution at one inlet was dyed with Rhodamine B (see Fig. 3a). After passing 30 grooves of flow promoting structures, the occurrence of cross-over can be readily detected. Fig. 3a includes a typical post-processed image of a situation in which no advective cross-over occurred (here: for sample S1 at low Reynolds number), i.e. the dyed and colorless solutions remained clearly separated. The second image to the right shows the onset of transversal cross-over for sample S4 at elevated Reynolds number, where the dye started to emerge also on the left side. To obtain a measure of the degree of cross-over we calculated the ratio of the amount of dye on the left half of the microchannel (c_cross-over) to the average amount of dye over the whole microchannel (c_total). This ratio is plotted in Fig. 3b as a function of Reynolds number. A value of 0.5 indicates total transversal mixing.

Fig. 3 Micro laser-induced fluorescence (μLIF) measurement of cross-over. (a) Illustration of measurement principle and typical images obtained for situations with (image to the right) and without advective cross-over (image to the left). (b) Ratio of the cross-over concentration of the dye Rhodamine B to the total concentration. Values of 0.5 indicate total transversal mixing.

Consistent with the previous electrochemical results (cf.Fig. 2c), the reference channel without flow promoters (S1) shows little to no cross-over, i.e. the ratio c_cross-over/c_total stays below 0.05. On the other hand, for samples S2–S4 with flow promoters, cross-over is clearly visible. Both S2 and S4 exhibit relatively high cross-over even below Re = 250. In difference to the electrochemical experiments, in which the electrodes were offset by 25 μm from the centerline, the μLIF measurements also capture any cross-over at the center of the channel. Thus, for samples S2 and S4 the μLIF measurements confirm the instability of the co-laminar regime and the cross-over appears more pronounced than the electrochemical approach (cf.Fig. 2c). However, sample S3, with the flow separation zone along the center-line, effectively pushes the onset of cross-over up to Reynolds numbers of ~325. It is especially worth noting that for S3, similar to S1, the ratio c_cross-over/c_total remains well below 0.05 for the entire measurement range up to Re ≈ 325. In this way, the μLIF measurements highlight the suitability of flow promoter design S3 to suppress transversal cross-over while promoting separate mixing of each co-laminar stream.

Mixing propensity

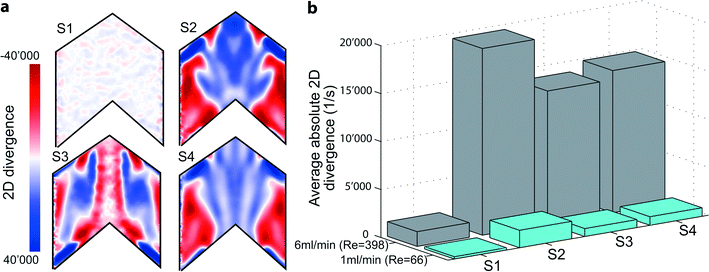
The employed flow promoter structures induce a 3-dimensional flow field in the microchannel. To gain a deeper understanding of the mechanism of flow promotion, 2-dimensional (2D) divergence maps are illustrative. The divergence maps in Fig. 4a show contour plots of the quantity div_2D:with the gradients of two velocity components u and v obtained by μPIV. The reason for the discussion of 2D divergence maps stems from the fact that flow visualization by μPIV is typically limited to the in-plane components of the velocity vectors u and v.⁴⁹ Yet, in the given device geometry the fluid has to move out-of-plane in order to reach the electrodes, which are in our case on the top channel wall opposite of the flow promoter structures. Although we do not have direct access to the out-of-plane velocity component w, the continuity equation yields the gradient of w:⁵⁰

Fig. 4 Fluid dynamically induced mixing propensity. (a) 2D divergence maps derived from μPIV experiments highlighting the generated gradients in the out-of-plane component of the velocity vector for samples S1–S4. (b) Average absolute divergence for the different designs and two different flow rates.

Therefore, the 2D divergence maps at z = 50 μm highlight the regions of a rapid change in the gradient of the out-of-plane velocity component. Fig. 4a shows such plots for Re = 400. For the plain channel (S1) we indeed observe low values of the 2D divergence since the flow is highly laminar and the out-of-plane velocity component is negligible. On the other hand, for all devices containing flow promoting structures (S2–S4) the 2D divergence maps show zones of highly positive and negative gradients indicating how the flow promoters guide the fluid. Due to the minus sign in eqn (8), negative values (red) represent regions where the fluid flow is diverted toward the electrodes, whereas positive values (blue) highlight a sink-like flow in this area. For all flow promoting structures the 2D divergence maps are highly symmetric, indicating that flow promoters induce two parallel, counter-rotating flow regions within each side of the microchannel.⁵¹ The position and the extent of regions with high gradients, however, depend on the three flow promoter designs. For all flow promoter designs these zones of high out-of-plane velocity gradients are positioned both on the very edge of the microchannel as well as at the center. Sample S4 shows a similar behavior in terms of 2D divergence as S2. Sample S3, however, yields a distinctly different view: at the centerline there is an almost continuous strip of zero 2D divergence, which is surrounded by a zone of highly negative gradients. With the actual geometry of S3 in mind, which includes a continuous ridge at the centerline, this backbone-like flow structure further explains why S3 performs best in keeping the two fluids separated over a larger range of Reynolds numbers. Neutral 2D divergence values at the centerline indicate that the flow remains stratified at the interface, thus only little additional advective mixing occurs at this location.

Moreover, the 2D divergence proves to be a powerful tool in judging the mixing propensity of the flow promoter designs. The arithmetic mean of the absolute 2D divergence,

where i and j are the indices of the pixels in x- and y-directions, respectively, is a measure of the overall mixing propensity. For low Re numbers this average remains relatively low regardless of the considered flow promoting structures (see Fig. 4b). At higher Re numbers this quantity increases distinctively for the devices including flow promoters. Sample S2 shows the highest average 2D divergence value of 19 500 s⁻¹, which constitutes a 13-fold increase in comparison to the plain channel sample (S1). For samples S3 and S4 we obtain slightly lower values of average divergence, but similar in magnitude (13 900 and 14 800 s⁻¹, respectively). This is in agreement with the trends observed for the electrochemical measurements with equimolar concentrations at both inlets (cf.Fig. 1b) and confirms that S2 has the greatest propensity for mixing. At the same time, S3 and S4 have a mixing propensity of similar magnitude. However, only S3 is able to cope with the constraint of no advective cross-over up to higher Re numbers due to small 2D divergence along the centerline (see Fig. 4a).

Flow separation to avoid cross-over

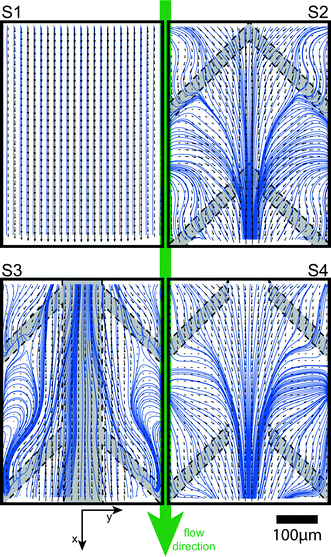
Time-averaged vector maps of the in-plane-velocity components u and v were obtained by μPIV at z = 50 μm. For optical guidance the vector plots in Fig. 5 are overlaid by the planar streamlines⁵² based on the u- and v-velocity components. At increased Reynolds numbers of Re = 400, the flow in the plain channel (S1) is laminar and the streamlines remain parallel. Thus, convection in the direction transverse to the main flow is negligible and the cross-over remains diffusion limited. The flow profiles for samples including flow promoters are symmetric with respect to the centerline. The flow profiles in S2 and S4 show the distinct feature of streamlines converging toward the center. This increases transverse transport of species across the co-laminar flow interface. However, sample S3 shows a distinctly different characteristic, where in a relatively broad zone at the interface of the two fluid streams the velocity vector field is aligned with the centerline of the channel. Streamlines starting at the center diverge to the outside and streamlines starting away from the center curl in regions away from the center. Therefore, along the centerline of the channel, the velocity field does not contribute to a reorientation of the iso-concentration lines which would cause transverse intermixing.⁵³ This confirms our earlier observation that S3 is a suitable choice for co-laminar devices where convective transport of species to the center must be avoided.

Fig. 5 Vector maps and corresponding streamlines. Visualization of the time-averaged flow profile (velocity vectors: black arrows, streamlines: blue lines) at Re = 400 for the different flow promoter designs.

Conclusion

We have demonstrated effective co-laminar flow mixing for a broad range of Reynolds numbers by enabling independent mixing of the individual reactants while maintaining a stratified flow field at the reactant interface. The flow field design S3 with an integrated separation zone and a well-defined flow promoter arrangement effectively suppressed transverse cross-over of electrochemical reactants up to Re ~325 while simultaneously significantly reducing the effective depletion boundary layer thickness due to enhanced mixing. This resulted in an improved scaling of collected current with respect to the Reynolds number.

Potential applications, which can benefit from such deeper understanding of microfluidic mixing, are analytical lab-on-chip devices, for which increased mass transfer rates could translate into a higher signal-to-noise ratio or a possible reduction of sampling volume. Another field is energy-related micro-devices such as redox flow batteries and fuel cells, for which higher rates of mass transfer would translate into increased power density and therefore further downscaling.⁸ The available potential for downscaling employing the herein demonstrated design concept is considerable. In the turbulent scaling regime we found Sh ~ Re^0.58L_e^−1/3 instead of Sh ~ Re^1/3L_e^−1/3 characteristic of purely laminar flow.³⁹ As a consequence, a 10-fold increase in Reynolds number enables a shortening of electrode length to 1/55 of the original length, whereas for a device operating in the laminar regime this shortening factor is 1/10. This example underpins the utility of this work for future microfluidic devices, which can be drastically downscaled making use of a rational flow promoter design.

Acknowledgements

We gratefully acknowledge the Swiss National Science Foundation for financially supporting this work within the REPCOOL project (grant 147661). JM is also grateful for support from the German National Academic Foundation. We thank Jovo Vidic for his hardware support with the μPIV/μLIF set-up and Ashish Asthana for fruitful discussions about microfluidic visualization techniques. Device fabrication and portions of the characterization were performed in the Binnig and Rohrer Nanotechnology Center. We especially thank Ute Drechsler for her advice while establishing the fabrication processes.

References

1. T. Gervais and K. F. Jensen, Chem. Eng. Sci., 2006, 61, 1102–1121.
2. L. P. Kadanoff, Phys. Today, 1983, 36, 46.
3. S. A. Mousavi Shaegh, N.-T. Nguyen and S. H. Chan, Int. J. Hydrogen Energy, 2011, 36, 5675–5694.
4. M.-A. Goulet and E. Kjeang, J. Power Sources, 2014, 260, 186–196.
5. A. Manz, N. Graber and H. M. Widmer, Sens. Actuators, B, 1990, 1, 244–248.
6. P. Neuži, S. Giselbrecht, K. Länge, T. J. Huang and A. Manz, Nat. Rev. Drug Discovery, 2012, 11, 620–632.
7. P. Ruch, T. Brunschwiler, W. Escher, S. Paredes and B. Michel, IBM J. Res. Dev., 2011, 55, 15:1–15:13.
8. M. N. Nasharudin, S. K. Kamarudin, U. A. Hasran and M. S. Masdar, Int. J. Hydrogen Energy, 2014, 39, 1039–1055.
9. E. R. Choban, L. J. Markoski, A. Wieckowski and P. J. A. Kenis, J. Power Sources, 2004, 128, 54–60.
10. E. R. Choban, P. Waszczuk and P. J. A. Kenis, Electrochem. Solid-State Lett., 2005, 8, A348–A352.
11. E. Kjeang, R. Michel, D. A. Harrington, N. Djilali and D. Sinton, J. Am. Chem. Soc., 2008, 130, 4000–4006.
12. J. W. Lee, M.-A. Goulet and E. Kjeang, Lab Chip, 2013, 13, 2504–2507.
13. J. W. Lee and E. Kjeang, J. Power Sources, 2013, 242, 472–477.
14. J. A. Trainham and J. Newman, Electrochim. Acta, 1981, 26, 455–469.
15. J. Lee, K. G. Lim, G. T. Palmore and A. Tripathi, Anal. Chem., 2007, 79, 7301–7307.
16. K. G. Lim and G. T. Palmore, Biosens. Bioelectron., 2007, 22, 941–947.
17. V. Hessel, H. Löwe and F. Schönfeld, Chem. Eng. Sci., 2005, 60, 2479–2501.
18. N.-T. Nguyen and Z. Wu, J. Micromech. Microeng., 2005, 15, R1–R16.
19. A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezic, H. A. Stone and G. M. Whitesides, Science, 2002, 295, 647–651.
20. M.-A. Goulet and E. Kjeang, Electrochim. Acta, 2014, 140, 217–224.
21. J. Xuan, D. Y. C. Leung, M. K. H. Leung, H. Z. Wang and M. Ni, J. Power Sources, 2011, 196, 9391–9397.
22. S. K. Yoon, G. W. Fichtl and P. J. Kenis, Lab Chip, 2006, 6, 1516–1524.
23. N. Da Mota, D. A. Finkelstein, J. D. Kirtland, C. A. Rodriguez, A. D. Stroock and H. D. Abruña, J. Am. Chem. Soc., 2012, 134, 6076–6079.
24. S.-M. Ha and Y. Ahn, J. Power Sources, 2014, 267, 731–738.
25. R. Huber, J. Conrad, L. Schmitt, K. Hecker, J. Scheurer and M. Weber, Microelectron. Eng., 2003, 67–68, 410–416.
26. Y. Temiz, R. D. Lovchik, G. V. Kaigala and E. Delamarche, Microelectron. Eng., 2014, 132, 156–175.
27. D. H. Angell and T. Dickinson, J. Electroanal. Chem. Interfacial Electrochem., 1972, 35, 55–72.
28. M. Odijk, A. Baumann, W. Lohmann, F. T. van den Brink, W. Olthuis, U. Karst and A. van den Berg, Lab Chip, 2009, 9, 1687–1693.
29. M. Hoffmann, M. Schlüter and N. Räbiger, Chem. Eng. Sci., 2006, 61, 2968–2976.
30. S.-S. Hsieh and Y.-C. Huang, J. Micromech. Microeng., 2008, 18, 065017.
31. M. G. Olsen and R. J. Adrian, Exp. Fluids, 2000, 29, S166–S174.
32. A. Renfer, M. K. Tiwari, T. Brunschwiler, B. Michel and D. Poulikakos, Exp. Fluids, 2011, 51, 731–741.
33. A. Renfer, M. K. Tiwari, R. Tiwari, F. Alfieri, T. Brunschwiler, B. Michel and D. Poulikakos, Int. J. Heat Mass Transfer, 2013, 65, 33–43.
34. A. Asthana, I. Zinovik, C. Weinmueller and D. Poulikakos, Int. J. Heat Mass Transfer, 2011, 54, 1456–1464.
35. J. Op de Beeck, W. De Malsche, J. Vangelooven, H. Gardeniers and G. Desmet, J. Chromatogr. A, 2010, 1217, 6077–6084.
36. V. R. Mokkapati, V. Di Virgilio, C. Shen, J. Mollinger, J. Bastemeijer and A. Bossche, Lab Chip, 2011, 11, 2711–2719.
37. T. P. Forbes and J. G. Kralj, Lab Chip, 2012, 12, 2634–2637.
38. A. Shrivastava, S. Kumar and E. L. Cussler, J. Membr. Sci., 2008, 323, 247–256.
39. J. Newman, Ind. Eng. Chem., 1968, 60, 12–27.
40. K. Yunus and A. C. Fisher, Electroanalysis, 2003, 15, 1782–1786.
41. D. Kaluza, W. Adamiak, T. Kalwarczyk, K. Sozanski, M. Opallo and M. Jonsson-Niedziolka, Langmuir, 2013, 29, 16034–16039.
42. E. Kjeang, B. Roesch, J. McKechnie, D. A. Harrington, N. Djilali and D. Sinton, Microfluid. Nanofluid., 2007, 3, 403–416.
43. S.-S. Hsieh, C.-Y. Lin, C.-F. Huang and H.-H. Tsai, J. Micromech. Microeng., 2004, 14, 436–445.
44. M. Smith, R. Donnelly, N. Goldenfeld and W. Vinen, Phys. Rev. Lett., 1993, 71, 2583–2586.
45. D. Liu and S. V. Garimella, J. Thermophys. Heat Transfer, 2004, 18, 65–72.
46. J. Bałdyga and J. R. Bourne, Turbulent Mixing and Chemical Reactions, 1999.
47. E. Kjeang, N. Djilali and D. Sinton, J. Power Sources, 2009, 186, 353–369.
48. R. F. Ismagilov, A. D. Stroock, P. J. A. Kenis, G. Whitesides and H. A. Stone, Appl. Phys. Lett., 2000, 76, 2376.
49. S. J. Williams, C. Park and S. T. Wereley, Microfluid. Nanofluid., 2010, 8, 709–726.
50. H.-W. Lu, F. Bottausci, J. D. Fowler, A. L. Bertozzi, C. Meinhart and C.-J. C. J. Kim, Lab Chip, 2008, 8, 456–461.
51. V. Somashekar, M. G. Olsen and M. A. Stremler, Mech. Res. Commun., 2009, 36, 125–129.
52. H. Klank, G. Goranovi, J. P. Kutter, H. Gjelstrup, J. Michelsen and C. H. Westergaard, J. Micromech. Microeng., 2002, 12, 862–869.
53. P. Tabeling, Lab Chip, 2009, 9, 2428–2436.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5lc00045a

---