An in situ technique for (U–Th–Sm)/He and U–Pb double dating

Abstract

We report on a new laser-based technique for rapid, quantitative and automated in situ double dating (U–Pb and (U–Th–Sm)/He) of minerals, for applications in geochronology, thermochronology and geochemistry. In situ laser microanalysis offers several advantages over conventional bulk crystal methods in terms of spatial resolution, productivity, and safety. This new approach/methodology utilizes an interoperable and integrated suite of analytical instruments including a 193 nm ArF excimer laser system, quadrupole ICP-MS, quadrupole helium mass spectrometry system and swappable flow-through and ultra-high vacuum analytical chambers. We describe the analytical protocols for zircon analysis including grain mounting in Teflon, parameters for parent and daughter isotopic measurement, and standard development, and provide a freeware application for determining (U–Th–Sm)/He ‘pairwise’ ages from analytical data. The in situ double dating method described is applied to the Ellendale lamproite pipe and country rocks, Western Australia and successfully replicates conventional U–Pb and (U–Th–Sm)/He age variations determined previously by conventional techniques.

---

Introduction

(U–Th–Sm)/He is a popular technique for studying a variety of geological processes.¹ The method involves the measurement of ⁴He, the daughter product of U, Th and Sm radioactive decay. Helium is quantitatively retained by minerals at low temperature, but is gradually lost from the mineral lattice by diffusion at elevated temperatures. Some minerals are more retentive of He than others (e.g., closure temperatures for zircon ≈180 °C (ref. 2 and 3) versus apatite ≈70 °C (ref. 4 and 5)). When integrated with other techniques such as U–Pb dating on the same mineral, complete rock time-temperature histories from 900 °C to 40 °C can be resolved.

Conventional (U–Th–Sm)/He dating involves microscopy observation of minerals of interest to characterize individual grains (clarity, morphology, presence/absence of inclusions/cracks/deformation, measurements of grain physical dimensions for alpha correction^6–8), loading selected grains into Pt or Nb microvials, extraction and quantification of total ⁴He content, grain dissolution for parent isotope measurement and, finally, age calculation.⁵ As comprehensively described by Tripathy-Lang, et al.,⁹ the limitations of conventional whole grain (U–Th–Sm)/He dating methods include the inability to avoid inclusions, crystallographic defects or ‘bad neighbors’ that can introduce excess ⁴He,^10–12 the uncertainties related to the alpha ejection correction (e.g., parent isotope zonation, potential inaccuracies of grain measurement, natural abrasion and breakage of grains^6,8,13–16), the length of time it takes to do a single analysis, and the safety issues associated with the use of aggressive acids such as hydrofluoric, nitric or perchloric for grain dissolution.¹⁷ These issues, combined with advances in laser ablation techniques have prompted a foray into in situ (U–Th–Sm)/He dating with encouraging results.^9,18–21

The earlier studies at Arizona State University applied ultraviolet laser microprobe analysis to monazite^18,19 and later, a combination of secondary ionization mass spectrometry (SIMS) for parent isotope measurement and microprobe for He determination on other U-bearing phases.^9,20 Recent work²¹ has introduced the notion of a ‘pairwise’ approach where standards of known age are compared to samples of interest using laser ablation inductively coupled plasma mass spectrometry (LA-ICPMS) for U, Th and He abundance. In situ (U–Th)/He dating permits us to target a selected area within a grain, thereby providing better spatial resolution than conventional methods (allowing us to avoid inclusions, crystallographic defects or zonation) and eliminating of the need for an alpha correction.^18,19 The increased productivity (less time required to generate an age relative to conventional methods), ability to circumvent the multiple-handling steps previously required for double dating (SHRIMP/LA-ICP-MS U–Pb and conventional (U–Th–Sm)/He),^22,23 and improved worker safety (does not require grain dissolution, thereby avoiding the use of acids) are added advantages.

As noted, previous approaches to in situ (U–Th–Sm)/He dating have utilized laser microprobe + SIMS^9,18–20,24 and laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS)²¹ for parent and daughter measurements. However, none of these approaches have integrated in situ (U–Th–Sm)/He and U–Pb dating on single crystals to obtain double dates. U–Pb and (U–Th–Sm)/He double dating has proven useful for sediment provenance and recycling studies^22,25 and in exploration applications (e.g., diamond exploration) where thermal processes are indicative of prospectivity.^23,26 These types of studies require large datasets (preferably >100 ages) for proper statistical evaluation.²⁷ In response to this need, we have developed the protocols for a novel analytical approach, suitable to rapid, automated in situ (U–Th–Sm)/He and U–Pb (+trace elements) single crystal double dating of zircon and other U-rich accessory phases. This innovation integrates several analytical instruments including (1) a 193 nm excimer laser equipped with an ultra-high vacuum (UHV) cell; (2) an ultra-high vacuum system with a ⁴He mass spectrometer, and (3) an ICP-MS. Items (1) and (2) are commercially known as the RESOchron instrument.

Methods

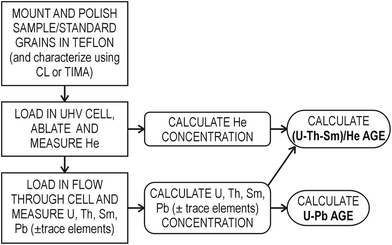
Our workflow for in situ dating is similar to that described previously^9,18,19,21 but with some differences in approach and instrumentation. The steps (Fig. 1) involve mounting, polishing and characterizing crystals, He extraction and measurement, pit volume determination, parent isotope analysis and age calculation, as outlined below.

Fig. 1 Flow chart showing steps required for pairwise U–Th–Sm–Pb–He (±trace elements) analysis.

1. Sample preparation – mounting and polishing

Zircon grains were mounted into Teflon using methods similar to those adopted for fission track etching.²⁸ The zircon grains were mounted with the c-axis parallel to the mount surface in order to maximize the surface area available for laser ablation. Zircon grains of known and unknown age (‘standards’ and ‘unknowns’, respectively) were arranged in a grid on Kapton polyimide film on a clean glass thin section slide and firmly pressed into a 25 mm round piece of Teflon (DuPont PFA, Type 6000LP) preheated on a hot plate at 230 °C until softened. We found that this type of Teflon does not excessively degas and allows us to reach the desired ultra-high vacuum pressure (i.e. <10⁻⁹ mbar) after 8 hours of pumping (usually overnight). When cold, the Teflon disc with embedded zircon grains was removed from between the glass slides and the Kapton was removed. Grains were ground to 4π geometry and polished using 1000 and 2000 grit SiC papers, and 12 μm, 6 μm, 3 μm and 1 μm diamond suspension, sequentially, in an effort to expose the interior surface of the grains and to achieve as flat a surface as possible. Similar to the methods employed by Tripathy-Lang, et al.,⁹ we examined polished zircon using a range of microscopy methods including reflected and transmitted light, scanning electron microscopy (backscattered electron (SEM-BSE), energy dispersive X-ray spectroscopy (SEM-EDS) and cathodoluminescence (CL)) imaging techniques in order to characterize the distribution of parent nuclides, reveal internal structures that could impact pit volume measurement (discussed below) and identify suitable areas for laser ablation.

2. Helium extraction and analysis

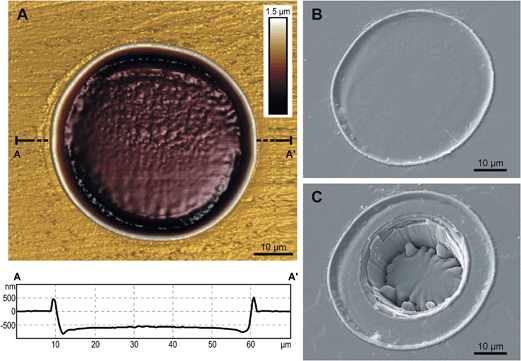
Helium extraction using laser microprobes or short-wavelength pulsed lasers has been shown to generate little or no heating of the surrounding material.^18–21,24 There are several potential approaches to in situ helium extraction. The approach developed at Arizona State University^9,18,19 employs a small pit (10–20 μm wide and 5–10 μm deep) for helium extraction and a larger pit overtop for U and Th (see Fig. 1b in Tripathy-Lang et al.⁹). Our experimental approach employed wide, shallow ⁴He pits followed by a narrower, deeper ablation for U, Th, Sm, Pb (+trace elements); Fig. 2, see details below. We found that this approach improves the accuracy of helium pit volume measurements, a key factor in accurate age determination.¹⁸

Fig. 2 (A) Topographic AFM image of a shallow ⁴He ablation pit in zircon. The volume of the raised rim surrounding the laser pit was excluded for volume analysis, with the volume calculated from the 3D topography of the pit below the surface level of the sample. Note the simple ‘top-hat’ cross-sectional profile with a well-defined, flat bottom. (B) SEM image of first, shallow ablation pit for helium measurement and (C) after second ablation pit for U, Th, Sm, Pb and trace element analysis.

For helium extraction, Teflon containing polished zircon was loaded into the UHV chamber connected to a RESOchron ⁴He analysis system, and pumped to <10⁻⁹ mbar. The standard operating procedure used in this study was to extract ⁴He from zircon using a 50 μm diameter laser spot (RESOlution M-50A-LR incorporating a Compex 102 excimer laser) directed at the polished zircon surface and ablated for 2 s at 5 Hz and 2–3 J cm⁻² fluence. The beam diameter can be altered depending on grain size, expected age and ⁴He content. The laser settings above typically result in a <2 μm deep ablation pit with a flat bottom. Laser spots were placed >20 μm from the edge of the grain in order to avoid issues related to alpha ejection. Gas from the ablated sample was purified using hot and cold Ti–Zr getters, spiked with ³He, and expanded to the quadrupole mass spectrometer (Pfeiffer PrismaPlus™) where it was analyzed for 65 s. ³He/⁴He ratios, corrected for HD and ³H by monitoring mass 1, were measured using a Channeltron detector operated in static mode. ⁴He was determined by isotope-dilution using ³He spike and ⁴He gas standards of known volume, analyzed throughout the run.

Ablation of zircon was always bracketed by a line blank (⁴He measured over the same expanded volume as a sample or gas standard, but without any ablation). A typical analysis sequence included a gas standard followed by at least three line blanks (to assure complete removal of gas standard memory effects), a zircon standard, a line blank, an unknown zircon, a line blank, a zircon standard, a line blank, an unknown zircon, a line blank, etc. with a gas standard run every 5 zircon ablations. The line blank used for ⁴He blank correction was typically in the range of 0.0012 ncc and the typical variation of the line blank throughout an analytical session was 1.2%. The magnitude of ⁴He in the line blank was two orders of magnitude lower than ⁴He in a typical sample analysis. The limit of detection was calculated as the ⁴He concentration in the line blank plus three times the standard deviation on ten sequentially measured line blanks, yielding a value of 0.002 ncc. Reproducibility of ⁴He gas standards during this study was better than 0.04% and 0.1% (both 1σ) on a daily and long-term basis, respectively. Uncertainty on individual ⁴He measurements (typically 0.2–2.5%) was calculated as the square root of the sum of the squares of the following: (i) precision of the ⁴He of the gas standard; (ii) precision of the ⁴He/³He of the sample after blank subtraction, and (iii) precision of the gas standard volume calibration, which in our case is 0.1%.

3. Pit volume measurement

The volume of the pit from which ⁴He was extracted is required in order to calculate the concentration of ⁴He.¹⁸ Choice/selection of the method for helium pit volume measurement will depend on the instrumentation available and the depth of the ablated pit. In our work, CLM is used to determine ⁴He pit volume for pits deeper than ∼3 μm and AFM is used on shallower ⁴He pits. All ages presented in this paper were generated using AFM pit volumes.

Confocal laser scanning microscopy. Accurate determination of laser pit dimensions for volume measurement, including diameter and depth, was achieved using a confocal laser scanning microscope (LSM 700, Carl Zeiss) located in the School of Earth Sciences, University of Melbourne. Laser light from the CLM strikes the sample at the confocal point of the objective lens. Only the light reflected/emitted from the focal plane is detected, which allows the acquisition of individual planar slices and the assembly of three-dimensional images using optical sectioning. In this study, the confocal images were obtained by scanning through the z-axis of the ablation pits using a small pinhole corresponding to an optical slice of ∼0.21 μm. The individual optical sections were then combined to build a three-dimensional image stack. CLM analysis was performed over a 127.8 μm × 127.8 μm area using a 50× objective, and a cut-off wavelength of 405 nm. Precision of this method is approximately 1% (1σ) as determined by repeatedly measuring volume dimensions of a well-defined ablation pit, although values may be higher in larger, steep-sided, imperfect pits.

Atomic force microscopy. AFM utilizes a sharp mechanical probe attached to a flexible cantilever to scan over the ablated pits creating a 3-dimensional topography image from which an apparent volume can be measured. The AFM images were acquired at the Nanochemistry Research Institute in the Dept of Chemistry at Curtin University with a Bruker Dimension Icon SPM system (Bruker, Santa Barbara, USA) operated in ScanAsyst Mode using a ScanAsyst-Air probe (Bruker, Santa Barbara, USA). The volume of each pit was extracted directly from the topography image (Fig. 2) using an in-house-written Matlab code (LPV.m, written by T. Becker). To test precision of this approach, surface topography reference standard (Bruker VGRP-15M) with a known volume (5.445 μm³) was repeatedly measured, yielding an agreement of 0.35% between the calculated (5.426 μm³) and known volumes. However, during routine in situ dating, additional uncertainty is introduced by the roughness of the polished zircon surface (measured to range from 5 to 10 nm in amplitude). Assuming an average roughness of 7 nm, a laser pit surface area of approximately 1900 μm² and a pit volume of 1200–1400 μm³, the sample surface roughness effect introduces an assumed additional uncertainty of ∼2%. Accordingly, a cumulative uncertainty of 2.4% was applied to all AFM pit volumes measured in this work.

4. U, Th, Sm and Pb measurement

After pit volume measurements, Teflon mounts were transferred to the Laurin Technics M50A flow-through cell for a second ablation to determine U, Th, Pb and Sm contents (in addition to a range of trace elements, if desired) using an Agilent 7700s ICP-MS. The CompexPro 102 has a pulse width of 25 ns and the effective cell volume of the Laurin Technic M50A cell is 1 cm³. The laser ablation spot was placed inside the previously ablated ⁴He pit as shown in Fig. 2 and samples and standards were treated identically. Isotopes were measured in time-resolved mode and the following elements were monitored for 0.07 s each: ⁴⁹Ti, ⁹¹Zr, ¹⁴⁷Sm, ²⁰²Hg, ²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb, ²⁰⁸Pb, with ²⁸Si, ²⁹Si, ²³²Th, and ²³⁸U monitored for 0.03 s each. Following a 10 s period of background analysis, samples were spot ablated for 30 s at a 7 Hz repetition rate using a 33 μm diameter beam and laser energy of 2.5 J cm⁻². The sample cell was flushed by ultrahigh purity He (0.68 L min⁻¹) and N₂ (2.8 mL min⁻¹) and high purity Ar was employed as the plasma carrier gas (flow rate 0.98 L min⁻¹). International glass standard NIST 610 was used as the primary standard to calculate elemental concentrations (using ²⁹Si as the internal standard element) and to correct for instrument drift. Mass spectrometer tuning was also performed on NIST 610 with a constant U–Th ratio of 1 obtained in each run. For U–Pb age determination, the primary age standard was 91500 (1062.4 ± 0.4 Ma (ref. 29)) with Plešovice (337.13 ± 0.37 Ma (ref. 30)), GJ-1 (601 ± 1.3 Ma (ref. 31)), and M257 (561.3 ± 0.3 Ma (ref. 32)) used as secondary age standards. The mass spectra were reduced using the trace element and U_Pb_Geochronology3 data reduction schemes in iolite.³³ Precision was better than 5% for most elements based on repeated analyses of secondary internal standards. ²⁰⁶Pb–²³⁸U ages calculated for all zircon age standards, treated as unknowns, were within 3% of the accepted value.

5. Age calculation

Currently there are two approaches used to calculate (U–Th–Sm)/He ages using in situ methods. In the first (absolute) approach, the age is calculated from the measured concentrations of U, Th, (Sm) and He using the following equation:¹⁸where U, Th and Sm are expressed in mol μm⁻³ or similar units, He is the molar abundance of helium released from the ablation pit (in moles) and V is the ablation pit volume (in μm³). Alternately, the pairwise dating approach²¹ can be used, where the concentrations and pit volumes are normalized to a mineral standard of known (U–Th)/He age. In this study, we have modified the method outlined by Vermeesch²¹ in the following ways:

(1) Whereas the original method combined the samples and standards on a one-by-one basis, we combined several standard measurements together in a single block. This was possible because the RESOchron is equipped with a ³He spike tank, making it immune to the sensitivity drift that was a concern in the magnetic sector mass spectrometer used by Vermeesch.²¹

(2) Whereas the calculations in the original method were performed on the raw data files, the modified method uses the processed elemental concentrations as input. This better fits the natural workflow of the method, that aims to determine trace elemental compositions as well as (U–Th–Sm)/He and U–Pb ages, however, a glass standard is required, introducing potential sources of uncertainty.³⁴

The measurements of U, Th, Sm and the ablation pit volume have associated systematic errors. These can be grouped into a single calibration factor, κ:

κ is unknown but can be estimated by analyzing a standard of known (U–Th–Sm)/He age. By measuring a series of standard zircon and normalizing the sample measurements to those of the standards, the age function can be solved and all uncertainties can be accounted for.

Although the maximum likelihood calculations used to determine κ are relatively straightforward to carry out, the details of taking the partial derivatives are rather tedious. We have implemented the method in a user-friendly browser-based calculator to facilitate the application of the κ-calibration method. The spreadsheet-like app is written in HTML and JavaScript and can either be downloaded and run offline or used as an online web service. The calculator is freely available at http://resochronometer.london-geochron.com and an example of input required can be found in Table 3.

Results and discussion

1. Empirical observations

Helium measurement. For in situ dating, it is critical that instrumentation is capable of measuring low ⁴He contents, on the order of pico cubic centimeters. Sensitivity tests were conducted on Mud Tank zircon, which has relatively low U and Th concentrations (10 ppm and 6 ppm, respectively) and a U–Pb age of 732 Ma.³⁵ We were able to measure ⁴He in Mud Tank zircon above detection limits in a ∼800 μm³ ablation pit which is equivalent to a cylindrical pit 10 μm in diameter and 10 μm deep. For younger zircon with relatively higher U and Th concentrations (e.g., Ellendale lamproite pipe zircon, 100 ppm U and 70 ppm Th; see Applications), an in situ (U–Th)/He age of 21.1 ± 1.2 Ma was determined from a ⁴He measurement close to the 0.002 ncc detection limit (Table 3). This in situ age (Table 4) compares well to the known age of the pipe determined by conventional (U–Th)/He and Ar–Ar geochronology methods (20.6 ± 2.8 Ma (ref. 23)).

Pit volume considerations. Typically, the shallow zircon laser ablation pits for helium analysis have a well-defined ‘top-hat’ profile geometry (see Fig. 2 and Marillo-Sialer, et al.³⁶), ideal for accurate pit volume determination. During ablation, we sometimes observed elongated positive structures protruding from the pit base, particularly where pit depth exceeded ∼7 μm (Fig. 3). The fact that the structures were not present in all ablation pits suggests that they do not result from a reduction in ablation efficiency due to a temporal fluctuation of the incident laser energy, as reported previously.³⁷ Viewed using transmitted light microscopy, ablation artifacts appear to coincide with microfractures cutting across the zircon crystal (Fig. 3). Although it is beyond the scope of this study to investigate in detail the processes leading to the formation of these structures, we believe that their development is related to nonlinear growth of surface irregularities, initiated by the scattering of light out of the irradiated laser beam by the microfracture surface.^38,39 The application of additional laser pulses then promotes the preferential ablation of the material surrounding the irregularities and the formation of hillocks, whose growth is enhanced by preferential re-deposition of ablated particulate between laser pulses.^40,41

Fig. 3 Laser ablation of zircon. (A) BSE image of two zircon grains showing pits ablated using the same operating conditions. Note the structures formed within two of the ablation pits. The features appear to be related to the presence of microfractures within the zircon grains, which are only visible under transmitted light (B). (C) Confocal laser microscope image and (D) cross section profile corresponding to the ablation pit in (C) showing that the structures formed within the ablation pits are cone-shaped. This is consistent with a nonlinear growth of surface irregularities during laser irradiation.

Considering that one of the advantages of in situ (U–Th–Sm)/He dating methods is the ability to analyze zircon grains or portions of grains that have crystal defects, such as fractures,⁹ the structures mentioned above, if undetected, have the potential to decrease the accuracy of age determinations. However, once identified, the number of rejected analyses will increase, thus reducing, to a certain extent, the internal precision of the analytical session and, for detrital studies, potentially biasing the results of age interpretations. Detailed examination of target grains using a range of microscopy methods and applying reasonable but higher uncertainties to pit volumes where features were noted, will minimize the effect of these uncertainties.

U, Th, Sm and Pb measurements. Our preferred protocol for U, Th and Sm analysis is to ablate directly over the ⁴He pits. The slightly smaller beam diameter for parent isotope analysis (33 μm, versus 50 μm for the ⁴He analysis) but deeper ablation (approximately 25 μm) provides enough material for reliable U–Pb age and trace element determinations. Initial tests of Sri Lanka zircon (B188 and RB140) showed that they contain <1.5 ppm Sm, so there was negligible contribution of ⁴He from this parent element, as is typical of most zircon.⁴² The initial ablation for helium determination had no discernable impact on the U and Th content of the underlying zircon as shown by the agreement between U and Th contents measured in our second ablation pit and that measured in fresh Sri Lanka zircon (Table 1) using conventional LA-ICP-MS methods. In situ RESOchron U and Th concentrations also agree within error with U and Th contents determined using SHRIMP (Table 1, notes) where zircon BR266 was used as the internal standard.⁴³

Table 1 Comparison of U, Th and Sm content of Sri Lanka zircon B188 and RB140 using both conventional LA-ICP-MS methods (single ablation) and methods described in this work (2nd ablation pit, over pit ablated for helium extraction)^a

	U (ppm)	2σ	Th (ppm)	2σ	Sm (ppm)	2σ
a All analyses were performed using a 33 μm beam, 30 second ablation, 7 Hz, 2–3 J cm^−2 fluence (measured at sample surface) with NIST610 as the primary reference material and ^28Si as the internal reference isotope. Nasdala^43 obtained U and Th values of 288 ± 3 and 122 ± 1 for RB140 and 556 ± 24 and 59 ± 4 for B188, respectively.
B188 (RESOchron, 2nd ablation pit) (n = 30)	529	18	58.6	2.2	1.4	0.2
B188 (LA-ICP-MS) (n = 54)	542	11	60.6	1.4	—	—
RB140 (RESOchron, 2nd ablation pit) (n = 13)	287	24	126	11	2.4	0.3
RB140 (LA-ICP-MS) (n = 19)	273	13	120	5.4	—	—

---

Zircon standards B188 and RB140. The pairwise dating approach requires the adoption of standard reference materials of similar matrix to the mineral being age dated. After testing a number of potential zircon candidates, it was determined that Sri Lanka zircon B188 fulfills the key attributes of an effective standard reference mineral because: (i) it yields reproducible (U–Th–Sm)/He ages of 435 ± 22 Ma, with a weighted mean age of 434.7 ± 4 Ma using conventional (U–Th–Sm)/He dating (Table 2), (ii) in laser ablation helium analysis mode it yields reproducible ⁴He abundances for pits ablated under constant conditions (<1% variation in ⁴He content; Table 3), and (iii) it showed negligible zonation in U and Th content during multiple LA-ICP-MS analyses (Table 1). Another Sri Lankan zircon RB140 is a potential alternative in that it has a known conventional (U–Th–Sm)/He age of 437 ± 20 Ma (ref. 43) and has reproducible ⁴He yields (<1% variation in ⁴He content; Table 3), however it was found to be relatively less homogeneous with respect to U and Th contents (Table 1). For this reason, B188 is preferred as the primary standard and was utilized in pairwise dating. Both ²⁰⁶Pb–²³⁸U ages and (U–Th–Sm)/He ages for pairwise in situ (U–Th–Sm)/He dated B188 and RB140 compare within error with ages determined using traditional methods (Fig. 4, Table 2). Neither of the pits for the two outliers (one of B188 yielding a too young He age and one RB140 yielding a too young U–Pb age) showed any unusual features.

Table 2 (U–Th–Sm)/He and U–Pb ages of prospective standards determined using both conventional methods and those described in this work

Sample	(U–Th–Sm)/He traditional^a (Ma)	2σ (Ma)	(U–Th–Sm)/He RESOchron^b (Ma)	2σ (Ma)	^206Pb–^238U LA-ICP-MS^c (Ma)	2σ (Ma)	^206Pb–^238U RESOchron (Ma)	2σ (Ma)
a Measured using methods in Evans.^17,23 b Determined using pairwise dating methods with B188 used as the standard against RB140 and vice versa with 2σ uncertainty calculated as the standard deviation on raw ages. c Determined using conventional LA-ICP-MS methods described in the text on grains that had not been ablated first for ^4He measurement. d Age from Nasdala et al., 2004 where B188 and RB140 SHRIMP ^206Pb–^238U ages were 559 ± 8 and 566 ± 3 Ma, respectively.
B188	434.7 (n = 27)	22	444 (n = 14)	23	566	9	560	8
RB140	437^d	20	422 (n = 13)	16	563	11	557	8

---

Table 3 Input required for online pairwise resochronometer. Data for Sri Lanka zircon B188 (standard) and single zircon grains from Ellendale, Western Australia^a

Sample	U (ppm)	2σ (ppm)	Th (ppm)	2σ (ppm)	Sm (ppm)	2σ (ppm)	He (ncc)	2σ (ncc)	Pit vol (μm^3)	± (μm^3)	Known He age (Ma)	2σ (Ma)
a All pit volumes measured by AFM. Uncertainty on AFM pit volume was 2.4% as described in the text.
B188-1	525	35	59	4	1.5	0.4	0.217	0.0004	1455	34.9	435	22
B188-2	544	26	60	3	1.4	0.3	0.202	0.0004	1216	29.2	435	22
B188-3	541	22	60	3	1.7	0.3	0.195	0.0004	1212	29.1	435	22
B188-4	578	28	64	4	1.5	0.4	0.204	0.0004	1266	30.4	435	22
B188-5	591	34	65	3	1.8	0.4	0.221	0.0004	1340	32.2	435	22
B188-6	503	22	55	3	1.2	0.3	0.198	0.0004	1231	29.5	435	22
B188-7	532	32	60	5	1.6	0.4	0.214	0.0004	1393	33.4	435	22
B188-8	700	120	78	14	1.9	0.6	0.177	0.0004	1095	26.3	435	22
B188-9	523	11	59	2	1.4	0.3	0.219	0.0004	1474	35.4	435	22
B188-10	524	9	59	1	1.2	0.2	0.239	0.0005	1613	38.7	435	22
B188-11	508	11	57	1	1.3	0.3	0.240	0.0005	1639	39.3	435	22
B188-12	510	10	58	1	1.3	0.2	0.213	0.0004	1443	34.6	435	22
B188-13	500	9	58	1	1.4	0.3	0.217	0.0004	1509	36.2	435	22
B188-14	511	9	58	1	1.3	0.3	0.245	0.0005	1689	40.5	435	22
RB140-1	298	12	133	6	3.2	0.6	0.119	0.0002	1363	32.7	437	20
RB140-2	303	15	136	6	2.5	0.5	0.102	0.0002	1135	27.2	437	20
RB140-3	303	16	136	8	2.8	0.5	0.111	0.0002	1264	30.3	437	20
RB140-4	277	12	124	6	2.4	0.4	0.131	0.0003	1503	36.1	437	20
RB140-5	288	15	125	6	2.3	0.4	0.113	0.0002	1292	31	437	20
RB140-6	298	17	132	7	2.8	0.4	0.114	0.0002	1285	30.8	437	20
RB140-7	285	6	130	3	2.2	0.3	0.133	0.0003	1634	39.2	437	20
RB140-8	273	6	126	3	2.4	0.3	0.137	0.0003	1660	39.8	437	20
RB140-9	266	6	123	3	2.2	0.3	0.122	0.0002	1498	36	437	20
RB140-10	262	6	121	3	2.1	0.4	0.125	0.0003	1434	34.4	437	20
RB140-11	276	7	128	4	2.4	0.4	0.122	0.0002	1502	36	437	20
RB140-12	271	5	125	2	2.2	0.4	0.133	0.0003	1602	38.4	437	20
RB140-13	278	6	129	3	2.5	0.4	0.122	0.0002	1466	35.2	437	20
Ellendale pipe 1	270	16	90	6	1.3	0.3	0.006	0.0001	1370	32.9
Ellendale pipe 2	250	12	100	4	2.0	0.4	0.006	0.0002	1446	34.7
Ellendale pipe 3	136	5	186	8	3.9	0.6	0.003	0.0001	1469	35.3
Ellendale pipe 4	202	10	134	7	2.7	0.4	0.005	0.0001	1390	33.4
Ellendale pipe 5	198	9	177	10	4.3	0.6	0.005	0.0001	1430	34.3
Ellendale pipe 6	642	25	354	16	14.5	2.0	0.012	0.0003	1374	33
Ellendale pipe 7	322	22	116	7	8.8	1.1	0.007	0.0002	1429	34.3
Ellendale pipe 8	700	42	138	6	5.0	0.7	0.012	0.0003	1353	32.5
Ellendale pipe 9	209	8	118	5	7.3	0.9	0.004	0.0001	1450	34.8
Ellendale pipe 10	418	25	112	8	2.2	0.4	0.007	0.0002	1413	33.9
Ellendale pipe 11	215	11	136	7	2.2	0.4	0.006	0.0002	1163	27.9
Ellendale pipe 12	241	6	225	6	4.4	0.5	0.006	0.0002	1840	44.2
Ellendale pipe 13	330	8	43	1	1.8	0.5	0.008	0.0002	1496	35.9
Ellendale pipe 14	103	3	80	2	1.1	0.3	0.003	0.0001	1840	44.2
Ellendale country rock-1	304	12	153	6	2.3	0.4	0.099	0.001	1225	29.4
Ellendale country rock-2	71	5	92	7	2.3	0.4	0.030	0.0003	1204	28.9
Ellendale country rock-3	69	6	34	2	1.8	0.4	0.034	0.0003	1306	31.3
Ellendale country rock-4	144	7	109	5	1.3	0.3	0.059	0.0006	1216	29.2
Ellendale country rock-5	76	4	218	12	18.7	1.4	0.073	0.0007	1249	30
Ellendale country rock-6	499	18	138	5	0.9	0.2	0.198	0.002	1327	31.8
Ellendale country rock-7	174	15	150	11	1.9	0.4	0.068	0.0007	1113	26.7
Ellendale country rock-8	95	7	63	4	3.2	0.6	0.067	0.0007	1423	34.1
Ellendale country rock-9	462	36	73	4	2.7	0.5	0.143	0.0014	1429	34.3
Ellendale country rock-10	81	6	92	9	6.4	1.1	0.068	0.0007	1258	30.2
Ellendale country rock-11	387	22	686	34	22.1	1.8	0.154	0.0015	1284	30.8
Ellendale country rock-12	91	7	43	2	1.5	0.3	0.126	0.0013	1619	38.8
Ellendale country rock-13	153	5	144	5	4.0	0.5	0.066	0.0013	1584	38
Ellendale country rock-14	106	4	114	3	2.2	0.4	0.047	0.0009	1812	43.5
Ellendale country rock-15	341	6	196	5	2.9	0.5	0.184	0.0037	1533	36.8
Ellendale country rock-16	156	3	205	4	6.7	0.5	0.078	0.0016	1678	40.3
Ellendale country rock-17	257	24	169	18	3.7	0.5	0.085	0.0017	1694	40.7

---

Table 4 Summary of in situ (U–Th–Sm)/He and U–Pb ages for Sri Lanka zircon (RB140, B188) and Ellendale lamproite/country rock

Sample	^206Pb–^238U (Ma)	2σ (Ma)	‘Pairwise’ (U–Th–Sm)/He (Ma)	2σ (Ma)
a ‘Pairwise’ (U–Th–Sm)/He age calculated using B188 standard. b ‘Pairwise’ (U–Th–Sm)/He age calculated using RB140 standard.
RB140-1^a	557	18	410	18
RB140-2^a	555	18	414	21
RB140-3^a	553	18	406	22
RB140-4^a	563	19	441	20
RB140-5^a	559	15	425	22
RB140-6^a	566	15	417	24
RB140-7^a	568	12	400	13
RB140-8^a	558	13	421	13
RB140-9^a	556	13	428	14
RB140-10^a	536	14	463	16
RB140-11^a	559	13	413	14
RB140-12^a	560	15	429	14
RB140-13^a	555	16	418	14
B188-1^b	565	14	442	34
B188-2^b	563	13	473	20
B188-3^b	565	15	462	27
B188-4^b	574	11	435	28
B188-5^b	551	14	435	31
B188-6^b	560	12	495	30
B188-7^b	557	13	450	32
B188-8^b	554	13	361	17
B188-9^b	565	9	441	22
B188-10^b	566	11	440	21
B188-11^b	559	9	448	22
B188-12^b	582	19	449	22
B188-13^b	553	9	448	21
B188-14^b	552	10	442	21
Ellendale pipe 1^a	1270	26	22.1	1.4
Ellendale pipe 2^a	598	18	25.5	1.5
Ellendale pipe 3^a	599	26	18.8	1
Ellendale pipe 4^a	607	17	26.2	1.4
Ellendale pipe 5^a	1175	29	21.5	1.1
Ellendale pipe 6^a	368	11	19.8	1
Ellendale pipe 7^a	2757	48	21.2	1.6
Ellendale pipe 8^a	2167	97	19.7	1.3
Ellendale pipe 9^a	578	19	18.6	0.9
Ellendale pipe 10^a	620	16	17.1	1.2
Ellendale pipe 11^a	1196	28	34.6	2.1
Ellendale pipe 12^a	895	17	18.3	0.9
Ellendale pipe 13^a	1122	21	23.6	1.1
Ellendale pipe 14^a	1147	27	18.6	1
Ellendale country rock-1^a	1756	28	371	17
Ellendale country rock-1^a	1613	46	418	25
Ellendale country rock-3^a	1066	40	524	39
Ellendale country rock-4^a	1133	25	444	21
Ellendale country rock-5^a	1161	43	696	32
Ellendale country rock-6^a	558	13	434	19
Ellendale country rock-7^a	1169	27	449	34
Ellendale country rock-8^a	875	33	650	42
Ellendale country rock-9^a	1830	34	325	25
Ellendale country rock-10^a	1208	40	793	49
Ellendale country rock-11^a	1811	28	341	17
Ellendale country rock-12^a	1727	54	1119	74
Ellendale country rock-13^a	1528	28	350	15
Ellendale country rock-14^a	1601	32	305	13
Ellendale country rock-15^a	1601	23	478	17
Ellendale country rock-16^a	1015	26	355	13
Ellendale country rock-17^a	304.8	9.2	265	23

---

Fig. 4 In situ U–Pb and (U–Th–Sm)/He ages for B188 and RB140 (squares and circles, respectively). Area inside shaded box indicates range of ages obtained on separate aliquots of B188 and RB140 using conventional methods (LA ICP-MS for U–Pb and conventional, whole grain gas extraction and dissolution (U–Th–Sm)/He techniques; Table 2). Prior to application of pairwise age calculation, standard analyses falling outside the range obtained using traditional methods should be closely examined and discarded if debris or structures that cause pit volume inaccuracies are detected.

2. Application: diamondiferous lamproite exploration

U–Pb and (U–Th–Sm)/He double dating has previously been applied to Australian diamond deposits^23,26 after recognition of the fact that xenocrystic zircon from kimberlitic and lamproitic intrusions have a unique age profile which is determined by the thermal resetting of zircon helium ages during the emplacement of the lamproite pipe in the upper crust. Zircon from the E9 lamproite at the Ellendale diamond mine (Western Australia) has been well characterised by conventional SHRIMP U–Pb and whole grain (U–Th–Sm)/He methods and, along with the surrounding country rock zircon, provides a convenient natural laboratory to test the viability of the in situ double dating methods described here. The zircon (U–Th–Sm)/He age of 21 Ma for the emplacement of the diamondiferous Ellendale lamproite was corroborated by phlogopite ⁴⁰Ar/³⁹Ar techniques, and is distinct from the 300–1500 Ma helium ages determined from detrital zircon originating from the regional sandstone country rock (sample located 20 km from the E9 pipe). In contrast, the range of SHRIMP U–Pb ages for the lamproite and detrital zircons in the sandstone were statistically indistinguishable.²³ Grains for pairwise in situ U–Pb and (U–Th–Sm)/He dating were selected from samples previously dated in the Evans, et al.²³ study. Fig. 5 demonstrates that the in situ U–Pb and (U–Th–Sm)/He double dating technique effectively reproduced the age distribution patterns observed using conventional (U–Th–Sm)/He and SHRIMP U–Pb dating. Although none of the 2–3 Ga (U–Pb age) grains were identified in the country rock samples, this is most likely an artefact of the small number of grains analysed here for demonstration purposes. In the original study, 55 zircon grains were double dated using conventional methods, as opposed to just 17 using in situ techniques.

Fig. 5 RESOchron pairwise double dated Ellendale lamproitic zircon (grey diamonds) and country rock (grey squares) plotted with zircon from the same samples, previously dated using conventional (U–Th)/He and SHRIMP methods (black diamonds and squares; from Evans et al., 2013). Pairwise in situ ages reproduce age distribution patterns identified by traditional analysis. A linear scale was used for U–Pb data as there was no significant difference between lamproite and country rock ages. Most 2σ uncertainties plot within the boundaries of the symbols.

The implications of Fig. 5 are that our in situ (U–Th–Sm)/He and U–Pb double dating technique is a viable tool for rapid, cost-effective analysis of a large number of grains, mitigating several of the primary obstacles to establishing double dating as a potentially viable diamond exploration tool. In addition, sediment provenance and landscape evolution studies^9,22,25,44 that require large numbers of double dates for legitimate statistical treatment and identification of significant age populations will benefit from this powerful tool.

Conclusions

We have demonstrated a new and effective analytical system for in situ U–Pb and (U–Th–Sm)/He double dating of zircon. The key dependencies in this approach are the need for accurate measurements of the volume of the ablation pits from which radiogenic helium has been extracted and a standard reference zircon with homogeneous He concentration and a known (U–Th–Sm)/He age. The determination of ablation pit volume is simplified by generating shallow craters (<2 μm deep) with cylindrical geometry and, while the development of zircon reference standards is ongoing, Sri Lanka zircon B188 (435 ± 22 Ma) is our current choice as a primary standard for the pairwise dating technique. We have provided the community with a freeware application (http://resochronometer.london-geochron.com) for in situ (U–Th–Sm)/He age calculation.

The successful application of in situ zircon (U–Th–Sm)/He and U–Pb to double dating at the Ellendale diamond mine demonstrates that geological this method is will provide a critical improvement over conventional methods of double dating when large numbers of analyses are required.

Acknowledgements

This project has been supported by the Australian Education Investment Fund and Curtin University via the AuScope Australian Geophysical Observation System project. Sri Lanka zircon was kindly provided by A. Kennedy (Curtin University). We are grateful for the support of B. Godfrey, E. Roberts, D. Gibbs, C. Gabay, A. Norris and M. Hamel throughout the development of the instrumentation and protocols. Solution U, Th and Sm analysis for conventional (U–Th–Sm)/He dating was performed at TSW Analytical, Perth. We are grateful to Elaine Miller (John de Laeter Centre, Microscopy and Microanalysis Facility, Curtin University) for help with SEM imaging. P. Vermeesch is financially supported by NERC grant #NE/K003232/1 and ERC grant #259505 (‘KArSD’). We thank R. Ickert, M. Tremblay and K. Hodges for comprehensive and constructive reviews of an earlier version of the manuscript and three anonymous reviewers for their insightful comments.

References

1. P. W. Reiners, T. A. Ehlers and P. K. Zeitler, in Thermochronology, ed. P. W. Reiners and T. A. Ehlers, Rev. Mineral. Geochem., 2005, vol. 58, ch. 1, pp. 1–18.
2. P. W. Reiners, T. L. Spell, S. Nicolescu and K. A. Zanetti, Geochim. Cosmochim. Acta, 2004, 68, 1857–1887.
3. K. V. Hodges, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Elsevier, Oxford, 2nd edn, 2014, vol. 4, ch. 8, pp. 281–308.
4. P. K. Zeitler, A. L. Herczeg, I. McDougall and M. Honda, Geochim. Cosmochim. Acta, 1987, 51, 2865–2868.
5. K. A. Farley, J. Geophys. Res., 2000, 105, 2903–2914.
6. K. A. Farley and B. I. A. McInnes, Rev. Mineral. Geochem., 2002, 47, 819–844.
7. K. A. Farley, R. A. Wolf and L. T. Silver, Geochim. Cosmochim. Acta, 1996, 60(21), 4223–4229.
8. T. A. Ehlers and K. A. Farley, Earth Planet. Sci. Lett., 2003, 206, 1–14.
9. A. Tripathy-Lang, K. V. Hodges, B. Monteleone and M. Van Soest, J. Geophys. Res., 2013, 118, 1333–1341.
10. C. Spiegel, B. Kohn, D. Belton, Z. Berner and A. Gleadow, Earth Planet. Sci. Lett., 2009, 285(1), 105–114.
11. M. Danišík, K. Pfaff, N. J. Evans, C. Manoloukos, S. Staude, B. McDonald and G. Markl, Chem. Geol., 2010, 278(1–2), 58–69.
12. C. Gautheron, L. Tassan-Got, R. A. Ketcham and K. J. Dobson, Geochim. Cosmochim. Acta, 2012, 96, 44–56.
13. A. G. C. A. Meesters and T. J. Dunai, Chem. Geol., 2002, 186, 333–344.
14. A. G. C. A. Meesters and T. J. Dunai, Chem. Geol., 2002, 186, 347–363.
15. J. K. Hourigan, P. W. Reiners and M. T. Brandon, Geochim. Cosmochim. Acta, 2005, 69, 3349–3365.
16. N. J. Evans, B. I. A. McInnes, A. P. Squelch, P. J. Austin, B. J. McDonald and Q. Qu, Chem. Geol., 2008, 257, 101–113.
17. N. J. Evans, J. P. Byrne, J. T. Keegan and L. E. Dotter, J. Anal. Chem., 2005, 60(12), 1159–1165.
18. J. W. Boyce, K. V. Hodges, W. J. Olszewski, M. J. Jercinovic, B. D. Carpenter and P. W. Reiners, Geochim. Cosmochim. Acta, 2006, 70, 3031–3039.
19. J. W. Boyce, K. V. Hodges, D. King, J. L. Crowley, M. Jercinovic, N. Chatterjee, S. A. Bowring and M. Searle, Geochem., Geophys., Geosyst., 2009, 10, Q0AA0,  DOI:10.1029/2009GC002497.
20. M. C. Van Soest, B. D. Monteleone, K. V. Hodges and J. W. Boyce, Geochim. Cosmochim. Acta, 2011, 75, 2409–2419.
21. P. Vermeesch, S. C. Sherlock, N. M. W. Roberts and A. Carter, Geochim. Cosmochim. Acta, 2012, 79, 140–147.
22. I. H. Campbell, P. W. Reiners, C. M. Allen, S. Nicolescu and R. Upadhyay, Earth Planet. Sci. Lett., 2005, 237, 402–432.
23. N. J. Evans, B. I. A. McInnes, B. J. McDonald, M. Danišík, F. Jourdan, C. Mayers, E. Thern and D. Corbett, Miner. Deposita, 2013, 48, 413–421.
24. M. C. Van Soest, B. D. Monteleone, J. W. Boyce and K. V. Hodges, AGU Fall Meeting Abstracts, San Francisco, 2008, p. B2161.
25. J. M. Rahl, P. W. Reiners, I. H. Campbell, S. Nicolescu and C. M. Allen, Geology, 2003, 31, 761–764.
26. B. McInnes, N. J. Evans, B. J. McDonald, P. Kinny and J. Jakimowicz, Lithos, 2009, 112S, 592–599.
27. P. Vermeesch, Earth Planet. Sci. Lett., 2004, 224, 441–451.
28. P. Zaun and G. A. Wagner, Nucl. Tracks Radiat. Meas., 1985, 10, 303–307.
29. M. Wiedenbeck, P. Allé, F. Corfu, W. L. Griffin, M. Meier, F. Oberli, A. Von Quadt, J. C. Roddick and W. Spiegel, Geostand. Newsl., 1995, 19(1), 1–23.
30. J. Sláma, J. Košler, D. J. Condon, J. L. Crowley, A. Gerdes, J. M. Hanchar, M. S. A. Horstwood, G. A. Morris, L. Nasdala, N. Norberg, U. Schaltegger, B. Schoene, M. N. Tubrett and M. J. Whitehouse, Chem. Geol., 2008, 249, 1–35.
31. A. R. C. Kylander-Clark, B. R. Hacker and J. M. Cottle, Chem. Geol., 2013, 345, 99–112.
32. L. Nasdala, W. Hofmeister, N. Norberg, J. M. Martinson, F. Corfu, W. Dörr, S. L. Kamo, A. K. Kennedy, A. Kronz, P. W. Reiners, D. Frei, J. Košler, Y. Wan, J. Götze, T. Häger, A. Kröner and J. W. Valley, Geostand. Geoanal. Res., 2008, 32(3), 247–265.
33. C. Paton, J. C. Hellstrom, B. Paul, J. D. Woodhead and J. M. Hergt, J. Anal. At. Spectrom., 2011, 26, 2508–2518.
34. P. Sylvester, in Laser Ablation in the Earth Sciences: Current Practices and Outstanding issues, ed. P. Sylvester, Mineralogical Association of Canada Short Course, 2008, vol. 40, ch. 5, pp. 67–78.
35. L. P. Black and B. L. Gulson, AGSO J. Aust. Geol. Geophys., 1978, 3, 227–232.
36. E. Marillo-Sialer, J. D. Woodhead, J. Hergt, A. Greig, M. Guillong, A. Gleadow, N. J. Evans and C. Paton, J. Anal. At. Spectrom., 2014, 29, 981–989.
37. J. Woodhead, J. Hergt, S. Meffre, R. R. Large, L. Danyushevsky and S. Gilbert, Chem. Geol., 2009, 262, 344–354.
38. A. J. Pedraza, S. Jesse, Y. F. Guan and J. D. Fowlkes, J. Mater. Res., 2001, 16, 3599–3608.
39. K. Kolasinski, Curr. Opin. Solid State Mater. Sci., 2007, 11, 76–85.
40. F. Sanchez, J. L. Morenza, R. Aguilar, J. Delgado and M. Varela, Appl. Phys. Lett., 1996, 69, 620.
41. F. Sanchez, J. L. Morenza and V. Trtik, Appl. Phys. Lett., 1999, 75, 3303.
42. P. W. Reiners and S. Nicolescu, ARHDL Report 1, http://www.geo.arizona.edu/~reiners/arhdl/arhdl.htm, 2006.
43. L. Nasdala, P. W. Reiners, J. I. Garver, A. K. Kennedy, R. A. Stern, E. Balan and R. Wirth, Am. Mineral., 2004, 89, 219–231.
44. P. W. Reiners, in Thermochronology, ed. P. W. Reiners and T. A. Ehlers, Rev. Mineral. Geochem., 2005, vol. 58, ch. 6, pp. 151–179.

---