Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determination of the kinetics underlying the pKa shift for the 2-aminoanthracenium cation binding with cucurbit[7]uril†
Suma S.
Thomas
and
Cornelia
Bohne
*
Department of Chemistry, University of Victoria, PO Box 3065, Victoria, BC V8W 3V6, Canada. E-mail: cornelia.bohne@gmail.com
First published on 19th June 2015
Abstract
The binding dynamics of the 2-aminoanthracenium cation (AH+) and 2-aminoanthracene (A) with cucurbit[7]uril (CB[7]) was studied using stopped-flow experiments. The kinetics was followed by measuring the fluorescence changes over time for AH+ and A, which emit at different wavelengths. The studies at various pH values showed different mechanisms for the formation of the AH+@CB[7] complex, with this complex formed either by the binding of AH+ or by the initial binding of A followed by protonation. In the latter case, it was possible to determine the protonation ((1.5 ± 0.4) × 109 M−1 s−1) and deprotonation (89 ± 7 s−1) rate constants for complexed A/AH+, which showed that the pKa shift of +3.1 for A/AH+ in the complex is mainly due to a lower deprotonation rate constant.
Introduction
Cucurbit[n]urils (CB[n]s) are macrocyclic host molecules formed from glycoluril units, which have a wide application as supramolecular hosts.1–7 One of the key features of supramolecular systems is their dynamics,8 which can be directly related to the intended function of a supramolecular system. CB[n]s have been developed for a wide variety of applications, such as photocatalysis9 or catalysis,10–13 drug stabilization and delivery,14–17 self-sorting and stimuli responsive systems,3,18–21 tandem enzyme assays,22,23 and control of supramolecular polymerization.24,25The dynamics of guest complex formation with CB[7] occurs over a wide time range, from milliseconds to hours,10,26–35 with rate constants for the association process as high as one order of magnitude below the diffusion controlled limit. The binding dynamics is affected by the size of the guest and the presence or absence of charges on the guest.10,26,30,34 Exclusion complexes can be formed between the positive charge of the guest and the carbonyl moieties at the portals of CB[n] before inclusion of the guest into the interior of the CB[n] cavity.27,30,31 However, in other cases, the formation of an exclusion complex is not detected in kinetic studies.32,34 There are still too few reported studies on guest binding dynamics to develop a mechanistic understanding of how the guest binding dynamics can be controlled. Such an understanding is required for the rational design of systems containing CB[n]s where the dynamics is directly related to the intended function.
The objective of the current work is to explore one aspect of the guest–CB[n] dynamics, namely, the protonation and deprotonation reactions of a guest@CB[n] complex. This aspect is important because CB[n]s were shown to stabilize positively charged guests. In the case of protonated guests, such stabilization led to an increase of the pKa of the CB[n]-complexed guest compared with the pKa for the guest in water.4,15,36-38 Therefore, CB[n]–guest complexation alters the protonation and deprotonation rates of bound guests compared with this reactivity in water. Understanding the origins for this change in kinetics is relevant to the design of supramolecular systems that alter chemical reactivity, including the ability to affect acid–base catalysis. In this context, CB[n]s were shown to catalyze the hydrolysis of included guests.39,40
The increase in the hydronium cation concentration at pH values where the guest is protonated led to slower kinetics when binding of the hydronium cation with CB[n] was competitive with guest binding.27,30,32 The protonation state of the guest affects its binding dynamics with CB[n]s. For example, the association and dissociation rate constants of the cyclohexylmethylammonium cation with CB[6] are lower than the same rate constants for cyclohexylmethylamine because, in the case of the cation, an exclusion complex is formed before the guest is included within the cavity.30,31 For pH values between the pKa values of the guest in water and in the complex, the association process corresponds to the binding of the neutral amine followed by fast protonation of the amine@CB[6] complex, whereas dissociation corresponds to the exit of the ammonium cation from CB[6].30 The kinetics for the cyclohexylmethylamine/CB[6] system occur on hour to day time scales, depending on the pH. Therefore, the acid–base equilibria for the guest in water or within the complex were fast compared to the complexation dynamics with CB[6]. On the other hand, no evidence for the formation of an exclusion complex was observed for the binding of the 2-naphthyl-1-ethylammonium cation with CB[7].32
In this work, we chose a guest, the 2-aminoanthracenium cation (AH+), with a lower pKa (4.0)41 than that of cyclohexylmethylamine (10.5)30 to study the effect of pH on the guest binding dynamics with CB[7] (Scheme 1). The pH values of the solutions were varied between 2.0, where the guest is completely protonated (AH+), and pH 5.5, where the guest is mostly deprotonated (A). The singlet excited state of AH+, which emits with a maximum at 422 nm (“blue” emission), has a much lower pK*a (−5.4 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water
1 water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol),42,43 leading to the formation of singlet excited A, which emits with a maximum at 503 nm (“green” emission).38 These photophysical properties provide a means of following the concentrations of AH+ and A separately.
ethanol),42,43 leading to the formation of singlet excited A, which emits with a maximum at 503 nm (“green” emission).38 These photophysical properties provide a means of following the concentrations of AH+ and A separately.
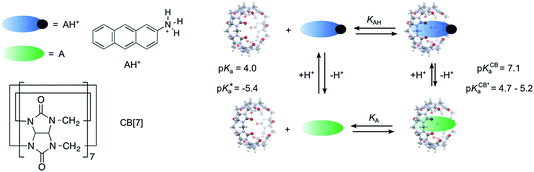 | ||
| Scheme 1 Structures of cucurbit[7]uril (CB[7]) and the 2-aminoanthracenium cation (AH+), equilibria between protonated AH+, neutral A, and CB[7], and pKa values for the ground (pKa, pKCBa) and singlet excited state (pK*a, pKCB*a) of AH+ in the absence41–43 and presence of CB[7].38 | ||
AH+ was shown to form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with CB[7] resulting in a shift in the pKa for ground state AH+ from 4.0 to 7.1, while the estimated excited state pK*a shifted from −5.4 to between 4.7 and 5.2.38 In acidic solution, AH+ was stabilized by complexation to CB[7], and its blue emission was observed.38 The changes in the pKa values for free and CB[7]-complexed AH+, as well as the ability to independently follow the concentrations of AH+ and A, were used to characterize the guest binding dynamics at pH values where only AH+ or predominantly A were present. At low pH, the kinetics was slower than at high pH because AH+ forms an encounter complex with CB[7], whereas at high pH, neutral A is in fast equilibrium with CB[7], and A@CB[7] is then protonated. Kinetic studies led to the determination of a protonation rate constant of (1.5 ± 0.4) × 109 M−1 s−1 for the A@CB[7] complex and a deprotonation rate constant of 89 ± 7 s−1 for AH+@CB[7], showing that the large pKa shift is mainly a reflection of the slow down of the deprotonation step.
1 complex with CB[7] resulting in a shift in the pKa for ground state AH+ from 4.0 to 7.1, while the estimated excited state pK*a shifted from −5.4 to between 4.7 and 5.2.38 In acidic solution, AH+ was stabilized by complexation to CB[7], and its blue emission was observed.38 The changes in the pKa values for free and CB[7]-complexed AH+, as well as the ability to independently follow the concentrations of AH+ and A, were used to characterize the guest binding dynamics at pH values where only AH+ or predominantly A were present. At low pH, the kinetics was slower than at high pH because AH+ forms an encounter complex with CB[7], whereas at high pH, neutral A is in fast equilibrium with CB[7], and A@CB[7] is then protonated. Kinetic studies led to the determination of a protonation rate constant of (1.5 ± 0.4) × 109 M−1 s−1 for the A@CB[7] complex and a deprotonation rate constant of 89 ± 7 s−1 for AH+@CB[7], showing that the large pKa shift is mainly a reflection of the slow down of the deprotonation step.
Experimental
Materials
2-Aminoanthracene (Aldrich, 96%) was recrystallized from ethanol once. Sodium chloride (Sigma-Aldrich, BioUltra, ≥99.5%), hydrochloric acid (Anachemia, ACS reagent grade), sodium hydroxide (Anachemia, ACS reagent grade), glacial acetic acid (ACP, ACS reagent grade), and methanol (Fisher, spectral grade, >99.9%) were used as received. Cucurbit[7]uril (CB[7]) was synthesized based on previous literature44–46 and was purified according to the procedure described in the ESI.† Deionized water (Barnstead NANOpure deionizing systems ≥17.8 MΩ cm) was used in the preparation of all aqueous solutions.Sample preparation
A 1 mM stock solution of 2-aminoanthracene was prepared in methanol. For the experiments at pH 2.0, 3.8, and 4.3, aqueous solutions were prepared by dissolving the required amounts of NaCl and 2.0 N HCl in water to achieve a final NaCl concentration of 20 mM and the required pH. The buffer solutions at pH 5.0 and 5.5 were prepared by adding the required quantity of 2.0 N NaOH to water to achieve a final sodium ion concentration of 20 mM and then titrating the solution with glacial acetic acid until the required pH was achieved. Aqueous AH+ or A solutions were prepared by diluting the methanol stock solution into the aqueous solutions of the required pH. CB[7] stock solutions (850 μM) were prepared by dissolving an appropriate amount of the solid in the aqueous solution of the required pH. The CB[7] stock solutions were titrated as described previously.47 For the binding isotherm experiments, small aliquots of the CB[7] stock solution were injected directly into 3 mL of the AH+/A solution with a gastight syringe. For stopped-flow experiments, a series of CB[7] solutions were prepared by diluting the stock solution into aqueous solutions of the required pH.Equipment
Absorption spectra were recorded on a Cary 100 UV-Vis spectrophotometer. Steady-state fluorescence measurements were performed on a PTI QM-40 spectrofluorimeter. Samples were excited at 365 nm and the emission was collected between 380 and 650 nm. A bandwidth of 2 nm was used for the excitation and emission monochromators. A baseline spectrum for a solution containing all chemicals except the fluorophore was subtracted from all emission spectra to obtain corrected spectra. All measurements were performed by maintaining the sample temperature at 20 °C. For the binding isotherm experiments, the area under each spectrum was integrated from 380 to 456 nm for the “blue” region and from 456 to 650 nm for the “green” region, corresponding to the emission of AH+ and A, respectively. These integrated intensities were then normalized by assuming unity for the integrated intensity in the absence of CB[7].Time-resolved fluorescence decays were recorded with an Edinburgh OB920 single photon counting system. The excitation source was a light emitting diode (EPLED-360, λex = 365 nm). The emission from the sample was collected at 405 or 510 nm using a monochromator with a bandwidth of 16 nm. The number of counts in the maximum intensity channel was 2000. The instrument response function (IRF) was recorded using a Ludox solution by collecting the emission at the excitation wavelength. The FAST (Edinburgh Instruments) software was used to fit the fluorescence decay traces. The IRF was reconvoluted with the decay during the fitting process. The quality of the fit was judged by the randomness of the residuals and the χ2 values (0.9–1.2).48 The data were fit to either a mono-exponential decay (i = 1, eqn (1)) or to a sum of two exponentials (i = 2, eqn (1)), where each species has a lifetime (τi) and a corresponding pre-exponential factor (Ai). A 10 × 10 mm quartz cell was used for the absorption, steady-state, and time-resolved fluorescence measurements.
 | (1) |
Binding dynamics studies were carried out with an Applied Photophysics SX20 stopped-flow system. The solutions were excited at 365 nm with a Hg–Xe vapor lamp. This wavelength was chosen because it corresponds to a peak of the Hg–Xe lamp and leads to a higher excitation efficiency of the sample, increasing the signal-to-noise ratio for the measurements. The excitation monochromator bandwidth was set to 2 nm. The monochromator wavelength was calibrated by comparing the wavelength reading for the maximum intensity reading for water with the wavelength for the maximum intensity provided by the manufacturer of the lamp. The emission was detected using an interference filter (385–423 nm) with a maximum at 405 nm for the “blue” region and a 515 nm cut-off filter for the green region. The solutions were mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in the mixing chamber. The temperature of the solutions was maintained at 20 °C throughout the experiment, and the samples were incubated at this temperature for 10 min before the start of an experiment. A minimum of 25 traces were averaged for each experiment performed on the stopped-flow. The intensity of the stopped-flow for a solution containing all chemicals except the fluorophore and CB[7] was taken as the baseline and subtracted from the stopped-flow traces to obtain the corrected traces.
1 ratio in the mixing chamber. The temperature of the solutions was maintained at 20 °C throughout the experiment, and the samples were incubated at this temperature for 10 min before the start of an experiment. A minimum of 25 traces were averaged for each experiment performed on the stopped-flow. The intensity of the stopped-flow for a solution containing all chemicals except the fluorophore and CB[7] was taken as the baseline and subtracted from the stopped-flow traces to obtain the corrected traces.
The stopped-flow traces were analyzed by fitting the individual traces to a sum of exponential functions (eqn (2)) or by using a global analysis method where all traces are simultaneously fit to a defined model. The fit to a sum of exponentials is defined by an offset (a0) and the sum of exponentials terms, each of which has a corresponding observed rate constant (kobsi) and an amplitude of ai.
| ΔI = a0 + a1e−kobs1t + a2e−kobs2t | (2) |
The analysis of the individual stopped-flow traces at pH 2.0 and 3.8 was done as follows: to obtain the rate constant for the slow relaxation time, the traces were fit to a mono-exponential function by starting the fit at incrementally longer times until the residuals became random and the observed rate constant was constant. The rate constant for the fast relaxation time was then obtained by fitting the traces to a sum of two exponentials and fixing the rate constant for the slow relaxation process. The stopped-flow traces at pH 5.0 and 5.5 were fit to a mono-exponential function to yield one relaxation time. In the global analysis method, all the kinetic traces for a particular experiment were fit simultaneously to a model defined in the Prokineticist II software from Applied Photophysics. The goodness of the fit was judged by the randomness of the residuals.
Results
The AH+/A absorption and emission spectra depend on the solution's pH. At pH 2.0, where only AH+ is present in the ground state, a small emission intensity is observed from AH+ around 400 nm in addition to the predominant emission centered at 510 nm from A formed adiabatically from excited AH+ (Fig. 1a). The emission from AH+ is absent at pH 6.0, which is two pH units higher than the pKa of AH+/A. At this pH, only A is present in solution. The absorption spectrum shows sharp peaks at pH 2.0 (Fig. 1b), whereas a broad absorption around 400 nm appears as the pH is raised (Fig. 1c and d). This broad absorbance is related to the presence of A.41 In the presence of 25 μM CB[7], where 91% AH+ (5 μM) is bound at pH 2.0, a red shift was observed in the absorption spectrum of AH+. At pH 3.8, with an approximately 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of AH+ and A in water, the shoulder around 400 nm decreased in the presence of CB[7], and the sharp peaks shifted to the same wavelengths observed at pH 2.0 in the presence of this host. These absorption spectra show that the equilibrium shifts toward AH+ when the guest is bound to CB[7]. At pH 5.5, the amount of AH+ is low (3%), and the absorption spectrum showed smaller changes in the presence of CB[7]. These results are consistent with the stabilization of AH+ when bound to CB[7].
2 mixture of AH+ and A in water, the shoulder around 400 nm decreased in the presence of CB[7], and the sharp peaks shifted to the same wavelengths observed at pH 2.0 in the presence of this host. These absorption spectra show that the equilibrium shifts toward AH+ when the guest is bound to CB[7]. At pH 5.5, the amount of AH+ is low (3%), and the absorption spectrum showed smaller changes in the presence of CB[7]. These results are consistent with the stabilization of AH+ when bound to CB[7].
The binding of AH+ with CB[7] was characterized at pH 2.0 where all of the guest molecules are protonated in water. Solubilization of CB[7] is enhanced in the presence of Na+ because cations bind to the portals of CB[7].27,49–51 The addition of Na+ cations was also required to adjust the solution's pH. The system is described by the equilibria between Na+ or AH+ with CB[7] (Fig. 2a). The competitive binding of Na+ to CB[7] was shown to slow the kinetics of AH+ binding with CB[7] and to decrease the amplitude of the kinetics (Fig. 2b). This behavior is the same as that previously reported for the 2-naphthyl-1-ethylammonium cation binding to CB[7].32 The smaller amplitude is due to the involvement of CB[7] in Na+ bound complexes. The slow down of the relaxation kinetics is a consequence of a slower bimolecular association process because of the lower effective concentration of free CB[7] in the presence of Na+ cations, while the dissociation is unaffected as it is a unimolecular reaction. Stopped-flow experiments were performed to determine the optimal Na+ cation concentration for the kinetic studies. The kinetics were followed in the “blue” region where AH+ emits because its excited state is not deprotonated owing to the higher pK*a of AH+@CB[7]. A concentration of 20 mM of Na+ cations was chosen for all experiments because the kinetics was sufficiently slow to be detected in stopped-flow experiments with reasonable amplitude.
Any parameter that is dependent on the concentration of CB[7] is an overall or apparent parameter because a fraction of the CB[7] molecules was non-reactive owing to the formation of CB[7] complexes with Na+ cations (Fig. 2a). The binding isotherms led to the determination of the overall binding constants (β), while the bimolecular rate constants for the reactions involving CB[7] are apparent rate constants and denoted k′. The individual equilibrium constants (K) or bimolecular rate constants (k) can be obtained following the procedure previously described.32 We chose to present the β and k′ values in the results section as these are the values derived directly from the experiments.
The addition of increasing concentrations of CB[7] to AH+ (1.0 μM) at pH 2.0 led to a decrease of the “green” emission of A around 510 nm and an increase of the AH+ emission below 450 nm (Fig. 2c). The dependencies of the intensities in the “blue” and “green” regions with the CB[7] concentration (Fig. 2d) were numerically fit to an overall equilibrium constant (β11, see ESI† for details) defined by the equations shown in Fig. 2a, where [CB[7]]GF corresponds to the guest-free CB[7] concentration that is not complexed to AH+. The residuals between the experimental data and the fits were random. The recovered average β11 values from two independent experiments were (4.92 ± 0.09) × 105 M−1 when the emission intensity for A was followed and (4.8 ± 0.2) × 105 M−1 when the intensity changes for AH+ were measured, leading to an overall average β11 value of (4.9 ± 0.1) × 105 M−1. The determination of the same β11 values for the two different emission bands and the presence of an isoemissive point support the assignment of the bands in the fluorescence spectra to AH+ and AH+@CB[7].
Binding isotherms were also measured at pH values of 3.8, 5.0, and 5.5 (Fig. S1 and Table S1 in the ESI†). The determined average β11 values from the binding isotherms measured for the “blue” and “green” emissions were (2.83 ± 0.03) × 105, (3.49 ± 0.09) × 104, and (1.52 ± 0.04) × 104 M−1 at pH values of 3.8, 5.0, and 5.5, respectively. At pH values of 3.8, 5.0, and 5.5, the percentage of AH+ is 61, 9, and 3%, while the percentage of A is 39, 91, and 97%, respectively. The decrease in the overall equilibrium constants as the pH was raised is a reflection of the lower equilibrium constant for the binding of A to CB[7] compared with that for the binding of AH+. The equilibrium constant for the binding of A to CB[7] can be calculated from the thermodynamic cycle shown in Scheme 1 since three of the equilibrium constants are known. It is important to note that the thermodynamic cycle is valid for overall equilibrium constants where the value for AH+ (βAH11) is the one determined at pH 2.0 and βA11 is related to the other equilibrium constants (eqn (3), see ESI† for derivation), leading to a value for βA11 of 390 ± 10 M−1, where the error is related to the measurement of βAH11. An attempt was made to measure directly the equilibrium constant between A and CB[7] at pH 12. The changes in the fluorescence intensity were small (Fig. S2 in the ESI†) and no saturation was achieved, which indicated the incomplete binding of A. The value of βA11 and the quantum yield of A in A@CB[7] are correlated, and for this reason, no unique value for βA11 could be obtained. Adequate fits were observed for βA11 values fixed between 100 and 700 M−1 (Fig. S3 in the ESI†), which are of the same order of magnitude as the value determined from the thermodynamic cycle.
 | (3) |
Time-resolved fluorescence experiments are used to identify fluorophores with different lifetimes; in the case of supramolecular systems, the same fluorophore in different environments can have different lifetimes.8,52 The decays for systems containing fluorophores with different lifetimes are fit to a sum of exponentials, where each term has an associated lifetime and pre-exponential factor Ai (eqn (1)). The Ai values are related to the abundance of each species; a positive value indicates the disappearance of the fluorophore, while a negative value indicates the formation of the fluorophore. The lifetime of excited A measured at 510 nm and pH 6.0 was 24.8 ± 0.1 ns. This value is of the same order of magnitude as the lifetimes previously determined in water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol (14 ns)43 or cyclohexane (25–33 ns).53 At pH 2.0, the kinetics at 510 nm for the emission of A showed a growth in kinetics with a lifetime of 1.0 ± 0.2 ns followed by a decay with a lifetime of 24.6 ± 0.1 ns (Fig. S4 and Table S2 in the ESI†). The growth corresponds to the adiabatic deprotonation of excited AH+ to form excited A, which decays with the same lifetime as excited A at the higher pH. This assignment at pH 2.0 is supported by the equal absolute values of the pre-exponential factors, which were −0.49 ± 0.02 and 0.51 ± 0.02 for the short- and long-lived components, respectively. The equal pre-exponential factors indicated that all the excited states of A were formed from AH+, as would be expected at a pH where the fluorophore is in the protonated form.
ethanol (14 ns)43 or cyclohexane (25–33 ns).53 At pH 2.0, the kinetics at 510 nm for the emission of A showed a growth in kinetics with a lifetime of 1.0 ± 0.2 ns followed by a decay with a lifetime of 24.6 ± 0.1 ns (Fig. S4 and Table S2 in the ESI†). The growth corresponds to the adiabatic deprotonation of excited AH+ to form excited A, which decays with the same lifetime as excited A at the higher pH. This assignment at pH 2.0 is supported by the equal absolute values of the pre-exponential factors, which were −0.49 ± 0.02 and 0.51 ± 0.02 for the short- and long-lived components, respectively. The equal pre-exponential factors indicated that all the excited states of A were formed from AH+, as would be expected at a pH where the fluorophore is in the protonated form.
In the presence of 16 μM CB[7] at pH 2.0, where all AH+ is bound, the fluorescence decay could only be measured at 410 nm because AH+ is stabilized in the complex and is the predominant species in the system. The decay was mono-exponential with a lifetime of 7.6 ± 0.1 ns, which corresponds to the emission of excited state AH+ complexed with CB[7]. This lifetime is not limited by the deprotonation of AH+@CB[7] because pH 2.0 is lower than both the pKCBa and pKCB*a values. In the presence of 2.6 μM CB[7], 50% of AH+ is bound to CB[7] and the remainder is free in water. For this reason, the fluorescence kinetics could be measured at 410 nm for the emission of AH+ and at 510 nm for the emission of excited A. The emission decay for AH+ at 410 nm led to the recovery of 0.9 ± 0.1 and 7.7 ± 0.1 ns lifetimes. The short lifetime corresponds to the deprotonation of AH+ in water, while the long lifetime corresponds to the emission of AH+ in the AH+@CB[7] complex. At 510 nm, where excited A emits, a growth with a 1.1 ± 0.1 ns lifetime was observed followed by a decay with a 24.5 ± 0.1 ns lifetime. This kinetics is the same as that observed for AH+ in water, and the absence of a longer-lived growth with a lifetime close to 8 ns suggested that AH+@CB[7] was not deprotonated during the excited state lifetime of AH+. Therefore, the intensity changes at 510 nm are diagnostic for the changes in the AH+ concentration in water and do not have a contribution from the concentration changes for AH+@CB[7].
The longest lifetime observed for the AH+/A system in the absence and presence of CB[7] is 25 ns, and the dynamics of the excited state occurs on a much faster time scale than the millisecond time scale for the formation of the AH+@CB[7] complex (see below). Therefore, the changes in emission intensity can be seen as instantaneous when analyzing the kinetics of AH+@CB[7] complex formation, and the excited state dynamics of AH+ is decoupled from the dynamics of CB[7] complex formation.
The kinetics for the formation of the AH+@CB[7] complex was studied in stopped-flow experiments. Two solutions, one containing CB[7] and a second containing AH+/A, were mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio. The concentrations stated are those for the final mixed solution. The kinetics was studied at pH 2.0, where only AH+ was present in water, and at pH 5.5, where A corresponds to 97% of the species present in water. A higher pH could not be used because the signals in the stopped-flow experiments became too small. The kinetics was also studied at intermediate pH values where a mixture of AH+ and A was present (pH 3.8: 61% AH+ and 39% A, pH 5.0: 9% AH+ and 91% A). At all pH values, mixing of the guest (AH+/A) with CB[7] led to a decrease of the emission intensity at 510 nm (Fig. 3a for pH 2.0 and Fig. S5 in the ESI†) and an increase of the emission intensity at 410 nm (Fig. S6 in the ESI†). It is important to note that at pH 2.0, the emission intensity at 510 nm corresponds to the concentration of AH+ in water, where excited A is formed from the deprotonation of excited AH+, as AH+ in the CB[7] complex is not deprotonated. The intensity increase at 410 nm corresponds to the formation of AH+@CB[7]. At pH 5.5, the emission intensity at 410 nm corresponds to the concentration of AH+@CB[7] because, at this pH, AH+ in water deprotonates readily. The intensity at 510 nm corresponds to the sum of the intensities of A in water and A@CB[7]. At the intermediate pH values of 3.8 and 5.0, the intensity at 510 nm corresponds to the concentrations of A in water, A@CB[7], and AH+ in water that forms excited A adiabatically. At all pH values, the same observed rate constants were recovered from the kinetics measured at 410 and 510 nm, indicating that the kinetics are coupled, as would be expected for the relaxation kinetics of a system where the various species are in equilibrium.
1 volume ratio. The concentrations stated are those for the final mixed solution. The kinetics was studied at pH 2.0, where only AH+ was present in water, and at pH 5.5, where A corresponds to 97% of the species present in water. A higher pH could not be used because the signals in the stopped-flow experiments became too small. The kinetics was also studied at intermediate pH values where a mixture of AH+ and A was present (pH 3.8: 61% AH+ and 39% A, pH 5.0: 9% AH+ and 91% A). At all pH values, mixing of the guest (AH+/A) with CB[7] led to a decrease of the emission intensity at 510 nm (Fig. 3a for pH 2.0 and Fig. S5 in the ESI†) and an increase of the emission intensity at 410 nm (Fig. S6 in the ESI†). It is important to note that at pH 2.0, the emission intensity at 510 nm corresponds to the concentration of AH+ in water, where excited A is formed from the deprotonation of excited AH+, as AH+ in the CB[7] complex is not deprotonated. The intensity increase at 410 nm corresponds to the formation of AH+@CB[7]. At pH 5.5, the emission intensity at 410 nm corresponds to the concentration of AH+@CB[7] because, at this pH, AH+ in water deprotonates readily. The intensity at 510 nm corresponds to the sum of the intensities of A in water and A@CB[7]. At the intermediate pH values of 3.8 and 5.0, the intensity at 510 nm corresponds to the concentrations of A in water, A@CB[7], and AH+ in water that forms excited A adiabatically. At all pH values, the same observed rate constants were recovered from the kinetics measured at 410 and 510 nm, indicating that the kinetics are coupled, as would be expected for the relaxation kinetics of a system where the various species are in equilibrium.
Two control experiments were performed: (i) comparison of the amplitudes for the kinetic and binding isotherm measurements and (ii) kinetic measurements with buffered and unbuffered solutions.
(i) It is important to establish whether the kinetics are measured for a sufficiently long time for the system to reach equilibrium. The normalized amplitudes from the stopped-flow experiments at 0.2 s were the same as the amplitudes from the binding isotherm experiments at all pH values (Fig. S7 and S8 in the ESI†). This result shows that the system is equilibrated within 0.2 s. Kinetic processes faster than the 1 ms mixing time of the stopped-flow experiment appear as initial offsets in the kinetic traces. In the current system, such a fast process would involve CB[7], and the amplitude of the offset would increase as the host concentration was raised. The kinetics at all pH values did not show a progressively increasing offset, indicating the absence of a relaxation process that occurred faster than 1 ms (Fig. S5 and S6 in the ESI†). Therefore, the whole kinetics of the system is captured in the stopped-flow experiments.
(ii) Experiments at pH 2.0 and 3.8 were performed in unbuffered solutions, where the pH was adjusted with the addition of HCl in the presence of 20 mM NaCl, while measurements at pH 5.0 and 5.5 required the use of sodium acetate as a buffer ([Na+] = 20 mM). A control experiment was performed at pH 4.3, where samples were prepared in the presence of HCl/NaCl or acetate buffer, and the kinetics for complex formation was measured. The dependence of the observed rate constants with CB[7] was similar, with a slightly lower slope observed for the experiments performed in acetate buffer (Fig. S9 in the ESI†). This difference is very similar to the variation observed between independent experiments, but it could also reflect the weak binding of acetic acid to CB[7]. However, this control experiment showed that the large differences in the dependencies of the observed rate constants with the CB[7] concentration (Fig. 3b) are not due to a counter-ion effect.
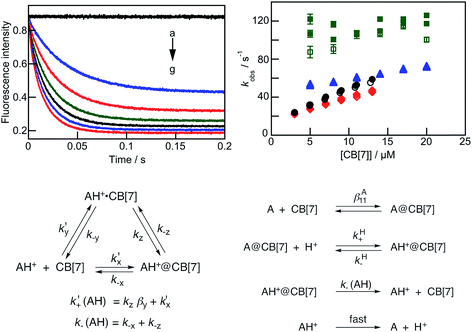
The kinetic behavior is different at the different pH values studied (Fig. 3b). A qualitative description will be provided first to guide the reader through the detailed analysis. The kinetics at pH 2.0 and 3.8 were fit to the sum of two exponentials, while the kinetics at pH 5.0 and 5.5 were mono-exponential. The relaxation kinetics for the lowest observed rate constant at pH 2.0 and 3.8 was slower than the relaxation kinetics at pH 5.5, and a steeper dependence of the observed rate constant with the CB[7] concentration was observed at the lower pH values. The errors for the measured rate constants are higher at pH 5.5 because the signal-to-noise ratio was lower, reflecting the smaller amount of CB[7] complex formed.
The slower kinetics observed at pH 2.0 is consistent with a mechanism where an exclusion complex is formed, denoted AH+·CB[7], in which the positively charged guest interacts with the carbonyl groups at the portal of CB[7] without the inclusion of the anthracene moiety into the CB[7] cavity in addition to a pathway where the anthracene moiety is included directly. Inclusion of the anthracene moiety to form AH+@CB[7] occurs either from the exclusion complex (pathway “z”, Fig. 3c) or directly (“pathway “x”).
At pH 5.5, deprotonated A is the predominant species in water (97%), but the hydronium ion concentration is sufficiently high to protonate the A@CB[7] complex and form AH+@CB[7]. The mechanism includes the fast equilibration between A and CB[7] followed by slow protonation and deprotonation steps (Fig. 3d). Deprotonation of AH+@CB[7] and the exit of AH+ from AH+@CB[7] are competitive, and the latter reaction needs to be accounted for in the fitting of the data.
The kinetics at pH 2.0 was fit to the sum of two exponentials, from which two observed rate constants, kobs1 and kobs2, were obtained. Similar dependencies were observed for the kobs2 values with the CB[7] concentration when the kinetics were measured for the “blue” and “green” emission intensity changes. The values for kobs1 were scattered, and this pattern is a reflection of the small amplitude of this component at low CB[7] concentrations. To improve the precision of the fits, the kinetics was fit to a mono-exponential function by starting the fit at incrementally longer delays after the start of the reaction until a constant value for kobs2 was obtained and the residuals were random (Fig. S10 and Table S3, see ESI† for details). These kobs2 values were then fixed for the fit of the entire kinetic trace to recover the values for kobs1.
In principle, the two relaxation times could correspond to two different processes. If kobs2 was related to the reaction of AH+ with CB[7] without the formation of an encounter complex, then the ratio of the slope of a linear dependence between kobs2 and the CB[7] concentration ((3.4 ± 0.2) × 106 M−1 s−1, average from two kinetic studies with the emission collected in the green region and one in the blue region) and the intercept (14.6 ± 0.8 s−1) should correspond to βAH11. However, this ratio ((2.3 ± 0.2) × 105 M−1) is much lower than the βAH11 value of (4.9 ± 0.1) × 105 M−1 determined from the binding isotherm studies. This analysis showed that the kinetics for the two relaxation processes are coupled.
Based on the precedence for the formation of exclusion complexes followed by cavity inclusion with CB[n]s as the host,27,30 the kinetics was analyzed using the mechanism shown in Fig. 3c. The formation of AH+·CB[7] was assumed to be in fast equilibrium. With this assumption, the two relaxation processes are related to the three equilibria (eqn (4) and (5)), where k′+(AH) and k−(AH) are defined in Fig. 3c:54
| kobs1 = k′y[CB[7]] + k−y | (4) |
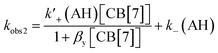 | (5) |
Fits of the dependence of kobs2 with the CB[7] concentration to eqn (5) (see Fig. S11 and Table S4 in the ESI† for individual values) led to an average βy value of (2.6 ± 0.6) × 104 M−1, a k′+(AH) value of (4.9 ± 0.4) × 106 M−1 s−1, and a k−(AH) value of 10 ± 1 s−1. The ratio between k′+(AH) and k−(AH) is (4.9 ± 0.6) × 105 M−1, which is equal to the βAH11 value ((4.9 ± 0.1) × 105 M−1) determined from the binding isotherm. The equality of these values suggests that the mechanism proposed is consistent with the kinetic and the binding isotherm data.
The kobs1 values increased with the CB[7] concentration; however, the data had large errors and showed significant scatter, indicating that fitting of the data was not warranted (Fig. S12 in the ESI†). The value of k−y is estimated to be between 100 and 130 s−1, which is ten times higher than the rate constant for the exit of AH+ from the inclusion complex (k−(AH) = 10 s−1), supporting the assumption that the formation of the exclusion complex occurs as a fast equilibrium. The value for ky estimated from the βy and k−y values is between 2.7 × 106 and 3.5 × 106 M−1 s−1, which would lead to an increment for the kobs1 value of ca. 30 s−1 for a 10 μM increase in the CB[7] concentration. This increment is within the scatter observed for the experimental data.
The data at pH 5.5 were analyzed using a global analysis method (Scheme S1 in the ESI†), where the kinetics at all CB[7] concentrations for two independent experiments collected for the “green” emission were analyzed simultaneously. The data from the kinetics in the “blue” region were not used because of the poor signal-to-noise ratio.
The value for the equilibrium constant for A@CB[7] was fixed as 390 M−1, and this equilibrium was assumed to be fast. Assuming that the association rate constant of A with CB[7] will be at least as high as the overall association rate constant for AH+ of 4.9 × 106 M−1 s−1, then the dissociation rate constant for A from A@CB[7] will be at least 1.3 × 104 s−1, which is ten times faster than the time resolution of the stopped-flow experiment. This calculation is consistent with the assumption of a fast equilibrium for A@CB[7].
The dissociation of AH+@CB[7] needs to be included in the model because the value for the rate constant of this process (10 s−1) corresponds to 10% of the observed rate constant. This value was also fixed in the model. The protonation and deprotonation reaction for A/AH+ in water is faster than the time resolution of the experiment, and the concentration of the hydronium ion is constant as the solution was buffered. For this reason, the deprotonation reaction for AH+ in water is not included in the model used for fitting the kinetics.
Global analysis of the kinetics at pH 5.5 (see Fig. S13 in the ESI† for the residuals) led to a recovery of the protonation rate constant (kH+) of (1.5 ± 0.4) × 109 M−1 s−1 for A@CB[7] and a deprotonation rate constant of (kH−) of 89 ± 7 s−1 for AH+@CB[7]. The pKCBa value calculated from these rate constants is 7.3 ± 0.2, which is in agreement with the reported value of 7.1 ± 0.2 determined from a pH titration experiment.38
A quantitative analysis of the kinetics at pH 3.8 and 5 is not feasible because the model requires the inclusion of both the low and high pH mechanisms observed for the binding of AH+ and A; the model would include too many parameters to fit the data. However, the changes can be explained qualitatively based on the relative contributions from the formation of the exclusion complex AH+·CB[7] and the complex with neutral A, A@CB[7]. The overall equilibrium constant for the formation of the former is 69 times higher than that for the latter. At pH 3.8, where 61% of the guest in water is in the protonated form and the remaining 39% is deprotonated, the kinetics is dominated by the binding of AH+ with CB[7] and the observed decay did not fit to a mono-exponential function. However, the amplitude of the fast component is smaller at pH 3.8 than at pH 2 (Table S5 in the ESI†). This difference increased from 11% for a CB[7] concentration of 5 μM to 32% for a CB[7] concentration of 13 μM. This increase is expected because the formation of A@CB[7] will be more prominent at a higher CB[7] concentration. The formation of A@CB[7] is followed by immediate protonation of the complex (∼2.4 × 105 s−1) because of the high hydronium ion concentration at this pH. This reaction path leads to a decrease in the contribution from AH+@CB[7] formation through the exclusion complex. This effect is observed as a decrease in the slope for the dependence of kobs2 with the CB[7] concentration without a large change in the intercept.
The kinetics at pH 5 was adequately fit to a mono-exponential function. In water, 9% of the guest is in the form of AH+ while 91% corresponds to A. The kinetics is dominated by the binding of A, but a slow down was observed for the kinetics when compared with the kinetics at pH 5.5. This slow down was caused by the formation of the AH+·CB[7] exclusion complex that removes A and free CB[7] from solution. The lower free concentrations of A and CB[7] decrease the amount of AH+@CB[7] formed through the faster reaction pathway, which is the protonation of the A@CB[7] complex.
Discussion
The guest binding dynamics of AH+ with CB[7] can be compared with the dynamics of previously studied guests. 2-Naphthyl-1-ethylammonium (Scheme 2) has a positive charge located in one extreme of the molecule in a similar fashion to AH+, whereas the positive charge in berberine is centrally located. In both cases, the kinetics was associated to one relaxation process without the observing the formation of an exclusion complex.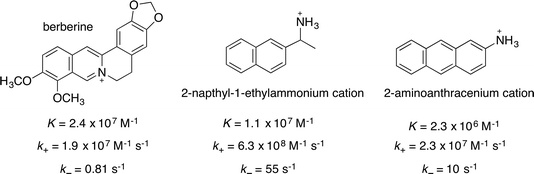 | ||
| Scheme 2 Structure, equilibrium constants and association and dissociation rate constants for the binding of berberine,34 the 2-naphthyl-1-ethylammonium cation32 and AH+ with CB[7]. The values of K and k+ for AH+@CB[7] were calculated from the overall values (see text). | ||
The equilibrium constant KAH was calculated to be (2.3 ± 0.3) × 106 M−1 (eqn (6)) using the previously determined values of 130 ± 10 M−1 and 21 ± 2 M−1 for the binding of the first and second Na+ cation to CB[7],32 and the average β11 value of (4.9 ± 0.1) × 105 M−1. The same multiplication factor was used to calculate the value of the association rate constant (k+(AH)) as (2.3 ± 0.2) × 107 M−1 s−1 from the overall association rate constant k′+(AH). It is important to note that the latter value includes the pathway for the formation of the exclusion complex.
| KAH = β11(1 + K01[Na] + K01K02[Na]2) | (6) |
A comparison of the binding of these three guests to CB[7] shows that the location of the positive charge and the size of the hydrophobic moiety of the guest influence the binding dynamics. The two modes of association of AH+ with CB[7], i.e. direct inclusion and formation of the exclusion complex, are probably related to the directionality of the approach of the guest with respect to the portal of CB[7]. Direct inclusion likely occurs when the anthracene moiety approaches the portal, whereas the exclusion complex is formed when the positive charge on the amino group interacts first with the carbonyl groups on the rim of the portal. In the case of the 2-naphthyl-1-ethylammonium cation, the guest is sufficiently small that if the exclusion complex is formed, the guest can rotate and enter the cavity. In this case, the rate constant of inclusion (kz in Fig. 3c) is higher than the dissociation of the exclusion complex (k−y), the association rate constant is high, and the exclusion complex is not detected as a defined intermediate. The association rate constant for AH+ is a factor of ∼25 lower than that of the 2-naphthyl-1-ethylammonium cation, which accounts for the formation of an exclusion complex where the dissociation of the exclusion complex is competitive with inclusion. The dissociation rate constant is a factor of ∼5 lower for AH+ than for the 2-naphthyl-1-ethylammonium cation. This slow-down is probably related to the larger hydrophobic moiety of AH+.
The aromatic moiety of berberine is included in the CB[7] cavity,34 and the central location of the charge likely precludes the formation of an exclusion complex. The complexation of berberine to CB[7] was shown to occur through constrictive binding, where the CB[7] needs to be distorted for inclusion of the guest to occur. This stereochemical effect led to lower association and dissociation rate constants. The association rate constant for berberine and AH+ are the same, but different mechanisms led to these values being lower than the association rate constant for the 2-naphthyl-1-ethylammonium cation. Distortion of the host is also responsible for the lower dissociation rate constant observed for berberine compared to those of AH+ and the 2-naphthyl-1-ethylammonium cation. These results show that the binding dynamics cannot be predicted from the values of the equilibrium constants because the mechanism for binding differs for the three guests. Berberine has a similar equilibrium constant to the 2-naphthyl-1-ethylammonium cation, but the association and dissociation rate constants of berberine are decreased to a similar extent because of the constricted binding. On the other hand, AH+ has a lower equilibrium constant because of the slow down of the association process where the exclusion complex is formed, but the dissociation rate constant is affected to a lesser extent because no constricted binding is operating. It is important to note that in the case of cyclohexylmethylamine binding to the smaller CB[6], the formation of an exclusion complex and constrictive binding were postulated, leading to very slow kinetics,30,31 showing that the binding dynamics with CB[n]s can occur over very different time scales.
The role of the protonation of the guest was previously studied for the cyclohexylmethylamine/CB[6] system, where the binding dynamics of the neutral and positively charged guest was uncoupled from the protonation/deprotonation dynamics.30,31 In the case of AH+ and A binding to CB[7], the binding dynamics is coupled to the protonation/deprotonation reactions for the CB[7]-bound guest. In both systems, the dynamics is faster for the formation of the CB[n] complex with the neutral guest. However, in the case of AH+/A binding to CB[7], it was possible to measure the kinetics of the system at different pH values. These studies led to the determination of the different mechanisms, where an exclusion complex is formed when AH+ binds to CB[7], whereas for A, complexation is fast and is followed by protonation of the complex (Scheme 3).
The protonation rate constant for ammonia in water is 4.3 × 1010 M−1 s−1,55 and this value constitutes the highest possible rate constant for the protonation of A in water, which is unknown. The protonation rate constant for A@CB[7] of 1.5 × 109 M−1 s−1 is ∼30 times lower than this upper limit, suggesting that protonation of A@CB[7] is not significantly impeded, which is consistent with the location of the amino group at the portal of CB[7]. The lower value for the protonation rate constant for A@CB[7] is probably related to fact that the approach of the hydronium ion towards the sides of CB[7] or the portal that does not contain the amino group leads to unproductive encounter complexes. In this respect, the protonation rate constant for a guest where the acid/base group was exposed to the water phase while a portion of the guest was bound to CB[7] was the same as for the guest in water,56 probably because the attack of the hydronium ion was not impeded. The deprotonation rate constant of AH+@CB[7] is higher (89 s−1) than the rate constant for the exit of AH+ from AH+@CB[7] (10 s−1). However, the deprotonation reaction is not observable at low pH values because the protonation process is too fast. For example, at pH 2.0, the protonation process for A@CB[7] has a pseudo-first order rate constant of 1.5 × 107 s−1.
In conclusion, the studies on the binding dynamics of AH+ and A with CB[7] provided further evidence that different mechanisms occur for the binding of guests with CB[n]. The binding dynamics of a neutral guest was shown to be faster than that for the corresponding positively charged guest. However, the binding constant is higher for the charged guest than for the neutral guest, mainly because of the charge–dipole interaction between the guest and the carbonyl groups at the portal of CB[n]. The size of the guest and the position of the positive charge on the guest affect the type of mechanism for the binding dynamics and affect the magnitude of the association and dissociation rate constants. Positive charges located at one end of the guest are more likely to lead to the formation of exclusion complexes when compared to molecules with centrally located positive charges. In addition, the requirement for distortion of CB[n] to accommodate the guest can lead to a significant slow down of the dynamics, but has a much smaller effect on the equilibrium constant as the required distortions of the host will occur for both the association and dissociation processes.
The coupling of the binding dynamics of A@CB[7] and AH+@CB[7] to the deprotonation and protonation reactions of these complexes made it possible to measure the protonation and deprotonation rate constants. The determination of these rate constants showed that the pKa shift observed for the CB[7]-bound guest was due mainly to a decrease in the deprotonation rate constant because of the stabilization of the charged species. This result has direct implications for the use of CB[n]s in any application, such as in catalysis, where the lifetime of a charged species is important.
Acknowledgements
This work was funded by the Natural Sciences and Engineering Council of Canada in the form of Discovery (DG) and Research Tools and Instrument (RTI) grants.References
- J. W. Lee, S. Samal, N. Selvapalam, H.-J. Kim and K. Kim, Acc. Chem. Res., 2003, 36, 621–630 CrossRef CAS PubMed.
- J. Lagona, P. Mukhopadhyay, S. Chakrabarti and L. Isaacs, Angew. Chem., Int. Ed., 2005, 44, 4844–4870 CrossRef CAS PubMed.
- L. Isaacs, Acc. Chem. Res., 2014, 47, 2052–2062 CrossRef CAS PubMed.
- R. N. Dsouza, U. Pischel and W. M. Nau, Chem. Rev., 2011, 111, 7941–7980 CrossRef CAS PubMed.
- Y. H. Ko, I. Hwang, D.-W. Lee and K. Kim, Isr. J. Chem., 2011, 51, 506–514 CrossRef CAS PubMed.
- W. M. Nau, M. Florea and K. I. Assaf, Isr. J. Chem., 2011, 51, 559–577 CrossRef CAS PubMed.
- E. Masson, X. Ling, R. Joseph, L. Kyeremeh-Mensah and X. Lu, RSC Adv., 2012, 2, 1213–1247 RSC.
- C. Bohne, Chem. Soc. Rev., 2014, 43, 4037–4050 RSC.
- N. Vallavoju and J. Sivaguru, Chem. Soc. Rev., 2014, 43, 4084–4101 RSC.
- W. L. Mock and N. Y. Shih, J. Org. Chem., 1986, 51, 4440–4446 CrossRef CAS.
- G. Parvari, O. Reany and E. Keinan, Isr. J. Chem., 2011, 51, 646–663 CrossRef CAS PubMed.
- B. C. Pemberton, R. Raghunathan, S. Volla and J. Sivaguru, Chem.–Eur. J., 2012, 18, 12178–12190 CrossRef CAS PubMed.
- K. I. Assaf and W. M. Nau, Chem. Soc. Rev., 2015, 44, 394–418 RSC.
- K. Kim, N. Selvapalam, Y. H. Ko, K. M. Park, D. Kim and J. Kim, Chem. Soc. Rev., 2007, 36, 267–279 RSC.
- D. H. Macartney, Isr. J. Chem., 2011, 51, 600–615 CrossRef CAS PubMed.
- S. Walker, R. Oun, F. J. McInnes and N. J. Wheate, Isr. J. Chem., 2011, 51, 616–624 CrossRef CAS PubMed.
- I. Ghosh and W. M. Nau, Adv. Drug Delivery Rev., 2012, 64, 764–783 CrossRef CAS PubMed.
- S. Liu, C. Ruspic, P. Mukhopadhyay, S. Chakrabarti, P. Y. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2005, 127, 15959–15967 CrossRef CAS PubMed.
- W. Jiang, Q. Wang, I. Linder, F. Klautzsch and C. A. Schalley, Chem.–Eur. J., 2011, 17, 2344–2348 CrossRef CAS PubMed.
- G. Ghale and W. M. Nau, Acc. Chem. Res., 2014, 47, 2150–2159 CrossRef CAS PubMed.
- H. Yang, B. Yuan, X. Zhang and O. A. Scherman, Acc. Chem. Res., 2014, 47, 2106–2115 CrossRef CAS PubMed.
- A. Hennig, H. Bakirci and W. M. Nau, Nat. Methods, 2007, 4, 629–632 CrossRef CAS PubMed.
- R. N. Dsouza, A. Hennig and W. M. Nau, Chem.–Eur. J., 2012, 18, 3444–3459 CrossRef CAS PubMed.
- E. A. Appel, J. del Barrio, X. J. Loh and O. A. Scherman, Chem. Soc. Rev., 2012, 41, 6195–6214 RSC.
- J. del Barrio, P. N. Horton, D. Lairez, G. O. Lloyd, C. Toprakcioglu and O. A. Scherman, J. Am. Chem. Soc., 2013, 135, 11760–11763 CrossRef CAS PubMed.
- W. L. Mock and N. Y. Shih, J. Am. Chem. Soc., 1989, 111, 2697–2699 CrossRef CAS.
- R. Hoffmann, W. Knoche, C. Fenn and H.-J. Buschmann, J. Chem. Soc., Faraday Trans., 1994, 1507–1511 RSC.
- W. L. Mock, Top. Curr. Chem., 1995, 175, 1–24 CrossRef CAS.
- R. Neugebauer and W. Knoche, J. Chem. Soc., Perkin Trans. 2, 1998, 529–534 RSC.
- C. Marquez and W. M. Nau, Angew. Chem., Int. Ed., 2001, 40, 3155–3160 CrossRef CAS.
- C. Márquez, R. R. Hudgins and W. M. Nau, J. Am. Chem. Soc., 2004, 126, 5806–5816 CrossRef PubMed.
- H. Tang, D. Fuentealba, Y. H. Ko, N. Selvapalam, K. Kim and C. Bohne, J. Am. Chem. Soc., 2011, 133, 20623–20633 CrossRef CAS PubMed.
- Z. Miskolczy and L. Biczók, Phys. Chem. Chem. Phys., 2014, 16, 20147–20156 RSC.
- Z. Miskolczy and L. Biczók, J. Phys. Chem. B, 2014, 118, 2499–2505 CrossRef CAS PubMed.
- Z. Miskolczy, J. G. Harangozó, L. Biczók, V. Wintgens, C. Lorthioir and C. Amiel, Photochem. Photobiol. Sci., 2014, 13, 499–508 CAS.
- W. L. Mock and J. Pierpont, J. Chem. Soc., Chem. Commun., 1990, 1509–1511 RSC.
- N. Barooah, J. Mohanty, H. Pal and A. C. Bhasikuttan, Proc. Natl. Acad. Sci., India, Sect. A, 2014, 84, 1–17 CrossRef CAS.
- R. Wang, L. Yuan and D. H. Macartney, Chem. Commun., 2005, 5867–5869 RSC.
- C. Klöck, R. N. Dsouza and W. M. Nau, Org. Lett., 2009, 11, 2595–2598 CrossRef PubMed.
- N. Basilio, L. García-Río, J. A. Moreira and M. Pessêgo, J. Org. Chem., 2010, 75, 848–855 CrossRef CAS PubMed.
- S. G. Schulman, P. J. Kovi, G. Torosian, H. McVeigh and D. Carter, J. Pharm. Sci., 1973, 62, 1823–1826 CrossRef CAS PubMed.
- E. Vander Donckt and G. Porter, Trans. Faraday Soc., 1968, 64, 3218–3223 RSC.
- K. Rotkiewicz and Z. R. Grabowski, Trans. Faraday Soc., 1969, 65, 3263–3278 RSC.
- A. Day, A. P. Arnold, R. J. Blanch and B. Snushall, J. Org. Chem., 2001, 66, 8094–8100 CrossRef CAS PubMed.
- J. Kim, I.-S. Jung, S.-Y. Kim, E. Lee, J.-K. Kang, S. Sakamoto, K. Yamaguchi and K. Kim, J. Am. Chem. Soc., 2000, 122, 540–541 CrossRef CAS.
- C. Marquez, F. Huang and W. M. Nau, IEEE Trans. Nanobiosci., 2004, 3, 39–45 CrossRef.
- S. Yi and A. E. Kaifer, J. Org. Chem., 2011, 76, 10275–10278 CrossRef CAS PubMed.
- C. Bohne, R. W. Redmond and J. C. Scaiano, in Photochemistry in Organized and Constrained Media, ed. V. Ramamurthy, VCH Publishers, New York, 1991, pp. 79–132 Search PubMed.
- R. Behrend, E. Meyer and F. Rusche, Justus Liebigs Ann. Chem., 1905, 339, 1–37 CrossRef PubMed.
- H.-J. Buschmann, E. Cleve and E. Schollmeyer, Inorg. Chim. Acta, 1992, 193, 93–97 CrossRef CAS.
- Y.-M. Jeon, J. Kim, D. Whang and K. Kim, J. Am. Chem. Soc., 1996, 118, 9790–9791 CrossRef CAS.
- C. Bohne, in Supramolecular Photochemistry: Controlling Photochemical Processes, ed. V. Ramamurthy and Y. Inoue, John Wiley & Sons, Singapore, 2011, pp. 1–51 Search PubMed.
- N. Nijegorodov, R. Mabbs and D. P. Winkoun, Spectrochim. Acta, Part A, 2003, 59, 595–606 CrossRef CAS.
- C. F. Bernasconi, Relaxation Kinetics, Academic Press, Inc., New York, 1976 Search PubMed.
- M. Eigen, Angew. Chem., Int. Ed. Engl., 1964, 3, 1–19 CrossRef PubMed.
- N. Basílio, C. A. T. Laia and F. Pina, J. Phys. Chem. B, 2015, 119, 2749–2757 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and purification of cucurbit[7]uril; model for the fitting of binding isotherms and binding isotherms at different pH values; singlet excited state lifetimes for AH+/A in water and in the presence of CB[7]; kinetics for AH+/A binding to CB[7] and models used for fitting. See DOI: 10.1039/c5fd00095e |
| This journal is © The Royal Society of Chemistry 2015 |