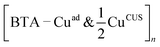Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio modeling of the bonding of benzotriazole corrosion inhibitor to reduced and oxidized copper surfaces
Anton
Kokalj
*
Department of Physical and Organic Chemistry, Jožef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia. E-mail: tone.kokalj@ijs.si; Web: http://www.ijs.si/ijsw/K3-en/Kokalj Fax: +386-1-251-93-85; Tel: +386-1-477-3523
First published on 2nd February 2015
Abstract
The bonding of benzotriazole—an outstanding corrosion inhibitor for copper—on reduced and oxidized copper surfaces is discussed on the basis of density functional theory (DFT) calculations. Calculations reveal that benzotriazole is able to bond with oxide-free and oxidized copper surfaces and on both of them it bonds significantly stronger to coordinatively unsaturated Cu sites. This suggests that benzotriazole is able to passivate the reactive under-coordinated surface sites that are plausible microscopic sites for corrosion attack. Benzotriazole can adsorb in a variety of different forms, yet it forms a strong molecule–surface bond only in deprotonated form. The bonding is even stronger when the deprotonated form is incorporated into organometallic adcomplexes. This is consistent with existing experimental evidence that benzotriazole inhibits corrosion by forming protective organometallic complexes. It is further shown that adsorption of benzotriazole considerably reduces the metal work function, which is a consequence of a large permanent molecular dipole and a properly oriented adsorption structure. It is argued that such a pronounced effect on the work function might be relevant for corrosion inhibition, because it should diminish the anodic corrosion reaction, which is consistent with existing experimental evidence that benzotriazole, although a mixed type inhibitor, predominantly affects the anodic reaction.
1 Introduction
There are various ways of corrosion protection and one of them is by means of corrosion inhibitors, which are substances that have the ability to considerably slow down the corrosion of metals and alloys by decreasing the rate of corrosion processes. Among efficient corrosion inhibitors are also organic molecules. It is commonly believed that strong interaction between an organic inhibitor molecule and a substrate is very important for achieving the inhibitory effect.1–3 In particular, Bockris stated that organic molecules must be adsorbed to become inhibitors.3 Despite the soundness of the strong adsorption premise, DFT (density functional theory) calculations have revealed—contrary to what might have been intuitively expected—that some outstanding inhibitor molecules, such as benzotriazole and several other azoles, interact only weakly in their intact form with substrates.4–6 For example, an intact benzotriazole molecule bonds only by about 0.5 eV to a Cu(111) surface,5,6 which is similar in strength to solvation interaction between benzotriazole and water.7,8 This implies that the net adsorption energy at the water/solid interface should be rather small, which may seem surprising, because if the bonding is that weak then aggressive corrosive species would easily replace benzotriazole from the surface (if it would adsorb at all). How then, can benzotriazole act against corrosion?Benzotriazole has been used for a long time as one of the most efficient copper corrosion inhibitors1,9–11 and there are numerous studies of its inhibition action on copper. Nevertheless, Finšgar and Milošev stated in a recent review:11 “… the exact mechanism of benzotriazole action on copper materials still remains to be elucidated. It is important to clarify why benzotriazole, and not other organic molecules with similar electronic structure, imparts corrosion protection. The answer to this question will provide the basis for predicting new and more effective corrosion inhibitors.”
The aim of this paper is to discuss the adsorption behavior of benzotriazole—as elucidated by DFT calculations—on reduced and oxidized copper surfaces (for the latter only the Cu(I) oxidation state is currently considered). The issue seems relevant, because controversial suggestions exist in the literature,11i.e., according to some researchers the presence of oxides is important,12–14 while others claimed that their presence is not needed for the adsorption of benzotriazole.15,16 It has to be emphasized that adsorption behavior is not synonymous with the mechanism of corrosion inhibition, yet it may nevertheless provide some useful information and insight. The literature is replete with numerous suggestions about possible adsorption mechanisms of benzotriazole on copper.11 There are at least two reasons of why this is so: the first is due to complexity of the investigated system. The interpretation of experimental data therefore involves various degree of assumptions and different assumptions may lead to different conclusions. The second reason is due to—as is argued in this paper—nontrivial adsorption behavior of benzotriazole, because it can adsorb in a variety of different forms. It all depends on the details and perhaps this is one of the strengths of benzotriazole and other inhibitor molecules; depending on different conditions they will adopt one of several possible forms and thus sustain various situations.
There are several important points to keep in mind when considering the results presented in this paper. The most important is that due to obvious modeling reasons the presented results refer to the solid/vacuum interface (solvent effects are estimated a posteriori when explicitly stated so), whereas in the context of corrosion the solid/water is the relevant interface. Apart from the fact that solvent considerably affects the energetics of adsorption, there is another distinction between the adsorption at solid/vacuum and solid/water interfaces. The adsorption at the latter is competitive (or substitutional), because the surface is always covered with solvent molecules and other possible species. So a given molecule will adsorb only if its adsorption is competitive enough to substitute other species from the surface. In contrast, at the solid/vacuum interface the surface is clean and the molecule adsorbs readily (say that surface temperature is low enough) unless its interaction with the surface is repulsive.
The paper is organized as follows: Section 2 contains a brief description of computational method along with some definitions, while Section 3 deals with bare metallic copper surfaces and reviews the pertinent computational DFT studies. These data are put into a new context and the relevance of the work function reduction upon adsorption of inhibitor is emphasized. Oxidized copper surfaces are considered in Section 4, where significant new results are presented. Section 5 finally contains the conclusions.
2 Technical details
2.1 Definitions
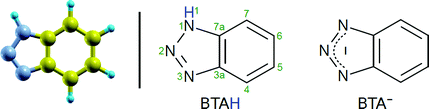
Term “copper surface” shall implicitly indicate the bare (reduced) metallic copper surface (oxidation state of 0); the oxidized surface shall be explicitly referred to as “oxidized”. The labels BTAH and BTA indicate the intact and dissociated (without H1 atom/proton) benzotriazole molecule, respectively (atom numbering and skeleton structures of neutral BTAH molecule and deprotonated BTA− anion are shown in Scheme 1). BTAH(g), BTAH(solv), BTAH(ads) stand for gas-phase, solvated, and adsorbed molecule, respectively (and analogously for other species). Notation BTA–Cu refers to organometallic complex, while the stand-alone chemisorbed form is designated as BTA(ads). Other labels are defined when first used.2.2 Computational
DFT calculations were performed with the plane-wave pseudo-potential method as implemented in the PWscf code from the Quantum ESPRESSO distribution,17 using the ultrasoft pseudopotentials18 and plane wave basis set with a kinetic energy cut-off = 30 Ry (240 Ry for the charge-density), while molecular graphics were produced by the XCRYSDEN19 graphical package. Calculations were performed with PBE20 and reparametrized PBE-D′ energy functionals; the former was used for chemisorption and the latter for parallel physisorption modes. PBE-D′ includes a semi-empirical dispersion correction of Grimme,21,22 which was reparametrized23 to match the experimental adsorption energy of benzene on Cu(111). Cu surfaces were modeled by periodic slabs with the in-plane lattice spacing fixed at the calculated equilibrium Cu bulk lattice parameter (3.67 Å for PBE24 and 3.64 Å for PBE-D′23). For Cu2O surfaces, the PBE calculated equilibrium bulk lattice parameter of 4.35 Å was used. Spin polarization was used when needed. For further computational details see our previous publications, in particular ref. 8 and also ref. 7.Molecular adsorption energies (at solid/vacuum interface) were calculated as:
| Eads = EA/surf − (Esurf + EA). | (1) |
3 Adsorption of benzotriazole on reduced copper surfaces: bare Cu(hkl) and defects thereon
Adsorption structures of benzotriazole on bare copper surfaces have been studied in detail by means of DFT calculations.5–8,23,25–28 The main findings of these studies are briefly explained below (Section 3.1 and, in part, also 3.2) to put them in context for the current discussion paper.3.1 Description of various DFT identified adsorption modes
Benzotriazole can adsorb either molecularly as BTAH(ads) or dissociatively as BTA(ads) + H(ads) (cleavage of N1–H bond). While the BTAH(ads) bonds weakly, the BTA(ads) is strongly chemisorbed on copper surfaces. The calculated activation energy of dissociation for weakly chemisorbed BTAH is about 1.1 eV on Cu(111), but on more open surfaces and step-edge defects the activation energy decreases below 1 eV.27 Dissociative adsorption of benzotriazole is experimentally well established, because it has often been observed that the H1 atom of benzotriazole is removed upon chemisorption on copper surfaces even under ultra high vacuum conditions.15,28–31Structures of different identified adsorption modes of BTAH(ads) and BTA(ads) are shown in Fig. 1 and binding energies as a function of coordination number of surface Cu atoms involved in the adsorption site are shown in Fig. 2.
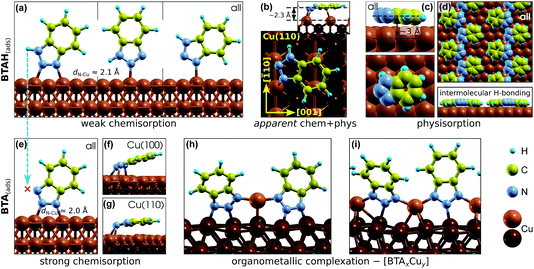 | ||
| Fig. 1 Various adsorption forms of benzotriazole on copper surfaces identified by means of DFT calculations5–8,23,25 (label “all” indicates that the form exists on all (several) Cu surfaces). Intact molecular forms (BTAH(ads), top row) and dissociated forms (BTA(ads), bottom row). (a) Weakly chemisorbed modes of BTAH bonded perpendicularly to the surface via triazole nitrogen atoms (dN–Cu stands for N–Cu bond length).5,6 (b) More strongly bonded parallel adsorption mode of BTAH on Cu(110) that is roughly oriented along the [001] direction; this mode was ascribed as apparent chemisorption + physisorption mode (labeled as “apparent chem + phys”).6 (c) Physisorption mode with BTAH molecular plane nearly parallel to the surface6,7 and (d) intermolecular H-bonded networks of physisorbed BTAH;7 this lateral H-bonding stabilizes the physisorbed BTAH by about 0.5 eV. (e) Strongly chemisorbed BTA(ads) bonded perpendicularly to the surface;7,8 on Cu(100) and Cu(110) also highly tilted (f) and almost parallel (g) variants were identified.8 (h and i) Benzotriazole–copper organometallic complexes: (h) [BTA–Cu–BTA] dimer25 and (i) [BTA–Cu]n polymer.7 | ||
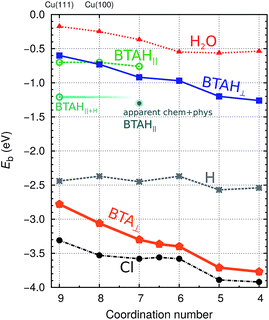 | ||
| Fig. 2 Dependence of low coverage adsorption (binding) energies of BTAH,6 BTA, Cl, H,8 and H2O-molecule on coordination number of surface Cu atoms at adsorption site (parallel BTAH modes are calculated with the PBE-D′ functional, while for all the others the PBE is used). Only the stablest identified adsorption energies at a given coordination number are reported [for BTAH, BTA, Cl, and H see ref. 6 and 8, whereas for H2O the points correspond to adsorption on (111), (100), (110), and adtetramer, adtrimer, and addimer defects on Cu(111)]. | ||
3.2 Adsorption characteristics
Adsorption forms of benzotriazole can be classified into four types: (i) weakly chemisorbed BTAH(ads), (ii) physisorbed BTAH(ads) (including the H-bonding networks of Fig. 1d), (iii) stand-alone strongly chemisorbed BTA(ads), and (iv) BTA–Cu adcomplexes. These four types display rather different adsorption features and for the first three types several adsorption related properties are listed in Scheme 2 (the BTA–Cu adcomplexes are treated separately later).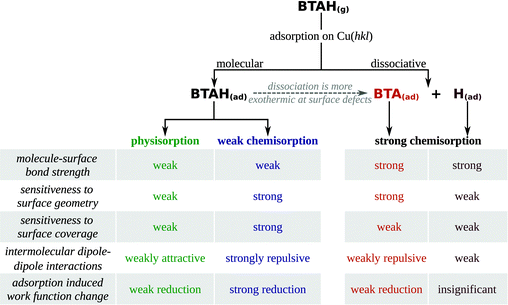 | ||
| Scheme 2 Characteristics of molecular and dissociative adsorption of benzotriazole on copper surfaces. | ||
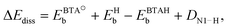 | (2) |
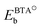 , EHb, and EBTAHb are binding energies of respective species to copper surface; DN1–H is the N1–H bond strength (4.7 eV). For Cu(111) the respective numbers in the limit of zero-coverage are: ΔEdiss = −2.8 + (−2.4) − (−0.6) + 4.7 eV = 0.1 eV.
, EHb, and EBTAHb are binding energies of respective species to copper surface; DN1–H is the N1–H bond strength (4.7 eV). For Cu(111) the respective numbers in the limit of zero-coverage are: ΔEdiss = −2.8 + (−2.4) − (−0.6) + 4.7 eV = 0.1 eV.
In order for dissociation to be exothermic, the following criterion has to be met (cf.eqn (2)):
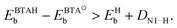 | (3) |
The bonding of H is rather insensitive to surface details and on Cu(hkl) the EHb ∈ [−2.4, −2.5] eV (see Fig. 2). Hence the BTA(ads) has to bond by about 2.3 eV stronger to the surface than BTAH(ads) for dissociation to be exothermic. This criterion is met on open surfaces and low coordinated defects, because the enhancement of the molecule–surface bond strength is larger for BTA(ads) than for BTAH(ads) as the coordination number of surface Cu atoms involved in the adsorption site decreases (see Fig. 2); consequently dissociation energy becomes more exothermic in the same direction (Fig. 3).
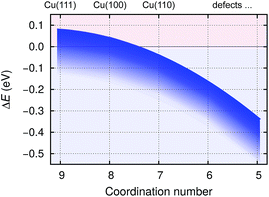 | ||
| Fig. 3 Schematically shown dependence of benzotriazole dissociation energies for stand-alone BTAH⊥ (BTAH(ads) → BTA(ads) + Hads, cleavage of N1–H bond) on coordination number of surface Cu atoms involved in the adsorption site; based on data of ref. 27. Dissociation energy (ΔE) is very sensitive to surface coverage due to a pronounced intermolecular long range repulsion between adsorbed BTAH⊥ (cf. Fig. 4). The dependence of ΔE on coverage is roughly indicated by the thickness of the blue band; the larger the coverage the more exothermic the ΔE. | ||
In addition to BTAH(ads), BTA(ads), and H(ads), Fig. 2 also plots the dependence of adsorption (binding) energy of Cl(ads) and H2O(ads) on the coordination number of surface Cu atoms involved in the adsorption site; the former may be seen as a prototype corrosive species and the latter is relevant due to the importance of water/metal interface for corrosion (though there is a large difference between a film of liquid water and a single water molecule).
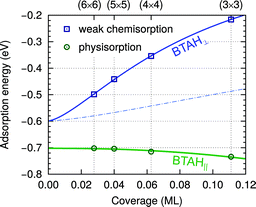 | ||
| Fig. 4 Dependence of adsorption energy on the coverage for stand-alone weakly chemisorbed (blue squares) and physisorbed (green circles) BTAH on Cu(111); adsorption energies are taken from ref. 6. The ML unit is defined as the number of molecules per surface Cu atom. Curves and zero-coverage adsorption energies are obtained with a polarizable point-dipole model extrapolation of ref. 32. The dependence is plotted up to a coverage of 0.12 ML, where the physisorbed BTAH∥ reaches optimum;23 at larger coverage the molecules start to feel intermolecular Pauli repulsion. At the water/solid interface the long range lateral intermolecular interactions would be screened by the solvent molecules; the effect is roughly estimated by a thin dash-dotted blue line, which approximates the lateral dependence for the permittivity of ε = 6, which is a typical value for water in the double-layer33 (note that continuum dielectric approximation is not expected to be valid at short intermolecular distances and also the magnitude of adsorption energy would be significantly altered by solvent effects). | ||
Due to the strong lateral intermolecular repulsion between weakly chemisorbed BTAH(ads) and much weaker lateral interactions for BTA(ads) the dissociation of benzotriazole becomes more favorable as the surface coverage increases (this effect is indicated schematically by the width of the blue band in Fig. 3).
| Species | Adsorption mode | Shown in | Coverage (ML) | μ (D) | ΔΦ (eV) |
|---|---|---|---|---|---|
| a Notation indicates which N atoms bond to Cu. The N1 and N3 atoms are symmetry equivalent for BTA. | |||||
| BTAH⊥ | N2 + N3a | Fig. 1a | 1/9 | 3.15 | −2.25 |
| 1/16 | 4.72 | −1.90 | |||
| BTAH∥ | stand-alone | Fig. 1c | 1/9 | 0.84 | −0.62 |
| H-network | Fig. 1d | 1/10 | 0.96 | −0.64 | |
| BTA(ads) | N2 + N3a | Fig. 1e | 1/16 | 0.51 | −0.21 |
| [BTA–Cu]n | N1 + N2 + N3a | Fig. 1i | 2/23 | 1.91 | −1.07 |
| 1/5 | 1.18 | −1.52 | |||
| Cl(ads) | fcc | — | 1/9 | −0.34 | +0.24 |
| H(ads) | fcc | — | 1/4 | −0.03 | +0.04 |
| H2O(ads) | top | — | 1/9 | +0.68 | −0.49 |
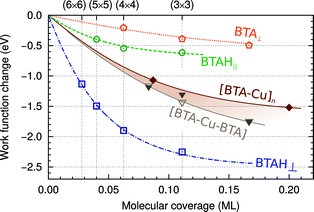 | ||
| Fig. 5 Dependence of ΔΦ of Cu(111) on the molecular coverage for various forms of adsorbed benzotriazole. The curves are drawn by fitting the data points with the polarizable point-dipole model of ref. 32. For organometallic complexes the dependence is emphasized by the brownish band. | ||
In this respect it should be noted that a large permanent molecular dipole of the inhibitor molecule does not automatically lead to a reduction in the work function. It depends on the adsorption structure of the inhibitor and for a weakly chemisorbed BTAH on copper, the adsorption structure is such that this is true.
3.3 Adsorption at water/metal interfaces
In the earlier discussion the adsorption of benzotriazole was considered at vacuum/copper interfaces, but in the context of corrosion inhibition the water/metal interface is more relevant. The presence of aqueous solvent considerably affects the energetics of adsorption due to an interplay of several competitive effects, i.e., molecule–metal, molecule–water, and metal–water interactions. In order to understand these effects, the presence of water has to be either implicitly or explicitly considered in calculations. The explicit modeling is, however, rather tedious. For this reason, the involved effects have been only roughly estimated7,8 by following an approach that utilizes a thermodynamic cycle,34 which is shown in Scheme 3. The adsorption energy of deprotonated BTA− or any other anion from the solution (A−(solv) → A(ads) + e−metal) can be written as:‡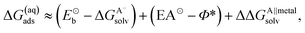 | (4) |
| ΔΔGA∥metalsolv = ΔGA|metalsolv − ΔGmetalsolv, | (5) |
| Φ* = Φ + ΔΦ, | (6) |
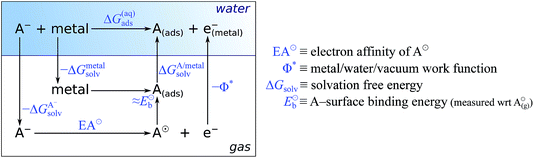 | ||
| Scheme 3 Thermodynamic cycle used to obtain a rough estimate for the adsorption energy of deprotonated molecule (or anion) in the aqueous phase (mnemonic: A stands for adsorbate or anion). | ||
For the adsorption of neutral species (A(solv) → A(ads)) the corresponding eqn is simpler, because there are no electron terms. Hence:
| ΔG(aq)ads ≈ (Eb − ΔGAsolv) + ΔΔGA∥metalsolv | (7) |
In this case the Eb and ΔGAsolv of BTAH are much smaller in magnitude than the corresponding terms for deprotonated BTA− (or any other anion).
A large mutual cancellation between the competitive terms in eqn (4) and (7) results in moderate adsorption energies. As a consequence the huge difference between the gas-phase adsorption energies of BTAH(ads) and BTA(ads) is greatly reduced in aqueous-phase. Solvent effects also relatively favor the adsorption of BTA− compared to Cl−, because Cl− is much smaller than BTA− and solvates by about 0.6 eV stronger; Cl also displays by ≈0.15 eV larger electron affinity than BTA⊙. While in gas-phase Cl adsorbs stronger than BTA(ads) (see Fig. 2), the two just mentioned effects seem to reverse the adsorption energy trend and BTA(ads)wins over Cl(ads) in aqueous-phase.8
Solvent effects also diminish the adsorption energy dependence on the coordination of surface metal atoms because the adsorbate has to displace water molecule(s) from the surface during specific adsorption and water displays a similar bonding enhancement trend as benzotriazole and Cl(ads) (Fig. 2). This effect is captured by the ΔΔGA∥metalsolv term in eqn (4) and (7). For anionic species (BTA− and Cl−) there is an additional effect that is even more pronounced and is due to dependence of Φ* on the surface geometry. Namely, the reduction of Φ* on going from (111) to (110) is so large§ that it reverses the adsorption trend, i.e., estimated magnitudes of aqueous-phase adsorption energies of BTA− and Cl− follow the (111) ≳ (100) > (110) sequence.8 This finding is in agreement with the analysis of electrochemical experiments of Trasatti et al.,38,39 who reported the same crystal-face specificity trend for the adsorption of halide anions on Ag.
By comparing Fig. 4 and 5, it can be seen that the effect of the molecular dipole on the work function is larger than on the adsorption energy. The effect of the molecular dipole on the inhibitor–surface bonding has often been discussed in studies that correlate inhibitor electronic parameters with their inhibition efficiency, but the effect on the work function has not been appreciated.
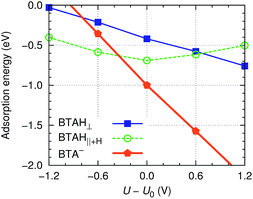 | ||
Fig. 6 Roughly estimated dependence of adsorption energy of benzotriazole on copper surfaces (i.e., values are averaged as 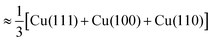 ) on the electrode potential relative to static potential of zero charge, U0.¶ The following species are considered: weakly chemisorbed BTAH (labeled as BTAH⊥, left structure shown in Fig. 1a), physisorbed BTAH intermolecularly associated into a H-bonded network (BTAH∥+H, Fig. 1d), and deprotonated BTA− (Fig. 1e). ) on the electrode potential relative to static potential of zero charge, U0.¶ The following species are considered: weakly chemisorbed BTAH (labeled as BTAH⊥, left structure shown in Fig. 1a), physisorbed BTAH intermolecularly associated into a H-bonded network (BTAH∥+H, Fig. 1d), and deprotonated BTA− (Fig. 1e). | ||
This figure should be understood only qualitatively, because the presented adsorption energies are subjected to significant uncertainty due to the nature of involved approximations. Nevertheless, the qualitative trends (i.e., the slopes/shapes of the curves) should be correctly captured. There are a few things to notice from the figure: (i) BTAH∥+H displays the well known parabolic dependence of simple organic molecules, with the strongest adsorption at the potential of zero charge.33 (ii) The adsorption energy of BTAH⊥ becomes more exothermic as the electrode potential becomes more positive (almost linearly). This distinctive behavior can be attributed to the orientation of molecular dipole of the two forms because the variation of molecule–surface bond with electric field is roughly proportional to −μ·E; for physisorbed BTAH the dipole points largely parallel to the surface, hence −μ·E ≈ 0 and the parabolic dependence stems from the enhancement of water–metal interaction with increasing E. On the other hand, the dipole of BTAH⊥ points outward and in this case ∂Eb/∂U ≈ μ/d = 0.3e (if d = 3 Å and μ is taken from Table 1).|| (iii) Finally, the slope of the BTA− line is largely dominated by the −e(U − U0) term, eqn (9), and is thus close to one.
According to Fig. 6, the BTAH∥+H form is the stablest among the three forms at low values of potential (U − U0 ≲ −0.3 V), but at larger values the deprotonated form becomes the stablest. The curves in Fig. 6 correspond to the following reactions:
| BTAH(solv) → BTAH(ads) and | (10) |
| BTA−(solv) → BTA(ads) + e−(metal), | (11) |
| BTAH(ads) ⇌ BTA(ads) + H(ads). | (12) |
Alternatively the H1 proton can be abstracted by a neighboring water molecule (which may then diffuse away from the surface):
| BTAH(ads) ⇌ BTA(ads) + H+ + e−. | (13) |
The argument applies to both cases. Consider, for example, the desorption of BTA(ads) under low pH conditions.** If the barrier for the reverse of reaction (12) or (13) is not too large, it may be more convenient for BTA(ads) to desorb as BTAH(ads); namely, the larger is the coverage of H(ads) (or concentration of H+) the more to the left the reaction (12) [or (13)] is pushed. This argument, together with Fig. 6, suggests that BTA(ads) is more relevant at higher potentials and higher pH, while BTAH(ads) may dominate at low potentials and low pH (relatively speaking); this is in fact self-evident from reaction (13). With respect to corrosion inhibition, it would be desirable to make reaction (12)irreversible or at least to push the dissociation reaction to the right as much as possible, because BTA(ads) bonds much stronger to the surface than BTAH(ads) and strong bonds imply larger desorption barriers than weak bonds. This may be the case on low coordinated surface defects, because Fig. 3 reveals that dissociation is more exothermic there. A step further in this direction is achieved by the BTA–Cu organometallic complexation, which is an issue that we turn to now.
3.4 Role of BTA–Cu organometallic complexes
The ability of benzotriazole to inhibit corrosion is often attributed to formation of protective BTA–Cu surface complexes.†† The arguments presented earlier may provide a sound rationale of why this is so. According to DFT calculations,7,8 the BTA–Cu organometallic complexes are thermodynamically more stable than stand-alone chemisorbed BTA(ads). For example, the two organometallic complexes—shown in Fig. 1h and i—are by about 0.1 to 0.2 eV per BTA more stable than the stand-alone form. This difference is not large, but it includes the cost for the Cu adatoms formation [0.76 eV per atom on Cu(111)] that are incorporated into the complex (for more details, see ref. 8). This implies that the gross bonding of BTA within the organometallic complex is much stronger than the BTA–surface bond of the stand-alone form. Moreover, within the complex all the BTA's N atoms are bonded to Cu atoms and are thus saturated (cf.Fig. 1h and i). Hence, the removal of BTA or the fusion of H into the BTA are more unlikely for the complex than for the stand-alone form. The organometallic complexes are therefore more resistant than the stand-alone BTA(ads) forms in the reverse of reaction (12) or (13), which eventually lead to desorption of benzotriazole. But they are still susceptible to potential and pH, according to the reaction of Youda:47nBTAH(ads) + nCu ⇌ [Cu–BTA]n + nH+ + ne−.According to some researchers the formation of protective BTA–Cu complex is faster on bare metallic surfaces,16 while others emphasized the importance of surface oxides in their formation.14,46 The latter is one amongst other reasons that the adsorption of benzotriazole on oxidized copper surfaces is considered below.
4 Adsorption of benzotriazole on oxidized copper surfaces
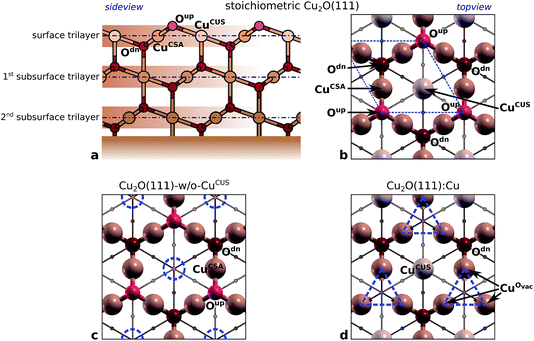
Up to this point the bonding of benzotriazole with reduced (oxide-free) copper surfaces was considered, which are more relevant at acidic pH, but in other conditions the copper surfaces are oxidized. It should be noted that bare metallic surfaces are structurally and electronically simpler than oxidized surfaces, which is the reason that the bonding of benzotriazole to oxidized copper surfaces has been considered by DFT calculations to a sufficiently smaller extent than to bare copper surfaces. Jiang and Adams48 studied the bonding of BTAH on stoichiometric Cu2O(111), while Peljhan and Kokalj49,50 extended the calculations and considered also the bonding on thermodynamically stablest so-called Cu2O(111)-w/o-CuCUS and Cu2O(110)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CuO. Currently, the adsorption of benzotriazole is considered in more detail on a broader set of potential surface sites on oxidized copper surfaces.
CuO. Currently, the adsorption of benzotriazole is considered in more detail on a broader set of potential surface sites on oxidized copper surfaces.
Because oxidized surfaces may display a plethora of different structures and stoichiometries, some of which might be rather complicated, a reductionistic approach is followed. The surfaces of Cu2O are well characterized in gas-phase and these are taken as a starting model of oxidized copper surface (Section 4.1). Subsequently also simple models of hydroxylated Cu2O surface are considered (Section 4.2), because several studies indicate that surface oxide layer is likely hydroxylated in aqueous solution.51–54 Due to obvious modeling reasons, the reported results again refer to the solid/vacuum interface and all the models are based on cuprous oxide [the Cu(II) oxidation state is not considered]. In this respect it should be noted that the Cu2O is more relevant than CuO for formation of the protective film of benzotriazole.13
4.1 Cu2O as a model of oxidized copper surfaces
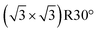 reconstructed surface, where one third of surface oxygens (Oup as defined in Fig. 7) are missing. A characteristic of the
reconstructed surface, where one third of surface oxygens (Oup as defined in Fig. 7) are missing. A characteristic of the 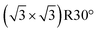 is the presence of the CuOvac sites that are described below. Under electrochemical conditions the Cu2O(111) surface can be Cu terminated (labeled as Cu2O(111)
is the presence of the CuOvac sites that are described below. Under electrochemical conditions the Cu2O(111) surface can be Cu terminated (labeled as Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu) and stabilized by adsorbed hydroxyls.51,52,58 Adsorption of benzotriazole on hydroxylated Cu2O(111) is considered in Section 4.2.
Cu) and stabilized by adsorbed hydroxyls.51,52,58 Adsorption of benzotriazole on hydroxylated Cu2O(111) is considered in Section 4.2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu. It also defines the naming of various atoms (ions) in the near surface region. Some atoms (ions) in the surface region are coordinatively saturated (CSA) and others are coordinatively unsaturated (CUS); caption of Fig. 7 explicitly lists all the CSA and CUS atoms. Note that the naming of atoms does not follow the coordinative CSA/CUS description (only the surface Cu atoms of stoichiometric Cu2O(111) are named CuCUS and CuCSA), but a rather more structural-like description, e.g., Oup and Odn indicate that they are above and below the surface Cu layer, respectively. The Cu atoms, which surrounds the Oup vacancy (Fig. 7d) are CUS, but they are named CuOvac as to differentiate them from CuCUS of Cu2O(111).
Cu. It also defines the naming of various atoms (ions) in the near surface region. Some atoms (ions) in the surface region are coordinatively saturated (CSA) and others are coordinatively unsaturated (CUS); caption of Fig. 7 explicitly lists all the CSA and CUS atoms. Note that the naming of atoms does not follow the coordinative CSA/CUS description (only the surface Cu atoms of stoichiometric Cu2O(111) are named CuCUS and CuCSA), but a rather more structural-like description, e.g., Oup and Odn indicate that they are above and below the surface Cu layer, respectively. The Cu atoms, which surrounds the Oup vacancy (Fig. 7d) are CUS, but they are named CuOvac as to differentiate them from CuCUS of Cu2O(111).
Calculations on Cu2O(111) surfaces were performed with slabs that consist of four trilayers. A (2 × 2) supercell was used. Its size would correspond to Cu(111)–(4 × 4), but the lattice parameter of Cu2O bulk (4.35 Å, PBE value) is larger than for Cu (3.67 Å), hence it actually corresponds to the size of Cu(111)–(4.7 × 4.7) supercell. Because of the coverage dependence of BTAH adsorption energies (cf.Fig. 4), this should be kept in mind when comparing the results between oxidized and reduced copper surfaces. The Cu2O(111)-w/o-CuCUS was taken as a reference; the adsorption on the CuCUS and CuOvac sites may be hence considered as adsorption on defect sites of Cu2O(111)-w/o-CuCUS. Two models—one based on Cu2O(111)-w/o-CuCUS and the other on Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu‡‡—were used for each defect so as to have an estimate of how susceptible the adsorption characteristics are on the specifics of the given model (the results were however not too different between different models). The results for adsorption of BTAH(ads) and BTA(ads) on various sites of Cu2O(111) are presented in Fig. 8.
Cu‡‡—were used for each defect so as to have an estimate of how susceptible the adsorption characteristics are on the specifics of the given model (the results were however not too different between different models). The results for adsorption of BTAH(ads) and BTA(ads) on various sites of Cu2O(111) are presented in Fig. 8.
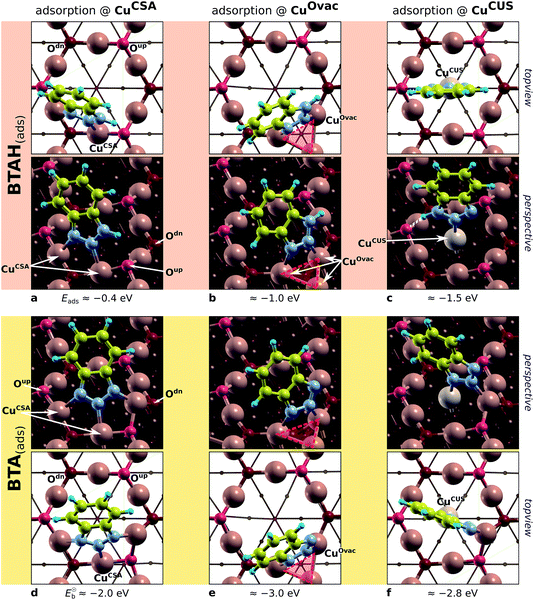 | ||
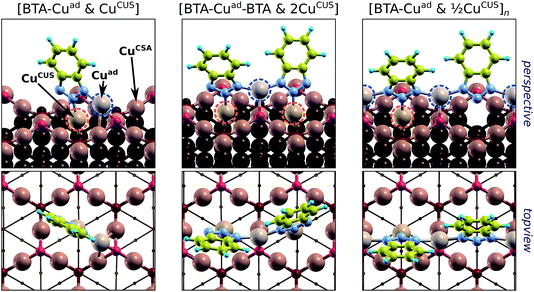
| Fig. 8 Top-view and perspective plots of representative structures of BTAH(ads) (top) and BTA(ads) (bottom) on various considered sites of Cu2O(111); partially based on ref. 49 and 50. Adsorption (binding) energies are also reported. From left to right: molecular bonding to CuCSA, CuOvac, and CuCUS sites. The Oup vacancy with the surrounding CuOvac atoms is indicated by reddish triangle. Note that in addition to direct N–Cu bonds, the BTAH adsorbed at CuCUS also forms the N1–H⋯Oup hydrogen bond. | ||
 condition is met only on CuOvac sites, which implies that dissociation of BTA(ads) is thermodynamically favored only thereon (the issue is confirmed by separate BTA(ads) + H(ads) coadsorption calculations). It should be noted, however, that under non-acidic conditions, the BTA− can also be supplied from solution; the BTAH's pKa constant at 25 °C is 8.4 for BTAH ⇌ BTA− + H+,60 hence at pH = 7 the BTA−(solv)
condition is met only on CuOvac sites, which implies that dissociation of BTA(ads) is thermodynamically favored only thereon (the issue is confirmed by separate BTA(ads) + H(ads) coadsorption calculations). It should be noted, however, that under non-acidic conditions, the BTA− can also be supplied from solution; the BTAH's pKa constant at 25 °C is 8.4 for BTAH ⇌ BTA− + H+,60 hence at pH = 7 the BTA−(solv)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTAH(solv) ratio is 4
BTAH(solv) ratio is 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96.
96.
4.2 Hydroxylated Cu2O(111) surfaces
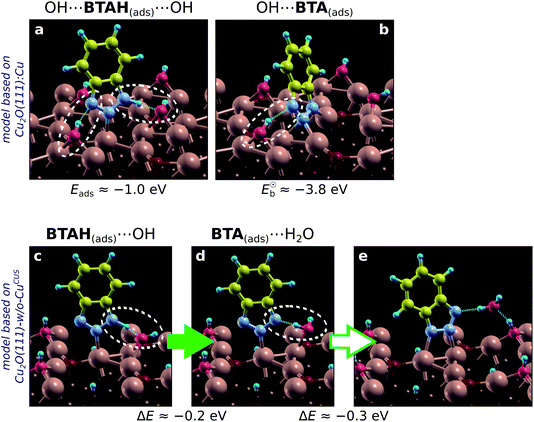
According to current calculations the OH bonds by about 1.9 eV to CuCSA, 3 eV to CuCUS, and 3.6 eV to CuOvac (with respect to OH radical in the gas-phase). Bonding enhancement is thus considerable—a trend similar to BTA(ads) (cf. Section 4.1.4). This enhancement helps us understand why, in contrast to gas-phase ambient, at water/solid interface the Cu2O surface can contain appreciable amounts of coordinatively unsaturated Cu ions, which are stabilized by adsorbates such as hydroxyls52 or inhibitor molecules (if present).Two simple models of the hydroxylated surface of Cu2O were used, one derived from Cu2O(111)-w/o-CuCUS and the other from Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu.|||| The first can be seen as a model of hydroxylated surface without (or an insignificant amount of) unsaturated Cu ions and the second as a model with considerable amounts of unsaturated Cu ions. Both models give rather similar benzotriazole–surface binding energies, which are about −1.0 eV for BTAH(ads) (a value similar to the one obtained on CuOvac sites of plain Cu2O(111) surface) and about −3.8 eV for BTA(ads) (Fig. 10a and b). BTA(ads) thus binds considerably stronger to the hydroxylated surface than to plain Cu2O. Consequently, the dissociation of benzotriazole is favored on hydroxylated surfaces. Calculations further reveal that benzotriazole forms hydrogen bonds with the OH(ads) more efficiently than with the Oup ions of plain Cu2O. The reason is that hydroxyls are much more flexible than O ions and can easily adjust so as to form hydrogen bonds with benzotriazole's N atoms (see Fig. 10). The flexibility of OH groups also leads to a new dissociation mechanism of benzotriazole. Namely, in addition to dissociation reaction (14), benzotriazole can also dissociate by interacting with the hydroxyl and forming a water molecule in the course of dissociation:
Cu.|||| The first can be seen as a model of hydroxylated surface without (or an insignificant amount of) unsaturated Cu ions and the second as a model with considerable amounts of unsaturated Cu ions. Both models give rather similar benzotriazole–surface binding energies, which are about −1.0 eV for BTAH(ads) (a value similar to the one obtained on CuOvac sites of plain Cu2O(111) surface) and about −3.8 eV for BTA(ads) (Fig. 10a and b). BTA(ads) thus binds considerably stronger to the hydroxylated surface than to plain Cu2O. Consequently, the dissociation of benzotriazole is favored on hydroxylated surfaces. Calculations further reveal that benzotriazole forms hydrogen bonds with the OH(ads) more efficiently than with the Oup ions of plain Cu2O. The reason is that hydroxyls are much more flexible than O ions and can easily adjust so as to form hydrogen bonds with benzotriazole's N atoms (see Fig. 10). The flexibility of OH groups also leads to a new dissociation mechanism of benzotriazole. Namely, in addition to dissociation reaction (14), benzotriazole can also dissociate by interacting with the hydroxyl and forming a water molecule in the course of dissociation:
| BTAH(ads) + OH(ads) → BTA(ads) + H2O. | (15) |
A snapshot of this reaction is shown in Fig. 10c and d. The corresponding elementary dissociative step is exothermic by 0.2 eV, but notice that the resulting BTA(ads) structure (Fig. 10d) is not the stablest possible; the BTA(ads) then further stabilizes by 0.3 eV by forming another N–Cu bond. Water formation has been proposed to form during BTAH dissociation in the literature, although due to interaction with oxygen.16,62
5 Conclusions
Controversial suggestions exist in the literature, concerning the role of copper oxides for the adsorption of benzotriazole.11 To shed some new light onto this question, the adsorption behavior of benzotriazole on reduced and oxidized copper surfaces was discussed on the basis of DFT results. DFT calculations reveal that benzotriazole is able to bond with oxide-free and oxidized copper surfaces. Its bonding is considerably enhanced on passing from Cu(111) to low coordinated defects on oxide-free surfaces. The bonding of aggressive chloride anions enhances in the same direction, but to a lesser extent. On oxide surfaces benzotriazole bonds considerably stronger to coordinatively unsaturated Cu sites. This suggests that benzotriazole is able to passivate the reactive under-coordinated surface sites that are plausible microscopic sites for corrosion attack.The adsorption behavior of benzotriazole is non-trivial, because it can adsorb (at least in principle) in a variety of different forms. Perhaps this is one of the strengths of benzotriazole; depending on different conditions it adopts one of several possible forms and thus sustains various situations. However, benzotriazole chemisorbs strongly only in the deprotonated form. Gross bonding is even stronger when BTA is incorporated into BTA–Cu organometallic adcomplexes. DFT results are therefore consistent with experimental evidence that the ability of benzotriazole to inhibit corrosion is due to the formation of organometallic complexes. This readily explains why benzotriazole is more effective at higher pH values. Namely, at low pH (and low potentials) the BTA transforms to BTAH(ads),47 which is bonded considerably weaker to the surface and may eventually desorb; according to the calculations the most strongly bonded adsorption form under such conditions is the BTAH physisorbed parallel to the surface and intermolecularly connected into a H-bonding network with other BTAH molecules.***
Strong inhibitor–surface bonding, as important as it may be, is by no means the only relevant factor for corrosion inhibition. BTAH⊥, [BTA–Cu–BTA] and [BTA–Cu]n considerably reduce the metal work function, which is a consequence of a large permanent molecular dipole and a properly oriented adsorption structure. It has been argued that such a pronounced effect on the work function should make any reaction that donates electron(s) to the metal less favorable (e.g., Cl−(solv) → Cl(ads) + e−(metal) or Cu(solid) → Cun+(solv) + ne−(metal)). This reasoning is consistent with the fact that benzotriazole predominantly affects the anodic reaction, although it is a mixed type inhibitor.11,63 A large permanent molecular dipole is a general characteristic of azoles [e.g., imidazole (3.8 D), triazole (4.4 D), tetrazole (5.4 D)].4 A mechanism based on the reduction of work function may be therefore operative also for other azole inhibitors. There are, however, significant differences between imidazole and triazole/tetrazole based inhibitors. Our recent DFT calculations suggest that imidazoles are active against corrosion in neutral molecular form, while tetrazoles—similar to triazoles—inhibit the corrosion in their deprotonated form.36 The reason for the different behaviour of imidazoles is two fold; the first is due to their more basic nature and the second is related to their molecular spatial structure, because of which they can form only one strong N–Cu bond, while triazoles and tetrazoles can form at least two.
An ability to form soluble complexes with dissolved metal ions as well as the solubility of stand-alone inhibitor are also relevant in the context of corrosion. A formation of soluble complexes between inhibitors and metal ions would help increase the dissolution of metal, thus having the effect of promoting the corrosion. This effect has been characterized for several imidazole based inhibitors in our parallel study.64 As for the solubility, it is known that the more soluble the molecule is, the smaller is its (relative) affinity for adsorption.3 Ideas of a similar kind were very recently used by Mondal and Taylor,65 who described a clever approach towards a rational design of corrosion inhibitors.
Last but not least, the ability of a molecule to inhibit corrosion of a metal is also given by the chemical nature of the metal itself, because molecules bond differently to various metals. For example, while Cu and Al are not reactive enough to interact with the azoles' π system,††† Fe can readily do so.26 This can have a pronounced effect on the structure of the adsorbed molecule.
Acknowledgements
This work has been supported by the Slovenian Research Agency (Grant no. P2-0148). The author is indebted to several researchers, first and foremost to Prof. Ingrid Milošev for bringing the subject of corrosion inhibitors to his attention. Sebastijan Peljhan and Nataša Kovačević are acknowledged for their many calculations and useful discussions on the subject azoles on metal surfaces. Prof. Phillipe Marcus is acknowledged for enlightening discussion about the growth of oxides on metal surfaces and surface hydroxylation. Dunja Peca and Matic Poberžnik are acknowledged for their careful reading of the manuscript.References
- M. M. Antonijević and M. B. Petrović, Int. J. Electrochem. Sci., 2008, 3, 1–28 Search PubMed.
- G. Schmitt, Br. Corros. J., 1984, 19, 165–176 CrossRef CAS PubMed.
- J. O. Bockris and A. K. N. Reddy, Modern Electrochemistry, Kluwer Academic/Plenum Publishers, New York, Boston, Dordrecht, London, Moscow, 2nd edn, 2000, vol. 2B Search PubMed.
- N. Kovačević and A. Kokalj, J. Phys. Chem. C, 2011, 115, 24189–24197 Search PubMed.
- Y. Jiang and J. B. Adams, Surf. Sci., 2003, 529, 428–442 CrossRef CAS.
- S. Peljhan and A. Kokalj, Phys. Chem. Chem. Phys., 2011, 13, 20408–20417 RSC.
- A. Kokalj, S. Peljhan, M. Finšgar and I. Milošev, J. Am. Chem. Soc., 2010, 132, 16657–16668 CrossRef CAS PubMed.
- S. Peljhan, J. Koller and A. Kokalj, J. Phys. Chem. C, 2014, 118, 933–943 CAS.
- J. B. Cotton and I. R. Scholes, Br. Corros. J., 1967, 2, 1–5 CrossRef CAS PubMed.
- G. W. Poling, Corros. Sci., 1970, 10, 359–437 CrossRef CAS.
- M. Finšgar and I. Milošev, Corros. Sci., 2010, 52, 2737–2749 CrossRef PubMed.
- D. Chadwick and T. Hashemi, Corros. Sci., 1978, 18, 39–51 CrossRef CAS.
- R. F. Roberts, J. Electron Spectrosc. Relat. Phenom., 1974, 4, 273–291 CrossRef CAS.
- V. Brusic, M. A. Frisch, B. N. Eldridge, F. P. Novak, F. B. Kaufman, B. M. Rush and G. S. Frankel, J. Electrochem. Soc., 1991, 138, 2253–2259 CrossRef CAS PubMed.
- B.-S. Fang, C. G. Olson and D. W. Lynch, Surf. Sci., 1986, 176, 476–490 CrossRef CAS.
- G. Xue, J. Ding, P. Lu and J. Dong, J. Phys. Chem., 1991, 95, 7380–7384 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 176–179 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- V. Barone, M. Casarin, D. Forrer, M. Pavone, M. Sambi and A. Vittadini, J. Comput. Chem., 2009, 30, 934–939 CrossRef CAS PubMed.
- A. Kokalj and S. Peljhan, Langmuir, 2010, 26, 14582–14593 CrossRef CAS PubMed.
- S. Peljhan and A. Kokalj, J. Phys. Chem. C, 2009, 113, 14363–14376 CAS.
- X. Chen and H. Häkkinen, J. Phys. Chem. C, 2012, 116, 22346–22349 CAS.
- N. Kovačević and A. Kokalj, Mater. Chem. Phys., 2012, 137, 331–339 CrossRef PubMed.
- A. Kokalj, S. Peljhan and J. Koller, J. Phys. Chem. C, 2014, 118, 944–954 CAS.
- F. Grillo, D. W. Tee, S. M. Francis, H. A. Früchtl and N. V. Richardson, J. Phys. Chem. C, 2014, 118, 8667–8675 CAS.
- J. F. Walsh, H. S. Dhariwal, A. Gutirrez-Sosa, P. Finetti, C. A. Muryn, N. B. Brookes, R. J. Oldman and G. Thornton, Surf. Sci., 1998, 415, 423–432 CrossRef CAS.
- J. O. Nilsson, C. Tornkvist and B. Liedberg, Appl. Surf. Sci., 1989, 37, 306–326 CrossRef CAS.
- F. Grillo, D. W. Tee, S. M. Francis, H. Fruchtl and N. V. Richardson, Nanoscale, 2013, 5, 5269–5273 RSC.
- A. Kokalj, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045418 CrossRef.
- J. O. Bockris, A. K. N. Reddy and M. Gamboa-Aldeco, Modern Electrochemistry, Kluwer Academic/Plenum Publishers, New York, Boston, Dordrecht, London, Moscow, 2nd edn, 2000, vol. 2A Search PubMed.
- M. T. M. Koper and R. A. van Santen, Surf. Sci., 1999, 422, 118–131 CrossRef CAS.
- S. Trasatti, Electrochim. Acta, 1991, 36, 1659–1667 CrossRef CAS.
- N. Kovačević and A. Kokalj, Corros. Sci., 2013, 73, 7–17 CrossRef PubMed.
- A. Kokalj, Chem. Phys., 2012, 393, 1–12 CrossRef CAS PubMed.
- S. Trasatti and L. M. Doubova, J. Chem. Soc., Faraday Trans., 1995, 91, 3311–3325 RSC.
- L. Doubova and S. Trasatti, Electrochim. Acta, 1997, 42, 785–791 CrossRef CAS.
- C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef.
- M. J. Weaver, Appl. Surf. Sci., 1993, 67, 147–159 CrossRef CAS.
- M. T. M. Koper, R. A. van Santen, S. A. Wasileski and M. J. Weaver, J. Chem. Phys., 2000, 113, 4392–4407 CrossRef CAS PubMed.
- S. A. Wasileski, M. T. M. Koper and M. J. Weaver, J. Phys. Chem. B, 2001, 105, 3518–3530 CrossRef CAS.
- J. B. Cotton, Proceedings of the 2nd International Congress on Metallic Corrosion, New York, USA, 1963, pp. 590–596 Search PubMed.
- J. C. Rubim, I. G. R. Gutz, O. Sala and W. J. Orville-Thomas, J. Mol. Struct.: THEOCHEM, 1983, 100, 571–583 CrossRef CAS.
- D. Chadwick and T. Hashemi, J. Electron Spectrosc. Relat. Phenom., 1977, 10, 79–83 CrossRef CAS.
- R. Youda, H. Nishihara and K. Aramaki, Electrochim. Acta, 1990, 35, 1011–1017 CrossRef CAS.
- Y. Jiang, J. B. Adams and D. Sun, J. Phys. Chem. B, 2004, 108, 12851–12857 CrossRef CAS.
- S. Peljhan, Ph.D. thesis, University of Ljubljana, 2012.
- A. Kokalj and S. Peljhan, J. Phys. Chem. C, 2015 DOI:10.1021/acs.jpcc.5b01677.
- V. Maurice and P. Marcus, Electrochim. Acta, 2012, 84, 129–138 CrossRef CAS PubMed.
- M. M. Islam, B. Diawara, V. Maurice and P. Marcus, Surf. Sci., 2009, 603, 2087–2095 CrossRef CAS PubMed.
- J. Kunze, V. Maurice, L. H. Klein, H.-H. Strehblow and P. Marcus, J. Phys. Chem. B, 2001, 105, 4263–4269 CrossRef CAS.
- V. Maurice, H.-H. Strehblow and P. Marcus, Surf. Sci., 2000, 458, 185–194 CrossRef CAS.
- A. Soon, M. Todorova, B. Delley and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125420 CrossRef.
- A. Soon, M. Todorova, B. Delley and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 129902 CrossRef.
- A. Önsten, M. Göthelid and U. O. Karlsson, Surf. Sci., 2009, 603, 257–264 CrossRef PubMed.
- X. Nie, G. L. Griffin, M. J. Janik and A. Asthagiri, Catal. Commun., 2014, 52, 88–91 CrossRef CAS PubMed.
- P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- L. D. Hansen, B. D. West, E. J. Baca and C. L. Blank, J. Am. Chem. Soc., 1968, 90, 6588–6592 CrossRef CAS.
- M. Finšgar, J. Kovač and I. Milošev, J. Electrochem. Soc., 2010, 157, C52–C60 CrossRef PubMed.
- H. Y. H. Chan and M. J. Weaver, Langmuir, 1999, 15, 3348–3355 CrossRef CAS.
- M. Finšgar, A. Lesar, A. Kokalj and I. Milošev, Electrochim. Acta, 2008, 53, 8287–8297 CrossRef PubMed.
- N. Kovačević, I. Milošev and A. Kokalj, Corros. Sci., 2015, submitted Search PubMed.
- S. K. Mondal and S. R. Taylor, J. Electrochem. Soc., 2014, 161, C476–C485 CrossRef CAS PubMed.
Footnotes | ||||||||
| † Terms chemisorption and physisorption refer to the type of molecule–surface interaction and not to the scale of the interaction energy. Molecule–surface bond length is a good descriptor to distinguish between the two. For chemisorption the benzotriazole–surface distances are about 2 Å, whereas for physisorption the distances are about 3 Å as inferred from respective covalent and van der Waals radii.23 | ||||||||
| ‡ Eqn (4) is a straight blend of energy contribution (E⊙b) and solvation free energy terms; neither the zero-point energy correction nor the concentration (translational) and roto-vibrational entropy contributions to free energy are taken into account. The equation is therefore very approximate, but it should suffice to illustrate the discussed points. | ||||||||
| § Both Φ and ΔΦ [cf. eqn (6)] reduce with reducing the coordination of surface Cu atoms; the PBE calculated Φ values are 4.84, 4.60, and 4.39 eV for Cu(111), Cu(100), and Cu(110), respectively,37 while the experimentally estimated ΔΦ at potentials of zero charge are −0.54, −0.57, and −0.65 eV, respectively,38 which result in Φ* values of 4.29, 4.03, and 3.74 eV for (111), (100), and (110) faces, respectively.8 | ||||||||
¶ The effects (i) and (ii) were estimated by putting the slab model (either adsorbate/copper or water-film/copper) in homogeneous electric field E and performing relaxation calculations at several different values of electric field. The relation between the electric field and electrode potential (U) was treated within the Helmholtz–Perrin parallel plate capacitor model of double layer, i.e.:
| ||||||||
| || This implies that Eb changes by ≈0.3 eV if potential is altered by 1 V. The actual calculations reveal that the variation is even larger due to molecular polarization, but this extra effect is largely cancelled by the enhancement of the water–metal interaction with increasing E (note that water has a considerably smaller dipole moment than BTAH); hence the slope of the BTAH⊥ line in Fig. 6 is close to 0.3e. | ||||||||
| ** Although the argument is similar for both reactions, (12) and (13), the atomistic mechanism is different. In the reverse direction of reaction (12) BTA(ads) reacts with H(ads) (Langmuir–Hinshelwood mechanism), while in the reverse of reaction (13) the H+ comes from solution and reacts with BTA(ads) directly (Eley–Rideal mechanism). | ||||||||
†† Linear polymeric structure consisting of alternating Cu+ and BTA− ions in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio that form a –Cu–BTA–Cu–BTA– bidentate structure is usually proposed;9,10,44–46 a corresponding model of such [BTA–Cu]n adstructure on bare copper surface, as obtained by DFT calculations, is shown in (Fig. 1i).7 Recently, Chen and Häkkinen proposed, on the basis of DFT calculations, a [BTA–Cu–BTA] dimer adstructure (Fig. 1h).25 This adcomplex was recently observed experimentally by STM (scanning tunneling microscopy) under ultra-high-vacuum conditions on Cu(111).28,31 1 ratio that form a –Cu–BTA–Cu–BTA– bidentate structure is usually proposed;9,10,44–46 a corresponding model of such [BTA–Cu]n adstructure on bare copper surface, as obtained by DFT calculations, is shown in (Fig. 1i).7 Recently, Chen and Häkkinen proposed, on the basis of DFT calculations, a [BTA–Cu–BTA] dimer adstructure (Fig. 1h).25 This adcomplex was recently observed experimentally by STM (scanning tunneling microscopy) under ultra-high-vacuum conditions on Cu(111).28,31 | ||||||||
‡‡ The adsorption on CuCUS and CuOvac sites of Cu2O(111)-w/o-CuCUS model was modeled by adding one CuCUS and removing one Oup ion per (2 × 2) supercell, whereas Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu model already consists of both CuCUS and CuOvac sites. Note, however, that Cu2O(111) Cu model already consists of both CuCUS and CuOvac sites. Note, however, that Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu is a polar terminated surface of Tasker type-3,59 hence it undergoes a reconstruction.52 In particular, the Odn ions upshift to the plane of surface Cu ions, the three CuOvac ions (marked by blue dashed triangles in Fig. 7d) move closer to one another and the CuCUS relaxes laterally as to bond with CuOvac. There are multiple ways of how this can occur and different reconstruction patterns display significantly different stability. For this reason the adsorption of benzotriazole on Cu2O(111) Cu is a polar terminated surface of Tasker type-3,59 hence it undergoes a reconstruction.52 In particular, the Odn ions upshift to the plane of surface Cu ions, the three CuOvac ions (marked by blue dashed triangles in Fig. 7d) move closer to one another and the CuCUS relaxes laterally as to bond with CuOvac. There are multiple ways of how this can occur and different reconstruction patterns display significantly different stability. For this reason the adsorption of benzotriazole on Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu is modeled using the following procedure: (i) the structure of Cu2O(111) Cu is modeled using the following procedure: (i) the structure of Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu is optimized, (ii) benzotriazole is added to the structure-(i) and relaxation is performed, and (iii) benzotriazole is removed and the surface is reoptimized. The adsorption energy is then calculated by using the total energies of (ii) and (iii). The reason for step (iii) is that step (ii) lowers the symmetry of the system (i.e., the molecule perturbs the system) and the surface may find a new relaxation pattern with lower energy; step (iii) therefore assures that structures (ii) and (iii) have a compatible relaxation pattern. A more sophisticated (but computationally much more expensive) approach would be to use a simulated annealing technique as was described by Islam et al.52 Cu is optimized, (ii) benzotriazole is added to the structure-(i) and relaxation is performed, and (iii) benzotriazole is removed and the surface is reoptimized. The adsorption energy is then calculated by using the total energies of (ii) and (iii). The reason for step (iii) is that step (ii) lowers the symmetry of the system (i.e., the molecule perturbs the system) and the surface may find a new relaxation pattern with lower energy; step (iii) therefore assures that structures (ii) and (iii) have a compatible relaxation pattern. A more sophisticated (but computationally much more expensive) approach would be to use a simulated annealing technique as was described by Islam et al.52 | ||||||||
§§ The BTAH bonding enhancement on passing from CuCSA to CuCUS is 1.1 eV, while the cost for the CuCUS formation is between 0.43 and 1.06 eV, taking into account the range of Cu chemical potential between that of Cu and Cu2O bulk, i.e., μmaxCu = EbulkCu and 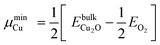 , where EbulkCu, , where EbulkCu,  and EO2 are DFT total energies of Cu atom in the Cu-bulk, formula unit of Cu2O bulk, and oxygen molecule, respectively. and EO2 are DFT total energies of Cu atom in the Cu-bulk, formula unit of Cu2O bulk, and oxygen molecule, respectively. | ||||||||
¶¶ Note that on Cu2O surfaces, H binds stronger to O than to Cu ion, hence the dissociation reaction should be correspondingly written as:
| ||||||||
|||| The Cu2O(111)-w/o-CuCUS derived model was made hydroxylated by substituting all Oup and all O ions below the CuCUS vacancies with OH groups; the model contains 8 hydroxyls per (2 × 2) supercell. For the Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu the model as used by Asthagiri et al.58 was used, where the Cu2O(111) Cu the model as used by Asthagiri et al.58 was used, where the Cu2O(111)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu–(2 × 2) supercell contains 4 hydroxyls, which bridge the CuCUS and CuOvac ions. Cu–(2 × 2) supercell contains 4 hydroxyls, which bridge the CuCUS and CuOvac ions. | ||||||||
| *** Only deprotonated BTA− and neutral BTAH were considered in this paper, because protonated BTAH2+ seems not to be competitive. According to DFT calculations, BTAH2+ bonds only marginally stronger than the neutral BTAH to Cu surfaces,26 but it solvates considerably stronger (for further DFT-based analysis of the adsorption of deprotonated, neutral, and protonated azoles, see our recent study36). This implies that BTAH2+ prefers being solvated rather than adsorbed. It was reported that it is the dominant adsorbed form only at pH ≲ 0.62 | ||||||||
| ††† Cu can do it only exceptionally: an example is the apparent chem + phys form of Fig. 1b and even then the interaction is driven by the dispersion van der Waals forces.6 |
| This journal is © The Royal Society of Chemistry 2015 |