A fixed bed column study for the removal of Pb²⁺ ions by watermelon rind

Abstract

The present study reports the feasibility of removing Pb²⁺ ions from aqueous solution using watermelon rind (WR) as a low cost adsorbent. Fixed bed column studies were employed to study the removal efficiency of Pb²⁺ ions by varying the column parameters such as flow rate, bed height and initial metal ion concentration. The results showed that breakthrough and exhaustion time increases with a decrease in flow rate, inlet concentration, and an increasing bed height. The breakthrough curves obtained were analyzed with Adams–Bohart, Thomas and Yoon–Nelson models. On comparison of the R² values, both the Thomas and Yoon–Nelson models were found to have a better fit than the Adams–Bohart model and these two models can be used to predict the adsorption of Pb²⁺ ions in a fixed bed column. Desorption of Pb²⁺ ions on WR was repeated for three cycles in 0.1 M HCl solution. The loading capacity of WR was compared with other adsorbents and was found to be high. These results show that watermelon rind, a non-hazardous agro waste, can be successfully employed for the elimination of Pb²⁺ ions from aqueous solution.

---

Water impact

The majority of adsorption studies have been carried out in batch modes which are limited to a laboratory process and generally not applicable to most of the long term treatment processes. Continuous column studies are the most valuable and economical treatment processes used in practice for the removal of heavy metal ions from industrial effluents. Activated carbon is a commonly used sorbent for the removal of inorganic and organic pollutants from waste water. In spite of its effectiveness in the removal of pollutants, high activation cost limits its use as an economical adsorbent. Hence, the present study reports the use of a low cost adsorbent such as watermelon rind for the removal of Pb²⁺ ions from aqueous solution.

1 Introduction

The increasing trend of industrialization in recent decades has resulted in severe environmental contaminations. Heavy metal ions are distinguished from other toxic pollutants, due to their non-biodegradability which causes severe physiological or neurological damage to human and aquatic life.¹ Various treatment methodologies include precipitation, oxidation/reduction, ion-exchange, membrane filtration, electrochemical reduction, and adsorption.² Each process has its own advantage and disadvantage; however adsorption produces high quality treated water with low cost.^3,4

Activated carbon is a commonly used sorbent for the removal of inorganic and organic pollutants from waste water. In spite of its effectiveness in the removal of pollutants, high activation cost limits its use as an economical adsorbent. Many waste by-products from the food industry have been evaluated for the removal of heavy metals from waste water as low cost economical sorbents.^5–8 Agricultural by-products are rich in functional groups like pectin, lignin and cellulose which can easily facilitate the binding of metal ions.⁹ The majority of adsorption studies have been carried out in batch modes which are limited to a laboratory process and generally not applicable to most of the long term treatment processes.¹⁰ Continuous column studies are the most valuable and economical treatment processes used in practice.^11,12 Hence, the study of the removal of heavy metals in continuous flow using agricultural by-products is desirable.

Watermelon (Citrullus lanatus), being the largest and heaviest fruit, is one of the most abundant and cheapest fruit available in India with 300 000 tons produced every year. Watermelon production occupies 6–7% of overall fruit production and is high during the summer because of its tropical nature. In watermelon, the red flesh present inside is sweet, edible and used for juices and salads but the outer rind is considered as waste and has no commercial value.¹³ Watermelon rind (WR) consists of phenols, citrulline, cellulose, proteins and caroteniods.^14–16 These polymers are rich in functional groups like hydroxyl (cellulose) and carboxylic (pectin) and can easily bind metal. Lead (Pb²⁺) is one of the prominent pollutants among the heavy metals which cause damage to the kidney, nervous system and liver, and can cause still births and sterility.^17,18 Hence, it is environmentally desirable to remove Pb²⁺ from waste water and industrial effluents.

The present study reports the removal of Pb²⁺ ions from aqueous solution through continuous column studies using WR, a green and economical sorbent. The influence of several operational parameters (flow rate, bed depth and influent concentration) has been studied and the experimental data were fit to various models that describe the breakthrough curves.

2 Materials and methods

2.1 Preparation of adsorbent

Watermelon rinds (WRs) were obtained from a local fruit market and washed under tap water several times followed by washing with double distilled water. After thorough washing the WR was cut in to small pieces and dried under sun light for 7 days to remove all the moisture content present. Later, the dried WR pieces were washed with hot water (70 °C) to remove any soluble matter present and dried in an oven at 85 °C for 48 h. The oven dried WR was powdered using conventional mixture and sieved between a 500–1000 BSS mesh. The sieved WR particles were stored in an air tight container and used for further column experiments.

2.2 Column adsorption studies

Continuous column adsorption experiments were performed in a laboratory glass column with an internal diameter of 1 cm and a length of 15 cm. Initially the column was packed with WR (0.354 g cm⁻³) and a synthetic Pb²⁺ ion solution was fed into the column from the top at a desired flow rate using a peristaltic pump. The samples were collected at the exit of the column at different time intervals and the concentration of the eluted samples was determined using a Flame atomic absorption spectrophotometer (AAS). To study the effect of flow rate on the adsorption of Pb²⁺ ions onto WR, experiments were conducted at three different flow rates: 1, 2 and 3 ml min⁻¹. The study of the effect of bed height on the column adsorption process was conducted at three different bed heights: 1, 3 and 5 cm, keeping other parameters constant. After optimizing the flow rate and bed height, the effect of the initial concentration of metal ion was studied at 500, 750 and 1000 mg L⁻¹. The flow to the column was continued until there was no adsorption i.e. the Pb²⁺ concentration of influent and effluent remained unchanged.¹⁹ In order to ensure the accuracy and reproducibility of all the data, all the column adsorption experiments were conducted in triplicate, and the mean values were used in the data analysis. The percentage standard deviation was found to be not more than 3%.

2.3 Column data analysis

The performances of the packed bed column studies are obtained in the form of breakthrough curves. The time for the breakthrough and the shape of the curve are very important characteristics for determining the operation and dynamic response of a sorption column.²⁰ The breakthrough point of an S shaped curve is considered to be when the effluent concentration (C_t) from the column reaches about 0.1% of the influent concentration. The column is considered to be saturated or exhausted at the point when the concentration of effluent reaches 95%. The breakthrough curve is generally expressed by C_t/C_o as a function of time or volume of the effluent. The effluent volume can be calculated from the equation:

V_eff = Qt_total (1)

Where Q is the volumetric flow rate and t_total is the total flow time (min).

The total metal adsorbed, M_ad (mg), in the fixed bed column can be calculated from the area under the curve multiplied by the flow rate eqn (2).

Where C_ad is the concentration of metal ion removal (mg L⁻¹).

The total amount of metal ions entering the column (M_total) is calculated from the following equation:

And the total metal removal percentage can be obtained from eqn 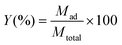(4):

2.4 Column breakthrough curve modeling

The successive operation of a lab scale column towards industrial applications can be well explained by simple mathematical models.^21,22 The breakthrough curves obtained for flow rate, bed height and initial metal ion concentration were predicted with well known mathematical models such as the Adams–Bohart, Thomas and Yoon–Nelson models.

The Adams–Bohart model²³ is one of the most widely used models for the prediction of column breakthrough curves. According to this model, the equilibrium is not instantaneous and the rate of sorption is proportional to the fraction of sorption capacity.^24,25 This model is used to explain the initial part of the breakthrough curve and the model equation is expressed as

where C_o and C_t are the inlet and outlet adsorbate concentrations (mg L⁻¹), k_AB is the kinetic constant (L mg⁻¹ min⁻¹), N_o is the saturation concentration (mg L⁻¹), z is the bed height (cm) and U_o is superficial velocity (cm min⁻¹).

One of the most general and widely used models for describing the performance theory of the sorption process in a fixed bed column is the Thomas model.²⁶ This model assumes the plug flow behavior in the bed and the equation is expressed as

where k_Th is the Thomas model constant (ml min⁻¹ g⁻¹) and q_o is the adsorption capacity (mg g⁻¹). The values of k_Th and q_o can be determined from the slope and intercept of ln (C_o/C_t − 1) against t.

Yoon–Nelson developed a relatively simple model for the adsorption of vapours or gases in activated coal.²⁷ This model assumes that the rate of decrease in the probability of adsorption for each adsorbate molecule is proportional to the probability of sorbate sorption and the probability of sorbate breakthrough on the sorbent. The linear form of the equation is:

where k_YN is the Yoon–Nelson proportionality constant in min⁻¹ and τ is the time required for retaining 50% of the initial sorbate (min). The values of k_YN and τ can be determined from the slope and intercept of plots ln (C_t/C_o − C_t) versus t.

3 Results and discussion

3.1 Characterization of adsorbent

The physico-chemical parameters of WR are summarized and represented in Table 1. The total acidic and basic sites of WR were determined using the traditional Boehm titration method. The acidic sites of WR were found to be high in number compared to the basic sites, suggesting that WR is capable of binding cations. The FTIR spectra of native watermelon rind (Fig. 1) displayed a number of peaks pertaining to different functional groups. The broad and intense peak at around 3371 cm⁻¹ corresponds to –OH (hydroxyl) stretching vibrations of cellulose and pectin, and the peaks at 2917 cm⁻¹ are attributed to –CH stretching vibrations of methyl groups. A peak at 1734 cm⁻¹ corresponds to –C=O stretching of carboxylic acid groups or esters, and asymmetric and symmetric vibrations of ionic carboxylic groups (–COO⁻), respectively, appeared at 1633, and 1423 cm⁻¹. These results suggest that WR is rich in metal ion binding functional groups such as hydroxyl, carboxyl and carbonyl groups. The SEM analysis was carried out to study the surface morphology of WR (Fig. 2). It is observed from the image that the surface was porous in nature. In general, porous surface materials act as very good adsorbents for sequestration of heavy metal ions.

Table 1 Physico-chemical parameters of native WR

Parameter	WR
Point zero charge (pHpzc)	4.9
Moisture (%)	13
Density (g cc^−1)	0.35
Acidic sites (mmol g^−1)	2.46
Basic sites (mmol g^−1)	0.71
Total cationic content (meq g^−1)	2.10

---

Fig. 1 FTIR spectra of native watermelon rind.

Fig. 2 SEM image of native watermelon rind without any pretreatment.

3.2 Fixed bed column studies

3.2.1 Effect of flow rate. Flow rate plays an important role in the fixed bed column adsorption process. In the present study, experiments were carried out by varying the flow rate of Pb²⁺ ions between 1–3 ml min⁻¹.

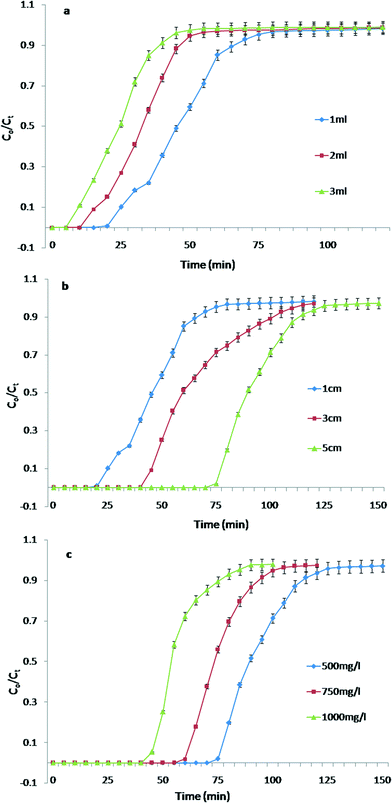
The breakthrough curves obtained are represented in Fig. 3a and the adsorption column data are summarized in Table 2. It was observed that with an increase in flow rate the breakthrough time decreases from 20 to 10 min. Similarly the saturation time of the column was also observed to decrease from 75 to 45 min. The removal efficiency of the WR substantially decreased with an increase in flow rate. This can be attributed to the fact that at a low flow rate, the residence time of the Pb²⁺ ions in the column increases and as result the Pb²⁺ ions have more time to diffuse into the pores of the WR through intraparticle diffusion resulting in a longer breakthrough time and saturation time.²⁸

Fig. 3 a) Effect of flow rate (bed height 1 cm, initial metal concentration 500 mg L⁻¹, room temperature, error bars represent the standard deviation at n = 3), b) effect of bed height (flow rate 1 ml min⁻¹, initial metal concentration 500 mg L⁻¹, room temperature, error bars represent the standard deviation at n = 3) and c) effect of initial metal ion concentration (flow rate 1 ml min⁻¹, bed height 5 cm, room temperature, error bars represent the standard deviation at n = 3) on the breakthrough curves for the removal of Pb²⁺ ions from aqueous solution.

Table 2 Parameters of the fixed bed column for the removal of Pb²⁺ ions by WR

Flow rate (ml)	Bed height (cm)	Initial metal concentration (mg L^−1)	Breakthrough time (min)	Saturation time (min)	M ad (mg)	M total (mg)	Total % removal	EBCT (min)
1	1	500	20	75	22.06	37.5	58.8	2.5
2	1	500	15	55	14.97	55	27.2	1.55
3	1	500	10	45	10.91	67.5	16.1	1.0
1	1	500	20	75	22.06	37.5	58.8	3
1	3	500	45	100	31.2	50	62.4	7.1
1	5	500	75	125	45.3	62.5	72.5	12.2
1	5	500	75	125	45.3	62.5	72.5	—
1	5	750	60	105	55.0	78.5	69.9	—
1	5	1000	45	90	54.0	90	61.0	—

---

3.2.2 Effect of bed height. The removal of Pb²⁺ ions at different bed heights was studied and the breakthrough curves obtained at different bed heights are shown in Fig. 3b. With the increase in bed height, the removal efficiency, breakthrough time and saturation time increases (Table 2). The increase in removal efficiency of Pb²⁺ ions by the WR is due to the availability of a higher number of adsorption sites and an increased volume of influent. The empty bed contact time (EBCT) also increased from 3 to 12.2 min. These observations suggest that the bed height of 5 cm offered optimum breakthrough curves and hence further experiments were carried out at this bed height.

3.2.3 Effect of initial metal ion concentration. At the optimized flow rate and bed height, the effect of the initial concentration of Pb²⁺ ions was studied and the breakthrough curves obtained are shown in Fig. 3c. The adsorption data are summarized in Table 2. The removal efficiency, breakthrough time and saturation time decreased with the increase in initial concentration of Pb²⁺ ions. The influent volume fed into the column also decreased with the increase in inlet concentration. The concentration of metal ions adsorbed onto the WR increased from 45.3 to 55.0 mg g⁻¹ with the increase in inlet concentration from 500 to 750 mg L⁻¹. Further increase in the inlet concentration of Pb²⁺ ions has no effect on the metal uptake capacity of the WR due to saturation of column. The increase in the Pb²⁺ uptake capacity of the WR is due to the fact that a higher inlet concentration provides a higher driving force for the transfer process to overcome the mass transfer resistance.

3.3 Breakthrough curve modeling

The breakthrough curves obtained at different parameters can be used for predicting the efficacy of a particular design of column. Several mathematical models have been proposed for predicting the efficacy of lab scale column studies for the purpose of industrial applications. In the present study, Adams–Bohart, Thomas, Yoon–Nelson models are employed for the best fit model in predicting the dynamic behaviour of the columns.

3.3.1 Adams–Bohart model. For evaluation of the parameters, the range of t taken into consideration was up to 0.5 (C₀/C_t) values of the breakthrough curves. The values of ln (C_t/C_o) were plotted against t and from the slope and intercept, k_AB and N_o were calculated. The values of k_AB and N_o for all the breakthrough curves are represented in Table 3, along with the respective correlation coefficients.

Table 3 Parameters of the Adams–Bohart model at different conditions

Parameter		K AB (L mg^−1 min)	N o (mg L^−1)	R ^2
Flow rate (ml)	1	3.2 × 10^−3	18 372	0.963
	2	2.7 × 10^−3	20 128	0.979
	3	2.5 × 10^−3	24 705	0.961
Bed height (cm)	1	3.2 × 10^−3	18 372	0.963
	3	4.3 × 10^−3	12 679	0.913
	5	7.6 × 10^−3	9562	0.833
Initial metal concentration (mg L^−1)	500	7.6 × 10^−3	9562	0.833
	750	5.4 × 10^−3	10 985	0.866
	1000	3.5 × 10^−3	11 278	0.892

---

The correlation coefficients obtained for the flow rate breakthrough curves were found to be high suggesting that the Adams–Bohart model is applicable for predicting the initial process of the present system. The correlation coefficients obtained for bed heights started to decrease with the increase in bed height and in the case of initial metal ion concentration, the correlation coefficient increases with the increase in initial metal ion concentration. These observations suggest that the Adams–Bohart model is not applicable to the present process at higher bed heights and initial metal ion concentrations.

3.3.2 Thomas model. One of the most widely used models for predicting breakthrough curves is the Thomas model. The values of k_Th and q_o obtained for all the breakthrough curves including correlation coefficients are represented in Table 4. It can be observed from Table 2, that the adsorption capacity of the WR increased with the increase in flow rate and initial metal ion concentration and decreased with the increase in bed heights. The correlation coefficients obtained for all the breakthrough curves are high compared to the Adams–Bohart model suggesting the goodness of fit of the experimental data. Thus, the observations suggest that external and internal diffusion were not the rate limiting steps.²⁹

Table 4 Parameters of the Thomas model at different conditions

Parameter		K Th (ml min^−1 mg)	q o (mg g^−1)	R ^2
Flow rate (ml)	1	4.7 × 10^−5	35.5	0.948
	2	9.9 × 10^−5	31.6	0.994
	3	1.5 × 10^−4	27.3	0.998
Bed height (cm)	1	1.1 × 10^−5	35.5	0.948
	3	1.0 × 10^−5	41.2	0.971
	5	1.1 × 10^−5	50.3	0.910
Initial metal concentration (mg L^−1)	500	1.5 × 10^−5	50.3	0.910
	750	1.5 × 10^−5	63.9	0.925
	1000	1.4 × 10^−5	59.4	0.920

---

3.3.3 Yoon–Nelson model. The values of k_YN and τ obtained for all the breakthrough curves including correlation coefficients are represented in Table 5. It can be observed from Table 5 that the correlation coefficients are found to be between 0.910–0.998 which shows the better fit to this model along with the Thomas model. The time necessary to reach 50% retention, τ, was found to be significantly decreasing with the increase in flow rate and initial inlet concentration. This is due to the fact that saturation of the column was attained quickly, while the τ values increased with an increase in bed height due to slower saturation of the column at higher bed heights. Based on the R² values it can be concluded that both the Thomas and Yoon–Nelson models can be used to predict the removal of Pb²⁺ ions by WR in a fixed bed column.

Table 5 Parameters of Yoon–Nelson model at different conditions

Parameter		K YN (min^−1)	τ (min)	R ^2
Flow rate (ml)	1	0.529	9.69	0.935
	2	0.733	6.44	0.992
	3	0.723	4.76	0.997
Bed height (cm)	1	0.529	9.69	0.935
	3	0.483	12.65	0.972
	5	0.587	18.90	0.904
Initial metal concentration (mg L^−1)	500	0.587	18.90	0.904
	750	0.739	15.66	0.885
	1000	0.633	11.63	0.905

---

3.4 Desorption studies

Desorption and regeneration of the adsorbent in a fixed bed column is of importance in practical applications. In order to study the desorption and regeneration efficiency of WR, the fixed bed column containing Pb²⁺ ions loaded on the adsorbent was eluted with 0.1 M HCl as a desorbing agent. Since 0.1 M HCl showed good desorption efficiency in batch studies the same agent was used in the present study. It is observed from Fig. 4 that a 95% desorption efficiency was achieved within 15 min of run time. The maximum desorption and regeneration efficiency achieved with 0.1 M HCl for three repeated cycles was found to be 95%. These results suggest that WR is a potential adsorbent for the removal of heavy metal ions in a fixed bed column with repeated usage.

Fig. 4 Plot of % decrease of Pb²⁺ ions from WR in a fixed bed column.

3.5 Maximum loading capacity

The maximum loading capacity of WR towards Pb²⁺ ions in the fixed bed column was found to be 55.0 mg g⁻¹. The loading capacity attained by the WR towards Pb²⁺ ions was compared with other adsorbents reported in literature and was found to be high (Table 6).

Table 6 Comparison of maximum Pb²⁺ ions loading capacity of WR with other reported adsorbents

Adsorbent	Loading capacity (mg g^−1)	Reference
a Fixed bed column study.
Ficus religiosa leaves	37.4	30
Mustard husk	30.4	31
Saw dust	21.0	32
Modified peanut husk	29.1	32
Sago waste	46.6	33
Papaya wood	17.4	34
Barley straws	23.2	35
Pomegranate peel	13.8	36
Banana peel	41.4	37
Watermelon rind^a	55.0	This study

---

4 Conclusion

Watermelon rind, an agro waste, was employed as an adsorbent for the removal of Pb²⁺ ions from aqueous solution. Fixed bed column studies were employed by varying the parameters such as flow rate, bed height and initial metal ion concentration. The column removal efficiency decreased with the increase in flow rate and the removal efficiency increased with the increase in bed height. The breakthrough curves obtained were successfully predicted with mathematical models such as the Adams–Bohart, Thomas and Yoon–Nelson models. It was found that the Thomas and Yoon–Nelson models fit well to the breakthrough curves and can be used in real time large scale industrial treatment processes. Successful desorption and regeneration of the adsorbent demonstrated the economical value of WR in the treatment of waste water.

Notes and references

1. S. Mohan and G. Sreelakshmi, J. Hazard. Mater., 2008, 153, 75.
2. O. Keskinkan, M. K. L. Goksu, A. Yuceer, M. Basibuyuk and C. F. Forster, Process Biochem., 2003, 39, 179.
3. E. Malkoc, Y. Nuhoglu and Y. Abali, Chem. Eng. J., 2006, 119, 61.
4. P. D. Saha, S. Chowdhury, S. Datta and S. K. Sanyal, Korean J. Chem. Eng., 2012, 29, 1086.
5. S. Y. Quek and B. Al-Duri, Chem. Eng. Process., 2007, 46, 477.
6. S. Chowdhury and P. D. Saha, Korean J. Chem. Eng., 2013, 30, 369.
7. S. Inbaraj and N. Sulochana, Bioresour. Technol., 2004, 94, 49.
8. P. D. Saha, S. Chakraborty and S. Chowdhury, Colloids Surf., B, 2012, 92, 262.
9. M. Iqbal, A. Saeed and S. I. Zafar, J. Hazard. Mater., 2009, 164, 161.
10. W. Li, Q. Yue, P. Tu, Z. Ma, B. Gao, J. Li and X. Xu, Chem. Eng. J., 2011, 178, 197.
11. S. Chowdhury and P. D. Saha, Environ. Prog. Sustainable Energy, 2013, 32, 633.
12. S. Chowdhury and P. D. Saha, Environ. Sci. Pollut. Res., 2013, 20, 1050.
13. L. R. Veeranjaneya, Y. K. Kumar, L. P. Anjaneya and O. V. Sarathi, Process Biochem., 2008, 43, 748.
14. A. M. Rimando and P. M. Perkins-Veazie, J. Chromatogr. A, 2005, 1078, 196.
15. A. Mort, Y. Zheng, F. Qiu, M. Nimtzc and G. Bell-Eunice, Carbohydr. Res., 2008, 343, 1212.
16. S. Y. Quek, N. K. Chok and P. Swedlund, Chem. Eng. Process., 2007, 46, 386.
17. A. G. El-Said, J. Am. Sci., 2010, 6, 143–150.
18. B. M. W. P. K. Amarasinghe and R. A. Williams, Chem. Eng. J., 2007, 132, 299.
19. S. S. Baral, N. Das, T. S. Ramulu, S. K. Sahoo, S. N. Das and G. R. Chaudhury, J. Hazard. Mater., 2009, 161, 1427.
20. A. A. Ahmad and B. H. Hameed, J. Hazard. Mater., 2010, 175, 298.
21. P. A. Kumar and S. Chakraborty, J. Hazard. Mater., 2009, 162, 1086.
22. V. Vinodhini and N. Das, Desalination, 2010, 264, 9.
23. G. Bohart and E. Q. Adams, J. Am. Chem. Soc., 1920, 42, 523.
24. W. W. Eckenfelder Jr, Industrial Water Pollution Control, McGraw Hill, USA, 1989, p. 273.
25. M. Lehman, A. I. Zouboulis and K. A. Matis, Environ. Pollut., 2001, 113, 121.
26. H. C. Thomas, J. Am. Chem. Soc., 1944, 66, 1466.
27. Y. H. Yoon and J. H. Nelson, Am. Ind. Hyg. Assoc. J., 1984, 45, 509.
28. G. Yan and T. Viraraghavan, Bioresour. Technol., 2011, 78, 243.
29. Z. Aksu and F. Gonen, Process Biochem., 2004, 39, 599.
30. T. K. Naiyaa, A. K. Bhattacharya, S. Mandal and S. K. Das, J. Hazard. Mater., 2009, 163, 1254.
31. A. K. Meena, K. Kadirvelu, G. K. Mishraa, C. Rajagopal and P. N. Nagar, J. Hazard. Mater., 2008, 150, 619.
32. Q. Li, J. Zhai, W. Zhang, M. Wang and J. Zhou, J. Hazard. Mater., 2007, 141, 163.
33. S. Y. Quek, D. A. Wase and C. F. Forster, Water SA, 1998, 24, 251.
34. A. Saeed, M. W. Akhtar and M. Iqbal, Sep. Purif. Technol., 2005, 45, 25.
35. E. Pehlivan, T. Altun and S. Parlayýcý, J. Hazard. Mater., 2009, 164, 982.
36. G. Annadurai, R. S. Juang and D. J. Lee, J. Hazard. Mater., 2002, 92, 263.
37. E. S. Z. El-Ashtoukhy, N. K. Amin and O. Abdelwahab, Desalination, 2008, 223, 162.

---