In situ tryptophan-like fluorometers: assessing turbidity and temperature effects for freshwater applications

Abstract

Tryptophan-like fluorescence (TLF) is an indicator of human influence on water quality as TLF peaks are associated with the input of labile organic carbon (e.g. sewage or farm waste) and its microbial breakdown. Hence, real-time measurement of TLF could be particularly useful for monitoring water quality at a higher temporal resolution than available hitherto. However, current understanding of TLF quenching/interference is limited for field deployable sensors. We present results from a rigorous test of two commercially available submersible tryptophan fluorometers (ex ∼ 285, em ∼ 350). Temperature quenching and turbidity interference were quantified in the laboratory and compensation algorithms developed. Field trials were then undertaken involving: (i) an extended deployment (28 days) in a small urban stream; and, (ii) depth profiling of an urban multi-level borehole. TLF was inversely related to water temperature (regression slope range: −1.57 to −2.50). Sediment particle size was identified as an important control on the turbidity specific TLF response, with signal amplification apparent <150 NTU for clay particles and <650 NTU for silt particles. Signal attenuation was only observed >200 NTU for clay particles. Compensation algorithms significantly improved agreement between in situ and laboratory readings for baseflow and storm conditions in the stream. For the groundwater trial, there was an excellent agreement between laboratory and raw in situ TLF; temperature compensation provided only a marginal improvement, and turbidity corrections were unnecessary. These findings highlight the potential utility of real time TLF monitoring for a range of environmental applications (e.g. tracing polluting sources and monitoring groundwater contamination). However, in situations where high/variable suspended sediment loads or rapid changes in temperature are anticipated concurrent monitoring of turbidity and temperature is required and site specific calibration is recommended for long term, surface water monitoring.

---

Environmental impact

Tryptophan-like fluorescence (TLF) has been highlighted as a viable method to address the increasing need to monitor organic matter in natural and engineered water bodies. The development of commercially available, field deployable, TLF fluorometers offers a sensitive, reagent-less method, for real-time monitoring of reactive organic carbon. However, understanding of turbidity and temperature effects are limited. We have developed a correction procedure to improve in situ TLF measurement. Real time monitoring of TLF, has the potential to improve monitoring resolution for a range of environmental applications including tracing polluting sources and monitoring groundwater contamination. However, if correction factors are not applied, in situ TLF fluorometers may be subject to significant error that must be considered when interpreting these data.

Introduction

Due to the recent developments in field-deployable optical sensor technology, continuous quantification and characterisation of dissolved organic matter (DOM) is now possible.^1–3 Tryptophan-like fluorescence (TLF), at excitation (emission) wavelengths of ∼280 nm (∼350 nm), has been identified as a useful indicator of human influence on surface water^4,5 and groundwater quality.^6–8 In urban or agricultural systems TLF peaks are often associated with the input of labile organic carbon (e.g. sewage or farm waste) and products of its microbial breakdown.⁵ The precise composition of the constituent compounds associated with TLF is still debated (most likely a heterogeneous mixture of free amino acids and proteinaceous materials).⁹ Nevertheless, strong correlations between TLF and a range of water quality parameters have been reported including: Biological Oxygen Demand (BOD);^5,10 Chemical Oxygen Demand (COD)^10,11 and bacteria index organisms.¹² Hence, real-time recording of TLF could potentially be invaluable for monitoring waste water and drinking water treatment processes, identifying inter alia cross connected sewers and contamination events, at higher temporal resolution than available hitherto.^11,13 However, despite the potential utility of this new sensor technology, particularly when compared to traditional wet chemistry methods, relatively little is known about performance in the laboratory or field.

Compared to marine systems, where many commercially available fluorometers were designed to be deployed, the environmental conditions of freshwater systems can be highly dynamic in space and time.^14,15 Hence, there are a number of challenges associated with monitoring fluorescence in freshwaters that need careful consideration before sampling regimes are designed or measurements interpreted.^16,17 In particular, the optical properties of fluorescent molecules or compounds (fluorophores) have been shown to display sensitivity to a wide range of quenchers (dynamic/static) and ‘matrix effects’.^17–19

The influence of solution or matrix temperature on fluorescence intensity has long been recognised.²⁰ Higher temperature increases collisional quenching and thus the chance that an excited electron will return to the ground energy state via a radiationless pathway.^21,22 A recent study has indicated that diurnal temperature variations are a key driver of uncorrected observation of diel CDOM (Chromophoric Dissolved Organic Matter) cycles and, in the absence of correction, spurious inferences regarding biogeochemical processing may be made.²³ However, while temperature compensation methods have been developed and corrections applied to in situ fluorometer records, the degree to which variability in: (i) DOM composition; and, (ii) sensor specific optical design and configuration, influences correction factors requires further study.^16,23,24

Suspended particles in the water column constitute another key challenge to in situ monitoring of TLF and can cause both increased scattering and attenuation of excitation and emission light.¹ A recent study investigating the challenges to deployment of in situ CDOM fluorometers identified that at >400 NTU (water turbidity was used a surrogate for suspended particle concentration) the fluorescence signal can be reduced by ∼80%.¹⁶ Yet despite the influence of particle size and shape for quantifying suspended sediment (SS) concentration using optical technologies,²⁵ the influence of such properties on TLF remains unknown. Saraceno et al.¹ highlighted the potential for in-line filtration of water samples as a method to remove particle interference. Analysis is possible bankside, using thru-flow fluorometers; however, the frequency of filter replacement and maintenance requirements in high sediment environments may render this approach impractical in systems with high SS loads.²⁶ Hence, further work is needed to constrain algorithms for correcting unfiltered optical systems.¹⁶

Given the need for high temporal resolution records of DOM,²⁷ real-time sensor technologies provide an increasingly viable and cost effective solution. However, proof of concept through rigorous testing is urgently required as tryptophan-like fluorometers are already beginning to be adopted by academics and practitioners alike. Furthermore, as changes to European legislation increasingly put the onus of water quality compliance on industry, a cost effective and robust solution for monitoring waste water discharge and infrastructure is required.²⁸ Hence, it is clear that an understanding of sensor measurement repeatability/transferability and interaction with environmental parameters (e.g. temperature and SS) is needed including correction of quenching/matrix interference.¹⁶ To address this knowledge gap rigorous laboratory tests, conducted on two commercially available, submersible tryptophan-like fluorometers, were coupled with field trials involving: (i) deployment in a ‘flashy’ urban stream, (the Bourn Brook, Birmingham, UK) with aging waste water infrastructure and known water quality problems;^21,29 and (ii) an urban multi-level borehole with low levels of sewage associated microbial contamination.³⁰

Methods

Sensor characteristics

Laboratory and field trials were conducted on two commercially available tryptophan-like field fluorometers. The sensors: Cyclops 7™ (Turner Designs, Sunnyvale, USA) and UviLux (Chelsea Technologies Group Ltd., West Molesey, UK), are herein referred to as TU and CH, respectively. The key optical, mechanical and electrical specifications are summarised in Table 1. Briefly, the differences between the sensors included sensor size, weight, output of the light-emitting diodes (LEDs), wavelengths of the excitation and emission peaks, unit age and manufacturer specified minimum detection limit and dynamic range (Table 1). Furthermore, sensor CH houses a photomultiplier tube and in this study was used as a stand-alone unit whereas TU was integrated with a multi-parameter Sonde (Manta 2, Eureka Environmental, Austin, USA). For initial calibration experiments and borehole tests two units for each manufacturer were used and are referred to as TU1, TU2, CH1 and CH2. For the temperature and turbidity trials, TU2 was not available.

Table 1 Manufacturer stated properties (mechanical, optical and electrical) of the tryptophan-like fluorometers used in this study

	Turner (Cyclops 7)	Chelsea (UviLux)
Dimensions	22 × 145 mm	70 × 149 mm
Weight (in air)	142 g	800 g
Depth rating	300 m	>50 m
Path type (detector angle)	Open (90°)	Open (90°)
Excitation (nm) ± bandpass (nm)	285 ± 10	280 ± 30
Emission (nm) ± bandpass (nm)	350 ± 55	365 ± 50
Detection limit (ppb)	3.00	0.02
Dynamic range (ppb)	0–20 000	CH1 0–1000, CH2 0–800
Supply voltage range	3–15 Vdc	3–15 Vdc
Power consumption	<0.3 Watt	<1 Watt
Signal output	0–5 Vdc	0–5 Vdc
Sensor age	TU1: 2 years, TU2: 1.5 years	CH1: 2 years, CH2: 2.5 years

---

Standard solutions and calibration

Calibration standards were prepared using L-tryptophan, purchased from Acros Organics, USA (≥98%), and Milli-Q ultra-pure water (18.2 MΩ⁻¹). A tryptophan stock solution (1000 ppm) was used to prepare standards that ranged from 1–1000 ppb. Standard solutions were prepared daily, while the stock solution was stored at 4 °C for a maximum of 72 h. Before analysis all standards were equilibrated in a temperature controlled dark room (20 °C) and their temperature confirmed using a HI 935005 meter (Hannah instrument, Rhode Island, USA: accuracy ± 0.2 °C). All solutions had a final volume of 1 L and were stored in acid washed (HCl 0.5 M), glass volumetric flasks. Measurements of standard solutions were completed in a 2 L glass beaker placed within a non-reflective black bucket to avoid spurious readings due to scattering and reflection. Sensors were clamped to ensure measurement location within the beaker was consistent between readings. Solution temperatures were periodically checked throughout the measurement runs to account for any increase in temperature. For the measurement of each standard the sensor was allowed 1 min to stabilize, before logging 10 readings at 10 s intervals. Between each solution measurement the sensors and beaker were thoroughly rinsed in ultra-pure water and the optics wiped with a lens cloth. The measurement series was repeated twice on separate days and varied by an average of ∼3%. A 10 mL sub-sample was taken from each standard solution and TLF intensity determined, within 1 h, using a bench-top scanning fluorometer (see below for analytical procedure).

Assessment of temperature effects

To determine the effect of temperature on the TLF signal of the experimental sensors, readings were logged over a warming and cooling cycle that ranged from 5–35 °C for four tryptophan concentrations (10, 25, 50 and 100 ppb). Sensors and standard solutions were first cooled in a dark room at constant temperature (5 °C) and then transferred to a MLR-352, 294 L programmable incubator (Sanyo, Osaka, Japan). The sensors were interfaced with a CR-1000 data logger (Campbell Scientific, Logan, USA: 1 min logging) and submerged in a 2 L glass beaker containing 1 L of tryptophan standard. A thermistor (Campbell Scientific, 107 L: ±0.2 °C) was also submerged in each beaker and interfaced with the data logger. For each concentration run (n = 4) the temperature was gradually increased to 35 °C over a period of 4 h and then cooled to 5 °C at the same rate.²³

Assessment of turbidity effects

Two sediment types were chosen for the experiment based on particle sizes that are commonly observed during baseflow and high flow conditions in urban river systems:^31–33 (i) Fuller's Earth, a clay material (D₅₀ = 11.9 μm); and, (ii) silt collected from the outwash of a retreating glacier (D₅₀ = 52.1 μm). Following Gray et al.,³⁴ sediments were first treated with 30% hydrogen peroxide (H₂O₂) to remove any organic material. The treated sediments were then rinsed in deionised water and dried in an oven at 65 °C.

The impacts of turbidity were assessed for seven standard solutions (0, 10, 25, 50, 100, 250, 500 ppb) with independent runs for the two sediment types. Prior to measurement, all sensors and solutions were equilibrated in a temperature controlled darkroom (20 °C). Subsequently, standard solutions (1 L) were transferred to a 2 L glass beaker and constantly stirred on a magnetic stir plate. Weighed sediment was added incrementally (n = 14) to each standard to give a range of turbidity (0–1000 NTU). For each increment, turbidity was measured on five occasions using a nephelometric turbidimeter (McVan; Analite NEP 390, Scoresby, Australia, ±1%). The sensors were given 1 min to stabilize, before taking 5 readings at 10 s intervals. During the experimental runs, all sensors (fluorometers and turbidimeter) were suspended at a fixed location in the beaker to avoid edge effects. Temperature was measured periodically during each run to account for any warming due to the sustained stirring.

Development of correction factors

Temperature. Two approaches were adopted to develop correction factors to compensate for thermal quenching of the fluorescence signal. First, Ordinary Least Squares (OLS) regression was used to model the relationship between temperature and TLF signal for each reference standard.^23,35 The ratio of the slope : intercept (m/c) has been shown to be relatively constant regardless of fluorophore concentration and thus provides a robust temperature compensation coefficient.²³ Following Watras et al.²³ fluorophore concentration can be temperature compensated using the following equation:where TLF is tryptophan concentration (ppb), T is temperature (°C) and subscripts mes and ref represent the measured and reference values respectively. As the calibration and turbidity experiments were conducted at 20 °C this was chosen as the reference temperature for this study, thus T_ref = 20 °C and TLF_ref represents the tryptophan concentration at 20 °C. Hence, ρ is calculated as the quotient (m/c) at the reference temperature. Therefore, in this study the intercept used was calculated by solving the linear regression equation for T = 20.

Second the relationship between temperature and TLF quenching was modelled using an exponential relationship of the form:

TLF_mes = TLF_stde^{α(T_mes−T_ref)} (2)

where TLF_std is the concentration of the tryptophan standard solution and the decay constant (α) is estimated using nonlinear least squares regression. TLF_ref was subsequently calculated as follows:

Turbidity. Prior to model development, the data were split on the basis of turbidity to create 14 groups of similar NTU. The 95% confidence interval overlap between sensor specific turbidity concentration runs was then tested. Here the observed tryptophan value is analogous to the response variable in a linear model and the concentration (treated as a factor) is the predictor. When an overlap was detected (i.e. no significant difference between concentration) all values greater than or equal to the specific NTU were disregarded and the remaining data used to create the correction algorithm.

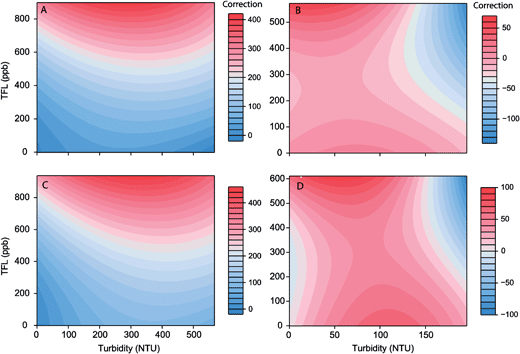
Due to the variability in turbidity response between sensors (see also ref. 16) and sediment types a generalized relationship could not be obtained. Hence, a statistical model fitting approach was adopted and complex polynomial regression models were developed for CH1 and TU1 (the sensors used in the urban river field trials) to provide correction values for scattering and attenuation of excitation and emission light related to suspended particles. The models consisted of two predictor variables: (i) turbidity (denoted below as a) and (ii) the difference between the measured and standard (i.e. 0 NTU) tryptophan signal (denoted below as b); and the response variable, correction factor (cf) that represented the differences between the measured and the blank signal (i.e. 0 NTU).

Preliminary analysis of the turbidity response suggested that a 3^rd order polynomial would be sufficient to model the data. A global model was first tested including all possible terms and interactions, followed by an iterative procedure to test all possible permutations of the terms in the global model. As we were wary of over fitting the model, the best correction algorithm was considered to be that which included only significant parameters (P < 0.05), retained high explanatory power, and had normally distributed residuals.³⁶ The final models for silt [eqn (4)] and clay [eqn (5)] were of the following forms:

cf = a + ab + a² + a²b² + b³ + a³b² (4)

cf = a + ab + a² + a²b² (5)

Data were then corrected by subtracting the cf (for the corresponding the turbidity and observed TLF signal) from the observed TLF signal.

Field trials

Urban stream. To assess the impact of: (i) field conditions on laboratory calibrated sensor readings and (ii) the suitability of the laboratory derived correction algorithms, continuous records and discrete samples were collected from the Bourn Brook, a tributary of the River Rea, Birmingham, UK (52°27′N, 1°54′W) between 23^rd Sept. and 15^th Oct. 2014. Carstea et al.³⁷ provide a detailed description of the basin characteristics; the catchment is 27.9 km² in area and urban/suburban land use covers ∼80% of the basin.³⁸ There are no wastewater treatment works within the catchment, but an extensive network of storm sewers and combined sewer overflows discharge to the main channel. Fluorometers TU1 and CH1 were deployed alongside: (i) a turbidimeter (Analite NEP 390), (ii) an integrated water temperature and electrical conductivity probe (247 L, Campbell Scientific); and (iii) a vented pressure transducer (CS420-L, Druck Inc., Billerica, Massachusetts). On three occasions, when high flow was anticipated, discrete 500 mL samples were collected at 30–60 min intervals, using an automatic pump sampler (3700, ISCO, Lincoln, USA). Samples were retained in acid washed HDPE bottles and kept cool within the pump sampler using ice packs. Samples were returned to the Water Sciences laboratory at the University of Birmingham for analysis within 24 h of collection. During Event 2 (see Fig. 5) six bulk water samples (10 L) were collected at roughly 1.5 h intervals during the rising and falling limbs of the hydrograph. Bulk samples were then analysed for particle size distribution using a Mastersizer 2000 (Malvern Instruments, Malvern, UK) following methods outlined by Phillips & Walling.³⁹

Groundwater. The borehole used in this study is located in Nottingham, UK (52°59′N, 1°10′W) and penetrates through the 42 m sequence of the unconfined Sherwood Sandstone Group aquifer.³⁰ There are multiple mudstone beds through the sequence, with the most significant positioned at 32 m below ground level (m bgl), which confines the underlying sandstones. The borehole is completed as a multi-level piezometer to enable samples to be obtained from eight specific intervals from 8.0–39.1 m bgl. In this locality, the aquifer is adversely impacted by sewer and septic tank leakage with bacteria index organisms and viruses detected throughout the sequence, but being more frequent at shallower depths.³⁰

Groundwater samples (∼5 L) were obtained from each piezometer, starting with the deepest, following the purging of three equivalent interval volumes. Samples were collected in an acid-washed black bucket (HDPE; previously confirmed not to leach fluorescent substances) in which field fluorometers, turbidimeter, thermometer (HI 935005), and pH and electrical conductivity (EC) sensors were submerged in-turn. All sensors were rinsed with the sample prior to submergence. Five TLF and turbidity readings were taken at 10 s intervals, having allowed 30 s for the sensors to stabilise. Finally, a fresh 10 mL sample was collected for each depth, kept in a cool box with ice, and analysed at the Birmingham Water Sciences Laboratory within 24 h of collection.

Analytical procedure and data processing

All field samples were filtered through Whatman GF/F glass fiber filter papers (pore size 0.7 μm) that had previously been rinsed in HCl and ultra-pure water then oven dried at 105 °C. Calibration standards and field samples were equilibrated in a temperature controlled lab (20 °C) before analysis. UV-visible absorbance spectra were collected using 10 mm path length quartz cuvettes on a Jenway 6800 dual beam spectrophotometer. Scans were conducted between 200–850 nm and continuously referenced to an ultra-pure water blank. For river samples dissolved organic carbon (DOC) was measured using a Shimadzu TOC-V CSH total organic carbon analyzer (Kyoto, Japan). Samples were acidified to pH 2, combusted at high temperature (0.5% platinum catalyst) and non-dispersive IR detection used to quantify DOC concentration. Replicate DOC readings (n = 3–5) indicated the coefficient of variation was ≤3%. Specific UV absorbance (SUVA₂₅₄) was calculated following Carstea et al.³⁷

Excitation-Emission Matrices (EEMs) were measured for each sample using a Varian Spectrofluorometer (Cary Eclipse) set to a scan rate of 9600 nm min⁻¹ and photomultiplier tube voltage of 725 V. A Raman blank (sealed cell) was recorded each instrument run and used to calibrate fluorescence intensity.⁴⁰ Standards and samples were excited between 200 nm and 400 nm (5 nm slit width), emission recorded 280–500 nm (2 nm slit width). EEMs were blank subtracted, corrected for inner-filter and instrument-specific spectral bias in Matlab (version 2011a) using the drEEM toolbox, following the protocol outlined by Murphy et al.⁴¹ TLF intensity was then extracted for the wavelength pairs matching those of the TLF fluorometers used in the study.

Statistical analysis

The minimum detection limit (MDL) of each sensor was calculated based on 10 replicate measurements of a series of low concentration samples (0–5 ppb) following Pellerin et al.⁴² Sensor precision was calculated as one over the coefficient of variation (i.e. precision = 1/CV) for repeated measurements (n = 10) taken for a low concentration (5 ppb) tryptophan standard.¹⁴ Sensor accuracy was calculated as one over the root mean square error (see eqn (3)) of the calibrated relationship (i.e. accuracy = 1/RMSE). Thus, for both sensor accuracy and precision a higher value represents greater accuracy/precision. Analysis of Variance (ANOVA) was used to test for differences between the MDL of the sensors. The Students t-test was adopted to test for difference between slopes (temperature quenching experiment) and temperature compensation factors for each sensor individually.

A suite of model efficiency statistics were employed to evaluate the performance of the temperature correction models following Moriasi et al.⁴³ The Nash–Sutcliffe coefficient (NS) for each model was calculated as follows:

Percent bias (PBIAS) was estimated using:

and the RMSE error to observation SD ratio (RSR):where Y^obs and Y^sim are the observed and corrected records respectively for n data records. PBIAS < 10% and RSR < 0.5 were considered to represent very good simulations.⁴³

To test the relationship between the submersible sensors during the surface water trial, Generalized Least Squares (GLS) regression was used. The regression model was of the following form:

C_lab = α + βC_field + ε (9)

where C = tryptophan concentration (ppb), α = the intercept, β = the regression coefficient and ε = the error term. Errors were treated as first order autoregressive correlation structures based on inspection and interpretation of autocorrelation functions.⁴⁴ To test the performance of the correction factors (turbidity and temperature) on the field data, RMSE and PBIAS was calculated for each event individually and all events combined. All plotting and statistical tests were carried out using R version 2.15.2.⁴⁵

Results and discussion

Response to calibration standards

All sensors tested displayed highly significant linear relationships (R² > 0.95, P < 0.001) with tryptophan concentration across the tested range (i.e. 0–1000 ppb for TU1, TU2, CH1 and 0–800 ppb for CH2) and no signal saturation or inner filtering effects were apparent (Fig. S1†). When converted to Raman Units (R.U) the upper limit of 1000 ppb equated to ∼2 R.U, which is a useful linear range for tracking point source pollution in both agricultural⁴⁶ and urban environments.⁴⁷

For the calibration curve and relationship with the Varian, all submersible sensor displayed similar slopes (∼1) and intercepts (≤0.15); however it is important to note that sensor TU1 was an older unit with an intercept significantly greater than the other three sensors (Table 2). This raises some important questions when considering the future development of real-time sensor networks, particularly the need to quantify inter-unit variability in optical configuration and deterioration of LED/photodiode efficiency.⁴⁸

Table 2 Calibration, precision and accuracy data for laboratory trial based on standard solution prepared with synthetic tryptophan (≥98%) in ultra-pure water (18.2 MΩ⁻¹)

	Turner 1	Turner 2	Chelsea 1	Chelsea 2
Calibrated relationship	y = 0.997x − 0.133	y = 1x + 0.0009	y = 1x − 0.00007	y = 1x + 0.00006
Relationship with Varian (ppb)	y = 0.99x − 0.1255	y = 1x + 0.0022	y = 1x + 0.0076	y = 0.99x + 0.0129
Relationship with Varian (R.U)	y = 0.002x + 0.0041	y = 0.002x + 0.0044	y = 0.002x + 0.0044	y = 0.002x + 0.0044
MDL ± SD	1.99 ± 0.53	1.92 ± 0.57	0.17 ± 0.06	0.19 ± 0.15
Precision (1/CV)	0.33	0.40	2.22	4.54
Accuracy (1/RMSE)	1.59	1.61	1.75	1.72

---

Minimum detection limits were significantly lower for CH sensors when compared to TU sensors (ANOVA; F_1,22 = 129.7, P < 0.001; Table 2). Sensor precision (1/CV) was greater for CH sensors compared to TU sensors (Table 2). Measurement accuracy (1/RMSE of the calibration curve) was greater for CH sensors when compared to TU sensors (TU sensors + 0.05 ppb; Table 2). Differences in the sensitivity and MDL can largely be attributed to sensor CH housing a photomultiplier tube,¹⁸ thus significantly increasing the intensity of emission light (Table 2). However, when planning field monitoring campaigns the greater sensitivity needs to be considered in combination with the increased size and weight of the unit relative to sensor TU (Table 1), making CH less readily integrated into a multi-parameter sonde for concurrent water temperature and turbidity measurement.

Temperature response and correction models

For all sensors tested (TU1, CH1 and CH2), TLF was negatively related to temperature and mean OLS slopes ranged from −1.57 ± 1.05 (TU1) to −2.50 ± 1.59 (CH1) (Fig. 1). Hysteresis loops were apparent for all sensors but were particularly pronounced for C sensors suggesting that the increased thermal capacity of the sensor housing (larger size; Table 1) contributed to lag times between solution and internal temperature of optics/electronics. Thermistor self-heating⁴⁹ and insufficient manufacturer LED temperature correction⁵⁰ could also lead to errors and potentially contributed to the hysteresis observed.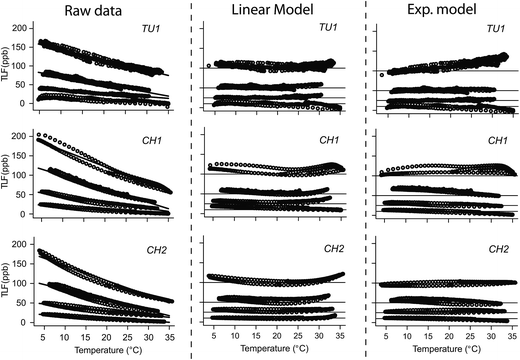

Fig. 1 Temperature effect on tryptophan-like fluorescence (TLF) at four concentrations (10, 25, 50 and 100 ppb) for three of the fluorometers listed in Table 2. The experimental temperature data (raw), ratio/linear temperature correction and exponential temperature correction are displayed.

A linear function fitted the data well for all sensors (R² > 0.9); however, for CH1 and CH2 there was a suggestion of non-linear behaviour at extreme high and low temperatures (>25 °C and <10 °C; Fig. 1). For both correction models the mean decay constant varied between sensors with the highest and lowest mean values for CH1 (ρ = −0.052, α = −0.051) TU1 (ρ = −0.039, α = 0.036) respectively (Table 3). For individual sensors values of α and ρ were comparable (see above) as were the CVs of α (range = 0.27–0.34) and of ρ (range = 0.27–0.37).

Table 3 The slope, regression coefficients (temperature compensation) and model performance results for the linear and exponential correction models. CV = coefficient of variation, NSE = Nash–Sutcliffe Efficiency, RSR = ratio of RMSE to the standard deviation of the observations and Bias% is the percent bias

Sensor type	Unit (fluorophore)	Linear model				Model performance			Exponential model		Model performance
		Slope (mean ± SD)	CV	Temperature coefficient (mean ± SD)	CV	NSE	RSR	Bias%	Decay constant (mean ± SD)	CV	NSE	RSR	Bias%
Tryptophan	TU1 (L-tryptophan)	−1.57 ± 1.05	0.67	−0.039 ± 0.0145	0.37	0.93	0.27	10.6	−0.036 ± 0.012	0.34	0.84	0.41	10.5
	CH1 (L-tryptophan)	−2.50 ± 1.59	0.63	−0.052 ± 0.0146	0.28	0.94	0.25	11.8	−0.051 ± 0.015	0.28	0.87	0.36	16.3
	CH2 (L-tryptophan)	−2.06 ± 1.44	0.70	−0.045 ± 0.0123	0.27	0.94	0.23	11.0	−0.044 ± 0.012	0.27	0.98	0.15	4.3

---

The changes in fluorescence intensity observed in this study are higher than those reported in studies exploring the thermal quenching of humic-like material in the laboratory^22,51 and where fluorometers have been deployed in the field (ρ = −0.009–−0.025).^16,23,52 This marked difference in temperature induced intensity attenuation highlights the need to consider DOM composition when developing temperature correction algorithms and correcting field data.^21,24,51 This is also supported by a recent study that identified the importance of seasonal changes in temperature compensation factors.⁵² The results also suggest that temperature quenching is more pronounced for TLF when compared to the fluorophore CDOM submersible fluorometers target.²¹ Further work is required to explore the influence of different matrix waters on the thermal quenching of TLF for submersible sensors and identify potential errors associated with using an idealized, pure tryptophan standard (i.e. ultra-pure water and a synthetic tryptophan standard).

The correction models for all sensors displayed positive bias, i.e. there was a tendency for the corrected data to be greater than the reference data, but this varied between sensor and correction model. While both correction approaches performed well for all sensors (Table 3), the linear correction model performed slightly better than the exponential correction model for TU1 and CH1 (i.e. lower NSE, RMSE and Bias) and the exponential model performed slightly better for CH2. These results highlight the need for current users of tryptophan-like fluorometers to consider temperature effects during calibration and field measurement, and ideally instrument specific correction algorithms should be developed pre/post deployment. Furthermore, instrument manufactures should begin to develop internal temperature correction factors, similar to those that are routine for electrical conductivity and pH sensors.⁵³

Turbidity response and correction models

The effects of turbidity on TLF were pronounced and appeared to be non-linear, but stable (i.e. smooth response shape and repeatable between tryptophan concentrations), across the range tested during this experiment (Fig. 2). Differences in the response shape and magnitude were greater between sediment types (i.e. clay vs. silt) than between sensor units (i.e. CH1 vs. TU1), though still apparent between the different sensors.

Fig. 2 Sensor response to turbidity for a range of tryptophan concentrations (0, 10, 50, 100, 250, 500 ppb). Each panel represents an individual sensor and sediment combination. Error bars displayed, horizontal and vertical, represent ±1SD.

For the silt runs, the TLF signal increased rapidly to a maximum between 100–300 NTU (depending on the sensor), and then decreased gradually to 1000 NTU with little evidence of signal attenuation, likely due to stray light leaking through the emission filter. The response was markedly different for the clay sediment; readings increased rapidly to a maximum between 25–100 NTU then decreased rapidly to 600 NTU and reached an asymptote. Signal attenuation was apparent at >200 NTU (Fig. 3).

Fig. 3 Representation of the regression surface as a function of the two predictor variables: (i) turbidity and (ii) observed tryptophan concentration. Filled contours represent the regression model output, i.e. the correction factor to be applied. Panels A and C represent the silt models for sensors TU1 and CH1 respectively. Panels B and D represent the clay models for sensors TU1 and CH1 respectively.

For the silt, TU1 (250 ppb standard) displayed the lowest increase in signal (75.3%) at 12.6 ± 2.2 NTU, while CH1 displayed the greatest increase (82.9%), at 296.2 ± 7.7 NTU (Fig. 3). Interestingly, at ∼1000 NTU the TLF was attenuated for TU1 but was still amplified for CH1 relative to the 0 NTU reference.

For the clay, TU1 (250 ppb standard) displayed the lowest increase 7.2% increase observed at 32.9 ± 0.9 NTU while the greatest increase in TLF 20.6% was observed for CH1 at 62.5 ± 9.6 NTU. At ∼1000 NTU the sensor reading was less than the 0 NTU reference for both TU1 (73%) and CH1 (70%).

When considering these results in the context of the generalized equations and theories describing the interaction of light and matter⁵⁴ there appears to be a plausible physical basis for the observed patterns. In the experimental situation presented here (and in most freshwater environments) particles are larger than the wavelength of the interacting UV light, thus the Mie approximation can be adopted.⁵⁵ Using this set of theoretical assumptions we would expect the larger silt particles to scatter light more efficiently than the smaller clay particles,⁵⁵ hence the differences in response between the clay and silt are likely to be due to increased stray light reaching the fluorometer photodiode for silt particles. This phenomenon of stray light leaking through the emission filter has been reported for Chl a fluorometers deployed in the marine environment.^56,57 Another plausible hypothesis is that as the adsorption capacity for proteinaceous material of clay particles is greater than silt particles,⁵⁸ an attenuated signal is observed for clay relative to silt.

The increase in TLF intensity at low to moderate turbidity observed in our study does not conform with the findings of Downing et al.¹⁶ or Saraceno et al.¹ who both reported attenuation of CDOM fluorescence intensity at both low and high turbidity. In a laboratory study Downing et al.¹⁶ reporting that at 35 NTU (clay-loam material) 22% of the fluorescence signal was lost. Similarly, Saraceno et al.¹ identified an 8% reduction at 50 NTU (predominately clay-loam) in a field based study. It is possible that an organic coating on particles could cause increased fluorescence at low to moderate turbidity; however, as we removed these using H₂O₂ prior to running the experiment this mechanism appears not to apply in this case (i.e. the increase in fluorescence intensity at low to moderate turbidity). Therefore we propose the most plausible explanations for differences observed between the two fluorometer types are (i) the shorter excitation wavelength (285 nm) used in tryptophan-like fluorometers is scattered more efficiently (i.e. increased potential for stray light reaching the photodiode⁵⁷) than the longer wavelength (360 nm) used in CDOM fluorometers,⁵⁵ and; (ii) the removal of organic material from the experimental sediments (H₂O₂ treatment) used in this study increased the ratio of ‘hard’ to ‘soft’ scatterers²⁵ and thus reduced absorption relative to the untreated sediments used by Downing et al.¹⁶

For the silt dataset, 95% CI (confidence interval) overlap was detected for the 700–800 NTU group for TU1, the 800–900 NTU group for CH1 and not detected for CH2. Hence, for comparability between sensors all turbidity correction models were created for data covering the range 0–700 NTU. For the clay dataset 95% CI overlap was detected for the 200–300 NTU group for all sensors, thus, models were created for records ≤200 NTU. For each sediment type the ‘best’ model consisted of the same terms for both sensors (silt: 7 terms; clay: 5 terms). All models appeared to reproduce the response observed in laboratory data reasonably well (R² > 0.6); however, the silt models displayed better agreement with the laboratory data than the clay model (Table 4). Whilst the model parameters were similar for both sensors when considering the silt particles, for the clay particles the model regression surface highlighted a marked difference in the values of the regression parameters (Fig. 3). This highlights the need for both site and sensor specific turbidity compensation.

Table 4 Turbidity correction model results. Here cf is the correction factor, a is the turbidity (NTU) and b is the difference between the standard (0 NTU) and the measured tryptophan-like fluorescence

Sensor (sediment)	Formula	F	R	P
TU1 (silt)	cf = a + ab + a^2 + a^2b^2 + b^3 + a^3b^2	15736,214	0.97	<0.001
CH1 (silt)	cf = a + ab + a^2 + a^2b^2 + b^3 + a^3b^2	24886,217	0.98	<0.001
TU1 (clay)	cf = a + b + a^2 + a^2b^2 + a^3	65.45,194	0.63	<0.001
CH1 (clay)	cf = a + b + a^2 + a^2b^2 + a^3	917.15,194	0.83	<0.001

---

Field trials

Urban stream.
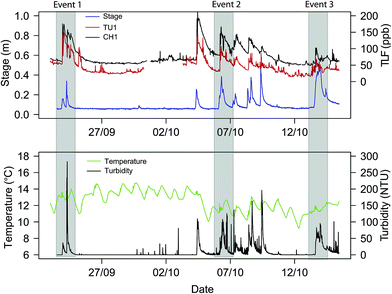
In situ records. For the storm events characterized, (n = 3; Fig. 4), the maximum river stage was recorded during Event 3 (0.54 m) and maximum turbidity during Event 1 (283.4 NTU). For all events the relationship between stage and turbidity was complex, with secondary peaks and ‘turbidity shoulders’ apparent, suggesting heterogeneous sediment sources.⁵⁹ However a reduction in maximum turbidity from Event 1–3 suggests sediment exhaustion may have occurred.²⁶ Water temperature ranged between 11.1–13.7 °C and storm events appeared to interrupt the diurnal cycle (Fig. 4). Raw TLF was relatively low (predominately <60 ppb) during base flow with the highest TLF value recorded during Event 1 of 175.8 ppb and 136.5 ppb for CH1 and TU1, respectively (Fig. 4). In Event 1 a classic ‘first flush’ type response was exhibited in which a large amount of labile organic matter was mobilized for a modest increase in flow (ESI, Fig. S2†). This was likely due to low antecedent rainfall (7 day = 1.6 mm) enabling a build-up of organic material that was then rapidly flushed from Combined Sewage Overflows (CSOs) and other drainage structures close to the sampling point.⁶⁰ A significant relationship between TU1 and CH1 was apparent (TU1: co-eff. = 1.19 ± 0.03, t-value = 36.75, P < 0.001); however, TU1 readings were lower during baseflow and high flow periods, for all events, when compared to CH1 (ESI, Fig. S2–S4†). The mean suspended sediment particle size (54.16 ± 17.15 μm) for Event 2 is similar to that of coarse silt; however, at low flow mean sediment size was smaller (36.82 μm; medium silt) than at peak flow (80.81 μm; very fine sand).

Fig. 4 Hydrological variables recorded at the Bourn Brook test site (23/09/2014–30/09/2014). Upper panel displays river stage and raw Tryptophan-Like Fluorescence (TLF); the lower panel displays water temperature and turbidity. The three events when discrete sampling was undertaken to complement the in situ sensor records are highlighted in grey.

Relationship between laboratory and in situ fluorescence. The general pattern displayed in the laboratory samples was similar to that of the in situ sensors. Low TLF was recorded during base-flow with an increase of between ∼80 ppb (Event 1) and ∼30 ppb (Event 3) during storm flow conditions. For both CH1 and TU1, systematic over-estimation of in situ TLF was apparent when compared to the discrete, laboratory analysed, samples (Table 5; Fig. 5). The temperature correction improved the agreement; however a significant positive bias (in situ > lab) was still apparent for both sensors but more pronounced for CH1 (Table 5), most likely due to the increased sensitivity to suspended particles (Fig. 2). The combined temperature and turbidity correction further improved agreement but, interestingly, the best fit appeared to differ for TU1 (silt + T_w) and CH1 (clay + T_w). This may have been due to fine scale hydraulic variability influencing SS particle size and load⁶¹ and as the turbidity sensor was mounted in the sonde (close to TU1) it was likely more representative of conditions close to TU1 rather than CH1. We therefore recommend that turbidity measurements are made as close as possible to TLF measurments to improve the accuracy of compensation algorithms for surface water installations.

Table 5 Summary of regression goodness of fit metrics testing agreement between in situ data correction methods and laboratory measurements

		RMSE (ppb)		PBIAS (%)
		TU1	CH1	TU1	CH1
All	Raw	31.46	49.6	49.6	82.2
	T w	16.8	21.99	21.99	32.1
	Clay	26.1	18.28	33.6	−0.6
	Silt	11.02	18.52	−1.2	−20.4
Event 1	Raw	45.4	34.05	62.7	74.3
	T w	20.43	23.19	27.6	31.4
	Clay	29.85	13.19	40.2	11.9
	Silt	10.02	29.15	8.41	−34.5
Event 2	Raw	27.59	63.54	47.2	112.9
	T w	19.18	27.33	25.7	43.3
	Clay	30.64	14.7	43.1	−11.2
	Silt	11.56	16.55	3.3	17.2
Event 3	Raw	11.86	26.21	17.2	54.1
	T w	8.19	6.88	9.8	10.3
	Clay	12.1	13.78	7.2	−23.5
	Silt	10.82	23.11	−15.5	−34.1

---

Fig. 5 Relationship between in situ and lab TLF for the storm events characterised. Raw records, temperature corrected (T_wcorr), clay particle size plus temperature corrected (clay + T_wcorr) and silt particle size plus temperature corrected (silt + T_wcorr) are displayed for comparison. Black line is 1 : 1.

The agreement between in situ and laboratory readings was generally improved when events were considered individually (Table 5). It is important to note that for Event 2 samples are distributed across the 1 : 1 line for both sensors when a silt correction is applied (Fig. 5) in agreement with the mean D₅₀ for this event (54.16 ± 17.16 μm; ESI, Fig. S3†). When examining relationships between raw/corrected (in situ) and laboratory TLF; Event 1 displayed the least scatter and appeared to represent a classic first flush type response (ESI, Fig. S2†).²⁶ Conversely for Events 2 & 3 scatter was apparent in the raw/T_w data and this was increased by turbidity correction. For both events rainfall was prolonged with episodes of varying intensity, and turbidity dynamics were also complex (ESI, Fig. S3 and S4†), suggesting multiple/varying sediment sources during these events.²⁶

Changes in organic matter source, concentration and composition were also likely between events, as DOC concentrations and SUVA₂₅₄ varied (ESI, Fig. S2–S4†). In particular the changes in the SUVA₂₅₄ from Event 1 (2.01 ± 0.14) to Event 3 (2.84 ± 0.14) suggest an increase in the hydrophobic, humic contribution to bulk DOM.⁶² It has been suggested that to represent changes in DOM quantity using a single excitation–emission pair the composition must be stable, thus to represent DOM dynamics completely it may be necessary to explore the use of multiple wavelength pairs.⁴⁶ A particularly promising approach would be the ratio of TFL to CDOM (peak T/C ratio) that can conceptually be considered a DOC/BOD ratio.^37,48 Furthermore increases in DOM concentration can lead to in situ signal attenuation due to inner filtering. While this was not explored in this study it has been suggested that at ∼0.2A₂₅₄ (the maximum absorbance observed in this study) ≤10% of the signal is attenuated for CDOM sensors.¹⁶

Groundwater. There was a clear gradient of decreasing TLF with depth for all submersible fluorometers (Fig. 6). Changes in turbidity (0.45 ± 0.33 NTU; mean ± SD), temperature (13.14 ± 0.53 °C), and pH (7.8 ± 0.07) were minimal between intervals. SEC data show a similar depth profile to TLF suggesting that increases in SEC are likely to be linked to waste water, i.e. leakage from the sewer network and septic tanks. Furthermore, it appears that the mudstone band at 32 m bgl is limiting the ingress of wastewater deeper into the aquifer.

Fig. 6 Depth profiles for tryptophan-like fluorescence signal, grey-scale bars represent the in situ measurements (temperature corrected) undertaken at the Nottingham borehole site, the red bar represents laboratory measurement using a Varian scanning fluorometer. RMSEs are displayed in the figure legend.

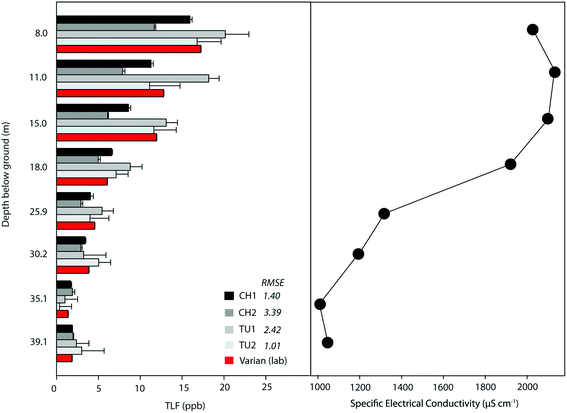
There was a strong correlation between laboratory and raw in situ TLF for all fluorometers (ρ > 0.95), with minimal differences (Fig. 6). Temperature correction of the data modified the TLF by between 12 and 22%, for TU1 and CH1, respectively. However, this only marginally improved the RMSEs given the low TLF (Fig. 6). This highlights the utility of in situ fluorometers for groundwater applications where, generally, temperature is perennially stable and turbidity is very low. Consequently, correction factors may be unnecessary in many groundwater systems, with the exception of shallow (e.g. riparian alluvials) and karstic aquifers.

Conclusions and recommendations

This study has highlighted the potential utility of field deployable, tryptophan-like fluorometers for monitoring surface- and ground-water quality. Due to their high sensitivity, small size (portable), relatively low cost, and maintenance requirements, this technology has distinct advantages enabling high resolution data in remote locations. There is; however, a need to carefully consider ambient environmental conditions as TLF intensity is sensitive to matrix water properties. Using laboratory and field data we have shown that with concurrent monitoring of potential TLF interferents, field data can be standardized to improve accuracy. Despite the apparent ease of this procedure it is important to remember that temperature quenching is sensitive to fluorophore composition.²⁴ Therefore when permanent (static) installation is expected, matrix waters should ideally be used for deriving compensation algorithms. If this is not feasible (i.e. when a fluorometer is used as a mobile unit) a standardized material, such as L-tryptophan, is recommended. Furthermore manufacturers should incorporate temperature compensation algorithms into frontend processing and practitioners should correct field data to 20 °C, or at a minimum report ambient temperature to allow comparisons between studies.

Our findings also highlight the sensitivity of TLF sensors to suspended particles and we recommend that when high/variable suspended sediment loads or rapid changes are anticipated concurrent monitoring of turbidity is required. Hence, for certain applications (e.g. surface water monitoring) compensation algorithms are essential or if high turbidity is expected in-line filtration may be the most viable option. While for other applications (such as groundwater monitoring) this may not be necessary. Sediment particle size specific responses to turbidity increases were also identified and warrant the need for both site and instrument specific calibrations when undertaking long term monitoring. Furthermore, it is important to acknowledge errors associated with compensation under high turbidity and report these accordingly.

The results also suggest circumstances when differences between field and laboratory measurements may be ‘real’, as larger biological particles (i.e. many microbial cells) have been shown to make a significant contribution to TLF⁶³ and could be removed through filtration. Hence, further work is required to optimize filter pore size to the size fraction TLF is anticipated to predominate, whilst still accounting for inorganic particle interference. Finally, we emphasize the need to consider carefully potential interferents and the likely range to be exhibited; and if frequent high sediment loads (NTU > 650) are anticipated then accuracy/repeatability may be severely impaired (i.e. pre-treated sewage). Hence, for surface water applications without site specific calibration TLF sensors are best employed as qualitative indicators of organic enrichment and can be used to trace point source pollution. However, for treated effluents, natural waters (with site specific calibration), drinking water infrastructure and groundwater aquifers quantitative in situ monitoring of reactive DOM using TLF submersible sensors represent a sensitive, cost-effective solution.

Acknowledgements

This research was supported by Innovate UK and represents outcomes from a Knowledge Transfer Partnership (KTP) between The University of Birmingham and RS Hydro (KTP no. 9623). The project was co-funded by The Engineering and Physics Research Council (EPSRC) and The Natural Environment Research Council (NERC). We are grateful to Peter Williams and Dr Philip Blaen for laboratory and field support. We also thank Richard Johnson, James Chapman and Ed Lang for logistical support and technical advice regarding installation and sensor calibrations. Finally, we thank Prof. Andy Baker and two anonymous reviewers for helpful comments that improved the manuscript.

References

1. J. F. Saraceno, B. A. Pellerin, B. D. Downing, E. Boss, P. A. M. Bachand and B. A. Bergamaschi, J. Geophys. Res., 2009, 114, G00F09.
2. M. Tedetti, P. Joffre and M. Goutx, Sens. Actuators, B, 2013, 182, 416–423.
3. P. Chen, D. Pan and Z. Mao, Opt. Laser Technol., 2014, 64, 213–219.
4. A. Baker and R. Inverarity, Hydrol. Processes, 2004, 18, 2927–2945.
5. N. Hudson, A. Baker, D. Ward, D. M. Reynolds, C. Brunsdon, C. Carliell-Marquet and S. Browning, Sci. Total Environ., 2008, 391, 149–158.
6. A. Baker and M. Curry, Water Res., 2004, 38, 2605–2613.
7. A. Baker and J. Lamont-Black, Groundwater, 2001, 39, 745–750.
8. D. J. Lapworth, D. C. Gooddy, A. S. Butcher and B. L. Morris, Appl. Geochem., 2008, 23, 3384–3390.
9. N. Maie, N. M. Scully, O. Pisani and R. Jaffé, Water Res., 2007, 41, 563–570.
10. J. Hur and J. Cho, Sensors, 2012, 12, 972–986.
11. J. Bridgeman, A. Baker, C. Carliell-Marquet and E. M. Carstea, Environ. Technol., 2013, 1–9.
12. S. A. Cumberland, J. Bridgeman, A. Baker, M. Sterling and D. Ward, Environ. Technol., 2012, 33, 687–693.
13. R. K. Henderson, A. Baker, K. R. Murphy, a. Hambly, R. M. Stuetz and S. J. Khan, Water Res., 2009, 43, 863–881.
14. M. Tedetti, C. Guigue and M. Goutx, Mar. Pollut. Bull., 2010, 60, 350–362.
15. C.-L. Ng, S. Senft-Grupp and H. F. Hemond, Limnol. Oceanogr.: Methods, 2012, 10, 978–990.
16. B. D. Downing, B. A. Pellerin, B. A. Bergamaschi, J. F. Saraceno and T. E. C. Kraus, Limnol. Oceanogr.: Methods, 2012, 10, 767–775.
17. J. A. Korak, A. D. Dotson, R. S. Summers and F. L. Rosario-Ortiz, Water Res., 2014, 49, 327–338.
18. J. R. Lackowicz, Principles of Fluorescence Spectroscopy, Springer, 3rd edn, 2006.
19. Z. Wang, J. Cao and F. Meng, Water Res., 2015, 68, 404–413.
20. R. W. Stoughton and G. K. Rollefson, J. Am. Chem. Soc., 1939, 62, 2264–2268.
21. A. Baker, Water Res., 2005, 39, 4405–4412.
22. A. Vodacek and W. D. Philpot, Rem. Sens. Environ., 1987, 21, 83–95.
23. C. J. Watras, P. C. Hanson, T. L. Stacy, K. M. Morrison, J. Mather, Y.-H. Hu and P. Milewski, Limnol. Oceanogr.: Methods, 2011, 9, 296–301.
24. E. M. Carstea, A. Baker, M. Bieroza, D. M. Reynolds and J. Bridgeman, Water Res., 2014, 61, 152–161.
25. C. J. Gippel, Hydrol. Processes, 1995, 9, 83–97.
26. D. M. Lawler, G. E. Petts, I. D. L. Foster and S. Harper, Sci. Total Environ., 2006, 360, 109–126.
27. R. C. Sandford, R. Bol and P. J. Worsfold, J. Environ. Monit., 2010, 12, 1678–1683.
28. EC, Seventh Report on the Implementation of the Urban Waste Water Treatment Directive (91/271/EEC), European Commission, Brussels, 2013.
29. E. M. Carstea, A. Baker, M. Bieroza and D. Reynolds, Water Res., 2010, 44, 5356–5366.
30. K. L. Powell, R. G. Taylor, A. A. Cronin, M. H. Barrett, S. Pedley, J. Sellwood, S. A. Trowsdale and D. N. Lerner, Water Res., 2003, 37, 339–352.
31. D. Walling, P. Owens, B. Waterfall, G. Leeks and P. Wass, Sci. Total Environ., 2000, 251–252, 205–222.
32. N. D. Williams, D. E. Walling and G. J. L. Leeks, Water Res., 2007, 41, 1081–1093.
33. G. Old, G. Leeks, J. Packman, B. Smith, S. Lewis, E. Hewitt, M. Holmes and A. Young, Sci. Total Environ., 2003, 314–316, 495–512.
34. A. B. Gray, G. B. Pasternack and E. B. Watson, Golotsen, 2010, 20, 293–301.
35. M. Hayashi, Environ. Monit. Assess., 2004, 96, 119–128.
36. M. C. Hill, Methods and Guidelines for Effective Model Calibration, US Geological Survey, Water Resources Investigation Report 98-4005, Denver, Colorado, USA, 1998.
37. E. M. Carstea, A. Baker, G. Pavelescu and I. Boomer, Hydrol. Processes, 2009, 23, 1937–1946.
38. D. Morton, C. Rowland, C. Wood, L. Meek, C. Marston, G. Smith, R. Wadsworth and I. C. Simpson, Final Report for LCM2007 – the new UK Land Cover Map, Lancaster, 2011.
39. J. Phillips and D. E. Walling, Water Res., 1995, 29, 2498–2508.
40. A. J. Lawaetz and C. A. Stedmon, Appl. Spectrosc., 2009, 63, 936–940.
41. K. R. Murphy, C. a. Stedmon, D. Graeber and R. Bro, Anal. Methods, 2013, 5, 6557.
42. B. A. Pellerin, B. A. Bergamaschi, B. D. Downing, J. F. Saraceno, J. Garrett and L. D. Olsen, Optical Techniques for the Determination of Nitrate in Environmental Waters: Guidelines for Instrument Selection, Operation, Deployment, Maintenance, Quality Assurance, and Data Reporting. U.S. Geological Survey Techniques and Methods 1-D5, 2013.
43. D. N. Moriasi, J. G. Arnold, M. W. Van Liew, R. L. Bingner, R. D. Harmel and T. L. Veith, Watershed Simulations, 2007, vol. 50, pp. 885–900.
44. A. F. Zuur, E. N. Ieno, N. Walker, A. A. Saveliev and G. Smith, Mixed effects models and extensions in ecology with R, Springer, New York, 2009.
45. R Development Core Team, 2012.
46. G. H. Old, P. S. Naden, S. J. Granger, G. S. Bilotta, R. E. Brazier, C. J. a. Macleod, T. Krueger, R. Bol, J. M. B. Hawkins, P. Haygarth and J. Freer, Sci. Total Environ., 2012, 417–418, 169–182.
47. A. Baker and R. G. M. Spencer, Sci. Total Environ., 2004, 333, 217–232.
48. P. G. Coble, J. R. Lead, A. Baker, D. M. Reynolds and R. G. M. Spencer, Aquatic Organic Matter Fluorescence, Cambridge University Press, 2014.
49. X. Lin and K. G. Hubbard, J. Atmos. Ocean. Technol., 2004, 21, 1025–1032.
50. X. A. Cao and S. F. Leboeuf, IEEE Trans. Electron Devices, 2007, 54, 3414–3417.
51. B. Seredyńska-Sobecka, A. Baker and J. R. Lead, Water Res., 2007, 41, 3069–3076.
52. E. Ryder, E. Jennings, E. de Eyto, M. Dillane, C. NicAonghusa, D. C. Pierson, K. Moore, M. Rouen and R. Poole, Limnol. Oceanogr.: Methods, 2012, 10, 1004–1010.
53. R. B. McCleskey, Environ. Sci. Technol., 2013, 47, 9874–9881.
54. M. Jonasz and G. R. Fournier, Light scattering of particle in water: theoretical and experimental foundations, Elsevier, 2007.
55. J. Gregory, Particles in Water: Properties and Proceses, CRC Press, 2004.
56. C. J. Lorenzent, Deep-Sea Res., 1966, 13, 223–227.
57. T. Leeuw, E. S. Boss and D. L. Wright, Sensors, 2013, 13, 7872–7883.
58. H. Wu, D. Jiang, P. Cai, X. Rong, K. Dai, W. Liang and Q. Huang, J. Soils Sediments, 2011, 12, 143–149.
59. D. E. Walling and B. W. Webb, in Recent developments in the explanation and prediction of erosion and sediment yield, IAHS Publication, 1982, vol. 137, pp. 327–337.
60. R. Sakrabani, J. Vollertsen, R. M. Ashley and T. Hvitved-Jacobsen, Sci. Total Environ., 2009, 407, 2989–2995.
61. L. C. van Rijn, J. Hydraul. Eng., 1984, 110, 1613–1641.
62. J. B. Fellman, E. Hood, R. T. Edwards and D. V. D'Amore, J. Geophys. Res., 2009, 114, G01021.
63. A. Baker, S. Elliott and J. R. Lead, Chemosphere, 2007, 67, 2035–2043.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5em00030k

---