Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Scalability and feasibility of photoelectrochemical H2 evolution: the ultimate limit of Pt nanoparticle as an HER catalyst†
E.
Kemppainen
 a,
A.
Bodin
b,
B.
Sebok
b,
T.
Pedersen
c,
B.
Seger
b,
B.
Mei
b,
D.
Bae
b,
P. C. K.
Vesborg
b,
J.
Halme
a,
O.
Hansen
c,
P. D.
Lund
a and
I.
Chorkendorff
*b
a,
A.
Bodin
b,
B.
Sebok
b,
T.
Pedersen
c,
B.
Seger
b,
B.
Mei
b,
D.
Bae
b,
P. C. K.
Vesborg
b,
J.
Halme
a,
O.
Hansen
c,
P. D.
Lund
a and
I.
Chorkendorff
*b
aDepartment of Applied Physics, New Energy Technologies Group, Aalto University, P.O. Box 14100, FI-00076 AALTO, Finland
bDepartment of Physics, CINF, Technical University of Denmark, DK-2800, Kgs. Lyngby, Denmark. E-mail: ibchork@fysik.dtu.dk
cDepartment of Micro- and Nanotechnology, Technical University of Denmark, DK-2800, Kgs. Lyngby, Denmark
First published on 27th August 2015
Abstract
The recent surge in investigating electrocatalysts for the H2 evolution reaction is based on finding a cheap alternative to Pt. However platinum's excellent catalytic activity means very little catalyst needs to be used. The present study combines model experiments with numerical modeling to determine exactly how little catalyst is needed. Specifically we investigate ultra-low Pt loadings for use in photoelectrochemical H2 evolution using TiO2–Ti-pn+Si photocathodes. At a current density of 10 mA cm−2, we photocathodically evolve H2 at +465, +450, +350 and +270 mV vs., RHE at Pt loadings of 1000, 200, 50, and 10 ng cm−2 corresponding to HER overpotentials of η1000ng = 32 mV, η200ng = 46 mV, η50ng = 142 mV, and η10ng = 231 mV. To put this in perspective, if 30% of the world's current annual Pt production was used for H2 evolution catalysis, using a loading of 100 ng cm−2 and a current of 10 mA cm−2 would produce 1 TWaverage of H2. The photoelectrochemical data matched the modeling calculations implying that we were near the fundamental maximum in performance for our system. Furthermore modeling indicated that the overpotentials were dominated by mass transfer effects, rather than catalysis unless catalyst loadings were less than 1000 ng cm−2.
Broader contextIn the last decade there has been an enormous push to find a cheaper, more earth-abundant catalyst than Pt for the hydrogen evolution reaction. This push is based on the theory that Pt is un-scalable if society would completely convert to a H2 based society. Interestingly, there have been relatively few works actually investigating if and how un-scalable using platinum as a H2 evolution catalyst actually is. In this manuscript we take the specific case of using a photoelectrochemical water splitting device, and determine how little Pt is needed (and thus the scalability) to effectively evolve H2 from both an experimental and a theoretical modeling standpoint. Our experimental results allow us to come very close to achieving our limit imposed by our modeling, but not surpass it. We feel this verifies the validity of our model, and thus the fundamental limits of Pt for H2 evolution in our system. From these results we find that the Pt consumed/terawatt would be on the order of 10% of the annual worldwide Pt production (depending upon photocurrent and overpotential). Thus this work should help to quantitatively put into perspective the scalability of Pt for photoelectrochemical water splitting. |
Introduction
Currently the primary energy source for electricity and transportation is from fossil fuels, and the replacement of these fuels by hydrogen is one of the ways to continue to fulfil society's energy demand, while simultaneously reducing greenhouse gas emissions.1,2 While we have ways to convert between hydrogen and electricity (via fuel cells and (photo)electrolysers), there are still several challenges that need to be addressed.2–5Renewable hydrogen can be produced using different approaches, i.e. electrolysis powered by a renewable source of energy, like wind energy or sunlight. Additionally, an integrated photoelectrocatalytic (PEC) approach, where solar energy is directly converted into hydrogen is also a possibility.2–5 Nevertheless, industrial scalability of both technologies requires reduction of capital costs to obtain hydrogen prices on a $ per J level compatible to those of today's fossil fuel prices. It is widely considered that capital costs of either electrolysers or PEC devices can be reduced by utilizing cheap and abundantly available materials to drive the hydrogen evolution reaction (HER) or the oxygen evolution reaction (OER) to replace platinum group metals, which are relatively scarce and expensive.6 In particular in the last 5–10 years fast progress has been made in the development of nonprecious metal HER catalysts to be implemented into these clean-energy technologies.2,7–14 Nevertheless, to date platinum is still the most widely used HER catalyst due to its world-record exchange current density and low Tafel slope. Additionally, Pt is known to be highly durable in the acidic environments used in electrolysers or PEC devices.15
While a low Tafel slope is certainly an important requirement for HER catalysts used in electrolysers, typically operated at high current densities (∼A cm−2), in photoelectrocatalytic devices high Pt exchange current density appears to be a more important criterion when chosen the HER catalyst.2 This is due to the lower current densities of 5–20 mA cm−2, which PEC devices will operate at due to solar flux limitations. Furthermore, it is often neglected in the development of efficient PEC devices that catalysts (HER or OER) will absorb light reducing the light limited current density provided by the photon absorber. Consequently, the catalysts amount used to drive HER or OER in such a device is a critical issue and significant light absorption by the catalyst material must be reduced.16
The best nonprecious metal HER catalysts reported so far can be separated into different classes of materials such as sulphides and phosphides, which usually contain transition metal cations of Mo, Co, Fe, or Ni.2,10–14 With an overpotential of 50 mV to produce current densities of 10 mA cm−2 in acidic electrolytes, FeP nanoparticles are the state-of-the-art nonprecious HER catalysts.17 Nevertheless exchange current densities are still an order of magnitude lower than that of conventional Pt HER catalysts. In general, high loadings are required for these non-noble HER catalysts to obtain low overpotentials. Hence, cost savings are lower than would be expected and the high-catalyst loading required might prevent the use in PEC devices. Indeed it was recently shown for CoP-modified Si photocathodes that significantly higher mass loadings (10 times) are required to achieve fill factors similar to those of Pt-modified electrodes, which is in agreement with the lower HER activity of CoP.18 These high loadings of CoP drastically reduced the photocurrent density due to parasitic light absorption decreasing the overall efficiency of the Si-based photocathode.18 While this might not be an issue for small band gap photocathodes on the backside of a monolithic device, the efficiency will be limited in a design with a large band gap photocathode and Pt appears to be still the optimal choice for HER catalysts in these PEC devices.16,19 Additionally the stability of these non-precious metal catalysts have yet to be proven. The state-of-the-art FeP dissolves rather fast17 and the reported data on Ni2P and CoP also suggest that these materials are far from being stable making it a challenge to utilize them with low coverage.11,12 It should also be mentioned that although there is no particular reason to believe Pt should not be stable under the conditions described here, there could also be long term issues that have not been realized yet.20 Thus even though these new classes of recently discovered HER materials are promising alternatives to the conventional Pt-group metals, a material matching the performance of Pt has not yet been reported. Taking this into account Pt appears to be still the optimal choice for HER catalysts in PEC devices and the question arises if Pt HER catalysts might be feasible on a TW level in a PEC device?
With an annual Pt production of 180 ton per year6 the Pt loading necessary to operate a photocathode at moderate current densities (on the order of 10 mA cm−2),2,21 and low overpotentials (<50 mV) determines the potential for Pt to be used in a PEC device. Only recently have researchers started to probe the idea that ultra-low Pt loadings for the HER could make this catalyst scalable even on the TW level. Dasgupta et al.22 used atomic layer deposition (ALD) to produce Pt nanoparticles on the surface of TiO2-coated Si microwire arrays. However, due to the procedure and the substrate used, defining an exact limit for the required Pt loading appears to be difficult. Thus, the Pt nanoparticle loadings that were studied ranged from ∼280 ng cm−2 (per geometrical electrode area) to several micrograms per cm2, and the Pt nanoparticle size-distribution was loading dependent. Another approach is to nanostructure or pattern the HER catalyst.23,24 Chen et al.24 investigated patterned Pt structures with different electrode filling fractions to reduce the parasitic light absorption effect of HER catalysts.24 While the authors obtained quite impressive results from these films, the exact loading was difficult to determine due to surface roughness of the films.
In this work we investigate ultra-low loadings of Pt nanoparticles for scalable photocathodic H2 evolution. This approach differs from the film based approach and allows us a uniform dispersion of platinum across our electrode. While we use a cluster-source sputtering approach to optimize the conditions, there are many methods to produce nanoparticles cheaper via solution based methods.
In this work we use well defined, size-selected Pt nanoparticles (diameter of 5 nm). The photoelectrocatalytic performance of planar TiO2-protected n+p-Si photocathodes in acidic solutions was investigated experimentally. Furthermore, a model combining the effects of mass transport, equilibrium hydrogen coverage and HER kinetics was used to describe the current–overpotential characteristics of these planar Si-photoelectrodes partially covered with Pt HER nanoparticles. The effect of mass transport and HER kinetics on the catalytic properties of individual Pt particles and the photoelectrode assemblies were assessed by this model and a good agreement between the experimental and theoretical data was obtained. Thus, using a combined experimental and theoretical approach the Pt HER catalyst amount needed for TW scale-up was assessed. The data provided here shows the dependence of Pt nanoparticle loading on overpotential for hydrogen evolution. For an acceptable HER overpotential of 50 mV, 54 tons of Pt metal, corresponding to a coverage of 100 ng cm−2 Pt (d = 5 nm) on a planar electrode, is required to achieve a TW scale-up with a PEC device operated at 10 mA cm−2 (12% solar-to-hydrogen efficiency). If larger overpotentials for HER are feasible, even lower Pt utilization is possible. This works shows that the use of Pt nanoparticles HER catalyst may potentially be a viable option for terawatt scale PEC applications.
It should be noted that for any PEC device, there needs to be a corresponding anodic reaction. While understanding these anodic reactions (such as O2 evolution) is important, this work only focuses on photocathodic H2 evolution and its corresponding overpotential and does not analyse anodic reactions or their corresponding overpotentials. For readers interested in how overpotentials at both electrodes effect photocatalytic efficiency we refer to the excellent review by Walter et al.25 and more recent works by Hu et al.26 and Seitz et al.27
Experimental
Preparation of TiO2-protected Si-based photocathodes
TiO2 protected silicon photocathodes with n+p junctions were produced as in our previous work.19,28Preparation of Pt nanoparticle and electrochemical characterization
Mass-selected Pt nanoparticles were produced in a five-step process by (1) sputtering a Pt target with Ar+-ions in a magnetron sputter head, (2) allowing the sputtered Pt to condense into nanoparticles in a LN2-cooled “aggregation zone”, where both He and Ar was present to facilitate faster aggregation,29 (3) super-sonic expanding the nanoparticles from the aggregation zone into UHV through an aperture and into an electronic lens system, which focuses the negatively charged particles into a narrow beam, (4) mass-selecting the nanoparticles in a lateral time-of-flight mass-selector,30 and (5) landing the particles on the substrate.The particle production was conducted in a Nano-Beam 2011 nanoparticle source (Birmingham Instruments Inc.) with a base pressure in the low 10−10 mbar range, which is connected to another UHV system (Omicron NanoTechnology), wherein the nanoparticles are deposited. This latter chamber is equipped with characterization techniques such as XPS (SPECS XR 50 X-ray gun coupled to Omicron NanoSAM 7 channel energy analyser), ISS (Omicron ISE100 ion gun) and SEM (ZEISS UHV-Gemini Supra), and has a base pressure in the low 10−11 mbar range. For further details about the preparation of mass selected nanoparticles see Hernandez-Fernandez et al.31
Platinum particles having a mass of 850![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 amu were deposited on the planar TiO2-protected Si photocathodes with calculated loadings of 10, 50, 200 and 1000 ng cm−2, respectively. The deposited photocathodes were characterized in UHV with XPS using Mg Kα radiation. Furthermore, one additional sample for each loading was made, for investigation with SEM. The 10 ng cm−2 sample was also investigated with ISS, in order to verify that Pt was on the surface.
000 amu were deposited on the planar TiO2-protected Si photocathodes with calculated loadings of 10, 50, 200 and 1000 ng cm−2, respectively. The deposited photocathodes were characterized in UHV with XPS using Mg Kα radiation. Furthermore, one additional sample for each loading was made, for investigation with SEM. The 10 ng cm−2 sample was also investigated with ISS, in order to verify that Pt was on the surface.
The mass of 850![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 amu was chosen for the time-of-flight mass-selector because it corresponds to a particle diameter of 5 nm. The size distribution of the deposited nanoparticles was determined with ex situ TEM imaging (Tecnai T20 G2) with samples prepared on TEM grids under the same deposition conditions as the photocathodes. (Higher resolution TEM images can be found in the ESI†.) The size of the nanoparticles on the pictures was examined using the software ImageJ. Only particles with circularity between 0.8–1 were analysed in order to avoid taking into account particles that were landed on top of each other. SEM images were taken of one sample of each loading. The images were obtained with an acceleration voltage of 7 kV, and a beam current of 400 pA with an in-lens detector, which detects almost exclusively secondary electrons in order to visualize the topography of the surface.
000 amu was chosen for the time-of-flight mass-selector because it corresponds to a particle diameter of 5 nm. The size distribution of the deposited nanoparticles was determined with ex situ TEM imaging (Tecnai T20 G2) with samples prepared on TEM grids under the same deposition conditions as the photocathodes. (Higher resolution TEM images can be found in the ESI†.) The size of the nanoparticles on the pictures was examined using the software ImageJ. Only particles with circularity between 0.8–1 were analysed in order to avoid taking into account particles that were landed on top of each other. SEM images were taken of one sample of each loading. The images were obtained with an acceleration voltage of 7 kV, and a beam current of 400 pA with an in-lens detector, which detects almost exclusively secondary electrons in order to visualize the topography of the surface.
All Pt wires were cleaned immediately before use in photoelectrochemical testing. Cleaning consisted first of a 15 second rinse in fresh aqua regia, then thorough washing in millipore water. Finally the electrodes were flame annealed.
For the photoelectrochemical measurements, a Bio-Logic VSP potentiostat along with EC Lab software was used. The photoelectrochemical H2 evolution experiments were performed in a three-electrode cell with an H-cell design and a glass frit between the working and counter electrode compartments to prevent any crossover. The experiments were carried out in an aqueous 1 M HClO4 (Aldrich 99.99%) solution. The electrolyte was cleaned overnight using a chronoamperometric measurement with two Pt mesh electrodes used as working and counter electrodes. For PEC measurements a Pt mesh counter electrode and saturated Hg/HgSO4 reference electrode (VWR International) were used. The solution was saturated with hydrogen gas 30 minutes before the start of any experiment, and for the entire duration of the experiment.
A 1000 W xenon lamp (Oriel) was used with a 635 nm cut-off filter and an AM1.5 filter to simulate the red part of the solar spectrum. The light intensity reaching the sample was calibrated to match that of the total light intensity of the red part of the solar spectrum (λ > 635 nm, 38.6 mW cm−2). For all cyclic voltammograms (CV's) the electrodes were scanned at a sweep rate of 50 mV s−1. The 3rd anodic sweep is shown in all graphs. The actual loading of Pt nanoparticles was verified using Inductively Coupled Plasma Mass Spectrometry (ICP-MS, iCAP-QC ICP-MS, Thermo Fisher Scientific) after dissolving the size-selected Pt nanoparticles in aqua regia solution. For all samples, the ICP-MS results closely matched that determined from the cluster source deposition.
Simulation details
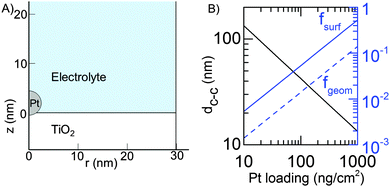
All calculations were done for a model system where spherical Pt nanoparticles of 5 nm diameter were simulated. It was assumed that each Pt nanoparticle was embedded 0.25 nm into a 100 nm thick TiO2 substrate (Fig. 1). This means that 95% of its (free sphere-) surface area was exposed to electrolyte. The conductivity of the TiO2 substrate was assumed to be 1 S m−1,32 corresponding to slightly reduced TiO2 but it could be much lower without affecting the modelling results (Table 1). The electrode was assumed to be an array of identical unit cells, so to simplify calculations it was simulated as a single Pt particle in a 2D cylindrical unit cell, corresponding to a diffusional domain approximation with uniform particle spacing.33,34 Periodic boundary conditions were replaced by zero-flux boundary conditions at the outer edge of the cell, whose area (i.e. radius, Rcell) corresponds to the average Pt loading (LPt) over the electrode area.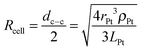 | (1) |
| Symbol | Explanation | Value |
|---|---|---|
| T | Temperature | 298.15 K |
| h el | Electrolyte diffusion layer thickness | 5 μm |
| h TiO2 | TiO2 layer thickness | 100 nm |
| σ TiO2 | Conductivity of TiO2 | 1 S m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 32 |
| d Pt | Pt particle diameter | 5 nm |
| ρ Pt | Pt density | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 kg m−3 450 kg m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
| σ Pt | Pt conductivity | 9.43 × 106 S m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
| i 0,V | Volmer reaction exchange current density | 100 mA cm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36 36 |
| r H | Ratio of Heyrovsky and Volmer rates | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36 36 |
| r T | Ratio of Tafel and Volmer rates | 9.5 |
| Θ 0 | Equilibrium H-coverage | 0.6737 |
| c H+,0 | Bulk proton concentration | 1.0 M |
| c H2,0 | Bulk H2 concentration | 0.7698 mM38 |
| D H+ | Proton diffusion coefficient | 9.3110 × 10−5 cm2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
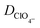
|
Perchlorate ion diffusion coefficient | 1.7908 × 10−5 cm2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
| D H2 | H2 diffusion coefficient | 5.1100 × 10−5 cm2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
| μ H+ | Proton mobility | 3.624 × 10−3 cm2 (V s)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
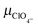
|
Perchlorate ion mobility | 6.970 × 10−4 cm2 (V s)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
| i ph | Si PV-cell photocurrent density | −22.0 mA cm−2 |
| V oc | Si PV-cell open circuit voltage | 0.495 V vs. RHE |
| i rec | Recombination current density | 9.8196 × 10−8 mA cm−2 |
The current density iPt/geom was calculated by integrating the local current density at the Pt surface over the exposed surface area and dividing it by either the exposed Pt area (APt) or the area of the unit cell (Ageom).
The steady state was calculated with a transient simulation starting from equilibrium conditions at 0 V vs. RHE. The concentration profiles took at most about 10 seconds simulation time to converge to steady state, and all simulations were run for 20 s simulation time to ensure steady state. IV-curves were calculated using the state at the last calculated time point.
To facilitate comparisons between simulated overpotential and measured IV-curves of the whole devices, the effect of the silicon PV cell was simulated with the IV-curve of an ideal PV cell
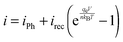 | (2) |
Results and discussion
Characterization of size-selected Pt nanoparticles
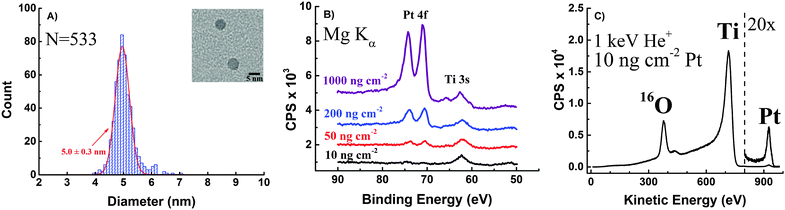
TEM images of the Pt nanoparticles were taken from different areas of the Cu TEM grids they were deposited on, and the resulting size distribution along with a close-up picture of typical particles (Fig. 2A) is shown in Fig. 2. According to the determined size-distribution, the average particle size is 5.0 ± 0.3 nm.Furthermore, Pt nanoparticles deposited on TiO2-protected Si photocathodes were investigated by XPS. Wide range survey spectra only showed O, Ti, C and Pt on the surface of the samples confirming that the Si surface was fully covered by a TiO2 film (Fig. S2 in ESI†).
Detailed spectra of the region around the Pt 4f peaks taken in case of each loading are shown in Fig. 2B.
The Pt 4f peak is decreasing with each loading and finally disappears in case of the 10 ng cm−2 Pt loading due to the low loading, which is below the detection limit of XPS. However, significant catalytic activity and reasonably low overpotentials were determined for the sample with 10 ng cm−2 Pt loading, meaning that Pt contaminations (e.g. during catalyst preparation or from the electrolyte) below the detection limit of XPS could significantly contribute to the activity of presumably Pt-free materials. Thus, XPS analysis is certainly not a reliable way to prove the absence of Pt in non-noble metal catalyst used in ORR or HER reaction and surface spectroscopic methods with much higher sensitivity are required to unambiguously show the absence of trace amounts of noble metals like Pt. Here, in order to have spectroscopic evidence for the successful deposition of 10 ng cm−2 Pt on TiO2-protected Si photocathodes, the sample was further investigated using ISS. The peak at approx. 927 eV can clearly be assigned to Pt (Fig. 2C). The intensity of the signal suggests that even lower Pt loadings can be easily identified using ISS which makes ISS more suitable for detecting trace amounts of Pt in non-noble metal catalysts.
Finally, each of the 4 different loading Pt samples were investigated with SEM. Pt particles can be seen as bright dots on the rough TiO2 substrate, and the differences in coverage's are clearly distinguishable (Fig. 3).
 | ||
| Fig. 3 SEM micrographs of four samples of different Pt nanoparticle loading. The particles in the lowest-loading image are marked by arrows. | ||
Photoelectrochemical hydrogen evolution with size-selected Pt nanoparticles on TiO2/np+-Si photocathodes
The mass-selected Pt nanoparticle (d = 5 nm) modified TiO2-protected Si photocathodes with Pt mass loadings of 10, 50, 200 and 1000 ng cm−2 (confirmed by ICP-MS) were tested in photoelectrochemical hydrogen evolution in acidic electrolyte. The respective IV-curves of the four different samples are shown in Fig. 4. For all samples an open-circuit photovoltage (Voc) of 495 ± 4 mV and a light-limited photocurrent of ∼22 mA cm−2 was obtained. These values are in good agreement with our previously reported TiO2-protected Si photocathodes modified with Pt nanoparticles using a conventional drop casting procedure of a Pt-salt solution.20,28 Furthermore, the results indicate that light blocking due to the HER catalyst is completely circumvented in these experiments.19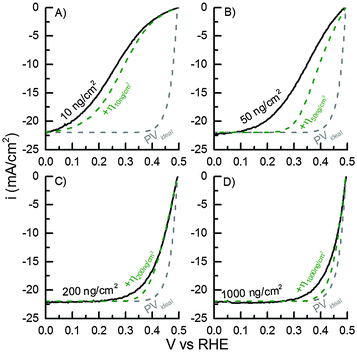 | ||
| Fig. 4 Measured IV-curves of 10, 50, 200 and 1000 ng cm−2 Pt loadings on TiO2-covered p+|p|n+-Si PV cell (black lines) and the simulated IV-curves for the same loadings including the calculated HER overpotentials (η) (green dashed lines). The IV-curve for an ideal PV cell with n = 1 (grey dashed line, eqn (2)) is shown for comparison. | ||
For comparison of the different Pt mass-loadings the overpotential η (defined as Voc – V10mA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−2) necessary to drive a current density of 10 mA cm−2 will be used as a figure of merit. The overpotentials required to achieve 10 mA cm−2 are highly dependent on the Pt nanoparticle loading. With the highest Pt loading (1000 ng cm−2) η1000ng = 32 mV was obtained, which is also in good agreement with similar previously reported Si-based photocathodes modified by drop casted Pt nanoparticles or compact Pt films.20,28 With lower loadings the required overpotential increases and overpotential of η200ng = 46 mV, η50ng = 142 mV, and η10ng = 231 mV were measured, respectively.
cm−2) necessary to drive a current density of 10 mA cm−2 will be used as a figure of merit. The overpotentials required to achieve 10 mA cm−2 are highly dependent on the Pt nanoparticle loading. With the highest Pt loading (1000 ng cm−2) η1000ng = 32 mV was obtained, which is also in good agreement with similar previously reported Si-based photocathodes modified by drop casted Pt nanoparticles or compact Pt films.20,28 With lower loadings the required overpotential increases and overpotential of η200ng = 46 mV, η50ng = 142 mV, and η10ng = 231 mV were measured, respectively.
One issue we did find with the ultra-low loading Pt samples was that even after extensive cleaning, there were still issues with contamination during photoelectrochemical testing. This was attributed to the epoxy resin encasing the photoelectrode. As expected, the issues due to contamination worsened with decreasing loading. Nevertheless for all of the samples shown in this work, at least 5 stable scans were completed before any noticeable drops in performance were measured. However, due to these contamination issues, we could not accurately do long term testing such as chronoamperometry measurements.
Simulations
Independent of the Pt nanoparticle loading, the deviation of the calculated overpotential and the experimental data increases with higher current densities and the simulation clearly underestimates the experimental HER overpotential. The difference between calculated and measured IV-curve at current densities higher than 15 mA cm−2 may be related to ideal PV cell characteristics overestimating the fill factor compared to the real silicon PV device used in the experiment.
| ηtotal = ηKinetic + ηMT | (3) |
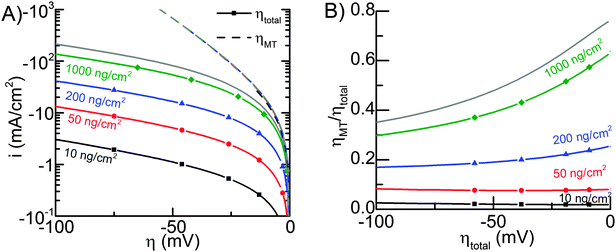
Fig. 5A shows the average current density, normalized by the geometric electrode area igeom as a function of total overpotential (solid lines), and pure mass transfer overpotential for the different Pt nanoparticle loadings used in Fig. 4. The mass transport overpotential was determined almost completely by H2 concentration, because the changes in the surface concentrations of protons and H2 were similar (both due to HER and mass transport), but the equilibrium concentration of H2 was small compared to the proton concentration, and therefore it dominated the Nernst potential.
The dashed lines in Fig. 5A overlap, which illustrates that mass transport losses are almost independent of Pt loading. The losses increase slightly when loading is decreased, but in all cases they correspond to approximately the same H2 transport rate. The fact that mass transfer losses are basically independent of Pt loadings can be rationalized by realizing that the H2 molecules have to travel a much longer distance in the axial direction (about 5 μm, see Fig. S5, ESI†) than the distance between two neighboring Pt particles (134 nm for 10 ng cm−2).
Although the H2 transport rate in simulations for Fig. 4 and 5 was unusually high, it explains the total overpotential with 1000 ng cm−2 better than our initial estimate that was based on typical literature values (Fig. S5, ESI†).41,42 The cause of high mass transport rate may be associated to the potential sweep rate used in the photoelectrochemical hydrogen evolution experiments, which was partly necessitated by contamination and performance drop with low loadings (for further details see ESI†).
Fig. 5B illustrates what fraction of the total overpotential is due to mass transfer, and it is evident that with 1000 ng cm−2, even with the high mass transport rate, mass transport losses correspond to more than half of the total overpotential up to about 20 mA cm−2 current density (25 mV total overpotential).
Considerations of Pt consumption for efficient PEC hydrogen evolution devices
Using the experimental and theoretical results obtained for the well-defined, mass-selected Pt nanoparticle modified photocathodes investigated in this study, the Pt consumption depending on an affordable overpotential for hydrogen evolution can be defined based on the calculated IV-curves. The amount of H2 needed to be produced if society switches to a completely sustainable future is unknown, but it will most likely be in the terawatt range. The average PEC power density is calculated using:| Pavg = 0.15 × i × 1.23V = 0.1854V × i | (4) |
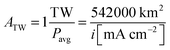 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 km2 and 27
200 km2 and 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 km2 for 10 mA cm−2 and 20 mA cm−2, respectively. Finally, Pt consumption is calculated by multiplying the area per TW by the Pt loading.
100 km2 for 10 mA cm−2 and 20 mA cm−2, respectively. Finally, Pt consumption is calculated by multiplying the area per TW by the Pt loading.
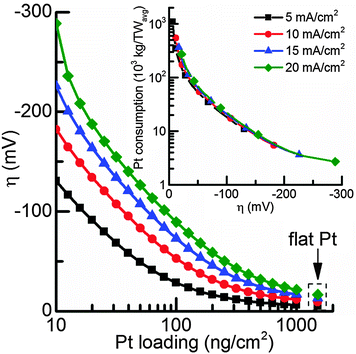
Depending on the acceptable overpotential the total Pt consumption can finally be calculated (Fig. 6). While the exact numbers for irradiation, capacity factor, and efficiency can be debated, the current numbers allow an order of magnitude determination of the feasibility of using Pt in photoelectrochemical devices and although some simulation parameters might not correspond to the actual reaction kinetics, they provide a reasonably good fit to experimental results for current densities up to 20 mA cm−2.
For a photocathode covered with a compact Pt film the overpotential to achieve a current density of 10 mA cm−2 in the simulated conditions is 9 mV, while for high Pt nanoparticle loadings of 1000 ng cm−2, 12 mV overpotential is required. The portion of mass transport losses is about 6.5 mV, so higher Pt loadings will not significantly improve the photoelectrode performance (Fig. 5) and a Pt loading of 1000 ng cm−2 can be considered as a compact Pt film electrode with negligible kinetic losses. Therefore, in a photoelectrochemical device with minimal overpotential losses, Pt nanoparticle loadings of 1000 ng cm−2 are sufficient for standard illumination conditions (AM1.5) and the total Pt consumption would be 542.4 tons per TW. On the other hand, if an increase in overpotential to 50 mV, which is well within the range of a good non-noble metal HER catalyst,10–13,17 is acceptable due to a sufficient photovoltage, the Pt consumption drops by an order of magnitude to about 100 ng cm−2, corresponding to 54 tons per TWavg (for Pt nanoparticles with d = 5 nm).
For comparison, the total global mining production of Pt is around 180 tons per year and the annual net consumption for jewelry and automotive catalytic converters are ∼70 ton and ∼65 ton respectively. In this light, the use of Pt in an efficient PEC system might be feasible even on a TW scale.6,44,45 The total energy demand could realistically be an order of magnitude larger (10 TW) but the investment will also be distributed over many years and furthermore Pt can be recovered.
When platinum is compared to the scalability of other well-known non-noble metal HER catalysts (Table 2), such as MoS2,46 CoP,12 Ni2P,11 and FeP17 it appears to be one of the most scalable. In Table 2 we assumed a photoelectrolysis capacity factor of 15% for all materials and used 2010 materials production data.6 In most cases the metal would be the limiting factor in production, however for FeP it would be the phosphorous. An overpotential of 75 mV was used because all of the optimal catalysts have data at this point. Choosing a lower overpotential would increase the amount of catalyst needed per TW for all of the materials, but it would have the least effect on Pt since it has the lowest Tafel slope. For our Pt data we used the modelled value at 50 ng cm−2 because at that loading we can reach the order of magnitude of current (∼10 mA cm−2) that will be needed in a photoelectrolysis device. It should be noted that if we used our experimental values at 50 ng cm−2 in Table 2, the amount needed would be slightly higher, but would still be relatively low in comparison to MoS2, CoP, and Ni2P.
An important thing to consider when reviewing Table 2 is to realize that the value for Pt is extremely optimized whereas materials such as MoS2 and phosphides still have a much larger potential to be optimized by nanoscaling and better dispersion. While FeP appears very promising from Table 1, it has severe durability issues (doubling of overpotential within ∼16 hours) thus limiting its current applicability. Since FeP has only recently been discovered, it is unknown whether these durability issues are fundamental or are simply a technical barrier that can be overcome.
In the present model, Pt nanoparticles with a diameter of 5 nm are assumed. It should be noted that the particle size also affects the overpotential for a given Pt loading: for larger particles less surface area per mass unit is available, so local current densities are higher and higher kinetic overpotentials are expected for the same mass loading. Correspondingly, the overpotential will decrease as the Pt nanoparticle diameter decreases and less Pt is needed to match a given overpotential for any current density. This effect is highlighted in Fig. S7 (ESI†) for Pt nanoparticles with different diameters (d = 2, 5, and 10 nm). However, this will come with a cost of stability as the surface energy will go up with decreasing diameter and the particles will be more prone to sintering and corrosion.47 Durability is an issue that we have not analyzed with respect to platinum's practical feasibility. Whether the Pt consumption/terawatt for a PEC water splitting device will be stable/durable for 1 month, 1 year or 10 years would obviously be of critical importance.
Interestingly, this approach of reducing the catalyst loading having well-dispersed nanoparticles may not work for a photoanode. In case of photoanode protection with TiO2 thin films we have recently shown that band bending in TiO2 protection layers should be avoided and a pinch-off effect will occur when using nanoparticular OER catalysts.48 Thus, even if another less scarce OER catalyst than IrO2 applicable for water oxidation in acidic environment will be found, the well-dispersed nanoparticle approach would not work using TiO2 protection layers. Unfortunately, except for compact IrO2 thin films, TiO2 protection layers, currently are the only known protection layers suitable in these conditions.20,28,48–50 On the other hand photoanode protection might be easier in alkaline electrolyte and NiO thin films might be most promising.51
Conclusions
In this work an experimental and theoretical approach was used to address the scalability of a photoelectrochemical device to the TW level using a TiO2–Ti-pn+Si photocathode as stable photon absorber and Pt as hydrogen evolution catalyst. The experimentally determined dependence of the HER overpotential with Pt nanoparticle loading was reproduced in the modelling approach. Thus, effects of mass-transport and hydrogen evolution kinetics could be investigated and the modelling results could be utilized to connect the Pt loadings and overpotentials required for hydrogen evolution. The presented data clearly shows that for an acceptable overpotential of 50 mV, which is the current state-of-the art overpotential for non-noble metal HER catalysts (FeP. 1 mg cm−2), only 100 ng cm−2 of Pt or 54 tons per TWavg are needed to scale-up a PEC device to the TW scale. Thus, this work demonstrated that 30% of the world's current annual Pt production could be utilized to achieve a 1 TWavg worth of H2 generation (assuming current densities of 10 mA cm−2 and a capacity factor of 15%) at overpotentials of 50 mV (Pt nanoparticles d = 5 nm).Acknowledgements
For funding we gratefully acknowledge the Danish National Research Foundation's Center for Individual Nanoparticle Functionality (DNRF54) and Nordic Energy Research for Nordic Initiative for Solar Fuel Development (N-I-S-F-D).Notes and references
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS
.
- P. C. K. Vesborg, B. Seger and I. Chorkendorff, J. Phys. Chem. Lett., 2015, 951–957 CrossRef CAS PubMed
.
- H. B. Gray, Nat. Chem., 2009, 1, 112 CrossRef CAS
.
- S. Dahl and I. Chorkendorff, Nat. Mater., 2012, 11, 100–101 CrossRef CAS PubMed
.
- N. S. Lewis, Science, 2007, 315, 798–801 CrossRef CAS PubMed
.
- P. C. K. Vesborg and T. F. Jaramillo, RSC Adv., 2012, 2, 7933 RSC
.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef PubMed
.
- B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, J. Am. Chem. Soc., 2005, 127, 5308–5309 CrossRef CAS PubMed
.
- T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS
.
- J. R. McKone, B. F. Sadtler, C. A. Werlang, N. S. Lewis and H. B. Gray, ACS Catal., 2013, 3, 166–169 CrossRef CAS
.
- E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, J. Am. Chem. Soc., 2013, 135, 9267–9270 CrossRef CAS PubMed
.
- E. J. Popczun, C. G. Read, C. W. Roske, N. S. Lewis and R. E. Schaak, Angew. Chem., Int. Ed., 2014, 53, 5427–5430 CrossRef CAS PubMed
.
- J. Kibsgaard and T. F. Jaramillo, Angew. Chem., Int. Ed., 2014, 53, 14433–14437 CrossRef CAS PubMed
.
- Y. Hou, B. L. Abrams, P. C. K. Vesborg, M. E. Björketun, K. Herbst, L. Bech, A. M. Setti, C. D. Damsgaard, T. Pedersen, O. Hansen, J. Rossmeisl, S. Dahl, J. K. Nørskov and I. Chorkendorff, Nat. Mater., 2011, 10, 434–438 CrossRef CAS PubMed
.
- S. Trasatti, Electrochim. Acta, 2000, 45, 2377–2385 CrossRef CAS
.
- B. Seger, I. E. Castelli, P. C. K. Vesborg, K. W. Jacobsen, O. Hansen and I. Chorkendorff, Energy Environ. Sci., 2014, 7, 2397–2413 CAS
.
- J. F. Callejas, J. M. McEnaney, C. G. Read, J. C. Crompton, A. J. Biacchi, E. J. Popczun, T. R. Gordon, N. S. Lewis and R. E. Schaak, ACS Nano, 2014, 8, 11101–11107 CrossRef CAS PubMed
.
- C. W. Roske, E. J. Popczun, B. Seger, C. G. Read, T. Pedersen, O. Hansen, P. C. K. Vesborg, B. S. Brunschwig, R. E. Schaak, I. Chorkendorff, H. B. Gray and N. S. Lewis, J. Phys. Chem. Lett., 2015, 2, 1679–1683 CrossRef PubMed
.
- D. Bae, T. Pedersen, B. J. Seger, M. Malizia, A. Kuznetsov, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, Energy Environ. Sci., 2015, 8, 650–660 CAS
.
- B. Seger, D. S. Tilley, T. Pedersen, P. C. K. Vesborg, O. Hansen, M. Grätzel and I. Chorkendorff, RSC Adv., 2013, 3, 25902–25907 RSC
.
- J. R. McKone, N. S. Lewis and H. B. Gray, Chem. Mater., 2014, 26, 407–414 CrossRef CAS
.
- N. P. Dasgupta, C. Liu, S. Andrews, F. B. Prinz and P. Yang, J. Am. Chem. Soc., 2013, 135, 12932–12935 CrossRef CAS PubMed
.
- L. Ji, M. D. McDaniel, S. Wang, A. B. Posadas, X. Li, H. Huang, J. C. Lee, A. a. Demkov, A. J. Bard, J. G. Ekerdt and E. T. Yu, Nat. Nanotechnol., 2014, 10, 84–90 CrossRef PubMed
.
- Y. Chen, K. Sun, H. Audesirk, C. Xiang and N. Lewis, Energy Environ. Sci., 2015, 8, 1736–1747, 10.1039/C5EE00311C
.
- M. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS
.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 CAS
.
- L. C. Seitz, Z. Chen, A. J. Forman, B. a. Pinaud, J. D. Benck and T. F. Jaramillo, ChemSusChem, 2014, 7, 1372–1385 CrossRef CAS PubMed
.
- B. Seger, T. Pedersen, A. B. Laursen, P. C. K. K. Vesborg, O. Hansen and I. Chorkendorff, J. Am. Chem. Soc., 2013, 135, 1057–1064 CrossRef CAS PubMed
.
- H. Haberland, J. Vac. Sci. Technol., A, 1992, 10, 3266 CAS
.
- B. von Issendorff and R. E. Palmer, Rev. Sci. Instrum., 1999, 70, 4497–4501 CrossRef CAS PubMed
.
- P. Hernandez-Fernandez, F. Masini, D. N. McCarthy, C. E. Strebel, D. Friebel, D. Deiana, P. Malacrida, A. Nierhoff, A. Bodin, A. M. Wise, J. H. Nielsen, T. W. Hansen, A. Nilsson, I. E. L. Stephens and I. Chorkendorff, Nat. Chem., 2014, 6, 732–738 CAS
.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS
.
- H. Reller, E. Kirowa-Eisner and E. Gileadi, J. Electroanal. Chem. Interfacial Electrochem., 1982, 138, 65–77 CrossRef CAS
.
- R. G. Compton, G. G. Wildgoose, N. V. Rees, I. Streeter and R. Baron, Chem. Phys. Lett., 2008, 459, 1–17 CrossRef CAS
.
-
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 95th edn, 2014 Search PubMed
.
- J. Durst, C. Simon and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, F190–F203 CrossRef CAS PubMed
.
- N. M. Markovic and P. N. J. Ross, Surf. Sci. Rep., 2002, 45, 117–229 CrossRef CAS
.
- K. Aoki, H. Toda, J. Yamamoto, J. Chen and T. Nishiumi, J. Electroanal. Chem., 2012, 668, 83–89 CrossRef CAS PubMed
.
- U. Stutenbaeumer and B. Mesfin, Renewable Energy, 1999, 18, 501–512 CrossRef CAS
.
-
A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, WILEY-VCH Verlag, 2001 Search PubMed
.
- K. Stephan and H. Vogt, Electrochim. Acta, 1979, 24, 11–18 CrossRef CAS
.
- C. A. C. Sequeira, D. M. F. Santos, B. Šljukić and L. Amaral, Braz. J. Phys., 2013, 43, 199–208 CrossRef CAS
.
- http://www.nrel.gov/analysis/tech_cap_factor.html .
-
P. J. Loferski, 2012 Minerals Yearbook, Platinum-group metals, 2013 Search PubMed
.
- World Platinum Investment Council, Platinum Quarterly Q1 2015, 2015.
- H. Wang, Z. Lu, D. Kong, J. Sun, T. M. Hymel and Y. Cui, ACS Nano, 2014, 8, 4940–4947 CrossRef CAS PubMed
.
- J. C. Meier, I. Katsounaros, C. Galeano, H. J. Bongard, A. A. Topalov, A. Kostka, A. Karschin, F. Schüth and K. J. J. Mayrhofer, Energy Environ. Sci., 2012, 5, 9319 CAS
.
- B. Mei, T. Pedersen, P. Malacrida, D. Bae, R. Frydendal, O. Hansen, P. C. K. Vesborg, B. Seger and I. Chorkendorff, J. Phys. Chem. C, 2015, 119, 15019–15027 CAS
.
- S. Hu, M. R. Shaner, J. A. Beardslee, M. Lichterman, B. S. Brunschwig and N. S. Lewis, Science, 2014, 344, 1005–1009 CrossRef CAS
.
- B. Mei, B. Seger, T. Pedersen, M. Malizia, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, J. Phys. Chem. Lett., 2014, 5, 1948–1952 CrossRef CAS PubMed
.
- B. Mei, A. A. Permyakova, R. Frydendal, D. Bae, T. Pedersen, P. Malacrida, O. Hansen, I. E. L. Stephens, P. C. K. Vesborg, B. Seger and I. Chorkendorff, J. Phys. Chem. Lett., 2014, 5, 3456–3461 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation details. See DOI: 10.1039/c5ee02188j |
| This journal is © The Royal Society of Chemistry 2015 |