Open Access Article
Open Access ArticleHolistic design guidelines for solar hydrogen production by photo-electrochemical routes†
Mikaël
Dumortier
,
Saurabh
Tembhurne
and
Sophia
Haussener
*
Laboratory of Renewable Energy Science and Engineering, EPFL, Station 9, 1015 Lausanne, Switzerland. E-mail: sophia.haussener@epfl.ch; Tel: +41 21 693 3878
First published on 6th October 2015
Abstract
Device and system design choices for solar energy conversion and storage approaches require holistic design guidelines which simultaneously respect and optimize technical, economic, sustainability, and operating time constraints. We developed a simulation platform which allows for the calculation of solar-to-hydrogen efficiency, hydrogen price, device manufacture and operation energy demand, and the component degradation and replacement time of photo-electrochemical water splitting devices. Utilizing this platform, we assessed 16 different design types representing all possible combinations of a system: (i) operating with or without irradiation concentration, (ii) utilizing high-performing and high-cost or low-performing but low-cost photoabsorbers, (iii) utilizing high-performing and high-cost or low-performing but low-cost electrocatalysts, and (iv) operating with or without current concentration between the photoabsorber and the electrocatalyst. Our results show that device types exist with a global optimum (a Pareto point), simultaneously maximizing efficiency, while minimizing cost and the energy demand of manufacture and operation. In our examples, these happen to be the device types utilizing high irradiation concentration, as well as expensive photoabsorbers and electrocatalysts. These device types and designs were the most robust to degradation, exhibiting the smallest price sensitivity for increasing degradation rates. Other device types did not show a global optimum, but rather a set of partially optimized designs, i.e. a Pareto front, requiring a compromise and prioritization of either performance, cost, or manufacture and operation energy demand. In our examples, these happen to be the device types using low-cost photoabsorbers. The targeted utilization of irradiation and current concentration predicted that even device types utilizing expensive components can provide competitive solutions to photo-electrochemical water splitting. The quantification of the influence of component degradation on performance allows the suggestion of best practice for device operational time and component replacement. The framework and findings presented here provide holistic design guidelines for photo-electrochemical devices, and support the decision-making process for an integral and practical approach to competitive solar hydrogen production in the future.
Broader contextSolar energy is the most abundant renewable energy source on earth. It is dilute, unequally distributed, and intermittent but can be stored, for example, in an energy-dense and transportable fuel such as hydrogen. Photo-electrochemical water-splitting devices convert solar energy into chemical energy integrating photo absorption, charge generation and separation, and electrocatalysis in a single device. The viability of such a device is only possible if four requirements are simultaneously fulfilled: (i) high performance, (ii) low cost, (iii) sustainability, and (iv) robustness. All devices developed up to now provide combinations of these aspects but do not simultaneously fulfill all of them. Holistic design guidelines outlining a pathway for scalable systems are required to provide a fast route to practical implementation. |
1. Introduction
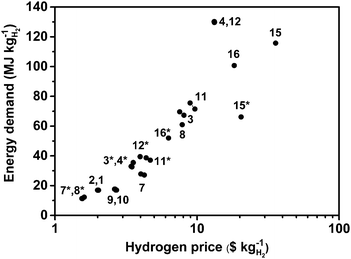
Since the first demonstrations of photo-electrochemical (PEC) water splitting devices more than 40 years ago,1 much research has focused on the development of efficient, low-cost, sustainable, and stable PEC components. As component performance has increased and synthesis approaches have matured, research has considered questions related to the integration of complete working PEC devices and systems, as well as corresponding performance, cost, sustainability, and stability assessment.2 Studies have assessed the economics of different PEC designs and systems ranging from particle-based to electrode-based systems,3 from closely integrated to decoupled systems,2 and from small to large scale facilities.4,5 These studies indicate that solar hydrogen has the potential to be produced for $2–$10 per kilogram.3 The sustainability of the devices has been assessed by examining the energy demand and the energy payback time in order to ensure that such devices produce more energy during their operating time than required for their manufacture.4,6,7 These studies indicated that PEC devices and systems can produce sustainable hydrogen when minimal efficiencies (in the range of 5%) and lifetimes (in the range of 10 years) can be guaranteed. Performance of PEC devices is usually assessed by solar-to-hydrogen (STH) efficiency, which has been used to compare novel device designs incorporating different components and materials as well as designs using concentration to reduce the mass of costly materials with energy intense processing steps.8,9 Measured STH efficiencies above 10% have been reported for lab-scale demonstration made of solely earth abundant materials,10 high-cost rare materials,11–13 and novel perovskite materials.14 In addition to cost, sustainability, and efficiency, the long-term stability and robustness of a device are also of major concern for a practical PEC device design.14,15 Measured device performance has shown stability up to several hours only.12,14 These four indicators provide an assessment as to whether hydrogen production by PEC devices and systems has the potential to provide a scalable solution and, consequently, contribute significantly to a future renewable energy economy.Recent detailed studies focusing on design improvement through a variety of material and component choices have shown that the lowest hydrogen cost of non-concentrating devices,5 and the largest energy yield ratios of concentrating devices,7 result from optimized material, component, and design choices. Therefore, life cycle assessments and economic studies which focus solely on one or few materials and components, or one or few device designs, provide limited guidance for integrated device design decisions. Moreover, these studies have only considered one indicator, e.g. price, energy input, or efficiency, ignoring whether at the maximized indicator the other indicators would still support a meaningful design, for example maximizing the device efficiency but providing a costly and energy-intense production design, or minimizing price but providing a low-efficiency and energy-intense production design. Maintaining this strategy will not provide holistic design guidelines, nor long-term meaningful guidance regarding which design strategies should be further investigated and optimized.
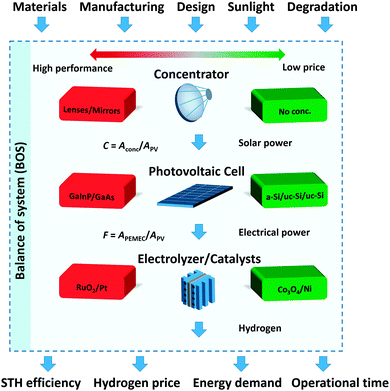
We proposed the use of multi-objective investigations to account for efficiency, price, manufacture and operation energy balance, and operating time in order to provide holistic guidelines for overall device design, material and component combinations and choices, operating conditions (e.g. using concentrated or non-concentrated irradiation), and component replacement time and degradation. We considered a device composed of photoabsorbers, membrane-separated electrocatalysts, and peripheral elements such as cables, wires, and pumps (balance of system, BOS). Multi-junction photovoltaics (PV) were considered as photoabsorbers, and polymer electrolyte membrane electrolyzers (PEMEC) as membrane-separated catalysts. A concentrator was used when concentrated irradiation was examined, together with a sun-tracking system to compensate for the low acceptance angle of concentrators. The photoabsorbers convert the incoming irradiation (concentrated or not) to electron and hole pairs, which are separated by internal electrical fields, and provide current at a sufficient potential to perform the anodic and cathodic electrochemical reactions, i.e. oxygen evolution and hydrogen evolution reactions, respectively. The modular nature of these devices was explored through the selection of two photoabsorber components (Si-based or III–V based cells) and two sets of electrocatalysts (Co3O4/Ni or RuO2/Pt). The component material choices were motivated by the desire to span a large range of possible material choices covering an exhaustive range of low-cost and low-performance, and high-cost but high-performance solutions. The material choices are examples and not preferential to, or selected to be optimal for our particular application. The components were combined in a range of device designs characterized by two concentration ratios: (i) irradiation concentration ratio, C, defined by the ratio of the irradiated concentrator area to the photoabsorber area (C = Aconc/APV), and (ii) the current concentration ratio, F, defined by the ratio of the catalyst-covered projected electrode area to the photoabsorber area (F = APEMEC/APV). The factor F generally indicates whether a system is closely coupled (F = 1), for example, in the case of traditional photoelectrochemical devices where the photoabsorber is closely integrated with the electrocatalyst, or indicates whether a system is loosely coupled or completely decoupled (F ≠ 1), for example, in the case of externally wired PV and electrolyzers. An obvious exception to this are nano-structured photoelectrodes such as catalyst covered micro-wires, which provide a similar effect as F. The device and the component choices are indicated in Fig. 1. The system boundary was set to only account for the device and immediate peripheral components (BOS) allowing for comparison of different device designs with different combinations of materials. Requirements associated with the installation, operation, maintenance, decommissioning, and overall management of a large scale H2 production plant were not considered.
The characteristic device types and designs studied in this work and the corresponding codes used are depicted in Table 1. Design types 1–4 and 9–12 are types using concentrated irradiation (C ≠ 1), and design types 5–8 and 13–16 are types using no concentration (C = 1). Design types 1–8 are loosely coupled PV-electrolyzer designs (F ≠ 1), and design types 9–16 are more closely coupled designs (F = 1). If not indicated otherwise, the replacement time of a device and its components is assumed to be 30 years, except for the PEMEC, whose replacement time is assumed to be 10 years. The four device indicators – performance, cost, sustainability, and degradation – were assessed using STH efficiency, hydrogen price ($ kgH2−1), energy input (MJ kgH2−1), and operational time (years).
| With current concentration (variable F) | No current concentration (F = 1) | ||||
|---|---|---|---|---|---|
| High quality catalyst (RuO2/Pt) | Low price catalyst (Co3O4/Ni) | High quality catalyst (RuO2/Pt) | Low price catalyst (Co3O4/Ni) | ||
| With concentrator (variable C) | High quality photoabsorber (III–V) | 1 | 2 | 9 | 10 |
| Low price photoabsorber (Si) | 3 | 4 | 11 | 12 | |
| No concentrator (C = 1) | High quality photoabsorber (III–V) | 5 | 6 | 13 | 14 |
| Low price photoabsorber (Si) | 7 | 8 | 15 | 16 | |
2. Methods and assumptions
The device types considered are integrated photo-electrochemical devices, composed of multiple protected photoabsorbers in the form of traditional multi-junction photovoltaics (PV), coupled to membrane-separated electrocatalysts in the form of a polymer electrolyte membrane electrolyzer (PEMEC). Current concentration was possible between the photoabsorber and the electrocatalyst, characterized by the factor F = APEMEC/APV. The device was irradiated by sunlight. Irradiation concentration was possible by using a concentrator with a characteristic irradiation concentration ratio C = Aconc/APV. The concentrator was composed of a concentrating module – Fresnel lenses, parabolic trough, or solar tower – and a sun-tracking system acting as a support. The efficiency of a concentrator was assumed 85% at the beginning of its lifetime.7Devices were modeled using equivalent circuit models for the photoabsorber and membrane-separated electrocatalysts. The influence of 1D and 2D on the performance has been investigated elsewhere.16,17 The PV cell was either a Si-based triple junction cell (a-Si/μc-Si/μc-Si) or a III–V dual-junction cell (GaInP/GaAs). The PV cells were modeled using either the Shockley–Queisser limits18 and an ideal diode equation, see eqn (Si) and (Sii) in ESI,† for the III–V based cells (band gaps 1.9 and 1.43 eV), or experimental data19,20 and equation fitting, see eqn (Siii) to (Sv) in ESI,† for the Si-based cells. Potentially, the radiation will be partially absorbed in the electrolyte before incident on the PV.21 This effect as well as phenomena related to two-phase flow were neglected as they heavily depend on the design. The electrolyzer model accounted for ohmic losses in the membrane and solid electrolyte (see eqn (Svi) and (Sviii) in ESI†), activation overpotentials of the anodic and cathodic reactions (see eqn (Svii) in ESI†), mass transport limitations due to concentration overpotentials (see eqn (Six) in ESI†), and potential losses due to degradation (see eqn (Sxiii) in ESI†).22–24 The proton conducting membrane had the properties of commercial Nafion (thickness 50 μm and conductivity of 10 S m−1). Two PEMEC types were considered with two selected sets of catalysts: expensive but efficient catalysts (Pt for the cathode and RuO2 for the anode with exchange current densities of 7.2 × 10−4 A cm−2 and 3.0 × 10−8 A cm−2, respectively) and catalysts made of earth abundant materials (Ni and Co3O4 with exchange current densities of 2.5 × 10−6 A cm−2 and 1.1 × 10−9 A cm−2, respectively).25 Typical current–voltage curves for devices with different irradiation and current concentrations are shown in Fig. S1 (ESI†).
The BOS specifications included a pump for the water cooling system, therefore device operation was assumed isothermal at T = 298 K for all types and concentrations. Potential temperature increase at high concentrations which could reduce the PV performance and increase the PEMEC performance were neglected.26 This assumption was justified as preliminary numerical analysis on thermal management in concentrated PEC suggested that the performance decrease due to increased temperature can be minimized.26,27
The materials were chosen as reasonable lower and upper limits in terms of price and efficiency. GaInP/GaAs cells were selected as an example of an efficient and costly technology, predominantly used in space applications. The double junction cells provided enough electrical potential for water splitting. Triple junction a-Si/μc-Si/μc-Si cells were chosen as a low price silicon cell technology able to provide enough potential for water splitting. The choice of electrocatalysts was based on the previous selection of Rodriguez et al.5 who reported the price and performance of 6 electrocatalysts. We selected the most efficient ones (RuO2 and Pt) and the cheapest ones (Co3O4 and Ni) for our study. All the selected materials needed available data to conduct the study, namely: price and energy demand, efficiency, electrochemical performance and photoabsorber behavior under concentrated irradiation, which was not available for other candidate device designs and materials such as highly efficient devices made of earth abundant materials10 or perovskite-based PECs,14 and hence were not chosen in our analysis. The material choices are examples and not preferential to, or selected to be optimal for our particular application.
The model was implemented in its transient form in order to account for the non-linear effects of degradation on operating performance. This transient investigation didn't account for the variation in solar irradiation during the day but assumed constant yearly-averaged irradiation values. Details on the effect of the irradiation variation on performance and sustainability of a device have been given elsewhere.7,26 Degradation of components and materials was included in the model to account for the decrease of the short circuit current of the PV cell and additional overpotentials in the PEMEC with time. Degradation rates were selected from literature and assumed the same for III–V and Si-based cells, i.e. 0.17% year−1 to 2.5% year−1 reduction in the short circuit current.28,29 The increase of the PEMEC overpotential with aging was 1 μV h−1 to 14 μV h−1.30,31 Mean degradation rates were chosen for the reference case, if not indicated otherwise, but the minimum (optimistic case) and maximum (conservative case) values were used in order to assess the effect of additional degradation sources such as high temperature, corrosion, and light intermittency. The degradation of the 85% efficient concentrator was assumed to be linear at 19.5% loss in optical efficiency after 30 years, i.e. a 0.65% loss per year.
Energy input and the price of devices were evaluated according to life cycle inventories and cost analysis of the four components: the concentrator device with tracking and support, the PV cells, the PEMEC, and the balance of system (BOS). BOS includes the peripheral components (cables, wires, control systems, pumps). The device cost accounted for materials and manufacturing. The energy assessment included the energy input required for materials mining, the manufacture of device components, and operation. We will call this energy input for the sustainability assessment the energy demand of the device. Details on device performance modeling, prices and energy inventory, and degradation and replacement time considerations are given in Table 2 and in the ESI.†
| e (MJ m−2) | p ($ m−2) | |
|---|---|---|
| Concentrators | ||
| Parabolic troughs | 163934,35 | 29536,37 |
| Solar tower heliostats | 235635 | 16436,37 |
| Flatcon | 188238 | 17039 |
| Dishes | — | 17640,41 |
| 2-Axis Fresnel | — | 20240,41 |
| Amonix 7700 | 312942 | 19843 |
| Average value | 2251 | 201 |
| Photoabsorbers | ||
| PV (Si) | 12307 | 1455 |
| PV (III–V) | 854044 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00045 00045 |
| Electrochemistry | ||
| PEMEC (RuO2/Pt) | 294846,47 | 1000 |
| PEMEC (Co3O4/Ni) | 2064 | 245 |
| Peripherals | ||
| BOS (with concentration) | 55042 | 13739,45 |
| BOS (no concentration) | 55048,49 | 7648,49 |
The hydrogen production of a given device type and design was determined by Faraday's law of electrolysis utilizing the operating current resulting from the simultaneous fulfillment of the current–voltage requirements in the PV cell and the PEMEC.
The hydrogen price was calculated as the ratio of the cumulated cost of the device to the cumulated hydrogen production at a given operational time L,
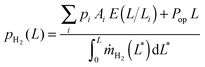 | (1) |
The hydrogen energy requirement in MJ kgH2−1 was calculated using the same approach, utilizing the energy requirements of materials instead of cost.
The yearly and operational time-averaged STH efficiencies at a given operational time were calculated as:
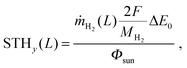 | (2) |
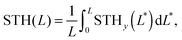 | (3) |
3. Results and discussion
The generally expected effects of the two design parameters – C and F – on each of the four indicators have been partially explored.5,7 Our observations followed these expected effects. An increase in C affected the PV cell by an increase in the photocurrent density, increased open circuit voltage, Voc, and reduced efficiency, unless the PV cell was specifically designed for large C. An increase in C affected the PEMEC through the PV provided current, which increased, consequently increasing the overpotentials in the PEMEC. An increased C reduced the importance of the PV cell and PEMEC to the device price and energy requirements, as their area and weight fractions in the device were decreased. An increase in F reduced the current density in the PEMEC and therefore the overpotentials. An increased F however also increased the price of the device because of the larger electrode area.Indicators' dependence on operational time
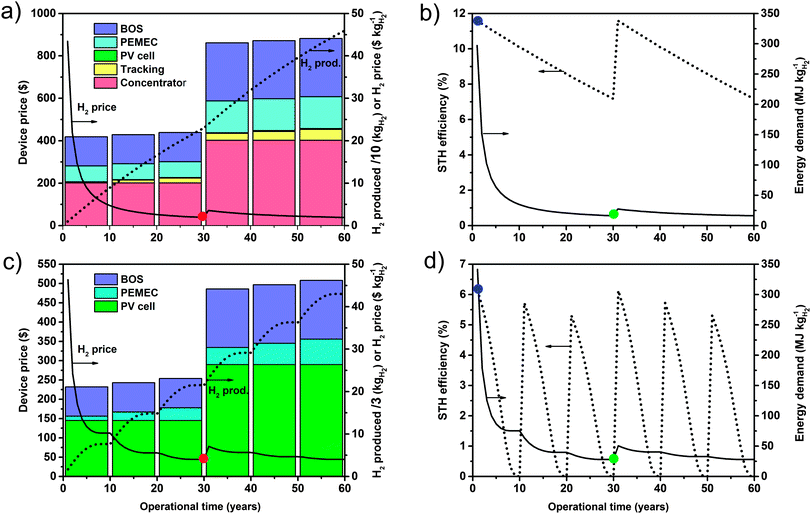
The performance of the PV cell, the PEMEC, and the concentrator (if used) decreased with time and an additional price and energy investment was required when components needed to be replaced. The hydrogen price decreased with operational time as a given set of components produced an increased cumulative quantity of hydrogen before replacement. Typical transient behaviors of the yearly STH efficiency, hydrogen price, component prices, and energy demand are depicted in Fig. 2 (for device type 2 – concentrating/III–V based PV cells/low-cost catalysts – with C = Copt = 1000 and F = Fopt = 3.2, and device type 7 – non-concentrating/Si-based PV cells/high-quality catalysts – with C = 1 and F = 0.013). Superscript “opt” indicates the irradiation and current concentration factors which lead to the lowest device price for a device type. The minimum hydrogen price, pmin ($ kgH2−1), was typically observed when the operational time was equal to the component replacement time (30 years or 60 years). The minimum energy demand for the device, emin (MJ kgH2−1), was also achieved when the operational time was equal to the component replacement time. Device types with concentrator and Si-based PV cells showed the lowest prices and energy demand already 1–3 years before the component replacement time (at years 27 to 29) as the continuous tracking expenses can't be compensated because of the low hydrogen production resulting from degradation in the components and relatively low Voc. The difference in price or energy requirement were however very low (less than 1%) compared to the values obtained for an operating time of 30 years. Therefore all the following results are shown for a 30 years operational time. The performance was lowest when the operational time was equal to the component replacement time, and maximal at the beginning of operation. The exact behavior differed between device types and between device designs. For example the influence of the degradation was more detrimental to device type 7 than device type 2. For device type 7 the hydrogen production dropped to almost zero already before the PEMEC was to be replaced (after 10 years in this case).The observation that device performance was maximal at operational debut, and cost and energy were minimal when the operational time was equal to the component replacement time, was generally true for all device types. Since a device operational time of one year, for which the yearly-averaged STH efficiency (eqn (2)) was maximized, was unrealistic, an operational time-averaged efficiency (eqn (3)), STH, was additionally used for characterization. Consequently, for each device type and design there were three possible strategic choices: (i) design for minimum hydrogen price (pmin), (ii) design for minimum energy demand (emin), and (iii) design for maximized performance over the operational time (STHmax). Fig. S7 (ESI†) quantifies the irradiation concentration, C, and current concentration, F, for each of 16 different device types for the three strategies.
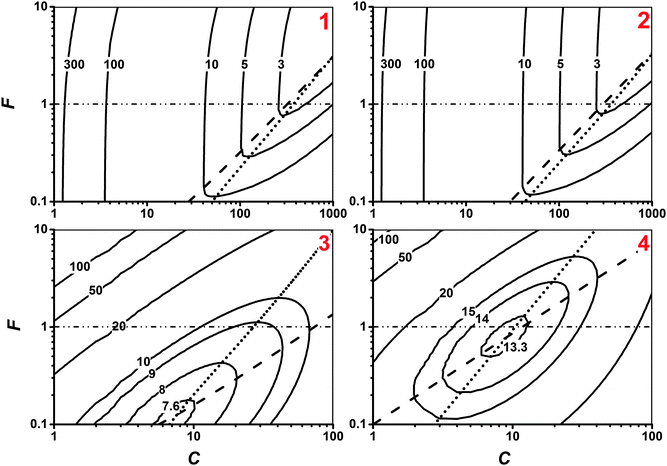
Influence of irradiation and current concentration on cost
The detailed influence of C and F on the hydrogen price is shown in Fig. 3 for design types 1–4 (F ≠ 1) and 9–12 (F = 1), the latter representing subsets of the plot and the corresponding C–F-space. Note that for device types 5–8 and 13–16, no concentrator and tracker are used and consequently the prices were different than indicated in Fig. 3 along the y-axis for C = 1. Device types 1 and 2, i.e. concentrating devices using III–V PV based cells, showed lowest hydrogen prices at highest irradiation concentration and slight current dilution (F > 1). The extremely high cost of the III–V based PV cells favors these irradiation concentrations. Slight current dilution is beneficial for the performance while acceptable for device cost as the PEMEC cost is negligible at these C, as shown in Fig. 4: Costs are dominated by the cost of the concentrator, BOS, and PV cells. Therefore also F can be freely adjusted to obtain maximum performance with a small variation in the hydrogen price (less than ±15% variation in hydrogen price when Fopt < F < 10), also shown in Fig. S2 (ESI†). The III–V based cells investigated exhibit a high Voc, providing enough potential to drive at these C and high operating currents. The slight current dilution ensures that mass transport limitations are not limiting in the PEMEC, as visible in Fig. S1 (ESI†). The maximum performance was not affected by the degradation of the PEMEC as the operating voltage was much smaller than the Voc provided by the PV cell. This allowed the device to cope with additional potential losses in the PEMEC while still operating in the maximum current plateau region of III–V PV cells during the complete operational time. This also explains why hydrogen prices showed little dependence on the choice of PEMEC in this case, with pmin = $2.03 kgH2−1 and $2 kgH2−1 for devices 1 and 2, respectively, with an optimum irradiation concentration of Copt = 1000 and an optimum current concentration of Fopt = 3.2. pmin was reached after 30 years before the concentrator and the BOS were replaced (see Fig. 2).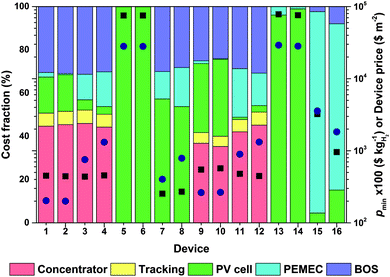 | ||
| Fig. 4 Cost (right y-axis) of overall device (black rectangle) and of produced hydrogen (blue circle), and cost fraction of the various components (left y-axis): concentrator, solar tracking, photoabsorber (PV), electrocatalysts and separator (PEMEC), and peripherals (BOS). The data is shown for cost-optimized device designs of type 1–16 (see Table 1). | ||
Device types 3 and 4, i.e. concentrating devices using Si-based PV cells, benefited from their low PV cell price and showed lowest hydrogen prices at only low irradiation concentration (Copt = 7 for device 3, and Copt = 9 for device 4) and low current concentration (Fopt = 0.12 and 0.74 for device types 3 and 4). Current concentration was beneficial for the cost while not yet limiting performance. The decreased performance of our chosen Si-based cell with increasing C and their low Voc limits the acceptable irradiation concentration, therefore the relative price of the PEMEC was larger compared to device types 1 and 2 (see Fig. 4) where F was still relatively large. If a maximization of the efficiency is targeted instead, the current concentration should be weak, i.e. F values should be maximized (F = 10, which was the maximum F investigated). The quality of the PEMEC was critical for device types 3 and 4 since hydrogen production was very sensitive to the small differences in the operating voltage as well as to degradation. Overall, the lower performance of these particular Si-based PV cells which we investigated did not compensate for their cost advantage, since pmin ($7.54 kgH2−1 and $13.2 kgH2−1 for device types 3 and 4, respectively) was 3.7 to 6.6 times higher than pmin of design types 1 and 2. The STH efficiency at the minimum price design was 3.8 to 6.4 times lower for device types 3 and 4 (STH = 2.4 and 1.4%, respectively) than for device types 1 and 2 (STH = 9% for both). This means that devices with an area of about 3.8 to 6.4 times larger are required for device types 3 and 4 to reach the same hydrogen production as device types 1 and 2.
p min was increased by 30% when comparing design type 1 to design type 9, and design type 2 to design type 10, i.e. when current concentration was suppressed (F = 1). The optimal concentration for minimized cost, Copt, decreased from 1000 (for device types 1 and 2) to 400 (for device type 9) and 380 (for device types 10) due to increased overpotentials in the PEMEC at smaller F. Consequently, the cost contribution of the PV cells to the overall device increased for device types 9 and 10 compared to device types 1 and 2.
Both pmin and Copt showed a moderate increase in device 11 (for which F = 1) compared with device 3 (18.5% increase in pmin, and an increase from 7 to 28 for Copt) and remained almost unchanged for device 12 (for which F = 1) compared with device 4 (0.3% increase in pmin, and an increase from 9 to 11 for Copt) since Fopt was already close to 1 for device types 4, as visible in Fig. 3.
For device types using no solar irradiation concentration and high-performing III–V PV cells (device types 5, 6, 13, and 14), the impact of the very high PV price was not compensated for by concentration, resulting in very high hydrogen prices (above $200 kgH2−1), making these devices not practical for scalable hydrogen production. Non-concentrating device types using Si-based PV cells with F = 1, device types 15 and 16, also resulted in unpractically high hydrogen prices ($35.7 kgH2−1 and $18.3 kgH2−1), stemming from low hydrogen production and the unmitigated high price of the PEMEC.
For device types using no solar irradiation concentration and Si-based PV cells (device types 7, 8, 15, and 16), not only the PV performance but also the PEMEC choice became important for performance and cost. This explains why Fopt (0.013 for device 7, and 0.066 for devices 8) was very sensitive to the choice of the PEMEC. Device types 7 and 8 had the potential to produce hydrogen at a price that was lower than their corresponding concentrating devices (pmin = $4 kgH2−1 for device 7, and pmin = $7.9 kgH2−1 for device 8), with a moderate sensitivity to F (±5% of variation in hydrogen price when changing F by a factor of two, see Fig. S2, ESI†). However, F values had to be kept low (F < 1) to avoid high PEMEC prices at the expense of reduced performance as the high current densities in the PEMEC led to larger overpotentials and consequently lower device operating currents. Consequently, minimum hydrogen prices were reached for low STH efficiencies (2.6% for device 7, and 1.4% for device 8) meaning that device areas of 3.5 to 6.4 times larger would be required to obtain equally affordable hydrogen production at a comparable magnitude as for device 1 and 2. This technical limitation resulted from the low Voc of the Si-based PV cell and a corresponding low flexibility in dealing with overpotentials in the PEMEC or losses in the PV fill factor resulting from high current densities, long operational times, or degradation.
Simultaneous consideration of performance, cost, and sustainability
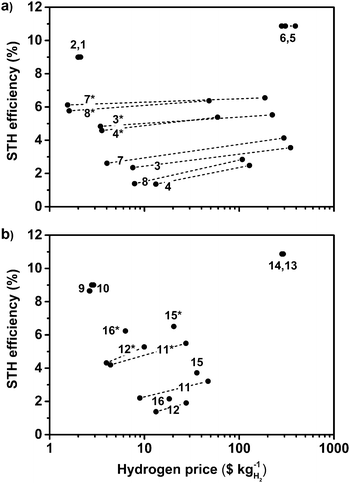
The ranges of operating time-averaged STH efficiency (assumed 30 years operation), hydrogen price (p for 30 years operation, usually pmin), and energy demand (e for 30 years operation, usually emin) spanned by the different device types for varying C and F are shown in Fig. 5 for a set of device types.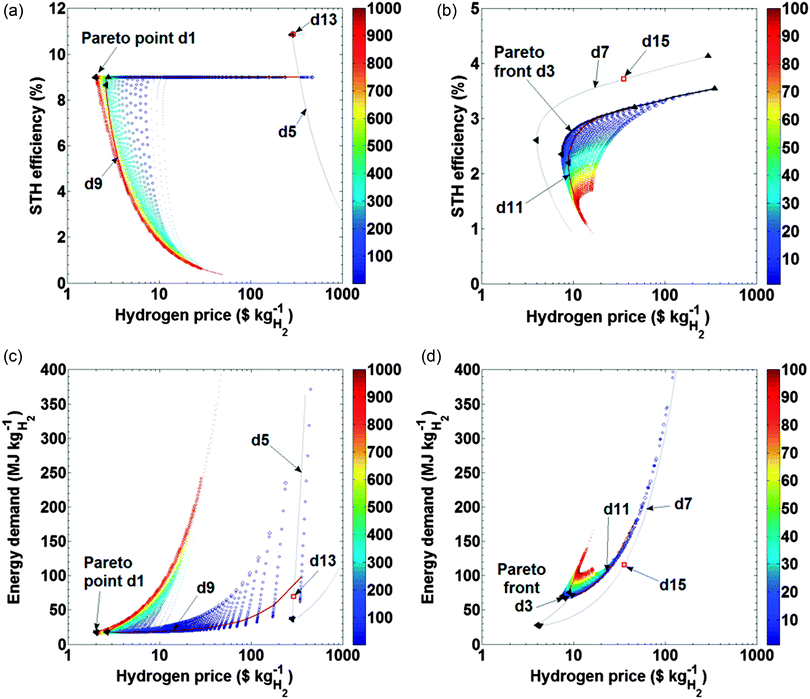 | ||
| Fig. 5 Operating time-averaged efficiency (a and b), and energy demand (c and d) as a function of hydrogen price, for (a and c) device types 1, 5 (gray line, C = 1), 9 (brown line, F = 1), and 13 (red rectangle, C = F = 1), and (b and d) device types 3, 7 (gray line, C = 1), 11 (brown line, F = 1), and 15 (red rectangle, C = F = 1). Device types j are indicated as dj in the plots. Point colors indicate the irradiation concentration (indicated by the color bar), C, for device types 1 and 3; point sizes indicate the log10 of the current concentration, F, for device types 1 and 3 (colored in Fig. S4, ESI†). Pareto front or point of device types 1 and 3 are indicated by the black line. Black triangles indicate the design for highest operational time-averaged STH efficiency (▲), lowest price (◀), and lowest energy demand (▼). | ||
Device type 1 predicted the existence of a single design choice (the Pareto point) which simultaneously maximized performance and minimized cost and energy demand. This design used irradiation and current concentration (C ≠ 1 and F ≠ 1). Generally, irradiation concentration increases the cost competitiveness of designs, while low C designs show higher efficiency and lower energy demand. Moderate current dilution (F ≈ 1–1.4) results in lowest cost design, but has no clear advantage for efficiency or energy demand, i.e. depending highly on the irradiation concentration (see Fig. S4, ESI†). The operating time-averaged efficiencies, STH, for device types 1 were 9% for a wide range of C values and for F > 3 (for larger C).
Device type 9, using irradiation concentration but no current concentration (F = 1), didn't predict a global optimum (a Pareto point) but rather a range of designs (Pareto front) with high efficiency, low cost and energy demand indicating a requirement for a strategic choice between highest performance, lowest cost, and lowest manufacturing energy demand. The Pareto front was below the Pareto point of device 1 indicating inferior indicator characteristics. Design types 5 and 13, not using a concentrator, showed significantly higher cost and higher as well as lower STH efficiency than device type 1. Note that the STH efficiencies of device type 5 shown in Fig. 5 were obtained for 0.01 ≤ F ≤ 10, while the efficiency data for device type 1 is shown only for 0.1 ≤ F ≤ 10. The cost inferiority of device types 5 and 13 compared to device types 1 and 9, stems from the use of the extremely expensive PV cells, for which the absence of concentrator and tracking cost couldn't compensate.
Device types 2, 6, 10, and 14, showed the same efficiency-cost-sustainability behavior as designs 1, 5, 9, and 13, even though they utilized low cost catalysts. Performance and cost were insignificantly influenced by this change as the PEMEC cost was negligible (see Fig. 4) while the performance stayed about the same. A recent demonstration of a non-concentrated III–V based cell using Ni-based catalysts operating with an efficiency of 8.6%13 could be seen as a demonstration of device design type 14, a type which proves unpractical unless the device is further developed to operate at high irradiation concentrations.
Device type 3 predicted the existence of a range of designs (Pareto front) with high efficiency, low cost and low energy demand with no single best design. Rather, compromises between efficiency, cost, and sustainability were required. Generally, low to no irradiation concentration is required for best performance. No clear trends of C on the price and energy demand are observed. Current concentration (F < 1) clearly benefits all design choices in terms of cost and energy demand, but has no clear trend on efficiency. Device type 11, using irradiation concentration but no current concentration (F = 1), predicted also a Pareto front. This front lay below the front of device type 3 indicating inferior indicator characteristics. Design types 7 and 15, not using a concentrator, showed a potential cost and STH efficiency advantage, and generally lower energy demand compared to device types 3 and 11. Current concentration (F < 1) clearly benefits the cost of non-concentrating device types, device type 15 is far away from the optimum. The cost and energy input advantage for some designs results from the absence of concentrator and tracker related cost and energy expenses, and generally from the low Si-based PV cell price.
Fig. 6 and 7 show the limiting points of the Pareto fronts and points of all device designs investigated, i.e. sensitivity of each design with optimized operational time-averaged efficiency towards cost-minimized designs and sensitivity of each design with optimized energy demand towards cost-minimized designs. The linear connection between the limiting points is introduced for better readability but doesn't represent the actual behavior of the Pareto front, as evident from Fig. 5.
Before we discuss the range of optimized devices for the various device types, we will introduce several additional device types. This was motivated by the observation that the choice of the Si-based cells was not well suited for this application, i.e. the low fill factor and low open circuit potential of the chosen Si-based cell were limiting for the overall performance and competitiveness of this device types (types 3, 4, 7, 8, 11, 12, 15, and 16). We examined the potential improvement of these device types by introducing new Si-based device types (indicated by superscript *) with an assumed higher Voc of 2.5 V, instead of 1.9 V. Parameter sweeps in the Voc of the Si-based PV cells were done (see Fig. S3, ESI†), which predicted that a Voc of at least 2.3 to 2.5 V was required to provide improved performance, cost, and sustainability characteristics. The assumed increase in Voc suggested the use of quadruple junction PV cells,52,53 or designed triple junction cells for high concentrations, both with a Voc of at least 2.5 V assuming no additional cost.
Fig. 6 shows that minimum prices of $1.55 kgH2−1 and $1.6 kgH2−1 can be reached for non-concentrating Si-based devices 7* and 8* with operational time-averaged STH efficiencies reaching 6.1% and 5.8% at this minimum price design for about an order of magnitude smaller area of PEMEC than for devices 7 and 8 (Fopt = 0.0043 for device 7*, and 0.011 for device 8*). An increase in Voc was also advantageous for Si-based device types using concentrated irradiation: minimal prices of $3.34 kgH2−1 for device 3* (with Copt = 6 and Fopt = 0.032), and $3.56 kgH2−1 for device 4* (with Copt = 5 and Fopt = 0.08) were observed, and maximal operational time-averaged STH efficiencies of 5.5% for device 3*, and 5.4% for devices 4* were achieved. This corresponded to a decrease of 2.3 (for 3*) and 3.7 (for 4*) fold in price, and an increase of 1.6 (for 3*) and 2.2 (for 4*) fold in efficiency when compared with device 3 and 4. The additional costs arising from a raise in the Voc of these PV cells were, however, not included in the calculations.
The comparison shown in Fig. 6 predicts that device types 1 and 2, and device types 7* and 8* are among the cheapest device types investigated. Irradiation concentration greatly benefits high-cost and high-performance PV cells, while its cost (including tracking) isn't compensated for in low-cost PV cells which additionally show reduced performance at large C. Current management (F ≠ 1) is essential for low-cost design types through either dilution (F > 1) to ensure that mass transport limitations are not present (critical for devices with large C) or through concentration (F < 1) to reduce the cost contribution of the usually expensive PEMEC (critical for devices with low C).
For concentrating devices using III–V PV cells (except devices 5, 6, 9, and 10) the most profitable design was also the most efficient one, i.e. the Pareto front collapsed into a point. Several combinations of C and F for these device types exhibited the same efficiency because the maximum current provided by the PV cell could be reached for these various combinations. This was not the case for device types using Si-based cells where the two design strategies (minimum price or maximum operational time-averaged efficiency) led to very different hydrogen prices. This was especially pronounced for design types with varying F (the price difference between the two design strategies ranged from $46.5 kgH2−1 for device 8* and $340.6 kgH2−1 for device 3). However, the difference in STH efficiency remained relatively low for these devices (maximum 1.5 point difference for all devices considered). This predicts that profitable designs might provide a better compromise than efficient designs.
Non-concentrating device types using Si-based PV cells with F = 1, device types 15 and 16, also resulted in unpractically high hydrogen prices ($35.7 kgH2−1 and $18.3 kgH2−1), even with an increased Voc, devices 15* and 16* ($20.4 kgH2−1 and $6.3 kgH2−1).
The sustainability, i.e. energy demand, and corresponding minimum hydrogen price calculated (see Fig. 7 with the corresponding Pareto points or limiting points of the Pareto front), suggest that hypothetical device types 7* and 8* are the most sustainable (11.4 MJ kgH2−1 for F = 0.0062, and 12.3 MJ kgH2−1 for F = Fopt = 0.011, respectively) followed by device types 1 and 2 (16.9 MJ kgH2−1 for F = Fopt = 3.2, C = Copt = 1000 and C = 980, respectively). Most of the devices showed a price per energy requirement of the same order of magnitude ($0.12 MJ−1 or $0.43 kW h−1 ± 17%), about 4.3 times a typical electricity price in the USA for a common energy mix.‡ Device type 15 showed a higher price per energy requirement ($0.3 MJ−1 or $1.1 kW h−1), 11 times the electricity price in the USA for a common energy mix.49 Devices 5, 6, 13 and 14 showed higher values (above $4 MJ−1), suffering from the very high price of III–V based PV cells, even though they show relatively good sustainability (emin between 36 MJ kgH2−1 and 69 MJ kgH2−1).
The estimated range of obtained price per unit energy requirement provides a better conversion factor when switching from sustainability to economic studies of such devices, which up to now have used typical electricity prices for a common energy mix, therefore underestimating the price by about one order of magnitude. Most devices reach emin and pmin for very similar choices of C and F, i.e. variations within ±22%, exceptions made for devices 3 and 7 with ±108% in F, and for devices 11 and 11* with ±50% variation in C.
After comparing the devices, it appears that concentrating devices using III–V PV cells are the best trade-off between profitability, sustainability and size. These device types also provide one single Pareto point, providing a design choice simultaneously optimizing efficiency, cost and sustainability. Their high STH efficiency implies lower space or aerial requirements than other devices for a given hydrogen production. Their optimum design lies at a high C value (C = 1000), meaning that price and energy requirement depend on the concentrator and the BOS without being impacted significantly by the price and design of the PV cell and the PEMEC. Consequently, PV and PEMEC can be chosen for maximized performance neglecting cost or energy requirement.
Non-concentrated and concentrated devices using Si-based cells can achieve low hydrogen prices and good sustainability, however for a STH efficiency 4.5 to 8.9 times lower than devices 1 and 2, implying a required solar collection area 4.5 to 8.9 times greater to obtain the same hydrogen production. These devices could compete with concentrating devices using III–V based PV cells when using Si-based PV cells with a higher Voc, of at least 2.5 V (see Fig. S3, ESI†), implying the use of additional junctions or targeted cell designs.
Degradation and replacement time
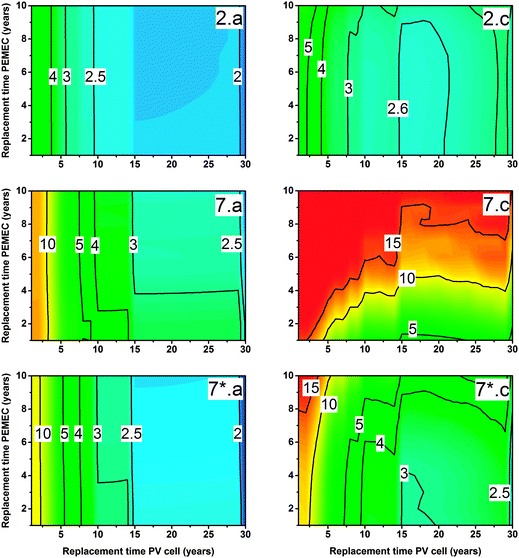
The replacement time of components is approached when the device has reached a certain threshold of degradation. For Si-based PV cells, a 20% efficiency decline has been considered a failure,29 but running a device with a PV cell with a 70% degraded efficiency may have less impact on hydrogen price than replacing it. We examined the relationships between degradation rate and hydrogen price to determine the optimum replacement time of components for the best-performing concentrating device type (device type 2 using III–V based PV cells and low cost electrocatalyst) and non-concentrating device types (device types 7 and 7* using Si-based PV cells and high quality electrocatalysts) in their most cost-effective C and F design configuration (i.e. at Copt and Fopt). We used the previously defined optimistic, reference, and conservative degradation cases since the degradation effects for solar water splitting devices caused by concentrated irradiation, temperature, or light intermittency is sparsely reported: Concentrator degradation was a linear decrease in efficiency of 0.65% loss per year for all degradation cases (optimistic, reference, conservative); PV short circuit current degradation ranged between 0.17% year−1 (optimistic) to 2.5% year−1 (conservative), with 0.7% year−1 as reference case; and PEMEC voltage degradation ranged between 1 μV h−1 (optimistic) to 14 μV h−1 (conservative), with 6 μV h−1 as reference case.We found that at low degradation rates, pmin was mostly dependent on the PV cell replacement time (see Fig. 8 and Fig. S5, ESI†) for device types 2 and 7*, while it slightly increased for longer PEMEC replacement times for device type 7. The impact of the PEMEC replacement time on the hydrogen price was negligible for device types 2 and 7* since the PV cell dominated the cost of the device. In this optimistic degradation configuration, the price of the components prevailed over their performance and the device worked at a sufficient performance for a long time, allowing the PV cell and the PEMEC to be replaced over their recommended operational times of 30 and 10 years, respectively. This explains why operational time-averaged STH efficiencies for cost-optimized designs did not change with replacement time (0.102 ± 1.2%, 0.0625 ± 3.3% and 0.0728 ± 2.8% for device types 2, 7 and 7*, respectively, see Fig. S6, ESI†). This conclusion didn't hold in the instance of high degradation rates, where the price and performance of the components defined the optimum replacement times. For device type 2, the PV cell and PEMEC needed to be replaced every 15 and 5 years, respectively. For device type 7, the PEMEC needed to be replaced almost every year to prevent device operation at a very low hydrogen production (see Fig. S6, ESI†). For device type 7* an interesting case arose: pmin presented a local minimum ($2.88 kgH2−1) for a PV cell replacement time of 15 years and PEMEC replacement time of 1 year, and showed an even lower value ($2.43 kgH2−1) for a PV cell replacement time of 30 years and PEMEC replacement time of 4 years. In the first case, the replacement of components increases the performance of the device, while in the second case, the longer replacement time alleviates the resulting additional cost.
In general, we observe that for low degradation rates pmin was lower at the optimal choice of component replacement times, with less sensitivity for device type 2 ($1.77 kgH2−1 for low degradation rates, and $2.53 kgH2−1 for high degradation rates) compared with device types 7 ($1.74 kgH2−1 for low, and $4.37 kgH2−1 for high rates) and 7* ($1.31 kgH2−1 for low, and $2.43 kgH2−1 for high rates). For a given degradation case, the ratio between maximum and minimum pmin obtained at different component replacement time combinations was also less sensitive to replacement time in device type 2 (2.8 and 2.4 for low and high degradation rates, respectively) than for device types 7 (7.1 and 17.1) and 7* (7.8 and 8.1).
The degradation analysis shows that there is a need for a beforehand accurate knowledge of the degradation rates before deciding on the replacement time of components. Additionally, an informed decision can then be made to select component replacement times e.g. with maximized hydrogen prices. This is especially pronounced for non-concentrating devices using the low-cost Si-based PV cells of this study (device type 7).
Sensitivity analysis for price, energy requirements and effective irradiation
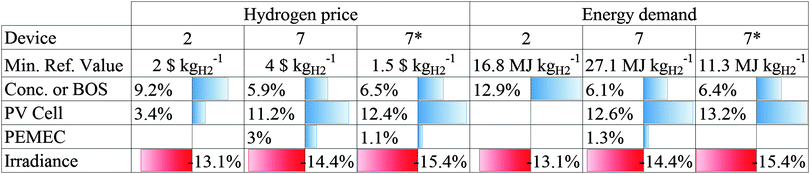
The sensitivity of pmin and emin for selected component prices and energy demand as well as incoming irradiation is presented in Fig. 9 for device types 2, 7, and 7* at their cost and energy demand optimized designs. pmin and emin displayed a four times higher PV cell requirement sensitivity for device types 7 and 7* compared to device type 2, despite the much higher energy requirements and cost of III–V based PV cells. The pmin and emin of device type 2 showed more sensitivity with respect to the concentrator and the BOS because of a high operating C (about 1/3 more sensitivity for device type 2 compared to device types 7 and 7*). Device types 2, 7, and 7* were not sensitive to the PEMEC requirements, mainly because of a high C and F ratios. The Voc improvement of the Si-based PV cells utilized in this study (device types 7* compared to 7) is generally more favorable to performance, cost, energy, and operational time behavior. Nevertheless, the Voc improvement was profitable only if it implied less than a 160% cost and energy requirement increase compared to the initial PV cell. A comfortable 750% increase in energy requirement in the PV cell was required for device type 7* to remain more sustainable than device type 2, but less than a 30% PV price increase was required to produce cheaper hydrogen than device 2. Device types using concentrated solar irradiation illustrate that a focus on reduction in cost and energy requirement of the concentrator and the BOS is most important. Price and energy demand showed a similar sensitivity to irradiation (and by extension to optical efficiency of the concentrator or of the PV cell) with a decrease of 0.65% to 0.77% per 1% increase in irradiation. This implies that the location of the device will strongly determine its outputs and that optical efficiency is a major parameter to be improved.The sensitivity analysis allowed for a quantification of the influence of the error margin in the collected data on the efficiency, cost, and energy demand results for a given device design type. Assuming a ±33% uncertainty on the cost and energy requirement of concentrators and PV cells (see Table 2) and a ±15% uncertainty on the collected data,38 the calculated variations in pmin and emin were 33% and 34% for device type 2, and 53% and 52% for device types 7 and 7*.
4. Conclusions
This study provides holistic and quantified design guidelines for hydrogen production through integrated photo-electrochemical water-splitting approaches, with the option to use irradiation concentration and current concentration. The results compared several design types (types 1–16, 3*, 4*, 7*, 8*, 11*, 12*, 15*, and 16*) and design choices (varying irradiation concentration, C, and varying current concentration, F) using four indicators: operation time-averaged STH efficiency, hydrogen cost, device manufacture and operation energy demand per mass unit of hydrogen produced, and operational time. The device types were built based on different material choices, which are examples and not preferential to, or selected to be optimal for our particular application.The operational dependence of performance, cost, and energy demand showed two trends. Due to the increase of the cumulative quantity of produced hydrogen, the cost and energy demand decreased with increasing operational time and was usually lowest right before the majority of the components were replaced. On the other hand, due to the degradation of the various components, the device performance decreased with operating time, with partial performance restoration when a few components were intermediately replaced. These trends were generally observed for all device types investigated. Nevertheless, if the performance of the device intermediately dropped to almost zero due to the failure of one component (high degradation rate or low performance components), a local minima for cost was observed a few years before the device operational lifetime was reached. This resulted from almost no increase in the cumulative generated hydrogen, while cost for tracking continued to increase. Generally, one can conclude that the operating time before complete device replacement should be as short as possible if maximum efficiency is the targeted indicator, while the replacement should be pushed towards the end of the device operational time if cost and energy demand minimization is targeted. For each device type there are, therefore, three possible strategic choices: (i) design for minimum hydrogen price, (ii) design for minimum energy demand, and (iii) design for maximized performance over the operational time. The latter strategy is unpractical and instead an optimization of the operational time-averaged performance should be approached.
Applying irradiation and current concentration to the design of the various concentrating device types provided significant advantages to all three indicators (performance, cost, and energy input). Thanks to this, hydrogen prices were significantly decreased and cost-competitive design solutions for device types utilizing very expensive components (e.g. the III–V based PV cells) were observed. As the performance didn't significantly decrease with increasing irradiation concentration for the III–V based PV cells modeled, the optimal irradiation concentration was reached for the largest investigated concentration C = 1000. For the Si-based device types modeled, on the other hand, an optimal irradiation (in the range of C = 10) and current concentration existed for which the cost was minimized. This concentration combination reduced the mass of expensive materials while still ensuring non-limiting losses in the PV cell and electrolyzer. Nevertheless, non-concentrating device types using Si-based PV cell showed a cost, efficiency, and energy demand advantage compared to the low concentrated case. This resulted from the requirement on direct irradiation of concentrating devices reducing the actual use of the total solar irradiation (composed of direct and diffuse fractions), the reduced performance of Si-based cells at higher concentrations, and the additional cost for a concentrator, all of which was not compensated by the lower device area and cost with increasing concentration. Generally, it was observed that in order to be commercially competitive and sustainable with minimum land use, concentrating devices must use PV cells which can produce high currents at large potentials and withstand high concentrations (up to C = 1000) without losing efficiency.
A holistic approach to photo-electrochemical water splitting devices requires a simultaneous optimization of cost, energy input, and performance over a long operational time. We observed two distinct behaviors for the various device types investigated: (i) device types which exhibited a design allowing for a global optimum (a Pareto point) simultaneously maximizing performance, while minimizing cost and energy input, and (ii) device types which exhibited a range of partially optimal designs (a Pareto front) with high efficiency, low cost, and low energy demand, indicating a tradeoff and the requirement for a strategic choice between highest performance, lowest cost, and lowest energy demand. Device types using high-performing and high-cost PV cells and allowing for an adaptation of C and F (device types 1 and 2) were device types which exhibited a Pareto point, i.e. provided a design which allowed for the simultaneous optimization of performance, cost, and energy demand. These designs perform best at high irradiation concentrations, and also showed the lowest variation in characteristics with respect to component replacement time and degradation rate. Hydrogen price and energy requirements were not affected by the current concentration, F, as long as F > 2. A decrease of F below 1 was detrimental for the hydrogen cost due to the occurrence of mass transport limitations at these high current densities (since C was already large). Further improvement in the performance characteristics of these device types can be achieved through the enhancements of the concentrator's optical efficiency without additional cost or energy requirement, and by lowering the cost of the balance of system (BOS). Generally, the cost-optimized devices were obtained for large C, therefore the PEMEC didn't play a significant role in the price or energy requirements. Consequently, best-performing catalysts could be used no matter their cost.
Device types using low-performing and low cost PV cells (types 3 and 4) were device types which exhibited a Pareto front. In other words, a set of device designs existed which optimized performance, cost, and energy input, but not simultaneously, therefore requiring a tradeoff between the indicators. Non-concentrating devices using our modeled Si-based cells showed the potential for higher profitability and sustainability than concentrating devices. The latter mainly resulted from the inability of concentrating devices to collect and absorb diffuse solar irradiation as well as the inability of compensating the performance losses at high concentrations by the reduction in device cost. These device types were highly sensitive to the degradation rate, replacement time choices, and variation in component price and energy requirement. In order to compete with device types 1 and 2, the Voc of the PV cell needed to be increased to higher values of around 2.5 V, with either no, or a tightly controlled increase in cost, potentially achievable with a Si-based PV technology with better performance such as crystalline Si.
The quantification of the influence of component degradation on the performance allows the suggestion of best practice for device operational time and component replacement. The results indicated that a detailed knowledge of the component degradation rates beforehand was required in order to determine the best replacement time for the various components. Generally, two competing effects were observed: (i) reduced performance with increasing replacement time, and (ii) reduced cost and energy demand due to the increase in cumulative hydrogen produced. For the low degradation scenarios investigated, PV replacement time was critical for the cost, while PEMEC replacement was insignificant. This was especially true for PV cell choices with significantly higher Voc than the operating potential. For high degradation scenarios, the PEMEC replacement time became more critical, especially for device types using PV cells with low Voc. For the device types with high performing PV cells (types 2 and 7*), local cost minima were observed, usually around a PEMEC replacement time of 5–6 years and a PV cell replacement of 15–16 years.
The methodology presented provides a pathway for a holistic assessment of photo-electrochemical water splitting device types and design. Obviously the concrete outcomes depend strongly on the material performance properties, and the cost and energy input assumed. We aim at providing a web-based version of the modeling framework presented here§ allowing for the assessment of, and guidance for specific device types, designs, and ideas, of which there are currently many existing in the community. A sensitivity study was conducted to get a general idea of the importance of various assumptions on the results. Optimized cost and energy demand displayed a four times higher PV cell requirement sensitivity for device types 7 and 7* compared to device type 2. The cost and energy demand sensitivity of the latter device type was highest with respect to the concentrator and BOS cost and energy input, as this device type operated at high irradiation concentration.
Since hydrogen compression, hydrogen storage, the end-of-life of a device, and all operational costs were not included in this study, and because of the uncertainties associated with the cost estimation of emerging technologies, the actual hydrogen prices and energy demands will likely vary. Accurate values for these devices will only be obtained once they are built and installed at a specific location with a specific irradiation, energy mix, and within a specific economic and policy environment. Furthermore, requirements associated with the installation, operation, maintenance, and overall management of a large scale H2 production plant were considered out of scope. Consequently, this study cannot comment on economy of scale. This study allows for comparison of systems on a device level (including their immediate peripherals) in order to compare different types of material selections under different designs. Price and energy requirement used in this study were reported per unit area of the device, implying that the results are valid for a variable device size.
Our study provides trends and guidelines for the meaningful focus of research concerning scalable hydrogen production technologies. The proposed framework allows for a quantifiable comparison between different device types, device designs, material choices, operating choices, and stability, and provides sensitivities of the obtained values to variations in the input data (performance, cost, energy demand, and degradation values) caused by fluctuations in the market and with technological improvement.
The findings presented here show that only the combined consideration of efficiency, price, sustainability, and operational time can provide a holistic approach for the design of integrated photo-electrochemical devices, and provide guidelines for a scalable, sustainable, and competitive solar hydrogen production for the future.
Acknowledgements
This material is based upon work performed with the financial support of the Nano-Tera.ch initiative as part of the SHINE project (Grant #145936), and the Starting Grant of the Swiss National Science Foundation as part of the SCOUTS project (Grant #155876). We thank Idrees Samim, Miguel Modestino, and Claudia Rodriguez for fruitful discussions.References
- A. Fujishima and H. Kenichi, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- M. A. Modestino and S. Haussener, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 13–34 CrossRef CAS PubMed.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 CAS.
- R. Sathre, C. D. Scown, W. R. Morrow, J. C. Stevens, I. D. Sharp, J. W. Ager, K. Walczak, F. a. Houle and J. B. Greenblatt, Energy Environ. Sci., 2014, 7, 3264–3278 CAS.
- C. Rodriguez, M. Modestino, D. Psaltis and C. Moser, Energy Environ. Sci., 2014, 7, 3828–3835 CAS.
- P. Zhai, S. Haussener, J. Ager, R. Sathre, K. Walczak, J. Greenblatt and T. McKone, Energy Environ. Sci., 2013, 6, 2380–2389 CAS.
- M. Dumortier and S. Haussener, Energy Environ. Sci., 2015 10.1039/C5EE01269D.
- S. Rau, S. Vierrath, J. Ohlmann, A. Fallisch, D. Lackner, F. Dimroth and T. Smolinka, Energy Technol., 2014, 2, 43–53 CrossRef CAS PubMed.
- F. Dimroth, G. Peharz, U. Wittstadt, B. Hacker and a. W. Bett, 2006 IEEE 4th World Conf. Photovolt. Energy Conf., 2006, 640–643.
- C. R. Cox, J. Z. Lee, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14057–14061 CrossRef CAS PubMed.
- S. Licht, B. Wang and S. Mukerji, J. Phys. Chem. B, 2000, 104, 8920–8924 CrossRef CAS.
- O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427 CrossRef CAS.
- E. Verlage, S. Hu, R. Liu, R. J. R. Jones, K. Sun, C. Xiang, N. S. Lewis and H. A. Atwater, Energy Environ. Sci., 2015 10.1039/c5ee01786f.
- J. Luo, J. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N. Park, S. D. Tilley, H. J. Fan and M. Grätzel, Science, 2014, 345, 1593–1596 CrossRef CAS PubMed.
- N. S. Lewis, Electrochem. Soc. Interface, 2013, 22, 43–50 CAS.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9936 CAS.
- A. Berger and J. Newman, J. Electrochem. Soc., 2014, 161, 3328–3340 CrossRef PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS PubMed.
- L. M. van Dam, W. G. J. H. van Sark, Proceedings of the 2011 MRS Spring Meeting, San Francisco, 2011.
- K. Söderström, G. Bugnon, R. Biron, C. Pahud, F. Meillaud, F.-J. Haug and C. Ballif, J. Appl. Phys., 2012, 112, 114503 CrossRef PubMed.
- H. Doscher, J. F. Geisz, T. G. Deutsch and J. A. Turner, Energy Environ. Sci., 2014, 7, 2951–2956 CAS.
- M. T. Winkler, C. R. Cox, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1076–E1082 CrossRef CAS.
- J. Kim, S. Lee, S. Srinivasan and C. E. Chamberlin, J. Electrochem. Soc., 1995, 142, 2670–2674 CrossRef CAS PubMed.
- M. Ni, M. K. H. Leung and D. Y. C. Leung, Energy Convers. Manage., 2007, 48, 1525–1535 CrossRef CAS PubMed.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. a. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- S. Haussener, S. Hu, C. Xiang, A. Z. Weber and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3605–3618 CAS.
- S. Tembhurne, M. Dumortier and S. Haussener, Proceedings of the 15th International Heat Transfer Conference, Kyoto, 2014.
- A. Skoczek, T. Sample and E. D. Dunlop, Prog. Photovoltaics, 2009, 17, 227–240 CAS.
- D. C. Jordan and S. R. Kurtz, Prog. Photovoltaics, 2013, 21, 12–29 Search PubMed.
- J. Wu, X. Z. Yuan, J. J. Martin, H. Wang, J. Zhang, J. Shen, S. Wu and W. Merida, J. Power Sources, 2008, 184, 104–119 CrossRef CAS PubMed.
- X.-Z. Yuan, S. Zhang, H. Wang, J. Wu, J. C. Sun, R. Hiesgen, K. A. Friedrich, M. Schulze, A. Haug and J. Colin, J. Power Sources, 2010, 195, 7594–7599 CrossRef CAS PubMed.
- V. Fthenakis, R. Frischknecht, M. Raugei, H. C. Kim, E. Alsema, M. Held and M. de Wild-Scholten, Methodology Guidelines on Life Cycle Assessment of Photovoltaic Electricity, International Energy Agency Report IEA-PVPS T12-03:2011, Upton, USA, 2011.
- M. Carmo, D. L. Fritz, J. Merge and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS PubMed.
- P. Krishnamurthy and R. Banerjee, Lecture Notes in Information Technology, 2012, vol. 9, pp. 509–514 Search PubMed.
- J. P. Caballero, Undergraduate thesis project, Universidad Carlos III de Madrid and Università degli studi de Perugia, 2012.
- C. Turchi, M. Mehos, C. K. Ho and G. J. Kolb, Presented at SolarPACES 2010, Perpignan, September 2010.
- G. J. Kolb, S. a. Jones, M. W. Donnelly, D. Gorman, R. Thomas, R. Davenport and R. Lumia, Heliostat Cost Reduction Study, Sandian report SAND2007-3, Sandia National Laboratories, Oak Ridge, TN, 2007.
- G. Peharz, F. Dimroth and H. P. V. System, Prog. Photovoltaics, 2005, 13, 627–634 Search PubMed.
- H. Lerchenmüller, A. W. Bett, J. Jaus and G. Willeke, presented at International Conference on Solar Concentrators for the Generation of Electricity or Hydrogen, Scottsdale, Arizona, 2005.
- S. Kurtz, Opportunities and Challenges for Development of a Mature Concentrating Photovoltaic Power Industry Opportunities and Challenges for Development of a Mature Concentrating Photovoltaic Power Industry, NREL report NREL/TP-5200-43208, National Renewable Energy Laboratory, Golden, Colorado, 2012.
- R. M. Swanson, Prog. Photovoltaics, 2000, 8, 93–111 CAS.
- V. M. Fthenakis and H. C. Kim, Prog. Photovoltaics, 2013, 21, 379–388 CAS.
- R. Stevenson, Compd. Semicond., 2013, 19, 18–19 Search PubMed.
- N. Mohr, A. Meijer, M. a. J. Huijbregts and L. Reijnders, Int. J. Life Cycle Assess., 2009, 14, 225–235 CrossRef CAS.
- R. R. King, D. Bhusari, D. Larrabee, X. Liu, E. Rehder, K. Edmondson, H. Cotal, R. K. Jones, J. H. Ermer, C. M. Fetzer, D. C. Law and N. H. Karam, Prog. Photovoltaics, 2012, 20, 801–815 CAS.
- M. Pehnt, Int. J. Hydrogen Energy, 2001, 26, 91–101 CrossRef CAS.
- Ecoinvent V3.0, Swiss Center for Life Cycle Inventories, 2013 Search PubMed.
- J. Mason and K. Zweibel, in Solar Hydrogen Generation, ed. K. Rajeshwar, R. McConnell and S. Licht, Springer, New York, 2008, vol. 1, pp. 273–313 Search PubMed.
- J. M. Mason, V. M. Fthenakis, T. Hansen and H. C. Kim, Prog. Photovoltaics, 2006, 14, 179–190 CAS.
- Geo Solar Model, Solar Resource Overview, 2014. SolarGIS report SG-0000-0000-1, SolarGIS, Bratislava, Slovakia, 2014.
- G. Peharz, F. Dimroth and U. Wittstadt, Int. J. Hydrogen Energy, 2007, 32, 3248–3252 CrossRef CAS PubMed.
- F. T. Si, D. Y. Kim, R. Santbergen, H. Tan, R. A. C. M. M. Van Swaaij, A. H. M. Smets, O. Isabella and M. Zeman, Appl. Phys. Lett., 2014, 105, 063902 CrossRef PubMed.
- J.-W. Schüttauf, B. Niesen, L. Löfgren, M. Bonnet-Eymard, M. Stuckelberger, S. Hänni, M. Boccard, G. Bugnon, M. Despeisse, F.-J. Haug, F. Meillaud and C. Ballif, Sol. Energy Mater. Sol. Cells, 2015, 133, 163–169 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ee01821h |
| ‡ http://www.eia.gov/electricity/monthly/epm_table_grapher.cfm?t = epmt_5_6_a |
| § Web-based version is currently under development and will be available on http://lrese.epfl.ch/research. |
| This journal is © The Royal Society of Chemistry 2015 |