Structure of the high voltage phase of layered P2-Na_2/3−z[Mn_1/2Fe_1/2]O₂ and the positive effect of Ni substitution on its stability

Abstract

A combination of operando X-ray diffraction, pair distribution function (PDF) analysis coupled with electrochemical measurements and Mössbauer spectroscopy elucidates the nature of the phase transitions induced by insertion and extraction of sodium ions in P2-Na_0.67[Ni_yMn_0.5+yFe_0.5−2y]O₂ (y = 0, 0.10, 0.15). When phase transitions are avoided, the optimal cathode material – P2-Na_0.67Fe_0.2Mn_0.65Ni_0.15O₂ – delivers 25% more energy than the unsubstituted material, sustaining high specific energy (350 Wh kg⁻¹) at moderate rates and maintains 80% of the original energy density after 150 cycles – a significant improvement in performance vs. the unsubstituted analogue. The crystal structure of the high voltage phase is solved for the first time by X-ray PDF analysis of P2-Na_0.67−zFe_0.5Mn_0.5O₂ (where z ∼ 0.5), revealing that migration of the transition metals – particularly Fe³⁺ – into tetrahedral sites in the interlayer space occurs at high potential. This results in new short range order between two adjacent layers. Although the transition metal migration is reversible as proven by electrochemical performance, it induces a large disfavourable cell polarization. The deleterious high voltage transition is mitigated by substitution of Fe³⁺ by Mn⁴⁺/Ni²⁺, giving rise to better cycling performance. Moreover, as demonstrated by ⁵⁷Fe Mössbauer spectroscopy, the much lower ratio of Fe⁴⁺O₆ to Fe³⁺O₆ observed systematically across the range of Ni content – compared to the values expected from a purely ionic model – suggests redox activity involves the O-2p orbitals owing to their overlap with the transition metal-3d orbitals.

---

Broader context

As the critical need for an energy transition from fossil fuel to more sustainable sources becomes clearer, the need for large scale electrochemical energy storage arises. Li-ion batteries, which have revolutionized portable electronics and electrical vehicles in just over two decades, will likely fail to meet the cost requirements for such technology, directing new focus towards sodium batteries. Development of low cost electrode materials for sodium based systems is rapidly becoming a topic of high interest in the scientific community. These future generation systems based on oxide insertion hosts employing the Fe³⁺/Fe⁴⁺ redox couple offer high energy density approaching that of Li-ion materials, low environmental impact and low cost; making these materials highly desirable positive electrode candidates. However, commercial use is so far hindered by several challenges that include capacity fading. In the present work, we have employed P2-Na_x[Fe_0.5−2yMn_0.5+yNi_y]O₂ layered oxides to study the phase transitions that impede the rate capability and capacity retention of these materials. Using in-depth structural and spectroscopic analysis, we unravel the nature of phenomena specific to the Fe³⁺/Fe⁴⁺ redox couple, highlighting the issues that will need to be addressed to improve the design of new iron containing positive electrodes for sodium batteries. This approach shows the way forward to diminish capacity fading by developing compositions with tailored substitution that minimize structural changes on cycling.

Introduction

Sodium-ion batteries have generated considerable interest recently with respect to developing sustainable and low-cost electrical energy storage systems. The high abundance of sodium and competitive energy densities of Na insertion host materials make Na-ion batteries an especially promising alternative to Li-ion battery technology for large scale applications such as electrical grid storage. Layered transition metal oxides Na_xMO₂, 0 ≤ x ≤ 1 and M = Ti, V, Cr, Mn, Fe, Co or Ni and their various combinations,^1–13 have been synthesized and their electrochemical properties investigated. Layered sodium transition metal oxides crystallize in several polymorphs dependent on their sodium content and synthesis conditions (temperature and partial pressure of oxygen). The transition metal ions reside within layers of edge sharing MO₆ octahedra while the sodium ions are accommodated between the layers. The most common polymorphs for Na_xMO₂ are O3 and P2, according to a classification by Delmas et al.¹⁴ in which sodium ions occupy octahedral (O) or trigonal prismatic (P) sites, respectively; structural distortion is denoted by a prime (i.e., P′2). The number following the sodium coordination environment describes the number of MO₂ layers in a unit cell. These polymorphs based on oxygen close packing differ in their oxygen arrays; namely ABCABC stacking for O3 and ABBA stacking for P2.

Sodium layered oxides offer significant advantages over their lithium counterparts. The ionic radius difference between Na⁺ and the transition metal ions prevents cation mixing which is frequently observed in lithium metal oxides. Redox couples that are inactive vs. Li can be used in sodium cells, such as Cr^3+/4+.⁴ Finally, the higher vacancy concentrations tolerated by sodium layered oxides offer larger capacities. However, the strong Na⁺/vacancy interactions result in multiple structural transitions upon cycling, considerably affecting the electrode ageing properties. For example, the sodium equivalent to the iconic LiCoO₂ follows an O3, O′3, P′3, P3, P′3 path as the sodium content decreases.¹⁵ Two approaches can be used to limit the extent of this problem. Limiting the cutoff voltage to 4.1 V to avoid the P2–O2 transition in Na_x[Mn_2/3Ni_1/3]O₂ results in an increase in capacity retention from 64% to over 95% after 10 cycles.¹⁶ Chemical modification can also retard structural transitions, as observed in P2-Na_0.80[Li_0.12Ni_0.22Mn_0.66]O₂ which maintains its structure up to 4.4 V and exhibits more than 95% of its initial capacity after 50 cycles.¹⁷

Following the initial report of the auspicious properties of P2-Na_xFe_0.5Mn_0.5O₂¹⁸ that demonstrated the activity of the Fe^3+/4+ redox couple in sodium cells, layered oxides Na_x[Mn_1−yFe_y]O₂ based on low-cost and non-toxic Mn and Fe have received considerable interest.^18–25 Their major drawbacks were identified as poor capacity retention due to structural transitions²⁴ and air sensitivity leading to carbonate insertion that inhibits electrode performance.²³ Nickel substitution seemed successful in addressing these points. P2-Na_x[Fe_0.5−yNi_yMn_0.5+y]O₂ oxides show improved air stability, better capacity retention and increase in the average discharge potential.^23,26,27 However, the structural transition at high voltage remains unexplained to date.

Here, we elucidate the nature of the structural evolution of P2-Na_0.67[Mn_0.5Fe_0.5]O₂ and P2-Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ upon cycling, and directly correlate this to electrochemical performance. The structure of rigorously air-protected pristine compounds was solved using combined X-ray and neutron powder diffraction (XRPD and NPD). The phase diagram of the two compositions as a function of sodium content is determined using operando diffraction experiments, and the structure of the unknown high voltage phase is solved by X-ray pair distribution function (PDF) analysis and ⁵⁷Fe Mössbauer spectroscopy for the first time. We demonstrate that the extended stability range of the P2 phase in the Ni substituted composition allows the storage of almost 25% more energy compared to the unsubstituted oxide when the cycling range is selected to prevent structural transitions.

Experimental

Synthesis

Na_0.67[Mn_0.5+yNi_yFe_0.5−2y]O₂ phases with y = 0, 0.1, 0.15 were synthesized by a solid state method. Na₂CO₃ (EMD Millipore, ≥99.5%), Mn₂O₃ (Sigma-Aldrich, 99%), NiO (Sigma-Aldrich, 99.8%), and Fe₂O₃ (Sigma-Aldrich, ≥99%) powders were used as starting materials. For each composition, a mixture of a stoichiometric amount of precursors was pelletized and heated in air at 750 °C for 4 hours followed by a final step at 900 °C for 6 hours. Due to the sensitivity of these materials under ambient atmosphere, samples were then subjected to an additional heat treatment under vacuum at 600 °C and transferred directly to an argon filled glovebox (MBraun, O₂ and H₂O < 0.1 ppm) as described in our previous study.²³

Na_0.14Fe_0.5Mn_0.5O₂ and Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂ were obtained by chemical oxidation of the corresponding air-protected P2 pristine materials in a 2 fold excess of NO₂BF₄ in acetonitrile. In an argon filled glovebox, 400 mg of sample were dispersed in 12 mL of acetonitrile (HPLC grade, Sigma Aldrich), and 688 mg of NO₂BF₄ (98%, Sigma-Aldrich) were added to the suspension. After 24 h under magnetic stirring, the solution was filtered and washed with 2 × 20 mL of acetonitrile.

Materials characterization

The X-ray powder diffraction (XRPD) data were recorded using Cu-K_α radiation on a PANalytical Empyrean diffractometer equipped with a PIXcel bidimensional detector. The samples were loaded in glass capillaries (Ø = 0.3 mm) in an argon filled glovebox and sealed in order to protect them from air exposure. Rietveld quality patterns were collected in Debye–Scherrer geometry using a parabolic X-ray mirror in the incident beam. Neutron powder diffraction (NPD) experiments were recorded on the time of flight spectrometer POWGEN at the Spallation Neutron Source at Oak Ridge National Laboratory. The powders were loaded in 8 mm vanadium sample cans in an argon filled glovebox and sealed with a copper gasket. The crystal structures of air protected samples were refined using combined Rietveld refinement of the NPD and XRPD datasets within the FullProf²⁸ software suite.

Operando diffraction experiments were conducted in a homemade cell, mounted on a PANalytical Empyrean diffractometer. The diffraction patterns were collected in Bragg–Brentano geometry using Cu-K_α radiation and a PIXcel detector with a Ni K_β filter. During the acquisition, the cells were cycled at a constant current rate of 13 mA g⁻¹ (C/20) with a pattern collection time of 30 min, i.e. Δx ≈ 0.02 in Na_xMO₂. The evolution of the lattice parameters during the operando diffraction experiments was determined by means of Le Bail fitting.²⁹

Reciprocal space data for pair distribution function (PDF) analysis were obtained using a PANalytical Empyrean outfitted with Ag-K_α radiation, a Rh K_β filter and a NaI scintillation point detector. In order to maximize the diffracted intensity, a divergent beam was used in combination with a 1 mm glass capillary (filled in an argon filled glovebox) and the receiving slits were set to 2 mm. The total collection time was 48 h per sample. The data reduction was performed using PDFGetX3 software³⁰ and real space data was fitted using PDFgui.³¹ The damping factor associated with this instrumental configuration was calibrated by refining the structure of a silicon sample.

Mössbauer spectrometry was performed with a conventional constant acceleration system with a radiation source of ⁵⁷Co in a Rh matrix. Velocity and isomer shift calibrations were performed with reference to a room-temperature α-Fe spectrum. The spectrometer linewidth obtained from the calibration is 0.31 mm s⁻¹. This was used as the linewidth for all spectral components resulting from fitting with Lorentzian doublets.

Energy dispersive X-ray spectroscopy (EDS) (EDAX) and inductively coupled plasma atomic emission spectroscopy (ICP-AES) (Prodigy high dispersion ICP, Teledyne Leeman Labs) were used to confirm the molar ratio of transition metals in each composition. The sodium content was determined to be 65% of transition metals in all three compositions by ICP-AES.

Electrochemistry

The electrochemical performance of the positive electrode materials was measured in 2325 coin cells using Na metal as the counterelectrode. Electrode fabrication was performed inside a glovebox under argon (O₂ and H₂O < 0.1 ppm) to avoid air contamination. Each active material was mixed with 10 wt% carbon black and 10 wt% polyvinylidene fluoride (PVDF) (Aldrich average M_w ∼ 534 000) suspended in N-methyl-2-pyrrolidinone (NMP) (Sigma-Aldrich, 99.5%) and cast on aluminum foil with a typical loading of 7–9 mg cm⁻². Electrodes were dried in a vacuum oven at 90 °C overnight. The electrolyte was 1 M NaClO₄ (Alfa Aesar, ≥98%) in propylene carbonate (BASF, 99.98%) with 2 vol% of 4-fluoro-1,3-dioxolan-2-one (FEC) (Sigma-Aldrich, 99%). The electrodes were separated with glass fiber separators (Merck Millipore). Galvanostatic cycling was performed using a MPG-2 (bio-logic) cycler at 24 °C with a current density of 13 mA g⁻¹ (C/20) or 26 mA g⁻¹ (C/10 rate).

Results and discussion

Structural and electrochemical overview

The crystal structures of rigorously air protected Na_0.67[Mn_0.6Ni_0.1Fe_0.3]O₂ and Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ were examined by combined Rietveld refinement of X-ray and neutron time of flight diffraction data (Fig. 1 and Table S1, ESI†). Both compositions crystallize in an undistorted P2 structure (P6₃/mmc) (Fig. 2; Table S1, ESI†), similar to Na_0.67[Mn_0.5Fe_0.5]O₂.²³ The substitution of Fe³⁺ by Mn⁴⁺/Ni²⁺ only impacts the cell parameters, which follow the evolution of the cation diameter, i.e. the cell parameters (a = 2.9429(1) Å, c = 11.1881(3) Å) for Na_0.67[Mn_0.5Fe_0.5]O₂ decrease as Fe³⁺ ions (radius 0.65 Å) are partially replaced by Mn⁴⁺/Ni²⁺ ions (radii of 0.53 Å, and 0.69 Å, respectively).³²

Fig. 1 Combined Rietveld refinement of (a,c) neutron and (b,d) X-ray powder diffraction data of (a,b) Na_0.67[Mn_0.6Ni_0.1Fe_0.3]O₂ and (c,d) Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂. For each pattern, the measured data is shown by red symbols, the calculated pattern is shown in black, the difference curve is shown in blue and the Bragg peak position are marked by green ticks.

Fig. 2 Schematic presentation of the P2-Na_xMO₂ (M = Ni, Fe, Mn) crystal structure.

In the P2 structure, sodium ions are distributed over two prismatic sites – Na_e and Na_f – that share edges and faces, respectively, with the MO₆ octahedra (Fig. 2). The occupancy of the Na_e site is about twice that of Na_f, showing that the former site is more stable than the latter due to longer Na–M distances. Configurational disorder in the sodium layer is frequently observed in the P2 structure and is thought to underlie the good mobility of sodium ions in the host structure.^23,33,34 Similar to those studies, this disorder is modelled here by splitting the Na_e(2d) and Na_f(2b) sites into lower symmetry 6 h Wyckoff positions. The combined refinement of the neutron and X-ray datasets confirms that the Ni, Fe, and Mn cations are statistically distributed over the transition metal site. This prevents the long range ordering of the sodium ion vacancies which are very common in sodium layered materials. These rearrangements trigger structural transitions that give rise to potential step features on the charge/discharge profiles in P2-Na_2/3VO₂,³⁵ P2-Na_2/3CoO₂,³⁶ and P2-Na_2/3[Mn_2/3Ni_2/3]O₂,³⁷ resulting in poor cyclability and limited rate capability. In contrast, smooth voltage profiles and perfectly superimposable electrochemical profiles on first and second charges of Na_0.67[Mn_0.5+yNi_yFe_0.5−2y]O₂ (y = 0, 0.10, 0.15) imply facile and reversible sodium (de)intercalation from all three compositions (Fig. 3) in agreement with previously published results.²³

Fig. 3 First two galvanostatic charge/discharge cycles and specific capacity of P2-Na_0.67[Mn_0.5+yNi_yFe_0.5−2y]O₂ (y = 0, 0.1, 0.15) over 25 cycles at 13 mAh g⁻¹ (C/20).

The initial capacity for the three compositions is about 200 mAh g⁻¹. They exhibit similar capacity fading, which is slightly exaggerated in the first five cycles. The electrochemical cycling curves of Na_0.67[Mn_0.5+yNi_yFe_0.5−2y]O₂ (y = 0, 0.10, 0.15) can be divided in two regions based on the magnitude of the cell polarization. Very small polarization is observed in the low voltage region. Greater polarization is noted in the high voltage range that clearly diminishes as the nickel content increases. The specific energy marginally increases (∼3%) with the nickel content, from 545 Wh kg⁻¹ for y = 0 to 561 Wh kg⁻¹ for y = 0.15.

The structural modifications induced by nickel substitution are minor, and thus it seems appropriate to conclude that the improved performance of the Ni-substituted materials arise from the change in charge compensation mechanism from the Fe^3+/4+ couple to Ni^2+/4+. Since Fe⁴⁺ has a d⁴ electronic configuration, it is expected to show significant Jahn–Teller stabilization, possibly explaining the large polarization observed at high voltage. In order to determine whether high polarization regions originate intrinsically from the Fe^3+/4+ couple or from structural features we carried out a comparative study on the structural evolution upon cycling of P2-Na_x[Fe_0.5Mn_0.5]O₂ and P2-Na_x[Fe_0.2Mn_0.65Ni_0.15]O₂. The results below disprove Jahn–Teller effects, showing instead that a mechanism involving transition metal migration is at hand.

Operando XRD study of P2-Na_xFe_0.5Mn_0.5O₂ and P2-Na_xFe_0.2Mn_0.65Ni_0.15O₂ upon cycling

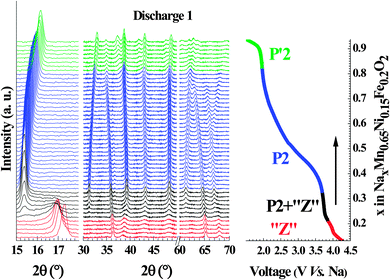
Operando monitoring of the structural evolution upon cycling shows that both title compositions undergo transitions to yield the same three phases. The evolution of the diffraction patterns is shown for the first discharge of Na_x[Fe_0.2Mn_0.65Ni_0.15]O₂ (Fig. 4) and the phase diagram over a complete cycle for both compositions (x = 0, 0.15) is displayed in Fig. 5. In agreement with previously published work on P2-Na_0.67[Fe_0.5Mn_0.5]O₂,^18,24 the initial P2 structure is preserved over a wide range of stoichiometry. It converts to a distorted P′2 phase at low voltage and to an uncharacterized high potential phase, labeled “Z”²⁴ or OP4.¹⁸ It will be referred here as the “Z” phase since the OP4 structure does not match our structural data (see below). All the observed transitions are fully reversible; the high and low voltage phases convert back to the pristine P2 phase as shown by the perfect overlap of the evolution of the cell parameters as a function of the sodium content during the first and second charge (Fig. S1, ESI†).

Fig. 4 Operando XRD data recorded during galvanostatic cycling of Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ at a rate of C/20 (left) along with illustration of sodium content vs. voltage of the cell (right) for the first discharge. The traces in the operando XRD patterns are colour-coded with respect to the electrochemical profile on the right to reflect the structural composition of the cathode material.

Fig. 5 Phase evolution within: (a) Na_0.67[Mn_0.5Fe_0.5]O₂ and (b) Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ as a function of the sodium content during first cycle. The sign * shows the starting point of cycling.

P2–P′2 transition. For sodium contents greater than ∼0.8 Na per formula unit the increasing concentration of Jahn–Teller active Mn³⁺ ions triggers a cooperative distortion that results in a hexagonal P2 (P6₃/mmc) to orthorhombic P′2 (Cmcm) transition. This orthorhombic phase was previously described for P2-Na_xMnO₂³⁸ and P2-Na_x[Fe_0.5Mn_0.5]O₂,²⁴ but is reported here for the first time in the nickel substituted composition. The hexagonal cell can be described in the orthorhombic space group using the following relationship, a_ortho = a_hex, b_ortho = a_hex + 2b_hex and c_ortho = c_hex, meaning that for an undistorted cell, a_ortho = b_ortho/√3. Owing to the similar concentration of Mn³⁺ in both compositions, the onset of the transition occurs at essentially the same sodium content. Na_xFe_0.5Mn_0.5O₂ does not undergo complete conversion to the orthorhombic cell, showing the presence of both P2 and P′2 in the lower voltage range. Consistent with a two-phase mechanism, no evolution of the cell parameters of the P′2-NaFe_0.5Mn_0.5O₂ phase are observed (Fig. 6a, green data points). Conversely, Na_xFe_0.2Mn_0.65Ni_0.15O₂ completely converts to the P′2 structure and the increasing concentration of Mn³⁺ ions enhances the orthorhombic distortion as the b_ortho/a_ortho ratio diverges from √3 (Fig. 6b, green data points).

Fig. 6 Evolution of lattice parameters, in-plane (a), (c) and out of plane (b), (d) of Na_0.67Fe_0.5Mn_0.5O₂ (a), (b); and Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ (c), (d) as a function of the sodium content during the first discharge.

P2 phase. As expected, the cell parameters of the P2 phase of both compositions evolve linearly with the concentration of sodium (Fig. 6, blue markers). As the sodium content decreases, the oxidation of the transition metal causes a contraction of the in-plane parameters. The interlayer distance follows the opposite trend: the decreasing sodium content implies less efficient screening of the electrostatic repulsion between the oxygen ions of two transition metal layers. Interestingly, the presence of nickel atoms in the transition metal layers allows the stability domain of the P2 struture to be pushed to higher voltage – from 4 V to 4.1 V – and to higher sodium vacancy concentration, from Na_0.35Fe_0.5Mn_0.5O₂ to Na_0.29Fe_0.2Mn_0.65Ni_0.15O₂.

P2–“Z” transition. The phase formed at high potential exhibits weak and broad diffraction peaks, characteristic of a very low crystallinity phase (Fig. 4). As pointed out in previous reports on P2-Na_xFe_0.5Mn_0.5O₂,^18,24 by analogy with the pattern of the P2 structure, the evolution of the (002) peak from ∼15° to ∼17° suggests an important contraction of the interlayer distance while the stability of the (100) reflection, at 36°, suggests very little change within the MO₂ layer. Yabuuchi et al. proposed an indexation in the P6̄m2 space group, compatible with the OP4 structure and consisting of a mixture of O and P type of stacking. As we show in the next section, this phase is not an OP4 type.

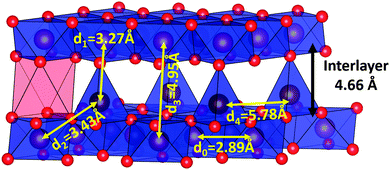
The sharp contraction of the interlayer spacing in moving from the P2 to the Z phase (Fig. 6b and d) can be related to a transition from a P to O stacking type, due to the fact that the oxygen atoms of two different transition metal layers are not aligned along the c-axis in O-type structures. However, the evolution of the interlayer distance is opposite to what is generally observed upon sodium de-intercalation in O and P structures.^{15,17,36,39–41} This means that, contrary to sodium extraction, the mechanism driving this transformation implies an increasingly strong inter-layer interaction. This transition occurs at different sodium content in the case of Na_xFe_0.5Mn_0.5O₂ (x = 0.35) and Na_xFe_0.2Mn_0.65Ni_0.15O₂ (x = 0.29). If the structural reorganization was driven by Na⁺/vacancies ordering as usually observed in sodium layer oxides, the transition would be expected to occur at the same sodium concentration.

Study of the transition from the P2 to the high voltage phase Z phase and its structure

PDF analysis. Due to the poor crystallinity (i.e., significant disorder) of the high voltage “Z” phase, traditional X-ray diffraction experiments provide little information about its structure, explaining the inconclusive previous reports. For this reason, we use X-ray pair distribution function (PDF) analysis to gain further structural insights. This powerful method has been successfully applied to understand the complex behavior of positive electrode materials.^42,43 In contrast to classical X-ray refinement, the PDF technique is sensitive to amorphous phases. The analyzed sample was synthesized by chemical oxidation of Na_0.67Fe_0.5Mn_0.5O₂, in order to avoid parasitic signals originating from the carbon additive and binder as would arise with an electrochemically oxidized sample.

The stoichiometry of a sample oxidized by an excess of NO₂BF₄ in acetonitrile, Na_0.14Fe_0.5Mn_0.5O₂, was determined by ICP-AES. The material showed a very similar diffraction pattern to that observed for samples in the high voltage region of the operando experiment (Fig. S2, ESI†). The in-plane cell parameter and interlayer spacing, 2.89 Å and 5.22 Å respectively, correspond to those for the operando composition Na_0.22Fe_0.5Mn_0.5O₂. Even by using a large excess of oxidant and successive oxidation steps, it was not possible to extract more sodium despite the high potential of the NO₂⁺/NO₂ couple (about 4.7 V vs. Na). The larger peak width of the electrochemically oxidized sample, as well as the appearance of small additional signals shows – as expected – that chemical oxidation produces a less homogeneous sample than the slower galvanostatic oxidation.

Pristine phase. The PDF profile of the pristine, air-protected P2-Na_0.67Fe_0.5Mn_0.5O₂ (Fig. 7a) reflects perfect agreement with the previously reported crystal structure.²³ This phase exhibits important disorder in the sodium layer and one expects significant discrepancies in the local structure. The good fit between the average structure, determined by diffraction, and the measured PDF is a consequence of the low occupancies and weak scattering coefficient of sodium atoms; the Na–Na correlations are masked by other features. Similarly, hkl-dependent peak broadening is observed in the XRD patterns, as reported, where it has been previously ascribed to stacking faults.^18,23 Yabuuchi et al. report good modelling of the broadening using a mixture of the perfectly ordered P2 phase, and a heavily disordered P2 phase with about 20% of P3-type stacking faults. However, as the ratio between these two phases was not determined, the overall concentration of stacking faults is unknown. This type of stacking fault should give rise to peaks at 5.85 Å and 6.55 Å, corresponding to the M–M interlayer distances in the P3 structure. The absence of these peaks in the measured PDF suggests that the overall concentration of these defects is negligible. Thus, although it appears that X-ray PDF is not best suited to analyze the disorder in P2-Na_0.67Fe_0.5Mn_0.5O₂, it is an excellent tool to understand the structural modifications occurring in the charged phase.

Fig. 7 Fit of the PDF of (a) P2-Na_0.67Fe_0.5Mn_0.5O₂ and (b) Na_0.14Fe_0.5Mn_0.5O₂. First neighbor M–O and M–M distances are highlighted in blue and yellow respectively; second neighbor in-plane M–O and M–M distances are highlighted in lavender, and characteristic interlayer M–M distances are highlighted in green (see text for details).

High voltage (charged) “Z” phase. As expected, the PDF curve of the electrochemically oxidized sample (Fig. 7b) shows many similarities with the pristine material. In particular, the first peak (Fig. 7, blue shading), related to the M–O pairs, shows a contraction from 1.98 Å to 1.91 Å as the average oxidation state of the transition metal increases. The fact that this peak is neither split nor broadened rules out Jahn–Teller stabilization of Fe(IV) as a driving force of the structural transition. The causes of the phase transition at low and high potential are therefore very different, as can be expected owing to the very different diffraction patterns.

The intensity of the second peak (Fig. 7, yellow shading) is largely dominated by the first neighbor M–M correlations (in-plane M_Oh–M_Oh) which are at 2.94 Å in the pristine material. As expected, this distance decreases slightly to 2.89 Å when the sample is oxidized, following the evolution of the in-plane cell parameter. The decrease in intensity of this peak (associated with the growth of a new signal at 3.35 Å) is direct evidence of modification of the hexagonal lattice of the transition metal element on oxidation. Since in-plane distortion due to a cooperative Jahn–Teller effect (as occurs in the low voltage orthorhombic phase) can be ruled out, differentiation of the M–M distance is attributed to the atomic displacement of transition metal atoms perpendicular to the close packed hexagonal lattice, i.e. along c. These shifted species will interact with the adjacent layers. This explains why the interlayer distance shrinks considerably as sodium continues to be extracted (Fig. 6b, red markers), while the opposite trend is usually observed (i.e. where sodium extraction triggers expansion of the interlayer distance).^{15,17,36,39–41} The mechanism proposed here is different from the cation mixing observed in lithium layered oxides. Sodium layered oxides are generally thought to be resistant to migration of the transition metal into the alkali layer, owing to the different ionic radii of Na⁺ and the transition metal ions. However, when the concentration of sodium vacancies is high, the transition metal ion migrates to an essentially empty layer. Migration of Li⁺ from the transition metal layer to the sodium layer has been demonstrated by NMR measurements in P2-Na_x[Li_0.12Ni_0.22Mn_0.66]O₂.¹⁷ Irreversible transition metal migration into the sodium layer was also proposed in O3-Na_xCrO₂⁴¹ and O3-Na_xFeO₂¹¹ based on the decrease of the interlayer distance and evolution of the pre-peak in X-ray absorption measurements. We show here, to the best of our knowledge, the first structural evidence of this mechanism.

The next group of peaks between 4 Å and 5.5 Å, due to in-plane M–M and M–O interactions (Fig. 7, lavender shading), remain similar in both pristine and oxidized samples, showing the overall conservation of the MO₂ layer. For distances larger than 6 Å, interlayer interactions start to be visible in the PDF profile of the pristine P2-Na_0.67Fe_0.5Mn_0.5O₂ sample. The disappearance of the interlayer M–M distances from the radial distribution curve of the chemically oxidized sample (6.32 Å, 8.14 Å, 9.57 Å; shown in green shading in Fig. 7) is particularly indicative of the destruction of the P2-type stacking. The fact that these very intense peaks cannot be found anywhere in the PDF curve of the oxidized sample is evidence that the long range ordering between the layers is completely destroyed. In order to model the PDF, supercells containing 20 metal transition layers were generated in the P1 space group and each MO₂ layer was randomly shifted in the ab plane. Owing to the low concentration of sodium and its weak scattering factor, it was not taken into account. The number of M cations moving out of plane was probed by gradually increasing the size of the supercell in the ab plane. Initially, the layers were evenly spaced along the c direction based on the assumption that the first diffraction peak observed at ∼5.22 Å was indeed a (00l) peak. Partial organization based on the P2, O2, P3 and O3 stacking schemes were tested but failed to explain the recorded PDF curve.

Bilayer model of the Z phase. A better approach coupled the layers in order to provide reasonable coordination polyhedra for the out-of-plane transition metal atom. The relative position of the two MO₂ planes in a bilayer were set according to the O2, O3, P2 and P3 stacking schemes and the interlayer distance was fixed to generate a symmetrical environment for the out-of-plane M cation. The in-plane position of each of the 10 bi-layers was randomized, where 5.22 Å represents half the distance between the centers of two bilayers. The best agreement with the measured PDF (Fig. 7b) was obtained for a bilayer with an O2 stacking scheme (Fig. 8). The cell used for the calculation of the PDF curve was a 2 × 2 × 10 supercell of an ideal O2 (P6₃mc) cell. As previously described, the position of each of the ten bilayers was randomized by an arbitrary translation in the ab plane. Transformation from a P2 to an O2 phase requires gliding of one MO₂ layer along a (1/3,2/3,0) translation. This structural transition is observed, for example, upon sodium extraction from P2-Na_0.67Ni_0.33Mn_0.67O₂ phases.³⁷ The transition metal atoms from the lower layer migrate through a triangular face of the original octahedron, directly to the tetrahedral site above it. The M–O distance is 1.90 Å, independent of the coordination polyhedron. The second peak in the yellow shaded region is the first neighbor M_Td–M_Oh distance between the tetrahedral and octahedral sites (depicted in Fig. 8); namely d₁ = 3.27 Å for the MO₂ layer connected to the corner of the tetrahedron and d₂ = 3.43 Å for the MO₂ layer connected to the face of the tetrahedron. This gives rise to the distinct splitting of the M–M correlations, and the appearance of a new first neighbor peak observed in the PDF curve at an average of 3.35 Å (Fig. 7, yellow shading).

Fig. 8 Representation of the bilayer used to fit the PDF curve of Na_0.14Fe_0.5Mn_0.5O₂ with interatomic distances shown in yellow. Transition metal atoms from the lower layer shift along the c direction to form interlayer MO₄ tetrahedra. A vacant octahedral site is represented in red for clarity.

Transition metal migration. In order to model the relative intensity of the M–M split peak, it was necessary to shift 25% of the transition metal atoms from the lower layer, i.e. doubling the MO₂ layer in the a and b direction. This process implies an organization of the tetrahedral sites, d₄ = 5.78 Å (Fig. 8), giving rise to an overestimation of the corresponding peak in the calculated PDF. Consistently, all the peaks corresponding to this in-plane correlation (2nd neighbor, 10.02 Å; 3rd neighbor = 11.56 Å; etc.) are overestimated. This suggests that the M cations do not move out of the layer in a cooperative fashion. Modelling the resultant disorder is not possible, however, owing to the prohibitively large size of the necessary supercell. Transition metal shifting from the upper layer was not considered since no tetrahedral site exists below the MO₆ octahedron; only a large octahedral site. This site normally hosts the sodium cation in the O2 structure, but with a center to oxygen distance of 2.18 Å, it is too large for a transition metal ion and too small for a sodium ion in the present configuration. Hence it probably remains empty. Thus, the distance between the two transition metal layers within the bilayer is 4.66 Å, resulting in a first neighbor M–M interlayer distance of d₃ = 4.95 Å that is well fit by the proposed model. It is worth noting that the construction of a symmetrical octahedral site would result in a much smaller bilayer thickness of about 3.2 Å, clearly ruling out this option. Interestingly, a small peak, not present in the XRD pattern of the electrochemically oxidized sample, appears at 18.9° (4.7 Å) in the diffraction pattern of the chemically oxidized sample (Fig. S2, ESI†). This suggests that a small fraction of the sample – most probably the surface of the grains – might actually reach a fully desodiated state with a homogeneous spacing of the layer, similar to what is observed in the bilayer.

The good agreement between measured and calculated PDF curves up to 30 Å shows that despite the poor diffraction pattern of the oxidized phase, the coherence length in the in-plane direction is large. The conservation of the primary structure of the layers clearly plays a major role in the good reversibility of the transition.

Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂. The structure of the high voltage phase of the nickel substituted oxide was similarly determined, using X-ray PDF analysis on a chemically oxidized “Z”-Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂ sample (Fig. 9). The sodium content reached by chemical oxidation of P2-Na_0.67Fe_0.2Mn_0.65Ni_0.15O₂ is slightly lower than what is achieved electrochemically (Fig. 3), resulting in an average interlayer spacing of 4.95 Å (smaller than anything measured by operando XRD), (Fig. 6d). Fitting of the PDF curve of “Z”-Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂ required a 4 × 4 × 10 supercell (Fig. 9a), revealing that the structure has the same bilayer arrangement previously solved for “Z”-Na_0.14Fe_0.5Mn_0.5O₂. However, there are two small differences. First, the fraction of tetrahedrally coordinated transition metals is reduced to only 3.1%, compared to 12.5% in “Z”-Na_0.14Fe_0.5Mn_0.5O₂. Second, the inter-bilayer distance of 4.55 Å of the nickel substituted sample is significantly smaller than the value of 4.66 Å observed in the non-substituted sample. This two effects are clearly visible when comparing the short range PDF profiles of the two compositions (Fig. 9b). The ratio of the split M–M peak (in yellow highlighting), clearly shows that nickel substitution induces a large increase of the M_Oh–M_Oh pair distance interaction with respect to the M_Oh–M_Td peak, as depicted in Fig. 9c. The contraction of the bilayer thickness is evidenced by the shift to smaller distance of the interlayer M–O and M–M peaks (shown in lavender highlighting).

Fig. 9 (a) Fit of the PDF curves of chemically oxidized Z-Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂ using a 4 ×4 × 10 supercell, (b) comparison of the short range experimental PDF of Z-Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂ and Z-Na_0.14Fe_0.5Mn_0.5O₂, showing the evolution in the MO₆/MO₄ ratio (yellow shading) and the contraction of the bilayer thickness (lavender shading); (c) representation of the two structures.

The smaller inter-bilayer distance observed for the nickel substituted compound indicates that the thickness of the bilayer is controlled by the nature of the tetrahedral species rather than their concentration. The MO₄ site in “Z”-Na_0.1Fe_0.2Mn_0.65Ni_0.15O₂ is smaller (M–O ∼ 1.8 Å) than in “Z”-Na_0.14Fe_0.5Mn_0.5O₂ (M–O ∼ 1.9 Å), suggesting that the average diameter of the tetrahedrally coordinated cation is smaller in the nickel substituted oxide (see below).

Mössbauer spectroscopy. Further insights into the phase transition were obtained with ⁵⁷Fe Mössbauer spectroscopy. The spectra of the pristine materials (x = 0.67, Fig. 10a–c) and the fully charged materials (x ∼ 0.15, Fig. 10d–f) were recorded at room temperature in sealed sample holders for the three compositions Na_x[Mn_0.5+yNi_yFe_0.5−2y]O₂ (y = 0, 0.10, 0.15). As expected, the pristine samples exhibit very similar spectra composed of a single sharp doublet with an isomer shift of ∼0.24 mm s⁻¹ and a quadrupolar splitting of ∼0.73 mm s⁻¹ (Table 1), consistent with Fe³⁺ in an octahedral environment. The removal of Na⁺ ions (charging) causes an asymmetry to develop in this doublet, with additional spectral weight shifted to negative velocity. This effect is more pronounced in the case of Na_0.15Fe_0.5Mn_0.5O₂ than Na_0.15Fe_0.2Ni_0.15Mn_0.65O₂, thus revealing a trend with Ni substitution.

Fig. 10 ⁵⁷Fe Mössbauer spectra of Na_x[Mn_0.5+yNi_yFe_0.5−2y]O₂ pristine (a–c) and charged to 4.3 V (d–f) for y = 0 (a and d), y = 0.1 (b and e), and y = 0.15 (c and f). Raw data is shown in black. Individual spectral components of Fe³⁺O₆, Fe³⁺O₄ and Fe⁴⁺O₆ from fitting are shown in grey and the sum of all spectral components results in the colored curves.

Table 1 Parameters resulting from fitting of ⁵⁷Fe Mössbauer spectra of Na_x[Mn_0.5+yNi_yFe_0.5−2y]O₂ (y = 0, 0.1, 0.15); pristine and charged to 4.3 V

		Component	IS (mm s^−1)	QS (mm s^−1)	area (%)
Ni = 0.15	Pristine	Fe^3+O6	0.24	0.72	100.0
	Charged	Fe^3+O6	0.25	0.71	84.2
		Fe^4+O6	0.00	0.70	15.8
Ni = 0.10	Pristine	Fe^3+O6	0.24	0.73	100.0
	Charged	Fe^3+O6	0.26	0.79	69.5
		Fe^3+O4	0.17	1.53	6.5
		Fe^4+O6	0.00	0.69	24.0
Ni = 0.00	Pristine	Fe^3+O6	0.25	0.75	100.0
	Charged	Fe^3+O6	0.28	0.76	50.9
		Fe^3+O4	0.17	1.51	16.7
		Fe^4+O6	0.00	0.69	32.5

---

The spectra of the charged materials (x ≈ 0.15, Fig. 10d–f) were fitted using three components (Table 1). The main component arises from Fe³⁺O₆ in an octahedral environment and has a nearly identical isomer shift and quadrupolar splitting values compared to its pristine counterpart. The second component with an isomer shift of 0.17 mm s⁻¹ and a large quadrupolar splitting of ∼1.5 mm s⁻¹ is assigned to Fe³⁺O₄ (tetrahedral coordination) owing to the non-centrosymmetry of its ligand environment. The third component with an isomer shift close to zero and a quadrupolar splitting of ∼0.7 mm s⁻¹ is consistent with Fe⁴⁺O₆ in sodium layered oxides.^44–47

We note that the refined ratio of Fe⁴⁺O₆ (Table 1) is systematically lower than what is expected for Na_0.15[Mn_0.5+yNi_yFe_0.5−2y]O₂ according to a simple, purely ionic model; i.e. 70%, 50% and 25% respectively for y = 0, 0.1, 0.15. This large discrepancy shows that the high voltage charge compensation mechanism is more complex than the straightforward oxidation of Fe³⁺ to Fe⁴⁺. Indeed, X-ray absorption measurements (XAS) of P2-Na_x[Mn_0.5Fe_0.5]O₂ have showed that in contrast to the Mn K-edge, the energy of the Fe K-edge transition was essentially unaffected by sodium extraction,¹⁸ suggesting that the electronic configuration of iron remains similar throughout the redox process.

It was recently proposed that ligand-to-metal charge transfer (LMCT) plays an important role in the electrochemical properties of sodium layered oxides.⁴⁴ It is particularly interesting to note that in perovskite structures containing Fe⁴⁺ such as CaFeO₃ and SrFeO₃, the LMCT energy was found to be null or negative.^48–50 The Fe(IV) oxidation state can be stabilized by transferring electrons from the oxide framework to the metal centers. This explains why the perovskites do not exhibit Jahn–Teller distortion, and accounts for the very small shift observed in the XAS spectra of non-stoichiometric AFeO_3−δ with A = Sr, Ca.⁵⁰ We propose that in the case of Na_0.15[Mn_0.5+yNi_yFe_0.5−2y]O₂ a similar mechanism occurs; however in contrast to the perovskites that exhibit metallic behavior, the electron hopping rate is sufficiently low in the case of the layered oxides to exhibit localized Fe³⁺ states by Mössbauer spectroscopy.

The charge transfer from the anionic framework to some of the iron atoms weakens the chemical bonding of the surrounding metal centers. The weakly bonded atoms are therefore more prone to the migration phenomena previously identified by PDF. Based on the intensity of the tetrahedral signal in Na_0.15Fe_0.5Mn_0.5O₂, we see that roughly 2/3 of the transition metal atoms in the tetrahedral sites are Fe³⁺, indicating preferential migration of iron. The fact that both iron and manganese ions migrate is further supported by previously reported XAS measurements¹⁸ which show the appearance of pre-peaks characteristic of non-centrosymmetric coordination polyhedra in both the Mn and Fe spectra, when the sample is charged from 3.8 V to 4.5 V vs. Na.

As the nickel content increases, the amount of tetrahedrally coordinated iron decreases from 16.6% in Na_0.15Fe_0.5Mn_0.5O₂ to 6.5% in Na_0.15Fe_0.3Mn_0.6Ni_0.1O₂. The signal was too small to be accurately refined in Na_0.15Fe_0.2Mn_0.65Ni_0.15O₂. This is in agreement with the PDF results obtained for this phase showing that the concentration of tetrahedral species is very low. Moreover, the smaller MO₄ (M–O ∼1.8 Å) site suggests that a cation smaller than Fe³⁺ migrates into this site. Tetravalent manganese is a likely candidate since its migration is observed in the non-substituted sample and the expected bond length for tetrahedral Mn⁴⁺ is 1.77 Å. Fe⁴⁺ and Ni⁴⁺ are usually not encountered in tetrahedral coordination but cannot be completely ruled out based on the data presented here.

Discussion of the mechanism. Based on these observations, we propose that sodium extraction from P2-Na_x[Fe_0.5−2yMn_0.5+yNi_y]O₂ cathodes occurs according to the following mechanism (see Fig. 8). The formation of Fe⁴⁺ species is stabilized by electron transfer from the oxygen orbitals. The localization of the donated electron on the Fe⁴⁺ cation weakens the bonding of the surrounding atoms, facilitating the migration of transition metal out of the MO₂ plane. Due to their larger size and absence of ligand field stabilization, Fe³⁺ cations are more likely to be expelled than Mn⁴⁺ from their octahedral site that shrinks upon charge due to the contraction of the in-plane cell parameter. The interaction of the expelled iron atoms with the adjacent MO₂ layer drives the glide that results in an O2 stacking type bi-layer, generating a stable tetrahedral environment for the interplanar cations. Once initiated, this process will likely propagate along the layer, favoring sodium depletion from the bilayer. The fact that this transformation does not extend to complete reorganization of the structure – i.e. collapse of the “interbilayer” spacing – can originate from two different phenomena. It might be significantly more difficult to oxidize Fe³⁺ in a tetrahedral environment given that Fe⁴⁺ is usually encountered in octahedral coordination. Another possibility is that the cation vacancies in the transition metal layer pin the Na⁺ ions, thus preventing their extraction.

Upon substitution of Fe by Mn/Ni, the lower concentration of Fe⁴⁺ implies that fewer atoms are impacted by the LMCT that stabilizes this valence state. Therefore the number of transition metal ions susceptible to migrate to the interlayer space is smaller, delaying the P2 to “Z” phase transition. This is consistent with the lower overpotentials observed in the electrochemical profiles of the nickel substituted oxides (Fig. 3); the lower number of MO₄ tetrahedra binding the bi-layers together implies a better reversibility of the transition. This has significant implications for the electrochemistry, as discussed below.

Electrochemistry: effect of structural transitions on cycling

Effect of voltage window on capacity. Structural transitions imply an abrupt change in the crystallographic cell volume and are significant sources of mechanical stress. These are expected to significantly affect the ageing properties of a positive electrode material subjected to deep cycling. The frequent occurrence of these phenomena in sodium layered oxides is a major drawback for application in sodium batteries. In that respect, P2-Na_x[Mn_0.5+yNi_yFe_0.5−2y]O₂ materials are very promising since the P2 phase is stable over a large range of stoichiometry. As previously demonstrated, nickel substitution not only increases the average cell voltage, but it also extends the stability domain of the P2 phase.

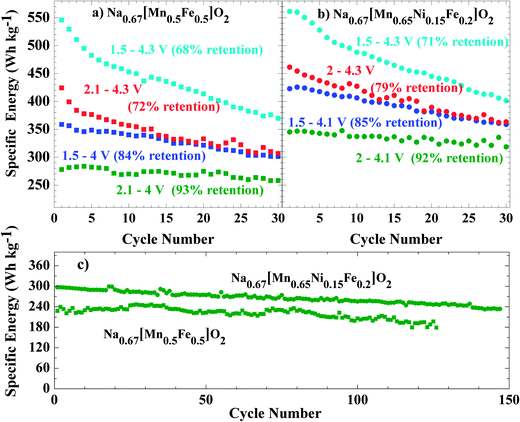
To investigate the effect of phase transitions on the electrochemical performance of Na_x[Mn_0.5Fe_0.5]O₂ and Na_x[Mn_0.65Ni_0.15Fe_0.2]O₂, these materials were cycled in four different voltage ranges allowing either: (i) both structural transitions to occur, (ii) and (iii) only one of the two, (iv) none at all (Fig. 11). Based on the operando study (Fig. 5), we determined that P2-Na_x[Mn_0.5Fe_0.5]O₂ is stable within the 4–2.1 V window, whereas the Ni substituted composition exhibits a larger stability window of 4.1–2 V. Preventing the formation of the orthorhombic P′2 phase by changing the low cutoff voltage does not induce significant change in the cycling profile of either composition. The observed polarization can then directly be related to intrinsic properties of the P2 phase such as the sodium mobility.

Fig. 11 The galvanostatic charge/discharge profile of Na_x[Mn_0.5Fe_0.5]O₂ and Na_x[Mn0_.65Ni_0.15Fe_0.2]O₂ cycled at C/20 in different voltage windows.

In contrast, when the high cutoff voltage is set to prevent formation of the bilayer phase, the cell polarization at high voltage drastically decreases. This shows that the polarization at high potential is solely due to the energy required to convert the bilayer structure of the Z phase to the original P2 structure. A small residual polarization is observed around the Na_0.5Fe_0.5Mn_0.5O₂ stoichiometry, i.e. around the potential jump, and was previously attributed to the decrease in electronic conductivity due to the absence of transition metals with a mixed valence state.²⁴ The absence of a similar jump in the Na_xMn_0.65Ni_0.15Fe_0.2O₂ shows that this composition remains electronically conductive over the whole range of sodium concentration. The oxidation of nickel and iron overlap, explaining why no potential jump is observed.

Improving the specific energy. Since modifying the cycling range changes the cell polarization and capacity at the same time, specific energy retention (Fig. 12a and b) is a more relevant parameter to study than capacity retention (Fig. S3, ESI†). Independent of the cycling range or the composition, the Coulombic efficiency measured is above 99.5% (Fig. S4, ESI†) showing that the capacity fading that is observed can be related to the mechanical stress within the positive electrode rather than chemical incompatibilities. Both compositions exhibit about 70% specific energy retention after 30 cycles when the full voltage range is used. Preventing the orthorhombic P′2 transition slightly increases the specific energy retention, whereas avoiding the formation of the bilayer phase boosts the retention by ∼15%. If the P2 structure is preserved during cycling, the specific energy retention is higher than 90% after 30 cycles. Within the same voltage range, at twice the current density (namely 26 mA g⁻¹ or C/10; compared to C/20), the Na_xFe_0.2Mn_0.65Ni_0.15O₂ cell maintained retention of ∼80% over 150 cycles (Fig. 12c). Considering that the electrodes were not optimized, and nor were issues at the negative Na electrode solved, this is highly promising for future development.

Fig. 12 Specific energy of (a) Na_0.67[Mn_0.5Fe_0.5]O₂ and (b) Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ as a function of cycle number, at C/20 within different voltage windows; (c) specific energy of Na_0.67[Mn_0.5Fe_0.5]O₂ and Na_0.67[Mn_0.65Ni_0.15Fe_0.2]O₂ at a rate of C/10 in the window from 2.1–4 V and 2–4.1 V, respectively; capacity fade rate for the latter is 0.13% per cycle.

Limiting the cycling range is an efficient way to greatly increase the life span of sodium batteries based on P2-Na_x[Mn_0.5+yNi_yFe_0.5−2y]O₂ electrodes benefitted by Ni substitution. Cycling in the 4.3–1.5 V window results in only a 3% energy density gain for Na_x[Mn_0.65Ni_0.15Fe_0.2]O₂ compared to Na_xFe_0.5Mn_0.5O₂, (561 Wh kg⁻¹ on the first discharge compared to 545 Wh kg⁻¹ for the latter). However reducing the voltage window in order to maintain the P2 structure increases the energy stored by the nickel containing sample by 25% (345 Wh kg⁻¹vs. 278 Wh kg⁻¹ for the non-substituted electrode).

Conclusions

We present here the phases of P2-Na_xFe_0.2Mn_0.65Ni_0.15O₂ as a function of the sodium content. The sodium (de)insertion mechanism is similar to that of the parent oxide P2-Na_xFe_0.5Mn_0.5O₂. The pristine P2 phase converts at low voltage to a P′2 orthorhombic phase due to a cooperative Jahn–Teller effect that stabilizes the Mn³⁺ cations. At high voltage, the migration of the transition metal into a tetrahedral coordination environment perturbs the long range stacking order of the MO₂ layers. The structure of this semi-crystalline phase, solved for the first time using X-ray PDF analysis, shows that the migration of the transition metal in the interlayer space induces the formation of short range order between two adjacent layers with the O2 stacking scheme. In contrast to other oxides for which this mechanism was proposed – O3-Na_xCrO₂⁴¹ and O3-Na_xFeO₂¹¹ – the structural transformation in P2-Na_x[Fe_0.5−2yMn_0.5+yNi_y]O₂ is fully reversible, despite the significant polarization that results. This difference between the O3 and P2 structures is most likely due to the fact that O2 stacking is not made accessible by translation of the MO₂ layers in an O3 structure. In this respect, P2 based structures are better suited for the design of high voltage positive electrode for sodium ion batteries.

The impact of both structural transitions on the cycling properties of the electrodes was investigated by adjusting the cutoff voltage. As expected, the high voltage structural transition has a much more significant impact due to the reorganization of the MO₂ layer stacking scheme. If both transitions are avoided, 80% specific energy is maintained after 150 cycles with non-optimized electrodes, representing a significant improvement vs. ∼70% after 30 cycles in the full electrochemical window. In other words, cycling is stabilized at the expense of capacity. Substitution of Fe³⁺ by Mn⁴⁺/Ni²⁺ decreases the concentration of species at the origin of the high voltage transition, effectively delaying its occurrence. This additional capacity allows P2-Na_xFe_0.2Mn_0.65Ni_0.15O₂ to deliver 25% more energy than the unsubstituted oxide when it is cycled in a voltage range that inhibits any structural transition.

The observations reported show that the Fe^3+/4+ redox couple is well suited to the design of high voltage positive electrodes for sodium ion batteries, provided that transition metal migration is prevented. Further studies are needed to fully understand the role of LMCT in these oxides and how to employ this effect to prevent cation migration. Mixing iron with larger cations should help increase the size of the MO₆ octahedra, hence inhibiting population of the tetrahedral site. Similarly, substituting Mn³⁺ by a higher voltage non-Jahn–Teller active cation should also greatly improve the material performance, bringing sodium ion batteries closer to market application.

Acknowledgements

We thank the Natural Sciences and Engineering Council of Canada for generous financial support of this work through their Discovery and Canada Research Chair programs, and BASF SE for ongoing support through the research network in Electrochemistry and Batteries. Mössbauer work, performed at Caltech, was supported as part of EFree, an Energy Frontier Research Center, under Award No. DE-SG0001057. Experiments performed at ORNL’s Spallation Neutron Source by UWaterloo were sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. We warmly thank A. Huq and M. Kirkham at the ORNL for their invaluable help during measurements on the POWGEN diffractometer, and Hiruy Haile for his assistance in the conception and realization of the operando cell. We also acknowledge M. Gateshki and M. Sommariva from PANalytical for their help with the PDF experimental setup.

References

1. J. Billaud, G. Singh, R. A. Armstrong, E. Gonzalo, V. Roddatis, M. Armand, T. Rojo and P. G. Bruce, Energy Environ. Sci., 2014, 7, 1387.
2. A. Maazaz, C. Delmas and P. Hagenmuller, J. Inclusion Phenom., 1983, 1, 45–51.
3. D. Hamani, M. Ati, J.-M. Tarascon and P. Rozier, Electrochem. Commun., 2011, 13, 938–941.
4. S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12, 355–358.
5. A. Mendiboure, C. Delmas and P. Hagenmuller, J. Solid State Chem., 1985, 57, 323–331.
6. S. Okada, Y. Takahashi, T. Kiyabu, T. Doi, J. Yamaki and T. Nishida, ESC Meet. Abstr., 2006, 201.
7. C. Delmas, J.-J. Braconnier, C. Fouassier and P. Hagenmuller, Solid State Ionics, 1981, 3, 165–169.
8. S. Miyazaki, S. Kikkawa and M. Koizumi, Synth. Met., 1983, 6, 211–217.
9. M. H. Han, E. Gonzalo, G. Singh and T. Rojo, Energy Environ. Sci., 2015, 8, 81–102.
10. J. Billaud, R. J. Clément, A. R. Armstrong, J. Canales-Vázquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243–17248.
11. N. Yabuuchi and S. Komaba, Sci. Technol. Adv. Mater., 2014, 15, 043501.
12. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682.
13. D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, Angew. Chem., 2015, 54, 3431–3448.
14. C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85.
15. Y. Lei, X. Li, L. Liu and G. Ceder, Chem. Mater., 2014, 26, 5288–5296.
16. D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312.
17. J. Xu, D. H. Lee, R. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269.
18. N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517.
19. B. Mortemard de Boisse, D. Carlier, M. Guignard and C. Delmas, J. Electrochem. Soc., 2013, 160, A569–A574.
20. J. S. Thorne, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2013, 160, A361–A367.
21. J. Xu, S. L. Chou, J. L. Wang, H. K. Liu and S. X. Dou, ChemElectroChem, 2014, 1, 371–374.
22. S. Kalluri, K. Hau Seng, W. Kong Pang, Z. Guo, Z. Chen, H.-K. Liu and S. X. Dou, ACS Appl. Mater. Interfaces, 2014, 6, 8953–8958.
23. V. Duffort, E. Talaie, R. Black and L. F. Nazar, Chem. Mater., 2015, 27, 2515–2524.
24. B. Mortemard de Boisse, D. Carlier, M. Guignard, L. Bourgeois and C. Delmas, Inorg. Chem., 2014, 53, 11197–11205.
25. E. Gonzalo, M. Han, J. L. del Amo, B. Acebedo, M. Casas-Cabanas and T. Rojo, J. Mater. Chem. A, 2014, 2, 18523–18530.
26. D. Yuan, X. Hu, J. Qian, F. Pei, F. Wu, R. Mao, X. Ai, H. Yang and Y. Cao, Electrochim. Acta, 2014, 116, 300–305.
27. I. Hasa, D. Buchholz, S. Passerini, B. Scrosati and J. Hassoun, Adv. Energy Mater., 2014, 4, 1400083.
28. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
29. A. Le Bail, Powder Diffr., 2005, 20, 316–326.
30. P. Juhas, T. Davis, C. L. Farrow and S. J. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566.
31. C. Farrow, P. Juhas, J. Liu, D. Bryndin, E. Božin, J. Bloch, T. Proffen and S. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
32. R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767.
33. Y. Ono, N. Kato, Y. Ishii, Y. Miyazaki and T. Kajitani, T., J. Jpn. Soc. Powder Powder Metall., 2003, 50, 469–474.
34. N. Yabuuchi, R. Hara, M. Kajiyama, K. Kubota, T. Ishigaki, A. Hoshikawa and S. Komaba, Adv. Energy Mater., 2014, 4, 1301453.
35. M. Guignard, C. Didier, J. Darriet, P. Bordet, E. Elkaïm and C. Delmas, Nat. Mater., 2013, 12, 74–80.
36. R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80.
37. Z. Lu and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A1225–A1229.
38. J.-P. Parant, R. Olazcuaga, M. Devalette, C. Fouassier and P. Hagenmuller, Solid State Chem., 1971, 3, 1–11.
39. M. Sathiya, K. Hemalatha, K. Ramesha, J. M. Tarascon and A. S. Prakash, Chem. Mater., 2012, 24, 1846–1853.
40. Y.-N. Zhou, J.-J. Ding, K.-W. Nam, X. Yu, S.-M. Bak, E. Hu, J. Liu, J. Bai, H. Li and Z.-W. Fu, J. Mater. Chem. A, 2013, 1, 11130–11134.
41. K. Kubota, I. Ikeuchi, T. Nakayama, C. Takei, N. Yabuuchi, H. Shiiba, M. Nakayama and S. Komaba, J. Phys. Chem. C, 2015, 119, 166–175.
42. Y.-Y. Hu, Z. Liu, K.-W. Nam, O. J. Borkiewicz, J. Cheng, X. Hua, M. T. Dunstan, X. Yu, K. M. Wiaderek, L.-S. Du, K. W. Chapman, P. J. Chupas, X.-Q. Yang and C. P. Grey, Nat. Mater., 2013, 12, 1130–1136.
43. D. Zeng, J. Cabana, J. Bréger, W.-S. Yoon and C. P. Grey, Chem. Mater., 2007, 19, 6277–6289.
44. X. Wang, G. Liu, T. Iwao, M. Okubo and A. Yamada, J. Phys. Chem. C, 2014, 118, 2970–2976.
45. J. S. Thorne, S. Chowdhury, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2014, 161, A1801–A1805.
46. J. Zhao, L. Zhao, N. Dimov, S. Okada and T. Nishida, J. Electrochem. Soc., 2013, 160, A3077–A3081.
47. Y. Takeda, K. Nakahara, M. Nishijima, N. Imanishi, O. Yamamoto, M. Takano and R. Kanno, Mater. Res. Bull., 1994, 29, 659–666.
48. A. E. Bocquet, T. Mizokawa, T. Saitoh, H. Namatame and A. Fujimori, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3771–3784.
49. M. Takano, N. Nakanishi, Y. Takeda, S. Naka and T. Takada, Mater. Res. Bull., 1977, 12, 923–928.
50. A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1561–1570.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ee01365h

‡ These authors contributed equally to this work.

---