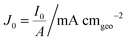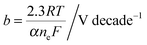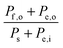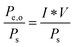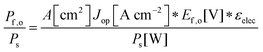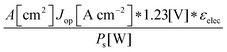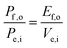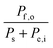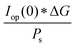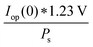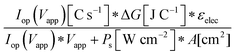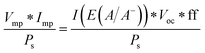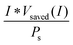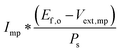Open Access Article
Open Access ArticleMethods for comparing the performance of energy-conversion systems for use in solar fuels and solar electricity generation
Robert H.
Coridan†
 a,
Adam C.
Nielander†
a,
Adam C.
Nielander†
 a,
Sonja A.
Francis
ab,
Matthew T.
McDowell
ab,
Victoria
Dix
a,
Shawn M.
Chatman
b and
Nathan S.
Lewis
*abc
a,
Sonja A.
Francis
ab,
Matthew T.
McDowell
ab,
Victoria
Dix
a,
Shawn M.
Chatman
b and
Nathan S.
Lewis
*abc
aDivision of Chemistry and Chemical Engineering, California Institute of Technology, 210 Noyes Laboratory, MC 127-72, 1200 E California Boulevard, Pasadena, CA 91125, USA. E-mail: nslewis@caltech.edu
bJoint Center for Artificial Photosynthesis, California Institute of Technology, Pasadena, CA 91125, USA
cBeckman Institute and Kavli Nanoscience Institute, California Institute of Technology, Pasadena, CA 91125, USA
First published on 13th April 2015
Abstract
The energy-conversion efficiency is a key metric that facilitates comparison of the performance of various approaches to solar energy conversion. However, a suite of disparate methodologies has been proposed and used historically to evaluate the efficiency of systems that produce fuels, either directly or indirectly, with sunlight and/or electrical power as the system inputs. A general expression for the system efficiency is given as the ratio of the total output power (electrical plus chemical) divided by the total input power (electrical plus solar). The solar-to-hydrogen (STH) efficiency follows from this globally applicable system efficiency but only is applicable in the special case for systems in which the only input power is sunlight and the only output power is in the form of hydrogen fuel derived from solar-driven water splitting. Herein, system-level efficiencies, beyond the STH efficiency, as well as component-level figures of merit are defined and discussed to describe the relative energy-conversion performance of key photoactive components of complete systems. These figures of merit facilitate the comparison of electrode materials and interfaces without conflating their fundamental properties with the engineering of the cell setup. The resulting information about the components can then be used in conjunction with a graphical circuit analysis formalism to obtain “optimal” system efficiencies that can be compared between various approaches. The approach provides a consistent method for comparison of the performance at the system and component levels of various technologies that produce fuels and/or electricity from sunlight.
Broader contextAs the fields of photoelectrochemical (PEC) energy conversion and solar fuels have grown, a number of metrics have been adopted for evaluating the performance of electrodes and systems. These metrics are often contradictory, irreproducible, or not properly standardized, which prevents researchers from accurately comparing the performance of materials. We explore herein these different metrics to evaluate their strengths and applicability, as well as to demonstrate the knowledge derived from each approach. We also present a framework for reporting these metrics in an unambiguous and reproducible manner. Additionally, we outline a method to estimate two-electrode system efficiencies from three-electrode electrochemical measurements, to accelerate the identification of promising system components without requiring the actual construction of a full system. Clarifying these issues will benefit the PEC community by facilitating the consistent reporting of electrode performance metrics, and will allow photoelectrodes and solar fuels systems to be appropriately compared in performance to other solar energy conversion technologies. |
I. Introduction
Many disparate technological approaches are being pursued to convert solar energy into electricity and fuels. For example, photovoltaic (PV) cells, photoelectrochemical (PEC) cells, and solar-thermal systems can directly produce electricity from sunlight. Similarly, fuels can be produced from sunlight either directly by PEC cells or by solar-driven electricity connected to electrolyzers, either as discrete, stand-alone units or as an integrated system.1,2 Fuels can also be generated by thermochemical systems3–5 or by engineering chemical reactions in biological systems.6 It is imperative to adopt a consistent approach to report the energy-conversion efficiencies for these various technologies. In all cases, the input power (sunlight, electricity) and output power (electricity, fuels) can be measured by a variety of analytical methods, and the absolute efficiency of any technology can be reported or compared directly to any other.For solar-fuels generating systems, the solar-to-fuels (STF) efficiency can be directly determined by analysis of the chemical products formed under solar illumination in the absence of an applied bias.7,8 The STF efficiency is an important metric for comparing solar-fuels systems to other technologies. However, this metric is reductive by definition, as it does not delineate the sources of loss or sub-optimal performance in a system. A STF metric provides little guidance regarding the potential for improvement because nearly all of the details of performance of the electrodes and of the system design are entangled in this single result. In addition, the STF efficiency is not applicable to systems that require electrical power as a partial input or that produce electrical power as a partial output. Conversely, the electrode components of a solar-fuels generating system can be isolated and characterized via electronic and electrochemical methods, and such results can be used to elucidate the catalytic and photovoltaic properties of a component as well as sources of energy-conversion inefficiencies for that component. The translation of these component measurements to STF device performance, however, must be done with care. Furthermore, many electrode component metrics that have traditionally been denoted and reported as efficiencies for single electrodes are not true efficiencies, because they are not a measurement of the ratio of the total power output to the total power input. Thus, there is a need to improve the evaluation of single prototypical electrodes and to relate their individual performance to their potential in solar-fuels systems.
Herein we first define the system efficiency generally and then more specifically for various technologies that convert sunlight into a combination of electricity and/or chemical fuels. Next we describe related figures of merit and discuss their value for the evaluation of single photoelectrodes within photoelectrochemical STF devices, as well as important considerations towards using such metrics appropriately. To link the properties of photoelectrodes to the performance of full systems, we present a method of graphical circuit analysis that permits evaluation of the optimal operating point of a hypothetical system comprising electrodes with well-characterized PEC properties. We also discuss how graphical circuit analyses can guide the engineering of an optimally efficient system architecture based on the characteristics of the chosen components. The methods for calculating the optimal system efficiency discussed herein are intended to provide a complementary and general system-analysis method relative to evaluating theoretical system efficiencies based on materials properties such as band gaps9,10 or relative to measurements of efficiencies in fully realized STF systems.7
II. System efficiencies
A. General treatment
Consider a system that generates output products in the form of chemical fuels and/or electrical power. The total system output power, Po, is the sum of the output power contained in the chemical fuel, Pf,o, and any output power in the form of electricity, Pe,o. When the incipient output currents, I, due to fuel and electricity production are equal (i.e. the circuit elements are electrically connected in series), this relationship can be expressed as:| Po = Pf,o + Pe,o = I * (Ef,o + Ve,o) | (1) |
The system inputs may, in general, consist of electrical power, Pe,i, and/or power from solar illumination, Ps. The total input power, Pi, is therefore:
| Pi = Ps + Pe,i | (2) |
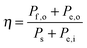 | (3) |
B. Solar-to-electricity systems
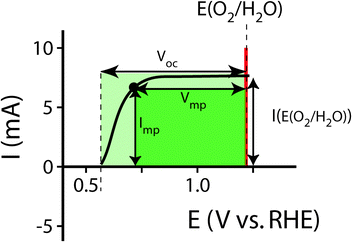
For systems that solely produce electricity, such as photovoltaic or regenerative photoelectrochemical cells,11 the maximum-power operating current Imp and voltage Vmp are the current and voltage that generate the maximum output power, Pmax = ImpVmp. The efficiency of the photovoltaic or regenerative PEC cell is simply the ratio of the electrical power output to the input power provided by solar illumination. This ratio can be calculated from the general efficiency expression (eqn (3)) by setting to zero the terms related to chemical fuel output and electrical power input (Pf,o = 0 and Pe,i = 0). Thus, the efficiency of a photovoltaic or regenerative PEC system at maximum power, ηPV, is given by: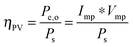 | (4) |
C. Solar-to-fuels systems
For comparing the performance of a solar-fuels generator to a solar-electricity generating system, we adopt herein the Gibbs free energy of the fuel as the standardized measure of the energy content of the fuel,7,8 where the fuel-forming reactions can be for e.g., hydrogen evolution from water or halide splitting, or the reduction of CO2 to hydrocarbons. For a system that produces only fuel as the output and that uses only solar power as the input, the efficiency can be calculated from eqn (3) by setting to zero the terms related to the electrical power input and output (Pe,i = 0 and Pe,o = 0), such that: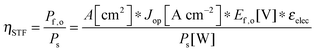 | (5) |
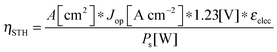 | (5′) |
D. Electricity-to-fuels systems
Electrolysis involves the input of electrical power to produce output power as chemical fuel, such as in the form of separated, pure streams of H2(g) and O2(g). Electrolyzers operate with no output electrical power (Pe,o = 0) and no power generated by illumination (Ps = 0). Assuming that all of the current is derived from Faradaic processes (εelec = 1), the efficiency of electrolysis is: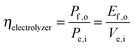 | (6) |
E. Mixed fuel/electricity/solar input and output systems
Efficiencies can also be evaluated from eqn (3) for systems that require electrical and optical energy inputs and/or produce both electrical and chemical energy as outputs. As an example of such a system, an n-Fe2O3|1.0 M KOH(aq)|Pt cell can be used as the photoanode in photo-driven water-splitting reactions, and could thus generate a portion of the photovoltage required for electrolysis. However, this system requires an external bias to split water, and therefore ηSTH is undefined by definition as eqn (5) makes no allowance for electrical input power. Nevertheless, the system still provides a net conversion of sunlight in the form of a reduced bias needed to drive the electrolysis reaction relative to the situation with two dark electrodes in the system. Throughout the manuscript, ‘dark electrode’ refers to an electrode which operates under negligible incident illumination or is not photoactive. Regardless of the details, the system efficiency can be determined from eqn (3). Because no excess electricity is drawn as output from this cell (Pe,o = 0), the expression for the resulting photo-assisted electrolysis system efficiency (ηPAE) is: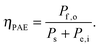 | (7) |
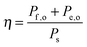 | (8) |
III. System figures of merit
Although the system efficiency is the key engineering-based figure of merit for fully operational electrochemical solar energy-conversion systems, understanding the electrochemical characteristics of the components of a system is crucial for understanding the results of a system efficiency measurement. Different metrics can be employed to characterize the performance of the photoactive components in systems by varying the components or other inputs of the system. In these cases, a ‘system’ refers to all of the components of a system that necessarily act in concert to produce harvestable power. This definition of a system can include, but does not necessarily include losses related to electricity generation, transmission, or control as would be considered for large-scale technical analyses for cross-technology comparisons. These measurements are often carried out on systems employing two electrodes in an electrochemical cell.One quantity that has been used to describe the performance of photoelectrodes is the applied-bias photon-to-current metric (often called an efficiency, and thus often abbreviated ABPE or ABCE, abbreviated here as ABPC).16,17 As given in eqn (9), this quantity is the difference of the power output in chemical fuel and any added electrical input power, divided by the solar power input:15,18
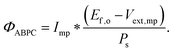 | (9) |
Φ ABPC is the IUPAC-suggested definition of the solar-conversion efficiency of a cell that has a dark electrode and a semiconductor-based photoelectrode.18 In general, however, ΦABPC is not a measurement of a system efficiency because ΦABPC is not a ratio of the total power output divided by the total power input to the system. Rather, ΦABPC measures the net chemical output power (rate of production of free energy of products less the input electrical power) of a system in units of incident solar power. The ΦABPC figure of merit represents the fraction of the energy stored in the chemical products that can be assigned to the photovoltage provided by the input solar illumination. The value of ΦABPC can be negative, meaning that the electrical energy input even under illumination is in excess of the free energy stored in the products. For systems that perform fuel-forming reactions without an applied bias (Vext), the expression for ΦABPC reduces to the analytical form of ηSTH (eqn (5)) if no electrical power is output by the system.
Another metric commonly used to evaluate the effects of input solar illumination is the system-level power-saved metric. This metric is quantified by determining the external voltage needed to achieve a current, I, for a system with a working photoelectrode and a given counter electrode, compared to the voltage needed to achieve that same current in a related system but comprising instead a dark working electrode and the same counter electrode:
| Psaved(I) = I * (Vdark,ext(I) − Vlight,ext(I)) = I * Vsaved(I) | (10) |
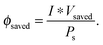 | (11) |
IV. Three-electrode measurements
Three-electrode electrochemical current density vs. potential (J–E) measurements provide a direct evaluation of the properties of an electrode under the relevant solution and illumination conditions and can be replicated readily by other researchers. This provides a distinct advantage over the less easily replicated two-electrode system measurements discussed above. This fundamental evaluation of electrode performance provides a basis to compare the relative metrics for different electrodes. Furthermore, three-electrode measurements allow identification of the optimal performance achievable in a system that would use the given components, without having to explicitly consider or develop the design, engineering, or operational details of the full system.In three-electrode voltammetric measurements, a potentiostat is used to control the potential difference between a working electrode and a reference electrode, while the current is measured between the working electrode and a counter electrode, with negligible current passed between the working and reference electrodes. The J–E behavior of the working electrode can therefore be determined independently of potential drops associated with electrochemical processes at the counter electrode. Kinetic overpotential and mass transport losses may be considered inherent to an electrode under the relevant conditions, but measurements of the J–E behavior should always be appropriately corrected for any uncompensated solution resistance, as this quantity is not a fundamental characteristic of an electrode/electrolyte interface.
For photoelectrode components, the J–E behavior can yield the open-circuit potential, Eoc, the current at the Nernstian potential (E(A/A−)) for the half-reaction of interest, I(E(A/A−)) (or J(E(A/A−)), the current density), and the photogenerated current, Iph,20 determined by finding the difference between the current under illumination and the dark current, prior to the observation of breakdown phenomena and under conditions that are not mass-transport limited. When Iph is potential-dependent (e.g. due to photogenerated carrier collection being dependent on drift in the depletion region) Iph should be measured separately at each potential of interest.
A. Power-saved metric
In a three-electrode system, the power saved16,21,22 at any current, I, is given by the product of the current I and the difference between the potential required to drive a half-reaction at a selected working electrode at this current in the dark, Edark(I) and the potential required to drive the same half-reaction at a photoelectrode in the light, Elight(I):| Psaved(I) = I * (Edark(I) − Elight(I)) = I * Vsaved(I) | (12) |
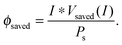 | (13) |
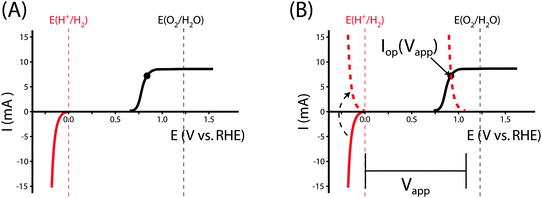
Fig. 1 illustrates the different methods by which three-electrode power-saved measurements can be used to characterize the photoelectrode performance.
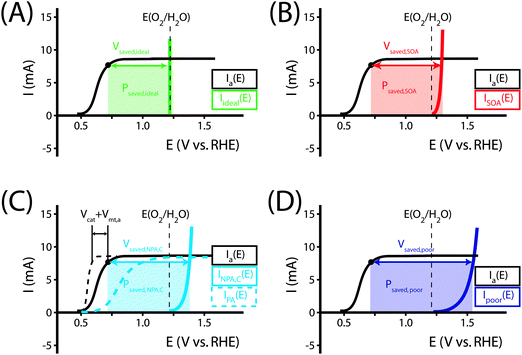 | ||
| Fig. 1 Examples demonstrating the effect of the chosen comparison dark electrode on the power-saved figure of merit in three-electrode I–E measurements. In each example, the same schematic voltammetric I–E characteristic (maximum power point designated by a black dot; Vmp = 0.71 V vs. RHE, Imp = 8 mA, electrode area = 1 cm2) for the photoanode of interest is compared to a chosen dark electrode performing the same anodic reaction. (A) The power saved compared to an ideally nonpolarizable dark electrode. The measured ratiometric power saved is ϕsaved,ideal = 4.2% (for Ps = 0.1 W cm−2). (B) The power saved compared to the state-of-the-art dark anode for the water-oxidation reaction (see Table 1). In this example, the dark electrode exhibits an overpotential of 100 mV at I = 8 mA, increasing the measured ratiometric power-saved value to ϕsaved,SOA = 5.0%. (C) The power saved by the photoanode compared to an identically engineered (semiconductor substrate, structure and mass loading of electrocatalyst, surface, etc.), non-photoactive, degenerately doped electrode (solid blue line). For the example that the catalyst and mass-transport overpotentials are 200 mV for this electrode configuration, the ratiometric power-saved value is ϕsaved,NPA,C = 5.8%. The intrinsic photovoltaic properties of the semiconductor VPV(I) = Edark,NPA,C(I) − Elight(I) (dashed black line). The catalyst/mass-transport effects can be observed using a photoelectrode prepared from the photoactive substrate without added electrocatalyst (Elight,PA(I)) (dashed blue line, PA = photoactive). (D) The power saved for the photoanode compared to a dark electrode with a non-optimal catalytic overpotential for water oxidation. An arbitrarily poor dark electrode can be chosen for comparison, which increases the ratiometric power-saved metric (ϕsaved,poor = 6.6% for the example dark electrode with overpotential of 300 mV at 8 mA) without any actual improvement in the photoelectrode characteristics. | ||
| Edark(I) − Elight(I) = E(A/A−) − [(E(A/A−) − VPV(I)) + Vcat(I) + Vmt(I) + Vsol(I)] | (14) |
Multiplying by the current and dividing by the input solar power yields:
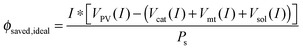 | (15) |
| Edark,SOA(I) − Elight(I) = (Vcat,dark(I) − Vcat,light(I)) + (Vmt,dark(I) − Vmt,light(I)) + VPV(I) | (16) |
As seen in eqn (16), comparison of a photoelectrode to a state-of-the-art dark electrode takes into account any differences in the catalytic activities of the electrodes, any differences in mass transport to the electrode surfaces, and accounts for the photovoltage generated by the photoelectrode. In the example from Fig. 1B, the measured ratiometric power saved at the maximum power point is ϕsaved,SOA = 0.008 A × (1.23 V + 0.10 V − 0.71 V)/Ps = 5.0%.
| Edark(I) − Elight(I) = (E(A/A−) + Vcat(I) + Vmt(I) + Vsol(I)) − (E(A/A−) − VPV(I) + Vcat(I) + Vmt(I) + Vsol(I)) | (17) |
The photovoltaic characteristics, VPV(I), of a photoelectrode can be described by the diode equation:
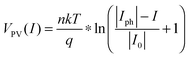 | (18) |
V. Predicting system efficiencies from three-electrode component measurements
A. Introduction
To determine how a particular component will affect the overall efficiency of a system, the most rigorous approach is to physically construct a full system that includes the component in question. However, this method introduces unreasonable barriers to component-level research because only those research groups capable of building and accurately testing full solar energy conversion systems would then be able to participate in component-level development. Additionally, a lack of standardization in device and system designs can lead to different conclusions between different laboratories regarding the contribution of the same component to the performance of the same device.An alternative approach is to hypothetically integrate the components into a theoretical, optimized system in which the resistive losses associated with the solution, membrane, and series resistances are negligible. This process allows estimation of an optimal system efficiency for a given photoelectrode, and the resulting optimal system efficiency value can be compared directly to efficiencies of other full systems. While this optimal system efficiency will always be greater than the measured efficiency for an actual, constructed device, calculation of the optimal system efficiency is nevertheless a valuable evaluation of how individual components will contribute to the system efficiency in an optimized device configuration. Below, we describe a method to determine the optimal system efficiency from half-cell measurements for three different systems: (1) an ideal regenerative photoelectrochemical cell, (2) a photoassisted electrolysis device and (2) a dual-photoelectrode photosynthetic cell.
B. Graphical circuit analysis for identifying system efficiencies from three-electrode measurements
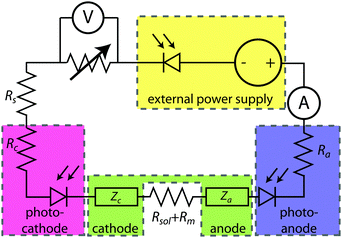
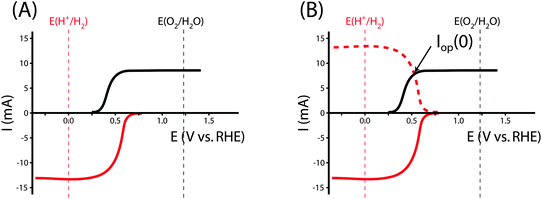
Fig. 2 shows an equivalent-circuit diagram for a two-electrode system. The photoelectrochemical characteristics of a photoanode/anode or of a photocathode/cathode are determined by their representative individual IR-corrected J–E measurements. To perform the graphical circuit analysis, the cathodic J–E characteristic (referenced to the Nernstian potential of the reaction at the cathode) is reflected across the x-axis and translated by Vapp, thus crossing the anodic J–E characteristic (referenced to the Nernstian potential of the reaction at the anode). The operating current Iop can be identified by the intersection point at which the current has the same absolute value through the anode and through the cathode. This constraint can be understood as a requirement of Kirchoff's current law that the current through each electrode must be the same. The value of the efficiency at zero applied bias, and the applied bias that results in the maximum efficiency, can then both be readily computed. This method is analogous to typical load-line analyses of photovoltaic cells and resistive loads. The J–E behavior of an electrode is dependent on the composition of the solution including the concentration of both electrolyte and gaseous species, the incident illumination on the electrode, and the temperature of the cell, among other factors. Whenever possible, the three-electrode measurements used in the graphical circuit analysis to produce predicted optimal system efficiencies should therefore be obtained under the same conditions that the electrode will experience during steady-state operation in the relevant two-electrode device. If both of the three-electrode measurements are not obtained under the same solution conditions (e.g. different counter ions, different pH, etc.) except for any separated products that may appear at one electrode but not the other (e.g. O2 gas at an anode and H2 gas at a cathode), correction for any junction potential that would form or equilibration of electrolyte that would take place in the two-electrode device is necessary.Ideal regenerative cells are fully analogous to solid-state photovoltaic cells, and therefore the efficiency of these systems is described by the same equation as was used to describe the efficiency of a PV device:
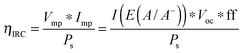 | (19) |
The ηIRC efficiency shares similarities with the two-electrode ΦABPC metric. As noted earlier, the voltage used to obtain a value for ηIRC is exactly the load voltage. Because ηIRC is designed to describe the behavior of a regenerative cell, the load is adjustable. However, the load is not adjustable for the fuel-forming systems that ΦABPC is used to describe. For fuel-forming reactions, in general, the free energy of formation of the chemical fuel is the load in an electrochemical solar-driven water-splitting cell. Thus, for water splitting, a value of 1.23 V is used for the load. This value appears in eqn (9), and the ΦABPC metric and ηIRC would thus have mutually identical numerical values for a fuel-forming system in which Vext = 0 and for which the counter electrode was ideally nonpolarizable.
Here, we propose the use of Pt and RuO2 as state-of-the-art cathodic and anodic counter electrodes, respectively, for the purpose of calculating optimized system efficiencies based on measurements of half-cell J–E characteristics. The performance characteristics of these suggested counter-electrode materials are shown in Table 1. The parameters j0 and b are the exchange-current density and Tafel slope, respectively, that fit the overpotential–current-density relationship of the exemplary planar dark electrocatalysts.1 The data in Table 1 were taken from previously reported electrochemical data on prepared Pt and RuO2 electrodes. The electrodes should be prepared using the same methods (see references in Table 1) to avoid any convolution of electrochemical activity with differences in catalyst structuring. Additionally, any future improvements on the preparation of these or other electrodes for HER and OER should supersede the data in this table. Other reference systems can be used instead, but their equivalent electrochemical parameters should be clearly specified when calculating such optimal solar-conversion efficiencies.
| Electrode | Electrolyte | Ref. | ||
|---|---|---|---|---|
a Note that the kinetic parameters used here to describe the performance of Pt in acid are summarized from studies conducted with planar Pt electrodes, which are appropriate as engineering parameters that approximate the measured Tafel behavior for a planar electrode. It has been suggested that planar Pt electrodes are sufficiently active in acidic conditions such that their kinetic parameters are analogous to the calculated Nernstian diffusion overpotential assuming infinitely fast reaction kinetics, and therefore may not be related to the true kinetics of the underlying reaction.29,33 Note that for this table, the expected overpotential can be calculated using the equation 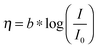 . .
|
||||
| Pt | Acid | 1a | 0.035a | 26–28 |
| Pt | Base | 0.7 | 0.120 | 29 |
| RuO2 | Acid | 10−5 | 0.035 | 30 and 31 |
| RuO2 | Base | 10−5 | 0.042 | 32 |
The solar-conversion efficiency of the optimized half-cell is then readily calculated (eqn (5)), by assuming that the series resistances are zero and using the measured photoelectrode characteristics in conjunction with the assumed counter-electrode behavior, in conjunction with the definition of a system efficiency presented in eqn (3).
The graphical circuit analysis can be used to determine the efficiency of a system that used this photoelectrode. Fig. 4B shows the shifted cathodic voltammogram required to determine the operating current as a function of the applied bias: Iop(Vapp). The system has negligible operating current until sufficient bias is supplied. In this example, the Iop(Vapp) relationship can be used to find the efficiency of this system for a given bias Vapp from eqn (3):
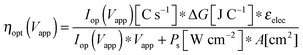 | (20) |
The properties of the counter electrode used in this analysis can be measured directly in another three-electrode measurement. Typically, ηopt at zero applied bias can be calculated as ηopt(Vapp = 0). However, the current is negligible for this example when Vapp = 0, and thus there is no reason to calculate the value of ηopt at zero bias in this system.
Fig. 5A shows the relevant I–E measurements for the example photocathode and photoanode materials under the same operating conditions. The intersection of the transformed photocathode voltammogram and the photoanode voltammogram in Fig. 5B indicates the Iop for which ηopt can be calculated.
The power output at the current density Iop(0) is given by:
| Pf,o = Iop(0) * ΔG | (21) |
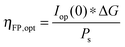 | (22) |
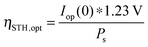 | (23) |
VI. System design considerations
A. Relating changes in component performance to changes in projected system efficiency
The graphical circuit analysis is required because neither ΦABPC nor power-saved measurements are robust predictors of system efficiencies. Consider, for example, the five hypothetical photoanodes shown in Fig. 6 as photoelectrodes for oxygen evolution in 1 M H2SO4(aq). Table 2 presents the ratiometric power-saved figure of merit as well as the value of ΦABPC, and the optimal system solar-conversion efficiency, ηopt, based on the half-cell performance of each electrode.| Electrode | V mp/V | I mp/mA |
Φ
ABPC,opt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/% a/% |
ϕ
saved![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b/% b/% |
η
PAE,opt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/% a/% |
I op/mA | η STH,opt/% |
|---|---|---|---|---|---|---|---|
| a Assumes an optimized Pt counter electrode with the performance metrics of Table 1. b Compared to an optimized, state-of-the-art dark RuO2 electrode. | |||||||
| 1 | 0.84 | 7.67 | 2.75 | 4.57 | 8.84 | — | 0.00 |
| 2 | 0.57 | 14.96 | 9.26 | 13.1 | 16.9 | 6.62 | 8.14 |
| 3 | 0.84 | 15.58 | 5.43 | 9.46 | 16.9 | — | 0.00 |
| 4 | 0.50 | 17.94 | 12.3 | 17.0 | 20.1 | 8.39 | 10.3 |
| 5 | 0.62 | 23.79 | 13.4 | 19.8 | 25.2 | 6.62 | 8.14 |
Clearly, the model I–E characteristics show disparities in the efficiency and performance figures of merit for the various model photoanodes. However, no individual component efficiency or figure of merit is an adequate descriptor of the overall performance of the optimized full system. As shown in Fig. 6, photoanode 5 has the highest ΦABPC and ratiometric power-saved (with respect to a state-of-the-art dark electrode) metric values of all of the photoanodes considered. A theoretical water-splitting system consisting of photoanode 3 operating at the maximum power point of the photoelectrode, in series with an optimal Pt counter electrode and an external bias, has a maximum system efficiency of 16.9%. However, a similar system using photoanode 2 also operates with a system conversion efficiency of 16.9%. Hence, the power-saved figures-of-merit for these two photoanodes do not indicate that the device incorporating photoanode 2 can operate with the same maximum solar-conversion efficiency as a system that instead uses photoanode 3.
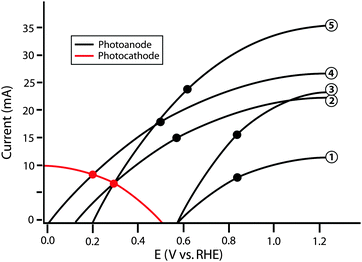 | ||
| Fig. 6 Schematic graphical circuit analysis showing five separate photoanodes (numbered on the right) and a single photocathode. The values in Table 2 are calculated based on this plot. The black points represent the maximum power point of each individual photoanode. | ||
A similar issue arises for the relationship between the actual system efficiencies of dual photoelectrode systems and trends in ΦABPC, ratiometric power-saved measurements, or even ηIRC values. For example, when used in conjunction with the example photocathode to produce a whole system, the system comprised of photoanode 5 operates with ηSTH,opt equal to that of the system comprised of photoanode 2. Moreover, using the example photocathode, neither photoanode 1 nor photoanode 3 are capable of providing the photovoltage necessary to operate in a dual-electrode full photosynthetic system with only solar power as the only source of input power. The graphical circuit analysis illustrates that although photoanode 5 yields a higher value of Imp than photoanode 4, the photoanode current is not the limiting factor in this example, because due to its higher photovoltage, photoanode 4 yields a higher ηSTH than photoanode 5 when paired with the specific photocathode used in the example of Fig. 6. This issue demonstrates the importance of current matching when combining photoanodes and photocathodes in systems designed for photoelectrolysis.
B. Limitations of using STH efficiencies relative to using system efficiencies
As demonstrated in Table 2, there are clear limitations to using ηSTH as the sole metric for the efficiency of a photovoltaic electrosynthetic or photoelectrochemical device. A motivating example is the case of two high-fill factor solar cells (e.g. GaAs) electrically connected in series driving electrolysis on a dark anode and a dark cathode (Fig. 7A). In this case, the component characteristics (i.e., the J–V characteristics of each photovoltaic) do not change, but the values of the computed figures of merit may change significantly when the system is organized in different ways. For example, consider two identical photovoltaic cells that each provide 1.0 V of open-circuit voltage, 28 mA cm−2 of short-circuit current density, a fill factor of 0.86, have optically active areas of 1 cm2, and thus each have efficiencies of 24%. The series connection of the two photovoltaics (laid out to cover twice the area of the incident optical plane and thus receive twice the illumination as an individual cell) still has an efficiency of 24%, but produces twice the voltage and the same, matched current through the whole circuit. If an electrolysis unit that is 75% efficient at the 28 mA cm−2 current density is then connected with these two series-connected PV cells, the whole system has an efficiency of 18% (0.75 × 0.24), as given by eqn (3).However, if the identical PV devices were wired individually to electrolysis units and ηSTH was calculated by treating the whole set of components as a full system, various values would be obtained for different configurations of the identical components. Specifically, if only one PV unit was wired to an electrolysis unit and the other was unused, ηSTH would be undefined, because ηSTH is limited to systems in which the production of H2 occurs spontaneously with only sunlight as the input power source, and the single PV unit does not provide sufficient voltage to perform water splitting. If the second PV was wired in series with the first and connected to the remainder of the system components, ηSTH would then be calculated to be (28 mA × 1.23 V)/(100 mW cm−2 × 2 cm) = 17.2%, provided that the electrolyzer was 75% efficient at the operating current density. If instead the electrolyzer were 60% efficient, which would require operation at a total of 1.23 V/60% = 2.05 V, ηSTH would be negligible, since the total open-circuit photovoltage of 2.0 V produced by both of the PV cells connected electrically in series would be insufficient to drive the water-splitting process at a useful rate. Note that in each case, however, if additional electrical power inputs and electrical power outputs were considered, the general expression of eqn (3) for the system efficiency and eqn (4) for the solar energy conversion efficiency would be applicable in each instance, and hence would provide for a consistent basis for comparison of the performance of these different systems.
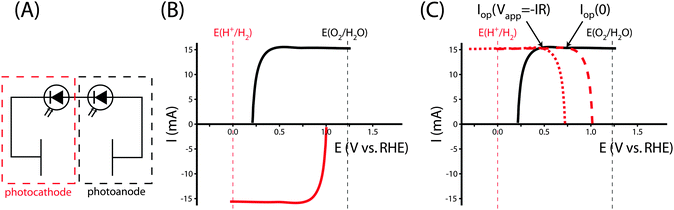
Specifically, the system can be analyzed with the graphical circuit method by dividing the system into a tandem configuration consisting of a single PV oxygen-evolving photoanode and a PV hydrogen-evolving photocathode. Separate voltammetric measurements in a three-electrode configuration can be used for each of these two components, as shown in Fig. 7A. Fig. 7B shows the J–E characteristics of each electrode in this schematic example. The potential of each electrode is defined relative to the fuel-forming reaction it performs, so the operating current for a water-splitting system built from these electrodes can be evaluated from the graphical circuit analysis. Neither electrode is capable of performing the full water-splitting reaction with only a dark counter electrode, but together both electrodes are able to drive water splitting when configured in tandem. The graphical circuit analysis shown in Fig. 7C demonstrates that an operating current can be found and the STH efficiency can be calculated from that quantity.
The tandem system provides a relatively large overvoltage for water splitting, which reduces the STH efficiency of the system compared to the solar-to-electricity efficiency that would be measured if the two PV units were connected in series across an optimized electrical load. Fig. 7C shows that the voltammograms are relatively flat in the region of the operating point, due to attaining their light-limited operating current. An electrical load can be added to the series circuit, which draws excess power without significantly affecting the operating current driving water splitting. In the graphical circuit analysis, the effect of the load drawing excess power is represented by shifting the transformed voltammogram of the photocathode to more negative potentials, effectively acting as a negative applied bias that can be utilized as electrical power. But more practically, this behavior demonstrates the necessity of load matching in solar fuels applications. A system designed from PV elements as described here would have a much higher efficiency if the architecture of the system matched the power supplied by the photocurrent-generating electrodes. A network of identical photoelectrodes, current–voltage transformers, and electrolysis units can be assembled to minimize these overvoltages, maximizing a measurement of ηSTH without any alteration to the PEC characteristics of the photoelectrodes.39 It is difficult to determine the optimal system architecture from a direct STH measurement, because the PEC performance of the electrode is convoluted with the design of the experimental system. The system architecture effects are eliminated in the calculation of ηopt from three-electrode cyclic voltammetry measurements, thereby allowing for the absolute ceiling of efficiency to be calculated for that specific photoelectrode or combination of electrodes. The value of ηopt calculated in this way is a significant metric by which to judge the technological potential of any photoelectrode for performing solar-driven, fuel-forming reactions.
C. Systems-level considerations for comparison between efficiencies of different types of photoelectrosynthetic cells
The systems described herein are generally part of larger processes, which may include energy needed to provide suitably pure input water streams, conditioning and pressurization of the output gas stream, and other processes involved with the storage, transportation and utilization of the fuel.40,41 The overall process efficiency will be affected by many variables; for instance a 12% efficient solar-driven water-splitting system that produces H2(g) at 1 atm pressure and thus requires a relatively inefficient three-stage compressor to produce pressurized H2(g) at the factory gate may be less preferred than a 10% efficient solar-driven water-splitting system that utilizes electrochemical compression and thus allows the use of a much more efficient two-stage compressor as part of the process. The key attributes of the system of interest must thus be clearly specified so that their utility in larger processes can be evaluated on a consistent basis.A second level of complexity is introduced in assessing the efficiency of a system that produces separated fuels from a system that co-evolves the gases in a mixture in the effluent stream. To be useful in a fuel cell, for example, or in a controllable combustion-based device, the gases must be separated and thus entropy is involved as well as energy inputs. Additionally, in the specific case of solar-driven water splitting (and likely in general for any fuel production), the H2 concentration in the O2 (and vice versa) must never exceed the lower explosive limits at any point in the system to be qualified as intrinsically safe and therefore to be practical, deployable, or even demonstrable at useful scale. The energy required to separate the products must therefore be included in any overall system efficiency measurement to provide a valid comparison between the system-level efficiency of a system that produces separate, pure gas streams relative to a system that co-evolves the gases. Additionally, due to impediments to practical implementation, systems that are not intrinsically safe should be so designated, and cannot directly be compared in efficiency to systems that are intrinsically safe.
A related, third level of complexity is that in the case of solar-driven water splitting, a pressure differential along a pipeline infrastructure is required to beneficially collect the H2 for use, and a further pressurization is required to supply, utilize, and distribute the H2 for conversion or other end-use. The efficiency of a mechanical compressor is a strong function of the ratio of the input and output pressures of the compressed gas, whereas electrochemical compression is inherently more efficient than mechanical compression. Hence, energy-conversion efficiencies at the systems level need to specify the output pressure of the (acceptably pure) H2 gas stream and systems will need to remain functional under pressure differentials that vary in both space and time.
VII. Conclusions
The key system-level figure of merit for power-conversion systems is the system efficiency, η, obtained from the ratio of the total output power in all forms to the total input power in all forms. Use of the system efficiency provides a consistent approach for comparing the performance of various methods for producing fuels and/or electrical power. The system efficiency reduces to the solar-to-hydrogen efficiency (ηSTH) for the special case of a system in which sunlight is the only input power and for which the only useful output power is the hydrogen obtained from solar-driven water splitting; thus, ηSTH is defined for characterizing this specific type of system.While efficiencies are the most important measure of the performance of a full system, other single-electrode and system metrics provide important characterizations of electrode performance. For example, a measured efficiency value does not provide insight into the detailed behavior of individual components within the system, and therefore pathways to improvement can be obscured. This issue is particularly relevant to photoelectrochemical systems for fuel or electricity production, where dual electrodes must be independently optimized to operate in tandem within the electrochemical device. Three-electrode electrochemical measurements should be used to probe the J–E behavior of a specific working electrode. To compare performance among individual electrodes, a variety of figures of merit have been discussed, each of which has a useful role, provided that they are clearly specified and quoted in the appropriate context.
The ideal regenerative cell efficiency (ηIRC) is defined as the efficiency of a photoelectrode component, after correcting for the mass-transport and uncompensated resistance overpotentials that arise because of the geometry of the electrochemical cell, used in conjunction with an ideally nonpolarizable counter electrode that is performing the reverse half-reaction of that performed at the photoelectrode. This figure of merit can be readily reproduced between laboratories, does not require constraints regarding cell design, and is not a function of the properties of the counter electrode used in the measurement. As the name suggests, ηIRC is designed to yield a standardized measure of the combined photo- and catalytic performance of a photoelectrode, and is thus suitable for comparing performance between electrodes for fuel- and electricity-forming systems.
The ratiometric power-saved (ϕsaved) figure of merit can also be used to decouple the fundamental properties of electrodes from systems-engineering considerations. This figure of merit provides a comparison of the behavior of a photoelectrode under illumination with the behavior of an appropriately chosen dark electrode. ϕsaved yields different information depending on the dark electrode chosen for comparison, as demonstrated in Fig. 1. If a state-of-the-art catalytic electrode for the reaction of interest is used for comparison (Table 1), ϕsaved,SOA is a measure of the combined photo- and catalytic performance of a photoelectrode. Alternatively, if a non-photoactive and oppositely and degenerately doped version of a photoelectrode is used for comparison, ϕsaved,NPA,C is a measure of the fundamental photovoltaic performance of the photoelectrode, because other losses in the cell (uncompensated solution resistance, mass transfer overpotential, catalytic overpotential, etc.) make identical contributions to each measurement and therefore cancel in the comparison. A judicious choice of the dark electrode must be made and specified for this calculation, as improper choices can result in arbitrarily high values of ϕsaved.
A third component metric, the applied bias photon-to-current figure of merit (ΦABPC), is useful for isolating the contribution of the photovoltage of an electrode to the energy stored in the chemical products produced by the system. For systems that produce fuel from sunlight and that do not require an applied bias, ΦABPC reduces to the solar-to-fuel efficiency (such as ηSTH).
Graphical circuit-analysis methods, where three-electrode voltammograms from two different (photo)electrodes are combined on one plot, and where the crossing point of the curves is the optimal operating current of the system (which is dependent on the applied bias), are required to predict system efficiencies from individual three-electrode I–E measurements. This information can be used to calculate an optimal system efficiency, ηopt, which represents the maximum possible efficiency attainable when these two electrodes are combined into a system. A method like this is useful because it is often difficult to build and test a full system, but a graphical circuit analysis allows for optimal efficiencies to be estimated based on separate three-electrode measurements of individual photoelectrodes. This method also offers the benefit of highlighting how changes within a single component electrode would affect the estimated efficiency of a full STH system, thus indicating effective utilization strategies for optimizing these components towards improving full system performance.
The various metrics described and discussed herein yield different information and all have some utility, in the proper context, for characterizing electrodes or systems for photoelectrochemical energy conversion (Table 3). It is imperative that researchers choose appropriate metrics to describe the performance of electrodes and materials for such systems, and that the measurements and methods used to calculate efficiencies and figures of merit are properly described and denoted in full. Such an approach is critical to facilitate accurate comparisons between laboratories, and to thereby accelerate progress in the field.
Glossary
| A | Geometric surface area |
| E(A/A−) | Half-cell Nernst potential for the electrochemical reaction at the electrode referenced to the reference electrode |
| E dark(I) | Potential needed to drive a reaction at current I in the dark during three-electrode measurements |
| E dark,SOA(I) | Potential needed to drive a reaction at current I on a state-of-the-art dark electrode during three-electrode measurements |
| E ext(I) | Potential at the working electrode when passing current I referenced to the reference electrode |
| E f,o | Potential difference corresponding to the Gibbs free energy difference between the two half-reactions of the fuels being produced |
| E light(I) | Potential needed to drive a reaction at current I in the light during three-electrode measurements |
| E oc | Open-circuit potential |
| ff | Photovoltaic fill factor |
| I | Current |
| I mp | Current at maximum power point |
| I(E(A/A−)) | Current at the Nernstian potential for a half-reaction (corrected for solution composition) |
| I 0 | Reverse-saturation current of an electrode |
| I op | System operating current (note that Iop can be a function of Vapp, Iop(Vapp)) |
| I ph | Photogenerated current |
| I sc | Photovoltaic short-circuit current |
| J | Current density |
| J(E(A/A−)) | Current density at the Nernstian potential for a half-reaction (corrected for solution composition) |
| J sc | Short-circuit current density |
| J fp | Current density at the formal potential of the half-reaction of interest |
| J op | System operating current density (note that Jop can be a function of Vapp, Jop(Vapp)) |
| k | Boltzmann's constant |
| n | Diode ideality factor |
| P i | Total input power |
| P e,i | Input electrical power |
| P e,o | Output power in the form of electricity |
| P f,o | Output power contained in the chemical fuel |
| P max | Maximum power output of a system or component |
| P o | Total output power |
| P s | Input power from solar illumination |
| P saved(I) | Power saved at current I |
| q | Elementary charge on an electron |
| R a | Resistance associated with the anode of a system |
| R c | Resistance associated with the cathode of a system |
| R m | Membrane ohmic resistance |
| R sol | Solution ohmic resistance |
| T | Temperature in Kelvin |
| V app | Electrical bias applied to a circuit |
| V cat(I) | Catalyst kinetic overpotential at current I |
| V cat,dark(I) | Catalyst kinetic overpotential at a dark electrode at current I |
| V cat,light(I) | Catalyst kinetic overpotential at a photoelectrode |
| V counter(I) | Overpotential at the counter electrode at current I |
| V dark(I) | External bias values needed to drive a reaction in the dark in a two-electrode system at current I |
| V e,i | External electrical voltage input |
| V ext | Voltage supplied by an external source |
| V e,o | Output voltage of the electrical power portion of the total system output |
| V light(I) | External bias values needed to drive a reaction at current I in the light in a two-electrode system |
| V mp | Voltage at maximum power point |
| V mt(I) | Mass-transport overpotential at current I |
| V mt,dark | Mass-transport overpotential at a dark electrode at current I |
| V mt,light | Mass-transport overpotential at a photoelectrode at current I |
| V oc | Photovoltaic open-circuit voltage |
| V PV(I) | Voltage across a photoelectrode at current I |
| V saved(I) | Difference between the external biases needed to drive a reaction at current I in the light and the dark on a photoactive working electrode and a related dark working electrode in a three-electrode measurement |
| V sol(I) | Total voltage drop across the solution resistance at current I |
| Z a | Impedance of the anode, related to the kinetic and mass transport overpotentials |
| Z c | Impedance of the cathode, related to the kinetic and mass transport overpotentials |
| ΔG | Gibbs free energy per electron of a heterogeneous reaction |
| ε elec | Faradaic efficiency |
| η | Efficiency |
| η electrolyzer | Electrolyzer (electricity-to-fuels) system efficiency |
| η FP,opt | Full photosynthetic system efficiency calculated from graphical circuit analysis of half-cell performances |
| η IRC | Ideal regenerative cell efficiency |
| η opt | System efficiency calculated from load-line analysis of half-cell performances |
| η PAE | Photo-assisted electrolyzer system efficiency |
| η PV | Photovoltaic (solar-to-electricity) component performance metric |
| η STF | Solar-to-fuels conversion efficiency |
| η STH | Solar-to-hydrogen conversion efficiency |
| η STH,opt | Maximum solar-to-hydrogen conversion efficiency calculated from load-line analysis of half-cell performances |
| Φ ABPC | Applied bias photon-conversion component metric |
| ϕ saved | Three-electrode ratiometric power-saved performance metric |
| ϕ saved,ideal | Three-electrode ratiometric power-saved performance metric for a photoelectrode compared to an ideally nonpolarizable working electrode |
| ϕ saved,SOA | Three-electrode ratiometric power-saved performance metric for a photoelectrode compared to the state-of-the-art (SOA) dark working electrode for the half-reaction of interest |
| ϕ saved,NPA,C | Three-electrode ratiometric power-saved performance metric for a photoelectrode compared to an identically engineered (catalyst, substrate), but non-photoactive, working electrode (NPA,C = non-photoactive, identical catalyst) |
| ϕ saved,PA | Three-electrode ratiometric power-saved performance metric for a photoelectrode compared to an identically engineered, but non-photoactive, working electrode without a catalyst |
| ϕ saved,poor | Three-electrode ratiometric power-saved performance metric for a photoelectrode compared to a non-state-of-the-art, high-overpotential working electrode |
Acknowledgements
The authors thank Dr Eric Miller for the motivation to participate in this review, and the members of the U.S. Department of Energy's Photoelectrochemical Working Group and Task 35 (Renewable Hydrogen) of the International Energy Agency's Hydrogen Implementing Agreement for providing helpful comments and suggestions. This work was supported through the Office of Science of the U.S. Department of Energy under Award No. DE-SC0004993 to the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub. This work was also supported by the Gordon and Betty Moore Foundation under Award No. GBMF1225. R.H.C. and V.D. acknowledge support from the Air Force Office of Scientific Research (AFOSR) through the Multidisciplinary University Research Initiative (MURI) under AFOSR Award Number FA9550-10-1-0572, and A.C.N. acknowledges the National Science Foundation for a Graduate Research Fellowship.References
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- T. J. Jacobsson, V. Fjällström, M. Edoff and T. Edvinsson, Energy Environ. Sci., 2014, 7, 2056–2070 CAS.
- A. Steinfeld, Sol. Energy, 2005, 78, 603–615 CrossRef CAS PubMed.
- M. A. Rosen, Energy, 2010, 35, 1068–1076 CrossRef CAS PubMed.
- Z. Wang, R. R. Roberts, G. F. Naterer and K. S. Gabriel, Int. J. Hydrogen Energy, 2012, 37, 16287–16301 CrossRef CAS PubMed.
- R. E. Blankenship, D. M. Tiede, J. Barber, G. W. Brudvig, G. Fleming, M. Ghirardi, M. R. Gunner, W. Junge, D. M. Kramer, A. Melis, T. A. Moore, C. C. Moser, D. G. Nocera, A. J. Nozik, D. R. Ort, W. W. Parson, R. C. Prince and R. T. Sayre, Science, 2011, 332, 805–809 CrossRef CAS PubMed.
- Z. Chen, T. F. Jaramillo, T. G. Deutsch, A. Kleiman-Shwarsctein, A. J. Forman, N. Gaillard, R. Garland, K. Takanabe, C. Heske, M. Sunkara, E. W. McFarland, K. Domen, E. L. Miller, J. A. Turner and H. N. Dinh, J. Mater. Res., 2010, 25, 3–16 CrossRef CAS.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 CAS.
- J. R. Bolton, S. J. Strickler and J. S. Connolly, Nature, 1985, 316, 495–500 CrossRef CAS PubMed.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 CAS.
- A. C. Nielander, M. R. Shaner, K. M. Papadantonakis, S. A. Francis and N. S. Lewis, Energy Environ. Sci., 2015, 8, 16–25 CAS.
- O. Khaselev, A. Bansal and J. A. Turner, Int. J. Hydrogen Energy, 2001, 26, 127–132 CrossRef CAS.
- Z. Chen, H. N. Dinh and E. Miller, Photoelectrochemical Water Splitting – Standards, Experimental Methods, and Protocols, Springer, 2013 Search PubMed.
- G. J. Conibeer and B. S. Richards, Int. J. Hydrogen Energy, 2007, 32, 2703–2711 CrossRef CAS PubMed.
- M. S. Wrighton, A. B. Ellis, P. T. Wolczanski, D. L. Morse, H. B. Abrahamson and D. S. Ginley, J. Am. Chem. Soc., 1976, 98, 2774–2779 CrossRef CAS.
- B. Parkinson, Acc. Chem. Res., 1984, 17, 431–437 CrossRef CAS.
- J. K. Dohrmann and N.-S. Schaaf, J. Phys. Chem., 1992, 96, 4558–4563 CrossRef CAS.
- A. J. Bard, R. Memming and B. Miller, Pure Appl. Chem., 1991, 63, 569–596 CrossRef.
- H. Dotan, N. Mathews, T. Hisatomi, M. Grätzel and A. Rothschild, J. Phys. Chem. Lett., 2014, 5, 3330–3334 CrossRef CAS PubMed.
- M. X. Tan, P. E. Laibinis, S. T. Nguyen, J. M. Kesselman, C. E. Stanton and N. S. Lewis, in Prog. Inorg. Chem., ed. K. D. Karlin, John Wiley & Sons, Inc., 1994, pp. 21–144 Search PubMed.
- A. Heller, Acc. Chem. Res., 1981, 14, 154–162 CrossRef CAS.
- A. Heller and R. G. Vadimsky, Phys. Rev. Lett., 1981, 46, 1153–1156 CrossRef CAS.
- H. Gerischer, Electrochim. Acta, 1990, 35, 1677–1699 CrossRef CAS.
- S. Hu, M. R. Shaner, J. A. Beardslee, M. Lichterman, B. S. Brunschwig and N. S. Lewis, Science, 2014, 344, 1005–1009 CrossRef CAS PubMed.
- K. Sun, F. H. Saadi, M. F. Lichterman, W. G. Hale, H.-P. Wang, X. Zhou, N. T. Plymale, S. T. Omelchenko, J.-H. He, K. M. Papadantonakis, B. S. Brunschwig and N. S. Lewis, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3612–3617 CAS.
- J. O. M. Bockris, B. Dandapani, D. Cocke and J. Ghoroghchian, Int. J. Hydrogen Energy, 1985, 10, 179–201 CrossRef CAS.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- H. Kita, S. Ye and Y. Gao, J. Electroanal. Chem., 1992, 334, 351–357 CrossRef CAS.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536 CrossRef CAS PubMed.
- G. Lodi, E. Sivieri, A. D. Battisti and S. Trasatti, J. Appl. Electrochem., 1978, 8, 135–143 CrossRef CAS.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 CAS.
- M. E. G. Lyons and S. Floquet, Phys. Chem. Chem. Phys., 2011, 13, 5314–5335 RSC.
- K. C. Neyerlin, W. Gu, J. Jorne and H. A. Gasteiger, J. Electrochem. Soc., 2007, 154, B631–B635 CrossRef CAS PubMed.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed.
- Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511–518 CrossRef CAS PubMed.
- S. Licht, Semiconductor Electrodes and Photoelectrochemistry, Wiley, 2002 Search PubMed.
- C. Levy-Clement, A. Heller, W. A. Bonner and B. A. Parkinson, J. Electrochem. Soc., 1982, 129, 1701–1705 CrossRef CAS PubMed.
- L. Fornarini, A. J. Nozik and B. A. Parkinson, J. Phys. Chem., 1984, 88, 3238–3243 CrossRef CAS.
- T. L. Gibson and N. A. Kelly, Int. J. Hydrogen Energy, 2008, 33, 5931–5940 CrossRef CAS PubMed.
- P. Zhai, S. Haussener, J. Ager, R. Sathre, K. Walczak, J. Greenblatt and T. McKone, Energy Environ. Sci., 2013, 6, 2380–2389 CAS.
- J. A. Herron, J. Kim, A. A. Upadhye, G. W. Huber and C. T. Maravelias, Energy Environ. Sci., 2014, 8, 126–157 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2015 |