Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Water desalination via capacitive deionization: what is it and what can we expect from it?
M. E.
Suss
*a,
S.
Porada
b,
X.
Sun
c,
P. M.
Biesheuvel
de,
J.
Yoon
f and
V.
Presser
*bg
aFaculty of Mechanical Engineering, Technion – Israel Institute of Technology, Haifa, 32000, Israel. E-mail: mesuss@tx.technion.ac.il
bINM – Leibniz Institute for New Materials, 66123 Saarbrücken, Germany. E-mail: volker.presser@leibniz-inm.de
cEST Water and Technologies Company Ltd, Changzhou 213034, People's Republic of China
dWetsus, European Centre of Excellence for Sustainable Water Technology, Oostergoweg 9, 8911 MA Leeuwarden, The Netherlands
eLaboratory of Physical Chemistry and Colloid Science, Wageningen University, Dreijenplein 6, 6703 HB Wageningen, The Netherlands
fSchool of Chemical and Biological Engineering, Institute of Chemical Processes, Seoul National University, Daehak-dong, Gwanak-gu, Seoul 151-742, Republic of Korea
gDepartment of Materials Science and Engineering, Saarland University, Campus D2 2, 66123 Saarbrücken, Germany
First published on 5th May 2015
Abstract
Capacitive deionization (CDI) is an emerging technology for the facile removal of charged ionic species from aqueous solutions, and is currently being widely explored for water desalination applications. The technology is based on ion electrosorption at the surface of a pair of electrically charged electrodes, commonly composed of highly porous carbon materials. The CDI community has grown exponentially over the past decade, driving tremendous advances via new cell architectures and system designs, the implementation of ion exchange membranes, and alternative concepts such as flowable carbon electrodes and hybrid systems employing a Faradaic (battery) electrode. Also, vast improvements have been made towards unraveling the complex processes inherent to interfacial electrochemistry, including the modelling of kinetic and equilibrium aspects of the desalination process. In our perspective, we critically review and evaluate the current state-of-the-art of CDI technology and provide definitions and performance metric nomenclature in an effort to unify the fast-growing CDI community. We also provide an outlook on the emerging trends in CDI and propose future research and development directions.
Broader contextCapacitive deionization (CDI) is an emerging technology for water desalination, and is based on the phenomenon of ion electrosorption. Especially for low molar concentration streams, like brackish water, CDI is a promising alternative to established technologies such as reverse osmosis. CDI research and commercialization efforts have exponentially grown over the past five years. This enhanced growth has been motivated by novel CDI architectures (such as flow-through or flow electrode design) and a deepened understanding of ion electrosorption. The performance of a CDI system depends on many parameters. A basic parameter to consider is the choice of electrode material, and different carbon materials have been explored so far (such as activated carbon, carbon nanotubes, and graphene). Yet, equally important is the system architecture and the operational mode. New developments using flow electrodes can even enable continuous operation of a CDI system. Lastly, new emerging applications of CDI beyond “just” generating potable water, are being discovered at a rapid pace. Our work is intended to support future growth by proposing standardized key CDI metrics, and critically examining current and emerging aspects of CDI theory, modeling, materials, system architectures, and operational modes. |
1 Introduction
Capacitive deionization (CDI) is an emerging technique for removing dissolved, charged species from aqueous solutions, and has been previously applied to brackish water desalination,1 sea water desalination,2 wastewater remediation,3 and water softening.4 The past decade has seen a remarkable number of innovations in the exponentially growing field of CDI, including significant theoretical,5–7 architectural,2,3,8–11 material,12–25 experimental methods,26–31 and performance advances.32–35 In this perspective paper, we briefly review key aspects of CDI, such as cell architecture, materials, applications, and theory with a focus on key recent advances. We further attempt to project future advances in the field of CDI, and facilitate these advances by framing key unsolved problems in CDI. We also provide guidelines for the fast-growing CDI field through standardization of key metrics and nomenclature. And finally, this perspective aims to serve as an accessible introduction to the field of CDI for newcomers, and thus to motivate further development of CDI technology and community. CDI shares many commonalities with other electrochemical systems such as supercapacitors and flow batteries, which we highlight in this perspective as a means of making CDI easily accessible to those (large) communities.A CDI cell consists of a pair of porous electrodes (either static or flow electrodes), with a separator (either an open channel or porous dielectric material) in-between. The electrodes are typically carbon, and the feed water flows either between or through the charging electrodes. The porous electrode pair is charged with an applied voltage difference of typically 1–1.4 V (called the cell voltage or charging voltage), and salt ions present in the feed migrate into electrical double layers (EDLs) along the pore surfaces at the carbon/water interface, removing salt from the feed water (a process known as “electrosorption”). Salt ions are electrostatically held in the double layer until the discharging step, where the external power supply is shorted or its polarity reversed. During discharge, the release of ions results in a brine stream, and the charge leaving the cell can be leveraged to recover energy (analogously to the energy from a discharging electric capacitor).36 The first work on a CDI-type system was published by Blair and Murphy in 1960,37,38 and the subsequent four decades saw only intermittent advances to this technology. Examples of advances during that time period include the development of the first macroscopic theory applied to CDI in 1971,39 and the use of carbon aerogels as a CDI electrode material in the mid-1990's.19 Incidentally, the term “CDI” was not used until 1996 when introduced by Farmer et al.40,41 By contrast to the slow initial development of CDI, the past decade has seen tremendous advances, including the development of membrane CDI,3,42 flow-through electrodes,8 flow electrodes,2,43–45 hybrid CDI,11 the modified Donnan mathematical model for CDI,6 and the discovery of key correlations between pore size and electrosorption performance.46 These scientific advances are accompanied by the growing commercial development of products utilizing CDI technology by various companies around the globe.
As a salt ion removal technology, CDI provides several unique advantages. Firstly, CDI enables salt removal at low (sub-osmotic) pressures and room temperatures, with the primary input being a small cell voltage (∼1 V) and an electric current whose magnitude depends on the system size. Thus, unlike reverse osmosis or distillation-based desalination systems, CDI does not need to be coupled to high pressure pumps or heat sources, allowing for facile system scaling. Secondly, in CDI the few salt ions (relative to the plentiful water molecules) are directly transported out of the feed water, similar to the case of electrodialysis. This allows for potentially highly energy efficient desalination of low salinity feed waters, such as brackish water.47 Thirdly, the operating principle of CDI shares many features with electrochemical capacitors, also known as supercapacitors,48 including reversible operation and energy storage capability (CDI can be crudely thought of as “desalination with a supercapacitor”). Thus, CDI systems have the unique ability to simultaneously store energy (similarly to a supercapacitor) and desalinate water upon being charged. Even if this energy storage capacity is not utilized, the once invested charge for ion removal is almost fully recovered during discharging of the electrode material, capitalizing upon the very high Coulombic efficiency inherent to EDL technologies. As such, CDI can potentially be an important part of future water purification solutions as well as potentially contributing to next generation distributed electrical grids.
2 CDI cell architectures
2.1 Types of CDI cell architectures
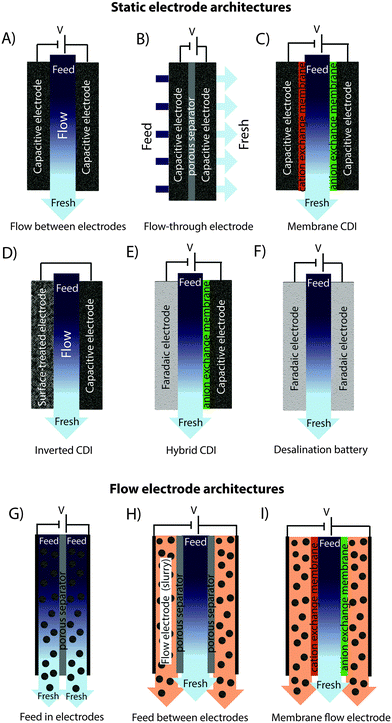
In recent years, there has been a proliferation of novel architectures for CDI cells, and these have introduced several unique features and novel functionalities to this field. In this section, we will briefly review the architectures which have been previously developed (Fig. 1). The first and historically most widely-utilized CDI cell architecture consists of a pair of porous carbon electrodes separated by a space in which the feed water flows (feed water flows perpendicular to the applied electric field direction, see Fig. 1A). This architecture is often called flow-by architecture,49,50 and has also been called CDI with flow-between electrodes.8 The flow-by cell was first seen in the pioneering work of Blair and Murphy in 1960,37 was re-visited in the 1970's and 1980's by Oren and Soffer,10,51 and again in the 1990's in the works of and Farmer et al.19,52 This architecture was subsequently utilized in a wide variety of works, including those demonstrating salt removal from various feed waters,53 investigating the performance of novel electrode materials,12,54 or performing fundamental studies of salt sorption on porous electrodes.29,55Early work on CDI-type systems in the 1970's by Johnson et al.56 developed a cell in which the feed flow was directed straight through the electrodes themselves and parallel to the applied electric field direction (Fig. 1B). Work on such flow-through CDI,29 or flow-through electrode8 cell architectures was seemingly abandoned for almost 40 years until Avraham et al.29,31,57 utilized flow-through electrodes in a three-electrode cell in order to study fundamental performance parameters, such as charge efficiency. The authors of the latter work noted that flow-through electrodes allowed for faster cell charging relative to flow-between systems.29 In 2012, Suss et al. studied the performance of a CDI cell with flow-through electrode architecture and novel hierarchical carbon aerogel monolith (HCAM) electrodes, and demonstrated a concentration reduction of up to 70 mM of a NaCl feed when operated in a stopped-flow mode (no flow during cell charging), with a mean sorption rate of nearly 1 mg g−1 min−1.8 The primary benefit of this architecture is to eliminate the need for a separator layer which also serves as the feed flow channel, thus allowing a minimization of separator thickness (from typically 200–500 μm to around 10 μm).8 This reduced spacer thickness can allow for more compact cells with lower cell ionic resistance, and potentially faster desalination by reducing the diffusion timescale governing salt removal from between the electrodes.27 This architecture requires the use of multi-scale porous electrodes, with both micrometer-scale pores to enable flow through the electrodes at moderate fluidic pressures, and micropores (nanoscale pores) to enable high salt sorption.8,29
A major variation of the basic CDI cell architecture (a cell with two porous electrodes and a separator) occurred with the development of membrane CDI (MCDI), with the first scientific demonstration of an MCDI system in 2006 by Lee et al.3 This architecture utilizes ion exchange membranes on the separator-side of each electrode (Fig. 1C). As in electrodialysis cells, the feed water channels in MCDI cells are bounded by an anion exchange membrane (AEM) and a cation exchange membrane (CEM). In MCDI, the most-often used configuration is a free-standing CEM placed at the cathode,50 and a free-standing AEM placed at the anode. Alternatively, using the porous electrode as structural scaffold, it is possible to directly coat the membrane onto the electrode, which can allow for a thinner membrane layer than when using a standalone membrane.58 The main benefit of adding membranes to the CDI cell is the improvement of charge efficiency (which is linked to cell energy efficiency, see Section 3.1), as the membranes block co-ions (ions with the same charge as the local electrode) from carrying parasitic current, and can increase the salt storage in electrode macropores.6 In addition, membranes may be tailored to have selectivity between different ions of the same charge sign which provides an additional level of tunability for complex multi-ion systems.59,60 The field of MCDI has seen intensive development in recent years, both in advancement of theoretical understanding,6,33 membrane materials, fabrication methods, and commercial applications.58,61 Also, the benefit of charging a CDI cell with constant current rather than constant voltage, namely that constant current allows for constant cell effluent concentration, was first demonstrated on an MCDI cell.26 The latter cell achieved a reduction in concentration of nearly 20 mM and an average salt adsorption rate (ASAR) of up to 2.3 mg g−1 min−1 with optimized operational parameters.33
Recently, the flow-by CDI cell was modified through the use of a surface-treated carbon anode, leading to the case of inverted-CDI (i-CDI, Fig. 1D).62 The latter cell utilized a carbon xerogel anode imbued with a negative surface charge via a chemical surface treatment, and pristine carbon xerogel as the cathode. The cell demonstrated inverted behavior, whereby cell charging resulted in desorption of ions from the electrode EDLs, and cell discharging resulted in ion electrosorption. The i-CDI cell sorption performance was maintained for 600 hours of continuous operation at a cell voltage of 0.8 V, in contrast to the relatively fast decay observed for a CDI cell with solely pristine carbon xerogels.62
In 2013, a new architectural class for CDI was demonstrated which leveraged carbon flow electrodes, or carbon slurry electrodes which can be pumped through electrode compartments (Fig. 1G–I).2 This concept of flow electrode CDI, or FCDI, follows that of slurry-based electrodes developed for electrochemical energy storage systems such as the electrochemical flow capacitor,63 and semi-solid lithium ion batteries.64,65 FCDI enables two major benefits relative to non-flowable or static electrode CDI systems. First, in FCDI, the feed water flowing through a single cell can be continuously desalinated, as the discharge of the active carbon particles (formation of brine) can occur as a separate process downstream of the cell.2 In all previous CDI architectures based on static electrodes, the cell can only desalinate for a finite time until the EDLs of the porous electrodes have been fully charged, and then desalination must cease while the cell is discharged to enable subsequent desalination cycles.50 This intermittent operation can also require complicated fluidic handling as desalinated streams (during charging) and brine streams (during discharging) emerge, at different times, from the same spacer between the electrodes. A second major benefit is that FCDI, by continuously introducing uncharged carbon particles into the charging cell, can effectively increase the capacitance available for desalination above that of static electrode CDI systems. Thus, FCDI can desalinate higher salinity streams than static CDI systems, and desalination of high salinity feeds (with a total dissolved salt concentration approximately that of sea water) was achieved with FCDI by Jeon et al. when using a total slurry flow rate of 50 mL min−1 and feed flow rate of 3 mL min−1 (Fig. 1I and 2A).2 In 2014, an FCDI architecture was proposed which desalinates without ion exchange membranes or a feed stream between electrodes (Fig. 1G).45 The latter architecture can potentially enable compact and low resistance systems (analogously to the benefits of flow-through CDI vs. flow-between CDI).45
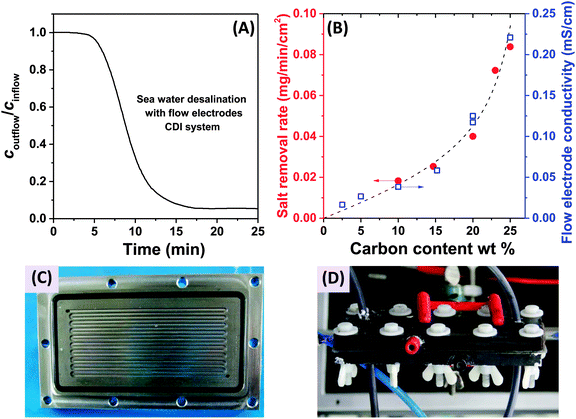 | ||
| Fig. 2 (A) Evidence of desalination of high salinity feedwater using a flow electrode CDI system (cin = 32 g L−1 of NaCl, roughly equivalent to the total dissolved salt concentration in sea water), from ref. 2. (B) Influence of carbon content of the flow electrodes on salt removal rate (red dots) and flow electrode conductivity (blue squares) in FCDI systems, from ref. 44. (C) and (D) Experimental setups employed for desalination using flow electrodes and membranes, where (C) shows a carved flow field in which the slurry flows,2 and in (D) a rectangular cut-out creating an empty space between current collector and ion-exchange membranes for slurry flow.44 | ||
Related to FCDI, Porada et al. introduced in 2012 another form of “electrodes in motion” through use of moving wires to perform desalination.9 In this system, the wires consist of a graphite rod coated with porous activated carbon and with an optional outer coating of an ion exchange membrane. Mechanical motion of the wires occurs between a feed and brine stream, where the wire is charged in the feed stream and discharged in the brine stream. Operating this system with multiple wires cycling between feed and brine streams (so called “merry-go-round” operational mode) may allow for continuous desalination of the feed stream.
Very recently, another advance has been made which combines a battery electrode (sodium manganese oxide) and a capacitive electrode (porous carbon) in a single desalination cell,11 (Fig. 1E) inspired by the previously developed desalination battery (Fig. 1G).66 Such a “hybrid CDI” system enabled high salt sorption of ∼31 mg g−1,11 as compared to purely capacitive CDI cells which achieve up to about 15 mg g−1 (see Section 4).67
2.2 Perspectives on CDI cell architectures
The fast proliferation of architectures available for CDI begs the question of which are the most promising. In our opinion, there is no clear answer as each of the architectures shown in Fig. 1 has unique advantages, and none should be neglected in future research work. Even the most traditional CDI architecture (Fig. 1A), dating back to 1960, has advantages over more recent designs due to its simplicity (no membranes or flow electrodes), which can potentially translate to lower system cost and reduced fouling potential. However, it is clear that the recent emergence of FCDI architectures (Fig. 1G–I) holds great promise, and is an important future research direction. While static electrode architectures (Fig. 1A–F) have been well-characterized and their performance limits are largely known, FCDI is still in its infancy and thus there is the potential for vast improvements in performance. For example, the conductivity of the flow electrodes can be orders of magnitude smaller than that of typical static electrodes, and recent experimental studies may point out design paths to improve their conductivity (see Fig. 2B).44 Also, many basic questions of flow electrode systems remain unanswered, including optimized flow cell design, and the kinetics and energy costs associated with regenerating the carbon particles (a key step in the complete system performance), along with practical consideration such as pumping energy requirements and effects of clogging on long term performance. In addition, FCDI is still far from being economically feasible for sea water desalination. For example, based on the system of Jeon et al., we calculate that it would require a total ion exchange membrane surface area as high as 250 m2 and total carbon suspension flow rate of 16 m3 h−1 in order to produce 1 m3 h−1 of water with final salt concentration of around 25 mM NaCl.2 Thus, significant work remains in understanding flow electrode systems, as well as demonstrating practical, round-trip performance for the slurry solutions.For architectures with static electrodes and no membranes, there is a choice between flowing through the electrodes (Fig. 1B) or between the electrodes (Fig. 1A). Flowing through the electrodes can enable more compact systems (and so potentially faster desalination with lower resistance cells), although at the cost of higher pressure requirements when compared to an open flow channel between electrodes.19 While over two hundred publications exist investigating the performance of flow-by CDI systems, far fewer exist which focus on flow-through electrode systems. Thus, more work is needed to compare these two architecture choices directly, and better understand the trade-offs between the two. Finally, adding ion exchange membranes to CDI systems (Fig. 1C) has the well-established advantage of improving the system's charge efficiency and sorption capacity,50 although at the cost of significantly more expensive cell components.
In addition to research focusing on improvements of existing CDI architectures, we expect as-of-yet unexplored architectures to continue to emerge. A potential example of this is the feed-between flow electrodes architecture of Fig. 1H, a mix of the architectures of Fig. 1G and I, but which to our knowledge has not been demonstrated. Other novelties left to explore include methods of effectively regenerating (discharging) the carbon particles used in FDCI. An alternative technique is to use the slurry exiting the anode to be then fed into the cathode compartment. In this “single slurry” architecture, the carbon particles that charge up (positively) in the anode, will be discharged/negatively charged in the cathode. A single recirculating slurry acting as both anode and cathode was described for electrodialysis in a patent by Kedem in 1980,68 but there it was not proposed as a desalination electrode (rather as a steady current sourcing electrode where desalination occurred elsewhere in the system).
It is also important to note that the development of CDI cells can occur in parallel with the intensive development of many other related electrochemical technologies. Thus, future advances in architectures of electrochemical systems such as batteries, flow batteries, supercapacitors, electrodialysis cells, and other such systems can often be translated to advances in CDI architectures, as has already occurred in the case of flow electrodes and hybrid CDI systems.
3 Standardization of CDI performance metrics
The field of CDI has progressed enormously in the past decade, and now requires standardization of key performance metrics to support future progress. In this section, we briefly review the historical development of metrics describing CDI cell performance, and we then propose such standardization, clearly explaining our rationale. This has been motivated by the emergence of a plethora of different terminology and difficult-to-compare CDI performance data over the past decade.Many CDI papers, starting from the inception of CDI in 1960,37,38 report exclusively the salt concentration reduction of the feed stream during constant voltage testing.19,39,52 The latter is a natural metric for a desalination technology; however, it has become evident that this metric alone is not an insightful indicator of electrode or cell performance. Many operational parameters can affect the salt concentration reduction, and it is possible for small reductions to be attained for systems which should be high performing (for example, if feed velocity is too high). Thus, the question remains, which metrics are insightful indicators of CDI performance. Another key question is if one should distinguish between cell and electrode performance – and if so, how that feat should be accomplished.
3.1 Maximum salt adsorption capacity
A growing trend in CDI is to report on the salt adsorption capacity (SAC) of a cell's charge–discharge cycle, a concept first introduced by Soffer and Folman.69 The charge–discharge cycle can have any duration, from very short, with little adsorption, to very long, when equilibrium is reached. For the latter, one measures the maximum salt adsorption capacity (mSAC), which is also known as equilibrium salt adsorption capacity (eqSAC). To reach equilibrium in a CDI salt adsorption experiment, a fixed cell voltage must be applied and maintained until the cell charging is complete (no gradients in charge remain in the electrode), and salt concentration is constant throughout the cell. At equilibrium, the measured conductivity of the cell effluent no longer changes over time. The salt removed from the feed water is calculated either by a time integral of the difference between the cell inflow and effluent concentration multiplied by the flowrate through the cell, from the start of the charge until equilibrium is reached (single pass method), or by multiplying the total solution volume in the system with the salt concentration decrease in the system (batch mode method).50Reporting of SAC and mSAC is mainly done by dividing the mass of salt removed from the feed water by a representative electrode mass, yielding a unit of mg g−1 (gravimetric SAC).46 An appropriate representative electrode mass is the combined mass of both the electrodes when dry.70 Typically, the mass of all solid components in the electrode is used in this calculation (including binder and other additives), not just the mass of the active ingredient (e.g., porous carbon),46 as is common in the field of supercapacitors.71 At the least, authors are strongly advised to state clearly whether SAC-numbers are based on the total electrode mass (including active carbon and binder), or based on the mass of the active electrode component. This is of high importance as the mass contribution of non-active components typically range between 5–15% of the total electrode mass. While it is most common to report a gravimetric mSAC, it is also possible to report a volumetric mSAC, which can give additional insight into the performance of an electrode material. For example, two CDI electrode materials, TiC-CDC and HIPE-CDC have similar values for gravimetric mSAC of 10.1 and 11.1 mg g−1, respectively, but because the electrode density is 0.54 vs. 0.11 cm3 g−1, the volumetric mSAC in mg cm−3 is very different: 5.5 mg cm−3 and 1.2 mg cm−3, respectively.46 Thus, to get the same salt adsorption, we would need roughly five times the electrode volume if using HIPE-CDC instead of TiC-CDC.
Importantly, for given operational parameters, mSAC is a property of only the electrodes, and should not be affected by any other cell component. Thus, it is a highly useful and insightful metric into CDI electrode sorption performance, and we recommend that it continue to be widely adopted as a standard metric in CDI cell characterization. Section 4 on carbon materials below describes the state-of-the-art and future trends in attained mSAC of CDI electrodes. Further, SAC (when the cell is not taken to equilibrium before measuring salt removed), may be used to characterize cell sorption up to a fixed, pre-equilibrium, charging time. It is important to note that SAC depends on many cell components, and is not purely a measurement characterizing the electrode material.
For a given electrode material, the measured value of mSAC depends on the cell voltage, where both the cell voltage during the charging step and the cell voltage in the preceding discharging step are of relevance. The discharge voltage is most often zero, that is, Vdisch = 0 V, but one can also perform such an experiment with a discharge voltage higher than zero,30 or even lower. The latter is more typically done in MCDI, and is also called reverse-MCDI.6 Another important point is that mSAC depends on the salt concentration in the cell both at the beginning and at the end of the charging step.
A commonly used value for the charging voltage is about Vch = 1.2 V (which allows for high salt adsorption while minimizing side reactions such as water electrolysis), while the optimum concentration range for salt adsorption is typically a salt concentration between 5–50 mM (0.5–5 mS cm−1), see Fig. 12.7 In batch-mode experiments performed with low initial salt concentration (<5 mM NaCl concentration) the final salt concentration can approach zero. In such an experiment the measured value of mSAC will likely be lower than what the electrode is capable of achieving when charging in the optimum concentration range.73 Therefore, when using a batch-mode experiment, it is favorable to start with high initial salinity such that the final salinity (after applying the voltage) is not below 5 mM. In this way, the measured value of mSAC is ensured to be representative of the electrode's maximum performance.
Another, widely used operational mode, called constant current operation (CC-mode), cannot be used for measuring mSAC, because during a CC-mode experiment equilibrium is never reached, with the requirements of equilibrium described above (such as absence of salt concentration gradients across the electrode). However, in CC-mode operation the non-equilibrium salt adsorption capacity (SAC) can still be determined.
In all cases, reporting must be avoided of values for mSAC based on the first adsorption cycle after a fresh material is dipped into the feed water and the voltage applied. Uncharged carbons can also adsorb salt,7 and this sorption may not be completely desorbed during discharge. Also other effects may occur in the first few cycles which result in unreliable mSAC measurements, for instance because full wetting of all pores in the electrode may only be reached after a few charge–discharge cycles. Thus, it is important to present only results of a later cycle in a series, when the measured mSAC is stable from cycle to cycle (or in other words, when the limit cycle is reached).
Besides operational conditions discussed above, also the type of porous carbon material has an impact on measured mSAC. In 2013, results were presented showing a strong correlation between the pore size distribution of porous carbons and their measured mSAC, where it was argued that micropores below 1.1 nm (and even more so those smaller than 0.7 nm) contributed most strongly to mSAC, with a more moderate contribution of pores beyond 2 nm.46 As such, rather than the specific surface area of the electrode, mSAC is determined by the size and specific volume of the electrode's micropores. These findings, along with those of an earlier study,12 went against the conventional thinking on the effect of pore size, which was that mesopores (>2 nm) were most useful for CDI.74,75 For example, in one instance it was stated in literature that only pores >20 nm size performed in an optimum way for CDI.76 The importance of micropores is in alignment with conventional wisdom in the field of EDL-capacitors (supercapacitors), where micropores allow for a significant increase in electrode capacitance (charge storage) over mesopores.77,78
3.2 Average salt adsorption rate
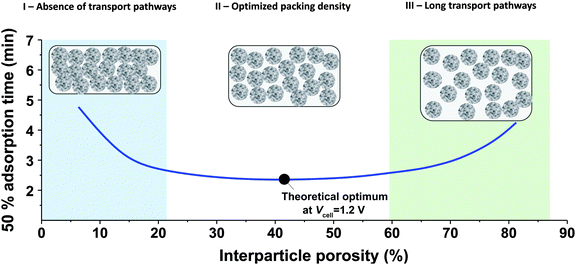
While the mSAC gives a sense of how much salt sorption is possible by the CDI electrodes, it gives no information on the rate of salt sorption. Thus, a second important metric to describe CDI or MCDI cell performance is the average salt adsorption rate (ASAR), described in detail in ref. 33. This metric has also been used by Xu et al.,53 and Suss et al.,8 among others, and has been reported in units of mg g−1 min−1, with “mg” referring to the mass of salt removed, “g” referring to the mass of the two electrodes together (as described in Section 3.1). The “min” referring to the charging time,8,53 or the total cycle time (which equals the duration of the charging and discharging steps combined).33 We recommend to standardize this metric by using the total cycle time, thus giving the most realistic portrayal of desalination rates via static electrode CDI (inherently a two-stage process). Note the charging time in the cycle could be the time to equilibrium, or could be a shorter time.Several operational parameters can affect the measured ASAR. For example, the choice of charging time can have a large effect on ASAR, especially in constant voltage operation.8,33 Shorter charging times (shorter than the time to reach equilibrium) at constant voltage generally allow for higher ASAR.33 Further, operating the cell at higher feed salinities will generally lead to faster charging (see Section 3.2) and so higher ASAR. ASAR is also dependent on cell architecture, for example, for two systems employing identical electrode materials and electrode thicknesses, higher ASAR may be attained when using flow-through rather than flow-by electrode architecture, as the flow-through system allows for minimizing the gap width between electrodes (lowering cell resistance and thus cell charging time).8 In addition, the electrode material itself can affect measured ASAR in several ways. For example, electrodes with sub-nanometer micropores allow for highest salt sorption,12,46 but they may also suffer from kinetic limitations associated with the small pore size, which can potentially limit the ion adsorption dynamics and thus limit ASAR (see Section 6.5 for a mathematical description of CDI where rate limitations exist between the nanoscale micropores and larger pathways for ion transport through the electrode bulk).79,80 Electrode thickness can also contribute to ASAR, with thinner electrodes generally exhibiting higher desalination rate capability.81 Finally, the effect of cell compression, electrode thickness, and electrode macroporosity are often coupled together and can affect ASAR in more complicated ways. Porada et al.46 calculated that the time to reach 50% of maximum salt adsorption was at a minimum value for intermediate values of the electrode macroporosity (see Fig. 3 and also ref. 46). Thus, further compressing the electrode from the optimized value can lead to a thinner electrode with less macroporosity and lower ASAR. To maximize ASAR, there exists an optimum degree of compression during electrode preparation.
Thus, ASAR is often a combination of many factors, such as cell architecture, charging time, electrode material, and electrode thickness, and thus should be considered a cell (system) property rather than an electrode (material) property. mSAC, by contrast, can be considered an actual electrode property. Still, we strongly recommend ASAR be widely adopted in the field as describing the rate capability of a given cell. However, it must be noted that comparing values of ASAR between different systems can be problematic without rigorously holding to the same charging times and electrode thicknesses. Thus, when reporting ASAR, all the relevant experimental conditions must be reported. The highest value of ASAR to our knowledge is 2.3 mg g−1 min−1 as reported by Zhao et al., who used sub-equilibrium charging times, roughly 300 μm thick electrodes, and a membrane CDI cell architecture.33
The above analysis applies to CDI with two static electrodes, where this cell necessarily operates in a non-continuous manner (with a discharge step following a charging step). For flow-electrode CDI, with continuous operation, it is recommended to present the steady-state value of salt removal rate in μg cm−2 s−1 rather than an ASAR value. Values presented in ref. 2 are ∼3.2 μg cm−2 s−1, and in ref. 44 are ∼0.35 μg cm−2 s−1. Here the “cm2” refers to the projected area of the cell.
3.3 Kim–Yoon diagram for salt adsorption rate vs. capacity
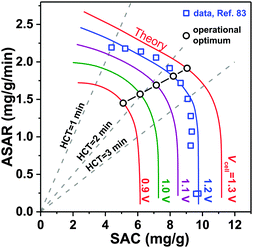
A novel representation of operational performance of static electrode CDI cells was recently proposed by Kim and Yoon in ref. 28 where salt removal rate was plotted against salt removal capacity. This plot was inspired by Ragone charts (named after Prof. David V. Ragone) commonly used to represent energy storage devices with respect to power (energy delivery rate) vs. energy stored.82 This “ASAR vs. SAC” chart, or as we propose the “Kim–Yoon” (KY) diagram, combines the two key metrics described previously in this section in a single plot. Further, this new representation allows for facile determination of optimal cell operational conditions, namely when both SAC and ASAR are close to their maximum attainable values. In Fig. 4 we show such a KY-diagram where we plot data and theory calculations of ASAR vs. SAC in CDI-cycles where we varied the half-cycle time (HCT; the charging and discharging steps are of the same duration). In all data and calculations the discharge voltage is 0 V, the charging voltage is set to values ranging from 0.9 to 1.3 V, and data were taken from ref. 83, which used film electrodes based on Kuraray YP50F activated carbon powder. Calculations are based on the model presented in ref. 83, which combines the i-mD model for the EDL structure with porous electrode ion transport theory.As Fig. 4 shows, it is possible to establish operation conditions with high ASAR while ensuring the adsorption capacity per cycle is close to the maximum achievable. This is a key operating point for CDI, especially for applications requiring significant salt removal. Higher values of ASAR can be achieved, but this requires sacrificing salt sorption per cycle. We propose defining the optimum HCT for a given charging voltage as that point along an ASAR-SAC curve for which the “response product”,84,85 which is ASAR multiplied by SAC, is maximized. Points satisfying this criterion for HCTmax-RP are shown with open circles in Fig. 4. We can observe that with increasing charging voltage, HCTmax-RP increases, i.e., longer cycles are more favorable. This is just one example of how the KY-diagram can be used in optimization studies for CDI.
3.4 Charge storage capacity
Besides measuring mSAC and salt removal rate, a third metric for CDI cells is the charge storage capacity, a metric shared with the supercapacitor community. This metric can be obtained from measured data for current vs. time during charging and discharging. Data for current in units of Ampères (A = C s−1) can be integrated with respect to time to obtain the electric charge transferred between electrodes of the cell (units of Coulombs, C). Further, by subtracting the leakage (non-capacitive) current, which is generally higher in magnitude during charging when compared to discharging, the calculated capacitive charge and the applied cell voltage can be converted to cell or electrode capacity in F g−1.71 For obtaining the capacitance of a single electrode, the capacitive charge in C must be divided by the mass of a single electrode and by half of the cell voltage (assuming cell symmetry), leading to a conversion factor of 4.70,71,86,87 This single electrode capacitance is often called “specific capacitance” in the supercapacitor field.48,70 Equivalently, we also find a “volumetric capacitance” in the supercapacitor community for single electrodes, which is four times larger than the cell volumetric capacitance (the cell capacitance divided by the volume of both electrodes). While many similarities exist between the fields of supercapacitors and CDI, the focus and key performance parameters are different. Especially important is not to directly deduce from a seemingly high specific capacitance automatically a high SAC value. In the following Section 3.5, we will describe how for CDI, capacitance and desalination (salt removal) are not equivalent, but are linked by a separate parameter known as charge efficiency. Thus, while charge storage is a key performance metric for supercapacitors (energy storage), we here focus on metrics which are most appropriate to capacitive desalination applications.3.5 Charge efficiency and current efficiency
The electric charge that accumulates in an electrode pair during charging (and is released during discharge) can simply be divided by Faraday's number, F = 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1, to arrive at charge expressed in units of moles, and this value can be compared to the measured salt adsorption per cycle (also expressed in moles). This leads to the definition of charge efficiency, Λ, as the ratio of adsorbed salt over charge. The concept and importance of the ratio between salt removed and invested electric charge stored was first described by Johnson and Newman in 1971,39 and the terminology “charge efficiency” was first used by Avraham in 2009.29,30 Zhao et al.86 proposed the symbol Λ for charge efficiency, and provided the first extensive data set for Λ as function of cell voltage and feed salinity. The metric Λ is used in the analysis of static electrode CDI cycles as an integral property of the entire cycle, and Λ must be less than unity (yet may approach unity). Λ is a function of the cell voltage during charging and discharging, as well as the feed water salt concentration. Generally, Λ increases with higher charging and discharging voltages, and with decreasing feed concentration.83,86
485 C mol−1, to arrive at charge expressed in units of moles, and this value can be compared to the measured salt adsorption per cycle (also expressed in moles). This leads to the definition of charge efficiency, Λ, as the ratio of adsorbed salt over charge. The concept and importance of the ratio between salt removed and invested electric charge stored was first described by Johnson and Newman in 1971,39 and the terminology “charge efficiency” was first used by Avraham in 2009.29,30 Zhao et al.86 proposed the symbol Λ for charge efficiency, and provided the first extensive data set for Λ as function of cell voltage and feed salinity. The metric Λ is used in the analysis of static electrode CDI cycles as an integral property of the entire cycle, and Λ must be less than unity (yet may approach unity). Λ is a function of the cell voltage during charging and discharging, as well as the feed water salt concentration. Generally, Λ increases with higher charging and discharging voltages, and with decreasing feed concentration.83,86
Λ is a crucially important parameter when evaluating CDI cells because of two important implications. First, the electrical energy requirements of a CDI cell are determined by the value of Λ, and generally higher values of Λ leads to lower energy consumption. Experimental results for CDI and MCDI reported in ref. 26 for constant–voltage operation and constant–current operation have been analyzed for the energy consumption per ion removed (“kT/ion”) and for charge efficiency. These two metrics are plotted against one another in Fig. 5. The plotted line is a simple inverse proportionality which captures both the magnitude and functional dependence of the data, according to: energy (kT/ion) = α/Λ, with α = 1/2·Vch/VT, and VT is the thermal voltage. This relation holds for all constant–voltage experiments that are at the same cell voltage during charging and discharging. As Fig. 5 shows, all data, also constant–current data, match closely with this dependency. Fig. 5 demonstrates that charge efficiency determines energy consumption (for a certain charging voltage), that higher values for charge efficiency lead to lower energy consumption, and thus that MCDI (higher charge efficiency) generally requires lower electrical energy inputs compared to CDI (lower charge efficiency). Second, in an equilibrium cycle, where both salt adsorption and charge stored reach equilibrium values, equilibrium EDL theory can be used to predict Λ, or vice versa, data for Λ can be used to validate an EDL model. As argued in Zhao et al.,86Λ is well-suited for such fundamental studies of the EDL as it is independent of the volume (area) of pores in which EDLs are formed, and thus independent of electrode mass.
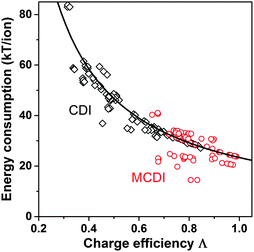 | ||
| Fig. 5 Data for energy consumption per ion removed, vs. charge efficiency, based on data reported in Zhao et al.26 for CDI and MCDI, for salt inflow concentrations from 5–200 mM. Energy recovery is not included. Divide energy in kT/ion by 200 to convert to MJ mol−1 salt. | ||
Related to charge efficiency, Λ, is the ratio of salt adsorption rate (in mol s−1) over current (in A s−1) divided by Faraday's constant, which is called the current efficiency, λ (Fig. 6B).44 Current efficiency λ relates two fluxes and can be used in place of Λ in a steady-state CDI processes such as constant current MCDI (CC MCDI) or FCDI (i.e., where all process parameters, such as current and effluent salt concentration, do not vary in time). This metric originates from the field of electrodialysis but can be used to characterize any FCDI cell, including those without ion-exchange membranes.45 The current efficiency is calculated from the effluent and inflow salinity, cout and cin, the water flow rate Φ and the applied current, I, according to λ = (cin − cout)Φ/(I/F), assuming the use of a monovalent 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt. For FCDI-experiments at the same level of the cell voltage, the energy used (“kT/ion”) scales as the inverse of the current efficiency.
1 salt. For FCDI-experiments at the same level of the cell voltage, the energy used (“kT/ion”) scales as the inverse of the current efficiency.
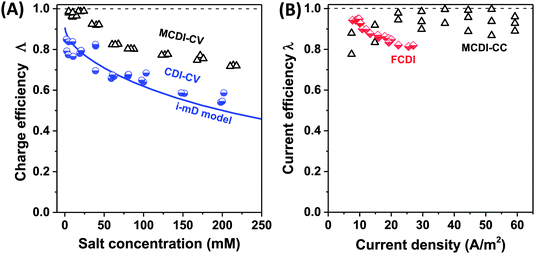 | ||
| Fig. 6 Selected data for charge efficiency Λ and current efficiency λ as function the salt concentration (A) and current density (B). Data for charge efficiency (A) are obtained for solid film electrodes at Vch = 1.2 V in a cycle where Vdisch = 0 V. Solid line denotes calculation results based on the improved mD model, see ref. 7. The data for current efficiency (B) is obtained for constant–current MCDI (open triangles; ref. 26), and for FCDI (half-filled diamonds; ref. 44). | ||
Fig. 6A presents as function of feed NaCl concentration, data for charge efficiency in constant–voltage CDI and MCDI (half-filled circles, commercial activated carbon electrodes Fig. 4 in ref. 7, open triangles, data from Fig. 5 in ref. 26). Fig. 6B shows measured current efficiency for the steady state processes of CC-MCDI from ref. 26 and FCDI from ref. 44. For all data in panel A, the charging voltage is Vch = 1.2 V, while discharge is at 0 V. As Fig. 6A shows, both for CDI and MCDI the charge efficiency decreases with feed salt concentration, and the application of ion-exchange membranes in CDI does not necessarily result in values of charge efficiency approaching unity. Though, as seen in Fig. 6A, Λ of approximately unity is achieved in MCDI for external salinities up to about 25 mM, beyond that value Λ starts to drop. The physical mechanism for this drop is likely an increase in co-ion leakage through the membrane (a reduced membrane selectivity) due to lower Donnan potential at the membranes' outer interfaces.88 Still, Fig. 6A shows that in MCDI the charge efficiency is consistently about 20% higher than in CDI (in absolute value) for all salinities up to 250 mM at these experimental conditions. In Fig. 6B we present data for current efficiency for flow-electrode CDI (FCDI) with both a cation- and anion-exchange membrane (half-filled diamonds, data from ref. 44) as a function of the applied current and for three salinities. Interestingly, data for different csalt of 25, 50, and 150 mM largely overlap. The decrease in λ with increasing applied current, observed for the FCDI-data in Fig. 6B, is as of yet unexplained. Also, Fig. 6B presents data for MCDI with static film electrodes based on cout of the effluent at steady state seen in constant-current operation (see Fig. 4 in ref. 26). This latter data was obtained with a feed salt concentration of 20 mM, and show values for λ that are invariant with current.
3.6 Perspectives on standardization of CDI metrics
The continuing rapid growth of the CDI community necessitates a standardization of key metrics. We strongly suggest that the CDI community uses the terms proposed here (see Table 1), which is in alignment with prior literature in the field of CDI and (for steady-state desalination) in the field of electrodialysis. Other efficiency-terms, such as salt removal efficiency and Coulombic efficiency, can be used as indicators for other aspects of CDI performance. Salt removal efficiency is mainly used in batch-mode CDI testing describing the relative decrease in salt concentration in the recycled feed when equilibrium has been reached and salt concentration no longer changes in time.50 This metric is highly dependent on many operational parameters including the volume of water in the system and, therefore, this efficiency can only be used for a direct comparison of electrode materials in the same test cell. Coulombic efficiency can be used for the ratio of output charge during discharging a cell, over the input charge. A value clearly below unity may indicate Faradaic reactions occurring in a CDI system.| CDI metric | Units | Best practices | Ref. |
|---|---|---|---|
| Salt adsorption capacity, SAC |
mg g−1,
mg mL−1 |
• Report which electrode weight or volume was used.
• Utilize a feedwater between 5–50 mM NaCl. • Cycle cell until limit cycle is reached before measurement. |
28 and 46 |
| Average salt adsorption rate, ASAR |
mg g−1 min−1,
mg mL−1 min−1 |
• Report key cell parameters (electrode thickness, charge and discharge times, cell materials used, etc.)
• Cycle cell until limit cycle is reached before measurement. |
28 and 33 |
| Charge efficiency, Λ |
• Report both charge and discharge voltages.
• Cycle cell until limit cycle is reached before measurement. |
39 and 86 | |
| Current efficiency, λ | • Wait until steady state to obtain current efficiency measurement. | 44 | |
Energy metrics are critical towards comparing between CDI systems, and further towards comparing water desalination by CDI with other desalination technologies such as reverse osmosis, distillation and electrodialysis. In Fig. 5, we presented the electrical energy requirements for CDI expressed per quantity of ions removed, which allowed for insight into the key parameters affecting CDI energy efficiency. However, we note here that to compare across technologies, reporting CDI energy requirements in terms of kW h m−3 is recommended, as this is widely used in the field of reverse osmosis.89 Future works in CDI should also report both the pump energy and electrical energy, especially for flow electrode systems which require more pump energy to flow the two slurry electrodes.
Another metric widely used in the field of water desalination is the water recovery ratio, which is the ratio of produced freshwater volume to the feedwater volume. Typical values for water recovery in sea water reverse osmosis plants range between 45–55%.89 By re-circulating the brine or reducing the feed flow rate during discharge, CDI systems have the potential to attain significantly higher than 50% water recovery ratios, although much work remains to explore the practical upper limits of water recovery, and the energy tradeoffs associated with operating at a high recovery. Brine management may be facilitated by high water recovery, as brine volume is minimized.
It is also clear that cost is an important metric with which to compare CDI systems, in order to elucidate which system may have the most commercial potential. In particular, performance-normalized capital costs are widely used for established energy or desalination systems, for example in the field of flow batteries (here cost per kW or per kWh). However, the field of CDI, while growing fast, is still a relatively immature technology, and so the cost data required to obtain performance-normalized capital cost metrics (such as cost per SAC or per ASAR) are still largely unavailable. In particular, more recent CDI technologies, such as flow electrode CDI (first published in 2013, Fig. 1I), hybrid CDI (first published in 2014, Fig. 1E), and inverted CDI (first published in 2015, Fig. 1D) are too novel to yet get a clear understanding of their ultimate performance-normalized costs. Future works in the field of CDI should utilize and develop these types of metrics.
Finally, the values of charge efficiency and current efficiency can serve as feedback on the correct execution of CDI experiments and construction of setups. For example, values for charge efficiency beyond unity are impossible according to current EDL structure models (see Section 6), while values below 0.4 at standard conditions of csalt = 5–20 mM and cell voltages of 1.0–1.2 V indicate that the system setup or electrode materials may not have been optimum.90
4 State-of-the-art and future of CDI electrodes
Electrode materials used in CDI cells have been extensively reviewed previously,50,91 and so we will here only briefly summarize the state-of-the-art and highlight ongoing and future trends. While the classic materials for CDI were either carbon aerogels1,19,41,52,53,92,93 or activated carbons,39,56,94 dozens of new materials for CDI electrodes have been proposed over the past decade. The latter materials are carbon-based, and include carbide-derived carbons,12,46 graphene,54,95–101 hierarchical carbon aerogels,8,27 carbon nanotubes,20,96,102,103 mesoporous carbons,18,24,72,104–106 and various composite electrodes (such as carbon–metal oxide composites).21,97,107–114 A detailed review on composite electrodes was recently published by Liu et al., and we refer readers to this work for further details on these types of electrodes.115 Overall, CDI electrodes come in various morphologies, including bound carbon particles, monolithic hierarchical porous media,8,116 aligned nanotubes,117 and woven carbon fibers.13,23,118–120Recently, advances in CDI electrode understanding and materials have driven an exciting and rapid rise in CDI cell sorption performance (see Section 3.1 on mSAC).67 In Fig. 7 we plot the achieved salt sorption by CDI systems vs. the year of publication, where the last 10 years alone have seen a rise from roughly 7 to nearly 15 mg g−1 achieved by systems with static, capacitive CDI electrodes (blue circles in Fig. 7), over 20 mg g−1 for systems with flow electrodes (green star in Fig. 7) or composite electrodes (black diamonds in Fig. 7), and over 30 mg g−1 for hybrid CDI systems with one capacitive and one Faradaic, or battery, electrode (red square in Fig. 7).
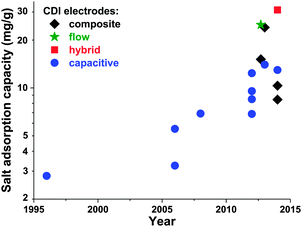 | ||
| Fig. 7 Historical evolution of maximum salt adsorption capacity (mSAC) for capacitive, composite, hybrid, and flow CDI electrodes. Capacitive CDI systems containing two static, capacitive porous carbon electrodes have increased in maximum salt adsorption capacity (mSAC) by a factor of approximately two over the past 10 years (to nearly 15 mg g−1). The recent advent of composite electrodes (capacitive electrodes with incorporated metal oxides) and hybrid architectures (one capacitive porous carbon electrode and one battery electrode), has allowed for boosts in mSAC to well over 20 mg g−1. Flow electrodes have also been able to achieve higher sorption, with over 25 mg g−1 reported. (*) For flow electrodes, a value of sorption capacity was reported as 40 mg g−1 in ref. 2; after personal communication with authors, this was corrected to 25 mg g−1. | ||
An interesting question now arises as to how far capacitive CDI electrodes can go in terms of mSAC (mgsalt gelectrode−1). To gain some insight into this question, we converted the capacitance achieved in state-of-the-art, aqueous supercapacitor cells to a predicted mSAC, in an effort to project the upper limit for mSAC achievable by CDI cells.121–126 For this conversion, we utilized the equation mSAC = α·C·V·Λ·M/(4F), where α is a conversion factor equal to 1000 mg g−1, C is the achieved specific capacitance of a single electrode in units F g−1, V is cell voltage which was assumed to be 1 V, F is Faraday's constant, Λ is cell charge efficiency which was assumed to be 0.8, M is the molar mass of NaCl in g mol−1, and the factor 4 relates the electrode specific capacitance to the cell specific capacitance. This conversion must be treated with caution, as capacitance for CDI cells may be lower than that of supercapacitor due to the lower ionic concentration of the electrolyte in CDI. As an example of the ionic concentration effects on capacitance, Kim et al.87 observed that for some electrodes made of activated carbons, capacitance measured in 1 M NaCl solution was approximately 25% higher than that in 10 mM NaCl. Based on this methodology, supercapacitors have achieved capacitances which would translate (without accounting for electrolyte or ionic strength effects on capacitance) to over 30 mg g−1 mSAC. Thus, it is conceivable that a cell with capacitive CDI electrodes can potentially reach significantly over today's level of 15 mg g−1, and that the field has not yet achieved the maximum possible mSAC. A related question can be posed as to what is an upper limit on mSAC for composite electrodes. The latter question is difficult to answer at this time, given the vast amount of possible active materials, and the current lack of understanding towards electrosorption in composite materials. As can be seen in Fig. 7, composite materials have been reported to allow for significantly higher mSAC than capacitive electrodes. One explanation offered is that composite electrodes with oxide nanoparticles can vary the point of zero charge of the electrodes, potentially enhancing charge efficiency and mSAC over that of capacitive electrodes.16
Recently, several groups have focused efforts on studying and improving the long-term performance of capacitive CDI electrodes. For example, the activated carbon cloth electrodes in the CDI system of Cohen et al. demonstrated significant declines in performance upon repeated charge–discharge cycling, which was attributed to the chemical oxidation of the positive CDI electrode (anode).127 Electrode stability was significantly improved through either operation under a nitrogen environment (to remove dissolved oxygen) or simply reversing the polarity of the electrodes intermittently. Gao et al. reported unstable and deteriorating performance upon cycling a CDI cell with carbon xerogel electrodes, which was also attributed to anode oxidation.62 However, upon chemically treating the anode and imbuing the anode with net negative surface charge (resulting in an “inverted” cell operation, with desalination during cell discharge), the electrode lifetime was extended by a factor of over 5 to over 600 h of continuous operation. Interestingly, in early CDI work with carbon aerogel electrodes, the cell was used for months of continuous operation with less than 10% decrease in salt removed per cycle (at 1.2 V charging voltage), and reversing the polarity after several months allowed for a recovery of the cell performance to nearly initial levels.19 These results collectively illustrate that capacitive electrode degradation extent and rate may be strongly material dependent. Electrode lifetime studies are a crucial component of the success of CDI technologies, and we expect to see many more such studies emerge in the near future for capacitive, composite, flow and hybrid CDI electrodes.
4.1 Designing electrode materials: differences between supercapacitor and CDI electrodes
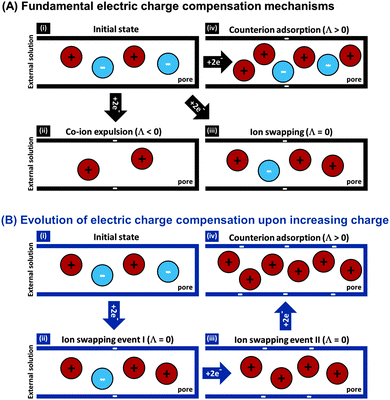
The features desirable for supercapacitor (more precisely, EDL capacitor) electrodes for aqueous electrolytes, namely the inhibition of electrochemical reactions within the water electrolysis voltage window and high specific capacitance, are also desirable features for CDI electrodes. In addition, the understanding of the impact of average pore size77 and pore size dispersity on energy storage performance developed in the supercapacitor community128 can typically be used directly towards improving desalination performance of CDI electrode materials.46 Yet, one important difference between CDI and supercapacitor electrode materials is that CDI material developers must be concerned with the electrode's charge efficiency (see Section 3.5), that is, considering not just charge, but the number of electrosorbed ions per invested charge. As mentioned in Sections 3.5 and ref. 83, in order to achieve the lowest energy requirements for desalination via CDI, one should minimize co-ion expulsion. The desire to boost charge efficiency is the reason CDI electrodes are often modified to include ion exchange membranes.3,6,33,36,42,61,129–137To illustrate the effect of charge efficiency, Λ, and its relation to the physical effect of co-ion expulsion and counterion adsorption, we show schematically in Fig. 8A several fundamental mechanisms of electric charge compensation inside micropores of carbon electrodes (where the pores open to an external solution). In Fig. 8A-i, we show an uncharged carbon pore, which possesses an equal amount of co- and counterions. In Fig. 8A-ii, we show the mechanism whereby charge screening occurs entirely due to co-ion expulsion. In such situations the charging current is not associated with ion removal from the feed water, but rather Λ < 0 would result and the ion concentration in the adjacent external solution would increase during charging, and decrease again during discharge. Though this scenario is not predicted by existing EDL theory, interestingly, desalination during CDI cell discharge has recently been demonstrated experimentally after anode oxidation or surface treatments of CDI electrodes.62,127Fig. 8A-iii shows the mechanism of electric-field driven ion swapping, which occurs at low voltages or high salt concentrations.138 In this scenario the ion concentration in the external solution does not change during the charging step, leading to the case where Λ = 0. The mechanism leading to desalination during charging is depicted in Fig. 8A-iv, where charge is balanced by counterion adsorption, leading to an increase in total number of ions in the pore and Λ > 0.
While Fig. 8A presents the three fundamental mechanisms of electric charge compensation in micropores, in Fig. 8B we present a realistic scenario of ion adsorption and expulsion upon increasing the electric charge, as occurs in CDI.7,50 Initially, we begin with an uncharged pore (i), and then begin to add electric charge. Subsequently, two ion swapping events occur (ii) and (iii) to fully empty the electrode of co-ions, without any increase in pore ion concentration (and thus no desalination of the external solution). Only upon further increasing the electrical charge in the electrode, does charge compensation of each extra electron involve adsorbing a counterion (iv), and only now is the external solution desalinated. This sequence of events is in line with the measured dependence of micropore ion concentration versus electrode charge as reported in ref. 7 and 50.
Another difference between CDI cells and supercapacitors is that for supercapacitors, charge (and so energy) is often in parallel stored by pseudocapacitive mechanisms that involve protons (e.g., quinone ↔ hydroquinone). Unfortunately, such mechanisms typically do not contribute to desalination, as they most often do not utilize the salt ions relevant to water desalination.
4.2 Perspectives on CDI electrode materials
Perhaps the most significant future research direction in capacitive CDI electrode materials is continuing the fast rise in mSAC via optimizing CDI electrode materials and pore structure (see blue circles in Fig. 7). Another important future research direction in CDI is improving the design, performance, and understanding of flow electrodes (slurry electrodes). While flow electrode architectures can enable desalination of high salinity feeds, they currently suffer from significantly inhibited electron transport when compared to static electrodes.44,45,139A parallel path in electrodes for CDI systems is the use of a single battery electrode (with Faradaic charge transfer) along with a single CDI electrode (a capacitive electrode). Analogously to the higher charge storage (energy density) achievable with batteries (bulk storage) than supercapacitors (surface storage), battery desalination electrodes have the potential to achieve higher salt sorption than CDI electrodes (although likely at a reduced desalination rate and possibly a lower performance stability over frequent charge–discharge cycles). This concept was demonstrated first by Lee et al.,11 who showed up to 31 mg g−1 salt sorption (see red square in Fig. 7). Finally, one step further from hybrid CDI systems are desalination batteries, which utilize two battery electrodes (Fig. 1F).66 The latter systems are promising for high salinity water desalination, allowing potentially higher salt sorption per charge than is possible with static electrode CDI. However, a key question with all desalination battery electrodes is on the stability against dissolution of the battery materials. In addition, a concern is how well they would perform in real water systems which contain a mixture of many ionic species. The Faradaic reactions in battery electrodes are currently tuned to consume a single species (such as chloride or sodium), and may not be able to significantly affect other present species (except, perhaps, by an additional capacitive mechanism).
Additionally, while the effect of pore size dispersity on salt sorption has been studied in detail,46 the effect of electrode micro-structure (e.g., bound spheres vs. monolithic vs. fibers) on the performance has not yet been fully determined and elucidated. It is clear that the structure must carefully balance the requirements of fast ion transport to micropores (e.g., with rates on the order of molecular diffusion), high microporosity, and fast ion transport within micropores. Generally, fast ion transport to micropores is ensured by placing the entrance to these micropores within a through-electrode network of macropores. However, future work must determine the optimized macropore network structure and pore size which allows for fast transport, yet also yields a maximum micropore volume (maximum salt storage). Generally, monolithic materials are especially promising, as they do not utilize inert binder material (which takes up volume but does not transport or store ions), and so the further development of these electrode materials is an important research direction.
Finally, another important aspect is to consider electrodes holistically; most current research focuses exclusively on the characterization of the porosity of the active material, such as microporous carbons, and exclusively reports the porosity parameters of this component. Yet, this ignores the presence of binder which effectively may block a large amount of pore volume140,141 apart from adding dead mass. Also, it is common practice for carbon electrodes to often mix in a conductive additive, such as carbon black; yet, again, we have to consider additional added dead mass when considering that common carbon blacks have a very small specific surface area (<100 m2 g−1). Incidentally, adopting recent results from the supercapacitor community, we see that adding any conductive additive is only beneficial if going to sufficiently high current densities during charging operation. Adding conductive additives generally leads to a lower mSAC value, because of mixing of the active carbon with a material with a low pore volume.142 Thus, key performance data should ideally relate to the properties of the entire electrode.
5 Current and future applications for CDI
The most widely investigated application for capacitive deionization (CDI) is the desalination of brackish waters towards the production of potable or agricultural water.1,19,33,53,81,130,143,144 Compared to established desalination technologies, such as reverse osmosis (RO) and multi-stage flash distillation (MSF), current CDI systems can require less energy for desalination at low levels of feed water salt concentration (at levels roughly one order of magnitude less salt than sea water and lower).26,33 Like electrodialysis, CDI is a technology which directly transports the (relatively few) dissolved salt ions out of the feed water, rather than transporting the (plentiful) water molecules away from the salt, as in RO and MSF.145,146 In the case of CDI, dissolved salts are transported by electromigration to EDLs, where they are stored until the desalination step is complete. In the case of RO, water molecules are transported through a semi-permeable membrane, with salt ions largely remaining on the upstream side.147 Thus, in CDI, the energy requirements are a strong function of the concentration of salt ions in the feed water, with a weaker relationship observed in RO.47 Energy requirements of MCDI and RO setups are compared in ref. 47 and show a salt concentration cross-over point below which MCDI becomes more energy efficient (roughly below 2 g L−1). CDI systems with static electrodes (Fig. 1A–F) are characterized by a limited amount of salt that can be adsorbed into the EDL per charge, and thus sea water desalination with static electrode CDI systems is impractical from an infrastructure and energy point of view (a roughly 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of electrode volume to feed water volume is needed to adequately desalinate sea water).
1 ratio of electrode volume to feed water volume is needed to adequately desalinate sea water).
The vast majority of CDI experimental works test novel CDI cell architectures or electrode materials using brackish feed water synthesized in a laboratory. Most typically, the feed water is a solution of sodium chloride in deionized water.50 The latter conditions allow for insightful, controlled experiments for proof-of-concept type work; however, they do not allow for a reliable prediction of the performance during continuous treatment of real brackish feed waters, such as river water or saline aquifers. In systems with real waters, such as that of Gabelich et al. using carbon aerogel electrodes,1 the natural organic matter present in river water appeared to reduce the sorption capacity of the electrodes, indicating some surface fouling. Similar conclusions were reached by Zhang et al.,148 who reported decreased performance in CDI systems when treating brackish waters with high concentrations (2 mg L−1) of dissolved organics. The latter performance decrease was reversed when a mild cleaning solution (0.01 M citric acid and 0.01 M sodium hydroxide) was flushed through the CDI cell.148
Conversely, field tests by Xu et al.53 on brackish produced water from natural gas generation sites indicated a stable performance of carbon aerogel-based CDI system over several hours of continuous operation, indicating no significant fouling of the electrodes in this timescale. Further, the work of Lee et al.3 treating brackish thermal power plant waste water using a membrane CDI cell reported no significant decay in cell performance for 500 desalination cycles. In yet another work it was shown that MCDI systems can be applied for treatment of brackish water containing 5–10 mg L−1 of oil compounds such as octane.149 Currently, it is difficult to draw broad conclusions on the lifetime of CDI cells, as it is clear the target parameters (water hardness, chemical composition etc.) play an important role for resulting CDI performance and stability.
The very recent advent of both flow electrode CDI (FCDI) and hybrid CDI systems has opened new areas of application for CDI systems.2,11 One advantage of these systems over CDI with two static porous carbon electrodes is to enable the desalination of higher salinity feeds than was previously possible. For example, FCDI, in which both electrodes are composed of a flowing carbon slurry, has demonstrated the desalination of feed water with total salt concentration roughly equal to that of sea water with a single cell charge.2 Hybrid CDI, in which one electrode is porous carbon and the other is a battery electrode such as sodium manganese oxide, has demonstrated over 30 mg g−1 equilibrium NaCl salt sorption per charge, nearly double that of static electrode CDI systems.11 Due to the nascent state of FCDI and hybrid CDI, many questions relating to their application remain currently unanswered. Will these systems compete with sea water reverse osmosis in terms of energy requirements? How many charge–discharge cycles will these systems be able to attain without significant performance degradation? It is clear that FCDI and hybrid CDI will be important research topics in the near future, with their most suitable applications yet-to-be determined.
Beyond the application of brackish and sea water desalination, CDI has also been utilized for other applications requiring removal of ions from an aqueous solution. For example, CDI for water softening was demonstrated by Seo et al.,4 where CDI cells were used to remove divalent dissolved minerals such as calcium and magnesium which can scale household appliances and interfere with their cleaning processes. Further, CDI systems have been employed as a method of removing weak acids, such as boric acid from RO-treated water.35 Other innovative application of CDI and MCDI relates to ion removal from biomass hydrolyzate,150 acetic and sulfuric acids from biomass hydrolyzate using a lime addition–capacitive deionization (CDI) hybrid process,151 insulin purification,152 microfluidic sample preparation,153 removal of phosphates and nitrates,154,155 chromium,156,157 copper,158,159 lithium,160,161 lead ions,162 and cadmium ions.163 It has to be noted that some of the applications mentioned above deal with treatment of feed waters containing amphoteric ions such as phosphate or bicarbonate ions which depending on electrolyte pH value can donate or accept protons. Such processes should be taken into account when performing desalination tests (as feed pH can be perturbed while charging (M)CDI cells).50,164 Yet, we would like to point out that some metal ions, for example copper, can undergo a reduction process and as a result be deposited as elemental copper on the electrodes.158,165 If this is the case, this process should not be classified as capacitive deionization but rather metal electroplating involving electron transfer reaction between electrodes and dissolved ions.
Also of note is that CDI systems can be integrated with other technologies to provide synergy towards achieving various end goals. One example is the integration of CDI cells with renewable energy sources such as solar energy,166 as solar panels are well suited towards providing the low voltage (approximately 1 V) required by a CDI cell. Such combined solar-CDI units can be used to treat water in remote locations without electrical grid access. A second example is combining CDI functionality with a microbial environment, the so-called integrated microbial capacitive desalination cell (MCDC).167 In the latter cells, it is reported that microbes present in the anode compartment oxidize organic matter in wastewater, yielding electrons which can be used to drive a CDI process. Thus, these cells have been reported to remove organic matter and salts simultaneously, (while generating the energy needed to desalinate). Lastly, CDI cells can be coupled together with other desalination systems, such as reverse osmosis (RO), where CDI systems have been used previously to treat brine water emerging from an RO unit.168 As the RO brine is typically of a high salinity, the cell's charge efficiency for this operation is likely low, and thus the process energy efficiency is likely poor (with respect to energy per ion removed, see Fig. 5).
Further, CDI has been investigated as a tool towards the selective removal or up-concentration of a certain ion from multicomponent electrolytes.55 The latter method leverages the time-dependent selectivity of charging EDLs, which preferentially adsorb species with higher bulk ionic concentrations at early times during charging, while at later times ions with higher valence are preferentially adsorbed.55 This concept can even be used to construct a cell for so called potential-controlled chromatography with improved separation (and detection) of charged species.169,170 An alternative approach to achieve preferential removal of a certain ion utilizes a material with high selectivity towards one ionic species placed either on electrodes' surfaces or between electrodes' carbon particles. This approach has been demonstrated towards the preferential removal of nitrate over chloride and sulfate ions.59,60 For example, Yeo et al.60 and Kim et al.59 demonstrated a 2.0- and 2.3-fold increase of nitrate ion removal compared with standard CDI and MCDI systems, respectively. Enhanced uptake of cations was demonstrated by using electrodes consisting of carbon particles and zeolite with high selectivity towards calcium.171 Another way of controlling the differential removal of ions carrying the same charge and valence was achieved by controlling current density during MCDI operation.172
We would like to point out that despite the many advances achieved in membrane technologies over the years, there is no membrane technology to our knowledge that is highly selective for one particular ion species. Development of such membranes will allow for new application possibilities in selective ion removal with MCDI. However, due to a lack of development of such membranes, this field is still largely unexplored, yet it remains a highly promising direction. The most known and studied membrane designed for ionic selectivity introduces selective molecules, often called “extractants”, into the membrane matrix. These molecules are responsible for selective binding with target molecules and transporting them across the membrane interface. It is believed that this concept can be applied in treating contaminated waters, but first, the price of extractants has to be significantly reduced to make large scale desalination systems economically feasible.173,174
In addition to research-level explorations of applications of CDI, there have been several commercial efforts based on CDI technologies. Early commercialization efforts emerged from LLNL (Lawrence Livermore National Laboratory, USA) in the 1990s (see ref. 19) but were eventually unsuccessful. In hindsight, the low salt adsorption capacity of the early carbon aerogels used in this work time may have played a role. Breakthroughs made since then, as described in this perspective, in material performance, cell design, and fundamental understanding, have allowed for large improvements in CDI system performance and energy efficiency. As a result, recent industrial efforts have arisen worldwide to commercialize CDI technologies. For example, the company Voltea B.V. (The Netherlands) has developed membrane CDI-based systems for commercial and domestic applications. Their MCDI pilot system performance data obtained from treating feed water of cooling tower facilities were published in ref. 175. In this work it was claimed that utilization of an MCDI system relative to traditional water treatment technologies is beneficial in terms of chemical, water and waste water savings. Additionally, this work demonstrated a low energy consumption of between 0.1 and 0.2 kW h m−3 of produced desalinated water for the desalination of cooling tower feed water with total conductivity of 0.37–0.65 mS cm−1. EST Water & Technologies (People's Republic of China) develops large-scale CDI systems (Fig. 9) for desalination which can be applied in a variety of industries. Examples include applications in municipal groundwater, petrochemical industry, steel mills, thermoelectric power plants, coal chemical manufacturing, paper mills, production of fertilizer, and high fluorine and high arsenic brackish water. Up to now more than 30 industrial systems are installed in China, where most of the facilities are for industrial/municipal waste water recovery/reuse with treatment capacities ranging from 100 to 2000 m3 h−1. In terms of energy consumption EST modules are attractive in comparison to RO modules, with values of energy consumption around 1.0 kW h m−3 for EST CDI and 1.5 kW h m−3 for RO.
5.1 Perspectives on applications for CDI technologies
Looking towards what the future may hold for applications for CDI, we believe that the research and commercial community has only scratched the surface of the potential of CDI. This is evidenced by the very recent proliferation of novel cell architectures with enhanced capabilities,2,11 and increased fundamental understanding of cell capabilities.46,55 We expect that the use of CDI cells as an electrosorption platform to selectively remove various charged species (ions, small organic molecules) from electrolytes will be a significant part of future efforts, as this aspect of CDI has only begun to be explored. Further, towards the application of water desalination, important future research in CDI will involve studying and reducing the fouling potential of CDI electrodes under real water conditions (sea, river, and other feed waters). This is especially important for novel and emerging architectures, such as flow electrode CDI and membrane CDI. More long-term studies of CDI cell performance with real waters will show the limits to cycle life of current systems, paving the way for a new generation of CDI systems which achieve breakthroughs in operation life. Yet, as real water systems have very unique composition and physicochemical properties that vary from source to source, we will yet have to (1) establish commonly accepted test protocols and (2) to modify such protocols for specific applications and local water properties.6 Theory for CDI: state-of-the-art and future developments
6.1 CDI vs. electrical double layer capacitors (supercapacitors): similarities and differences
As mentioned before: there exist many similarities between supercapacitors cells for energy storage and CDI cells. Architecturally, both consist of a pair of conductive porous electrodes (either static or flow electrodes) which are charged capacitively to store ions in EDLs at the interface between the solid carbon matrix and the liquid electrolyte. The dynamics of supercapacitors are often modeled via linear circuits, with the most common circuit known as the transmission line model (TL-model; Fig. 10).176,177 This circuit model can capture the charging/discharging of a porous medium consisting of two continuous interpenetrating conductive media, such as an electrically conductive solid carbon material (the pore walls), and an electrolyte filling the pore void volume. For supercapacitor applications, charge is stored capacitively at the carbon/electrolyte interface. Typically, for simplicity, the resistance in the electron conducting carbon is assumed to be negligible,73,177 although the treatment of carbon as an ideal metal is factually incorrect.178Fig. 10 shows a schematic of the equivalent circuit used to model supercapacitors. Here, resistor elements represent the ionic resistance of the electrolyte in the pore, while capacitor elements represent the EDLs forming at pore walls. Let us stress, in the CDI models discussed further on, the concept of a “pore wall” is not used. Instead, EDLs are formed within a third type of volumetric continuous medium, in transport theory called the micropores. This nomenclature for micropores and macropores (for the ion transport pathways across the electrode) dates back to Johnson and Newman (1971),39 and is different from IUPAC definitions for pore sizes. From this circuit model, a simple partial differential equation can be formulated to describe the dynamics of local electric potential in the electrolyte (eqn (1)):176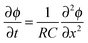 | (1) |
Although similar in architecture, significant differences in charging dynamics can be observed between supercapacitor and CDI cells. In a CDI cell, the concentration of ions is significantly lower than in supercapacitors (typically 1–100 mM), so that during charging the pore bulk is significantly depleted of ions (i.e., desalinated). Thus, a key difference between supercapacitors and CDI cell dynamics is that in CDI cells, the dynamics cannot be captured by linear circuit elements (eqn (1)), as the process of desalination necessarily introduces time-varying electrolyte resistances into the system.73 Further, modeling the salt concentration dynamics requires an additional parameter known as charge efficiency (see Section 3.5). CDI models also may have to consider complexities associated with ionic mixtures, for instance containing multiple species of cations.55 As a result, the dynamics of CDI cells can be significantly more complex than that of the supercapacitor, but, nevertheless, understanding supercapacitors provides an excellent foundation onto which one can build an understanding of CDI cells. In the following section, we will cover methods of modeling CDI cells which go beyond linear circuit theory.
6.2 Advances in macroscopic porous electrode theory applied to CDI: multiscale porous electrodes and storing salt in micropore volumes
To capture the dynamics of charging (and discharging) of CDI cells, the most-utilized approach is to employ macroscopic porous electrode theory.5,39,73,182 This theory, pioneered in the 1970's by Newman,39,183 models the dynamics within charged porous electrodes by using judiciously chosen volume elements. These volumes are larger than pore sizes, yet much smaller than the overall electrode length scale, and variables such as electrolyte ion concentration and electric potential are averaged over this volume element.184 In this manner, transport equations can be formulated without considering the microscopic, pore-level geometry. This theory is widely used in electrochemical systems,184 and was first applied to CDI in 1971 by Johnson and Newman.39In order to model ion uptake into EDLs, the transport model must couple to an EDL structure model, which can relate the local potential drop across the EDL in porous carbon particles, or at any pore walls, to the local ion flux into the EDL. Thus, obtaining accurate CDI model results depends crucially on the use of an accurate EDL structure model. Initial CDI models utilized well-known EDL structure models such as a Helmholtz EDL model8,39 or a Gouy–Chapman–Stern (GCS) EDL model (Fig. 11A).86 However, neither of these models accurately captures the EDL structure along typical CDI electrodes' pore walls. First, the Helmholtz model assumes that the liquid side of the EDL consists entirely of counterions in a fixed plane. The latter has the advantage of being the simplest EDL structure model; however, this model necessitates a charge efficiency of unity: for each electronic charge injected locally in the micropore, one ionic countercharge is adsorbed, as co-ions are absent from the EDL. This is clearly in contrast with typical CDI experimental data, which always demonstrates a sub-unity charge efficiency (see Section 3.5). For the GCS-model, as implemented by Biesheuvel and Bazant,73 it was assumed that the diffuse layer forming at pore walls can extend freely. Rather, in typical multi-scale CDI electrodes, the pores where strong desalination occurs are strongly confined (pores < 2 nm), and so the EDLs are strongly overlapped.
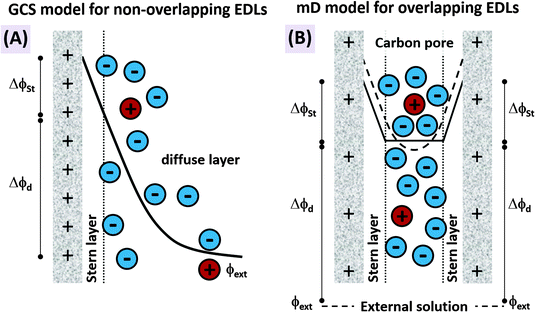 | ||
| Fig. 11 Classic GCS EDL model (A) vs. modified Donnan model (B) to describe ion storage in carbon pores. | ||
An advance in the equilibrium EDL structure model accounted for the confined nature of the micropores in CDI electrodes, and this was the so-called modified Donnan (mD) model formulated in 2011 (Fig. 11B).5–7 This model considers salt storage to occur within the volume of micropores (i.e., pores smaller than 2 nm) rather than along pore surfaces (as was assumed for previously developed models utilizing Helmholtz or GCS double layer structure models8,39,86). In the mD model, the micropores are considered to have strongly overlapped double layer and so the classical Donnan assumption of a uniform pore electrostatic potential can be utilized. The Donnan assumption allows for a mathematically compact description of the EDL structure, and it also more accurately captures the typical pore structure of CDI electrodes (see Section 4). Further, the use of “modified” referred to two extensions of classical Donnan models, one by including a Stern layer in the micropores' EDL, and two, by including an extra term describing an adsorption of ions into micropores due to forces separate from the applied electric field. The latter extension captures the effect that also uncharged carbons can adsorb salt from electrolytes, which is a well-known and well-characterized phenomenon.7,185,186 In addition to being a more realistic portrayal of CDI electrodes, the mD-model also overcame numerical difficulties in using classical GCS EDL structure models in cases of strong desalination and salt concentration gradients.50,73 The robustness of implementing the mD model in porous electrode theory is evidenced by the presence of very steep gradients of salt concentration in the transport pathways in the mD model solutions, without numerical difficulties, with the macropore salinity dropping to small values (order 10 ppm) (see ref. 50).
However, initial formulations of the mD-model overpredicted salt adsorption at high salinity (Fig. 4 in ref. 7). Supported by an analysis of ion–ion correlation forces in metallic nanopores, a correction was established where the extra attraction term was made inversely dependent on total pore ion concentration. This improved mD model allowed for a much better fit of theory to equilibrium data for salt adsorption and charge over a wide range of feed salinities (5–200 mM) and cell voltages (up to 1.2 V).7,83 Future analysis must show whether the i-mD model can accurately capture data for ionic mixtures containing both mono- and multivalent cations and anions.55
6.3 On the use of adsorption isotherms in CDI modeling
A very different approach of modeling salt adsorption in CDI electrodes is the use of classical Langmuir or Freundlich isotherms. While this approach has been used frequently in the field of CDI, we caution that this is not appropriate for several reasons. Such isotherms are general equations to fit data for the equilibrium adsorption of uncharged molecules from a gas or liquid phase onto an uncharged surface, and do not capture ion electrosorption at a charged interface. From fitting the equation to, for example, data for nitrogen gas adsorption onto an uncharged surface, an adsorption energy and a maximum adsorption can be derived. However, such isotherm equations are inappropriate to model CDI which has very different underlying physical characteristics, based primarily on ion storage in the EDL by an electrostatic attraction. This electrostatic force can be tuned by injecting more or less electronic charge in the carbon, a feature which is not captured by Langmuir or Freundlich isotherms. Further, CDI cells typically consist of two electrodes, and thus there may be an asymmetry between the electrodes, an effect not captured by classical isotherm models. Instead, only EDL models (such as the modified Donnan model) can correctly describe the underlying physics of ion adsorption in CDI via electrostatic forces, can be extended to consider ionic mixtures or salt systems that undergo acid/base reactions, and in the future extended to include chemical surface charge (e.g., due to carboxylic groups), and pseudocapacitive reactions (e.g., the quinone ↔ hydroquinone reaction, which involves the joint “adsorption” of an electron and proton).182 In short, classical isotherms only describe the effect of salt concentration on salt adsorption in the absence of a charged surface, whereas many additional effects are needed to describe electrosorption via CDI (see Fig. 12). The data in Fig. 12 demonstrates that isotherm modeling alone is inappropriate for CDI, as here the measured decrease in salt adsorption for salt concentrations beyond 6 g L−1 (∼100 mM NaCl) can only be described by the i-mD model, and not by the isotherm equations.7 Classical isotherms can be used to compare and contrast the sorption of technologies not using applied voltages, such as ion exchange, to the electrosorption predicted by CDI models.6.4 Future directions in CDI theory: cell level modelling
The previous sections focused on transport in a single porous electrode used for CDI. However, additional considerations are important when modeling the complete CDI cell, and these will be described in this section. Firstly, porous electrode theory applied to CDI has up to now always been solved for one-dimensional transport through a charging or discharging electrode. However, an actual flow-by (or flow between) CDI cell (see Fig. 1A) typically has two important directions: one in the direction of the flow of water between the electrodes, and one in the direction of the applied electric field (perpendicular to the flow direction). Thus, to model a flow-by CDI cell, a coupling of the macroscopic porous electrode theory (a one-dimensional transport of species through the electrode) to a model that encompasses the two-dimensional cell architecture is required. Until now this coupling has been established by mathematically dividing the flow channel and its neighboring electrode regions into “stirred tank” sub-cells with only fluid flow from sub-cell to sub-cell in the spacer (the region between porous electrodes).6,187 A fully 2D CDI model would allow for more realistic determination of the transport and concentration profile within the separator region. For flow-by CDI, often only half of a cell is considered (see the modeling geometry in Fig. 13). This is a good approach for a simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt solution when there is evidence of symmetry in the EDL structure between positively and negatively charged electrodes. Extensive experimental work with CDI using asymmetric electrode mass ratios showed that indeed this assumption of symmetry is appropriate for a simple salt solution such as NaCl (despite the slightly different diffusivities between the sodium and chloride ions).187 However, the use of a full model including both electrodes is unavoidable when a strongly asymmetric salt is used such as CaCl2, as well as for complex ionic mixtures. Also when the transport of H+- and OH−-ions is to be included, important to model pH fluctuations, a two electrode model is required due to the large diffusivity difference between H+, OH−, and salt ions.
1 salt solution when there is evidence of symmetry in the EDL structure between positively and negatively charged electrodes. Extensive experimental work with CDI using asymmetric electrode mass ratios showed that indeed this assumption of symmetry is appropriate for a simple salt solution such as NaCl (despite the slightly different diffusivities between the sodium and chloride ions).187 However, the use of a full model including both electrodes is unavoidable when a strongly asymmetric salt is used such as CaCl2, as well as for complex ionic mixtures. Also when the transport of H+- and OH−-ions is to be included, important to model pH fluctuations, a two electrode model is required due to the large diffusivity difference between H+, OH−, and salt ions.
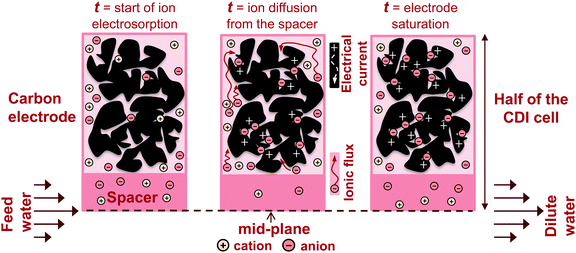 | ||
| Fig. 13 Outline of a macroscopic CDI cell model combining fluid flow through a spacer channel (left-right direction) with ion transport and adsorption in solid fixed CDI film electrodes, first through transport pathways (or, macropores), then into carbon particles where EDLs are formed (reproduced with permission).46 | ||
In contrast to flow-by CDI, flow-through electrode CDI is an architecture that can be well described by a purely one-dimensional model, as here the flow of electrolyte is in the same direction as the applied electric field (see Fig. 13). Another key difference in modeling flow-through electrode vs. flow-between systems is that desalination is not symmetric about the cell centerline. For flow-through CDI, in the upstream electrode, the co-ion (ions with the same valence sign as the electrode wall charge) must transport faster than the fluid, while the counterions are held back (these effects occur via an electromigration drift flux). In this way, local electroneutrality in the transport pathways of the upstream electrode is assured while counterions can be adsorbed in the local EDLs. In the downstream (second) electrode, the situation is reversed (not symmetric to the first electrode) with the counterion transporting faster than the fluid velocity, and the co-ion held back. Such effects should be explored in future works on the theory of flow-through electrode CDI.
CDI architectures with static and flow electrodes often use ion exchange membranes (IEMs) (see Section 2.1). Ion transport in these IEMs can be described by the same Nernst–Planck flux equations as also used for the electrodes. The membrane fixed charge density, “X”, however, is now a constant, which simplifies matters significantly (in the electrodes, charge density varies temporally and spatially during charging). Because X, which is defined per unit volume of electrolyte, is very high, of the order of 5 M, the ionic conductivity of the membranes is very high, and its ionic content is relatively invariant upon changing external conditions, and thus ion accumulation (unsteady behavior) is typically neglected. Also, because of the high charge X, ionic concentration profiles and electrical potentials can be assumed to be linear across the membrane. All of these assumptions lead to a simplified semi-analytical model for the membrane that is easily included in a full CDI transport model.26 Note that the membrane charge X is defined as a positive number, with a factor ω used to describe the sign of the membrane charge, being positive (ω = 1) for an anion-exchange membrane, negative (ω = −1) for a cation exchange membrane. This is the classical Teorell–Meyers–Sievers (TMS) model, or “leaky membrane model”.6,33,188,189 This TMS model allows the passage of counterions and also a limited number of co-ions (as opposed to a perfect membrane, which does not allow co-ion transport). The TMS model self-consistently models all ionic fluxes and currents, taking as input only the ionic diffusivities in the membrane and the membrane charge density, and has been applied to model MCDI in ref. 26, 33 and 190.
A final task to be taken up is the modeling of flow-electrode CDI. Assuming that steady-state is reached with all local parameters unvarying in time, modeling here is actually much simplified44 and the system can be described by the current efficiency, λ, unvarying in time, see Fig. 6. This key parameter of current efficiency is defined as the salt removal rate from the (central) water channel over the current (assuming the testing of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt), where current is expressed in mol s−1 (or mol m−2 s−1) by dividing current (density) by Faraday's number. In flow-electrode CDI one of the main challenges is the description and optimization of slurry viscosity and slurry electrical conductivity: how do electrons “hop” from one carbon particle to the next and how does ion- and charge-redistribution in floating carbon particles affect the overall performance and efficiency?
1 salt), where current is expressed in mol s−1 (or mol m−2 s−1) by dividing current (density) by Faraday's number. In flow-electrode CDI one of the main challenges is the description and optimization of slurry viscosity and slurry electrical conductivity: how do electrons “hop” from one carbon particle to the next and how does ion- and charge-redistribution in floating carbon particles affect the overall performance and efficiency?
6.5 Future directions in CDI theory: accounting for slow transport into EDLs
A key assumption implicit in typical porous electrode CDI models, is that the local ion transport from the interparticle pores (macropores) into the EDLs (micropores) occurs with negligible resistance to transport, and so the rate-limiting step in desalination by CDI is macroscopic transport across the electrode. This assumption may be correct for thick electrodes that are composed of small (relative to the electrode size) carbon particles that have a fair degree of mesopores, as this configuration results in small transport distances from macropore to the intraparticle EDL, and mesopores (2–50 nm size) do not have the transport resistances that may occur when the pore size approaches the ion size (as for micropores).80,181 However, in situations with longer macropore to EDL transport distances, or intraparticle pore space with primarily micropores, it may be required to include this additional transport resistance.In modified Donnan CDI theory with fast transport between macropores and EDLs, the Boltzmann equilibrium describes ion concentration in the micropores (eqn (2)):
cmi,i = cmA,i·exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−ziΔϕd + μatt), (−ziΔϕd + μatt), | (2) |
Instead of using eqn (2), it is possible to use an equation for the rate of transport of ions between macro- and micropores. We here account for finite transport rates by using an overpotential-like expression mentioned first in ref. 46 and 50. Namely, we can describe the ion flux from macro- to micropore according to the following equation (eqn (3)):
ji = k·(cmA,i·exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (α·(−zi·Δϕd + μatt)) − cmi,i·exp (α·(−zi·Δϕd + μatt)) − cmi,i·exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ((1 − α)·(zi·Δϕd − μatt))) ((1 − α)·(zi·Δϕd − μatt))) | (3) |
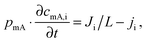 | (4a) |
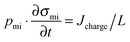 | (4b) |
6.6 Perspectives on the field of CDI theory
The ultimate aim of CDI modeling is to derive a mathematical code that not just describes previously recorded data, but can predict CDI performance in all its facets including desalination degree, pH fluctuations, energy consumption, and so on. Such a design model should be able to do that for wide ranges of input parameters of electrode architecture (thickness, porosities), cell design and external conditions such as switching times, applied current and voltage signals, and more. The design model can then be combined with a cost calculation module that contains prices for energy and materials, and these elements together should go into a cost optimization code to calculate the optimum CDI cell design and operational mode, for a precisely-defined application. This optimum can then be compared to the respective optimum of competing water treatment technologies.This aim is still far from being realized, but the CDI-community has covered quite some distance towards the ultimate development of a design model that confidently predicts the performance of all possible data sets (e.g., including/excluding membranes; constant voltage vs. constant current) with all model parameters at constant values. This is a significant challenge, given that many elements of a CDI cell have not yet been included, such as effects of protons/hydroxyl ions, chemical surface charge and redox functionalities, and also details of membrane transport, such as co-ion leakage and possible water flow through the membrane. Thus, the challenge of a predictive CDI model can be put into context as part of the larger challenge in the electrokinetics community of predicting ion transport in charged porous media and EDL structure.
As improved EDL structure models are developed, we must emphasize that it is also important that EDL structure models are simple enough to be easily integrated into porous electrode transport models, see for example ref. 83. They should furthermore ideally remain mathematically concise when extending the model to situations with mixtures of ions as is typical in environmental applications. Also the fact that the ions may undergo acid/base equilibria reactions should be implementable.190,191
A key issue in membrane transport modeling is the range of phenomena occurring at “overlimiting currents” when the ion concentration near one of the membrane interfaces drops to zero. This condition very likely also exists in MCDI, but has not been investigated at all. Note that this may happen on either side of the membrane: on the side of the spacer channel during charging, and on the electrode side during discharge. It may therefore well be that phenomena such as fluid flow vortices, or current-induced membrane discharge (CIMD) play a role also in MCDI.192 In summary, membrane modeling for CDI is still in its infancy: no papers exist that describe the effect of membrane thickness, or possibly the role of monovalent selective membranes for CDI, which are membranes where a thin nm-thick coating is applied on the membrane of an opposite sign (e.g., a thin anion-exchange coating on a cation-exchange IEM).
7 Conclusion and outlook
The field of CDI has seen tremendous growth over the last decade, and has grown from a laboratory curiosity into a capable technology of which we have only started to understand the limitations. Perhaps the most intriguing aspect of CDI is its many parallels with the field of supercapacitors. In both fields, we have seen a trend first towards high capacitance (CDI: salt adsorption capacity), which is now transitioning also towards high performance at high rates (CDI: salt adsorption rate), and exploring novel architectures for applications very small (micro-supercapacitors; CDI: desalination on a chip) and very large (electrochemical flow capacitors; CDI: flow-CDI). Also, Faradaic reactions have entered the scope of both fields as a facile way to allow an enhanced amount of charge transfer. For CDI, enhanced charge transfer alone is not required, the enhanced transfer must also remove targeted salt ions from the feedwater (as has been very recently demonstrated via hybrid CDI). A controllable surface functionality may also open new pathways for alternative CDI systems, like the recently proposed “inverted” CDI concept.62 Like in the case of Ragone plots with capacitors, supercapacitors, and batteries, we may see in the future competition between electrochemical ion removal technologies with different removal rates, sorption capacities, and cycle lifetimes.For CDI to reach its full application potential, we still need to better understand the mechanisms of performance degradation and eventual device failure. This applies in particular when transitioning from very controlled systems (like 5 mM NaCl in de-aerated water) to surface water. As our expertise in applying CDI with more robust performance and stability improves, the versatility of the method will grow. Beyond the scope of providing drinking water, CDI and adaptions thereof will continue to be explored for closed-circuit treatment and recycling of industrial water, ion separation, and possibly increasing ion concentration for mining waste water or selective synthesis routes in the chemical and pharmaceutical industry.
Performance and stability are intrinsically tied to the electrode material, which until recently was exclusively carbon. With the emergence of hybrid CDI the desalination battery, this strict limitation to carbon materials has ended, but also first exploratory studies have shed some light on the perspective of using heteroatom carbons or carbon hybrid materials. This field is widely unexplored and the community will only be able to benefit from novel and possibly exotic materials if thorough performance benchmarking is provided. For example, while adding heteroatoms to carbons and utilizing hybrid materials may be a way to modify and tune wettability and electrical conductivity, we also have to consider that the emergence of possibly redox-active sites may negatively impact the charge efficiency and cycle lifetime.
One exciting development in the field of CDI is the emergence of flow electrodes. Not only has it impacted on system engineering, but has also introduced the idea of decoupling maximum salt sorption capacity and ion removal rates by employing a continuous process without the need for in-cell electrode regeneration. The latter is having a potentially transformative impact on the selection of carbon materials and their synthesis. After all, the complex interplay of viscosity, conductivity, and flow rates allows for less of an emphasis on employing carbons with the highest salt sorption capacity, but rather with the highest salt sorption rate and the best performance stability.
Acknowledgements
This work is part of the ongoing efforts of the CDI&E working group to foster the science and technology of capacitive deionization and electrosorption (http://www.cdi-electrosorption.org). SP and VP thank Prof. Eduard Arzt for his continuing support. SP acknowledges financial support of the Alexander von Humboldt Foundation. VP acknowledges funding from the Hans Meier Leibniz Award of the German Research Foundation (DFG). This work was supported by the Grand Technion Energy Program (GTEP), and comprises part of The Leona M. and Harry B. Helmsley Charitable Trust reports on Alternative Energy series of the Technion, Israel Institute of Technology, and the Weizmann Institute of Science.References
- C. J. Gabelich, T. D. Tran and I. H. M. Suffet, Environ. Sci. Technol., 2002, 36, 3010–3019 CrossRef CAS PubMed.
- S.-I. Jeon, H.-R. Park, J.-G. Yeo, S. Yang, C. H. Cho, M. H. Han and D.-K. Kim, Energy Environ. Sci., 2013, 6, 1471–1475 CAS.
- J.-B. Lee, K.-K. Park, H.-M. Eum and C.-W. Lee, Desalination, 2006, 196, 125–134 CrossRef CAS.
- S.-J. Seo, H. Jeon, J. K. Lee, G.-Y. Kim, D. Park, H. Nojima, J. Lee and S.-H. Moon, Water Res., 2010, 44, 2267–2275 CrossRef CAS PubMed.
- P. M. Biesheuvel, Y. Q. Fu and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061507 CrossRef CAS.
- P. M. Biesheuvel, R. Zhao, S. Porada and A. van der Wal, J. Colloid Interface Sci., 2011, 360, 239–248 CrossRef CAS PubMed.
- P. M. Biesheuvel, S. Porada, M. Levi and M. Z. Bazant, J. Solid State Electrochem., 2014, 18, 1365–1376 CrossRef CAS.
- M. E. Suss, T. F. Baumann, W. L. Bourcier, C. M. Spadaccini, K. A. Rose, J. G. Santiago and M. Stadermann, Energy Environ. Sci., 2012, 5, 9511–9519 CAS.
- S. Porada, B. B. Sales, H. V. M. Hamelers and P. M. Biesheuvel, J. Phys. Chem. Lett., 2012, 3, 1613–1618 CrossRef CAS PubMed.
- Y. Oren and A. Soffer, J. Electrochem. Soc., 1978, 125, 869–875 CrossRef CAS.
- J. Lee, S. Kim, C. Kim and J. Yoon, Energy Environ. Sci., 2014, 7, 3683–3689 CAS.
- S. Porada, L. Weinstein, R. Dash, A. van der Wal, M. Bryjak, Y. Gogotsi and P. M. Biesheuvel, ACS Appl. Mater. Interfaces, 2012, 4, 1194–1199 CAS.
- G. Wang, Q. Dong, Z. Ling, C. Pan, C. Yu and J. Qiu, J. Mater. Chem., 2012, 22, 21819–21823 RSC.
- L. Zou, G. Morris and D. Qi, Desalination, 2008, 225, 329–340 CrossRef CAS.
- K. C. Leonard, J. R. Genthe, J. L. Sanfilippo, W. A. Zeltner and M. A. Anderson, Electrochim. Acta, 2009, 54, 5286–5291 CrossRef CAS.
- L. Han, K. G. Karthikeyan, M. A. Anderson, K. Gregory, J. J. Wouters and A. Abdel-Wahab, Electrochim. Acta, 2013, 90, 573–581 CrossRef CAS.
- H. J. Oh, J. H. Lee, H. J. Ahn, Y. Jeong, Y. J. Kim and C. S. Chi, Thin Solid Films, 2006, 515, 220–225 CrossRef CAS.
- L. Li, L. Zou, H. Song and G. Morris, Carbon, 2009, 47, 775–781 CrossRef CAS.
- J. C. Farmer, D. V. Fix, G. V. Mack, R. W. Pekala and J. F. Poco, J. Electrochem. Soc., 1996, 143, 159–169 CrossRef CAS.
- D. Zhang, L. Shi, J. Fang, K. Dai and X. Li, Mater. Chem. Phys., 2006, 97, 415–419 CrossRef CAS.
- X. Z. Wang, M. G. Li, Y. W. Chen, R. M. Cheng, S. M. Huang, L. K. Pan and Z. Sun, Electrochem. Solid-State Lett., 2006, 9, E23–E26 CrossRef CAS.
- H. Wang, L.-Y. Shi, T. Yan, J. Zhang, Q. Zhong and D. Zhang, J. Mater. Chem. A, 2014, 2, 4739–4750 CAS.
- Y. Bai, Z.-H. Huang, X.-L. Yu and F. Kang, Colloids Surf., A, 2014, 444, 153–158 CrossRef CAS.
- G. Wang, B. Qian, Q. Dong, J. Yang, Z. Zhao and J. Qiu, Sep. Purif. Technol., 2013, 103, 216–221 CrossRef CAS.
- Y. Bouhadana, E. Avraham, M. Noked, M. Ben-Tzion, A. Soffer and D. Aurbach, J. Phys. Chem. C, 2011, 115, 16567–16573 CAS.
- R. Zhao, P. M. Biesheuvel and A. Van der Wal, Energy Environ. Sci., 2012, 5, 9520–9527 CAS.
- M. E. Suss, P. M. Biesheuvel, T. F. Baumann, M. Stadermann and J. G. Santiago, Environ. Sci. Technol., 2014, 48, 2008–2015 CrossRef CAS PubMed.
- T. Kim and J. Yoon, RSC Adv., 2015, 5, 1456–1461 RSC.
- E. Avraham, Y. Bouhadana, A. Soffer and D. Aurbach, J. Electrochem. Soc., 2009, 156, 95–99 CrossRef.
- E. Avraham, M. Noked, Y. Bouhadana, A. Soffer and D. Aurbach, J. Electrochem. Soc., 2009, 156, 157–162 CrossRef.
- E. Avraham, M. Noked, I. Cohen, A. Soffer and D. Aurbach, J. Electrochem. Soc., 2011, 158, 168–173 CrossRef.
- X. Gao, A. Omosebi, J. Landon and K. Liu, Electrochem. Commun., 2014, 39, 22–25 CrossRef CAS.
- R. Zhao, O. Satpradit, H. H. M. Rijnaarts, P. M. Biesheuvel and A. van der Wal, Water Res., 2013, 47, 1941–1952 CrossRef CAS PubMed.
- A. Omosebi, X. Gao, J. Landon and K. Liu, ACS Appl. Mater. Interfaces, 2014, 6, 12640–12649 CAS.
- E. Avraham, M. Noked, A. Soffer and D. Aurbach, Electrochim. Acta, 2011, 56, 6312–6317 CrossRef CAS.
- P. Dlugolecki and A. van der Wal, Environ. Sci. Technol., 2013, 47, 4904–4910 CrossRef CAS PubMed.
- J. W. Blair and G. W. Murphy, Adv. Chem. Ser., 1960, 27, 206 CrossRef.
- J. W. Blair and G. W. Murphy, Saline Water Conversion, American Chemical Society, 1960, pp. 206–223 Search PubMed.
- A. M. Johnson and J. Newman, J. Electrochem. Soc., 1971, 118, 510–517 CrossRef CAS.
- J. C. Farmer, D. V. Fix, G. V. Mack, R. W. Pekala and J. F. Poco, Low Level Waste Conference, Orlando, 1995.
- J. C. Farmer, D. V. Fix, G. V. Mack, J. F. Poco, J. K. Nielsen, R. W. Pekala and J. H. Richardson, Pacific Rim Environmental Conference, San Francisco, 1995.
- H. Li, Y. Gao, L. Pan, Y. Zhang, Y. Chen and Z. Sun, Water Res., 2008, 42, 4923–4928 CrossRef CAS PubMed.
- S.-I. Jeon, J.-S. Park, J.-G. Yeo, S. Yang, J. Choi and D. K. Kim, J. Mater. Chem. A, 2014, 2, 6378–6383 CAS.
- S. Porada, D. Weingarth, H. V. M. Hamelers, M. Bryjak, V. Presser and P. M. Biesheuvel, J. Mater. Chem. A, 2014, 2, 9313–9321 CAS.
- K. B. Hatzell, E. Iwama, A. Ferris, B. Daffos, K. Urita, T. Tzedakis, F. Chauvet, P.-L. Taberna, Y. Gogotsi and P. Simon, Electrochem. Commun., 2014, 43, 18–21 CrossRef CAS.
- S. Porada, L. Borchardt, M. Oschatz, M. Bryjak, J. Atchison, K. J. Keesman, S. Kaskel, P. M. Biesheuvel and V. Presser, Energy Environ. Sci., 2013, 6, 3700–3712 CAS.
- R. Zhao, S. Porada, P. M. Biesheuvel and A. van der Wal, Desalination, 2013, 330, 35–41 CrossRef CAS.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2219–2251 CrossRef PubMed.
- Y. Bouhadana, E. Avraham, A. Soffer and D. Aurbach, AIChE J., 2010, 56, 779–789 CAS.
- S. Porada, R. Zhao, A. van der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 CrossRef CAS.
- Y. Oren and A. Soffer, J. Appl. Electrochem., 1983, 13, 473–487 CrossRef CAS.
- J. C. Farmer, D. V. Fix, G. V. Mack, R. W. Pekala and J. F. Poco, J. Appl. Electrochem., 1996, 26, 1007–1018 CrossRef CAS.
- P. Xu, J. E. Drewes, D. Heil and G. Wang, Water Res., 2008, 42, 2605–2617 CrossRef CAS PubMed.
- H. Li, L. Zou, L. Pan and Z. Sun, Environ. Sci. Technol., 2010, 44, 8692–8697 CrossRef CAS PubMed.
- R. Zhao, M. van Soestbergen, H. H. M. Rijnaarts, A. van der Wal, M. Z. Bazant and P. M. Biesheuvel, J. Colloid Interface Sci., 2012, 384, 38–44 CrossRef CAS PubMed.
- A. M. Johnson, A. W. Venolia, R. G. Wilbourne, J. Newman, C. M. Wong, W. S. Gilliam, S. Johnson and R. H. Horowitz, U. S. Dept. of the Interior, Washington, 1970.
- I. Cohen, E. Avraham, M. Noked, A. Soffer and D. Aurbach, J. Phys. Chem. C, 2011, 115, 19856–19863 CAS.
- Y.-J. Kim and J.-H. Choi, Water Res., 2010, 44, 990–996 CrossRef CAS PubMed.
- Y.-J. Kim and J.-H. Choi, Water Res., 2012, 46, 6033–6039 CrossRef CAS PubMed.
- J.-H. Yeo and J.-H. Choi, Desalination, 2013, 320, 10–16 CrossRef CAS.
- J.-Y. Lee, S.-J. Seo, S.-H. Yun and S.-H. Moon, Water Res., 2011, 45, 5375–5380 CrossRef CAS PubMed.
- X. Gao, A. Omosebi, J. Landon and K. Liu, Energy Environ. Sci., 2015, 8, 897–909 CAS.
- V. Presser, C. R. Dennison, J. Campos, K. W. Knehr, E. C. Kumbur and Y. Gogotsi, Adv. Energy Mater., 2012, 2, 895–902 CrossRef CAS.
- M. Duduta, B. Ho, V. C. Wood, P. Limthongkul, V. E. Brunini, W. C. Carter and Y.-M. Chiang, Adv. Energy Mater., 2011, 1, 511–516 CrossRef CAS.
- V. E. Brunini, Y.-M. Chiang and W. C. Carter, Electrochim. Acta, 2012, 69, 301–307 CrossRef CAS.
- M. Pasta, C. D. Wessells, Y. Cui and F. La Mantia, Nano Lett., 2012, 12, 839–843 CrossRef CAS PubMed.
- S. Porada, P. M. Biesheuvel and V. Presser, Adv. Funct. Mater., 2015, 25, 179–181 CrossRef CAS.
- O. Kedem and T. Robinson, US Pat., 4,226,688, 1980 Search PubMed.
- A. Soffer and M. Folman, J. Electroanal. Chem. Interfacial Electrochem., 1972, 38, 25–43 CrossRef CAS.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294–1301 CAS.
- S. Zhang and N. Pan, Adv. Energy Mater., 2015, 5 DOI:10.1002/aenm.201401401.
- C. Tsouris, R. Mayes, J. Kiggans, K. Sharma, S. Yiacoumi, D. DePaoli and S. Dai, Environ. Sci. Technol., 2011, 45, 10243–10249 CrossRef CAS PubMed.
- P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031502 CrossRef CAS.
- C.-H. Hou, C. Liang, S. Yiacoumi, S. Dai and C. Tsouris, J. Colloid Interface Sci., 2006, 302, 54–61 CrossRef CAS PubMed.
- K.-L. Yang, T.-Y. Ying, S. Yiacoumi, C. Tsouris and E. S. Vittoratos, Langmuir, 2001, 17, 1961–1969 CrossRef CAS.
- J. Gabelich, P. Xu and Y. Cohen, Sustain. Sci. Eng., 2010, 2, 295–326 Search PubMed.
- E. Raymundo-Piñero, K. Kierzek, J. Machnikowski and F. Béguin, Carbon, 2006, 44, 2498–2507 CrossRef.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- M. E. Suss, T. F. Baumann, M. A. Worsley, K. A. Rose, T. F. Jaramillo, M. Stadermann and J. G. Santiago, J. Power Sources, 2013, 241, 266–273 CrossRef CAS.
- S. Kondrat, P. Wu, R. Qiao and A. A. Kornyshev, Nat. Mater., 2014, 13, 387–393 CrossRef CAS PubMed.
- T. Kim, H. D. Yoo, S. M. Oh and J. Yoon, Electrochim. Acta, 2014, 139, 374–380 CrossRef CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- T. Kim, J. E. Dykstra, S. Porada, A. van der Wal, J. Yoon and P. M. Biesheuvel, J. Colloid Interface Sci., 2015, 446, 317–326 CrossRef CAS PubMed.
- J. Veerman, M. Saakes, S. J. Metz and G. J. Harmsen, J. Appl. Electrochem., 2010, 40, 1461–1474 CrossRef CAS.
- J. Veerman, R. M. de Jong, M. Saakes, S. J. Metz and G. J. Harmsen, J. Membr. Sci., 2009, 343, 7–15 CrossRef CAS.
- R. Zhao, P. M. Biesheuvel, H. Miedema, H. Bruning and A. van der Wal, J. Phys. Chem. Lett., 2010, 1, 205–210 CrossRef CAS.
- T. Kim and J. Yoon, J. Electroanal. Chem., 2013, 704, 169–174 CrossRef CAS.
- A. H. Galama, J. W. Post, M. A. Cohen Stuart and P. M. Biesheuvel, J. Membr. Sci., 2013, 442, 131–139 CrossRef CAS.
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CrossRef CAS PubMed.
- A. Omosebi, X. Gao, J. Rentschler, J. Landon and K. Liu, J. Colloid Interface Sci., 2015, 446, 345–351 CrossRef PubMed.
- Y. Liu, C. Nie, X. Liu, X. Xu, Z. Sun and L. Pan, RSC Adv., 2015, 5, 15205–15225 RSC.
- K.-L. Yang, T.-Y. Ying, S. Yiacoumi, C. Tsouris and E. S. Vittoratos, Langmuir, 2001, 17, 1961–1969 CrossRef CAS.
- T.-Y. Ying, K.-L. Yang, S. Yiacoumi and C. Tsouris, J. Colloid Interface Sci., 2002, 250, 18–27 CrossRef CAS PubMed.
- G. W. Murphy, J. L. Cooper and J. A. Hunter and U. S. Dept. of the Interior, Washington, 1969.
- H. B. Li, T. Lu, L. K. Pan, Y. P. Zhang and Z. Sun, J. Mater. Chem., 2009, 19, 6773–6779 RSC.
- H. Li, L. Pan, T. Lu, Y. Zhan, C. Nie and Z. Sun, J. Electroanal. Chem., 2011, 653, 40–44 CrossRef CAS.
- H. Li, L. Pan, C. Nie, Y. Liu and Z. Sun, J. Mater. Chem., 2012, 22, 15556–15561 RSC.
- H. Wang, D. Zhang, T. Yan, X. Wen, L. Shi and J. Zhang, J. Mater. Chem., 2012, 22, 23745–23748 RSC.
- Z. Wang, B. Dou, L. Zheng, G. Zhang, Z. Liu and Z. Hao, Desalination, 2012, 299, 96–102 CrossRef CAS.
- H. Wang, D. Zhang, T. Yan, X. Wen, J. Zhang, L. Shi and Q. Zhong, J. Mater. Chem. A, 2013, 1, 11778–11789 CAS.
- Z. Li, B. Song, Z. Wu, Z. Lin, Y. Yao, K.-S. Moon and C. P. Wong, Nano Energy, 2015, 11, 711–718 CrossRef CAS.
- K. Dai, L. Shi, J. Fang, D. Zhang and B. Yu, Mater. Lett., 2005, 59, 1989–1992 CrossRef CAS.
- C. Nie, L. Pan, H. Li, T. Chen, T. Lu and Z. Sun, J. Electroanal. Chem., 2012, 666, 85–88 CrossRef CAS.
- L. Zou, L. Li, H. Song and G. Morris, Water Res., 2008, 42, 2340–2348 CrossRef CAS PubMed.
- Z. Peng, D. S. Zhang, L. Y. Shi, T. T. Yan, S. A. Yuan, H. R. Li, R. H. Gao and J. H. Fang, J. Phys. Chem. C, 2011, 115, 17068–17076 CAS.
- K. Sharma, R. T. Mayes, J. O. Kiggans Jr, S. Yiacoumi, J. Gabitto, D. W. DePaoli, S. Dai and C. Tsouris, Sep. Purif. Technol., 2013, 116, 206–213 CrossRef CAS.
- L. Pan, X. Wang, Y. Gao, Y. Zhang, Y. Chen and Z. Sun, Desalination, 2009, 244, 139–143 CrossRef CAS.
- J. W. Lee, H. I. Kim, H. J. Kim and S. G. Park, Appl. Chem. Eng., 2010, 21, 265–271 CAS.
- J. Yang, L. Zou, H. Song and Z. Hao, Desalination, 2011, 276, 199–206 CrossRef CAS.
- C. Nie, L. Pan, Y. Liu, H. Li, T. Chen, T. Lu and Z. Sun, Electrochim. Acta, 2012, 66, 106–109 CrossRef CAS.
- Z. Peng, D. Zhang, L. Shi and T. Yan, J. Mater. Chem., 2012, 22, 6603–6612 RSC.
- D. Zhang, T. Yan, L. Shi, Z. Peng, X. Wen and J. Zhang, J. Mater. Chem., 2012, 22, 14696–14704 RSC.
- H. Li, S. Liang, J. Li and L. He, J. Mater. Chem. A, 2013, 1, 6335–6341 CAS.
- Y. Wimalasiri and L. D. Zou, Carbon, 2013, 59, 464–471 CrossRef CAS.
- Y. Liu, C. Nie, X. Liu, X. Xu, Z. Sun and L. Pan, RSC Adv., 2015, 5, 15205–15225 RSC.
- G. Rasines, P. Lavela, C. Macías, M. C. Zafra, J. L. Tirado, J. B. Parra and C. O. Ania, Carbon, 2015, 83, 262–274 CrossRef CAS.
- Z. Lin, Z. Li, K.-s. Moon, Y. Fang, Y. Yao, L. Li and C.-p. Wong, Carbon, 2013, 63, 547–553 CrossRef CAS.
- G. Wang, C. Pan, L. Wang, Q. Dong, C. Yu, Z. Zhao and J. Qiu, Electrochim. Acta, 2012, 69, 65–70 CrossRef CAS.
- M. Wang, Z.-H. Huang, L. Wang, M.-X. Wang, F. Kang and H. Hou, New J. Chem., 2010, 34, 1843–1845 RSC.
- Y. Z. Chen, M. B. Yue, Z. H. Huang and F. Y. Kang, Chem. Eng. J., 2014, 252, 30–37 CrossRef CAS.
- C.-T. Hsieh and H. Teng, Carbon, 2002, 40, 667–674 CrossRef CAS.
- X. Xiang, E. Liu, Z. Huang, H. Shen, Y. Tian, C. Xiao, J. Yang and Z. Mao, J. Solid State Electrochem., 2011, 15, 2667–2674 CrossRef CAS.
- M. Rose, Y. Korenblit, E. Kockrick, L. Borchardt, M. Oschatz, S. Kaskel and G. Yushin, Small, 2011, 7, 1108–1117 CrossRef CAS PubMed.
- B.-J. Yoon, S.-H. Jeong, K.-H. Lee, H. Seok Kim, C. Gyung Park and J. Hun Han, Chem. Phys. Lett., 2004, 388, 170–174 CrossRef CAS.
- E. Frackowiak, S. Delpeux, K. Jurewicz, K. Szostak, D. Cazorla-Amoros and F. Béguin, Chem. Phys. Lett., 2002, 361, 35–41 CrossRef CAS.
- S. R. C. Vivekchand, C. S. Rout, K. S. Subrahmanyam, A. Govindaraj and C. N. R. Rao, J. Chem. Sci., 2008, 120, 9–13 CrossRef CAS.
- I. Cohen, E. Avraham, Y. Bouhadana, A. Soffer and D. Aurbach, Electrochim. Acta, 2015, 153, 106–114 CrossRef CAS.
- S. Kondrat, V. Presser, C. R. Perez, Y. Gogotsi and A. A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 CAS.
- Y. Liu, L. Pan, X. Xu, T. Lu, Z. Sun and D. H. C. Chua, Electrochim. Acta, 2014, 130, 619–624 CrossRef CAS.
- J.-B. Lee, K.-K. Park, S.-W. Yoon, P.-Y. Park, K.-I. Park and C.-W. Lee, Desalination, 2009, 237, 155–161 CrossRef CAS.
- J.-S. Kim and J.-H. Choi, J. Membr. Sci., 2010, 355, 85–90 CrossRef CAS.
- Y.-J. Kim and J.-H. Choi, Sep. Purif. Technol., 2010, 71, 70–75 CrossRef CAS.
- H. Li and L. Zou, Desalination, 2011, 275, 62–66 CrossRef CAS.
- C. Nie, Y. Zhan, L. Pan, H. Li and Z. Sun, Desalin. Water Treat., 2011, 30, 266–271 CrossRef CAS.
- J.-H. Lee and J.-H. Choi, J. Membr. Sci., 2012, 409–410, 251–256 CrossRef CAS.
- H. Li, C. Nie, L. Pan and Z. Sun, Desalin. Water Treat., 2012, 42, 210–215 CrossRef CAS.
- C. Yan, Y. W. Kanaththage, R. Short, C. T. Gibson and L. Zou, Desalination, 2014, 344, 274–279 CrossRef CAS.
- M. Deschamps, E. Gilbert, P. Azais, E. Raymundo-Piñero, M. R. Ammar, P. Simon, D. Massiot and F. Béguin, Nat. Mater., 2013, 12, 351–358 CrossRef CAS PubMed.
- S. Porada, J. Lee, D. Weingarth and V. Presser, Electrochem. Commun., 2014, 48, 178–181 CrossRef CAS.
- M. Aslan, D. Weingarth, P. Herbeck-Engel, I. Grobelsek and V. Presser, J. Power Sources, 2015, 279, 323–333 CrossRef CAS.
- M. Aslan, D. Weingarth, N. Jäckel, J. S. Atchison, I. Grobelsek and V. Presser, J. Power Sources, 2014, 266, 374–383 CrossRef CAS.
- N. Jäckel, D. Weingarth, M. Zeiger, M. Aslan, I. Grobelsek and V. Presser, J. Power Sources, 2014, 272, 1122–1133 CrossRef.
- M. T. Z. Myint, S. H. Al-Harthi and J. Dutta, Desalination, 2014, 344, 236–242 CrossRef CAS.
- E. Garcia-Quismondo, C. Santos, J. Lado, J. Palma and M. A. Anderson, Environ. Sci. Technol., 2013, 47, 11866–11872 CrossRef CAS PubMed.
- R. K. McGovern, S. M. Zubair and J. H. Lienhard V, Desalination, 2014, 348, 57–65 CrossRef CAS.
- L. F. Greenlee, D. F. Lawler, B. D. Freeman, B. Marrot and P. Moulin, Water Res., 2009, 43, 2317–2348 CrossRef CAS PubMed.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- W. Zhang, M. Mossad and L. Zou, Desalination, 2013, 320, 80–85 CrossRef CAS.
- Y.-J. Kim, J. Hur, W. Bae and J.-H. Choi, Desalination, 2009, 253, 119–123 CrossRef.
- C. Huyskens, J. Helsen, W. J. Groot and A. B. de Haan, Sep. Purif. Technol., 2013, 118, 33–39 CrossRef CAS.
- S.-J. Kim, J.-H. Choi and J.-H. Kim, Process Biochem., 2012, 47, 2051–2057 CrossRef CAS.
- S.-M. Jung, J.-H. Choi and J.-H. Kim, Sep. Purif. Technol., 2012, 98, 31–35 CrossRef CAS.
- S. H. Roelofs, B. Kim, J. C. T. Eijkel, J. Han, A. van den Berg and M. Odijk, Lab Chip, 2015, 15, 1458–1464 RSC.
- C. Macías, P. Lavela, G. Rasines, M. C. Zafra, J. L. Tirado and C. O. Ania, J. Appl. Electrochem., 2014, 44, 963–976 CrossRef.
- G.-H. Huang, T.-C. Chen, S.-F. Hsu, Y.-H. Huang and S.-H. Chuang, Desalin. Water Treat., 2013, 52, 759–765 CrossRef.
- H. Wang and C. Na, ACS Appl. Mater. Interfaces, 2014, 6, 20309–20316 CAS.
- J. C. Farmer, S. M. Bahowick, J. E. Harrar, D. V. Fix, R. E. Martinelli, A. K. Vu and K. L. Carroll, Energy Fuels, 1997, 11, 337–347 CrossRef CAS.
- S.-Y. Huang, C.-S. Fan and C.-H. Hou, J. Hazard. Mater., 2014, 278, 8–15 CrossRef CAS PubMed.
- C.-C. Huang and J.-C. He, Chem. Eng. J., 2013, 221, 469–475 CrossRef CAS.
- T. Ryu, D.-H. Lee, J. C. Ryu, J. Shin, K.-S. Chung and Y. H. Kim, Hydrometallurgy, 2015, 151, 78–83 CrossRef CAS.
- Y. Liu, L. Pan, X. Xu, T. Lu and Z. Sun, RSC Adv., 2013, 3, 16932–16935 RSC.
- L. F. Yang, Z. Shi and W. H. Yang, Surf. Coat. Technol., 2014, 251, 122–127 CrossRef CAS.
- Y. Chen, L. Peng, Q. Zeng, Y. Yang, M. Lei, H. Song, L. Chai and J. Gu, Clean Technol. Environ. Policy, 2014, 1–9 Search PubMed.
- J.-H. Lee, W.-S. Bae and J.-H. Choi, Desalination, 2010, 258, 159–163 CrossRef CAS.
- D. Grujicic and B. Pesic, Electrochim. Acta, 2002, 47, 2901–2912 CrossRef CAS.
- W. Zhang, M. Mossad, J. S. Yazdi and L. Zou, Desalin. Water Treat., 2014, 1–7 Search PubMed.
- C. Forrestal, P. Xu and Z. Ren, Energy Environ. Sci., 2012, 5, 7161–7167 CAS.
- L. Y. Lee, H. Y. Ng, S. L. Ong, G. Tao, K. Kekre, B. Viswanath, W. Lay and H. Seah, Water Res., 2009, 43, 4769–4777 CrossRef CAS PubMed.
- R. S. Deinhammer, K. Shimazu and M. D. Porter, Anal. Chem., 1991, 63, 1889–1894 CrossRef CAS.
- F. Kocak, K. Vuorilehto, J. Schrader and D. Sell, J. Appl. Electrochem., 2005, 35, 1231–1237 CrossRef CAS.
- Y. Liu, W. Ma, Z. Cheng, J. Xu, R. Wang and X. Gang, Desalination, 2013, 326, 109–114 CrossRef CAS.
- Y.-J. Kim, J.-H. Kim and J.-H. Choi, J. Membr. Sci., 2013, 429, 52–57 CrossRef CAS.
- L. D. Nghiem, P. Mornane, I. D. Potter, J. M. Perera, R. W. Cattrall and S. D. Kolev, J. Membr. Sci., 2006, 281, 7–41 CrossRef CAS.
- M. I. G. S. Almeida, R. W. Cattrall and S. D. Kolev, J. Membr. Sci., 2012, 415–416, 9–23 CrossRef CAS.
- B. van Limpt and A. van der Wal, Desalination, 2014, 342, 148–155 CrossRef CAS.
- R. de Levie, Electrochim. Acta, 1963, 8, 751–780 CrossRef.
- E. Conway, Electrochemical Supercapacitors, Springer, New York, 1999 Search PubMed.
- D. Weingarth, M. Zeiger, N. Jäckel, M. Aslan, G. Feng and V. Presser, Adv. Energy Mater., 2014, 4 DOI:10.1002/aenm.201400316.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021502 CrossRef.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- R. K. Kalluri, M. M. Biener, M. E. Suss, M. D. Merrill, M. Stadermann, J. G. Santiago, T. F. Baumann, J. Biener and A. Striolo, Phys. Chem. Chem. Phys., 2013, 15, 2309–2320 RSC.
- P. M. Biesheuvel, Y. Fu and M. Z. Bazant, Russ. J. Electrochem., 2012, 48, 580–592 CrossRef CAS.
- J. Newman and W. Tiedemann, AIChE J., 1975, 21, 25–41 CrossRef CAS.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems, John Wiley & Sons, Inc Publications, Hoboken, 3rd edn, 2004 Search PubMed.
- H. A. Arafat, M. Franz and N. G. Pinto, Langmuir, 1999, 15, 5997–6003 CrossRef CAS.
- B. Kastening and M. Heins, Electrochim. Acta, 2005, 50, 2487–2498 CrossRef CAS.
- S. Porada, M. Bryjak, A. van der Wal and P. M. Biesheuvel, Electrochim. Acta, 2012, 75, 148–156 CrossRef CAS.
- T. Teorell, Discuss. Faraday Soc., 1956, 21, 9–26 RSC.
- T. Teorell, in Progress in biophysics and biophysical chemistry, ed. J. A. V. Butler and J. T. Randall, Academic Press, London, 1953, pp. 305–369 Search PubMed.
- J. E. Dykstra, P. M. Biesheuvel, H. Bruning and A. Ter Heijne, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013302 CrossRef CAS.
- J. M. Paz-Garcia, O. Schaetzle, P. M. Biesheuvel and H. V. M. Hamelers, J. Colloid Interface Sci., 2014, 418, 200–207 CrossRef CAS PubMed.
- M. B. Andersen, M. van Soestbergen, A. Mani, H. Bruus, P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. Lett., 2012, 109, 108301 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |