Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tracking the structural arrangement of ions in carbon supercapacitor nanopores using in situ small-angle X-ray scattering†
C.
Prehal
a,
D.
Weingarth
b,
E.
Perre
b,
R. T.
Lechner
a,
H.
Amenitsch
c,
O.
Paris
*a and
V.
Presser
bd
aInstitute of Physics, Montanuniversitaet Leoben, Franz-Josef Strasse 18, 8700 Leoben, Austria. E-mail: oskar.paris@unileoben.ac.at
bINM-Leibniz Institute for New Materials, Campus D2 2, 66123 Saarbrücken, Germany
cInstitute of Inorganic Chemistry, Graz University of Technology, Stremayrgasse 9/V, 8010 Graz, Austria
dDepartment of Materials Science and Engineering, Saarland University, Campus D2 2, 66123 Saarbrücken, Germany
First published on 17th March 2015
Abstract
The charge storage mechanism and ion arrangement inside electrically charged carbon nanopores is a very active research field with tremendous importance for advanced electrochemical technologies, such as supercapacitors or capacitive deionization. Going far beyond the state of art, we present for the first time a comprehensive study of tracking ion electrosorption in aqueous electrolytes during charging and discharging of porous carbon electrodes using in situ X-ray scattering. We provide novel and quantitative insights into the local concentration of anions and cations and demonstrate that the global number of ions within the pores does not vary during charging and discharging. In addition, we have unique access to the spatial arrangement of ions inside carbon nanopores by using a simple, yet powerful two-phase model. Applying this model to our data, we show that double-layer formation is accomplished by a unique combination of preferred counter-ion adsorption directly at the pore wall which drains ions from their local surrounding inside carbon nanopores. Effectively, this leads to a situation which globally appears as ion swapping.
Broader contextThe demand for green energy technologies has increased tremendously over the past few years. A serious bottleneck for sustainable energy management on large- and small-scales (from renewable energy sources to e-mobility or microelectronics) is efficient energy storage. Among such systems, supercapacitors have emerged as an advanced technology for rapid energy storage and recovery at high efficiency and long life expectancy. Yet, further advancement of supercapacitor technology requires a better understanding of the fundamental charge storage mechanisms via ion electrosorption in nanoporous carbon materials. This is also the basis to capitalize advanced modelling for an improved design of electrode materials and structures. Yet, even the most advanced experimental in situ methods fall short in combining global information on charge and ion concentration with the local arrangement of ions inside carbon nanopores. The present work illustrates the potential of in situ small-angle X-ray scattering as a complementary experimental approach providing novel insights into ion transport and charge storage within carbon nanopores. |
1 Introduction
Electrical double-layer capacitors (EDLCs), also known as supercapacitors or ultracapacitors, are advanced electrochemical energy storage devices preferred for high power handling and long lifetime applications.1 Energy storage is accomplished by fast ion electrosorption at the electrostatically charged electrode surface and this mechanism effectively mitigates kinetic limitations caused by slow faradaic reactions or limited ion transport during ion intercalation notoriously found in battery systems.2 Over the last few years, significant improvements in the basic understanding of ion charge storage mechanisms in nanopores of highly porous carbon electrodes have been obtained.3–7 Tremendous efforts have been made recently to design new electrodes and electrolytes to optimize performance parameters such as power- and energy density or cycling stability. On the theory side, models for charge storage mechanisms have advanced vastly by applying atomistic modelling approaches, and also new experimental in situ methods have rapidly developed.5,6,8–13As one of the first, Chmiola et al. demonstrated an enhanced capacitance for nanopores with a size comparable to the desolvated ion diameter, which implies that ions partly or fully lose their solvation shell in order to fit into such pores.14 The importance of ion size with respect to the pore size has been shown for electrolytes with or without solvent,1,14,15 and has also been supported by molecular dynamics (MD) studies using aqueous electrolytes.16 Moreover the specific arrangement of ions (and solvent molecules) across the pore is crucial to understand the dependency of the areal capacitance (F m−2) on the micropore size (i.e., pores smaller than 2 nm).5,16–19
Based on these findings, we have started to gain a better understanding of the rather complex process of charge storage via double-layer formation from a structural point of view. There are different ways by which ion electrosorption can accomplish charge storage (Fig. S1a, ESI†).20 In the simplest case, one could assume counter-ion adsorption, where each electrode charge carrier is compensated by the adsorption of an ion of opposite charge compared to the pore wall leading to an increase in the total number of ions in nanopores.21 The other extreme would be pure co-ion expulsion, leading to a decrease in the total ion number of pores.20 A third possibility is the combination of both mechanisms via ion swapping, where every two electrode charge carriers are compensated by a counter-ion entering and a co-ion leaving the pore.6 In the latter case, the total number of ions (i.e., anions plus cations inside pores) remains constant. Whether ion swapping or preferred counter-ion adsorption/co-ion desorption dominates may depend on a variety of parameters, such as the ion concentration, the cation-to-anion size ratio, or hydration energies.20
Standard electrochemical methods are commonly used to determine the total amount of accumulated/depleted charge per time unit, thus failing in probing the nature of the actual charge storage mechanism.22 Advanced electrochemical testing, for example by using impedance spectroscopy, deconvoluting time constants, and fitting equivalent circuit models, can greatly help to advance our knowledge on charge transfer and storage, but still requires validation by a complementary method. Until now, there exist only very few experimental tools that allow a distinction between the different species (cations, anions, and solvent molecules) involved in the charging process.6,23,24 The electrochemical quartz crystal microbalance (eQCM) for instance is very powerful to measure the mass change of a thin film electrode during electrosorption, yielding mass-related information on the ions for one electrode.11 This information can be used to get global information on the ion transport in- and out of a working electrode. However, no information on the local arrangement of ions with respect to the charged electrode surface within the pore space is obtained by this method. In contrast, spectroscopic techniques such as nuclear magnetic resonance (NMR) spectroscopy are highly sensitive to the local ion environment,6 and thus provide rather specific information on whether a certain ion species is preferentially adsorbed to the electrode surface or not. Yet, information on the ion concentration in different sized pores and the local ion arrangement remains limited using this method.
In this study, we employ small-angle X-ray scattering (SAXS) as a powerful technique sensitive to track ion kinetics and local concentrations across the nanopores. X-ray or neutron scattering methods generally have the advantage of providing direct access to structural parameters from molecular length scales up to several tens of nanometers, which has been capitalized by only a few initial studies so far. In the ideal case of ordered mesopores with small size distribution, the electron density distribution of a liquid within the pores can be determined, as was recently shown for the density distribution of water in confinement.25In situ SAXS has been applied previously to study electrosorption of sodium ions or the electrochemical activation in activated carbons.26,27 Also, small-angle neutron scattering (SANS) has been applied successfully to study supercapacitors, where the change in the SANS signal was related to the equilibrium ion concentration within carbon nanopores.28,29 For the first time, these studies demonstrated the unique ability of small-angle neutron scattering to extract pore-size dependent information on electrowetting and electrosorption within microporous electrodes.
However, the full potential of small-angle scattering has not been unlocked so far to obtain selective information on cation and anion concentrations independent from each other and, at the same time, on the specific re-arrangement of ions within carbon nanopores during charging and discharging. In the present study, we demonstrate for the first time that in situ SAXS is a powerful technique to provide this unique information for aqueous electrolytes in highly disordered activated carbons. Following complementary analysis, we combine the information derived from SAXS with the X-ray transmission (XRT) signal, which allows evaluating the photoelectric absorption of the X-rays in order to track changes of the absolute ion concentration during voltage cycling of an actual supercapacitor cell. We investigate three different salts (CsCl, KCl, and NaCl) in aqueous solution at 1 M concentration to make use of their different absorption and scattering cross-sections for X-rays within the pores of an activated carbon with an average pore size of 1.3 nm. This pore size was important for our study to exclude the presence of strong ion size related effects, such as ion sieving.30,31 The choice of aqueous electrolytes is motivated by the simplicity of the ions on the one hand, but also by the renaissance of water-based electrolytes for high-power supercapacitors32 and their importance for capacitive deionization33 or capacitive mixing energy harvesting.34
2 Experimental
Materials
Electrolytes were prepared by mixing distilled water and salts with high purity (CsCl: 99.9%; NaCl: 99.99%; both provided by Alfa Aesar). The 1 M KCl aqueous solution was used as received (Alfa Aesar). As an electrode material a 300 μm thick activated carbon (AC) film was made employing YP-80 (Kuraray Chemicals). Activated carbon and polytetrafluoroethylene (PTFE in a 60 wt% aqueous solution from Sigma Aldrich) were mixed using a mortar and pestle in a 95 to 5 wt% ratio. Ethanol was added to the blend and the final films with a thickness of 300 ± 15 μm (determined via a microcaliper) were obtained by using a hot rolling press. Finally, the electrodes were dried for 24 h at 120 °C under vacuum. Nitrogen gas sorption measurements at −196 °C revealed an average pore diameter of 1.3 nm from micro- (<2 nm) and mesopores (2–50 nm) which yielded a specific surface area of 1672 m2 g−1 for the electrode film (Fig. S2, ESI†). The AC particles had a size of up to several μm, leading to an additional volume of macropores (>50 nm) within the electrode for the space comprised between such particles; yet, in terms of the specific surface area their contribution is negligible (<1 m2 g−1). A sketch of the pore system in AC is given in the ESI,† Fig. S1, where the basic mechanisms of charge accommodation within single micropores are also indicated. For the cell assembly, a thin platinum paper (Dukatshop.de; ∼200 nm) was used as a current collector (CC) and a porous Whatman (GF/A) membrane as a separator.Electrochemical in situ experiments
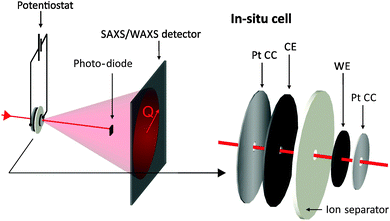
X-ray experiments were conducted at the SAXS beamline of the synchrotron radiation source ELETTRA in Trieste, Italy.35 A monochromatic X-ray beam with a wavelength of 0.154 nm was selected. The beam spot at the sample was quadratic with a size of 1 mm2.Fig. 1 shows schematically the experimental setup to record simultaneously the X-ray transmission (XRT) signal and a two-dimensional (2D) SAXS pattern during the cyclic voltammetry measurement of an activated carbon electrode. While applying the cyclic voltage signal with a potentiostat, each transmission value and SAXS pattern are measured in a period of 10 s. The small-angle scattering signal is recorded using a 2D position sensitive X-ray detector (SAXS: Pilatus 1M) and the transmission signal using an X-ray sensitive photodiode. In addition to the small-angle data, the wide-angle X-ray scattering (WAXS) intensity was also recorded using a second 2D detector (Pilatus 100K). The specific design of the in situ supercapacitor cells enables us to selectively probe only one electrode at a time, so that all data can be related just to the working electrode. As outlined in Fig. 1, the in situ cells were tested in a two-electrode arrangement with a ca. 4 time oversized counter electrode (CE). The assembly of the platinum current collector/working electrode/separator/counter electrode (YP-80)/platinum current collector was sandwiched in a polyether ether ketone (PEEK) housing and was kept in contact with titanium end plates similar to the in situ cell developed by Ruch et al.27 Moreover, two sticky polyimide (Kapton) tapes sealed the cell at the X-ray entrance holes between the platinum current collectors and the titanium/PEEK casing. Electrochemical measurements were carried out using a Gamry Ref 600 Potentiostat and cyclic voltammetry was performed at a scan rate of 5 mV s−1. Additional transmission measurements were carried out using a laboratory SAXS instrument (Nanostar, Bruker AXS) using Cu-Kα radiation and the Glassy Carbon Method for transmission measurements.36
SAXS data treatment
Before analyzing the in situ SAXS data, the scattering raw data were treated in the following way. First, the 2D scattering data were averaged azimuthally using the software FIT2D.37 The resulting scattering intensity as a function of the scattering vector length Q was normalized by the corresponding transmission value and divided by the exposure time of 9 s. Finally, background contributions from air scattering and the polyimide tape were subtracted.The so-called radius of gyration is a parameter sensitive to any structural change within the system of ions, water molecules, and the carbon pore structure. It is easily assessable from the SAXS signal by performing a conventional Guinier analysis.38,39 The Guinier analysis was conducted for Q-values larger than 1.2 nm−1 in order to avoid any impact of the scattering contribution from the large carbon particles. Moreover, an ion concentration dependent background contribution originating from the carbon and electrolyte structure factor (see Fig. 4b) was subtracted from the SAXS intensity. This background was evaluated by a modified Porod analysis.39 In a perfect two-phase material, the intensity at large Q decays with a power law I(Q) ∼ Q−4. In disordered microporous carbons on the other hand the exponent might be significantly smaller than 4. This fact is explained by a breakdown of the validity of the ideal two-phase model with sharp interfaces due to the small size of the pores with a rough or fractal surface.40–42 From a power law fit, an exponent of −3.28 was obtained for Q-values between 4 nm−1 and 8 nm−1. Assuming a SAXS intensity of the form AQ−3.28 + BG, the background was evaluated by the common Porod procedure and then subtracted from the data.
3 Results and discussion
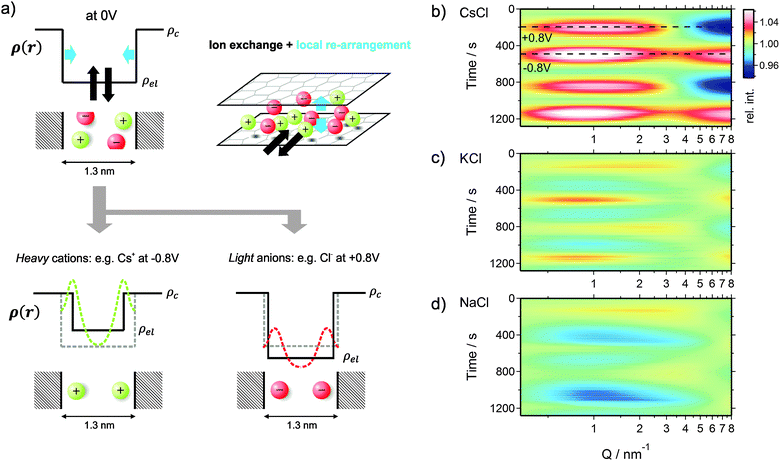
Electrochemical performance
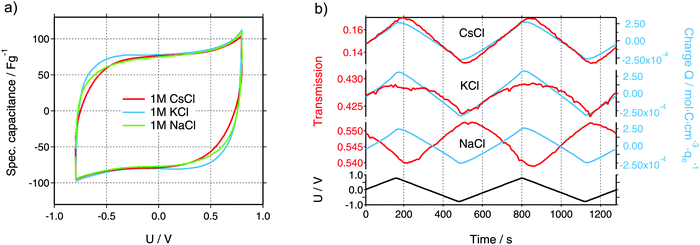
Characteristic cyclic voltammograms (CVs) at a scan rate of 5 mV s−1 of three aqueous electrolytes are shown in Fig. 2a. Each of the in situ experiments was carried out in a new cell, with identical geometry and components except for the electrolyte. All tested electrolytes reveal near-ideal EDLC performance with specific capacitance values of about 75 F g−1 and the absence of detrimental effects like electrochemical degradation, ion sieving, or parasitic faradaic reactions.30 Slight differences are visible at the vertex potentials, which can be attributed to differences in the ionic conductivity of the electrolytes or the differences in the ion size and, therefore, different ion transport properties inside the porous structure. Furthermore, the size of the hole, cut in all materials except WE, determines the kinetics of the in situ cells. In the case of the CsCl measurement, this hole (6 mm) was larger as compared to KCl and NaCl (3 mm), leading to a larger equivalent serial resistance due to an increased ion diffusion pathway. In conclusion, the in situ cell shows an electrochemical performance comparable to conventional cells and, thus, can be used as an ideal platform for meaningful operando testing.Integral ion concentrations from XRT
While the electrochemical data for all three tested electrolytes were roughly identical, we see that the XRT data during charging and discharging exactly differentiate the different ionic systems (Fig. 2b). In general, the XRT signal of the WE is determined by the ratio of the intensities of the transmitted beam (I) and the primary beam (I0). Thus, it relates to the concentrations ci of the different ion species in the electrode, their thickness di, their molar masses Mi and their mass attenuation coefficients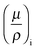 via the Lambert–Beer law (eqn (1)).
via the Lambert–Beer law (eqn (1)).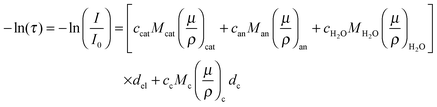 | (1) |
| Cs+ | K+ | Na+ | Cl− | H2O | |
|---|---|---|---|---|---|
| Mass attenuation coefficients [cm2 g−1] | 330 | 151 | 31 | 111 | 10 |
| Electron number of dehydrated ions n | 54 | 18 | 10 | 18 | 10 |
| Effective electron number neff | 59 | 31(40) | 32(40) | 24 | 10 |
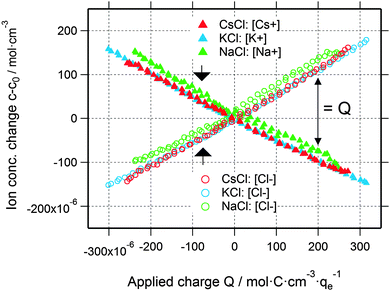
Using the data shown in Fig. 2b, it is possible to obtain quantitative information on the change in the ion concentration with time. Eqn (1) constitutes an equation with two unknown concentrations can and ccat. A second independent equation containing the same two unknown concentrations is obtained from the total charge Q calculated by integrating the current signal I(t) over time and normalized by the electrolyte volume Vel (eqn (2)).
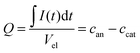 | (2) |
Assessing complementary information from SAXS
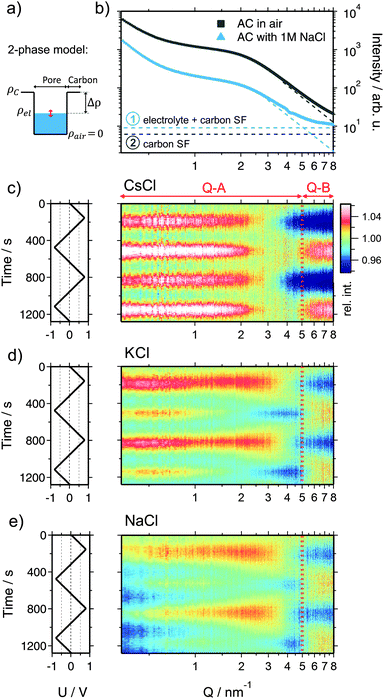
Beyond information on the ion concentration from XRT, SAXS allows to unravel more details about the ion electrosorption mechanism. The SAXS curves from carbon electrodes in air or when soaked with electrolyte are shown in Fig. 4. These curves can be categorized into three main regions, having their origin in different levels of hierarchy of the carbon structure. At very small values of the scattering vector modulus Q (Q < 0.7 nm−1), the power law decay of the SAXS intensity is at least partly attributed to large pores between the micrometer-sized AC particles (macroporosity).44 Scattering from disordered micropores dominates the intermediate region between 0.7 nm−1 and 5 nm−1. This region is often described by the so-called Debye–Anderson–Brumberger (DAB) model45 to obtain average correlation parameters that are related to the size and surface area of the pores.44 At larger Q-values (i.e., Q > 5 nm−1), the molecular structure factors of the carbon matrix and the electrolyte dominate, corresponding to the correlation of individual carbon atoms and electrolyte ions.46When the electrode is infiltrated with the electrolyte, the SAXS intensity (Fig. 4b, blue curve) at low and medium Q significantly decreases due to the decreased electron density difference (SAXS contrast) (Δρ)2 = (ρc − ρel)2 between the carbon matrix and electrolyte-filled pores (Fig. 4a).39 At the same time, the intensity at large Q increases due to the contribution of the electrolyte molecular structure factor in addition to the carbon structure factor (Fig. S4a, ESI†). If the ions are randomly distributed within the water matrix, the electrolyte structure factor contribution is constant in the SAXS regime47 (indicated in Fig. 4b), its value being determined by the concentration and the type of ion within the irradiated sample volume.48 A more detailed description of the small- and wide-angle scattering intensity (SAXS & WAXS) of both dry and wet AC is given in the ESI.† Moreover, SAXS intensities of all three cells at 0 V cell potential are also shown.
When a voltage is applied to the electrolyte-filled carbon electrode, the change in the electron density contrast in the pores (red arrow in Fig. 4a) is expected to lead to a change in the SAXS intensity, as was previously demonstrated.26–28 However, not only the mean electron density within the pores is expected to change, but also the re-arrangement of the ions within the pores due to counter-ion adsorption at the pore walls. Qualitatively, this causes a change in the shape of the SAXS curve, which goes beyond a simple vertical shift of the intensity due to an average contrast change considered widely in the literature so far.
In order to visualize the voltage-dependence of the SAXS signal, all SAXS curves were normalized by the first curve measured at 0 V and are displayed in Fig. 4c–e as color-coded relative intensity versus time and Q. As the very low-Q region is not of primary interest here, the scattering curves were conveniently classified into two main regions Q-A (<5 nm−1) and Q-B (>5 nm−1) (indicated in Fig. 4c–e), emphasizing essentially the SAXS region and the onset of the molecular structure factor region.
As shown in the ESI,† the electrolyte structure factor for the given systems can be approximated by eqn (3):
| I(QB) ≅ A[ϕcat(ncat − nH2O)2 + ϕan(nan − nH2O)2 + C] | (3) |
A possible explanation for this unexpected behavior of the scattering intensity for KCl and NaCl can be given when we also consider the role of the solvent, that is, exchange or densification of water. An increased amount of water molecules transported by small cations has been proposed in a recent eQCM study.21 Instead of just considering the bare ions in eqn (3), a densified water layer surrounding each ion is taken into account.47 This leads to the concept of an effective electron number. The numbers of tightly bound water molecules evaluated by Levi et al.21 for carbon nanopores were used to calculate these effective values, which are listed in Table 1. The effective electron numbers of the K+ and Na+ ions are now similar, and both are larger than the one of the Cl− ion, in qualitative agreement with the experimental observation.
We shall now discuss the SAXS intensity in region Q-A (Fig. 4). If a simple two-phase model of a homogeneous electrolyte within the pores of the carbon matrix is applicable, the intensity in the SAXS regime should behave just opposite to the electrolyte structure factor in Q-B, since it is determined by the scattering contrast (Δρ)2 = (ρc − ρel)2. This is obviously not the case for any of the used electrolytes (Fig. 4c–e). Again, for CsCl the situation should be the simplest one, since the scattering intensity changes will be dominated by the Cs+ concentration changes. When assuming pure ion swapping, one would expect an intensity increase at positive voltage (when Cs+ is expelled) and a decrease at negative voltage (when Cs+ is adsorbed). However, at negative voltage not a minimum, but a strong intensity maximum is observed experimentally, which cannot be simply related to ion concentration changes. In the case of the KCl electrolyte at intermediate Q-values (1 nm−1 < Q < 5 nm−1), the intensity signal reveals maxima at positive and minima at negative voltages (Fig. 4d). This behavior would be consistent with the simple two-phase model considering the results from the electrolyte scattering. However, similar to the CsCl sample, an additional intensity maximum is observed at negative voltages at Q < 1 nm−1, although this maximum is less pronounced. Finally, considering the effective electron number of Na+ ions (Table 1) and the measured concentration changes (Fig. 3), the intensity change in the Q-A region should be rather similar to KCl, which is obviously the case (Fig. 4d and e).
We conclude that a simple two-phase model with an essentially homogeneous electron density distribution of the electrolyte within the micropores is not able to explain the behavior of the SAXS intensity within the Q-A regime. A peculiar feature, namely an intensity maximum at negative voltages, occurs for all electrolytes at medium to low Q-values. This maximum scales roughly with the effective electron number of the cations adsorbed, being largest for Cs+ and smaller for K+ and Na+.
The radius of gyration as a correlation length parameter
The deviation from a simple two-phase model is not unexpected, since – at least for large enough pores – the counter-ions are expected to accumulate close to the pore walls during double-layer formation. Yet, SAXS from a multiphase system in connection with the complex disordered pore structure of activated carbons is not treatable without introducing too many ad hoc assumptions. Therefore, in order to understand the basic features of the structural arrangement of the ions within the pore space, Guinier analysis of the SAXS data is a convenient tool.38 As the Guinier approximation is strictly applicable only for particulate systems of low volume fraction, the radius of gyration obtained from this analysis is merely a correlation length parameter without direct connection to a real size in the system.In Fig. 5, the relative change of the radius of gyration (Rg) is plotted as a function of the applied charge, with the values being normalized to the Rg value at zero voltage. The magnitude of the normalized radius of gyration is high for CsCl and lower for KCl and NaCl at maximum negative voltage. Going from zero to maximum positive charge, all electrolytes show an increase of Rg. The increase of Rg left and right to the minimum is clearly correlated with the effective electron number (Table 1) of the individual counter-ions (Cs+, K+, or Na+ at negative charge and Cl− at positive charge). Hence, the change in the correlation length rather than the change in the intensity seems to open a way to a better understanding of the in situ SAXS signals. This will be discussed in the following section.
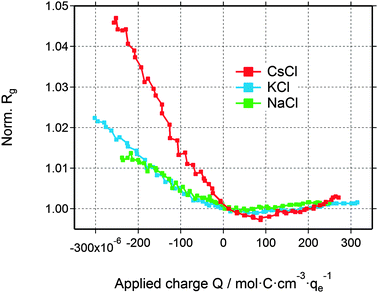 | ||
| Fig. 5 Relative change of the radius of gyration for all three electrolytes as a function of the applied charge. | ||
Probing local ion arrangement
As seen from gas sorption data (see ESI†), the volume fraction of micropores in the electrode materials is 69% and the average pore size is about 1.3 nm. Hence, on average, there is enough space for two solvated ions next to each other to build up a layer of electrosorbed ions at the charged carbon surface. Such preferred arrangement of ions should lead to a significant change in the electrolyte electron density close to the carbon surface not only in the case of Cs+ ions, but also for K+ and Na+ taking their effective electron numbers into account. Yet, the resolution of the SAXS setup is not sufficient to deduce unambiguously the real electron density profile.As sketched in Fig. 6a, the increase of the actual electron density near the surface may be represented within a two-phase model by an effective decrease of the pore size. Upon charging, an excess amount of counter-ions will be attracted by the pore walls leading to an electron density profile as sketched in Fig. 6a on the bottom. The green dashed line represents this profile within the pore for heavy cations like Cs+ (large effective electron number) and the red dashed line indicates the electron density profile caused by light ions like Cl− (having a small effective electron number). In our resolution limited SAXS experiment, the electron density near the pore walls can be replaced by the black line to represent again a two-phase model, leading to an effective decrease of the pore volume fraction. Furthermore, the average electrolyte electron density ρel changes upon changing the average ion concentrations within the pore. This model is very useful and may be employed even for pores smaller than the double-hydrated ion diameter, as the probability of ions in proximity to the pore wall is still higher compared to the pore center.
 | ||
| Fig. 6 (a) Sketch of the electron density profile of a carbon pore filled with the electrolyte at 0 V (top). The size of the sketched ions corresponds roughly to the dehydrated ion size with respect to the average pore size of 1.3 nm. Water molecules in the hydration shell and the solvent are not visualized. When applying a voltage, the average ion concentration within the pores will change (ion exchange in and out of the pores: indicated as black arrows on the top). Moreover the ions will re-arrange locally within the nanopore (local re-arrangement: blue arrows on the top). These changes lead to electron density profiles as sketched on the bottom. In the case of heavy ions (large effective electron number), the preferably adsorbed ions next to the pore walls will lead to a significant increase of the electron density close to the pore walls. The sketch of the real electron density across the pore (green dashed line) can be replaced by the profile shown by the black solid line suggesting an apparent decrease of the pore size. The same argument is valid for negative voltages when Cl− ions are situated preferably near the pore walls, but due to their lower effective electron number the apparent decrease of the effective pore width is smaller. The sketched profiles on the bottom describe the situation exemplarily for −0.8 V and +0.8 V. These two points are indicated as dashed lines within the simulated scattering intensities in (b). (b)–(d) Simulated scattering intensities of all three electrolytes, covering changes of the pore volume fraction, the average electrolyte density and the electrolyte structure factor. (b) CsCl, (c) KCl, (d) NaCl. The simulations reproduce very well the main features of the measured scattering intensity changes (Fig. 4c–e). | ||
We can now implement the data obtained from our Guinier analysis. As we are still in a two-phase approximation, the radius of gyration can be related to the actual volume fraction of pores and the carbon matrix. Within the Debye–Anderson–Brumberger (DAB) model, which has been used extensively to describe the structure of disordered carbons, this relationship is explicitly given in ref. 44, 45 and 50viaeqn (4):
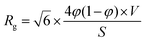 | (4) |
Fig. 6b shows that the scattering intensity increases at small Q-values when the radius of gyration is increased (in particular at negative voltages). The simulations of all three electrolytes are in excellent agreement with the measured scattering data (Fig. 4c–e). Using only two independent signals from the XRT evaluation (ion concentrations) and the SAXS measurements (Rg) as an input for a simple model, we were able to fully reproduce the complex changes of the SAXS intensity. Hence, the relative change of the radius of gyration in Fig. 5 can be understood as a measure for ions preferably adsorbed on the pore walls and weighed by a factor related to the effective electron number (see sketch in Fig. 6a). With this we can come to a qualitative explanation of Fig. 5 as being a measure of the local ion concentration close to the pore walls.
Interestingly, the local ion concentration near the pore walls (Fig. 5) behaves quite differently as compared to the global ion concentration (Fig. 3) which was interpreted as pure ion swapping. The radius of gyration signals increase strongly at negative applied charge, but only slightly at positive values. In the simplest scenario, we expect the local ion concentration near the pore walls to behave similar to the globally measured ion swapping. In this case, we should see an increase of Rg at negative and a decrease of Rg at positive applied charge, since the Rg signal is dominated by the local ion concentration changes of cations (having a larger effective electron number). This is actually not the case, as we have observed an increase in both directions of the applied charge. In fact, the Rg signal suggests the preferred arrangement of counter-ions locally close to the pore walls, depending on the polarization of the electrode. However, on a global scale, the ion transport in and out of the pores on the other hand is accommodated by ion swapping.
Moreover, we have to point out the unique similarity between Rg (Fig. 5) and eQCM data (i.e., mass change vs. charge). To our knowledge, eQCM has, so far, only shown counter-ion adsorption as the dominant charge compensating mechanism for a variety of electrolytes and salt concentrations. Yet, pure ion swapping has not been observed so far at large enough potentials.11,21,51 In this study only counter-ions are involved in the local re-arrangement, which explains the similarity between the Rg and eQCM data. On the other hand, the ion exchange in and out of the micropores is realized by pure ion swapping, which corresponds to the actual mechanism counterbalancing the electrode charge. The minimum of the curves in Fig. 5 might be taken as an indication for the point of zero charge (PZC), similar as proposed in recent eQCM studies.52 However, since the actual charge compensating mechanism seems to be ion swapping, the Rg signal (local ion redistribution) is probably not suitable for the determination of the “overall” (global) PZC.
Since only relative changes of Rg are discussed, the arrangement of ions under 0 V conditions can be only estimated. Hence, the presented electron density profiles and ion concentrations represent excess values with respect to the 0 V situation. MD simulations have shown the preferred position of ions near the pore walls already at 0 V.53 However, independent of the distribution of ions across the pore at 0 V, the change of Rg corresponds to a local re-arrangement of ions from the center towards the pore walls. Using combined in situ SAXS and XRT one is sensitive to both the global ion concentration (corresponding to the average ion concentration within the micropores) and the local ion arrangement within the pores. Finally, we should mention that the profiles in Fig. 6c and d were simulated by using effective electron numbers of 40 for both, the hydrated Na+ and K+ ions. When using instead the literature values of 31 and 32 electrons, respectively (see Table 1), the basic features are qualitatively reproduced, but the correspondence between Fig. 4d, e and Fig. 6c, d is not good. We speculate that detailed confinement effects, being different for different carbons, may be responsible for this deviation. Furthermore deviations might be induced by the different nature of the methods. However, a detailed investigation of the role of water (and hydration) must be left open for future investigations.
4 Conclusions
We have presented the first comprehensive and complementary in situ (operando) SAXS and XRT study of a carbon supercapacitor in aqueous media which revealed novel insights into the structural and concentration dependent changes of ions within the confinement of nanopores. X-ray transmission represents a fast, reliable, and easy-to-measure signal to study the integral ion flux independent of the pore size. SAXS data, on the other hand, allow to simultaneously investigate processes at different length scales. In this way, we combine the advantage of eQCM (global ion accounting) with in situ NMR (in pore probing) and obtain information on the local ion arrangement. The latter has, so far, only been accessible via simulation53 or on flat plates using X-ray reflectometry54 which is difficult to translate to the complex situation in confinement of carbon nanopores inside activated carbon particles.Our data help to draw a clearer picture of ion electrosorption in aqueous media with high ionic strength (i.e., 1 M). Globally, charge accommodation is accomplished without changing significantly the global number of ions in the pores, that is, cations plus anions. Effectively, this corresponds to what is we call ion swapping. Only for highly charged electrodes, our data imply the onset of transition towards preferred counter-ion adsorption. Yet, ion electrosorption also entails a second component, namely local in pore ion re-arrangement. Compared to the uncharged state, counter-ions move much closer to the pore wall and facilitate the formation of a dense ion layer. This process is intimately tied with the ionic system and the solvent, in our case water. In particular, we have shown that we have to consider a much “denser” hydration shell with an increased amount of water molecules transported by small cations. This experimental fact should further motivate modeling groups to take the solvent (water) properly into account in atomistic simulations.13,16,55
The ability to distinguish between cation and anion processes sets the stage to provide novel experimental insights into the complex mechanism of ion electrosorption in carbon nanopores. Even more important is the unique usefulness and the plethora of complementary information when we consider the advanced stage of modeling that now even taps into charge/discharge kinetics and adopts more realistic pore networks.4,56–58 Yet, most experimental techniques fall short to provide a molecular picture of the ion electrosorption process and we believe that our approach adds an advanced technique to the limited number of electrochemical in situ methods. More generally, this novel approach might be of interest for a variety of fields where ion adsorption within confined geometry plays an important role. Most importantly, we think that our results and the potential of this method may help to advance the growing field of capacitive deionization for which exact quantitative knowledge of the dominant charge storage mechanism (ion swapping versus counter-ion adsorption) determines the so-called charge efficiency.
Acknowledgements
The INM is part of the Leibniz Research Alliance Energy Transition (LVE). EP, DW, and VP acknowledge funding from the German Federal Ministry for Research and Education (BMBF) in support of the nanoEES3D project (award number 03EK3013) as part of the strategic funding initiative energy storage framework. EP, DW, and VP thank Prof. Eduard Arzt (INM) for his continuing support. CP and OP gratefully acknowledge financial support by the Austrian Federal Government (in particular from Bundesministerium für Verkehr, Innovation und Technologie and Bundesministerium für Wissenschaft, Forschung und Wirtschaft) represented by Österreichische Forschungsförderungsgesellschaft mbH and the Styrian and the Tyrolean Provincial Government, represented by Steirische Wirtschaftsförderungsgesellschaft mbH and Standortagentur Tirol, within the framework of the COMET Funding Programme.Notes and references
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2219–2251 CrossRef PubMed
.
- P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210–1211 CrossRef CAS PubMed
.
- E. Raymundo-Pinero, K. Kierzek, J. Machnikowski and F. Béguin, Carbon, 2006, 44, 2498–2507 CrossRef CAS
.
- C. Péan, C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, B. Daffos, M. Salanne and P. Simon, ACS Nano, 2014, 8, 1576–1583 CrossRef PubMed
.
- C. Merlet, B. Rotenberg, P. A. Madden, P. L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed
.
- M. Deschamps, E. Gilbert, P. Azais, E. Raymundo-Pinero, M. R. Ammar, P. Simon, D. Massiot and F. Beguin, Nat. Mater., 2013, 12, 351–358 CrossRef CAS PubMed
.
- S. Kondrat, N. Georgi, M. V. Fedorov and A. A. Kornyshev, Phys. Chem. Chem. Phys., 2011, 13, 11359–11366 RSC
.
- T. M. Arruda, M. Heon, V. Presser, P. C. Hillesheim, S. Dai, Y. Gogotsi, S. V. Kalinin and N. Balke, Energy Environ. Sci., 2013, 6, 225–231 CAS
.
- F. Bonhomme, J. C. Lassègues and L. Servant, J. Electrochem. Soc., 2001, 148, E450–E458 CrossRef CAS
.
- J. Huang, B. G. Sumpter and V. Meunier, Angew. Chem., Int. Ed., 2008, 47, 520–524 CrossRef CAS PubMed
.
- M. D. Levi, G. Salitra, N. Levy, D. Aurbach and J. Maier, Nat. Mater., 2009, 8, 872–875 CrossRef CAS PubMed
.
- F. W. Richey and Y. A. Elabd, J. Phys. Chem. Lett., 2012, 3, 3297–3301 CrossRef CAS
.
- R. K. Kalluri, M. M. Biener, M. E. Suss, M. D. Merrill, M. Stadermann, J. G. Santiago, T. F. Baumann, J. Biener and A. Striolo, Phys. Chem. Chem. Phys., 2013, 15, 2309–2320 RSC
.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed
.
- J. Chmiola, C. Largeot, P.-L. Taberna, P. Simon and Y. Gogotsi, Angew. Chem., 2008, 120, 3440–3443 CrossRef
.
- G. Feng, R. Qiao, J. Huang, B. G. Sumpter and V. Meunier, ACS Nano, 2010, 4, 2382–2390 CrossRef CAS PubMed
.
- G. Feng and P. T. Cummings, J. Phys. Chem. Lett., 2011, 2, 2859–2864 CrossRef CAS
.
- D.-e. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11, 5373–5377 CrossRef CAS PubMed
.
- D.-e. Jiang, Z. Jin, D. Henderson and J. Wu, J. Phys. Chem. Lett., 2012, 3, 1727–1731 CrossRef CAS PubMed
.
- J. M. Griffin, A. C. Forse, H. Wang, N. M. Trease, P. L. Taberna, P. Simon and C. P. Grey, Faraday Discuss., 2015, 176, 49–68 RSC
.
- M. D. Levi, S. Sigalov, D. Aurbach and L. Daikhin, J. Phys. Chem. C, 2013, 117, 14876–14889 CAS
.
- R. Zhao, P. M. Biesheuvel, H. Miedema, H. Bruning and A. van der Wal, J. Phys. Chem. Lett., 2010, 1, 205–210 CrossRef CAS
.
- F. W. Richey, B. Dyatkin, Y. Gogotsi and Y. A. Elabd, J. Am. Chem. Soc., 2013, 135, 12818–12826 CrossRef CAS PubMed
.
- H. Wang, A. C. Forse, J. M. Griffin, N. M. Trease, L. Trognko, P.-L. Taberna, P. Simon and C. P. Grey, J. Am. Chem. Soc., 2013, 135, 18968–18980 CrossRef CAS PubMed
.
- M. Erko, D. Wallacher, A. Hoell, T. Hauss, I. Zizak and O. Paris, Phys. Chem. Chem. Phys., 2012, 14, 3852–3858 RSC
.
- D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 4428–4431 CrossRef CAS
.
- P. W. Ruch, M. Hahn, D. Cericola, A. Menzel, R. Kötz and A. Wokaun, Carbon, 2010, 48, 1880–1888 CrossRef CAS
.
- S. Boukhalfa, L. He, Y. B. Melnichenko and G. Yushin, Angew. Chem., Int. Ed., 2013, 52, 4618–4622 CrossRef CAS PubMed
.
- S. Boukhalfa, D. Gordon, L. He, Y. B. Melnichenko, N. Nitta, A. Magasinski and G. Yushin, ACS Nano, 2014, 8, 2495–2503 CrossRef CAS PubMed
.
- V. Lorrmann, G. Reichenauer, C. Weber and J. Pflaum, Electrochim. Acta, 2012, 86, 232–240 CrossRef CAS
.
- L. Eliad, G. Salitra, A. Soffer and D. Aurbach, J. Phys. Chem. B, 2001, 105, 6880–6887 CrossRef CAS
.
- Q. Gao, L. Demarconnay, E. Raymundo-Pinero and F. Beguin, Energy Environ. Sci., 2012, 5, 9611–9617 CAS
.
- S. Porada, R. Zhao, A. Van Der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 CrossRef CAS
.
- S. Porada, D. Weingarth, H. V. Hamelers, M. Bryjak, V. Presser and P. M. Biesheuvel, J. Mater. Chem. A, 2014, 2, 9313–9321 CAS
.
- H. Amenitsch, M. Rappolt, M. Kriechbaum, H. Mio, P. Laggner and S. Bernstorff, J. Synchrotron Radiat., 1998, 5, 506–508 CrossRef CAS PubMed
.
- J. Pedersen, J. Appl. Crystallogr., 2004, 37, 369–380 CrossRef CAS
.
- A. Hammersley, ESRF Internal Report ESRF97HA02T, 1997.
-
A. Guinier and G. Fournet, Small angle scattering of X-rays, Wiley, New York, 1955 Search PubMed
.
-
O. Glatter and O. Kratky, Small angle X-ray scattering, Academic Press Inc. Ltd., London, 1982 Search PubMed
.
- W. Ruland, J. Appl. Crystallogr., 1971, 4, 70–73 CrossRef
.
- R. Perret and W. Ruland, J. Appl. Crystallogr., 1970, 3, 525–532 CrossRef CAS
.
- R. Diduszko, A. Swiatkowski and B. J. Trznadel, Carbon, 2000, 38, 1153–1162 CrossRef CAS
.
- P. M. Biesheuvel, S. Porada, M. Levi and M. Z. Bazant, J. Solid State Electrochem., 2014, 18, 1365–1376 CrossRef CAS
.
- A. Gibaud, J. S. Xue and J. R. Dahn, Carbon, 1996, 34, 499–503 CrossRef CAS
.
- P. Debye, H. R. Anderson and H. Brumberger, J. Appl. Phys., 1957, 28, 679–683 CrossRef CAS
.
-
A. Guinier, X-ray diffraction in crystals, imperfect crystals, and amorphous bodies, Courier Dover Publications, 1994 Search PubMed
.
- I. Waluyo, C. Huang, D. Nordlund, U. Bergmann, T. M. Weiss, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2011, 134, 1–10 Search PubMed
.
- C. J. Pings and J. Waser, J. Chem. Phys., 1968, 48, 3016–3018 CrossRef CAS
.
- C. T. Chantler, K. Olsen, R. A. Dragoset, J. Chang, A. R. Kishore, S. A. Kotochigova and D. S. Zucker, NIST, Physical Measurement Laboratory, 1995, 1996, 2001.
- G. Laudisio, R. K. Dash, J. P. Singer, G. Yushin, Y. Gogotsi and J. E. Fischer, Langmuir, 2006, 22, 8945–8950 CrossRef CAS PubMed
.
- W.-Y. Tsai, P.-L. Taberna and P. Simon, J. Am. Chem. Soc., 2014, 136, 8722–8728 CrossRef CAS PubMed
.
- M. D. Levi, S. Sigalov, G. Salitra, D. Aurbach and J. Maier, Phys. Chem. Chem. Phys., 2011, 12, 854–862 CAS
.
- M. C. F. Wander and K. L. Shuford, J. Phys. Chem. C, 2010, 114, 20539–20546 CAS
.
- H. Zhou, M. Rouha, G. Feng, S. S. Lee, H. Docherty, P. Fenter, P. T. Cummings, P. F. Fulvio, S. Dai, J. McDonough, V. Presser and Y. Gogotsi, ACS Nano, 2012, 6, 9818–9827 CrossRef CAS PubMed
.
- C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, Electrochim. Acta, 2013, 101, 262–271 CrossRef CAS
.
- C. Merlet, D. T. Limmer, M. Salanne, R. van Roij, P. A. Madden, D. Chandler and B. Rotenberg, J. Phys. Chem. C, 2014, 118, 18291–18298 CAS
.
- D. Bedrov, J. Vatamanu and Z. Hu, J. Non-Cryst. Solids, 2015, 407, 339–348 CrossRef CAS
.
- D.-e. Jiang and J. Wu, J. Phys. Chem. Lett., 2013, 4, 1260–1267 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ee00488h |
| This journal is © The Royal Society of Chemistry 2015 |