Spinel compounds as multivalent battery cathodes: a systematic evaluation based on ab initio calculations

Abstract

Batteries that shuttle multivalent ions such as Mg²⁺ and Ca²⁺ ions are promising candidates for achieving higher energy density than available with current Li-ion technology. Finding electrode materials that reversibly store and release these multivalent cations is considered a major challenge for enabling such multivalent battery technology. In this paper, we use recent advances in high-throughput first-principles calculations to systematically evaluate the performance of compounds with the spinel structure as multivalent intercalation cathode materials, spanning a matrix of five different intercalating ions and seven transition metal redox active cations. We estimate the insertion voltage, capacity, thermodynamic stability of charged and discharged states, as well as the intercalating ion mobility and use these properties to evaluate promising directions. Our calculations indicate that the Mn₂O₄ spinel phase based on Mg and Ca are feasible cathode materials. In general, we find that multivalent cathodes exhibit lower voltages compared to Li cathodes; the voltages of Ca spinels are ∼0.2 V higher than those of Mg compounds (versus their corresponding metals), and the voltages of Mg compounds are ∼1.4 V higher than Zn compounds; consequently, Ca and Mg spinels exhibit the highest energy densities amongst all the multivalent cation species. The activation barrier for the Al³⁺ ion migration in the Mn₂O₄ spinel is very high (∼1400 meV for Al³⁺ in the dilute limit); thus, the use of an Al based Mn spinel intercalation cathode is unlikely. Amongst the choice of transition metals, Mn-based spinel structures rank highest when balancing all the considered properties.

---

Broader context

The high price and limited volumetric capacity of the lithium ion battery (LIB) challenges its application in electric vehicles and portable electronics. Multivalent batteries, such as those utilizing Mg²⁺ or Ca²⁺ as the working ions, are promising candidates for beyond LIB technology due to the increase in volumetric capacity and reduced cost. In the present work, we use first-principles calculations to systematically evaluate the theoretical performance of the spinel structure host with the general formula AB₂O₄ across a matrix of chemical compositions spanning A = {Al, Y, Mg, Ca, Zn} and B = {Ti, V, Cr, Mn, Fe, Co, Ni} for multivalent battery applications. The evaluation incorporates screening on voltage, capacity, thermodynamic structural and thermal stability as well as ion mobility and discusses the results in the context of available host structure sites, preference of the intercalating cation, and the oxidation state of the redox-active cation. Overall, the Mn₂O₄ spinel phases paired with Mg²⁺ or Ca²⁺ emerge as the most promising multivalent cathode materials. As the first comprehensive screening of multivalent intercalation compounds across size, valence, and redox-states of the involved cations, our work is intended to provide guidance for future theoretical as well as experimental multivalent cathode development and design.

Introduction

To support the rapidly growing energy storage demands of future technologies such as electric vehicles, improved battery technologies are needed. Lithium (Li) ion batteries with good energy density, rechargeability and cycle life¹ have been used to advance portable consumer electronics and recently, electric vehicles. However, further advancement of Li ion technology faces limits on the energy density of electrode materials,^2,3 safety, and high cost. A multivalent battery technology, where an intercalation cathode host is paired with a metal anode, has the potential to store energy at significantly lower cost and volume.^4–6 For example, Mg metal has much higher volumetric capacity (3833 mA h cm⁻³) than graphite (∼800 mA h cm⁻³)^7,8 or even lithium metal (2046 mA h cm⁻³). Furthermore, as many known intercalation hosts are limited by the available cation insertion sites rather than by redox capability, one can expect improvements using multivalent intercalation on the cathode side. For instance, Mg²⁺ carries two charges per ion while maintaining an ionic radius as small as that of a Li⁺ ion, hence the charge storage capability is doubled at the same cation volumetric concentration. In addition, the natural abundance of multivalent elements, such as Mg and Ca, is significantly higher than that of Li (the atomic abundance of Mg is ∼10⁴ times larger than Li in the earth crust), which may decrease the cost of materials and guarantee supply even for multi-fold increases in the size of the energy storage market.

To date, there have been limited examples demonstrating the feasibility of rechargeable multivalent batteries, and among them, most of the focus has been on Mg technology. In the seminal work of Aurbach et al., it was demonstrated that Mg²⁺ can intercalate into the Chevrel phase Mo₆S₈ at a potential of ∼1.0–1.3 V and a maximum charge capacity of 135 mA h g⁻¹ for several hundreds of cycles.^6,9 Other materials have shown initial promise for multi-valent intercalation, such as layered V₂O₅ where Mg²⁺ is inserted into the V₂O₅ inner layer spacing.^10,11 Ca²⁺ has also been shown to intercalate into V₂O₅, supplying a voltage of ∼3.0 V and an initial capacity of ∼450 mA h g⁻¹.¹² Other materials claimed to accommodate Mg²⁺ insertion include MoO₃,^13–15 TiS₂ in both the cubic phase and layered phases,¹⁶ NbS₃,¹⁷ graphitic fluoride,¹⁸ and CoSiO₄.¹⁹ However, due to limited Mg mobility in the host and possibly concurrent water and/or proton insertion, the cycling stability of these materials has so far been insufficient, resulting in rapid decomposition of the host material.^20,21

From the limited experimental studies performed to date, the feasibility of a battery technology based on multivalent intercalation is not yet clear. As the cathode will be a critical component of such a technology, it is important to assess the feasibility of multivalent insertion cathodes. In this work, we present a systematic computational study of multivalent intercalation within a fixed spinel-based host structure, using a set of seven redox-active cations and spanning size and valence differences between a set of intercalating {Ca, Zn, Mg, Al and Y} cations to establish design trends and guidelines for future experimental work.

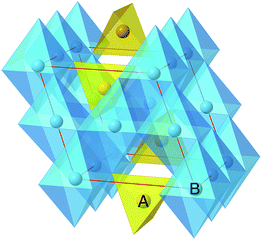
The spinel (prototype MgAl₂O₄, space group Fd3̄m) structure provides an excellent candidate for this study, encompassing a family of materials with the general formula AB₂O₄. The A and B ions are tetrahedrally and octahedrally coordinated by oxygen, respectively (Fig. 1). The B octahedrons form a network with percolating empty sites interconnecting in three directions. Spinel LiMn₂O₄ was first prepared by Thackeray et al.²² and exhibits excellent performance as a cathode for Li intercalation with a voltage of 3–4 V versus Li metal.²³ The properties of the spinel structure are tunable, for example it has been observed that partially replacing Mn with Ni increases the voltage to 4.7 V,^24,25 and mixing Mn with Co and/or Cr increases the voltage even higher to ∼5 V.^25–27

Fig. 1 The spinel crystal structure where the ‘A’ atoms occupy the tetrahedral sites, and the ‘B’ atoms occupy the octahedral site. Throughout this paper, the ‘A’ atoms are multivalent intercalating ions selected from the set {Mg²⁺, Ca²⁺, Zn²⁺, Y³⁺, Al³⁺}, and the ‘B’ atoms are transition redox-active ions, selected from the set {Ti, V, Cr, Mn, Fe, Co, Ni}.

Experiment shows that spinel LiMn₂O₄ can be electrochemically converted to MgMn₂O₄ in aqueous Mg(NO₃)₂ electrolyte, and exhibits Mg²⁺ reversible intercalation/deintercalation.²⁸ Spinel ZnMnO₂ has also demonstrated Zn²⁺ insertion/deinsertion, providing a capacity of 210 mA h g⁻¹ for 50 cycles.²⁹ Recently, it was shown that Mg²⁺ can intercalate/deintercalate into spinel-type Mn₂O₄ with a retained capacity of 155.6 mA h g⁻¹ after 300 cycles in 1 mol dm⁻³ MgCl₂ aqueous electrolyte,³⁰ suggesting that further development could lead to a viable cathode with good energy density. Against this background it is intriguing to broadly consider a multivalent spinel cathode with possible intercalating cations A = {Mg, Ca, Zn, Al, Y} that could theoretically produce a higher capacity than its Li counterpart due to the greater charge carried by each ion. Hence, in this paper, our aim is to evaluate the cathode performance of spinel phases for multivalent intercalation; we computationally evaluate the feasibility of a matrix of spinel compounds with different redox ion species and intercalating cation species. The redox ion was selected from the set {Ti, V, Cr, Mn, Fe, Co, Ni}, and the intercalating cation was selected from the set {Mg, Ca, Zn, Al, Y}. By substituting the cations in the A and B sites, respectively, we created 35 charged/discharged topotactic pairs and performed first-principles density functional theory (DFT) calculations for each of these pairs. We evaluate cathode performance through such quantities as the capacity, average voltage, energy density, and intercalating cation mobility. We also evaluate the thermodynamic structural and thermal stability. The detailed methodology can be found in previous literature.³¹

Methods

We use the Vienna ab initio software package (VASP)³² to perform the density functional theory calculations, with the projector augmented-wave method³³ to describe the ion–electron interactions and the generalized gradient approximation (GGA)³⁴ within the Perdew–Burke–Ernzerhof (PBE) framework³⁵ as the exchange–correlation functional. The calculation parameters are the same as those adopted by the Materials Project³⁶ and as implemented in the pymatgen software package,³⁷ which have been previously tested to be appropriate to study Li-intercalation cathode materials.³¹ In the calculations, the U–J parameters to correct for non-cancellation of the self-interaction error in the d orbitals of the redox active species are set to U_V = 3.25 eV, U_Cr = 3.7 eV, U_Mn = 3.9 eV, U_Fe = 5.3 eV, U_Co = 3.32 eV, and U_Ni = 6.45 eV.³⁸ The primitive spinel unit cell as illustrated in Fig. 1 is used for voltage and stability calculations. Brillouin zone sampling is performed on a 5 × 5 × 5 grid in k-space. Throughout this work, the cell shape, volume and atomic positions are relaxed, unless otherwise stated. All magnetic ions are initialized ferromagnetically.

All calculations in this paper assume that the transition metal host framework ‘B₂O₄’ remains structurally invariant during the operation of the battery (i.e., during intercalation and de-intercalation of ‘A’ cations). Additionally, we assume that the host can be synthesized with little/no disorder and remains that way during the operation of the cell. We acknowledge that spinels are well known to show varying degrees of cation disorder that may impact important material properties relevant for battery operation such as the activation energies and voltages reported herein. However, in the interest of providing a preliminary view of what is possible in multivalent systems, we have simplified our calculations and analysis.

The voltages of the compounds can be obtained from the difference in the total energy between the charged and discharged phases following Aydinol et al.^39,40 The average voltage can be calculated as V̄ = ΔE/nz, where ΔE = (E_charge + E_MV − E_discharge) denotes the total energy change in the reaction, E_charge and E_discharge are the energy of the charged and discharged compounds respectively; E_MV is the energy of multivalent intercalating species in metal form; n is number of intercalating atoms participating in the reaction; and the z represents the oxidation state of the intercalant. We adopt the units of eV and e for ΔE and nz, respectively, so that no normalization factor (i.e., Faraday's constant) needs to be introduced into the equation. We estimate the thermodynamic stability of the phases by the energy above the convex hull of stable phases, which is the energy released by decomposing the compound to the most stable combination of compounds at the same overall composition.^41,42 The energy above the hull is always a non-negative number with the unit of eV per atom. The detailed procedure for the computation of the energy above the hull can be found in previous literature.^41,42 As explained later in this paper, the thermal stability was determined by evaluating the critical chemical potential at which O₂ gas becomes favorable according to the methodology presented in Ong et al.⁴³ Since the entropy of a reaction is dominated by the gas entropy and the entropy of the solid phase at room temperature,³⁸ for the any reactions containing molecular O₂, we use the corrected O₂ chemical potential to include the well-known O₂ DFT calculation error³⁸ as well as the PΔV contribution to the oxygen enthalpy⁴³ by comparing with the experimental thermodynamic data⁴⁴ for O₂ at 0.1 MPa at 298 K throughout the paper. For the thermal stability calculation, the temperature effect has been taken into account by adjusting the entropy term (−TΔS) of the O₂ chemical potential at given temperature.⁴⁵ A more detailed description can be found in the ESI.†

The calculations were automatically executed and analyzed using the FireWorks software package.⁴⁶ In this work, hundreds of DFT calculations are performed across 70 compounds to generate the thermodynamic stability and thermal stability data.^41,43

Activation barriers were calculated with the nudged elastic band (NEB) method⁴⁷ using the GGA-PBE functional.^34,35 A U term was not included in these calculations as NEB is difficult to converge with GGA+U due to pronounced metastability of electronic states along the ion migration path. Furthermore, while GGA+U clearly improves the accuracy of redox reactions,³¹ there is no conclusive evidence that GGA+U performs better in predicting cation migration.^48–52 The minimum energy paths (MEP) in the NEB procedure were initialized by linear interpolation of 8 images between the two fully relaxed end-point geometries, and each image is converged to <1 × 10⁻⁴ eV per super cell. The MEPs were obtained in both the high vacancy limit and dilute vacancy limit, i.e. one mobile species per unit cell or one vacancy per unit cell. To ensure that fictitious interactions between the diffusing species are removed, a 2 × 2 × 2 supercell of the primitive cell was used, for which the inter-image distance is never less than 8 Å.

Results and discussion

The average intercalation voltage was calculated from the reaction energy B₂O₄ + A → AB₂O₄ for the matrix of intercalating A = {Mg, Ca, Zn, Y, Al} ions and redox active transition B = {Ti, V, Cr, Mn, Fe, Co, Ni} metal cations. Fig. 2 shows the resulting voltage vs. the gravimetric capacity, where the color and shape of a data point indicate the intercalating ion, and the redox-active transition metal is given next to each data point. Voltages are referenced to the bulk metal of the intercalating ion, e.g., Mg metal for MgMn₂O₄ and Zn metal for ZnMn₂O₄.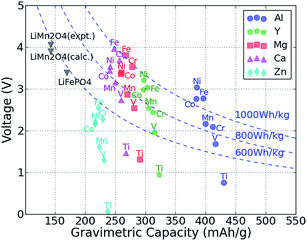

Fig. 2 The computed average voltage vs. gravimetric capacity for intercalation of A = Zn, Ca, Mg, Y and Al in various M₂O₄ spinels up to composition AM₂O₄. The redox-active metal is marked next to each point. Dashed curves show the specific energy of 600 W h kg⁻¹, 800 W h kg⁻¹ and 1000 W h kg⁻¹, respectively. The spinel LiMn₂O₄ and olivine LiFePO₄ data points are also marked on the plot for comparison.^22,36,43

As expected from the electrochemical series, and evidenced in Fig. 2, multivalent compounds have lower voltages than Li cathodes. The Li spinel usually exhibits a voltage between 4 and 5 V,^22,26,53 whereas we find that for multivalent spinel cathodes, the voltage is always less than 4 V versus the corresponding metal. Most Mg and Ca intercalation voltages vary between 2 and 4 V, which is lower than the values for Li (e.g., calculated voltage of LiMn₂O₄ is ∼0.7 V higher than CaMn₂O₄);^22,54 however, considering the additional charge carried by multivalent cations, a multivalent spinel cathode can still exhibit a significantly higher energy density than the corresponding Li version. For example, the gravimetric capacity of LiMn₂O₄ is 143 mA h g⁻¹,^22,36 whereas the gravimetric capacity of MgMn₂O₄ is almost double ∼270 mA h g⁻¹, which more than makes up for the slightly lower voltage. Hence, of the considered intercalating ions, Al, Y, Ca and Mg are all viable candidates from the perspective of energy density. However, the voltage of the Zn spinel compounds ranges between 1.3 V and 2.5 V, which even in the best case scenario amounts to approximately 600 W h kg⁻¹, about equal to the specific energy of LiFePO₄.^36,43

The voltage for each multivalent intercalant is plotted as a function of the active redox metal in Fig. 3(a): the bi-valent ions Ca, Mg, and Zn follow a common trend as the redox couple is varied, different from the voltage trend of the tri-valent intercalants Al and Y. The difference originates largely from the different valence state of the transition metal in the discharged state. Insertion of the bi-valent cations induces a change in redox state from 4+ to 3+, whereas the tri-valent cation corresponds to a redox change from 4+ to 2.5+ for insertion into AB₂O₄.

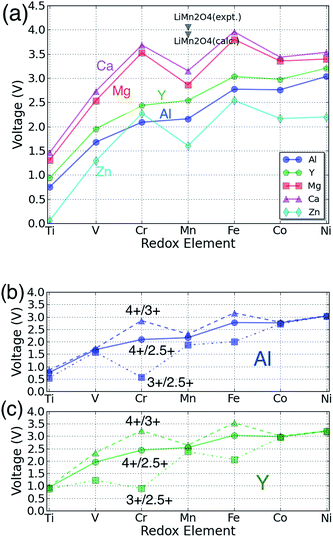Fig. 3 (a) The calculated voltage of each spinel phase for the reaction B₂O₄ + A → AB₂O₄ as a function of the redox-active transition metal and intercalating cation. The different colors denote different intercalating species as specified by the legend. The black triangle point indicates the data corresponding to the spinel LiMn₂O₄;^22,36 (b) and (c): for Y and Al the voltage for separate 3+/2.5+ and 4+/3+ redox reactions is compared to the overall voltage for the 4+/2.5+ redox change corresponding to the full intercalation range, as in (a).

In general, the Ca spinel has the highest voltage, followed by the Mg spinel compounds, Y compounds, Al compounds, and Zn compounds, in that order. For all the redox active cations {B = Ti, V, Cr, Mn and Ni} the voltage of the Mg compounds is lower than that of the Ca compounds by ∼0.2 V, and the voltages of Mg compounds are ∼1.4 V higher than Zn compounds. The three bi-valent intercalants show the same trend of voltage verses redox active metal: Ti₂O₄ always has the lowest voltage among the transition metals considered. V₂O₄ is the second lowest one but ∼1.2 V higher than Ti₂O₄. Mn₂O₄ is ∼0.3 V higher than V₂O₄, Co₂O₄ is ∼0.6 V higher than Mn₂O₄, and Ni₂O₄ is slightly higher than Co₂O₄ by ∼0.1 V. The Cr₂O₄ and Fe₂O₄ spinels have the highest voltage, respectively ∼0.6 V and ∼0.9 V higher than Mn₂O₄. Bhattacharya et al. found a similar trend for the Li insertion voltage in spinels.⁵⁴ We find that Li insertion⁵⁴ occurs on average at about ∼0.7 V higher voltage than Ca insertion and ∼0.9 V higher than Mg insertion. Comparing this with the aqueous electrochemical series (E⁰_Li = −3.04, E⁰_Ca = −2.86, E⁰_Mg = −2.37, E⁰_Zn = −0.76) we find that the voltages are ordered according to the electrochemical series of the intercalating metal ion. However, while the voltage shift between Li and Mg is close to what is expected, the voltage reduction in moving from Li to Ca in the solid state is considerably larger than expected from the electrochemical series. This is likely due to the fact that the intercalant enters a tetrahedral site in the spinel, which for Ca is not nearly as favorable as for Mg and Li, and thus reduces the Ca intercalation voltage from what one would expect from the electrochemical series. Experimentally, Li has indeed been found to exhibit a higher voltage than Mg. In the Chevrel phase Mo₆S₈, the voltage difference between Li and Mg insertion is ∼1.0–1.2 V.^9,55,56 For V₂O₅, the Li voltage is usually ∼0.2 V higher than that of Mg.^57–59

Because the data in Fig. 3(a) for trivalent cations averages the voltage over both the 3+/2.5+ and 4+/3+ redox couples, the intermediate 3+ states of the transition metals were calculated for the trivalent intercalants to investigate the impact of different redox states. Fig. 3(b) and (c) show the calculated voltage of the different redox pairs for the Al and Y spinel compounds, respectively. As expected, the 3+/2.5+ redox pairs exhibit a lower voltage compared to the 4+/3+ reactions, in good agreement with existing literature.² In particular, when restricting focus to the 4+/3+ redox reaction, the Al and Y spinel compounds follow largely the same trend as Ca, Mg and Zn as shown in Fig. 3(a).

The capacity of cathode materials is important as it strongly influences the overall energy density of a cell. Fig. 4(a) shows the volumetric capacity of each AB₂O₄ spinel as a function of the redox-active species and intercalating cation. The volumetric capacity of all the cathodes is higher than that of a Li spinel cathode at the same cation concentration due to the extra charge carried by each of the multivalent intercalants. Not surprisingly, Al³⁺ leads to the highest capacity density, while Ca²⁺ has the lowest. For a fixed valence of the intercalant, the volumetric capacity follows the ionic size of the intercalating cation. Hence, the volumetric capacities of Al³⁺ compounds are higher than Y³⁺ compounds by approximately 300 A h L⁻¹. For bi-valent cations, the capacities of Mg and Zn compounds are almost the same, consistent with the similar ionic size of Mg²⁺ or Zn²⁺.

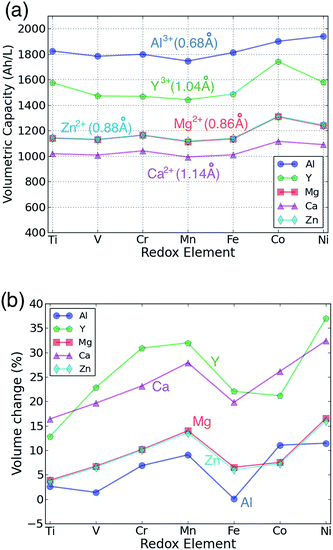Fig. 4 The calculated (a) volumetric multivalent capacity and (b) volume change of the spinel structure as a function of the redox-active cation, assuming intercalation to composition AB₂O₄.

Fig. 4(b) presents the volume expansion associated with the intercalation of each multivalent ion as function of the redox metal. Volume change is an important parameter as it needs to be accommodated at the particle, electrode and cell level. At the particle level, large volume changes can lead to particle fracture and loss of contact. The total volume change associated with intercalation is the combined result of the intercalant insertion and the transition metal reduction, and can be very small for some Li-insertion systems.^60,61 The contribution from the intercalating ion will depend on its size and charge. For example, Y³⁺ leads to larger volume increase than Al³⁺ as the ion is much larger. The effect of charge cannot as easily be extracted from Fig. 4(b) as the +3 cations also cause a larger reduction of the transition metal than the 2+ cations. Reduction of the transition metals generally leads to an increase in volume, although the magnitude of the change depends on the nature of the metal-d orbital that is being filled. Filling of t_2g orbitals, which are to first order non-bonding,⁴⁰ tends to cause only a small increase in volume, while the anti-bonding e_g orbitals lead to a larger volume change.⁶⁰ This explains why in general the early transition metals, such as Ti and V exhibit lower volume changes. They have several unoccupied t_2g orbitals, which are available for reduction. On the other hand, Mn and Ni-based spinels show the largest volume changes as their reduction occurs by filling one or more e_g orbitals. For both Mn³⁺ and Ni³⁺ this volume increase is compounded by the fact that these ions are Jahn–Teller active which, in its anharmonic form, leads to additional volume increase.⁶² The combined small size and high charge of Al³⁺ lead to almost zero volume change for several spinels.

For Mg, Zn and Al insertion, the magnitude of the volume change normalized by the capacity is very similar to the volume changes observed for Li insertion compounds, and hence is not likely to lead to any practical design problems. For Ca and Y the volume change is larger – up to 30% increase in some cases.

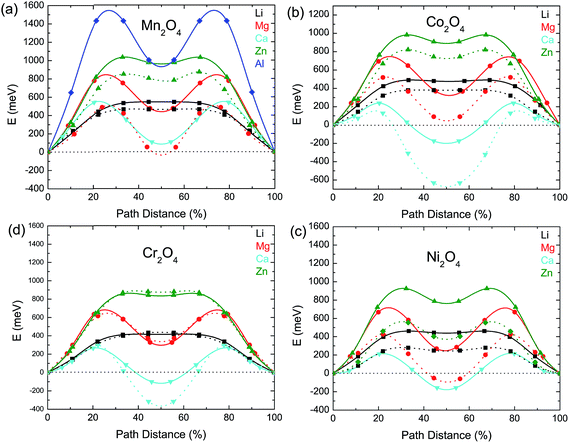
The thermodynamic stabilities of the charged and discharged state are important considerations for possible cathode materials, as they may influence the cycle life as well as the synthesizability of the compounds. Thermodynamic stability can be measured by the driving force for a compound to separate into its most stable combination of compounds. From first principles, this is determined by comparing the energy of the compound with the convex energy hull of all ground states in the relevant phase diagram (see the ESI† for a detailed explanation). Fig. 5(a) and (b) provide this energy above the hull of each compound. The ground state hulls were determined from all the calculated compounds in the Materials Project database.³⁶ A smaller energy above the hull implies that the material has a greater chance of being stable,⁶³e.g. at synthesis and upon cycling.

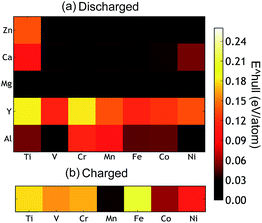Fig. 5 (a) The calculated thermodynamic stability of the AB₂O₄ spinel compounds as a function of the intercalating ion (vertical axis) and redox metal (horizontal axis). (b) The energy above hull of the charged state which is calculated as the formation energy difference between a compound and the convex hull (see ESI† for a detailed explanation).

The Mg and Zn spinel phases (except ZnTi₂O₄) are all quite stable, exhibiting an energy above hull less than 0.011 eV per atom. Such a small value of the decomposition energy falls well within the accuracy of our calculations⁶³ or within relative changes between competing phases due to finite temperature effects. The Ca spinel structures are more thermodynamically unstable compared to the equivalent Mg and Zn compounds. This is consistent with Ca²⁺ normally preferring coordination environments larger than tetrahedral, though it is not excluded that this coordination can be achieved through electrochemical intercalation. The Y spinel compounds are the most unstable phases among all the candidates, due to the large ionic size of Y³⁺. The Al³⁺ spinels are also relatively unstable in the discharged state. Among the chemistries of the charged host spinel, Mn₂O₄ forms the most stable structure. The high energy above hull for Fe₂O₄ suggests the difficulty to synthesize such a phase. Indeed, Fe⁴⁺ is only known to exist in ternary and higher component compounds⁶⁴ where the formation energy is lowered by the interaction with other cations. In terms of phase stability across both charged and discharged states, we conclude that MgMn₂O₄, CaMn₂O₄ and ZnMn₂O₄ provide the best opportunities.

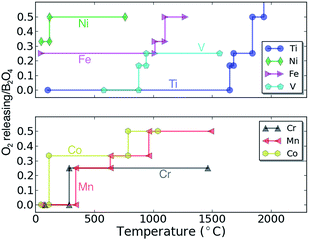
A way to gauge the intrinsic safety of a potential cathode material is by the thermal stability of the compound against O₂ release. The thermal stability can be estimated by calculating the temperature at which O₂ gas release is predicted thermodynamically (see ref. 43 and the ESI† for more details on the methodology). Fig. 6 shows the calculated O₂ amount released as a function of temperature for the charged spinel compounds (e.g. for B₂O₄), determined by the equilibrium chemical potentials at which O₂ release can be expected. At low temperature the oxygen release is likely limited by kinetics and the decomposition temperatures should only be used to rank compounds relative to their oxidation strength. Clearly, the data in Fig. 6 indicates that Fe₂O₄ and Ni₂O₄ are highly oxidizing, and are unlikely to be stable in their stoichiometric configuration at room temperature. Co₂O₄ decomposes to 2/3(Co₃O₄ + O₂) at a temperature slightly above 100 °C. The Cr₂O₄ and Mn₂O₄ spinels are predicted to decompose to Cr₂O₃ + 1/2O₂ and Mn₂O₃ + 1/2O₂ at 285 °C and 342 °C, respectively. Since the Mn spinel exists as a metastable phase in some Li batteries, the Cr and Mn spinel phases should operate well at room temperature. Finally, the V₂O₄ and Ti₂O₄ spinels are predicted as fairly stable against O₂ release as indicated by their higher decomposition temperatures; 876 °C and 1646 °C, respectively. In summary, Ti₂O₄, V₂O₄, Cr₂O₄ and Mn₂O₄ are expected to exhibit superior thermal stability against O₂ release among the considered spinel compounds. Comparing the calculated voltage (Fig. 3) and thermodynamic stability (Fig. 5), a stable discharged phase and unstable charged phase naturally lead to higher voltage, and vice versa (as expected). For example, fairly unstable Fe₂O₄ and Ni₂O₄ result in a higher voltage, while Mn₂O₄ generally results in lower voltages.

Fig. 6 The calculated thermodynamic O₂ evolution diagram of charged host spinel compounds as a function of temperature. The vertical axis denotes how much O₂ is predicted to be released from the compound per formula unit of B₂O₄ as the material decomposes.

The previous voltage, capacity and stability results for multivalent cathode materials show great potential to go beyond current Li-ion. However, a major remaining challenge is overcoming the sluggish diffusion expected for multivalent-ions. The slower diffusion of high-valent cations has been attributed to the stronger cation–anion interaction, which makes migrating 2+ or 3+ ions more difficult than moving 1+ ions, though no quantitative information is available on mulit-valent ion diffusion.⁵ Hence, we calculate the migration energy barriers of the various multivalent ions (A = Mg²⁺, Zn²⁺, Ca²⁺, Al³⁺, and also Li⁺ for comparison) in the spinel structure AB₂O₄ (B = Mn, Co, Ni, Cr) from first-principles as shown in Fig. 7. The Nudged Elastic Band method was used in both high vacancy limit and dilute vacancy limit corresponding a single migrating intercalant or a vacancy in an empty host or fully intercalated structure, showing the upper and lower limit of the intercalant migration activation barrier. To provide a general idea of how the migration energy barrier affects the diffusivity, a rough estimation can be given as follows: a migration barrier of ∼525 meV corresponds to a typical ionic diffusivity of ∼10⁻¹² cm² s⁻¹ at room temperature, which approximately represents the lower limit for reasonable charge and discharge time (∼2 h in micron-size active particles). Also, a 60 meV increase (decrease) in the migration energy corresponds to an order of magnitude decrease (increase) in the intercalant migration activation barrier. With smaller particle sizes a somewhat larger barrier can be tolerated: every order of magnitude in size reduction allows for two orders of magnitude smaller diffusion constant. Hence for 100 nm particulates, migration barriers up to ≈645 meV may be acceptable.

Fig. 7 Computed minimum energy paths for migration of different intercalants between the tetrahedral sites in the spinel B₂O₄ (B = Mn, Co, Ni, Cr) at the high vacancy limit (solid line) and dilute vacancy limit (dotted line), i.e. one mobile specie per supercell (2 × 2 × 1 of primitive cell).

In spinel Mn₂O₄, which has been successfully commercialized for use in Li-ion batteries, Al³⁺ displays the highest diffusion barrier of ∼1400 meV. Among the divalent cations, Zn²⁺ (∼850–1000 meV) and Mg²⁺ (∼600–800 meV) have the highest barriers, while Ca²⁺ is comparable to Li⁺ (∼400–600 meV). The migration barriers obtained for Li⁺ in M₂O₄ (M = Mn, Co, Ni, Cr) all lie within ∼400 to 600 meV in the empty lattice limit, in good agreement with first-principles Li mobility calculations performed by Bhattacharya et al. in the spinel Li_1+xTi₂O₄ system (−1 < x < 1).⁶⁵ Excluding the CrO₂ spinels and some of Ca-containing spinels, the migration barrier at high vacancy limit is always higher compared to the dilute vacancy limit, agreeing with Bhattacharya et al. that migration barrier is reduced by nearly 300 meV as Li is intercalated from the Li-deficient to the Li-rich limit (from ∼600 meV for Li migration in Ti₂O₄ to ∼300 meV for vacancy migration in LiTi₂O₄).⁶⁵ From kinetic Monte Carlo simulations, the room temperature self-diffusivity of Li was shown to span ∼10⁻¹⁰ to 10⁻⁹ cm² s⁻¹ between Li_0.5Ti₂O₄ and LiTi₂O₄, in good agreement with the excellent experimental rate-capability typically observed in Li spinel cathodes. Except in Mn₂O₄, we could not converge the NEB for Al³⁺ due to the very large forces along the transition path, which is usually symptomatic of a very high barrier. The divalent barriers vary significantly with the chemical nature of the intercalant: Zn²⁺ (∼800–1000 meV), Mg²⁺ (∼600–800 meV), and Ca²⁺ (∼200–500 meV). Although Ca²⁺ migration appears to be facile in our calculations, only in Mn₂O₄ does Ca²⁺ prefer to occupy the tetrahedral site as opposed to the octahedral site (which can be observed in Fig. 7 as the energy along the migration path becomes negative when Ca is near the octahedral site in the Ni, Cr, and Co spinel). For this case, the migration barrier should be measured as the energy increase from the octahedral site to the maximum along the path (see Fig. 7). We find that for all fully intercalated phases, the tetrahedral sites are more stable than the octahedral sites, which indicates a cross-over in site preference with concentration for some of the intercalating cations.

Discussion

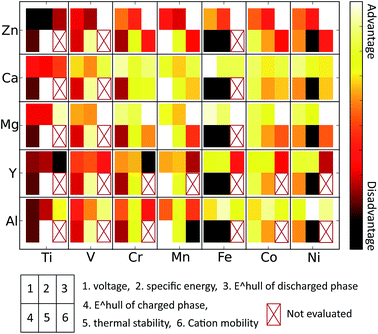
Technical extrapolations of projected multivalent chemistries to the cell level have shown that multivalent intercalation is one of the few technologies that can outperform Li-ion batteries in terms of energy density. In this paper we have used first principles calculations, well established in Li-cathode research,^2,3,43,63,66 to evaluate the properties of multivalent-ion intercalation in spinel structures with different chemistries. We evaluated average insertion voltage, stability in the charged and discharged state, volume change upon intercalation, oxidation strength of the charged cathode, and the mobility of the multi-valent cations. Such first principles screening is important for this new field as multi-valent ion electrochemistry is not well established and, due to incompatibility between electrolytes and electrode materials, it can be difficult to obtain unambiguous experimental results on the performance of a specific cathode material.^4,67,68 We found that the insertion voltage of Ca²⁺, Mg²⁺, Zn²⁺, Al³⁺ and Y³⁺ against their respective metal anodes in general follows the electrochemical series but with quantitative variations due the nature of the site preference of the intercalating ion. For example, Ca insertion voltages in spinels are lower than expected, as Ca in general prefers higher coordination than tetrahedral (commonly the most favorable site in the spinel structures). The Fe₂O₄ and Ni₂O₄ spinels are unlikely to function across the full capacity range due to the highly oxidizing and unstable nature of their fully charged states. As expected, Ti₂O₄ spinels have low insertion voltage for most intercalants, and in addition, are fairly unstable. The V₂O₄ and Cr₂O₄ spinels are also fairly unstable in the charged state, and the V spinel exhibits a low insertion voltage for all intercalants besides Mg and Ca. From the perspective of stability, the most promising spinel chemistry is Mn₂O₄ as it is stable in the charged state and fairly stable in the discharged state for several intercalating ions. Intercalant mobilities are generally low due to the high activation energies when transitioning between the tetrahedral and octahedral site, though they are clearly not only controlled by charge. For example, among the divalent ions Zn mobility is inferior to Mg, and Ca may have fairly good mobility in the spinel. Al³⁺ intercalation into the spinel structure can likely be excluded from consideration even though it has the peculiar feature that volume changes upon insertion are very small. The activation barrier for motion is very high for Al³⁺ in Mn₂O₄ and its discharged spinels are all highly unstable. Somewhat surprisingly, and in contrast to experimental claims,²⁹ we find that mobility of Zn in the spinel structure is very low, which in addition to its low insertion voltage, should exclude this system from further consideration for high energy density cathodes. The large intercalating ions such as Y³⁺ and Ca²⁺ are interesting, though the Y-spinels become unstable in the discharged limit. Both of these ions have reasonable insertion voltages and Ca²⁺ has better than expected migration barriers, due to its relative instability in the tetrahedral site. While this effect lowers the voltage from what would be expected by considering the electrochemical scale, it also seems to lower the migration barrier for motion. This may be similar to the more general principle that high energy defects in materials often have higher mobility.

Considering all computed properties, Mn₂O₄ spinels are particularly interesting due to their stability (Fig. 8). Among the divalent cations, both Mg²⁺ and Ca²⁺ may potentially be mobile in the spinel structure, warranting further experimental and computational investigation (particularly at small particle sizes). Mixed spinel structures may provide a further promising avenue, as the Ni^4+/3+ and Co^4+/3+ show higher voltage than the Mn^4+/3+ redox couple and compounds such as LiNiMnO₄ are known to combine higher operating voltage with a relatively stable charged state.^24,25 Improving the diffusivity should be a focus for all multivalent cathode materials.

Fig. 8 Qualitative summary of multivalent spinel compounds based on multiple performance metrics, such as voltage, specific energy, thermodynamic stability of charged and discharged phases, thermal stability and intercalant mobility. The favorable (unfavorable) properties are represented with light (dark) color.

Finally, a concern with spinels, as with all intercalation materials, is the occurrence of cation disorder. In the extreme case, normal spinels can convert to inverse spinels with part of the transition metals on the tetrahedral site. While in more common layered materials, lowering of the intercalant mobility by cation disorder is well understood through the contraction of the interlayer slab space by disorder,⁶⁹ we are not aware of an equivalent study for spinels. Given the 3D and more rigid nature of the framework and the 3D diffusion network, one would expect spinels to be more tolerant to cation disorder. Nonetheless, we have performed a preliminary investigation into the driving force inverse spinel formation by adopting the same methodology as in Bhattacharya et al.⁵⁴ Based on small supercell calculations, we find that the normal spinel is always energetically favorable for Ca, Mg, Zn compounds (See Fig. S2 in the ESI†). Further information can be obtained from the study of Burdett et al. who elucidated that cation disorder is strongly correlated to the relative size of the A and B ions.⁷⁰ Hence, Li and Zn prefer to form normal spinels, and we do not expect cation disorder. Ca is large and has the possibility to occupy octahedral sites that forms inverse spinel. Similarly, Mg may show cation site disorder for Ni, Fe, Co when synthesized at high temperature. However, in the case that well ordered spinels cannot be formed at high temperature synthesis conditions, it may be still be possible to create the normal ordered spinel phase by chemical or electrochemical delithiation of the lithium spinels^28,30 and inserting multivalent cations.

In summary, we have performed systematic calculations to screen for and discover improved multivalent cathode materials using the spinel structure as a general host. On the basis of all property calculations, the spinel Mn₂O₄ is found to be a superior candidate with Ca²⁺ and possibly Mg²⁺ as mobile cations. It is our hope that our work provides a general guide and standard for future theoretical as well as experimental multivalent cathode development and design.

Acknowledgements

This work was intellectually led and fully supported by of the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U. S. Department of Energy, Office of Science, Basic Energy Sciences. Work at the Lawrence Berkeley National Laboratory was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, under Contract no. DEAC02-05CH11231. We also thank the National Energy Research Scientific Computing Center (NERSC) for providing computing resources. The Materials Project (BES DOE Grant no. EDCBEE) is acknowledged for infrastructure and algorithmic support.

References

1. J. B. Goodenough and K.-S. Park, The Li-Ion Rechargeable Battery: A Perspective, J. Am. Chem. Soc., 2013, 135, 1167–1176.
2. G. Hautier, A. Jain, S. P. Ong, B. Kang, C. Moore, R. Doe and G. Ceder, ChemInform Abstract: Phosphates as Lithium-Ion Battery Cathodes: An Evaluation Based on High-Throughput Ab Initio Calculations, Chem. Mater., 2011, 42, 3495.
3. G. Hautier, A. Jain, T. Mueller, C. Moore, S. P. Ong and G. Ceder, Designing Multielectron Lithium-Ion Phosphate Cathodes by Mixing Transition Metals, Chem. Mater., 2013, 25, 2064–2074.
4. H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Mg Rechargeable Batteries: An on-Going Challenge, Energy Environ. Sci., 2013, 6, 2265.
5. E. Levi, M. D. Levi, O. Chasid and D. Aurbach, A Review on the Problems of the Solid State Ions Diffusion in Cathodes for Rechargeable Mg Batteries, J. Electroceram., 2007, 22, 13–19.
6. A. Mitelman, M. D. Levi, E. Lancry, E. Levi and D. Aurbach, New Cathode Materials for Rechargeable Mg Batteries: Fast Mg Ion Transport and Reversible Copper Extrusion in CuyMo6S8 Compounds, Chem. Commun., 2007, 4212.
7. K. Persson, Y. Hinuma, Y. S. Meng, A. Van der Ven and G. Ceder, Thermodynamic and Kinetic Properties of the Li-Graphite System from First-Principles Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125416.
8. E. Lee and K. A. Persson, Li Absorption and Intercalation in Single Layer Graphene and Few Layer Graphene by First Principles, Nano Lett., 2012, 12, 4624–4628.
9. D. Aurbach, Z. Lu, A. Schechter, Y. Gofer, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Prototype Systems for Rechargeable Magnesium Batteries, Nature, 2000, 407, 724–727.
10. W. Yu, D. Wang, B. Zhu and Z. Gui-en, Intercalation of Mg in V₂O₅, Solid State Commun., 1987, 63, 1043–1044.
11. W. Yu, B. Zhu, S. Wang and L. Xus, Insertion of Bi-Valence Cations Mg²⁺ and Zn²⁺ into V₂O₅, Solid State Commun., 1987, 61, 271–273.
12. M. Hayashi, H. Arai, H. Ohtsuka and Y. Sakurai, Electrochemical Insertion/Extraction of Calcium Ions Using Crystalline Vanadium Oxide, Electrochem. Solid-State Lett., 2004, 7, A119.
13. M. E. Spahr, P. Novak, O. Haas and R. Nesper, Electrochemical Insertion of Lithium, Sodium, and Magnesium Molybdenum(VI) Oxide, J. Power Sources, 1995, 54, 346–351.
14. T. Sian and G. B. Reddy, Infrared and Electrochemical Studies on Mg Intercalated a-MoO₃ Thin Films, Solid State Ionics, 2004, 167, 399–405.
15. T. D. Gregory, R. J. Hoffman and R. C. Winterton, Nonaqueous Electrochemistry of Magnesium Applications to Energy Storage, J. Electrochem. Soc., 1990, 137, 775.
16. N. Amir, Y. Vestfrid, O. Chusid, Y. Gofer and D. Aurbach, Progress in Nonaqueous Magnesium Electrochemistry, J. Power Sources, 2007, 174, 1234–1240.
17. W. Yuan and J. R. Giinter, Insertion of Bivalent Cations into Monoclinic NbS₃ Prepared under High Pressure and Their Secondary Batteries, Solid State Ionics, 1995, 76, 253–258.
18. J. Giraudet, D. Claves, K. Guérin, M. Dubois, A. Houdayer, F. Masin and A. Hamwi, Magnesium Batteries: Towards a First Use of Graphite Fluorides, J. Power Sources, 2007, 173, 592–598.
19. Y. Zheng, Y. NuLi, Q. Chen, Y. Wang, J. Yang and J. Wang, Magnesium Cobalt Silicate Materials for Reversible Magnesium Ion Storage, Electrochim. Acta, 2012, 66, 75–81.
20. D. B. Le, S. Passerini, F. Coustier, J. Guo, T. Soderstrom, B. B. Owens and W. H. Smyrl, Intercalation of Polyvalent Cations into V₂O₅ Aerogels, Chem. Mater., 1998, 4756, 682–684.
21. R. Imhof and O. Haas, Magnesium Insertion Electrodes for Rechargeable Nonaqueous Batteries – a Competitive Alternative to Lithium?, Electrochim. Acta, 1999, 45, 351.
22. M. M. Thackeray, P. G. Bruce, J. B. Goodenough and S. P. Road, Lithium Insertion into Manganese Spinels, Mater. Res. Bull., 1983, 18, 461–472.
23. M. M. Thackeray, C. T. Division and E. T. Program, Manganese Oxides for Lithium Batteries, Prog. Solid State Chem., 1997, 25, 1–71.
24. K. Amine, H. Tukamoto, H. Yasuda and Y. Fujita, A New Three-Volt Spinel Li_1+xMn_1.5Ni_0.5O₄ for Secondary Lithium Batteries, J. Electrochem. Soc., 1996, 143, 1607–1613.
25. Y. Terada, K. Yasaka, F. Nishikawa, T. Konishi, M. Yoshio and I. Nakai, In Situ XAFS Analysis of Li(Mn, M)₂O₄ (M = Cr, Co, Ni) 5 V Cathode Materials for Lithium-Ion Secondary Batteries, J. Solid State Chem., 2001, 156, 286–291.
26. H. Kawai, M. Nagata, H. Kageyama, H. Tukamoto and A. R. West, 5 V Lithium Cathodes Based on Spinel Solid Solutions, Electrochim. Acta, 1999, 45, 315–327.
27. D. Liu, Y. Lu and J. B. Goodenough, Rate Properties and Elevated-Temperature Performances of LiNi_0.5−xCr_2xMn_1.5−xO₄ (0 ≤ 2x ≤ 0.8) as 5 V Cathode Materials for Lithium-Ion Batteries, J. Electrochem. Soc., 2010, 157, A1269.
28. N. N. Sinha and N. Munichandraiah, Electrochemical Conversion of LiMn₂O₄ to MgMn₂O₄ in Aqueous Electrolytes, Electrochem. Solid-State Lett., 2008, 11, F23.
29. C. Xu, H. Du, B. Li, F. Kang and Y. Zeng, Reversible Insertion Properties of Zinc Ion into Manganese Dioxide and Its Application for Energy Storage, Electrochem. Solid-State Lett., 2009, 12, A61.
30. C. Yuan, Y. Zhang, Y. Pan, X. Liu, G. Wang and D. Cao, Investigation of the Intercalation of Polyvalent Cations (Mg²⁺, Zn²⁺) into λ-MnO₂ for Rechargeable Aqueous Battery, Electrochim. Acta, 2014, 116, 404–412.
31. F. Zhou, M. Cococcioni, C. Marianetti, D. Morgan and G. Ceder, First-Principles Prediction of Redox Potentials in Transition-Metal Compounds with LDA+U, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121.
32. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
33. P. E. Blochl, Projector Augmented-wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
34. J. P. Perdew, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
35. J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1, 011002.
37. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319.
38. L. Wang, T. Maxisch and G. Ceder, Oxidation Energies of Transition Metal Oxides within the GGA+U Framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
39. M. K. Aydinol and G. Ceder, First-Principles Prediction of Insertion Potentials in Li–Mn Oxides for Secondary Li Batteries, J. Electrochem. Soc., 1997, 144, 1–4.
40. M. Aydinol, A. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Ab Initio Study of Lithium Intercalation in Metal Oxides and Metal Dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365.
41. S. P. Ong, L. Wang, B. Kang and G. Ceder, Li–Fe–P–O2 Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 77, 1798–1807.
42. A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Formation Enthalpies by Mixing GGA and GGA+U Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115.
43. S. P. Ong, A. Jain, G. Hautier, B. Kang and G. Ceder, Thermal Stabilities of Delithiated Olivine MPO₄ (M = Fe, Mn) Cathodes Investigated Using First Principles Calculations, Electrochem. Commun., 2010, 12, 427–430.
44. M. W. Chase, NIST-JANAF Thermochemical Tables, American Chemical Society, New York, 1998, p. 2013.
45. L. Wang, T. Maxisch and G. Ceder, A First-Principles Approach to Studying the Thermal Stability of Oxide Cathode Materials, Chem. Mater., 2007, 19, 543–552.
46. http://pythonhosted.org/FireWorks .
47. G. Henkelman, B. P. Uberuaga and H. Jonsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904.
48. G. K. P. Dathar, D. Sheppard, K. J. Stevenson and G. Henkelman, Calculations of Li-Ion Diffusion in Olivine Phosphates, Chem. Mater., 2011, 23, 4032–4037.
49. S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Voltage, Stability and Diffusion Barrier Differences between Sodium-Ion and Lithium-Ion Intercalation Materials, Energy Environ. Sci., 2011, 4, 3680.
50. H. Lin, Y. Wen, C. Zhang, L. Zhang, Y. Huang, B. Shan and R. Chen, A GGA+U Study of Lithium Diffusion in Vanadium Doped LiFePO₄, Solid State Commun., 2012, 152, 999–1003.
51. B. Xu and S. Meng, Factors Affecting Li Mobility in Spinel LiMn₂O₄—A First-Principles Study by GGA and GGA+U Methods, J. Power Sources, 2010, 195, 4971–4976.
52. D. Morgan, A. Van der Ven and G. Ceder, Li Conductivity in Li_xMPO₄ (M = Mn, Fe,  Co,  Ni) Olivine Materials, Electrochem. Solid-State Lett., 2004, 7, A30.
53. K. Amine, H. Tukamoto, H. Yasuda and Y. Fujita, Preparation and Electrochemical Investigation of LiMn₂Me_xO₄ (Me: Ni, Fe, and x = 0.5, 1) Cathode Materials for Secondary Lithium Batteries, J. Power Sources, 1996, 68, 604–608.
54. J. Bhattacharya and C. Wolverton, Relative Stability of Normal vs. Inverse Spinel for 3d Transition Metal Oxides as Lithium Intercalation Cathodes, Phys. Chem. Chem. Phys., 2013, 15, 6486–6498.
55. E. Gocke, R. Schollhorn, G. Aselmann and W. Muller-Warmuthf, Molybdenum Cluster Chalcogenides Mo6X8: Intercalation of Lithium via Electron/Ion Transfer, Inorg. Chem., 1987, 26, 1805–1812.
56. W. R. McKinnon and J. R. Dahn, Structure and Electrochemistry of Li_xMo₆S₈, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3084–3087.
57. M. Morita, N. Yoshimoto, S. Yakushiji and M. Ishikawa, Rechargeable Magnesium Batteries Using a Novel Polymeric Solid Electrolyte, Electrochem. Solid-State Lett., 2001, 4, A177.
58. S. Wang, Z. Lu, D. Wang, C. Li, C. Chen and Y. Yin, Porous Monodisperse V₂O₅ Microspheres as Cathode Materials for Lithium-Ion Batteries, J. Mater. Chem., 2011, 21, 6365.
59. K. H. Seng, J. Liu, Z. P. Guo, Z. X. Chen, D. Jia and H. K. Liu, Free-Standing V₂O₅ Electrode for Flexible Lithium Ion Batteries, Electrochem. Commun., 2011, 13, 383–386.
60. A. Van der Ven, C. Marianetti, D. Morgan and G. Ceder, Phase Transformations and Volume Changes in Spinel Li_xMn₂O₄, Solid State Ionics, 2000, 135, 21–32.
61. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Unlocking the Potential of Cation-Disordered Oxides for Rechargeable Lithium Batteries, Science, 2014, 343, 519–522.
62. C. Marianetti, D. Morgan and G. Ceder, First-Principles Investigation of the Cooperative Jahn–Teller Effect for Octahedrally Coordinated Transition-Metal Ions, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 224304.
63. G. Hautier, S. P. Ong, A. Jain, C. J. Moore and G. Ceder, Accuracy of Density Functional Theory in Predicting Formation Energies of Ternary Oxides from Binary Oxides and Its Implication on Phase Stability, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155208.
64. G. Bergerhoff and I. D. Brown, et al., Crystallographic Databases, ed. F. H. Allen, International Union of Crystallography, Chester, 1987.
65. J. Bhattacharya and A. Van der Ven, Phase Stability and Nondilute Li Diffusion in Spinel Li_{1 − x}Ti₂O₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 104304.
66. A. Jain, G. Hautier, C. Moore, B. Kang, J. Lee, H. Chen, N. Twu and G. Ceder, A Computational Investigation of Li₉M₃(P₂O₇)₃(PO₄)₂ (M = V, Mo) as Cathodes for Li Ion Batteries, J. Electrochem. Soc., 2012, 159, A622.
67. R. Zhang, X. Yu, K.-W. Nam, C. Ling, T. S. Arthur, W. Song, A. M. Knapp, S. N. Ehrlich, X.-Q. Yang and M. Matsui, A-MnO₂ as a Cathode Material for Rechargeable Mg Batteries, Electrochem. Commun., 2012, 23, 110–113.
68. W. Song; T. S. Arthur; C. Bucur; M. Matsui; J. Muldoon; N. Singh and R. Zhang, High Voltage Rechargeable Magnesium Cell, U.S. Pat. 0004830 A1, 2013.
69. K. Kang and G. Ceder, Factors That Affect Li Mobility in Layered Lithium Transition Metal Oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094105.
70. J. K. Burdett, G. D. Price and S. L. Pricelb, Role of the Crystal-Field Theory in Determining the Structures of Spinels, J. Am. Chem. Soc., 1982, 104, 92–95.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ee03389b

‡ M. Liu and Z. Rong contributed equally to this work.

---