Mechanical degradation and stability of organic solar cells: molecular and microstructural determinants
Suchol
Savagatrup
,
Adam D.
Printz
,
Timothy F.
O'Connor
,
Aliaksandr V.
Zaretski
,
Daniel
Rodriquez
,
Eric J.
Sawyer
,
Kirtana M.
Rajan
,
Raziel I.
Acosta
,
Samuel E.
Root
and
Darren J.
Lipomi
*
Department of NanoEngineering, University of California, 9500 Gilman Drive, Mail Code 0448, San Diego, La Jolla, CA 92093-0448, USA. E-mail: dlipomi@ucsd.edu
First published on 3rd November 2014
Abstract
The mechanical properties of organic semiconductors and the mechanical failure mechanisms of devices play critical roles in the yield of modules in roll-to-roll manufacturing and the operational stability of organic solar cells (OSCs) in portable and outdoor applications. This paper begins by reviewing the mechanical properties—principally stiffness and brittleness—of pure films of organic semiconductors. It identifies several determinants of the mechanical properties, including molecular structures, polymorphism, and microstructure and texture. Next, a discussion of the mechanical properties of polymer–fullerene bulk heterojunction blends reveals the strong influence of the size and purity of the fullerenes, the effect of processing additives as plasticizers, and the details of molecular mixing—i.e., the extent of intercalation of fullerene molecules between the side chains of the polymer. Mechanical strain in principle affects the photovoltaic output of devices in several ways, from strain-evolved changes in alignment of chains, degree of crystallinity, and orientation of texture, to debonding, cohesive failure, and cracking, which dominate changes in the high-strain regime. These conclusions highlight the importance of mechanical properties and mechanical effects on the viability of OSCs during manufacture and in operational environments. The review—whose focus is on molecular and microstructural determinants of mechanical properties—concludes by suggesting several potential routes to maximize both mechanical resilience and photovoltaic performance for improving the lifetime of devices in the near term and enabling devices that require extreme deformation (i.e., stretchability and ultra-flexibility) in the future.
Broader contextOrganic solar cells (OSCs) are potentially an inexpensive source of renewable energy that can be manufactured at speeds that dwarf the rate at which wafer-based devices (i.e., silicon) can be fabricated. While low efficiencies of OSCs have historically been regarded as a major roadblock, the performance of this class of printable devices is improving rapidly, and module efficiencies of ten percent now seem possible. The susceptibility of polymer-based active layers to undergo thermally activated phase separation, photochemical damage, and other forms of degradation has motivated large and expanding literature devoted to understanding and improving the long-term stability of modules. Conspicuously absent from the literature, however, is a similar effort directed toward understanding the mechanical properties of organic semiconductors and their effects on the lifetime of devices against mechanical failure. The principal advantage of OSCs and all printed electronic devices is, nonetheless, roll-to-roll manufacturing on flexible substrates. Manufacturing, installation, and use of these devices will thus require substantial mechanical resilience. Moreover, the ability to make devices on ultrathin plastic sheets—necessary to achieve low production energy for whole modules—requires that the active materials withstand at least some mechanical strain. This article reviews the literature on the mechanical properties of organic semiconductors, the ways in which strain impacts the photovoltaic performance of modules, and what can be done to understand and mitigate these effects. The goal of this review is thus to connect the molecular structure and solid-state microstructure to mechanical properties and mechanical forms of degradation. In addition to increasing the mechanical stability of devices envisioned in the near term, understanding how mechanical resilience and high-performance semiconducting properties can coexist could enable devices for extreme deformation, for example, in portable and wearable applications. Our analysis reveals that there are several potential routes toward co-engineering both mechanical resilience and photovoltaic performance. |
1. Motivation
Organic solar cells (OSCs) have achieved benchmarks in the research laboratory that may have seemed out of reach only a decade ago: power conversion efficiencies over 10 percent,1 projected lifetimes of devices on rigid substrates of over seven years,2 power-to-mass ratios of 10 W g−1,3 and projected energy payback times on the order of days.4 These achievements have been realized, in general, by an approach that uses power conversion efficiency (PCE) or some other figure of merit to guide the design and selection of materials and parameters for processing. For organic solar cells to reach the performance and robustness needed to provide inexpensive power on the scale of gigawatts or—in a best-case scenario—terawatts,5 significant work remains to be done to translate the progress made in the research laboratory toward the production of modules in a roll-to-roll manner.6 Krebs and coworkers have suggested an alternative approach in which the requirements for manufacturing inform the design of materials.7 The minimum requirements for low-cost and green8,9 materials to be amenable to manufacturing include stability while printing from solution,10 in air,11 at low temperatures, from environmentally benign solvents,12,13 without vacuum steps,14 and with tolerance of inhomogeneities in thickness and morphology that appear in printed films.7,15 (Fundamental and theoretical studies designed to understand the mechanism of operation, of course, inform all efforts to improve the efficiencies of devices.16–19) One aspect of the design of materials that is seldom considered20,21—but that is critical to the stability and lifetime of thin, flexible, lightweight modules destined for outdoor or portable use—is mechanical stability.22–24 This attribute is generally excluded from an approach that is centered on efficiency,7 but is included in one that is centered on the requirements for manufacturing and viability under conditions in outdoor25 and portable environments.26It may seem, because thin films of virtually any material are flexible relative to thicker specimens, that organic semiconductors are already sufficiently compliant for flexible applications and for high yield in roll-to-roll manufacturing. An examination of the modest literature on the mechanical properties of organic semiconductors reveals that their responses to mechanical deformation are highly variable22,24,27–33 (see Fig. 1 for structures referred to in the text, and Table 1 for a summary of the mechanical properties of pure organic semiconductors and composites). Moreover, good electronic performance—associated with long conjugation lengths and high degrees of crystallinity—seems to correlate with stiffness and brittleness.24,28,33 Some studies, however, have shown that this correlation is not a fundamental trade-off and that it is, in principle, possible to achieve the “best of both worlds” of mechanical and electronic performance.27,29,34–36 Predicting trends in mechanical properties requires an understanding of the ways in which a molecular structure produces a solid-state microstructure,28 and how structures at both length scales influence the mechanical and electronic properties of a solid material.24,27,33
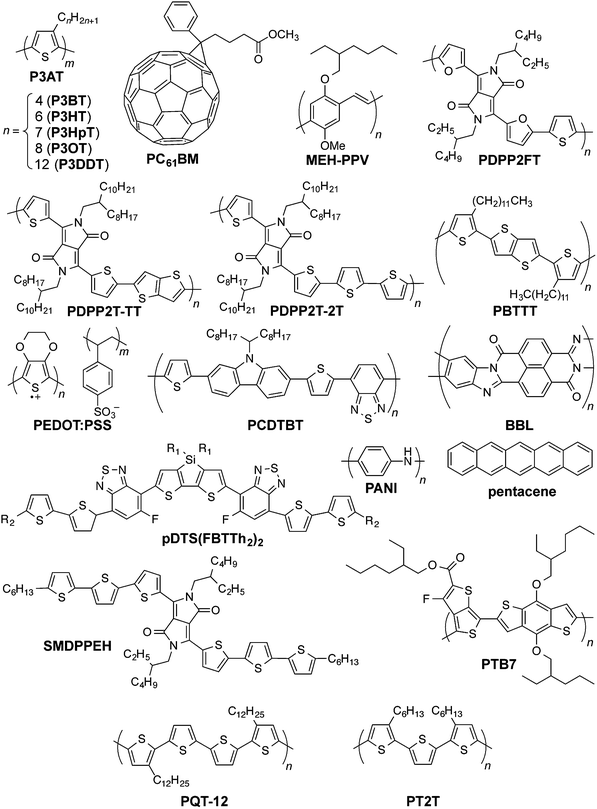 | ||
| Fig. 1 Chemical structures of organic conductors and semiconductors discussed in the text. Another variation of PBTTT has side chains with two additional methylene units. | ||
| Materials | Notes | Tensile modulus [GPa] | Crack on-set strain [%] | Reference |
|---|---|---|---|---|
| a Ratios are reported in weight ratio. Films with thermal annealing treatments are denoted as annealed (AN), while untreated films are denoted as as-cast (AC). Films are spin-coated from chloroform or otherwise noted. | ||||
| P3HT | AC | 1.33 ± 0.01 | 32 | |
| 1.3 | 88 | |||
| 0.92 | 31 | |||
| 0.252 ± 0.06 | >150 | 33 | ||
| 1.09 ± 0.15 | 9 ± 1.2 | 28 | ||
| 0.22 ± 0.03 | 24 | |||
| P3HT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8, AC 0.8, AC |
6.02 ± 0.03 | 32 | |
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AC 1, AC |
4.3 | 31 | ||
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AC 1, AC |
1.97 ± 0.07 | 131 | ||
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AN 1, AN |
2.75 ± 0.09 | 131 | ||
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, AC 0.5, AC |
2.02 ± 0.48 | 3 ± 1.5 | 28 | |
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AN (ODCB) 1, AN (ODCB) |
∼1.74 to 1.97 | ∼2% to >80% | 24 | |
| P3HT–Fullerene | PC71BM (90%), AC | 0.67 ± 0.07 | 125 | |
| PC71BM (90%), AN | 1.76 ± 0.04 | 125 | ||
| PC71BM (90%), AC | 2.72 ± 0.40 | 125 | ||
| PC71BM (90%), AN | 3.21 ± 0.06 | 125 | ||
| ICBA (99%), AC | 3.27 ± 0.86 | 125 | ||
| ICBA (99%), AN | 6.53 ± 1.88 | 125 | ||
| P3BT | AC | 1.87 ± 0.52 | 6 ± 1.5 | 28 |
| P3BT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, AC 0.5, AC |
5.2 ± 0.61 | 2 ± 0.6 | 28 |
| P3PT | AC | 1.33 ± 0.14 | 27 | |
| P3HpT | AC | 0.07 ± 0.01 | 58 | 27 |
| AN | 0.13 ± 0.01 | 131 | ||
| P3HpT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AC 1, AC |
0.61 ± 0.09 | 131 | |
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AN 1, AN |
1.46 ± 0.16 | 131 | ||
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AN (ODCB) 1, AN (ODCB) |
1.79 ± 0.35 | 27 | ||
| P3OT | AC | 0.15 ± 0.05 | 65 ± 2.5 | 28 |
| P3OT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, AC 0.5, AC |
0.52 ± 0.16 | 47 ± 2.1 | 28 |
| P3DT | AC | 0.12 ± 0.4 | 27 | |
| P3DDT | AC | 0.16 ± 0.07 | 47 ± 3.1 | 28 |
| P3DDT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, AC 0.5, AC |
0.47 ± 0.17 | 44 ± 1.4 | 28 |
| DPPT-TT | AC | 0.99 | 31 | |
| DPPT-TT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AC 1, AC |
1.4 | 31 | |
| DPPT-2T | AC | 0.74 | 31 | |
| DPPT-2T–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AC 1, AC |
0.84 | 31 | |
| PT2T | AC | 1.11 ± 0.19 | 29 | |
| AN | 1.01 ± 0.27 | 131 | ||
| PT2T–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, AC 2, AC |
1.6 ± 0.36 | 29 | |
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AC 1, AC |
2.0 ± 0.36 | 131 | ||
Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AN 1, AN |
2.61 ± 0.39 | 131 | ||
| PDPP2FT | AC | 2.17 ± 0.35 | 29 | |
| PDPP2FT–PCBM | Ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, AC 2, AC |
2.76 ± 0.77 | 29 | |
| MEH–PPV | AC | 0.119 ± 0.005 | 131 | |
| AN | 0.023 ± 0.001 | 131 | ||
| MEH–PPV–PCBM | AC | 3.79 ± 0.07 | 131 | |
| AN | 4.92 ± 0.09 | 131 | ||
| PBTTT | AC (ODCB) | 0.879 ± 0.243 | <2.5 | 33 |
| AN (ODCB) | 1.8 ± 0.345 | <2.5 | 33 | |
| AC | 1.8 ± 0.19 | 131 | ||
| AN | 2.9 ± 0.30 | 131 | ||
| PBTTT–PCBM | AC | 3.76 ± 0.8 | 131 | |
| AN | 4.38 ± 0.68 | 131 | ||
| PEDOT–PSS | 2.26 ± 0.05 | 32 | ||
| 5% DMSO, 10% Zonyl | 0.03 ± 0.01 | 71 | ||
| 5% DMSO, 1% Zonyl | 3.14 ± 0.12 | 71 | ||
| 5% DMSO, 0.1% Zonyl | 7.49 ± 1.5 | 71 | ||
| PANI | 0.03 | 32 | ||
| Pentacene | 16.09 | 32 | ||
| PCBM | C60 | 3.06 ± 0.17 | 24 | |
| C60 | 6.2 | 88 | ||
The range over which mechanical properties vary will have significant consequences for the long-term stability of devices, and will thus influence the selection of materials for particular applications. Annealed films of pure PBTTT and composite films of P3HT–PCBM—the Drosophila of organic solar cells—crack at strains <2.5% on polydimethylsiloxane (PDMS) substrates under typical processing conditions.33 Evaporated films of the molecular semiconductor pentacene (and presumably other van der Waals solids) are likely to be more brittle than are films of P3HT–PCBM.32 Other researchers have noted the importance of understanding the mechanical failure mechanisms.21 In the report of a Workshop on Key Scientific and Technological Issues for Development of Next-Generation Organic Solar Cells, sponsored by the US National Science Foundation and the Office of Naval Research, researchers asked, “What has been done to prevent solar cells from failing mechanically?”37 Moreover, in a well-known paper in which researchers deployed roll-to-roll fabricated, OSC-powered, LED lanterns in rural Zambia, one of the principal conclusions was that “…mechanical failure mechanisms were dominant during the field test and therefore these would have to be improved significantly before the photochemical stability of the [semiconducting] polymer becomes a problem.”26 Mechanical stability is of critical importance not only for portable applications—for which accommodation of strain is an operational requirement38—but also for roll-to-roll production, transportation, and for utility-scale applications.7,25
In large-scale solar farms and in portable applications, thin organic solar modules will be subject to a range of stresses due to environmental forces.25 The pressure of wind and the weight of rain and snow will strain the devices to an extent that depends on the compliance and thermal expansion of the encapsulants and support structures. Robust encapsulants and support structures will add significant expense to the modules,39 and it is thus desirable to use active materials that can accommodate at least some strain without the need for expensive, rigid supports. Even the thinnest support structures add significantly to the production costs of thin-film PV modules: Anctil et al. calculated that a 130 μm poly(ethyleneterephthalate) (PET) substrate contributes approximately 10% of the embodied energy (along with a roughly equal amount for the encapsulants) of organic modules made using conventional materials, and nearly double that amount in ITO-free devices.39 One inevitable mode of mechanical deformation that will occur even in the presence of protective layers is thermal expansion and contraction due to diurnal and seasonal variations in temperature. Materials and devices must thus tolerate the extreme conditions in a given geographical area, as well as exhibit resistance to fatigue in the face of cyclic loading due to modest thermal cycling. It is possible that the surface of a highly absorbing device may reach temperatures of 70 °C in the Southwestern US, and a range of as much as 100 °C over the lifetime of a device in the Midwest, if one accounts for inevitable extremes in temperatures. One of the goals of the community interested in the mechanical properties of organic semiconductors is thus to mitigate the effects of thermal expansion and contraction on the lifetime and performance of OSCs.
There are a large number of competing technologies in the field of solar photovoltaics. All of these technologies ostensibly have the same goal: achieving the most favorable cost per watt, amortized over the lifetime of the device, for utility-scale installations.40 Organic solar cells, however, have several characteristics that would be difficult or impossible to replicate in conventional or other thin-film technologies. These characteristics include: semitransparency41,42 and tunable color for aesthetic considerations,43 thermally activated charge transport44 and possibly increased efficiency at elevated temperature, high-speed manufacturing under ambient conditions,6,25 extreme thinness and light weight,3 and the potential to tolerate high strains without loss of function.30,31 One strategy to hedge against a winner-take-all outcome (if a non-organic PV technology becomes dominant for utility-scale applications) is to focus on areas in which OSCs could “run away” with part of the PV market.22 Mechanical compliance is the fundamental attribute that provides the basis for all advantages of OSCs.45 Physical robustness is a prerequisite for fabricating devices on ultrathin substrates, because small forces can produce strains large enough to crack, delaminate, or plastically deform thin films of semiconducting polymers.3,46,47 Moreover, in some portable,26 wearable,38 and implantable48 applications, extreme mechanical compliance30 and resistance to mechanical failure is at least as important as photochemical49 and morphological21 stability.50–52
This article reviews the current state of knowledge of the mechanical failure of organic solar cells. The focus is on the ways in which molecular structure influences the microstructure of conjugated materials in the solid state, and how these parameters combine to dictate mechanical properties. The focus on molecular structure and microstructure reflects the expertise of the authors, and we thus invite readers interested in other important aspects of mechanical stability, such as continuum theories of deformation and fracture, to consult references herein.
2. Mechanical properties of organic semiconductors
The factors that ultimately control the mechanical stability of OSCs can be reduced to intermolecular and surface forces present in samples of organic semiconductors and ancillary materials, and how they influence the properties of thin films (mediated by the conditions of processing). The early literature—in the 1980s and early 1990s—contained several studies of the mechanical properties of some of the first-reported conjugated polymers.53–57 It is apparent, however, that the discovery of the polymer solar cell by Heeger and Wudl,58 and independently by Friend,59 along with the discovery of the organic light-emitting device by Friend,60 and invention61 and refinement62 of the polymer thin-film transistor, shifted the focus from bulk properties—i.e., mechanical properties—familiar to polymer scientists and mechanical engineers, to electronic properties familiar to physicists and electrical engineers. Mechanical properties thus took a back seat to electronic performance, during which time important work was done on improving electronic figures of merit (e.g., power conversion efficiency, PCE, in organic solar cells). Much of the success of the field in improving the performance of devices came through the proliferation of the molecular structures accessible by synthetic chemistry.8,63–67 Mechanical properties, such as tensile modulus, ductility, fracture toughness, and other parameters of new materials, however, are seldom reported and would be difficult to judge based only on molecular structure. Nevertheless, recent work has attempted to produce some generalities about the ways in which molecular structure and solid-state microstructure influence the mechanical properties of these materials. Far more is known about the mechanical properties of semiconducting polymers than is known about their small-molecule counterparts, and thus Section 2.1 begins with a discussion of the structural determinants of the mechanical properties of pure conjugated polymers.There is no single figure of merit possessed by an organic semiconductor or composite that will predict the mechanical stability of a whole module: desirable properties will depend largely on the application and on the properties of other materials in the device. The substrate and encapsulant provide structural support, and if the substrate fails mechanically then the device will most likely fail electronically, so it is not necessary that the organic semiconductors provide structural support (e.g., high tensile strength may be desirable, but not if the film fractures at low strains). In general, the active materials should deform with the substrate. That is, they should have a low modulus and high elastic limit. The strain at which cracks appear in a film on an elastic substrate is often taken as a measure of the ductility of a thin film, but the so-called crack-onset strain is highly dependent on the adhesion between the film and the substrate (poorly adhered films crack at smaller strains than well adhered films of the same modulus).28 Adhesive68,69 and cohesive23,52,70 fracture energies have been proposed to predict the mechanical modes of degradation within the active materials and electrodes in whole modules, and we will return to these figures of merit in more detail in Section 3.2.2. Adhesive energy, however, is sensitive to the order in which layers are deposited,68,69 and cohesive energy often depends on thickness.50 Of all these figures of merit, tensile modulus has the advantages of being easily measured, intrinsic to the material (as opposed to its interaction with a substrate or overlayer), insensitive to thickness for those typically used in devices (≥50 nm), and easily relatable (and sometimes predictable) on the basis of chemical structure and microstructure. Additionally, tensile modulus and crack-onset strain (i.e., effective brittleness) are correlated for every system of conjugated polymers in which both quantities are reported in the same paper,24,27,28,33,71 and thus a low tensile modulus can be used as a proxy for a favorable response to deformation in mechanically robust applications. Tensile modulus, however, will not predict the mechanical response past the elastic limit, nor will it predict the elastic limit (though we have observed that low tensile modulus is correlated with high elastic limit in P3ATs).30
2.1. Mechanical properties of pure organic semiconductors
The mechanical buckling technique has proven useful in determining the tensile modulus of a range of inorganic and organic thin films,85,86,88 and even of individual single-walled carbon nanotubes.89 The method is based on the buckling instability that gives rise to wrinkles in a relatively rigid film on a relatively compliant substrate under compressive strain.90,91 The wavelength of the wrinkling pattern, λb, can be related to the tensile modulus of the film, Ef, in terms of the modulus of the substrate, Es, the thickness of the film, df, and the Poisson ratios of the film and substrate, νf and νs, in eqn (1).86
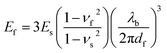 | (1) |
In practice, plotting λb as a function of df for a series of samples (or for a single sample bearing a gradient in thickness) and inserting the slope into eqn (1) yields the modulus of the film. The modulus scales with the cube of the slope, and this sensitivity thus requires that the measurement be carried out with strict adherence to established procedures.86 Poor interfacial adhesion92 and surface defects—such as pre-existing wrinkles, delamination, and cracking—can produce apparent buckling wavelengths that lead to measurements that deviate significantly from the intrinsic values of the films. Table 1 is a comprehensive table containing the modulus of every organic electronic material and composite measured by the buckling method.
 | ||
| Fig. 2 Tensile moduli of poly(3-alkylthiophenes) (P3ATs). (a) Tensile modulus vs. the length of the alkyl side chain (n). A sharp drop-off occurs with increasing n as the glass transition drops below ambient temperature, from n = 6 to n = 7. (b) Moduli of three “hybrid” materials with equimolar ratios of hexyl and octyl side chains: a block copolymer (P3HT-b-P3OT), a statistical copolymer (P3HT-co-P3OT), and a physical blend (P3HT–P3OT). Reproduced with permission from ref. 28. Copyright 2014, American Chemical Society. (c) Overlay of the experimental and theoretical tensile moduli of P3ATs vs. the length of the alkyl side chains. Reproduced with permission from ref. 28 Copyright 2014 Wiley-VCH Verlag GmbH & Co. KGaA. | ||
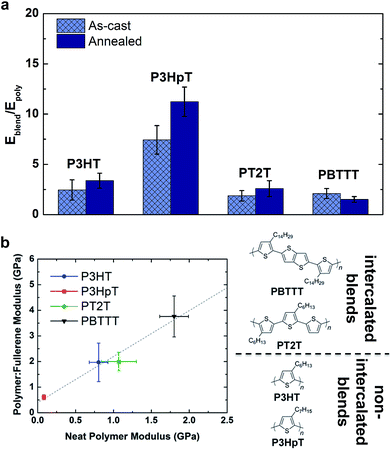
The interesting mechanical behavior of P3ATs in which 6 ≤ n ≤ 8 led us to investigate “hybrid” systems, comprising equal molar fractions of hexyl and octyl side chains (Fig. 2b).27 These hybrid systems were a physical blend of P3HT and P3OT (P3HT–P3OT), a block copolymer (P3HT-b-P3OT), and a statistical copolymer (P3HT-co-P3OT). The modulus of the block copolymer sat on a line extrapolated between P3HT and P3OT. This average modulus can be attributed to the covalent connectivity of the relatively stiff P3HT and the relatively plastic P3OT. The modulus of the physical blend, in contrast, sat below the extrapolated modulus, possibly because the P3OT domains—unconstrained by covalent tethering to the P3HT domains—absorbed the strain and thus dominated the mechanical response of the composite material.27 None of these hybrid materials, however, exhibited as low a tensile modulus as did P3HpT, and the factors governing the combination of high compliance and good photovoltaic properties of this interesting material are still under investigation. It appears, however, that the percent aggregate and the order within the crystalline domains of P3HpT are similar to that of P3HT, while these quantities for P3OT are substantially reduced.
The presence or absence of interdigitation of the side chains of conjugated polymers could be a predictor of the mechanical properties of the solid film.75 The side chains of the P3ATs generally do not interdigitate,75 and thus the lamellae within the crystallites should not be as highly registered vertically as in materials in which the side chains do interdigitate (such as PBTTT33,66 and PT2T97). The decreased number of van der Waals interactions between side chains in non-interdigitated polymers should produce crystallites that are more easily deformable than those in which the side chains are interdigitated. Evidence for interdigitation of the side chains in PBTTT comes by way of a reduction in the (a00) lamellar spacing (measured by GIXD) compared to the spacing predicted by the addition of the lengths of two opposing alkyl side chains in their fully extended conformations.66 Smaller lamellar spacing thus implies interdigitation. Mechanical measurements of PBTTT by O'Connor et al. are highly correlated with its thermal history and thin-film morphology.33 As-cast samples of PBTTT, which have small crystallites,66 exhibited tensile moduli that were half those of annealed films,33 which exhibited large crystallites (and low amorphous fractions) in an earlier study by AFM.66 Both the as-cast film and the annealed film were highly brittle, and both cracked at strains <2.5% on PDMS substrates.33 PT2T (Fig. 1), a structural analogue of P3HT that differs from P3HT on the basis of the regioisomerism and density of attachment of hexyl side chains (which are incorporated in two of every three monomers for PT2T, and in every monomer for P3HT), forms a solid film in which interdigitation is the preferred packing structure.97 Interestingly, the tensile modulus of PT2T was similar to that of P3HT when cast under similar conditions.29
Different crystalline polymorphs of the same material are expected to have substantially different mechanical properties.75 For example, the crystalline domains of P3ATs have two known packing structures.76 Form I is the polymorph found under most conditions. It is characterized by side chains that do not interdigitate. Form II occurs in oligomers of 3-hexylthiophene,75 and for both P3BT and P3HT, conversion from Form I to Form II can occur by exposure to certain solvent vapors (e.g., carbon disulfide).98,99 The defining characteristic of Form II is a shortened lamellar spacing, which is attributed to interdigitation of the side chains.76 Koch et al. made qualitative observations about the mechanical properties as “somewhat brittle in form II while plastic crystalline behavior was observed for form I,” but the mechanical properties were not quantified.75
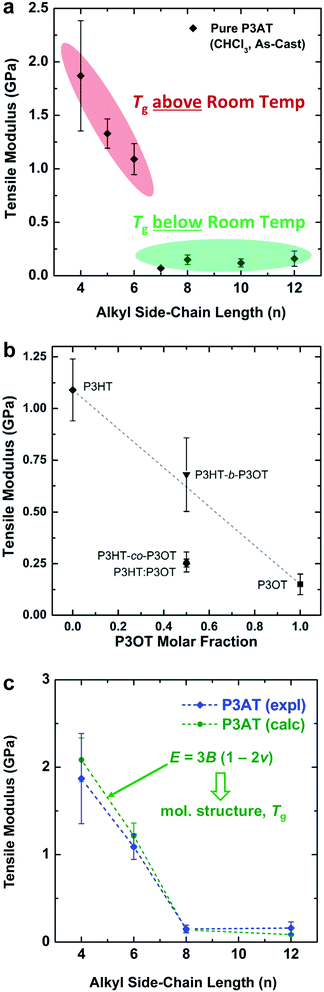
The tensile modulus, Ef, of a thin film (or any material under small strains) is related to the bulk modulus (B) and the Poisson ratio (νf) by eqn (2).
| Ef = 3B(1 − 2νf) | (2) |
The bulk modulus is related, through the Lennard-Jones potential, to the cohesive energy (Ecoh), the van der Waals volume at 0 K (V0), and the volume at the temperature of interest (V) by eqn (3).
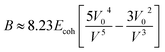 | (3) |
The cohesive energy can, in turn, be calculated from semi-empirical parameters derived from the bond connectivity indices assigned to each atom in the structure of the monomer, in a method described by Fedors.107 The bond connectivity indices are parameters that embody the size and the structure of the monomer as well as the conformational freedom of its bonds. The Poisson ratio is related empirically to the cross-sectional area of the monomer (A), by eqn (4).
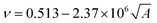 | (4) |
The area is determined by eqn (5).
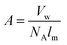 | (5) |
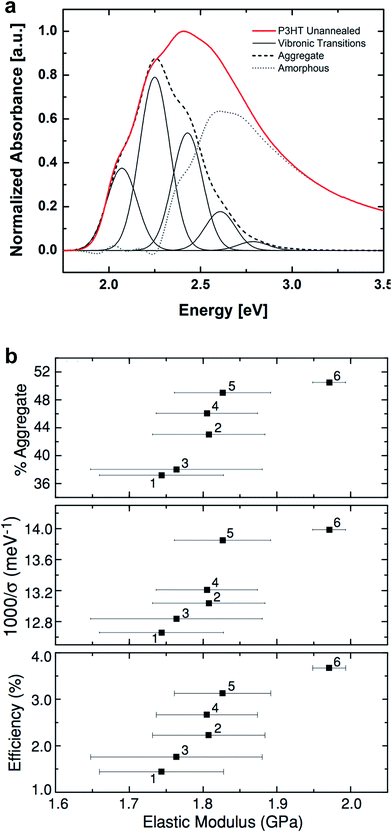 | ||
| Fig. 3 Determination of order within P3HT films by the weakly interacting H-aggregate model. (a) Deconvolution of UV-vis absorption spectrum of P3HT into vibronic peaks associated with aggregated—i.e., crystalline—phases and higher energy absorption of the amorphous domains. Reproduced with permission from ref. 24. Copyright 2013 Wiley-VCH Verlag GmbH & Co. KGaA. | ||
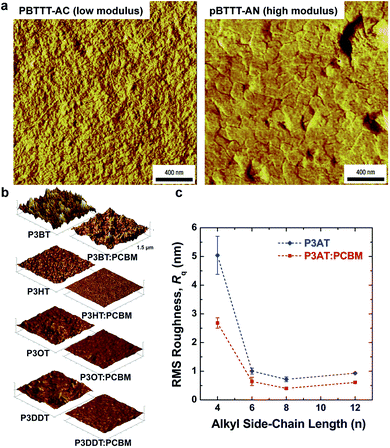 | ||
| Fig. 4 Correlation of surface morphology by atomic force microscopy with mechanical properties. (a) PBTTT undergoes a transition upon thermal annealing from an as-cast form with small crystallites, which is relatively compliant, and a highly crystalline annealed form, which is relatively stiff. Reproduced with permission from ref. 66 Copyright 2006, Nature Publishing Group. (b and c) Roughness is loosely correlated to tensile modulus in P3ATs. Reproduced with permission from ref. 28 Copyright 2014 Wiley-VCH Verlag GmbH & Co. KGaA. | ||
2.2. Mechanical properties of polymer–fullerene composites
While the mechanical properties of pure polymer films have begun to receive some attention, and conclusions and design rules can be drawn, blending pure polymers with electron acceptors—usually fullerenes—produces effects that can be difficult to predict. The general outcome is that a polymer–PCBM composite is stiffer, more brittle, and has decreased interlayer adhesion than does the pure polymer. The current model that describes the P3HT–PCBM blend comprises (at least) a three-phase system: a crystalline polymer domain, a fullerene-rich domain, and a mixed phase.19,121–124 Each phase is expected to contribute to the overall mechanical properties of the film. Processing conditions—e.g., the rate at which the bulk heterojunction forms—affects the order within the crystalline polymer phase, and thus affects the mechanical properties.24 Intercalation of fullerenes between the side chains of conjugated polymers to form bimolecular crystallites117,118 or to prevent crystallization97 is known to have dramatic effects on the tensile modulus and fracture behavior of polymer–fullerene blends.23 Other factors, such as the size and purity of the fullerene samples, also play an important role.125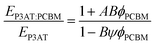 | (6) |
 | (7) |
The results from this model are plotted in Fig. 5 on the same set of axes as the experimental data.28 These composite theories do not account, however, for the ways in which the presence of the fullerene changes the morphology of the polymer phase. In particular, miscibility123 and intercalation118 of the PCBM between the side chains of the polymer, can have profound effects on the mechanical properties of films.23
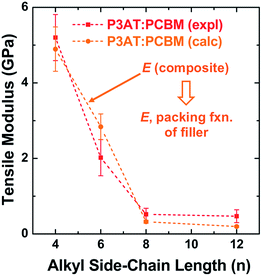 | ||
Fig. 5 Tensile modulus vs. alkyl side chain length for P3AT–PCBM composites in a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The composite theory described in Section 2.2.1 nearly overlaps with the experimental values. Reproduced with permission from ref. 28 Copyright 2014, Wiley-VCH Verlag GmbH & Co. KGaA. 1. The composite theory described in Section 2.2.1 nearly overlaps with the experimental values. Reproduced with permission from ref. 28 Copyright 2014, Wiley-VCH Verlag GmbH & Co. KGaA. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.118
4.118
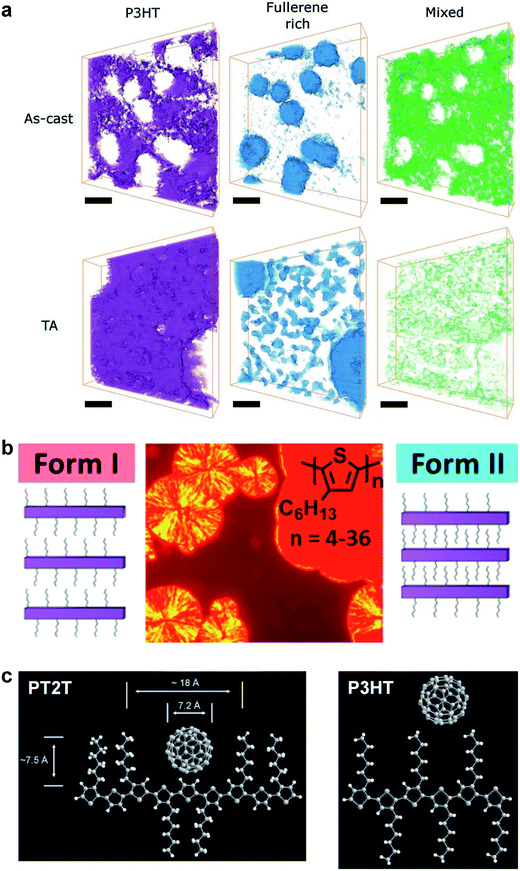 | ||
| Fig. 6 Morphology and packing of organic semiconductor films. (a) Electron tomography using endohedral fullerenes reveals a three-phase system comprising polymer- and fullerene-rich phases, and a mixed phase, which is substantially reduced by thermal annealing. Reproduced with permission from ref. 121 Copyright 2013, Wiley-VCH Verlag GmbH & Co. KGaA. (b) Two crystalline polymorphs of P3HT exist, a thermodynamically favored Form I (spherulites), in which the side chains do not interdigitate, and a kinetically favored Form II (solid red phase), in which they do. Form II is expected to have a greater modulus and higher brittleness than does Form I. Reproduced with permission from ref. 75 Copyright 2013, American Chemical Society. (c) Schematic drawings of PT2T and P3HT, and the hypothesized way in which fullerene molecules can fit between the side chains of PT2T, but not P3HT. Reproduced with permission from ref. 97 Copyright 2007, Wiley-VCH Verlag GmbH & Co. KGaA. | ||
The mechanical properties of polymer–fullerene blends were previously reported to be intimately related to the details of molecular mixing.23 The tensile moduli of most P3AT–fullerene blends are a factor of 3–5 greater than those of the neat polymers.28,32 The typical rationale for the increased modulus of P3AT–PCBM relative to the neat polymer is the stiffness of the fullerene-rich phase.28,32Fig. 7a plots the factor by which selected polymer–fullerene composites are greater than that of the neat polymer both before and after annealing. The salient example is P3HpT–PCBM (factor of 7 greater than neat P3HpT).131 As discussed in Section 2.1.3, P3HpT is the P3AT that maximizes mechanical compliance and electronic performance. Differential compliance and ductility of the P3ATs is largely a function of the fluidity of the amorphous domains at room temperature.27 In a P3AT–fullerene composite, however, the current model predicts the absence of pure amorphous domains of P3ATs,130 and thus we conclude that the presence of fullerenes produce stiffened mixed domains, which dominate the mechanical properties of the blend.
The dominance by the stiffened mixed domains on the mechanical properties of polymer–fullerene blends was observable not only in blends with P3ATs, which do not allow fullerene intercalation, but also in other polythiophenes which do allow fullerene intercalation. Fig. 7b plots the tensile modulus of selected polymer–fullerene blends against the tensile modulus of the neat polymers. Interestingly, for these polythiophenes, there is a linear correlation between the tensile moduli of the neat polymers and the polymer–fullerene blends. This linear correlation suggests that the effects of molecular mixing play a relatively small role in the tensile modulus of polymer–fullerene blends. A striking example is PT2T–PCBM. The neat polymer is relatively highly aggregated due to the interdigitation of the alkyl side chains, though the modulus is similar to that of neat P3HT (∼1 GPa, depending on batch-to-batch variability).28,29 Blending with PCBM, however, destroys the aggregate microstructure of PT2T. Remarkably, the tensile modulus of even a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 blend of PT2T–PCBM is similar to that of P3HT–PCBM, despite the completely different microstructures. The mechanical properties of bulk heterojunction composites—due to the complex nature of the blend, which has at least three phases—can vary widely, and offer interesting opportunities for studying nanocomposite materials.
1 blend of PT2T–PCBM is similar to that of P3HT–PCBM, despite the completely different microstructures. The mechanical properties of bulk heterojunction composites—due to the complex nature of the blend, which has at least three phases—can vary widely, and offer interesting opportunities for studying nanocomposite materials.
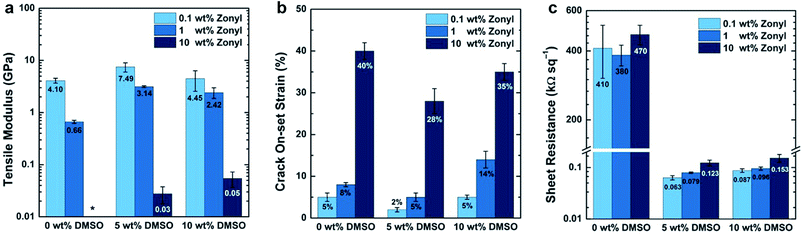
Additives and cosolvents are essentially always used in solution-processed films of PEDOT–PSS,140,141 and these adjuncts have effects on the modulus (Fig. 8a) and ductility (Fig. 8b),71 along with effects on the sheet resistance (Fig. 8c),140 some of which are already known.142 High-boiling liquids and polar additives, such as dimethylsulfoxide (DMSO) and sorbitol, are associated with increasing the size of the conductive PEDOT-rich grains, and thus increasing the conductivity of the film.143,144 Zonyl fluorosurfactant (now called Capstone by DuPont) is used to enable wetting of aqueous dispersions of PEDOT–PSS on hydrophobic plastic substrates,140,145 or on the hydrophobic surface of the bulk heterojunction film in the inverted architecture.146 Poly(ethyleneimine) (PEI),147 and other amine-containing polymers and small molecules,148,149 is used to lower the work function of PEDOT–PSS to permit its use as the cathode (as well as the anode) in all-organic devices. While the use of a thin-layer of PEI seems to have a stiffening effect, Zonyl, when present in the ink in concentrations up to 10%, has a very strong plasticizing effect.71 It seems, thus, that additives may serve a dual purpose: as cosolvents for one or more components of the bulk heterojunction, and as plasticizers for increased mechanical stability. Interestingly, the concentration of DMSO in the ink of 5%, which produced the most conductive films when the concentration of Zonyl was kept constant, also produced films of greater stiffness and brittleness.71 The interconnected morphology that supports good charge transport may thus embrittle the films, but this effect can be mitigated by adding Zonyl (or perhaps another surfactant) without degrading the electronic performance substantially.
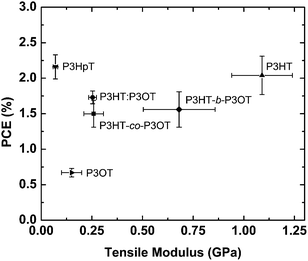 | ||
| Fig. 9 Power conversion efficiency (PCE) of polymer–fullerene blends vs. tensile modulus of the pure poly(3-alkylthiophenes): P3HT, P3OT, a physical blend of the two (P3HT–P3OT), a block copolymer (P3HT-b-P3OT), a random copolymer (P3HT-co-P3OT), and P3HpT. Materials occupying the top-left quadrant (e.g., P3HpT) in principle exhibit a favorable combination of mechanical compliance and photovoltaic performance. Reproduced with permission from ref. 27 Copyright 2014 American Chemical Society. | ||
3. Behavior of materials and devices under strain
All thin-film technologies are susceptible to damage by environmental forces. If changes in the photovoltaic output of devices upon imposition of mechanical stress are not prevented, they should at least be anticipated, so that their effects can be mitigated downstream. We divide the response to strain into two regimes: (1) pre-catastrophic failure and (2) catastrophic failure. The behavior in the first regime, characterized by small-strains (prior to cracking or delamination that produces substantial loss of function) is in principle affected by elastic or plastic deformation of the active materials and contacts. Deformation of the materials continues throughout the second regime, but the photovoltaic output is dominated instead by cracking of the active materials and contacts, failure of the barrier films, and short-circuiting of the electrodes. We define catastrophic failure as occurring when the device loses most or all of its photovoltaic efficiency. This section also discusses the factors that control interfacial debonding, cracking, and the molecular and environmental determinants of this type of failure.3.1. Pre-catastrophic failure behavior
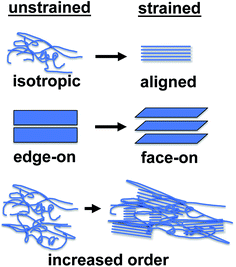
This section reviews the evolution in photovoltaic properties in response to strain-evolved microstructures, change in interfacial energies, and the formation of small cracks. The defining characteristic of this regime is that the photovoltaic properties remain generally intact. Many of the strain-evolved changes in microstructure observed in some conjugated polymers—alignment of chains,78 change in texture from edge-on to face-on,78,79 and increased degree of crystallinity78—might actually increase the photovoltaic performance of devices under some circumstances.The most well known effect of tensile strain on a conjugated polymer is alignment of the chains along the strained axis. This effect has been known since early work on conjugated polymers, and is responsible for the extraordinarily high tensile strength of uniaxially aligned polyacetylene.53,54 Drawn films of P3HT exhibit highly anisotropic hole mobility, which has been noted by Vijay et al.112 and O'Connor et al.78 These studies highlight the importance of along-chain transport in the overall ability of a film to transport charge. This fact was reinforced in a paper by Heeger and coworkers, in which low-bandgap polymers aligned in nanoimprinted grooves exhibited among the highest charge-carrier mobilities reported to date.157 Aligned films also exhibit polarization-dependent absorption, because of the orientation of the π–π* transition, which is perpendicular to the molecular axis.158 Awartani et al. has shown substantial birefringence in stretch-aligned bulk heterojunction films, and thus organic solar cells with polarization-dependent absorption and efficiency.80 The increase in charge-carrier mobility induced by stretch aligning may benefit field-effect transistors, but the anisotropy is in the wrong direction to benefit organic solar cells, in which charges are transported through the thickness of a film.
A secondary effect of strain on the microstructure of conjugated polymer films, as seen in P3HT, is on the texture. O'Connor et al. noted that strain produced realignment of the π system of the molecules from predominantly edge-on (regarded as the preferred orientation for P3ATs and other conjugated polymers) to largely face-on.78,79 The latter orientation may be favorable for OSCs. O'Connor, DeLongchamp, and coworkers have observed this effect in P3HT films under both uniaxial78 and biaxial79 deformation. The mechanism and fundamental basis for this realignment remains an interesting and important question for further inquiry, and has implications for the photovoltaic output of devices under strain.
A third effect of strain, observed by increases in the intensities of the vibronic transitions of P3ATs, is an increase in the percent crystalline aggregate within the film.78 This strain-evolved microstructural change could, in principle, produce greater photovoltaic performance, as percent aggregate in the polymer phase is correlated with increased efficiency in P3HT–PCBM devices.24 While such increases in crystalline order produced by other means—i.e., thermal annealing,159 solvent-vapor annealing,160 and slowness of evaporation of the solvent during solution casting24—are generally correlated with increases in PCE; in a solar cell, tensile strain has possibly detrimental effects on the other components of the device, such as the substrates, interfaces, barrier films, and electrodes, which make it difficult to isolate the effects of strain itself on the overall properties of the device.31Fig. 11a and b shows the evolution in photovoltaic properties with tensile strain for two types of devices fabricated on PDMS substrates, one based on P3HT–PCBM, and the other based on PDPP2T-TT–PCBM, from 0 to 20% strain.31 The apparent increase in VOC with small strains for the brittle P3HT–PCBM was attributed to fracturing of the oxide “skin” that forms on the liquid eutectic gallium–indium (EGaIn) cathode—used because it is stretchable—when extruded in air. The same effect is observed if the EGaIn is extruded in air, placed in the glovebox, and then agitated with a wooden applicator, but the effect disappears when the EGaIn is extruded in a nitrogen atmosphere. The effect is more pronounced for P3HT–PCBM than it is for PDPP2T-TT–PCBM, because the former bulk heterojunction is more brittle, and the opening and closing of cracks in the active layer perturb the top electrode to a greater extent. This experiment highlights the difficulty in isolating the effects of the change in microstructure of the active materials from the detrimental effects on the electrodes and other materials.
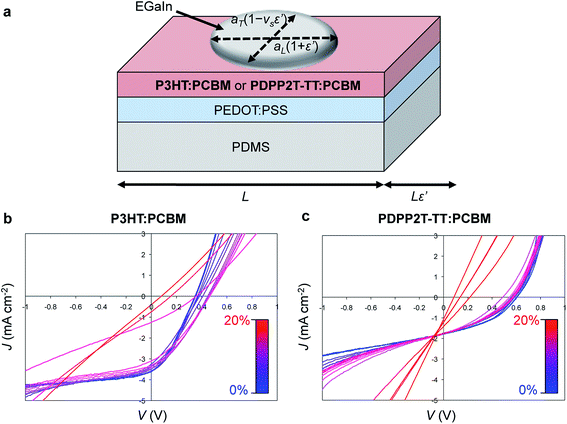 | ||
| Fig. 11 Evolution in photovoltaic output with tensile strain, ε. (a) Schematic diagram of a stretchable device. (b) Current density vs. voltage for a P3HT–PCBM device from 0% to 20% strain. (c) A similar plot for a PDPP2T-TT–PCBM device. Current densities were calculated using the area of the footprint of the drop of eutectic gallium indium (EGaIn), which deformed with strain, by the equation A(ε′) = πaL(1+ε′)aT(1 − νSε′), where ε′ = ε/100%, aL and aT are the longitudinal and transverse semi-major axes, and νS is the Poisson ratio of PDMS (and assumed to be constant within the relatively small range of strains, between 0 and 20%.) Reproduced with permission from ref. 31 Copyright 2012, Elsevier. | ||
Global strains, applied to whole devices, can manifest as damage at interfaces. While the effects of pre-catastrophic bending strains on interfaces have not been rigorously determined for organic solar cells, Sokolov et al. has performed relevant studies on field-effect transistors.161 The authors' principal conclusion was that the strains applied to these transistors changed the alignment of polymer chains and altered the field-effect mobility of the strained devices due to reorientation of the surface dipoles.161 Poor interfacial adhesion can produce cracks at sites of local delamination that propagate through multiple layers in the device.30,142 Adhesion promoters can reduce this effect substantially, as has been observed for PEDOT–PSS,30,142 which behaves as a prime coat that increases adhesion of bulk heterojunction films to hydrophobic substrates. Lu et al. observed a similar effect in films of copper on polyimide substrates, which could be stretched up to 50%, without cracking, if a chromium adhesion layer was used.162
3.2. Catastrophic fracture
In contrast to Section 3.1.1, which dealt largely with the theoretical effects of strain-evolved changes in microstructure on the photovoltaic properties, the effects of cracking are easily seen in plots of current density vs. voltage, and are nearly always deleterious.31 The detail to which these effects are characterized in the literature is, however, not fine-grained. In general, bending studies are performed to illustrate the superior mechanical flexibility of one material (e.g., the transparent electrode) over a control device that uses a conventional material (e.g., ITO, though the mechanism by which ITO itself degrades under strain is an active area of research166).167 Degradation of function is attributed to cracking within the control device, however, strain is almost never estimated based on the bending radius and thickness of the substrate, and the specific ways in which the damage manifests in the degraded J–V plots are generally not identified. This section is subdivided on the basis of the relative orientation of the strain to the plane of the device: (1) strain applied parallel to the device plane that generally produces cracking and cracking-induced delamination in one or more layers,31,145 and (2) strain applied normal to the device plane, which is associated with cohesive and adhesive failure of the thin films that make up the device. | ||
| Fig. 12 Images of cracks and buckles that appear in organic thin-film devices. (a) A cracked film of pentacene evaporated on a PDMS substrate and subjected to a 10% compressive strain. (b) A surface wrinkling pattern characteristic of the deformation that occurs in rigid films under compression due to direct application of mechanical force or because of thermal contraction. Reproduced with permission from ref. 32 Copyright 2009, American Chemical Society. | ||
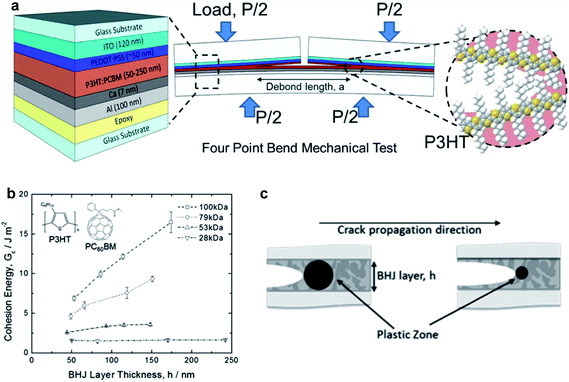 | ||
| Fig. 13 Schematic diagrams and data summarizing cohesive and delaminative fracture under different conditions. (a) Schematic diagram of the four bend mechanical test designed to measure the cohesive fracture energy of the P3HT–PCBM active layer in an organic solar cell as a function of molecular weight of the P3HT. (b) Cohesive energy vs. thickness of the BHJ layer with different molecular weights. Extremely high values of cohesion were obtained for thick films of high molecular weight. (c) Schematic illustration of the effect of the size of the plastic zone at the crack tip on the cohesion; brittle materials with small plastic zones exhibit less of a dependence on layer thickness, because the plastic zone is smaller than the distance between plates. Reproduced with permission from ref. 50 Copyright 2014, American Chemical Society. | ||
The range of values of Gc for cohesion of the P3HT–fullerene bulk heterojunction were found to be 1–20 J m−2, although the high end of this range was only measured for P3HT–ICBA23 and in systems of thick P3HT–PCBM films in which the P3HT had high molecular weight.50 Typical values of 1–5 J m−2 are lower (more unfavorable) than those of other dielectric materials—e.g., crosslinked polymers and oxides—commonly used in microelectronics.52 The cohesion was found to be strongly dependent on the composition of the bulk heterojunction. In particular, cohesion decreased with increasing PCBM concentration, from 0.5 J m−2 for pure PCBM to a maximum of 2.5 J m−2 for BHJs containing 75% P3HT.52 The cohesive energy was not found to be affected by thickness, at least in the initial report, which the authors noted was different from the behavior of more-ductile polymers.52 The cohesion, trajectory of the propagation of the crack, and the roughness after cohesive fracture depends on the mechanical properties of the material encountered by the crack during propagation. In examples of polymers exhibiting substantial plasticity (e.g., high-molecular-weight P3HT, Fig. 13b), a plastic zone forms at the crack tip and expands until it is confined by either crystalline domains in the film or by the rigid top and bottom substrate (Fig. 13c)—i.e., glass or epoxy in these experiments.52 This plastic zone dissipates energy of the deformation, and decreases the cohesion measured in thin films of polymers with high ductility as thickness decreases, in which the volume of the plastic zone is confined by the hard substrate and backing.50,52 Dependence of cohesion on thickness is, however, present in high molecular weight P3HT,50 which is consistent with a lowered degree of crystallinity and a larger plastic zone of the crack tip that is relatively unconstrained by rigid crystallites of samples with lower molecular weight. Formation of bimolecular crystals, in the case of PQT-12 and PBTTT and their mixtures with monofunctionalized PCBM, tends to produce bulk heterojunction films with relatively high cohesion (Gc ∼ 2–5 J m−2).23 While this is an important observation that informs the selection of materials for mechanical robustness, bulk heterojunctions with bimolecular crystals at ratios of polymer–fullerene of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (i.e., below the concentration at which pure PCBM domains form) are inefficient, and those with ratios of 1
1 (i.e., below the concentration at which pure PCBM domains form) are inefficient, and those with ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 fail cohesively more readily (Gc ∼1 J m−2) because of the fragility of the pure PCBM phase.23
4 fail cohesively more readily (Gc ∼1 J m−2) because of the fragility of the pure PCBM phase.23
In roll-to-roll processed flexible devices with the inverted architecture, adhesive failure was found to occur most commonly between the bulk heterojunction layers and PEDOT–PSS, with values of Gc between 0.1 to 1.6 J m−2.68 The adhesion decreased with increasing concentration of PCBM, which can be attributed to low interaction volume of fullerenes100 and relatively weak van der Waals attraction to adjacent layers. We note that the order in which the layers are deposited has an effect on mechanical stability. For cells with the conventional geometry, in which the P3HT–PCBM is coated on top of the PEDOT–PSS, this interface survived, whereas the P3HT–PCBM failed cohesively.52 The adhesion in the inverted geometry could be increased by increasing the time and temperature of annealing, or by replacing the PEDOT–PSS with another hole-transporting layer, such as vanadium oxide (V2O5). Use of V2O5, deposited from solution, produced an interface that was dramatically stronger (up to 150 J m−2), but a device that was very inefficient.68 Increased adhesion was attributed to a 10 nm-thick mixed layer between V2O5 and P3HT–PCBM. Depth profiling XPS determined that failure occurred between this mixed layer and the active layer. Reduced mixing and a weaker interface was found when solution processed V2O5 was replaced with vapor-deposited molybdenum oxide (MoO3).69 A mixed interfacial layer has also been invoked to explain the good adhesion between PEDOT–PSS and the active layer, if the PEDOT–PSS has been deposited first, and is possibly concomitant with the formation of P3HT+–PSS− species where the polymer chains interact.69 (The pure PEDOT–PSS phase itself is, however, subject to decohesion that accelerates in the presence of atmospheric moisture, attributed by DuPont et al. to hydrogen bonds of PSS− to water which disrupt the existing PSS−–H+–PSS− that give the polymer its cohesive strength.70)
4. Possible routes of increasing the mechanical stability of organic solar cells
The experiments described in this review point to several routes that can be explored toward the end goal of increasing the mechanical robustness of organic solar cells. We identify several approaches that have been proposed explicitly or suggested by the results of experiments in the literature, and comment on the probability of success in a large-scale environment.4.1. Buckled or wavy solar cells
The concepts introduced by Whitesides,90 Rogers,170 Wagner171,172 and others,173 involving the production of thin-film devices whose active materials are buckled on pre-strained surfaces, and which accommodate strain by local bending and unbending of the buckles, has been exploited by Lipomi et al.145 and then later by Kaltenbrunner et al.3 to form unencapsulated stretchable organic solar cells. (Buckles and deep folds were later used as structures to increase light trapping by Loo and coworkers.174) This concept would be difficult to apply in a roll-to-roll scheme, because of the requirement that the substrate be under tension and the low probability that a multilayered device could be buckled by compressive strain without introducing substantial interfacial stress. The authors' experience suggests that under compressive strain, metallic electrodes, or solution processed oxides to modify the work function of one or more of the electrodes, would almost certainly crack and have a deleterious effect on the photovoltaic output of the devices. Furthermore, surface wrinkling requires a substantial mismatch in moduli between the substrate (∼1 MPa for PDMS) and the thin films (≥10 MPa). The use of such deformable substrates in roll-to-roll coating apparatuses may not be straightforward.4.2. Use of highly compliant conjugated polymers
A promising strategy to increase the mechanical robustness of OPV devices is to increase the elasticity, plasticity, or both, of the conjugated polymer. The highly compliant nature of P3HpT, a material with well ordered crystalline aggregates, is attributed to the amorphous domains whose glass transition is below room temperature, and suggests one possible way to achieve the “best of both worlds” of electronic and mechanical properties.27 Another strategy is to take a material with a low bandgap and high mobility (such as a DPP-based material depicted in Fig. 1) and introduce unlike conjugated monomers at random into the backbone, to decrease the degree of crystallinity (which would be effective so long as the material maintained high charge-carrier mobility in the absence of high crystallinity).29 In general, factors that increase the compliance and ductility (independent of their effects on charge transport) are long alkyl side chains,57 high molecular weight (at least in P3HT),50 substitution of fused rings in the polymer backbone to isolated rings,31 and structural randomness to reduce the degree of crystallinity.29 All things being equal, highly cohesive and non-brittle conjugated polymers will perform better than brittle ones. The extent to which one component of the active material influences the failure behavior of the entire device, however, is an open question, and requires more testing. It also requires knowledge of the effects of other materials not only in the device stack, but within the active layer itself.4.3. Substitution of PCBM
The ubiquitous acceptor PCBM has many deleterious effects on the mechanical stability of OPV devices. Pure PCBM phases have low cohesive energy,52 high tensile moduli,125 low crack-onset strains,125 and weak interfaces with other layers in the device.68 They can also substantially stiffen active materials that have low moduli by themselves (e.g., P3HpT).27 Decreasing the purity of the fullerene might suppress crystallization and therefore reduce the modulus, but this is not a guaranteed strategy.125 Another potential route would be to find a different acceptor,136 but our (very) preliminary observations on the mechanical properties of solution-processed small molecule films suggest that they are brittle. Polymer–polymer heterojunctions59,175 might represent a way forward, and indeed all-polymer solar cells have achieved high efficiencies in trials by several groups.176,177 The mechanical properties of electron-acceptor polymers are relatively unexplored, but we suspect that the design rules for robust donors would be easily translated to acceptors.4.4. Plasticizers
The use of plasticizers represents an approach that is familiar to the engineering plastics community. For example, small molecules that increase the free volume in a polymer sample also tend to reduce its Tg and modulus, and increase its ductility. As discussed in Section 2.2.4, our group has found that compounds that are added to bulk heterojunction blends to increase efficiency (for example DIO or PDMS)28 and to PEDOT–PSS to improve conductivity and wettability (DMSO or Zonyl),71 can also have plasticizing effects on thin films. Since only a few plasticizers have been thoroughly tested in a laboratory setting, their success leads us to believe other combinations of additives could play a key role in improving mechanical stability. The effect of these plasticizers on the failure mechanisms of whole devices, however, is an open question; plasticizers may segregate to the surface and change the interfacial adhesive properties.68 Another question is mechanistic: do these additives increase the compliance and ductility simply by increasing the free volume (if they remain in the film) or by altering the morphology or extent of mixing, or some combination thereof?4.5. Importance of adhesion
Strong interlayer adhesion is an important design characteristic, irrespective of the mechanical properties of the isolated materials. Interlayer adhesion68 is generally increased if at least one of the interacting partners has a high surface energy, which is typically produced by a high dipolar contribution to the van der Waals coefficient of the material. Specific interactions, such as hydrogen bonding surfaces could also increase the adhesive fracture energy of the interfaces. Adhesion promoters would be beneficial, provided they do not have deleterious effects on charge transport in the device stack. In some cases, materials behave as serendipitous “prime coats,” which is the case for PEDOT–PSS,30 which improves the adhesion of bulk heterojunction films to hydrophobic substrates.1424.6. Toward standardization of mechanical testing
As of yet, there is no standardized procedure for characterization of the mechanical stability of organic solar cells. Any international standards must begin with a full description of the dimensions and composition of all layers in the device, and the way in which it was processed. In particular, the order in which layers are processed will influence which materials or interfaces fail. The temperature and relative humidity must be reported, as the mechanical properties of the materials can be highly sensitive to these parameters. Devices intended for outdoor use must be tested for the effects of thermal cycling, and the effects of thermal expansion and contraction should be isolated from those that occur because of thermal cycling independent of the concomitant mechanical deformation. Bending and tensile tests should be performed in a way that most realistically mimics the deformation expected in the environment. Simply reporting bending radius is insufficient for tests of flexibility; the depth of the active materials within the device stack must be specified, and their proximity to the mechanically neutral plane should be stated so that it is possible to calculate—in most cases by finite-element modeling—the strain on the active materials. Stresses that will produce cracks within or between layers will be highly dependent on the mechanical properties of the substrates and encapsulants. For devices on flexible substrates, torsion should also be tested, and the angle of torsion (e.g., 180° vs. 360°) and number of cycles should be reported. Diligence in reporting these parameters will allow for a more thorough understanding of failure mechanisms and streamline the process for developing robust organic electronic devices.5. Outlook and future work
The majority of all work on the stability of organic electronic devices in general—and organic solar cells in particular—has focused on photochemical, thermal, oxidative, morphological, and other thermodynamic modes of degradation.20,21 The exclusion of mechanical modes of degradation is somewhat surprising, because both the production and use of thin-film flexible solar modules requires—often substantial—bending, shear, and tensile deformations and thus requires resistance or at least a predictable response to mechanical strain. This review described the literature on the mechanical response of organic semiconductors and whole devices with the aim of identifying design principles for robust materials and devices to determine avenues of future research on the topic. We find several areas in which very little work has been done. For example, while the mechanical properties of polymers is a mature field, and many of the principles can be applied directly to the properties of semiconducting polymers, the mechanical properties of films of small-molecule semiconductors and their effects on the yield of devices in roll-to-roll production are unexplored.Much of the work has focused on the mechanical properties of single materials or interfaces. Only one study to our knowledge used a module fabricated in an industrially relevant manner.68 The study of whole modules will require a close connection between experiments and computational modeling to determine which materials will absorb strain at different depths within the device stack. It might turn out, for example, that the barrier foils, which are often multilayered laminate structures of polymers and ceramic films, will crack first, and thus mechanical deformation may lead to failure by photochemical damage. As the field has not yet “settled” on the ideal barrier technology, attention toward the mechanical properties of barrier materials should be increased.
In the past, thermal stability has implied accelerated degradation by chemical processes, or by phase segregation within the bulk heterojunction. The suspected mechanism by which phase separation degrades the performance of solar cells is that the domains grow to critical dimensions that are larger than the diffusion lengths of excitons. Phase segregation is not, however, the only potential pathway of degradation initiated by heat. Differential thermal expansion and contraction of the different layers in an outdoor environment will inevitably produce large-scale buckling of support structures in pilot organic photovoltaic installations, just as smaller scale deformations will tend to place shear stress on the layers and could be especially problematic for the interfaces, which are often weak.
While the topics discussed in this review suggest that all deformation leads to fracture and therefore is deleterious to the long-term stability of devices, it is conceivable that strain in the pre-fracture regime may produce changes that are either non-degrading or perhaps even beneficial to the photovoltaic output of devices. Very little is known about the effects of strain on device performance in the pre-fracture regime, but some ideas can be put forth. For example, strain has at least three effects on the morphology of P3HT–PCBM blends (as illustrated in Fig. 11): (1) alignment of polymer chains along the axis of strain, (2) increase in the percentage of crystalline aggregates and order within the aggregated phase, and (3) evolution in texture from one in which the axis of π-stacking is parallel to the substrate (edge-on), to one in which the π-stacking axis is perpendicular to the substrate (face-on). While it is difficult to predict the effect of (1) on the photovoltaic properties, since the direction of charge-transport is orthogonal to the stretch-aligned chains, the effects of (2), and especially (3), would seem to be beneficial in a device whose charge carriers move vertically through the stack.
One intriguing aspect of research on the mechanical stability of organic solar cells is its interdisciplinarity. It requires teams whose members have expertise in organic chemistry, microstructural determination, polymeric science and engineering, device physics, manufacturing engineering, and solid mechanics. It is our hope that this review served to stimulate interest in the field in an effort to produce low-cost renewable power sources that are both highly efficient and also mechanically stable.
Acknowledgements
This work was supported by the Air Force Office of Scientific Research (AFOSR) Young Investigator Program, Grant FA9550-13-1-0156 and laboratory startup funds from the University of California, San Diego. S.S. acknowledges a fellowship from the National Science Foundation Graduate Research Fellowship Program under Grant DGE-1144086. A.V.Z. acknowledges a fellowship from SoCal Clean Energy Technology Acceleration Program from the von Liebig Center at UCSD sponsored by the U.S. Department of Energy. The authors acknowledge helpful discussions with Prof. Frederik C. Krebs.References
- L. T. Dou, J. B. You, Z. R. Hong, Z. Xu, G. Li, R. A. Street and Y. Yang, Adv. Mater., 2013, 25, 6642–6671 CrossRef CAS PubMed.
- C. H. Peters, I. T. Sachs-Quintana, J. P. Kastrop, S. Beaupre, M. Leclerc and M. D. McGehee, Adv. Energy Mater., 2011, 1, 491–494 CrossRef CAS.
- M. Kaltenbrunner, M. S. White, E. D. Glowacki, T. Sekitani, T. Someya, N. S. Sariciftci and S. Bauer, Nat. Comm., 2012, 3, 770 CrossRef PubMed.
- N. Espinosa, M. Hosel, D. Angmo and F. C. Krebs, Energy Environ. Sci., 2012, 5, 5117–5132 CAS.
- T. R. Cook, D. K. Dogutan, S. Y. Reece, Y. Surendranath, T. S. Teets and D. G. Nocera, Chem. Rev., 2010, 110, 6474–6502 CrossRef CAS PubMed.
- Y. Galagan, E. W. C. Coenen, B. Zimmermann, L. H. Slooff, W. J. H. Verhees, S. C. Veenstra, J. M. Kroon, M. Jorgensen, F. C. Krebs and R. Andriessen, Adv. Energy Mater., 2014, 4, 1300498 Search PubMed.
- F. C. Krebs, N. Espinosa, M. Hosel, R. R. Sondergaard and M. Jorgensen, Adv. Mater., 2014, 26, 29–39 CrossRef CAS.
- D. J. Burke and D. J. Lipomi, Energy Environ. Sci., 2013, 6, 2053–2066 CAS.
- T. P. Osedach, T. L. Andrew and V. Bulovic, Energy Environ. Sci., 2013, 6, 711–718 CAS.
- F. C. Krebs, M. Jorgensen, K. Norrman, O. Hagemann, J. Alstrup, T. D. Nielsen, J. Fyenbo, K. Larsen and J. Kristensen, Sol. Energy Mater. Sol. Cells, 2009, 93, 422–441 CrossRef CAS PubMed.
- F. C. Krebs, Sol. Energy Mater. Sol. Cells, 2008, 92, 715–726 CrossRef CAS PubMed.
- K.-S. Chen, H. L. Yip, C. W. Schlenker, D. S. Ginger and A. K. Y. Jen, Org. Electron., 2012, 13, 2870–2878 CrossRef CAS PubMed.
- I. Burgues-Ceballos, F. Machui, J. Min, T. Ameri, M. M. Voigt, Y. N. Luponosov, S. A. Ponomarenko, P. D. Lacharmoise, M. Campoy-Quiles and C. J. Brabec, Adv. Funct. Mater., 2014, 24, 1449–1457 CrossRef CAS.
- J. E. Carle, M. Helgesen, M. V. Madsen, E. Bundgaard and F. C. Krebs, J. Mater. Chem. C, 2014, 2, 1290–1297 RSC.
- R. Po, A. Bernardi, A. Calabrese, C. Carbonera, G. Corso and A. Pellegrino, Energy Environ. Sci., 2014, 7, 925–943 CAS.
- J. L. Bredas, J. E. Norton, J. Cornil and V. Coropceanu, Acc. Chem. Res., 2009, 42, 1691–1169 CrossRef CAS PubMed.
- A. J. Heeger, Adv. Mater., 2014, 26, 10–28 CrossRef CAS PubMed.
- A. Salleo, R. J. Kline, D. M. DeLongchamp and M. L. Chabinyc, Adv. Mater., 2010, 22, 3812–3838 CrossRef CAS PubMed.
- M. A. Brady, G. M. Su and M. L. Chabinyc, Soft Matter, 2011, 7, 11065–11077 RSC.
- M. Jorgensen, K. Norrman and F. C. Krebs, Sol. Energy Mater. Sol. Cells, 2008, 92, 686–714 CrossRef PubMed.
- M. Jorgensen, K. Norrman, S. A. Gevorgyan, T. Tromholt, B. Andreasen and F. C. Krebs, Adv. Mater., 2011, 24, 580–612 CrossRef PubMed.
- D. J. Lipomi and Z. N. Bao, Energy Environ. Sci., 2011, 4, 3314–3328 CAS.
- C. Bruner, N. C. Miller, M. D. McGehee and R. H. Dauskardt, Adv. Funct. Mater., 2013, 23, 2863–2871 CrossRef CAS.
- O. Awartani, B. Lemanski, H. W. Ro, L. J. Richter, D. M. DeLongchamp and B. T. O'Connor, Adv. Energy Mater., 2013, 3, 399–406 CrossRef CAS.
- M. Hosel, R. Sondergaard, M. Jorgensen and F. C. Krebs, Adv. Energy Mater., 2014, 4, 1301625 Search PubMed.
- F. C. Krebs, T. D. Nielsen, J. Fyenbo, M. Wadstrom and M. S. Pedersen, Energy Environ. Sci., 2010, 3, 512–525 CAS.
- S. Savagatrup, A. D. Printz, D. Rodriquez and D. J. Lipomi, Macromolecules, 2014, 47, 1981–1992 CrossRef CAS.
- S. Savagatrup, A. S. Makaram, D. J. Burke and D. J. Lipomi, Adv. Funct. Mater., 2014, 24, 1169–1181 CrossRef CAS.
- A. D. Printz, S. Savagatrup, D. J. Burke, T. Purdy and D. J. Lipomi, RSC Adv., 2014, 4, 13635–13643 RSC.
- T. F. O'Connor, A. V. Zaretski, B. A. Shiravi, S. Savagatrup, A. D. Printz, M. I. Diaz and D. J. Lipomi, Energy Environ. Sci., 2014, 7, 370–378 Search PubMed.
- D. J. Lipomi, H. Chong, M. Vosgueritchian, J. G. Mei and Z. N. Bao, Sol. Energy Mater. Sol. Cells, 2012, 107, 355–365 CrossRef CAS PubMed.
- D. Tahk, H. H. Lee and D. Y. Khang, Macromolecules, 2009, 42, 7079–7083 CrossRef CAS.
- B. O'Connor, E. P. Chan, C. Chan, B. R. Conrad, L. J. Richter, R. J. Kline, M. Heeney, I. McCulloch, C. L. Soles and D. M. DeLongchamp, ACS Nano, 2010, 4, 7538–7544 CrossRef PubMed.
- C. Muller, S. Goffri, D. W. Breiby, J. W. Andreasen, H. D. Chanzy, R. A. J. Janssen, M. M. Nielsen, C. P. Radano, H. Sirringhaus, P. Smith and N. Stingelin-Stutzmann, Adv. Funct. Mater., 2007, 17, 2674–2679 CrossRef CAS.
- J. J. Liang, L. Li, X. F. Niu, Z. B. Yu and Q. B. Pei, Nat. Photonics, 2013, 7, 817–824 CrossRef CAS.
- Z. B. Yu, Q. W. Zhang, L. Li, Q. Chen, X. F. Niu, J. Liu and Q. B. Pei, Adv. Mater., 2011, 23, 664–668 CrossRef CAS PubMed.
- B. Hu, Workshop on Key Scientific and Technological Issues for Development of Next-Generation Organic Solar Cells, Arlington, VA, 2012 Search PubMed.
- F. C. Krebs, M. Biancardo, B. Winther-Jensen, H. Spanggard and J. Alstrup, Sol. Energy Mater. Sol. Cells, 2006, 90, 1058–1067 CrossRef CAS PubMed.
- A. Anctil, C. W. Babbitt, R. P. Raffaelle and B. J. Landi, Prog. Photovolt.: Res. Appl., 2013, 21, 1541–1554 CrossRef CAS.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20142–20142 CAS.
- J. Y. Lee, S. T. Connor, Y. Cui and P. Peumans, Nano Lett., 2010, 10, 1276 CrossRef CAS PubMed.
- G. Li, R. Zhu and Y. Yang, Nat. Photonics, 2012, 6, 153–161 CrossRef CAS.
- C. M. Amb, M. R. Craig, U. Koldemir, J. Subbiah, K. R. Choudhyry, S. A. Gevorgyan, M. Jorgensen, F. C. Krebs, F. So and J. R. Reynolds, ACS Appl. Mater. Interfaces, 2012, 4, 1847–1853 CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva, Y. Olivier, R. Silbey and J. L. Bredas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- S. Savagatrup, A. D. Printz, T. F. O'Connor, A. V. Zaretski and D. J. Lipomi, Chem. Mater., 2014, 26, 3028–3041 CrossRef CAS.
- S. Bauer, S. Bauer-Gogonea, I. Graz, M. Kaltenbrunner, C. Keplinger and R. Schwodiauer, Adv. Mater., 2014, 26, 149–162 CrossRef CAS PubMed.
- M. Kaltenbrunner, T. Sekitani, J. Reeder, T. Yokota, K. Kuribara, T. Tokuhara, M. Drack, R. Schwodiauer, I. Graz, S. Bauer-Gogonea, S. Bauer and T. Someya, Nature, 2013, 499, 458–463 CrossRef CAS PubMed.
- D. Ghezzi, M. R. Antognazza, R. Maccarone, S. Bellani, E. Lanzarini, N. Martino, M. Mete, G. Pertile, S. Bisti, G. Lanzani and F. Benfanati, Nat. Photonics, 2013, 7, 400–406 CrossRef CAS.
- M. Manceau, E. Bundgaard, J. E. Carle, O. Hagemann, M. Helgesen, R. Sondergaard, M. Jorgensen and F. C. Krebs, J. Mater. Chem., 2011, 21, 4132–4141 RSC.
- C. Bruner and R. H. Dauskardt, Macromolecules, 2014, 47, 1117–1121 CrossRef CAS.
- V. Brand, K. Levi, M. D. McGehee and R. H. Dauskardt, Sol. Energy Mater. Sol. Cells, 2012, 103, 80–85 CrossRef CAS PubMed.
- V. Brand, C. Bruner and R. H. Dauskardt, Sol. Energy Mater. Sol. Cells, 2012, 99, 182–189 CrossRef CAS PubMed.
- Y. Cao, P. A. Smith and A. J. Heeger, Synthetic Met., 1991, 41–43, 181–184 CrossRef.
- Y. Cao, P. Smith and A. J. Heeger, Polymer, 1991, 32, 1210–1218 CrossRef CAS.
- S. Tokito, P. Smith and A. J. Heeger, Synth. Met., 1990, 36, 183–194 CrossRef CAS.
- A. R. Postema, K. Liou, F. Wudl and P. Smith, Macromolecules, 1990, 23, 1842–1845 CrossRef CAS.
- J. Moulton and P. Smith, Polymer, 1992, 33, 2340–2347 CrossRef CAS.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CAS.
- J. J. M. Halls, C. A. Walsh, N. C. Greenham, E. A. Marseglia, R. H. Friend, S. C. Moratti and A. B. Holmes, Nature, 1995, 376, 498–500 CrossRef CAS.
- J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539–541 CrossRef CAS.
- A. Tsumura, H. Koezuka and T. Ando, Appl. Phys. Lett., 1986, 49, 1210–1212 CrossRef CAS PubMed.
- Z. N. Bao, A. Dodabalapur and A. J. Lovinger, Appl. Phys. Lett., 1996, 69, 4108–4110 CrossRef CAS PubMed.
- A. Fachetti, Chem. Mater., 2011, 23, 733–758 CrossRef.
- J. G. Mei and Z. N. Bao, Chem. Mater., 2014, 26, 604–615 CrossRef CAS.
- H. Bronstein, Z. Y. Chen, R. S. Ashraf, W. M. Zhang, J. P. Du, J. R. Durrant, P. S. Tuladhar, K. Song, S. E. Watkins, Y. Geerts, M. M. Wienk, R. A. J. Janssen, T. Anthopoulos, H. Sirringhaus, M. Heeney and I. McCulloch, J. Am. Chem. Soc., 2011, 133, 3272–3275 CrossRef CAS PubMed.
- I. McCulloch, M. Heeney, C. Bailey, K. Genevicius, I. MacDonald, M. Shkunov, D. Sparrowe, S. Tierney, R. Wagner, W. M. Zhang, M. L. Chabinyc, R. J. Kline, M. D. McGehee and M. F. Toney, Nat. Mater., 2006, 5, 328–333 CrossRef CAS PubMed.
- A. J. Heeger, Chem. Soc. Rev., 2010, 39, 2354–2371 RSC.
- S. R. Dupont, M. Oliver, F. C. Krebs and R. H. Dauskardt, Sol. Energy Mater. Sol. Cells, 2012, 97, 171–175 CrossRef CAS PubMed.
- S. R. Dupont, E. Voroshazi, P. Heremans and R. H. Dauskardt, Org. Electron., 2013, 14, 1262–1270 CrossRef CAS PubMed.
- S. R. Dupont, F. Novoa, E. Voroshazi and R. H. Dauskardt, Adv. Funct. Mater., 2013, 24, 1325–1332 CrossRef.
- S. Savagatrup, E. Chan, S. Renteria-Garcia, A. D. Printz, A. V. Zaretski, T. F. O'Connor, D. Rodriquez, E. Valle and D. J. Lipomi, Adv. Funct. Mater., 2014 Search PubMed , in revision.
- A. J. Heeger, Angew. Chem., Int. Ed., 2001, 40, 2591–2611 CrossRef CAS.
- S. M. Aharoni, Polymer, 1981, 22, 418–419 CrossRef CAS.
- R. D. McCullough, Adv. Mater., 1998, 10, 93–116 CrossRef CAS.
- F. P. V. Koch, M. Heeney and P. Smith, J. Am. Chem. Soc., 2013, 135, 13699–13709 CrossRef CAS PubMed.
- M. Brinkmann, Polym. Phys., 2011, 49, 1218–1233 CrossRef CAS.
- J. Rivnay, M. F. Toney, Y. Zheng, I. V. Kauver, Z. H. Chen, V. Wagner, A. Facchetti and A. Salleo, Adv. Mater., 2010, 22, 4359–4363 CrossRef CAS PubMed.
- B. O'Connor, R. J. Kline, B. R. Conrad, L. J. Richter, D. Gundlach, M. F. Toney and D. M. DeLongchamp, Adv. Funct. Mater., 2011, 21, 3697–3705 CrossRef.
- D. Gargi, R. J. Kline, D. M. DeLongchamp, D. A. Fischer, M. F. Toney and B. T. O'Connor, J. Phys. Chem. C, 2013, 117, 17421–17428 CAS.
- O. Awartani, M. W. Kudenov and B. T. O'Connor, Appl. Phys. Lett., 2014, 104, 093306 CrossRef PubMed.
- F. E. Arnold and V. Rl, Macromolecules, 1969, 2, 497–503 CrossRef CAS.
- M. R. Vanlandingham, J. S. Villarrubia, W. F. Guthrie and G. F. Meyers, Macromol. Symp., 2001, 167, 15–43 CrossRef CAS.
- P. G. Karagiannidis, S. Kassavetis, C. Pitsalidis and S. Logothetidis, Thin Solid Films, 2011, 519, 4105–4109 CrossRef CAS PubMed.
- C. Koidis, S. Logothetidis, S. Kassavetis, P. G. Kapnopoulos, P. G. Karagiannidis, D. Georgiou and A. Laskarakis, Sol. Energy Mater. Sol. Cells, 2013, 112, 36–46 CrossRef CAS PubMed.
- J. Y. Chung, A. J. Nolte and C. M. Stafford, Adv. Mater., 2011, 23, 349–368 CrossRef CAS PubMed.
- C. M. Stafford, C. Harrison, K. L. Beers, A. Karim, E. J. Amis, M. R. Vanlandingham, H. C. Kim, W. Volksen, R. D. Miller and E. E. Simonyi, Nat. Mater., 2004, 3, 545–550 CrossRef CAS PubMed.
- C. M. Stafford, B. D. Vogt, C. Harrison, D. Julthongpiput and R. Huang, Macromolecules, 2006, 39, 5095–5099 CrossRef CAS.
- D. Y. Khang, J. A. Rogers and H. H. Lee, Adv. Funct. Mater., 2009, 19, 1526–1536 CrossRef CAS.
- D. Y. Khang, J. L. Xiao, C. Kocabas, S. MacLaren, T. Banks, H. Q. Jiang, Y. Y. G. Huang and J. A. Rogers, Nano Lett., 2008, 8, 124–130 CrossRef CAS PubMed.
- N. Bowden, S. Brittain, A. G. Evans, J. W. Hutchinson and G. M. Whitesides, Nature, 1998, 393, 146–149 CrossRef CAS PubMed.
- N. Bowden, W. T. S. Huck, K. E. Paul and G. M. Whitesides, Appl. Phys. Lett., 1999, 75, 2557–2559 CrossRef CAS PubMed.
- J.-B. Lee, S.-S. Yoon and D. Y. Khang, RSC Adv., 2013, 3, 17364–17372 RSC.
- J. Y. Kim and C. D. Frisbie, J. Phys. Chem. C, 2008, 112, 17726–17736 CAS.
- J. Zhao, A. Swinnen, G. V. Assche, J. Manca, D. Vanderzande and B. V. Mele, J. Phys. Chem. B, 2009, 113, 1587–1591 CrossRef CAS PubMed.
- S. A. Chen and J. M. Ni, Macromolecules, 1992, 25, 6081–6089 CrossRef CAS.
- H. K. Reimschuessel, J. Polym. Sci., Part A: Polym. Chem., 1979, 17, 2447–2457 CrossRef CAS.
- M. Koppe, M. Scharber, C. J. Brabec, W. Duffy, M. Heeney and I. McCulloch, Adv. Funct. Mater., 2007, 17, 1371–1376 CrossRef CAS.
- A. Buono, N. H. Son, G. Raos, L. Gila, A. Cominetti, M. Catellani and S. V. Meille, Macromolecules, 2010, 43, 6772–6781 CrossRef CAS.
- J. G. Liu, Y. Sun, X. Gao, R. Xing, L. D. Zheng, S. P. Wu, Y. H. Geng and Y. C. Han, Langmuir, 2011, 27, 4212–4219 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier, Waltham, MA, 2011 Search PubMed.
- H. L. Zhong, Z. Li, F. Deledalle, E. Collado Fregoso, M. Shahid, Z. P. Fei, C. B. Nielsen, N. Yaacobi-Gross, S. Rossbauer, T. D. Anthopoulos, J. R. Durrant and M. Heeney, J. Am. Chem. Soc., 2013, 135, 2040 CrossRef CAS PubMed.
- D. J. Lipomi, R. C. Chiechi, W. F. Reus and G. M. Whitesides, Adv. Funct. Mater., 2008, 18, 3469–3477 CrossRef CAS.
- D. J. Lipomi, R. C. Chiechi, M. D. Dickey and G. M. Whitesides, Nano Lett., 2008, 8, 2100–2105 CrossRef CAS PubMed.
- F. S. Kim, G. Q. Ren and S. A. Jenekhe, Chem. Mater., 2011, 23, 682–732 CrossRef CAS.
- A. L. Briseno, S. C. B. Mannsfeld, P. J. Shamberger, F. S. Ohuchi, Z. N. Bao, S. A. Jenekhe and Y. N. Xia, Chem. Mater., 2008, 20, 4712–4719 CrossRef CAS.
- J. T. Seitz, J. Appl. Polym. Sci., 1993, 49, 1331–1351 CrossRef CAS.
- R. F. Fedors, Polym. Eng. Sci., 1974, 14, 147–154 CAS.
- B. S. Hsiao, Nanostructure development in semicrystalline polymers during deformation by synchrotron X-ray scattering and diffraction techniques, Taylor & Francis, 2005 Search PubMed.
- S. T. Salammal, E. Mikayelyan, S. Grigorian, U. Pietsch, N. Koenen, U. Scherf, N. Kayunkid and M. Brinkmann, Macromolecules, 2012, 45, 5575–5585 CrossRef CAS.
- F. Padinger, R. S. Rittberger and N. S. Sariciftci, Adv. Funct. Mater., 2003, 13, 85–88 CrossRef CAS.
- S. E. Shaheen, C. J. Brabec, N. S. Sariciftci, F. Padinger, T. Fromherz and J. C. Hummelen, Appl. Phys. Lett., 2001, 78, 841–843 CrossRef CAS PubMed.
- V. Vijay, A. D. Rao and K. S. Narayan, J. Appl. Phys., 2011, 109, 084525 CrossRef PubMed.
- J. Rivnay, S. C. B. Mannsfeld, C. E. Miller, A. Salleo and M. F. Toney, Chem. Rev., 2012, 112, 5488–5519 CrossRef CAS PubMed.
- J. Clark, C. Silva, R. H. Friend and F. C. Spano, Phys. Rev. Lett., 2007, 98, 206406 CrossRef.
- R. J. Kline, M. D. McGehee, E. N. Kadnikova, J. S. Liu, J. M. J. Frechet and M. F. Toney, Macromolecules, 2005, 38, 3312–3319 CrossRef CAS.
- A. J. Pearson, T. Wang, A. D. F. Dunbar, H. N. Yi, D. C. Watters, D. M. Coles, P. A. Staniec, A. Iraqi, R. A. L. Jones and D. G. Lidzey, Adv. Funct. Mater., 2013, 24, 659 CrossRef.
- N. C. Miller, R. Gysel, Z. Beiley, C. E. Miller, M. F. Toney, M. Heeney, I. McCulloch and M. D. McGehee, Nano Lett., 2009, 9, 4153–4157 CrossRef PubMed.
- N. C. Miller, E. K. Cho, R. Gysel, C. Risko, V. Coropceanu, C. E. Miller, S. Sweetnam, A. Sellinger, M. Heeney, I. McCulloch, J. L. Bredas, M. F. Toney and M. D. McGehee, Adv. Energy Mater., 2012, 2, 1208–1217 CrossRef CAS.
- J. Rivnay, R. Noriega, R. J. Kline, A. Salleo and M. F. Toney, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045203 CrossRef.
- E. Verploegen, R. Mondal, C. J. Bettinger, S. Sok, M. F. Toney and Z. Bao, Adv. Funct. Mater., 2010, 20, 3519–3529 CrossRef CAS.
- J. D. Roehling, K. J. Batenburg, F. B. Swain, A. J. Moule and I. Arslan, Adv. Funct. Mater., 2013, 23, 2115–2122 CrossRef CAS.
- W. Ma, J. R. Tumbleston, M. Wang, E. Gann, F. Huang and H. Ade, Adv. Energy Mater., 2013, 3, 864–872 CrossRef CAS.
- N. D. Treat, A. Varotto, C. J. Takacs, N. Batara, M. Al-Hashimi, M. J. Heeney, A. J. Heeger, F. Wudl, C. J. Hawker and M. L. Chabinyc, J. Am. Chem. Soc., 2012, 134, 15869–15879 CrossRef CAS PubMed.
- N. D. Treat, M. A. Brady, G. Smith, M. F. Toney, E. J. Kramer, C. J. Hawker and M. L. Chabinyc, Adv. Energy Mater., 2011, 1, 82–89 CrossRef CAS.
- S. Savagatrup, D. Rodriquez, A. D. Printz, A. Sieval, J. C. Hummelen and D. J. Lipomi, 2014, in revision.
- L. H. Nguyen, H. Hoppe, T. Erb, S. Gunes, G. Gobsch and N. S. Sariciftci, Adv. Funct. Mater., 2007, 17, 1071–1078 CrossRef CAS.
- H. Hoppe and N. S. Sariciftci, J. Mater. Chem., 2006, 16, 45–61 RSC.
- H. Hoppe, M. Niggemann, C. Winder, J. Kraut, R. Hiesgen, A. Hinsch, D. Meissner and N. S. Sariciftci, Adv. Funct. Mater., 2004, 14, 1005–1011 CrossRef CAS.
- F. Liu, Y. Gu, X. B. Shen, S. Ferdous, H. W. Wang and T. P. Russell, Prog. Polym. Sci., 2013, 38, 1990–2052 CrossRef CAS PubMed.
- H. W. Ro, B. Akgun, B. T. O'Connor, M. Hammond, R. J. Kline, C. R. Snyder, S. K. Satija, A. L. Ayzner, M. F. Toney, C. L. Soles and D. M. DeLongchamp, Macromolecules, 2012, 45, 6587–6599 CrossRef CAS.
- A. D. Printz, S. Savagatrup, D. Rodriquez and D. J. Lipomi, Sol. Energy Mater. Sol. Cells, 2014 Search PubMed , in press.
- H. Y. Li, B. C.-K. Tee, G. Giri, J. W. Chung, S. Y. Lee and Z. N. Bao, Adv. Mater., 2012, 24, 2588–2591 CrossRef CAS PubMed.
- T. Liu and A. Troisi, Adv. Mater., 2013, 25, 1038–1041 CrossRef CAS PubMed.
- A. Anctil, C. W. Babbitt, R. P. Raffaelle and B. J. Landi, Environ. Sci. Technol., 2011, 45, 2353–2359 CrossRef CAS PubMed.
- Y.-S. Zimmermann, A. Schaffer, C. Hugi, K. Fent, P. F.-X. Corvini and M. Lenz, Environ. Int., 2012, 49, 128–140 CrossRef CAS PubMed.
- P. Sonar, J. P. F. Lim and K. L. Chan, Energy Environ. Sci., 2011, 4, 1558–1574 CAS.
- J. Peet, A. J. Heeger and G. C. Bazan, Acc. Chem. Res., 2009, 42, 1700–1708 CrossRef CAS PubMed.
- J. Peet, J. Y. Kim, N. E. Coates, W. L. Ma, D. Moses, A. J. Heeger and G. C. Bazan, Nat. Mater., 2007, 6, 497–500 CrossRef CAS PubMed.
- K. R. Graham, J. G. Mei, R. Stalder, J. W. Shim, H. Cheun, F. Steffy, F. So, B. Kippelen and J. R. Reynolds, ACS Appl. Mater. Interfaces, 2011, 3, 1210–1215 CAS.
- M. Vosgueritchian, D. J. Lipomi and Z. N. Bao, Adv. Funct. Mater., 2012, 22, 421–428 CrossRef CAS.
- N. Kim, S. Kee, S. H. Lee, B. H. Lee, Y. H. Kahng, Y. R. Jo, B. J. Kim and K. Lee, Adv. Mater., 2014, 26, 2268–2272 CrossRef CAS PubMed.
- D. J. Lipomi, J. A. Lee, M. Vosgueritchian, B. C.-K. Tee, J. A. Bolander and Z. N. Bao, Chem. Mater., 2012, 24, 373–382 CrossRef CAS.
- X. Crispin, F. L. E. Jakobsson, A. Crispin, P. C. M. Grim, P. Andersson, A. Volodin, C. van Haesendonck, M. Van der Auweraer, W. R. Salaneck and M. Berggren, Chem. Mater., 2006, 18, 4354–4360 CrossRef CAS.
- D. S. Hecht, L. B. Hu and G. Irvin, Adv. Mater., 2011, 23, 1482–1513 CrossRef CAS PubMed.
- D. J. Lipomi, B. C.-K. Tee, M. Vosgueritchian and Z. N. Bao, Adv. Mater., 2011, 23, 1771–1775 CrossRef CAS PubMed.
- M. M. Voigt, R. C. I. Mackenzie, C. P. Yau, P. Atienzar, J. Dane, P. E. Keivanidis, D. D. C. Bradley and J. Nelson, Sol. Energy Mater. Sol. Cells, 2011, 95, 731–734 CrossRef CAS PubMed.
- Y. H. Zhou, C. Fuentes-Hernandez, J. W. Shim, J. Meyer, A. J. Giordano, H. Li, P. Winget, T. Papadopoulos, H. Cheun, J. Kim, M. Fenoll, A. Dindar, W. Haske, E. Najafabadi, T. M. Khan, H. Sojoudi, S. Barlow, S. Graham, J. L. Bredas, S. R. Marder, A. Kahn and B. Kippelen, Science, 2012, 336, 327–332 CrossRef CAS PubMed.
- L. Lindell, A. Burquel, F. L. E. Jakobsson, V. Lemaur, M. Berggren, R. Lazzaroni, J. Cornil, W. R. Salaneck and X. Crispin, Chem. Mater., 2006, 18, 4246–4252 CrossRef CAS.
- F. L. E. Jakobsson, X. Crispin, L. Lindell, A. Kanciurzewska, M. Fahlman, W. R. Salaneck and M. Berggren, Chem. Phys. Lett., 2006, 433, 110–114 CrossRef CAS PubMed.
- J. E. Coughlin, Z. B. Henson, G. C. Welch and G. C. Bazan, Acc. Chem. Res., 2013, 47, 257–270 CrossRef PubMed.
- M. Shin, J. H. Song, G. H. Lim, B. Lim, J. J. Park and U. Jeong, Adv. Mater., 2014, 26, 3706–3711 CrossRef CAS PubMed.
- Z. B. Yu, X. F. Niu, Z. Liu and Q. B. Pei, Adv. Mater., 2011, 23, 3989–3994 CrossRef CAS PubMed.
- G. Giri, E. Verploegen, S. C. B. Mannsfeld, S. Atahan-Evrenk, D. H. Kim, S. Y. Lee, H. A. Becerril, A. Aspuru-Guzik, M. F. Toney and Z. Bao, Nature, 2011, 480, 504–509 CrossRef CAS PubMed.
- Y. Diao, B. C.-K. Tee, G. Giri, J. Xu, D. H. Kim, H. A. Becerril, R. M. Stoltenberg, T. H. Lee, G. Xue, S. C. B. Mannsfeld and Z. N. Bao, Nat. Mater., 2013, 12, 665–671 CrossRef CAS PubMed.
- Z. L. Rang, A. Haraldsson, D. M. Kim, P. P. Ruden, R. J. Chesterfield and C. D. Frisbie, Appl. Phys. Lett., 2001, 79, 2731–2733 CrossRef CAS PubMed.
- C.-Y. Liu and A. J. Bard, Nature, 2002, 418, 162–164 CrossRef CAS PubMed.
- H. R. Tseng, H. Phan, C. Luo, M. Wang, L. A. Perez, S. N. Patel, L. Ying, E. J. Kramer, T. Q. Nguyen, G. C. Bazan and A. J. Heeger, Adv. Mater., 2014, 26, 2993–2998 CrossRef CAS PubMed.
- H. C. Wu, S. J. Benight, A. Chortos, W. Y. Lee, J. G. Mei, J. W. F. To, C. Lu, M. Q. He, J. B.-H. Tok, W. C. Chen and Z. N. Bao, Chem. Mater., 2014, 26, 4544–4551 CrossRef CAS.
- D. Chirvase, J. Parisi, J. C. Hummelen and V. Dyakonov, Nanotechnology, 2004, 15, 1317–1323 CrossRef CAS.
- G. Li, Y. Yao, H. C. Yang, V. Shrotriya, G. W. Yang and Y. Yang, Adv. Funct. Mater., 2013, 17, 1636–1644 CrossRef.
- A. N. Sokolov, Y. Cao, O. B. Johnson and Z. N. Bao, Adv. Funct. Mater., 2012, 22, 175–183 CrossRef CAS.
- N. S. Lu, X. Wang, Z. G. Suo and J. Vlassak, Appl. Phys. Lett., 2007, 91, 221909 CrossRef PubMed.
- A. Chortos, J. Lim, J. W. F. To, M. Vosgueritchian, T. J. Dusseault, T. H. Kim, S. W. Hwang and Z. N. Bao, Adv. Mater., 2014, 26, 4253–4259 CrossRef CAS PubMed.
- A. L. Shu, A. Dai, H. Wang, Y. L. Loo and A. Kahn, Org. Electron., 2013, 14, 149–155 CrossRef CAS PubMed.
- A. Dai, Y. H. Zhou, A. L. Shu, S. K. Mohapatra, H. Wang, C. Fuentes-Hernandez, Y. D. Zhang, S. Barlow, Y. L. Loo, S. R. Marder, B. Kippelen and A. Kahn, Adv. Funct. Mater., 2013, 24, 2197–2204 CrossRef.
- G. Lubineau and M. N. Saleh, Sol. Energy Mater. Sol. Cells, 2014, 130, 199–207 CrossRef PubMed.
- S. K. Hau, H. L. Yip, J. Y. Zou and A. K. Y. Jen, Org. Electron., 2009, 10, 1401–1407 CrossRef CAS PubMed.
- D. H. Kim and J. A. Rogers, Adv. Mater., 2008, 20, 4887–4892 CrossRef CAS.
- F. Nickel, T. Haas, E. Wegner, D. Bahro, S. Salehin, O. Kraft, P. A. Gruber and A. Colsmann, Sol. Energy Mater. Sol. Cells, 2014, 130, 317–321 CrossRef CAS PubMed.
- W. M. Choi, J. Z. Song, D. Y. Khang, H. Q. Jiang, Y. Y. Huang and J. A. Rogers, Nano Lett., 2007, 7, 1655–1663 CrossRef CAS PubMed.
- J. Jones, S. P. Lacour, S. Wagner and Z. G. Suo, J. Vac. Sci. Technol., A, 2004, 22, 1723–1725 CAS.
- S. P. Lacour, S. Wagner, Z. Y. Huang and Z. Suo, Appl. Phys. Lett., 2003, 82, 2404–2406 CrossRef CAS PubMed.
- H. S. Wu, S. Kustra, E. M. Gates and C. J. Bettinger, Org. Electron., 2013, 14, 1636–1642 CrossRef CAS PubMed.
- J. B. Kim, P. Kim, N. C. Pegard, S. J. Oh, C. R. Kagan, J. W. Fleischer, H. A. Stone and Y. L. Loo, Nat. Photonics, 2012, 6, 327–332 CrossRef CAS.
- X. M. He, F. Gao, G. Tu, D. Hasko, S. Huttner, U. Steiner, N. C. Greenham, R. H. Friend and W. T. S. Huck, Nano Lett., 2010, 10, 1302–1307 CrossRef CAS PubMed.
- W. W. Li, W. S. C. Roelofs, M. Turbiez, M. M. Wienk and R. A. J. Janssen, Adv. Mater., 2014, 26, 3304–3309 CrossRef CAS PubMed.
- Y. Zhou, T. Kurosawa, W. Ma, Y. K. Guo, L. Fang, K. Vandewal, Y. Diao, C. G. Wang, Q. F. Yan, J. Reinspach, J. G. Mei, A. L. Appleton, G. I. Koleilat, Y. L. Gao, S. C. B. Mannsfeld, A. Salleo, H. Ade, D. H. Zhao and Z. N. Bao, Adv. Mater., 2014, 26, 3767–3772 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |