Pressure induced separation of phase-transition-triggered-abrupt vs. gradual components of spin crossover

Abstract

The application of pressure on [Co^II(dpzca)₂], which at ambient pressure undergoes abrupt spin crossover (SCO) with thermal hysteresis, gives unique insights into SCO. It reversibly separates the crystallographic phase transition (I4₁/a ↔ P2₁/c) and associated abrupt SCO from the underlying gradual SCO, as shown by detailed room temperature (RT) X-ray crystallography and temperature dependent magnetic susceptibility studies, both under a range of 10 different pressures. The pressure effects are shown to be reversible. The crystal structure of the pressure-induced low-spin state is determined at RT at 0.42(2) and 1.78(9) GPa. At the highest pressure [1.78(9) GPa] the Co–N bond lengths are consistent with the complex being fully LS, and the conjugated terdentate ligands are significantly distorted out of plane. The abrupt SCO event can be shifted up to RT by application of a hydrostatic pressure of ∼0.4 GPa. These magnetic susceptibility (vs. temperature) and X-ray crystallography (at RT) studies, under a range of pressures, show that the SCO can be tuned over a wide range of temperature and pressure space, including RT SCO.

---

Introduction

When the ligand field in octahedral d⁴–d⁷ transition metal complexes is in the ‘Goldilocks’ zone, not too big and not too small, the application of an external stimulus can cause the complex to switch between the low spin (LS) and high spin (HS) states, an event known as spin crossover (SCO).^1–7 The types of stimuli employed include temperature,^2,3,7 pressure,^6,8–10 light irradiation,^11,12 variation in external magnetic field,¹³ and the presence or absence of a guest.¹⁴ The most commonly studied of these is temperature, which is also the simplest experimentally. Here, we focus on the use of a change in pressure to induce SCO (usually increased pressure favors the smaller volume LS state).^2,9 Pressure is a relatively uncommonly employed stimulus that has mainly been applied to iron(II) systems, mostly because (a) this is the most common class of SCO-active complexes and (b) iron(II) is expected to show the greatest change in M–L bond lengths on SCO.^2,4,7

In contrast, there is only a handful of studies of the effect of pressure on SCO in cobalt(II) systems – excluding valence tautomerism as it also involves redox¹⁵ (i.e. considering only ‘true’ cobalt(II) SCO^1,2,16) – all of which were probed only by spectroscopic methods (infrared, Raman or X-ray absorption).¹⁷ This includes our Raman spectroscopy study of the hysteretic spin transition (ST) of [Co^II(dpzca)₂] (Fig. 1; dpzca = N-(2-pyrazylcarbonyl)-2-pyrazinecarboxamide) under pressure, which showed that the application of ∼0.4 GPa induced SCO at ambient temperature.¹⁸

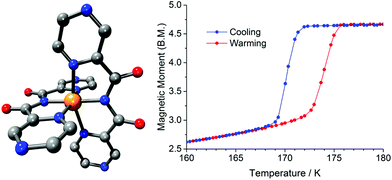Fig. 1 [Co^II(dpzca)₂] at ambient pressure. Left: Structure at 298 K. Right: Magnetic moment vs. temperature.¹⁸

Single crystal X-ray or neutron structure determinations of metal complexes under pressure are very informative but also challenging experimentally and have been limited to a handful of iron(II) complexes^10,19,20 and a single manganese(III) example.²¹ The pressure-induced LS structure has only been reported in four of those studies, all concerning iron(II).^10,19 This is despite interest in probing the similarities and differences between the structures of the pressure-induced and temperature-induced LS states,²² especially for metal ions which undergo anisotropic M–L changes (Jahn Teller), such as cobalt(II). Rather than full structure determinations, the effect of pressure is more commonly followed crystallographically by monitoring changes to the unit cell constants. Such studies also include those on a variety of minerals, including examples of cobalt(III) spin crossover,²³ something which is extremely rare in cobalt(III) coordination complexes.²⁴

The combination of detailed crystal structure and magnetic studies of SCO behaviour for any coordination complex under pressure is rare,^10,19,20 and is without precedent in cobalt(II) SCO. The present study, monitoring both the structure and the magnetism of [Co^II(dpzca)₂] under pressure, gives unique insight into the interplay between phase transition and hysteretic ST, and shows that we can tune the abrupt ST over a wide region of temperature and pressure space, including room temperature (RT).

At ambient pressure the room temperature HS phase of [Co^II(dpzca)₂] is tetragonal (I4₁/a) with a quarter of the complex forming the asymmetric unit, whereas the thermally induced LS phase is monoclinic (P2₁/c) with the entire complex forming the asymmetric unit at 100 K.¹⁸ In both cases there are 4 complexes per unit cell. This phase transition is the likely cause of the observed abrupt spin transition with thermal hysteresis (Fig. 1).

Results and discussion

Unit cell constants vs. pressure at RT

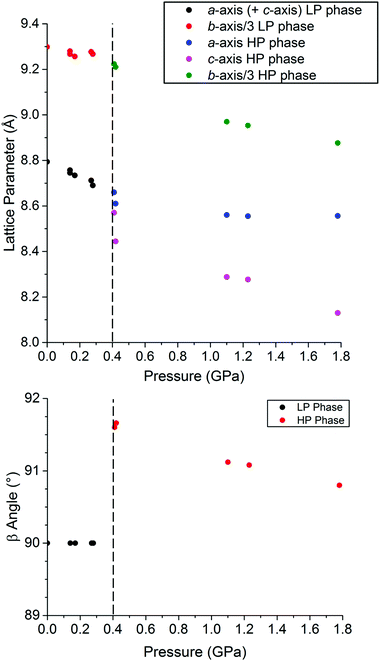
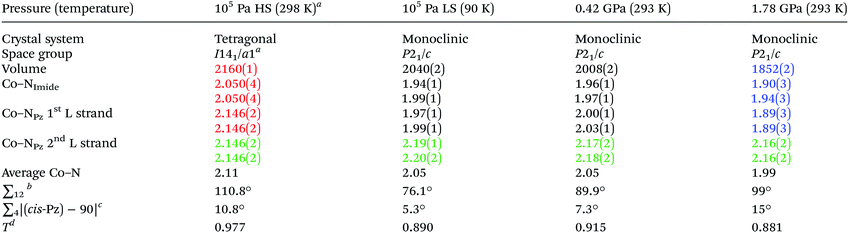
The hydrostatic pressure on a single crystal was ramped in 10 steps from ambient to 1.8 GPa and back to ambient, monitoring the unit cell dimensions, at room temperature (293 K). A plot of the resulting cell constants (Fig. 2), and of the unit cell volume (Fig. S1†), as a function of pressure reveals a discontinuity at ca. 0.4 GPa in both cases, consistent with a phase transition from the HS I4₁/a space group to the LS P2₁/c space group occurring at this pressure (at 293 K, Table 1).

Fig. 2 Unit cell beta angle and axis lengths of [Co^II(dpzca)₂] as a function of pressure at room temperature (293 K). The low-pressure (LP) phase is tetragonal (I4₁/a) whereas the high-pressure (HP) phase is monoclinic (P2₁/c). Note that the b and c axes in the tetragonal HS (298 K and 10⁵ Pa) structure have been swapped to facilitate comparison with the monoclinic structures.

Table 1 Crystal system, space group, unit cell volume (ų), selected Co–N bond lengths (Å), N–Co–N angles (°), and octahedral distortion parameters (°) at ambient pressure (1 × 10⁻⁴ GPa; 298 and 90 K),¹⁸ and at 0.42(2) GPa and 1.78(9) GPa (293 K). text highlights fully HS; text highlights fully LS; text highlights the almost constant pair of trans ‘long’ axes across all structures

a Note the non-standard setting to facilitate comparison to the monoclinic form. Symmetry-generated distances are shown for clarity. See also footnote to Fig. 2. b Octahedral distortion parameter (0 for perfect O_h) is the sum of the deviation of the twelve cis N–Co–N angles from 90°. c ∑₄ Sum of the deviation of the four cis pyrazine-Co-pyrazine angles from 90°. d Tetragonality factor T is ratio of average equatorial over average axial Co–N bond length (compressed T > 1; elongated T < 1).²⁵ Note: for the purpose of these calculations the equatorial plane is kept constant, comprising the first four bonds in the above table.

---

Single crystal structure determinations under pressure at RT

In the structure of [Co^II(dpzca)₂] at ambient pressure,¹⁸ the average Co–N bond length in the HS, 298 K structure is 2.11 Å, whereas in the LS, 90 K structure it is 2.05 Å, with four short equatorial bonds, and two long axial bonds to the pyrazine nitrogen atoms on the second ligand strand (Table 1).

Here we report single crystal structure determinations carried out at pressures of 0.42(2) GPa, and at 1.78(9) GPa, at room temperature (Fig. S2,†Table 1). The Co–N bond lengths in the structure at 0.42 GPa (293 K) are similar to those for the temperature-induced LS state, except that those involving the first ligand strand are slightly longer (Table 1), consistent with the presence of some residual HS character. When the pressure is increased further to 1.78 GPa (293 K), the Co–N bond lengths are more clearly indicative of the complex being fully LS cobalt(II), with the Jahn-Teller distortion resulting in an equatorial plane of four short bonds (1.89–1.94 Å) and two long axial bonds (both 2.162 Å) to the pyrazine nitrogen atoms (N_Pz) of the second ligand strand (Fig. S2† and Table 1). Within the equatorial plane, the shortest Co–N bonds now involve the two trans N_Pz atoms on the first ligand strand, rather than the two trans imide nitrogen donors (N_Im) as is seen in the other three structures (Table 1). Overall this results in an average Co–N bond length of just 1.99 Å and in a unit cell volume 14% smaller than for the 298 K ambient pressure structure and also nearly 10% smaller than for the 90 K ambient pressure mostly LS structure. These pressure-induced structural changes are reversible (Table S2, Fig. S3†).

At 1.78 GPa, the pressure is causing significant distortions to the complex (Fig. 3). These are correlated to the substantially different pressure sensitivity of the a and c axes, which were equivalent in the HS tetragonal crystal system (making the tetragonal b axis unique for ease of comparison with the monoclinic LS structures). The Co–N(11) and Co–N(15) bonds (Jahn-Teller axis) lie almost parallel to the a-axis and are almost unchanged over the range 0.43–1.78 GPa, whereas the Co–N(1) and Co–N(5) bonds lie almost parallel to the more compressible c-axis and are considerably shortened over this pressure range (Table 1).

Fig. 3 Perspective view of [Co^II(dpzca)₂] at 100 K and atmospheric pressure (left) and at 293 K and 1.78(9) GPa (right) highlighting the twisting of the N11/N12 pyrazine ring: In order to minimise the volume of the complex, whilst maintaining the elongation in the second ligand strand, one of the pyrazine rings on the second ligand strand [the N11/N12 ring], has shifted significantly further out of the plane defined by the Co(1) centre, the other two donors on the same ligand strand [N(13) and N(15)], and the imide nitrogen [N(3)] on the other ligand strand. The mean plane of the N11/N12 pyrazine ring is at an angle of 16.9° to that plane in the 1.8 GPa LS structure, compared to just 3.3° in the low temperature LS structure. This also distorts the octahedron significantly (Table 1), which is best identified by looking at the ∑₄, rather than the ∑₁₂ where the effect is diluted by the other (relatively unchanged) cis angles, and even more clearly by the tetragonality factor T which shows maximum axial elongation of the octahedron at 1.78 GPa, consistent with this being fully LS, hence showing maximum Jahn Teller distortion.

Magnetic susceptibility vs. pressure and temperature

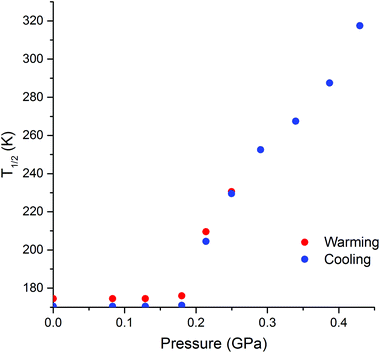
The pressure dependence of the hysteretic ST in [Co^II(dpzca)₂] was also monitored by variable-temperature magnetic susceptibility (Fig. 4). The hydrostatic pressure was taken from ambient pressure to 0.43(2) GPa in 10 steps, then back to ambient. The effect of pressure on the magnetic behaviour of [Co^II(dpzca)₂] is completely reversible (Fig. S6†).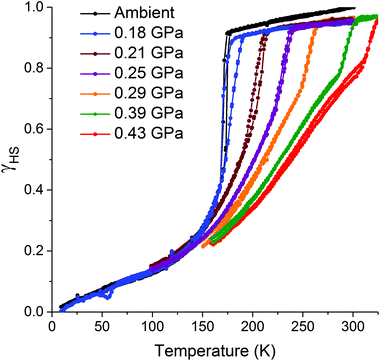

Fig. 4 Fraction HS (γ_HS) versus temperature for [Co^II(dpzca)₂], obtained from magnetic data collected as a function of increasing pressure for selected isobars from ambient to 0.43(2) GPa.

As expected,²⁶ the SCO event is shifted to higher temperatures with increased hydrostatic pressure (Fig. 4). However, the single-step abrupt ST observed at ambient pressure (Fig. 1) is split into two distinct processes as the hydrostatic pressure is increased from 0 to 0.43(2) GPa (Fig. 4): an abrupt ST, which is hysteretic at low pressures, and a gradual, Boltzmann-like SCO. As the pressure is increased, less of the material undergoes the abrupt ST, and instead more of it undergoes gradual SCO.

We propose that the gradual process is associated with lengthening (on heating; or shortening on cooling) of the LS Co–N bonds whilst remaining in the space group P2₁/c, whereas the abrupt process is associated with the crystallographic phase transition²⁷ between P2₁/c and I4₁/a (Table S1†). This hypothesis is supported by the literature examples of thermally induced cobalt(II) SCO, where, to the best of our knowledge, abrupt and hysteretic SCO is always accompanied by a crystallographic phase transition (Table S3†).⁵ The application of pressure to [Co^II(dpzca)₂] induces the phase transition at higher temperatures, so the associated abrupt SCO event shifts to higher temperatures, and the fraction of HS material undergoing this abrupt ST decreases as the pressure increases. This in turn leads to a somewhat less abrupt event, due to dilution of the remaining SCO centres by HS centres.

At ambient pressure and high temperatures the cobalt(II) centres can be thought of as ‘locked in’ the HS state (by lattice ‘negative pressure’ effects²⁸) until the temperature is low enough to induce the phase transition.

The previously reported Raman spectroscopy results under pressure at room temperature¹⁸ are consistent with these observations, showing some mixed HS/LS character over a range of moderate pressures rather than a single complete ST [0.32(5)–0.49(5) GPa, Table 2 and Fig. S7†]. Given the different pressure cells, gauges and resolutions used in these three very different high-pressure experiments, these data are in good agreement.

Table 2 A comparison of the results of three methods used to study the pressure dependence of SCO in [Co^II(dpzca)₂]

	Pressure (GPa)	Spin state at ∼295 K
Raman^18	0.32(5)–0.49(5)	Mixed HS/LS
Magnetic susceptibility	0.38(2)	Mixed HS/LS
Crystallography	1 × 10^−4	HS
	0.42(2)	Mixed HS/LS
	1.78(9)	LS

---

When T_1/2↑ and T_1/2↓ are defined as the midpoints of the abrupt section of the SCO, there are two distinct regions in their pressure dependence (Fig. 5). Firstly, below a ‘threshold pressure’ there is no shift in the T_1/2 values, which may be the consequence of some lattice compressibility (i.e. at low pressures the lattice acts as a ‘shock absorber’) such that it is not ‘felt’ by the cobalt(II) centre via a shortening of the Co–N bonds.²⁹ Secondly, above the threshold pressure the T_1/2 value increases with pressure, as predicted by the Clausius–Clapeyron relationship.²⁶ Projecting to higher pressure one can see that eventually the structural phase transition will no longer involve a change in HS : LS fraction, as at the temperature of this transition the monoclinic phase will be entirely in the HS state. We expect this to occur when P ≥ 0.75 GPa at a temperature exceeding about 500 K. This is outside our current measurement capability.

Fig. 5 The T_1/2 for the abrupt component of the SCO in [Co^II(dpzca)₂] versus applied hydrostatic pressure, obtained from the magnetic data. The four lowest pressure data points (T_1/2 ∼ constant) are consistent with a threshold pressure being reached before the expected approximately linear change of T_1/2 with P is observed.

The information gained from this study gives one the ability to tune the T_1/2 of [Co^II(dpzca)₂] spin transition across a wide region of temperature and pressure space (Fig. 6), including the capability to induce spin crossover at room temperature.

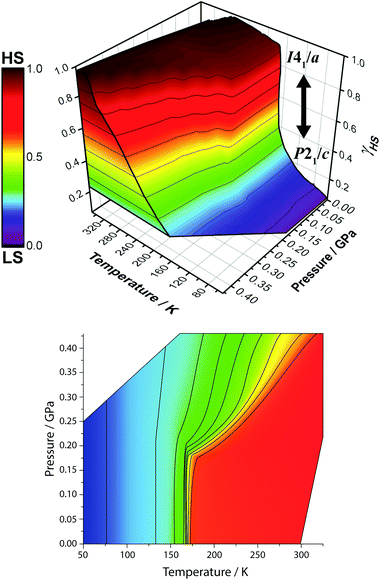Fig. 6 Two different representations of the 3D temperature and pressure dependence of the fraction HS (γ_HS) during the SCO (data shown were obtained in the cooling mode) in [Co^II(dpzca)₂], as monitored by magnetic measurements. (top): Note that the colours on the cut-through (left wall) are only guides for the eyes. (bottom): Projection of the surface shown in the top panel. The tight bunching of contour lines denoting γ_HS (colour scale similar to that used for the top image) corresponds to the abrupt structural phase transition from P2₁/c to I4₁/a due to phase-locking at low pressures (p < 0.20 GPa). See also Fig. 5.

Conclusions

In summary, these magnetic measurements, Raman and crystallographic data give unique insight into the interplay between phase transitions and hysteretic SCO, and are consistent with the abrupt SCO event being intimately associated with the crystallographic phase transition from I4₁/a to P2₁/c. The application of pressure shifts this phase transition to higher temperatures, removing the barrier to SCO at low temperatures, and therefore allowing the observation of the previously unresolved underlying gradual SCO. Relative to the 90 K ambient pressure mostly LS structure, the RT 1.78 GPa structure accommodates the pressure by becoming completely LS with shortened Co–N bond lengths and with considerable distortion of the conjugated ligand.

Experimental section

The ligand Hdpzca, and powder and single crystal samples of [Co^II(dpzca)₂], were prepared as described previously.¹⁸

Isobaric variable temperature magnetic susceptibility measurements

An 8.2 mg powder sample of [Co^II(dpzca)₂] was suspended in Fluorinert FC70:77 as a pressure medium in a homebuilt pressure cell.³⁰ This is a cylindrical hydrostatic pressure cell of 8.8 mm diameter made of non-magnetic BeCu outer body. The sample is loaded in a 7 mm long Teflon capsule along with, optionally, a piece of high-purity Pb as pressure manometer and Fluorinert FC70:77 pressure medium. The cell is loaded at room temperature and the pressure is calibrated at low temperature from the superconducting transition temperature of Pb. The width of the Pb transition is a measure of pressure inhomogeneity along the Pb manometer and it is ±0.02 GPa. In addition the pressure is determined at ambient temperature from the force on the cell when it is initially loaded and clamped in a press. Since the pressure cell has been very well calibrated with a Pb standard³⁰ the measurements on [Co^II(dpzca)₂] were carried out without using an internal pressure standard. Whilst there will be some pressure change from the initial loading due to the differential thermal contraction between the metallic components and the transmitting medium when the pressure cell is cooled, the effects of this are minimal: typically the pressure variation as a function of temperature over a 6–300 K range, with Pb and F70:77 pressure medium in the cell, is ±4%. For susceptibility measurements, the cell background was determined by doing ‘dummy runs’ at 1 T magnetic field and the same temperature sweep rate of 1 K min⁻¹, with the pressure cell containing only the pressure medium, at ambient and 0.45 GPa.

The possibility of an experimental artifact, such the presence of air bubble, causing the observation of the ‘threshold pressure’ effect (Fig. 5) is ruled out. A well-practiced standard procedure was followed when loading the sample with the pressure medium, in order to avoid any possibility of a trapped air bubble. If, despite the care taken, air bubbles were present then the manometer would show no shift in T_c at that load. As a further check of this threshold pressure, a couple of the pressure steps were repeated, in two different experiments, and the results were found to be consistent. Finally, the pressure cell has been very well calibrated with both Pb and high purity Sn. Some of the repeat experiments were done without internal manometer. The pressure was determined from the previously calibrated fit with applied load using the Sn manometer.

Variable temperature magnetic dc susceptibility was measured by Dr Suresh Narayanaswamy on a Quantum Design MPMS5 SQUID magnetometer with an applied magnetic field of 1 T at the Robinson Research Institute. The variable temperature data were measured at a sweep rate of 1 K min⁻¹ and were corrected for thermal lag by adjusting the measured temperature to

for equal values of χ outside the spin transition where the susceptibility is featureless, reversible and more or less linear in temperature. Extensive studies over a broad range of sweep rates confirm that this rigid shift approach to thermal lag is accurate and reliable.

High pressure X-ray crystallography

Data were collected on beamline 12.2.2 of the Advanced Light Source (ALS), Lawrence Berkeley National Laboratory, by Dr Simon Clark and Dr Przemyslaw Dera.³¹ This beamline benefits from hard X-radiation produced by an ALS superbend magnet. This beamline is equipped with a set of brightness preserving optics, which focuses the X-ray beam to a virtual source point mounted on the experimental table inside the X-ray safety enclosure. The beam diverges from this source point and is then focused to a 10 × 10 μm spot by a set of Kirkpatrick-Baez mirrors. A pair of silicon crystals, mounted in the synchrotron beamline, cut parallel to the (111) direction is used to select a single X-ray wavelength. For these measurements we selected an X-ray energy of 30 keV (0.4133 Å) so as to minimise absorption in the diamonds of our high-pressure cell and to maximise the d-spacing coverage of our data. X-ray diffraction images were collected using a MAR345 image plate detector. The distance from the sample to the detector was calibrated using the NIST LaB6 standard. High-pressures were generated using a symmetrical four-post type diamond anvil cell (DAC) designed explicitly for single crystal measurements. The DAC is equipped with Boelher cut diamond anvils of 0.4 mm culet.³² This gives an opening angle of ±30° two-theta. Gaskets were prepared by pressing 300 μm rhenium foil in the DAC to give a 70–100 μm thick indent. Gaskets holes of 200 μm diameter were cut using an automated laser cutting system. One or two crystals were loaded into the gasket hole together with a few 20 μm ruby spheres, for pressure determination, and a methanol : ethanol : water mixture (16 : 3 : 1) which acted as the pressure transmitting fluid. Pressure was determined using the ruby fluorescence method.³³ The fluorescence lines were found to be symmetric throughout all of our measurements implying that hydrostatic conditions were maintained. Pressure was measured before and after each measurement and found to vary by less than the calibration error (±5%).³⁴ Data were collected in 1 degree slices from −30 to 30 degrees. The data were processed using the GSE-ADA and RSV packages³⁵ to find the orientation matrices and produce sets of structure factors, as intensities I_hkl with their associated estimated standard deviations. At 30 keV both the sample and the diamond absorptions are fairly negligible, and were accounted for by intensity data scaling using the GSE_ADA software³⁵ [by fitting a polynomial function dependent on the angle between incident and diffracted beams with respect to the DAC axis to minimise R(int)].

The structures were refined using the SHELX package.³⁶ The X-ray data sets collected, on two different crystals, at 0.42(2) and 1.78(9) GPa, were both highly redundant and equivalent reflections merged very well, but in the case of the 1.78 GPa measurement the data set was ineluctably incomplete due to unfortunate crystal orientation. Crystallographic data for the room temperature structures, at 0.42(2) and 1.78(9) GPa, have been deposited with the Cambridge Crystallographic Data Centre, CCDC 1404670–1404672.

Acknowledgements

We thank the Marsden Fund (RSNZ) and the University of Otago (including the award of a postgraduate scholarship and a publishing bursary to RGM) for supporting this research. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We acknowledge the MacDiarmid Institute for Advanced Materials and Nanotechnology (NZ) for purchasing and providing access to the SQUID magnetometer. We thank Lisa Bucke (Otago) for help with Figure 6 and Michael Crawford (Dunedin) for creating the front cover image from a concept provided by SB.

References

1. J. G. Haasnoot, 1,2,4-Triazoles as ligands for iron(II) high spin-low spin crossovers, ed. O. Kahn, Kluwer Academic Publishers, 1996; B. Weber, Coord. Chem. Rev., 2009, 253, 2432; E. Coronado and G. Minguez Espallargas, Chem. Soc. Rev., 2013, 42, 1525; R. G. Miller, S. Narayanaswamy, J. L. Tallon and S. Brooker, New J. Chem., 2014, 38, 1932.
2. P. Gütlich and H. A. Goodwin, Top. Curr. Chem., 2004, 233, 1.
3. C. Atmani, F. El Hajj, S. Benmansour, M. Marchivie, S. Triki, F. Conan, V. Patinec, H. Handel, G. Dupouy and C. J. Gómez-García, Coord. Chem. Rev., 2010, 254, 1559; M. A. Halcrow, Spin-Crossover Materials: Properties and Applications, John Wiley & Sons, Ltd, 2013.
4. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313.
5. S. Hayami, Y. Komatsu, T. Shimizu, H. Kamihata and Y. H. Lee, Coord. Chem. Rev., 2011, 255, 1981.
6. P. Gütlich, A. B. Gaspar and Y. Garcia, Beilstein J. Org. Chem., 2013, 9, 342.
7. S. Brooker, Chem. Soc. Rev., 2015, 2880.
8. V. Ksenofontov, A. B. Gaspar and P. Gutlich, Top. Curr. Chem., 2004, 235, 23; J. A. Real, A. B. Gaspar and M. C. Muñoz, Dalton Trans., 2005, 2062; A. Galet, A. B. Gaspar, M. C. Muñoz, G. V. Bukin, G. Levchenko and J. A. Real, Adv. Mater., 2005, 17, 2949; S. Bonnet, G. Molnár, J. S. Costa, M. A. Siegler, A. L. Spek, A. Bousseksou, W.-T. Fu, P. Gamez and J. Reedijk, Chem. Mater., 2009, 21, 1123; J. A. Rodríguez-Velamazán, O. Fabelo, C. M. Beavers, E. Natividad, M. Evangelisti and O. Roubeau, Chem. – Eur. J., 2014, 7956; N. F. Sciortino, S. M. Neville, C. Desplanches, J.-F. Létard, V. Martinez, J. A. Real, B. Moubaraki, K. S. Murray and C. J. Kepert, Chem. – Eur. J., 2014, 20, 7448.
9. P. Gütlich, V. Ksenofontov and A. B. Gaspar, Coord. Chem. Rev., 2005, 249, 1811.
10. H. J. Shepherd, P. Rosa, L. Vendier, N. Casati, J.-F. Létard, A. Bousseksou, P. Guionneau and G. Molnár, Phys. Chem. Chem. Phys., 2012, 14, 5265.
11. S. Decurtins, P. Gütlich, C. P. Kohler, H. Spiering and A. Hauser, Chem. Phys. Lett., 1984, 105, 1.
12. A. Hauser, J. Jeftić, H. Romstedt, R. Hinek and H. Spiering, Coord. Chem. Rev., 1999, 190–192, 471; O. Sato, J. Tao and Y.-Z. Zhang, Angew. Chem., Int. Ed., 2007, 2152.
13. A. Boussekou, F. Varret, M. Goiran, K. Bouckheddaden and J. P. Tuchagues, Top. Curr. Chem., 2004, 235, 65; S. Kimura, Y. Narumi, K. Kindo, M. Nakano and G.-e. Matsubayashi, Phys. Rev. B: Condens. Matter, 2005, 72, 064448; S. Bonhommeau, G. Molnár, M. Goiran, K. Boukheddaden and A. Bousseksou, Phys. Rev. B: Condens. Matter, 2006, 74, 064424.
14. G. J. Halder, C. J. Kepert, B. Moubaraki, K. S. Murray and C. S. Cashion, Science, 2002, 298, 1762; X. Bao, H. J. Shepherd, L. Salmon, G. Molnár, M.-L. Tong and A. Bousseksou, Angew. Chem., Int. Ed., 2013, 125, 1236.
15. T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23.
16. V. Ksenofontov, G. Levchenko, S. Reiman, P. Gütlich, A. Bleuzen, V. Escax and M. Verdaguer, Phys. Rev. B: Condens. Matter, 2003, 68, 024415.
17. L. Sacconi and J. R. Ferraro, Inorg. Chim. Acta, 1974, 9, 49; C. Roux, J. Zarembowitch, J. P. Itié, M. Verdaguer, E. Dartyge, A. Fontaine and H. Tolentino, Inorg. Chem., 1991, 30, 3174; C. Hannay, M.-J. Hubin-Franskin, F. Grandjean, V. Briois, J. P. Itié, A. Polian, S. Trofimenko and G. J. Long, Inorg. Chem., 1997, 36, 5580.
18. M. G. Cowan, J. Olguín, S. Narayanaswamy, J. L. Tallon and S. Brooker, J. Am. Chem. Soc., 2012, 134, 2892.
19. T. Granier, B. Gallois, J. Gaultier, J. A. Real and J. Zarembowitch, Inorg. Chem., 1993, 32, 5305; P. Guionneau, C. Brigouleix, Y. Barrans, A. E. Goeta, J.-F. Létard, J. A. K. Howard, J. Gaultier and D. Chasseau, C. R. Acad. Sci., Ser. IIc: Chim., 2001, 4, 161; J. A. Rodriguez-Velamazan, L. Canadillas-Delgado, M. Castro, G. J. McIntyre and J. A. Real, Acta Crystallogr., Sect. B: Struct. Sci., 2014, 70, 436.
20. J. Jeftić and A. Hauser, J. Phys. Chem. B, 1997, 101, 10262; V. Legrand, F. Le Gac, P. Guionneau and J.-F. Letard, J. Appl. Crystallogr., 2008, 41, 637; H. J. Shepherd, S. Bonnet, P. Guionneau, S. Bedoui, G. Garbarino, W. Nicolazzi, A. Bousseksou and G. Molnár, Phys. Rev. B: Condens. Matter, 2011, 84, 144107; H. J. Shepherd, T. Palamarciuc, P. Rosa, P. Guionneau, G. Molnár, J.-F. Létard and A. Bousseksou, Angew. Chem., Int. Ed., 2012, 51, 3910.
21. P. Guionneau, M. Marchivie, Y. Garcia, J. A. K. Howard and D. Chasseau, Phys. Rev. B: Condens. Matter, 2005, 72, 214408.
22. V. Legrand, S. Pechev, J.-F. Letard and P. Guionneau, Phys. Chem. Chem. Phys., 2013, 15, 13872.
23. J.-M. Chen, Y.-Y. Chin, M. Valldor, Z. Hu, J.-M. Lee, S.-C. Haw, N. Hiraoka, H. Ishii, C.-W. Pao, K.-D. Tsuei, J.-F. Lee, H.-J. Lin, L.-Y. Jang, A. Tanaka, C.-T. Chen and L. H. Tjeng, J. Am. Chem. Soc., 2014, 136, 1514; K. Oka, M. Azuma, W.-t. Chen, H. Yusa, A. A. Belik, E. Takayama-Muromachi, M. Mizumaki, N. Ishimatsu, N. Hiraoka, M. Tsujimoto, M. G. Tucker, J. P. Attfield and Y. Shimakawa, J. Am. Chem. Soc., 2010, 132, 9438.
24. W. Kläui, Angew. Chem., Int. Ed. Engl., 1990, 29, 627; W. Kläui, W. Eberspach and P. Gütlich, Inorg. Chem., 1987, 26, 3977.
25. A. B. P. Lever, Studies in Physical and Theoretical Chemistry 33: Inorganic Electronic Spectroscopy, Elsevier, 1997; B. J. Hathaway and D. E. Billing, Coord. Chem. Rev., 1970, 5, 143; B. J. Hathaway, Struct. Bonding, 1984, 57, 55.
26. E. Meissner, H. Köppen, H. Spiering and P. Gütlich, Chem. Phys. Lett., 1983, 95, 163; P. Adler, L. Wiehl, E. Meibner, C. P. Köhler, H. Spiering and P. Gütlich, J. Phys. Chem. Solids, 1987, 48, 517; A. B. Gaspar, V. Ksenofontov, M. Seredyuk and P. Gütlich, Coord. Chem. Rev., 2005, 249, 2661; A. Bhattacharjee, V. Ksenofontov, J. A. Kitchen, N. G. White, S. Brooker and P. Gütlich, Appl. Phys. Lett., 2008, 92, 174104.
27. M. Shatruk, H. Phan, B. A. Chrisostomo and A. Suleimenova, Coord. Chem. Rev., 2015, 289–290, 62.
28. J.-P. Martin, J. Zarembowitch, A. Dworkin, J. G. Haasnoot and E. Codjovi, Inorg. Chem., 1994, 33, 2617.
29. V. Ksenofontov, A. B. Gaspar, G. Levchenko, B. Fitzsimmons and P. Gütlich, J. Phys. Chem. B, 2004, 108, 7723.
30. N. Suresh and J. L. Tallon, Phys. Rev. B: Condens. Matter, 2007, 75, 174502.
31. M. Kunz, A. A. MacDowell, W. A. Caldwell, D. Cambie, R. S. Celestre, E. E. Domning, R. M. Duarte, A. E. Gleason, J. M. Glossinger, N. Kelez, D. W. Plate, T. Yu, J. M. Zaug, H. A. Padmore, R. Jeanloz, A. P. Alivisatos and S. M. Clark, J. Synchrotron Radiat., 2005, 12, 650.
32. R. Boehler and K. De Hantsetters, High Pressure Res., 2004, 24, 391.
33. H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., [Solid Earth], 1986, 91, 4673.
34. R. T. Downs and D. C. Palmer, Am. Mineral., 1994, 79, 9.
35. P. Dera, K. Zhuravlev, V. Prakapenka, M. L. Rivers, G. J. Finkelstein, O. Grubor-Urosevic, O. Tschauner, S. M. Clark and R. T. Downs, High Pressure Res., 2013, 33, 466.
36. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112.

---

Footnote

† Electronic supplementary information (ESI) available: Including full experimental details and crystallographic information files. CCDC 1404670–1404672. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt03795f

---