Synthesis, crystal structure, optical and thermal properties of lanthanide hydrogen-polyphosphates Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho)

Abstract

Lanthanide hydrogen-polyphosphates Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) were synthesised as colourless (Ln = Tb, Dy) and light pink (Ln = Ho) crystalline powders by reaction of Tb₄O₇/Dy₂O₃/Ho₂O₃ with H₃PO₃ at 380 °C. All compounds crystallise isotypically (P2₁/c (no. 14), Z = 4, a_Tb = 1368.24(4) pm, b_Tb = 710.42(2) pm, c_Tb = 965.79(3) pm, β_Tb = 101.200(1)°, 3112 data, 160 parameters, wR₂ = 0.062, a_Ho = 1363.34(5) pm, b_Ho = 709.24(3) pm, c_Ho = 959.07(4) pm, β_Ho = 101.055(1)°, 1607 data, 158 parameters, wR₂ = 0.058). The crystal structure comprises two different infinite helical chains of corner-sharing phosphate tetrahedra. In-between these chains the lanthanide ions are located, coordinated by seven oxygen atoms belonging to four different polyphosphate chains. Vibrational, UV/Vis and fluorescence spectra of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) as well as Dy[H(PO₃)₄]:Ln (Ln = Ce, Eu) and the magnetic and thermal behaviour of Tb[H(PO₃)₄] are reported.

---

1 Introduction

In general, phosphates exhibit a large variety of structures and composition. Besides monophosphates, various condensed oligo-, long-chain polyphosphates and cyclophosphates exist.^1,2 Phosphates doped with lanthanides or stoichiometric lanthanide phosphates, such as Sr₃(PO₄)₅Cl:Eu³⁺/Eu²⁺, LaPO₄:Ce³⁺,Tb³⁺, (Y,Gd)PO₄:Eu³⁺,^3–7 Ln(PO₃)₃:Eu³⁺ (Ln = Y, Gd, Lu),⁸ α-Sr(PO₃)₂:Eu²⁺,Mn²⁺, SrM(P₂O₇):Eu²⁺,Mn²⁺ (M = Zn, Sr)^9,10 and BaCa(PO₃)₄:Eu²⁺ (ref. 11), reveal great potential for optical applications as luminescent materials. Many transitions between the energy levels of the Ln³⁺ ions are in the visible range (12500–25000 cm⁻¹).^12,13 Due to the strong shielding of the 5s and 5p orbitals, crystal field splitting is very small, and weak 4f–4f transitions occur, leading to the characteristic line emissions.^4,7,14 Since these are parity forbidden, they only become allowed by an admixture of states of the opposite parity.^12,13 Despite the rather low emission, a good colour rendering can be achieved.^4,7

Acid polyphosphates with the sum formula Ln[H(PO₃)₄] (Ln = Sm, Eu) are known to crystallise isostructurally to Bi[H(PO₃)₄]¹⁵ in the triclinic space group P1̄.¹⁶ Surprisingly, acid polyphosphates of the elements at the origin of the lanthanide row (La, Pr, Nd) and at the end (Tm, Yb) have not yet been observed. Instead, only non-protonated polyphosphates and ultraphosphates are formed depending on the synthesis temperature.¹⁷ Ln[H(PO₃)₄] (Ln = Tb–Er) crystallises in the monoclinic space group P2₁/c. Gd[H(PO₃)₄] represents an exception, which crystallises in both configurations at the same time. Up to now only the crystal structure of Er[H(PO₃)₄] was solved from single-crystal data.¹⁷ With regard to optical applications, both the spectroscopic properties and the thermal stability of the host lattice are important characteristics.

Herein we study the crystal structures of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) determined from single-crystal data (Ln = Tb, Ho) and refined via a Rietveld refinement (Ln = Dy) as well as their optical, magnetic and thermal properties.

2 Crystal structure

Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) crystallise isotypically to Er[H(PO₃)₄]¹⁷ in the centrosymmetric monoclinic space group P2₁/c (no. 14) (Tables 5–9 and 11). The anionic partial structure of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) consists of two different infinite helical corner-sharing phosphate chains arranged parallel to each other along [010] with alternating poly-hydrogenphosphate and polyphosphate chains (Fig. 1).

Fig. 1 Infinite, parallel hydrogen polyphosphate (A) and polyphosphate (B) chains of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) along [010] (viewed along direction [001]); phosphorus blue, oxygen red, hydrogen white.

Table 1 MAPLE calculations for Ln[H(PO₃)₄] (Ln = Tb, Ho)

Tb[H(PO3)4]	α-TbP3O9 ^22 + 0.5H2O ^34 + 0.5P2O5 ^35
MAPLE = 98 590 kJ mol^−1	MAPLE = 98 466 kJ mol^−1
(Δ = 0.1%)

---

Ho[H(PO3)4]	α-HoP3O9 ^22 + 0.5H2O ^34 + 0.5P2O5 ^35
MAPLE = 98 811 kJ mol^−1	MAPLE = 98 326 kJ mol^−1
(Δ = 0.5%)

---

Table 2 Absorption band energies for the strongest transitions in Tb[H(PO₃)₄] and in free Tb³⁺ ions between 225 and 800 nm

No.	Absorption	λ/nm	Tb[H(PO3)4] energy/10^3 cm^−1	Free Tb^3+ (ref. 42) energy/10^3 cm^−1
1	^7F6 → ^5H7	319	31.3	31.6
2	^7F6 → ^5G2	336	29.8	29.6
3	^7F6 → ^5L9	351	28.5	28.5
4	^7F6 → ^5G5	358	27.9	27.8
5	^7F6 → ^5L10	369	27.1	27.1
6	^7F6 → ^5G6	377	26.5	26.4
7	^7F6 → ^5D4	486	20.6	20.5

---

Table 3 Absorption band energies for the strongest transitions in Dy[H(PO₃)₄] and in free Dy³⁺ ions between 225 and 800 nm

No.	Absorption	λ/nm	Dy[H(PO3)4] energy/10^3 cm^−1	Free Dy^3+ (ref. 42) energy/10^3 cm^−1
1	^6H15/2 → ^4D7/2	295	33.9	33.8
2	^6H15/2 → ^6P3/2	325	30.8	30.8
3	^6H15/2 → ^4F5/2 + ^4D5/2	338	29.6	29.6
4	^6H15/2 → ^6P7/2	350	28.6	28.6
5	^6H15/2 → ^6P5/2	364	27.5	27.5
6	^6H15/2 → ^4K17/2	378	26.5	26.4
7	^6H15/2 → ^4I13/2	386	25.9	25.9
8	^6H15/2 → ^4G11/2	425	23.5	23.3
9	^6H15/2 → ^4I15/2	452	22.1	22.3
10	^6H15/2 → ^4F9/2	473	21.1	21.1
11	^6H15/2 → ^6F3/2	753	13.3	13.2

---

Table 4 Absorption band energies for the strongest transitions in Ho[H(PO₃)₄] and in free Ho³⁺ ions between 225 and 800 nm

No.	Absorption	λ/nm	Ho[H(PO3)4] energy/10^3 cm^−1	Free Ho^3+ (ref. 41) energy/10^3 cm^−1
1	^5I8 → ^3H6 + ^1I6	219	45.7	45.7
2	^5I8 → ^3F4 + ^5D4	241	41.6	41.5
3	^5I8 → ^5D3	250	40.0	40.0
4	^5I8 → ^3I7	261	38.2	38.5
5	^5I8 → ^3P0	278	36.0	36.0
6	^5I8 → ^5G4 + ^5D4 + ^3G4	290	34.5	34.8
7	^5I8 → ^3F4 + ^3H4 + ^3G4	334	29.9	30.0
8	^5I8 → ^3L9	346	28.9	29.0
9	^5I8 → ^3H6	361	27.7	27.7
10	^5I8 → ^5G4	386	25.9	25.8
11	^5I8 → ^5G5 + ^3G5	417	24.0	24.0
12	^5I8 → ^5F1	451	22.2	22.4
13	^5I8 → ^3K8	468	21.4	21.3
14	^5I8 → ^5F2	473	21.1	21.1
15	^5I8 → ^5F3	485	20.6	20.7
16	^5I8 → ^5F4	538	18.6	18.6
17	^5I8 → ^5F5	648	15.4	15.5

---

Table 5 Single-crystal data and structure refinements of Ln[H(PO₃)₄] (Ln = Tb, Ho)

	Tb[H(PO3)4]	Ho[H(PO3)4]
Temperature/K	293(2)	296(2)
Molar weight/g mol^−1	475.81	481.77
Crystal system	Monoclinic	Monoclinic
Space group	P21/c (no. 14)	P21/c (no. 14)
Crystal shape	Plate	Irregular
Crystal size/mm^3	0.047 × 0.018 × 0.019	0.050 × 0.018 × 0.020
Colour	Colourless	Pink/yellow
a/pm	1368.24(4)	1363.34(5)
b/pm	710.42(2)	709.24(3)
c/pm	965.79(3)	959.07(4)
β/°	101.200(1)	101.055(1)
Volume/10^6 pm^3	920.89(5)	910.15(6)
Z	4	4
Calculated density Dx/g cm^−3	3.432	3.499
Absorption coefficient μ/mm^−1	8.440	9.462
F(000)	888	896
Radiation (λ/Å)	Mo-Kα (0.7093)	Mo-Kα (0.7093)
Diffractometer	Bruker D8 Venture	Bruker D8 Venture
Absorption correction	Multi-scan	Multi-scan
Transmission factor (min./max.)	0.6359/0.7457	0.6029/0.7458
Index range h|k|l (min./max.)	0/16|−8/0|−11/11	−16/16|−8/8|−11/11
Theta range/°	3.04 ≤ Θ ≤ 25.00	3.04 ≤ Θ ≤ 25.00
Reflections collected	3112	27195
Independent reflections	3111	1607
Observed reflections (I > 2σ)	2790	1421
R int	—	0.0537
Refined parameters	160	158
R 1 (all data)	0.028	0.029
wR2 (all data)	0.062	0.058
Weighting scheme	w^−1 = σ^2Fo^2 + (0.0389P)^2	w^−1 = σ^2Fo^2 + (0.0423P)^2 + 1.5847P
	P = (Fo^2 + 2Fc^2)/3	P = (Fo^2 + 2Fc^2)/3
GooF	1.131	1.030
Residual electron density (min./max.)/e^− Å^−3	−0.499/0.144	−0.841/1.981

---

Table 6 Refined atomic coordinates, Wyckoff symbols and isotropic displacement parameters U_eq/Ų in Tb[H(PO₃)₄]

Atom	Wyckoff symbol	x	y	z	U eq
Obr = bridging oxygen atom; Oterm = terminal oxygen atom; OH = hydroxyl group.
Tb1	4e	0.729401(15)	0.05792(3)	0.05897(2)	0.00704(9)
P1	4e	0.90133(8)	−0.32485(16)	0.12591(13)	0.0083(3)
P2	4e	0.90026(9)	0.15142(17)	−0.18737(12)	0.0080(3)
P3	4e	0.61157(9)	−0.20990(17)	0.29579(12)	0.0077(2)
P4	4e	0.59385(9)	0.40127(16)	0.20937(12)	0.0078(3)
Obr1	4e	0.9446(3)	−0.4771(5)	0.2377(3)	0.0135(7)
Obr2	4e	0.9990(2)	−0.2305(4)	0.0948(3)	0.0114(7)
Obr3	4e	0.5802(2)	−0.3766(4)	0.1876(3)	0.0117(7)
Obr4	4e	0.5152(2)	−0.1724(4)	0.3594(3)	0.0098(7)
Oterm1	4e	0.8343(3)	−0.1896(5)	0.1741(3)	0.0145(8)
Oterm2	4e	0.8414(3)	0.0764(5)	−0.0888(3)	0.0174(8)
Oterm3	4e	0.8587(3)	0.2914(5)	−0.2952(3)	0.0156(8)
Oterm4	4e	0.6343(3)	−0.0457(4)	0.2130(3)	0.0132(7)
Oterm5	4e	0.6902(3)	−0.2722(4)	0.4168(3)	0.0123(7)
Oterm6	4e	0.6158(2)	0.3586(5)	0.3627(3)	0.0115(7)
Oterm7	4e	0.6615(2)	0.3364(4)	0.1191(3)	0.0114(7)
OH1	4e	0.8569(3)	−0.4300(5)	−0.0105(4)	0.0158(8)
H1	4e	0.804(3)	−0.350(8)	−0.048(5)	0.05

---

Table 7 Anisotropic displacement parameters U_ij/Ų in Tb[H(PO₃)₄]

Atom	U 11	U 22	U 33	U 12	U 13	U 23
Tb1	0.00640(13)	0.00779(13)	0.00678(13)	−0.00024(9)	0.00093(10)	0.00006(9)
P1	0.0056(6)	0.0087(6)	0.0100(6)	0.0002(5)	0.0001(5)	−0.0004(5)
P2	0.0051(6)	0.0086(6)	0.0104(6)	0.0007(5)	0.0017(5)	0.0010(5)
P3	0.0068(6)	0.0074(6)	0.0082(5)	0.0005(5)	−0.0005(5)	−0.0001(5)
P4	0.0070(6)	0.0062(6)	0.0094(6)	−0.0008(5)	−0.0001(5)	−0.0002(5)
Obr1	0.0099(18)	0.0108(17)	0.0184(19)	0.0068(14)	−0.0009(14)	0.0002(15)
Obr2	0.0129(19)	0.0104(17)	0.0091(14)	0.0030(14)	−0.0025(13)	−0.0011(14)
Obr3	0.0195(19)	0.0051(16)	0.0087(16)	−0.0010(13)	−0.0021(14)	0.0022(15)
Obr4	0.0076(17)	0.0136(19)	0.0084(16)	0.0024(13)	0.0021(13)	0.0023(14)
Oterm1	0.020(2)	0.0089(18)	0.0137(17)	0.0017(14)	0.0021(15)	0.0029(16)
Oterm2	0.0116(18)	0.027(2)	0.0156(17)	−0.0013(16)	0.0066(15)	−0.0042(15)
Oterm3	0.0087(19)	0.0172(18)	0.0182(17)	0.0070(16)	−0.0042(14)	0.0015(16)
Oterm4	0.0148(19)	0.0093(18)	0.0171(18)	0.0040(14)	0.0068(15)	0.0012(14)
Oterm5	0.0082(19)	0.0111(18)	0.0155(15)	0.0013(14)	−0.0032(13)	0.0025(13)
Oterm6	0.012(18)	0.0126(17)	0.0075(16)	0.0000(14)	−0.0025(14)	−0.0054(15)
Oterm7	0.0073(17)	0.0113(18)	0.0168(18)	−0.0026(14)	0.0054(14)	−0.0006(14)
OH1	0.012(2)	0.0154(19)	0.0176(18)	−0.0077(15)	−0.0019(15)	−0.0002(14)

---

Table 8 Refined atomic coordinates, Wyckoff symbols and isotropic displacement parameters U_eq/Ų in Ho[H(PO₃)₄]

Atom	Wyckoff symbol	X	y	z	U eq
Ho1	4e	0.729532(17)	0.05657(3)	0.05931(3)	0.00637(13)
P1	4e	0.90118(10)	−0.3250(2)	0.12488(15)	0.0080(3)
P2	4e	0.89935(9)	0.1530(2)	−0.18799(15)	0.0073(3)
P3	4e	0.38820(10)	0.2885(2)	0.20467(15)	0.0070(3)
P4	4e	0.59443(10)	0.3988(2)	0.21039(15)	0.0070(3)
Obr1	4e	0.9438(3)	−0.0209(6)	−0.2624(4)	0.0138(9)
Obr2	4e	0.9995(3)	−0.2308(5)	0.0942(4)	0.0101(8)
Obr3	4e	0.4186(3)	0.1212(5)	0.3132(4)	0.0111(8)
Obr4	4e	0.4853(3)	0.3257(6)	0.1412(4)	0.0107(8)
Oterm1	4e	0.8334(3)	−0.1891(5)	0.1737(4)	0.0117(8)
Oterm2	4e	0.8395(3)	0.0788(6)	−0.0889(5)	0.0166(9)
Oterm3	4e	0.8581(3)	0.2080(6)	0.2034(4)	0.0154(9)
Oterm4	4e	0.6349(3)	−0.0475(5)	0.2120(4)	0.0125(9)
Oterm5	4e	0.6904(3)	−0.2267(6)	−0.0824(4)	0.0119(8)
Oterm6	4e	0.6161(3)	0.1414(6)	−0.1351(4)	0.0132(9)
Oterm7	4e	0.6633(3)	0.3331(5)	0.1200(4)	0.0121(9)
OH1	4e	0.8568(3)	−0.4297(6)	−0.0126(5)	0.0178(10)
H1	4e	0.795(3)	−0.394(12)	−0.068(7)	0.050

---

Table 9 Anisotropic displacement parameters U_ij/Ų in Ho[H(PO₃)₄]

Atom	U 11	U 22	U 33	U 12	U 13	U 23
Ho1	0.00672(16)	0.00555(17)	0.00677(17)	−0.00023(10)	0.00109(10)	−0.00002(10)
P1	0.0072(6)	0.0059(7)	0.0103(7)	0.0007(6)	0.0004(6)	−0.0001(6)
P2	0.0053(6)	0.0069(7)	0.0094(7)	−0.0003(6)	0.0008(5)	−0.0011(6)
P3	0.0066(6)	0.0054 (7)	0.0088(7)	−0.0006(6)	0.0010(5)	−0.0006(5)
P4	0.0069(6)	0.0048(7)	0.0090(7)	−0.0015(6)	0.0002(6)	0.0001(5)
Obr1	0.0094(19)	0.012(2)	0.019(2)	−0.0050(18)	−0.0009(17)	0.0009(17)
Obr2	0.0121(19)	0.011(2)	0.0064(18)	0.0006(17)	0.0004(15)	−0.0025(16)
Obr3	0.018(2)	0.0037(19)	0.010(2)	0.0033(17)	0.0002(17)	−0.0011(17)
Obr4	0.0084(18)	0.015(2)	0.0093(19)	−0.0018(17)	0.0029(15)	−0.0026(16)
Oterm1	0.0139(19)	0.010(2)	0.011(2)	0.0014(17)	0.0020(16)	0.0033(16)
Oterm2	0.014(2)	0.019 (2)	0.018(2)	0.0005(19)	0.0064(18)	−0.0033(17)
Oterm3	0.0119(19)	0.014(2)	0.018(2)	−0.0014(19)	−0.0037(17)	−0.0012(17)
Oterm4	0.014(2)	0.010(2)	0.016(2)	0.0020(17)	0.0069(17)	−0.0008(16)
Oterm5	0.0091(18)	0.010(2)	0.0015(2)	0.0004(18)	−0.0015(16)	0.0002(16)
Oterm6	0.016(2)	0.010(2)	0.013(2)	−0.0019(17)	0.0000(17)	0.0043(17)
Oterm7	0.0105(18)	0.010(2)	0.018(2)	−0.0016(18)	0.0068(17)	0.0006(16)
OH1	0.015(2)	0.018(2)	0.017(2)	−0.0100(19)	−0.0039(18)	0.0004(17)

---

Table 10 Selected interatomic distances/pm and angles/°

	Tb[H(PO3)4]	Dy[H(PO3)4]	Ho[H(PO3)4]
Ln–O	228.0(3)–245.1(3)	224(2)–247(2)	2.254(4)–2.427(4)
P–Obr	156.1(3)–161.1(3)	145(3)–188(3)	1.568(4)–1.601(4)
P–Oterm	146.2(3)–149.4(3)	130(2)–160(3)	1.463(4)–1.495(4)
P–OH	153.3(3)	171 (3)	1.533(4)
POH–Obr–PO	135.8(2)–135.90(2)	126.5(18)–134.9(16)	135.8(2)–136.3(3)
PO–Obr–PO	129.9(2)–132.5(2)	129.5(19)–141.5(19)	129.8(3)–132.6(3)
Oterm–P–Oterm	117.4(2)–121.4(2)	111(2)–118(3)	117.4(2)–121.2(2)
Oterm–P–Obr	105.9(2)–114.3(2)	94(2)–130(3)	105.9(2)–114.1(2)
Oterm–P–OH	115.1(2)	135(2)	115.0(2)
Obr–P–Obr	99.4(2)–104.1(2)	93(2)–111(2)	99.1(2)–104.2(2)
Obr–P–OH	104.6(2)–106.9(2)	98.1(20)–108.9(20)	104.7(2)–106.7(2)

---

Table 11 Rietveld refinement parameters of Dy[H(PO₃)₄]

Molar weight/g mol^−1	479.40
Crystal system	Monoclinic
Space group	P21/c (no. 14)
Colour	Colourless
a/pm	1365.85(3)
b/pm	709.74(1)
c/pm	962.15(2)
β/°	101.116(1)
Volume/10^6 pm^3	915.21(3)
Z	4
Calculated density Dx/g cm^−3	3.479
Radiation	Cu-Kα
Wavelength λ/Å	1.5406
Diffractometer	Bruker D8 Advance
Theta range/°	5.00 ≤ 2θ ≤ 140.00
Refined parameters	62
R p	0.009
R wp	0.012
χ ^2	4.04

---

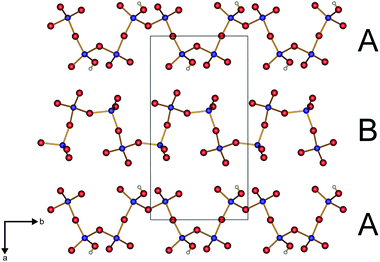
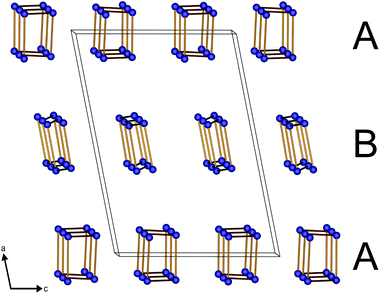
The protonated chain (A) reveals a larger diameter compared to the non-protonated polyphosphate chain (B) (Fig. 2) due to the widened P–O–P angles (136° in A vs. 130–133° in B).

Fig. 2 Reduced presentation of the infinite helical poly-hydrogenphosphate (A) and polyphosphate (B) chains of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) viewing in the [010] direction. O and H atoms are omitted for clarity; phosphorus blue.

The adjacent A and B chains in the a and c directions, respectively, exhibit a phase shift of 180° towards each other (Fig. 3).

Fig. 3 Phase-shifted chains of poly-hydrogenphosphate (A) and polyphosphate (B) tetrahedra (blue: front, violet: back) of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) in [001]; phosphate tetrahedra blue, oxygen red, hydrogen white.

In the phosphate tetrahedra P–O bond lengths range between 146 and 161 pm. The P–O_H bond is 153 pm long. P–O_br distances range between 156 and 161 pm, whereas P–O_term distances range between 146 and 150 pm. These values correspond very well to the data found for other poly-hydrogenphosphates^15–17 or polyphosphates.^18–23 In general, P–O distances increase from P–O_term to P–O_H and up to P–O_br due to the decreasing effective negative charge on the involved oxygen atom which leads to weaker electrostatic interactions between P and O. Angles of the P_OH–O_br–P_O and P_O–O_br–P_O bridges range between 135 and 137° and between 129 and 133°, respectively. Selected bond lengths and angles of Ln[H(PO₃)₄] (Ln = Tb, Ho) are listed in Table 10.

An appropriate method for the calculation of the deviation of tetrahedra from ideal symmetry was introduced by Balić-Žunić and Makovicky.^24,25 We adopted and explained the application of this method with the example of α-BaHPO₄;²⁶ in the course of our recent results we assigned deviations of less than 1% to regular tetrahedra. The four crystallographically different phosphate and hydrogenphosphate tetrahedra in Tb[H(PO₃)₄] and Ho[H(PO₃)₄] show the values of −0.32% (P1), −0.29 (P2), −0.22 (P3), −0.20 (P4) and −0.32 (P1), −0.29% (P2), −0.21 (P3), −0.21 (P4), respectively. These values are on the typical scale for phosphate tetrahedra.^22,26–29 Exhibiting a deviation far below 1%, all tetrahedra are classified as regular.

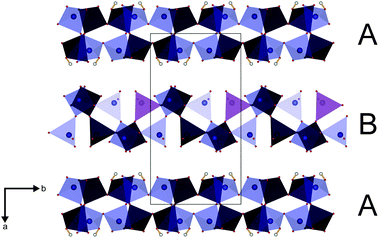
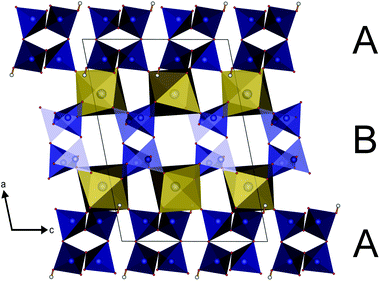
The parallel poly-hydrogenphosphate and polyphosphate chains of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) are interconnected via common O corners of LnO₇ polyhedra (Fig. 4). The single-crystal structure reveals a single site of Ln³⁺, which is coordinated capped trigonal prismatic by seven terminal oxygen atoms of the polyphosphate chains (Fig. 5 and 6). The Ln–O bond lengths range between 225 and 245 pm (Table 10). These values are in the same range as the Er–O bond lengths in Er[H(PO₃)₄] determined by Palkina et al.¹⁷

Fig. 4 Infinite helical chains of poly-hydrogenphosphate (A) and polyphosphate (B) tetrahedra in Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) in the [010] direction interconnected via LnO₇ polyhedra (yellow); phosphate tetrahedra blue, oxygen red, hydrogen white.

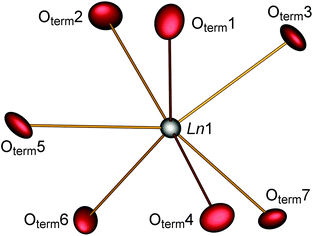Fig. 5 Coordination sphere of the lanthanide in Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho). The displacement ellipsoids are drawn on a probability level of 70%.

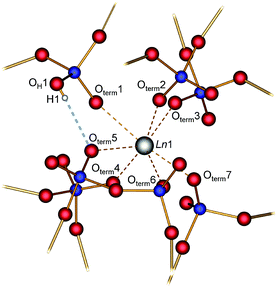Fig. 6 Moderate hydrogen bond (dotted blue line) and coordination sphere of the Ln atom in Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho); phosphorus blue, oxygen red, hydrogen white.

In Ln[H(PO₃)₄] (Ln = Tb, Ho) a single hydrogen bond was found which can be considered as moderate according to Steiner.³⁰ Tb[H(PO₃)₄] exhibits a hydrogen to acceptor distance d(H1–O_term5) of 176 pm and a bond angle ∢(DHA) of 165° (the donor to hydrogen distance d(O_H1–H1) = 93 pm, and the donor to acceptor distance d(O_H1–O_term5) = 267 pm). In Ho[H(PO₃)₄] the hydrogen to acceptor distance d(H1–O_term5) is 185 pm and the bond angle ∢(DHA) is 145° (the donor to hydrogen distance d(O_H1–H1) = 94 pm, and the donor to acceptor distance d(O_H1–O_term5) = 266 pm) (Fig. 6). In contrast to moderate hydrogen bonds with a hydrogen to acceptor distance between 150 and 220 pm and bond angles ∢(DHA) larger than 130°, strong hydrogen bonds exhibit a distance of 120–150 pm and an angle of 170–180°.

The crystal structure of Dy[H(PO₃)₄] was refined via the Rietveld method (Fig. 8 and Table 11) based on the structure model of Tb[H(PO₃)₄].

Fig. 7 X-ray powder diffraction patterns of Tb[H(PO₃)₄] (red) and Ho[H(PO₃)₄] (blue) and the calculated X-ray powder diffraction pattern from single-crystal data of Tb[H(PO₃)₄] (black) (λ_Cu-Kα = 1.54178 Å).

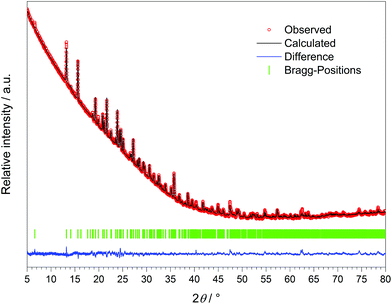Fig. 8 X-ray powder diffraction pattern and the result of the Rietveld refinement of Dy[H(PO₃)₄] (λ_Cu-Kα = 1.54178 Å).

3 Electrostatic calculations

The coordination numbers of the lanthanide ions and the electrostatic consistency of the structure model were confirmed by calculations based on the MAPLE concept (Madelung Part of Lattice Energy).^31–33 The presence of one proton could also be proven. A structure model is electrostatically consistent if the sum of MAPLE values of chemically similar compounds deviates from the MAPLE value of the compound of interest by less than approximately 1%. Thus the structure models of Tb[H(PO₃)₄] and Ho[H(PO₃)₄] show electrostatic consistency (Table 1).

4 Infrared spectroscopy

The infrared spectra of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) were recorded between 4000 and 400 cm⁻¹ and are shown in Fig. 9.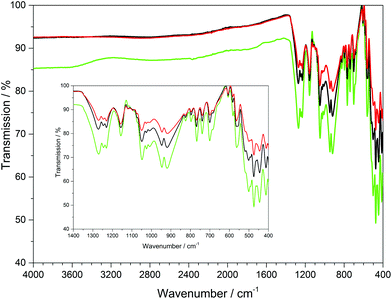

Fig. 9 Infrared spectra of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho); terbium green, dysprosium black, holmium red.

The bands between 1350 and 1200 cm⁻¹ can be assigned to the asymmetric stretching vibrations of PO₂, while vibrations between 1200 and 990 cm⁻¹ can be assigned to the stretching vibrations of PO_term. The ν_as(PO_br) and ν_as(POP) vibrational bands range between 985 and 845 cm⁻¹.^11,36–38 The four symmetric stretching modes of the PO_br vibrations are detected between 780 and 650 cm⁻¹ peaking at 681, 700, 741 and 770 cm⁻¹, which had been empirically correlated with the periodicity of polyphosphate chains in catena-polyphosphates.^11,36,39 This also holds for Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho), due to the periodicity P = 4 of its poly-hydrogenphosphate chains. Vibrations observed below 620 cm⁻¹ are assigned to the bending vibrations of the PO₄ tetrahedra.^11,36–38 Surprisingly, no vibrations of the hydroxyl groups were detected, which leads to the assumption that presumably the ratio of O–H/P–O vibrations of 1 : 16 is too small to be detected via ATR.

5 UV/Vis spectroscopy

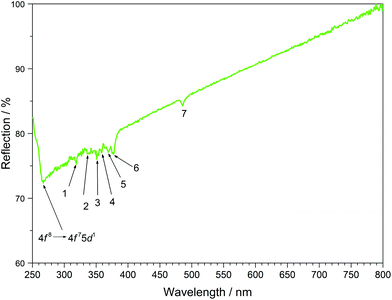
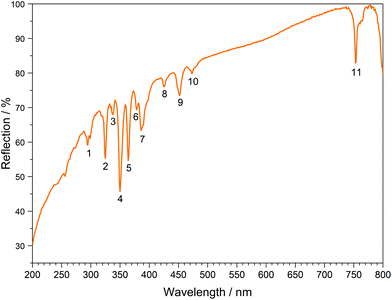
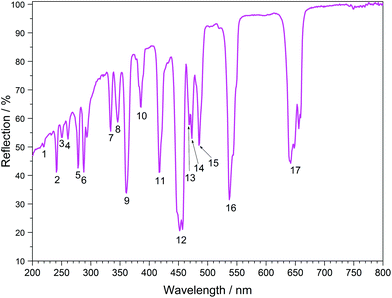
The UV/Vis reflection spectra of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) (Fig. 10–12) reveal the typical absorption bands of the f–f transitions of Tb³⁺, Dy³⁺ and Ho³⁺ ions, according to the well-known energy level schemes.^40,41 All transitions start from the respective ground states ⁷F₆, ⁶H_15/2 and ⁵I₈ with the electronic configuration [Xe] 4f⁸, [Xe] 4f⁹ and [Xe] 4f¹⁰, respectively. The corresponding assignments are listed in Tables 2–4.

Fig. 10 UV/Vis spectrum of Tb[H(PO₃)₄].

Fig. 11 UV/Vis spectrum of Dy[H(PO₃)₄].

Fig. 12 UV/Vis spectrum of Ho[H(PO₃)₄].

No significant deviations from the spectra of other inorganic salts of terbium, dysprosium and holmium were detected and the spectra are in accordance with the powder colours white (Tb[H(PO₃)₄] and Dy[H(PO₃)₄]) and pink/yellow (Ho[H(PO₃)₄]). Like other holmium compounds Ho[H(PO₃)₄] shows the alexandrite effect.^43,44 Due to an absorption gap in the yellow region, it exhibits a yellow body colour in ambient day light. In artificial light, e.g. fluorescent lamps, exhibiting distinct emissions in the blue (∼450 nm), green (∼540 nm) and red (∼610 nm) range, it reveals a pink body colour, due to the reflection of the wavelengths between 550 and 620 nm.⁴

6 Fluorescence spectroscopy

The fluorescence spectra of Tb[H(PO₃)₄] (Fig. 13) and Dy[H(PO₃)₄] (Fig. 14) reveal the characteristic f–f emissions of Tb³⁺ and Dy³⁺, respectively.^40–42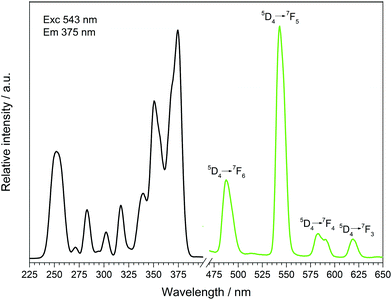

Fig. 13 Excitation (black), recorded at λ_Em = 543 nm, and emission (green) spectrum, recorded at λ_Exc = 375 nm, of Tb[H(PO₃)₄].

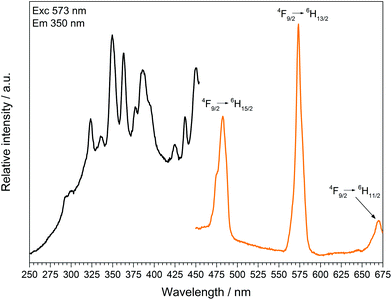Fig. 14 Excitation (black), recorded at λ_Em = 573 nm, and emission (orange) spectrum, recorded at λ_Exc = 350 nm, of Dy[H(PO₃)₄].

Between 230 and 267 nm a broader band in the excitation spectrum of Tb[H(PO₃)₄] reveals the parity allowed 4f⁸ → 4f⁷5d¹ transition. Under excitation at 375 nm Tb[H(PO₃)₄] exhibits sharp emission lines between 475 and 630 nm, which can be assigned to the ⁵D₄ → ⁷F₆ (488 nm), ⁵D₄ → ⁷F₅ (543 nm) showing the highest intensity, ⁵D₄ row ⁷F₄ (583 nm) and ⁵D₄ → ⁷F₃ (619 nm) transitions.⁴²

The excitation spectrum of Dy[H(PO₃)₄] exhibits a broad band around 290 nm, which reveals the 4f⁹ → 4f⁸5d¹ transition. Under excitation at 349 nm Dy[H(PO₃)₄] exhibits sharp emission lines between 460 and 675 nm, which correspond to the f–f electronic transitions ⁴F_9/2 → ⁶H_15/2 (482 nm), ⁴F_9/2 → ⁶H_13/2 (573 nm) and ⁴F_9/2 → ⁶H_11/2 (671 nm).⁴¹ The most intense transition ⁴F_9/2 → ⁶H_13/2 is sensitive to the surrounding of Dy³⁺, and is thus called hypersensitive. The surrounding of Dy³⁺ in Dy[H(PO₃)₄] is of relatively low symmetry (single capped trigonal prismatic), therefore the intensity of the hypersensitive transition is increased with respect to the ⁴F_9/2 → ⁶H_15/2 transition.^45,46

Doping of Dy[H(PO₃)₄] with increasing concentrations of Ce³⁺ (5, 10, 30 mol%) was carried out to investigate the effect of Ce³⁺ as a sensitizer. The presence of cerium and the corresponding ratios of Dy : Ce were investigated via EDX spectroscopy. The resulting ratios are 1 : 0.04 (expected: 1 : 0.05), 1 : 0.07 (1 : 0.10) and 1 : 0.26 (1 : 0.30), which are within the limits of accuracy of the measurements very close to the expected values. Due to an overlap in the wavelength range of the emission bands of Ce³⁺ and the excitation spectrum of Dy³⁺ energy transfer could be expected. Transitions in Ce³⁺ are f–d transitions, which are allowed due to the selection rules, and thus lead to broad and intense bands in the fluorescence spectrum.¹³ The fluorescence spectra of the doped samples Dy[H(PO₃)₄]:Ce³⁺ are shown in Fig. 15. The excitation spectra exhibit strongly increasing broad band intensities of Ce³⁺ at 302 nm (²F_5/2 → 5d). In the emission spectra, next to the typical broad band emissions of Ce³⁺ peaking at 317 nm (5d → ²F_5/2) and 336 nm (5d → ²F_7/2)^47,48 two comparably weak emission bands of Dy³⁺, corresponding to the f–f electronic transitions ⁴F_9/2 → ⁶H_15/2 and ⁴F_9/2 → ⁶H_13/2, can be observed. Despite the low Dy³⁺ emission intensities the hypersensitive transition ⁴F_9/2 → ⁶H_13/2 can still be observed with higher intensity compared to the ⁴F_9/2 → ⁶H_15/2 transition. Doubling the content of Ce³⁺ from 5 to 10% the emission intensity of Dy³⁺ also increases equally (⁴F_9/2 → ⁶H_15/2), whereas the hypersensitive transition ⁴F_9/2 → ⁶H_13/2 even triples. A further increase of the Ce³⁺ content to 30% leads to a raised intensity of a factor of 2.5 for the ⁴F_9/2 → ⁶H_15/2 transition and a factor of 1.7 for the ⁴F_9/2 → ⁶H_13/2 transition. Thus the emission intensities of Dy³⁺ increase slightly with the increasing Ce³⁺ content but do not prove efficient Ce³⁺ → Dy³⁺ energy transfer. The intensity of the f–d transition in the excitation spectrum increases corresponding to the increasing Ce³⁺ content. According to Luo and Yang satisfying energy transfer rates in the system Dy³⁺/Ce³⁺ could be reached, if the ratio of Dy³⁺ to Ce³⁺ ions is decreased to about 1 : 3, before the luminescence quenching of Ce³⁺ occurs.^49–51 By reversing the Dy³⁺/Ce³⁺ ratio and increasing the content of Ce³⁺ to Ce_0.75Dy_0.25[H(PO₃)₄] efficient energy transfer might be reached, which represents a substitution process rather than a doping process.

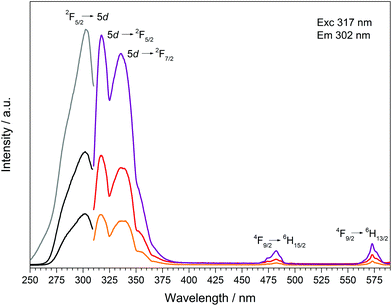Fig. 15 Excitation, recorded at λ_Em = 317 nm, and emission spectra, recorded at λ_Exc = 302 nm, of Dy[H(PO₃)₄]:Ce³⁺(5% black/orange, 10% dark grey/red, 30% grey/violet).

Doping Dy[H(PO₃)₄] with 5 mol% Eu³⁺ leads to the typical sharp excitation and emission bands of Dy³⁺ and Eu³⁺ (Fig. 16). The ratio of Dy : Eu was investigated via EDX spectroscopy exhibiting a ratio of 1 : 0.04, which is very close to the expected ratio (1 : 0.05). Under excitation at 392 nm Dy[H(PO₃)₄]:Eu³⁺ exhibits sharp emission lines between 530 and 757 nm, which can be assigned to the ⁵D₁ → ⁷F₁ (536 nm), ⁵D₀ → ⁷F₀ (553 nm), ⁵D₀ → ⁷F₁ (593 nm), ⁵D₀ → ⁷F₂ (614 nm), ⁵D₀ → ⁷F₃ (646 nm), ⁵D₁ → ⁷F₅ (663 nm), ⁵D₀ → ⁷F₄ (700 nm) and ⁵D₀ → ⁷F₅ (750 nm) transitions of Eu³⁺.⁵² The most intense transition ⁵D₀ → ⁷F₂ at 614 nm is called hypersensitive due to its sensitivity to the surrounding of Eu³⁺ and is responsible for the weak red emission. It is dominant over the ⁵D₀ → ⁷F₁ transition because of the asymmetric surrounding of Eu³⁺ in Dy[H(PO₃)₄]:Eu³⁺, which proves its partial substitution of Dy³⁺.^53,54 Besides the emission bands of Eu³⁺ two emission bands of Dy³⁺ can be observed at 573 and 722 nm, which can be assigned to the ⁴F_9/2 → ⁶H_13/2 and ⁶F_1/2 → ⁶H_15/2 transitions of Dy³⁺, respectively.⁴¹

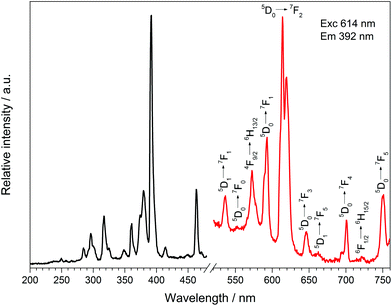Fig. 16 Excitation (black), recorded at λ_Em = 614 nm, and emission (red) spectrum, recorded at λ_Exc = 392 nm, of Dy[H(PO₃)₄]:Eu³⁺.

7 Magnetic properties

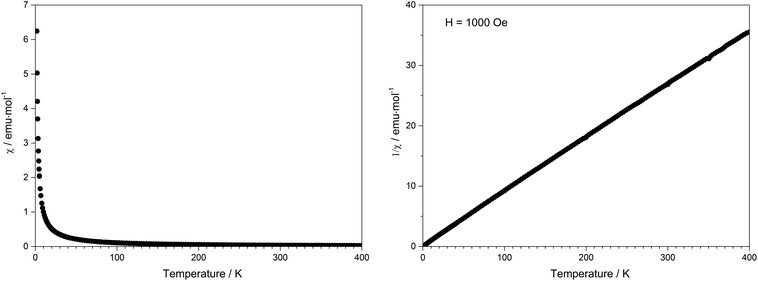
Due to the presence of one proton and the thus postulated sum formula of Tb[H(PO₃)₄], the valence state of terbium was confirmed by the magnetic susceptibility measurement, which was recorded in a field of 1000 Oe over the temperature range of 1.8 K < T < 400 K (Fig. 17). In the whole temperature range the molar susceptibility obeys Curie's law (χ_m = C/T) very well with a Curie constant of C = 11.3792 emu mol⁻¹ K⁻¹. The Curie constant corresponds to an effective magnetic moment per Tb³⁺ ion of μ_eff = 9.54μ_B, which is close to the theoretical value (μ_eff = 9.72μ_B) and to experimental effective magnetic moments of Tb³⁺ ions (9.7–9.8μ_B).⁵⁵

Fig. 17 Temperature dependence of the magnetic susceptibility χ of Tb[H(PO₃)₄].

8 Thermal analysis

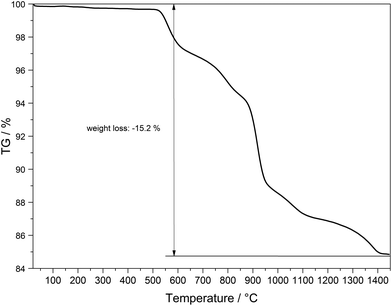
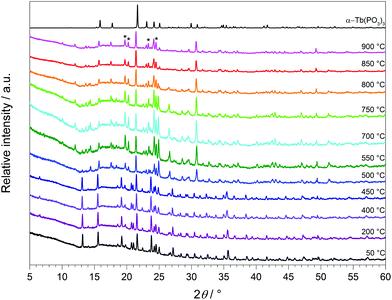
The thermal behaviour of Tb[H(PO₃)₄] was investigated between room temperature and 1450 °C (Fig. 18). The thermogravimetric curve revealed several undefined steps with a total mass loss of 15.2 wt% in the temperature range of 500–1450 °C. Assuming that besides 0.5 moles of H₂O a further 0.5 moles of P₂O₅ evaporate (theor. mass loss: 16.8 wt%) a final composition of TbP₃O₉ may be assumed. After the thermal treatment the product was glazed and the expected composition could not be confirmed via X-ray powder diffraction.

Fig. 18 Thermogravimetric analysis of Tb[H(PO₃)₄].

Temperature-dependent X-ray powder diffraction confirms that Tb[H(PO₃)₄] is stable up to 500 °C (Fig. 19). At 900 °C α-TbP₃O₉ (grey) represents the main phase next to a small part of TbP₅O₁₄ (marked with *).⁵⁶ This leads to the conclusion that the assumption of losing half a mole of each, H₂O and P₂O₅, in the thermal analysis is correct. Tb[H(PO₃)₄] exhibits infinite chains of [H(PO₃)₄]³⁻ and [P₃O₉]³⁻ anions. Hence it is not surprising that thermal decomposition leads to the elimination of the hydroxyl groups by evaporation of water. Astonishingly, under nitrogen flow this process does not occur below 500 °C.

Fig. 19 Temperature-dependent X-ray powder diffraction patterns of Tb[H(PO₃)₄] recorded between 50 and 900 °C and the calculated powder diffraction pattern from the single-crystal data of α-TbP₃O₉ (grey) (λ_Cu-Kα = 1.54178 Å).

The thermal decomposition of Ln[H(PO₃)₄] (Ln = Y, Gd–Er) was determined between 350 and 600 °C by Selevich et al.⁵⁷ According to the authors all investigations were carried out in atmospheric humidity. Thus thermal analysis was carried out in air and naturally proceeds in a shorter and lower temperature range (350–600 °C) rather than under an inert atmosphere (500–1440 °C) as performed in this work. Since an increasing stability is to be expected with an increasing connectivity, the thermal stability of Tb[H(PO₃)₄], exhibiting infinite polyphosphate chains, is estimated to be higher than for non-condensed cyclotetraphosphates, e.g. Ba₂(P₄O₁2)·3.5H₂O,²⁷ which decomposes around 380 °C. In contrast, thermal decomposition of the ultraphosphate YP₅O₁4, which reveals a higher degree of condensation, does not occur until 760 °C.⁵⁸

9 Conclusions

In this contribution we demonstrated the crystal structures of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho), which were solved and refined based on single-crystal X-ray diffraction (Tb and Ho) and refined by a Rietveld refinement (Dy), respectively. Via MAPLE calculations the presence of a single proton could be proved on the one hand, and on the other hand the electrostatic consistency of the structure model of Ln[H(PO₃)₄] (Ln = Tb, Ho) was confirmed. All the observed bands in the IR spectrum are in agreement with our structure model. The optical properties reveal the typical UV/Vis reflection and fluorescence spectra of Tb³⁺, Dy³⁺ and Ho³⁺ ions exhibiting their characteristic absorption and emission bands. Doping of Dy[H(PO₃)₄] with increasing amounts of Ce³⁺ revealed only slightly more intense emission bands of Dy³⁺ in the blue and yellow regions. Doping of Dy[H(PO₃)₄] with Eu³⁺ leads to a partial occupancy of Dy³⁺ sites, which is in accordance with the relatively high intensity of the hypersensitive ⁵D₀ → ⁷F₂ transition of Eu³⁺ in a non-centrosymmetric surrounding. The magnetic measurements reveal no interaction between the Tb³⁺ centres and confirmed the oxidation state of Tb³⁺ and thus the composition of Tb[H(PO₃)₄]. Though Tb[H(PO₃)₄] only reveals a condensation in one dimension, it exhibits a remarkable thermal stability up to 500 °C before presumably H₂O and P₂O₅ are released.

10 Experimental section

10.1 Syntheses of Ln[H(PO₃)₄] (Ln = Tb, Dy)

Ln[H(PO₃)₄] (Ln = Tb, Dy) were synthesised via solid-state reactions starting from the respective lanthanide oxides and phosphorous acid. Tb₄O₇ (94.70 mg, 0.14 mmol, Chempur, 99.9%) and Dy₂O₃ (94.00 mg, 0.25 mmol, Kristallhandel Kelpin, 99.99%), respectively, and H₃PO₃ (264.10 mg, 3.22 mmol, Sigma Aldrich, 99%) were ground in an agate mortar and transferred into a silica glass crucible. The reaction mixtures were covered with H₂O₂ (20 ml, Merck, 30%) to suppress the formation of LnP₃O₉ (Ln = Tb, Dy) as the side phase and heated up to 380 °C with a heating rate of 100 °C/h using a muffle furnace. The temperature was maintained for three hours before cooling down to room temperature by switching off the furnace. The products were washed with hot water and dried in air overnight. Different experiments showed that addition of H₂O₂ to the reaction mixtures leads to phase pure samples of colourless Tb[H(PO₃)₄] and Dy[H(PO₃)₄].

10.2 Synthesis of Ho[H(PO₃)₄]

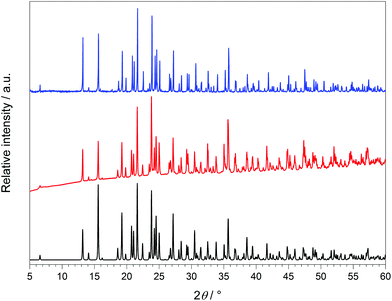
Ho[H(PO₃)₄] was synthesised analogously to Ln[H(PO₃)₄] (Ln = Tb, Dy) but could be obtained as phase pure yellow/pink powder without addition of H₂O₂ to the reaction mixture.

10.3 X-Ray powder diffraction

The crystalline sample was finely ground, enclosed in a Hilgenberg glass capillary of 0.3 mm outer diameter and investigated at room temperature with a Bruker D8 Advance diffractometer using Cu-K_α radiation (LynxEye 1-D detector, steps of 0.2°, acquisition time 7 s per step, Soller slits 2.5°, fixed divergence slit 8 mm, transmission geometry). The obtained products were phase pure according to X-ray powder diffractometry (Fig. 7). The structure models of Tb[H(PO₃)₄] and Ho[H(PO₃)₄] were confirmed and the structure model of Dy[H(PO₃)₄] was refined by Rietveld analysis^59,60 (Fig. 8) using the FullProf program suite and the WinPlotR graphical user interface.⁶¹ The single-crystal data of Tb[H(PO₃)₄] served as the starting structure model. The structure of Dy[H(PO₃)₄] was refined to excellent residuals of R_p = 0.009, R_wp = 0.012 and χ² = 4.04 (Table 11). The phase purity of Dy[H(PO₃)₄] could thus be confirmed. In Table 11 the data of the Rietveld refinement of Dy[H(PO₃)₄] are summarised.

The composition of Ln[H(PO₃)₄] (Ln = Tb, Dy, Ho) was checked via EDX (Energy-dispersive X-ray) spectroscopy. For the doped samples Dy[H(PO₃)₄]:Ce and Dy[H(PO₃)₄]:Eu the ratios of Dy : Ce and Dy : Eu were also confirmed. Within the accuracy of the measurement limits no other elements were found.

10.4 Crystal structure determination of Ln[H(PO₃)₄](Ln = Tb, Ho)

Single-crystals suitable for single-crystal X-ray diffraction analysis were selected under a polarizing microscope. Diffraction data were collected with a Bruker D8 Venture diffractometer using Mo-K_α radiation (λ = 0.7093 Å) at a temperature of 293 ± 2 (Ln = Tb) and 296 ± 2 K (Ln = Ho), respectively.

The structure of the non-merohedrally twinned crystal of Tb[H(PO₃)₄] was solved by defining the twinned components using TWINABS (twin matrix: 0 0 1 0 −1 0 1 0 0; BASF = 0.430).⁶² Both crystal structures were solved by direct methods and refined by the full-matrix least-squares technique with the SHELXTL crystallographic software package.^63,64 The Tb/Ho, P and O atoms could be clearly located. The hydrogen atom was added geometrically and was confirmed by MAPLE calculations.^31–33 Relevant crystallographic data and further details of the structure determination are summarised in Table 5. Tables 6–9 show the atomic coordinates and displacement parameters.

Further details of the crystal structure investigations presented in this work may be obtained from the Fachinformationszentrum Karlsruhe, D-76344 Eggenstein-Leopoldshafen, Germany (Fax: +49-7247-808-666; E-mail: crysdata@fiz-karlsruhe.de, http://www.fiz-karlsruhe.de/request for depositeddata.html) on quoting the depository numbers CSD 429861 (Tb[H(PO₃)₄]) and CSD 429860 (Ho[H(PO₃)₄]).

10.5 Infrared spectroscopy

Infrared spectra were recorded at room temperature with a Bruker Equinox 55 FT-IR spectrometer using a Platinum ATR device with a scanning range from 4000 to 400 cm⁻¹.

10.6 UV/Vis spectroscopy

The optical reflection spectra were recorded with a Varian Cary 300 Scan UV/Vis spectrophotometer in the range of 200–800 nm.

10.7 Fluorescence spectroscopy

Excitation and emission spectra were recorded at room temperature with a Fluoromax-4 spectrofluorometer with a Xe plasma lamp (Horiba Scientific, Unterhaching).

10.8 Magnetic investigations

The temperature-dependent magnetic susceptibility data were recorded with a Quantum Design MPMS-XL super-conducting quantum-interference device (SQUID) magnetometer in the field of 1000 Oe between 1.8 K < T < 400 K.

10.9 Thermal analysis

The thermal analysis was carried out with a Netzsch STA-409 PC thermal analyzer in the temperature range of 25–1450 °C in air with a heating rate of 5 K min⁻¹.

Acknowledgements

The authors thank Dana Vieweg, Lehrstuhl für Experimentalphysik V, Universität Augsburg, for recording the magnetic susceptibility measurements and Dr Stefan Riegg, Lehrstuhl für Experimentalphysik V, Universität Augsburg, for valuable discussions about the magnetic measurement and the Rietveld refinement.

References

1. A. Holleman and E. Wiberg, Lehrbuch der Anorganischen Chemie, deGruyter, Berlin, New York, 102nd edn, 2007.
2. A. Durif, Crystal Chemistry of Condensed Phosphates, Plenum Press, New York, 1995.
3. C. Feldmann, T. Jüstel, C. Ronda and P. Schmidt, Adv. Funct. Mater., 2003, 13, 511–516.
4. T. Jüstel, H. Nikol and C. Ronda, Angew. Chem., Int. Ed., 1998, 37, 3084–3103.
5. T. Jüstel, C. Feldmann and C. R. Ronda, Phys. Biol., 2000, 56, 55–58.
6. T. Jüstel, J.-C. Krupa and D. U. Wiechert, J. Lumin., 2001, 93, 179–189.
7. C. R. Ronda, T. Jüstel and H. Nikol, J. Alloys Compd., 1998, 275–277, 669–676.
8. H. A. Höppe, K. Kazmierczak, S. Kacprzak, I. Schellenberg and R. Pöttgen, Dalton Trans., 2011, 40, 9971–9976.
9. H. A. Höppe, M. Daub and M. C. Bröhmer, Chem. Mater., 2007, 19, 6358–6362.
10. H. A. Höppe, Angew. Chem., Int. Ed., 2009, 48, 3572–3582.
11. H. A. Höppe and J. M. U. Panzer, Eur. J. Inorg. Chem., 2009, 3127–3130.
12. G. H. Dieke and H. M. Crosswhite, Appl. Opt., 1963, 2, 675–686.
13. K. Ogasawara, S. Watanabe, H. Toyoshima and M. G. Brik, Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 2007, vol. 37.
14. L. Ozawa, Chem. Rev., 2003, 103, 3835–3855.
15. K. Palkina and K. H. Jost, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 2285–2290.
16. K. Palkina, N. Kuzmina, A. Selevich and A. Lesnikovich, Russ. J. Inorg. Chem., 2003, 48, 161–164.
17. K. Palkina, N. Chudinova and G. Balagina, Izves. Akad. Nauk SSSR, 1982, 18, 1337–1341.
18. K. H. Jost, Z. Kristallogr., 1963, 16, 623–626.
19. M. Rzaigui and K. Arigiub, J. Solid State Chem., 1983, 50, 240–246.
20. M. Graia, A. Driss and T. Jouini, Solid State Sci., 2003, 5, 393–402.
21. H. A. Höppe, Solid State Sci., 2005, 7, 1209–1215.
22. H. A. Höppe, J. Solid State Chem., 2009, 182, 1786–1791.
23. S. J. Sedlmaier and W. Schnick, Z. Anorg. Allg. Chem., 2008, 634, 1501–1505.
24. T. Balić-Žunić and E. Makovicky, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 78–81.
25. E. Makovicky and T. Balić-Žunić, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 766–773.
26. H. A. Höppe, M. Daub and O. Oeckler, Solid State Sci., 2009, 11, 1484–1488.
27. H. A. Höppe, K. Kazmierczak and M. Daub, Z. Anorg. Allg. Chem., 2010, 636, 1106–1110.
28. H. A. Höppe and M. Daub, Z. Kristallogr., 2012, 227, 535–539.
29. M. Daub, A. J. Lehner and H. A. Höppe, Dalton Trans., 2012, 41, 12121–12128.
30. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
31. R. Hoppe, Angew. Chem., Int. Ed. Engl., 1966, 5, 95–106.
32. R. Hoppe, Angew. Chem., Int. Ed. Engl., 1970, 9, 25–34.
33. R. Hübenthal, MAPLE, MAPLE, Program for the Calculation of the Madelung Part of Lattice Energy, University of Gießen, Germany, 1993.
34. A. Goto, T. Hondoh and S. Mae, J. Chem. Phys., 1990, 93, 1412–1417.
35. C. H. MacGillavry, H. C. J. de Decker and L. M. Nijland, Nature, 1949, 164, 448–449.
36. M. Weil, M. Puchberger, J. Schmedt auf der Günne and J. Weber, Chem. Mater., 2007, 19, 5067–5073.
37. J. Weidlein, U. Müller and K. Dehnicke, Schwingungsfrequenzen I Hauptgruppenelemente, Georg Thieme Verlag Stuttgart, New York, 1981.
38. A. Rulmont, R. Cahay, M. Liegeois-Duyckaerts and P. Tarte, Eur. J. Solid State Inorg. Chem., 1991, 28, 207–219.
39. O. Y. Miroshnichenko and V. V. Mombelli, Russ. J. Inorg. Chem. Engl. Transl., 1979, 24, 1631–1634.
40. W. T. Carnall, J. Phys. Chem., 1963, 67, 1206–1211.
41. W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4424–4442.
42. W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4447–4449.
43. H. A. Höppe, G. Kotzyba, R. Pöttgen and W. Schnick, J. Mater. Chem., 2001, 11, 3300–3306.
44. K. Kazmierczak and H. A. Höppe, J. Solid State Chem., 2011, 184, 1221–1226.
45. Y.-C. Li, Y.-H. Changa, Y.-F. Lin, Y.-S. Changb and Y.-J. Lin, J. Alloys Compd., 2007, 439, 367–375.
46. Z.-J. Zhang, J.-L. Yuan, H.-H. Chen, X.-X. Yang and J.-T. Zhao, Solid State Sci., 2009, 11, 549–555.
47. D. Bimberg, D. J. Robbins, D. R. Wight and J. P. Jeser, Appl. Phys. Lett., 1975, 27, 67–68.
48. M. Guan, J. Sun, T. Shang, Q. Zhou, J. Han and A. Ji, J. Mater. Sci. Technol., 2010, 26, 45–48.
49. C. Yang, Y. Pan and Q. Zhang, Mater. Sci. Eng., B, 2007, 137, 195–199.
50. Q. Luo, X. Qiao, X. Fan, H. Yang, X. Zhang, S. Cui, L. Wang and G. Wang, J. Appl. Phys., 2009, 105, 043506.
51. H. Yu, W. Zi, S. Lan, S. Gan, H. Zou, X. Xu and G. Hong, Luminescence, 2013, 28, 679–684.
52. W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4450–4455.
53. G. Blasse, A. Bril and W. Nieuwpoort, J. Phys. Chem. Solids, 1966, 27, 1587–1592.
54. G. Blasse and A. Bril, J. Chem. Phys., 1967, 47, 5442–5443.
55. H. Lueken, Magnetochemie, B. G. Teubner Stuttgart, Leipzig, 1999.
56. A. Durif, Bull. Soc. Fr. Miner. Crystallogr., 1971, 94, 314–318.
57. A. Selevich, A. Lyakhov and A. I. Lesnikovich, Phosphorus Res. Bull., 1999, 10, 171–176.
58. A. Mbarek, M. Graia, G. Chadeyron, D. Zambon, J. Bouaziz and M. Fourati, J. Solid State Chem., 2009, 182, 509–516.
59. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
60. H. M. Rietveld, Z. Kristallogr., 2010, 225, 545–547.
61. J. Rodríguez-Carvajal, Phys. Rev. B: Condens. Matter, 1993, 192, 55–69.
62. G. M. Sheldrick, TWINABS, Universität Göttingen, 1996.
63. G. Sheldrick, SHELXTL, Version 6.14, Bruker AXS, 2003.
64. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5dt02648b

---