 Open Access Article
Open Access ArticleField-induced slow relaxation of magnetization in a pentacoordinate Co(II) compound [Co(phen)(DMSO)Cl2]†
Ivan
Nemec
 a,
Raphael
Marx
b,
Radovan
Herchel
a,
Raphael
Marx
b,
Radovan
Herchel
 a,
Petr
Neugebauer
b,
Joris
van Slageren
b and
Zdeněk
Trávníček
*a
a,
Petr
Neugebauer
b,
Joris
van Slageren
b and
Zdeněk
Trávníček
*a
aRegional Centre of Advanced Technologies and Materials, Department of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic. E-mail: zdenek.travnicek@upol.cz
bInstitute of Physical Chemistry, University of Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany
First published on 20th July 2015
Abstract
The static and dynamic magnetic properties of a pentacoordinate [Co(phen)(DMSO)Cl2] compound (phen = 1,10′-phenanthroline, DMSO = dimethyl sulfoxide) were thoroughly studied by experimental (SQUID magnetometry and HF-EPR spectroscopy) and theoretical methods (DFT and CASSCF calculations). It has been found from temperature/field-dependent magnetization measurements that the studied compound possesses a large and negative magnetic anisotropy (D = −17(1) cm−1) with large rhombicity (E/D = 0.24(5)), and these experimental results are in agreement with ab initio calculations (D = −17.7 cm−1, E/D = 0.31). Interdoublet resonances were not observed in the HF-EPR measurements, but the large rhombicity was confirmed (DEPR = −17.7 cm−1 (fixed from CASSCF calculations), E/DEPR = 0.33). A frequency dependent out-of-phase susceptibility signal was observed only in a non-zero static magnetic field (B = 0.1 T) and the following parameters of slow-relaxation of magnetisation were derived from the experimental data: either the energy of spin reversal barrier, Ueff = 10.4 K, and the relaxation time, τ0 = 5.69 × 10−9 s using the Debye model, or Ueff = 21.4–40.3 K and τ0 = 0.248–58.3 × 10−9 based on a simplified model.
Introduction
Single-molecule magnets (SMMs) are molecular compounds in which each molecule exhibits slow-relaxation of magnetisation and thus it behaves as a molecular nanomagnet. The energy barrier of spin reversal is defined as Δ = |D|(S2 − 1/4) for odd values of the ground spin state S, under the condition that D is negative. This means that magnetic anisotropy is uniaxial and, in the case of Co(II) with S = 3/2, the lowest energy level of the ground state is the Kramers doublet |±3/2> and the energy separation from the adjacent Kramers doublet |±1/2> is equal to 2D.1SMMs were discovered 24 years ago with the famous Mn12 compound2 and it was believed for a long time that the total spin might be an important variable regarding spin reversal barrier (Ueff) which defines the basic properties of SMMs. However, it has turned out that magnetic anisotropy is the key factor in the design of SMM compounds and this was further confirmed by the discovery of the first mononuclear lanthanide SMM3 and other theoretical studies.4 Other coordination compounds containing only one paramagnetic metal centre and exhibiting slow-relaxation of magnetization followed: Fe(I5/II6/III7), Ni(I)8 or Mn(III).9
The first two mononuclear Co(II) compounds exhibiting slow-relaxation of magnetization were reported by Jurca et al. in 2011.10 Both compounds were pentacoordinate possessing a distorted square-pyramidal geometry with bis(imino)pyridine and thiocyanido ligands ([Co(bip1)(NCS)2] (I), [Co(bip2)(NCS)2] (II), where bip1 = [2,6-bis{1-[(2,6-diisopropylphenyl)imino]-ethyl}pyridine], bip2 = [2,6-bis{1-[(2,6-diisopropylphenyl)imino]benzyl}pyridine]). This discovery was followed by further reports on SMM behaviour in tetra-,11 penta-,12 hexa-13 or heptacoordinate14 Co(II) compounds, but in most of the cases, the slow relaxation of magnetisation was observed only in a non-zero static magnetic field. Only a few examples of slow-relaxation of the magnetisation in pentacoordinate Co(II) compounds have been reported,15 in all cases described as compounds consisting of a tridendate heterocyclic N-donor ligand and two halido or pseudohalido ligands: [Co(bpp)Cl2] (III),16 [Co(terpy)Cl2] (IV) and [Co(terpy)(NCS)2] (V)17 (terpy = terpyridine, bpp = 4-hept-1-ynyl-2,6-dipyrazol-1-ylpyridine). Remarkably, all the previously reported pentacoordinate Co(II) SMMs (I–V) are of the same structural type. They are composed of a tridentate N-donor aromatic ligand and two monodentate halido/pseudohalido ligands.
Herein, we report on the magnetic behaviour of the mononuclear compound [Co(phen)(DMSO)Cl2] (1), phen = 1,10-phenanthroline, DMSO = dimethyl sulfoxide, the crystal structure of which was reported previously.18 Interestingly, as it is apparent from the chemical formula of 1, this compound is of a completely different structural type than compounds I–V, possessing a {CoN2Cl2O} chromophore and a combination of bidentate and monodentate ligands. The static magnetic properties were studied by temperature- and field-dependent SQUID magnetometry measurements which were analysed using the spin Hamiltonian formalism and by HF-EPR. Experimental studies were supported by theoretical calculations. Dynamic magnetic properties were studied by measuring AC susceptibility in zero and non-zero static magnetic fields.
Results and discussion
Synthesis and crystal structure
[Co(phen)(DMSO)Cl2] compound (1) was prepared by recrystallization of [Co(phen)2(μ-Cl)2Co(Cl)2] from DMSO and by slow diffusion of diethyl ether into it.18It has to be stressed that all the synthetic operations must be carried out under very dry conditions for the successful preparation of 1.18
The crystal structure was well described (CCDC number: 193345)18 but some aspects will be emphasized for the purposes of this article. The geometry of a coordination polyhedron is in between a square pyramidal and a trigonal bipyramidal as can be deduced from the Addison parameter τ (τ = 0.54, τ = 0 for ideally square pyramidal and 1 for trigonal bipyramidal geometry).19 The Co–Cl bonds (2.3100(8) and 2.3556(8) Å) are the longest metal–ligand bond lengths in the {CoCl2N2O} chromophore, while the Co–O bond is the shortest −2.052(2) Å. The Co–N bonds are dissimilar in lengths and they adopt the values of 2.119(2) and 2.169(2) Å (Fig. 1a). From the above mentioned structural parameters it is apparent that the coordination polyhedron in 1 is much distorted in view of the significant differences found in the metal–ligand bond lengths.
The crystal structure of 1 is rich in weak non-covalent intermolecular contacts such as C–H⋯Cl, C–H⋯O, or π–π stacking interactions. There are two repeating dimeric [Co(phen)(DMSO)Cl2]2 synthons, which can be distinguished in the crystal structure of 1. One dimer is linked by weak C–H⋯O hydrogen bonds (Fig. 1b, d = 3.212(4) Å, further abbreviated as syn1), while the second one is held by C–H⋯Cl non-covalent contacts (Fig. 1c, d = 3.710(2) Å, syn2). These two structural fragments are assembled into a ladder-like substructure by stacking the phen rings (the shortest C⋯C distances are 3.515(4) Å in syn1, 3.484(5) Å in syn2; in syn1 there is also a short C⋯N distance equal to 3.453(4) Å). The detailed discussion of intermolecular interactions in 1 is necessary, because the non-covalent contacts such as hydrogen bonds20 or stacking of aromatic rings21 are capable of mediating magnetic exchange interactions which might have a strong influence on dynamic magnetic properties of SMMs.16
Static magnetic properties and theoretical calculations
The static magnetic properties (Fig. 2) were measured in two different ways, i.e. (i) as temperature dependence (1.9–300 K) of mean susceptibility and (ii) field dependence of magnetization (0–7 T). The effective magnetic moment (μeff) adopts a value close to 4.84 μB at room temperature which is significantly higher than the spin-only value for high-spin Co(II) with g = 2.00 and S = 3/2 (μeff = 3.87 μB). This indicates a significant contribution of spin–orbit coupling to the ground state magnetic moment. Below 50 K μeff continuously decreases to approximately 3.54 μB, which is a sign of zero-field splitting (ZFS) of the CoII atom and/or weak antiferromagnetic interactions between the individual molecules presented in the solid state. | ||
| Fig. 2 Temperature dependence of the effective magnetic moment and molar magnetization measured at B = 0.1 T in the inset, and isothermal reduced magnetizations measured at T = 2 and 5 K. Empty circles: experimental data. Red full lines: calculated data using eqn (1), with g = 2.44(1), D = −17(1) cm−1, E/D = 0.24(5) cm−1, zj = −0.16(2) cm−1 and χTIP = 7(2) × 10−9 m3 mol−1. Blue full lines: calculated data using the CASSCF/NEVPT2 energy levels in eqn (7). | ||
Due to the possible mediation of antiferromagnetic interactions via non-covalent contacts (as mentioned above) we decided to investigate the effectivity of magnetic exchange coupling within the supramolecular dimers syn1 and syn2 (Fig. 3). This was done by broken-symmetry DFT calculations using ORCA software in order to decide which model, i.e. for isolated mononuclear, dimeric or polymeric compounds, would describe the magnetic properties in the best way (Fig. 1b–d). Therefore, the well-established B3LYP functional and scalar relativistic contracted version of def2-TZVP(-f) basis functions together with the zero order regular approximation (ZORA) was utilized to calculate the energy difference Δ between the high spin (HS) and broken-symmetry (BS) spin states:
| Δ = EBS − EHS | (1) |
 | (2) |
The calculations resulted in Δsyn1 = −0.279 cm−1 and Δsyn2 = +0.018 cm−1. Afterwards, the isotropic exchange J-values were calculated by Ruiz's approach22,23 as
| J = 2Δ/[(S1 + S2)(S1 + S2 + 1)] | (3) |
Therefore, the following spin Hamiltonian involving the single ion axial (D) and rhombic (E) ZFS parameters, Zeeman term and molecular field correction zj was postulated24
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ).
θ).
The molar magnetization in the a-direction of the magnetic field, Ma, was numerically calculated as:
 | (5) |
 | (6) |
Both temperature and field dependent magnetic data were fitted simultaneously in order to obtain a reliable set of parameters. As a result, negative D = −17(1) cm−1 with a relatively large rhombicity (E/D = 0.24(5)) was obtained (Fig. 2).25
In order to support the results of the magnetic data fitting we also performed an ab initio calculation based on state-averaged complete-active-space self-consistent field (SA-CASSCF, the active space on metal-based d-orbitals was CAS(7,5)) wave functions complemented by N-electron valence second-order perturbation theory (NEVPT2) using ORCA software (for more detailed description of the calculations see the Experimental section).
From the list of the excited states contributing to the D-tensor (Tables S1 and S2, ESI†) it is apparent that the first excited state is well separated from the ground state by more than 1864 cm−1 and thus the spin Hamiltonian formalism is applicable.
The calculated values of the ZFS parameters were as follows: D = −17.7 cm−1 and E/D = 0.313 leading to the separation between the two lowest Kramers doublets equal to 40.1 cm−1. These values of the single-ion ZFS parameters are in very good agreement with those determined from fitting of the experimental magnetic data (D = −17(1) cm−1, E/D = 0.24(5) cm−1). A similar quality of agreement between the theory and the experiment was also achieved for other tetracoordinate Co(II)26 and hexacoordinate Co(II)27 field-induced single-ion magnets, hence showing that this theoretical approach is suitable for studying Co(II) complexes in relation to their ZFS tensor and magnetic properties. Also, the g-tensor values were found as: g1 = 2.176, g2 = 2.321, g3 = 2.461 resulting in giso = 2.320. The main axes of the g-tensor and the D-tensor are depicted in Fig. 3a. It can be concluded that there is a small non-coincidence between these two tensors; despite this fact we can approximate their mutual relationship as gx = g2, gy = g1, and gz = g3. Furthermore, the two Kramers doublets were also analysed using the effective spin Hamiltonian with Seff = 1/2, and the outcome of this procedure is visualized in Fig. 3b, where geff-tensor's axis is shown. The lowest doublet has g1a = 1.546, g1b = 2.187, g1c = 6.774 and the second doublet has g2a = 1.898, g2b = 2.435, g2c = 5.895. Thus, both doublets have a large axial type of magnetic anisotropy, but have different orientations of easy axes.
In the next step, we utilized the respective ab initio CASSCF/NEVPT2 spin–orbit coupling, orbital and spin angular momentum matrices:
| H = HSOC + μB(L + geS)·B | (7) |
EPR spectroscopy
We have also recorded high-frequency electron paramagnetic resonance spectra at different frequencies between 175 and 1000 GHz (Fig. 4 and S3†) with the aim of obtaining a better estimate of the g tensor and zero-field splitting values. At the lowest frequency of 175 GHz, three resonance lines are observed at 2.09, 4.80 and 7.27 T. With increasing frequencies, these resonance lines move to higher fields. Extrapolating the resonance line positions to zero field gives resonance frequencies close to zero. We therefore attribute the observed three resonance lines to transitions within the ground doublet along the three principal directions. Even at frequencies of 1000 GHz, we did not see any resonance line that can be attributed to interdoublet transitions. As a consequence, we cannot equivocally determine the sign and magnitude of D, which we have therefore fixed to the CASSCF value of D = −17.7 cm–1. We obtained the best fit for E/D = 0.33, gx = 2.6, gy = 2.4, gz = 2.3. These values differ from those obtained from the CASSCF calculation, but it must be remarked that E/D and the g tensor values are strongly correlated in the EPR fit. | ||
| Fig. 4 HFEPR spectra recorded on pressed powder pellets of 1 at 5 K and different frequencies (in GHz) as indicated. | ||
Dynamic magnetic properties
The analysis of the static magnetic data of 1 showed that there is a uniaxial type of anisotropy, and therefore dynamic AC susceptibility data were also acquired. In the zero static magnetic field, there was no out-of-phase susceptibility signal, but the field dependent measurement performed at T = 1.9 K confirmed a slow relaxation of magnetization (Fig. S1, ESI†).Therefore, AC susceptibility measurements were performed in the non-zero static field, Bdc = 0.1 T at various temperatures, showing a typical pattern for slow-relaxation of magnetization typically observed for SMM species (Fig. 5). The outcome of the analysis of the AC susceptibility data for each temperature using the one-component Debye's model:
| χ(ω) = χS + (χT − χS)/[1 + (iωτ)1−α] | (8) |
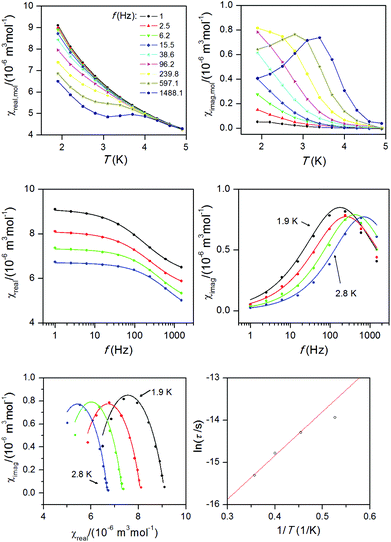 | ||
| Fig. 5 Top: In-phase χreal and out-of-phase χimag molar susceptibilities for 1 at the applied external field Bdc = 0.1 T. Lines serve as guides for the eyes. Middle: Frequency dependence of the in-phase χreal and out-of-phase χimag molar susceptibilities for 1 at Bdc = 0.1 T. Full points – experimental data, full lines – fitted data using eqn (8). Bottom: The Argand (Cole–Cole) plot with full lines showing the fitted data using eqn (8) (left) and fit of resulting relaxation times according to the Arrhenius equation (right). | ||
Then, the Argand (Cole–Cole) plot was constructed (Fig. 5) and the Arrhenius equation was applied to analyse the temperature dependence of relaxation times, which resulted in τ0 = 5.69 × 10−9 s and the spin reversal barrier U = 10.4 K (7.2 cm−1) (Fig. 5), where only data having maxima in the Argand diagram were used. The effective value of U is much lower than the theoretical prediction based on the parameters derived from magnetic analysis, Umag = 2(D2 + 3E2)1/2 = 52.5 K, or from the CASSCF/NEVPT2 calculations, Uab initio = 57.7 K. However, this kind of discrepancy is observed also in other pentacoordinate Co(II) SIMs I–V as listed in Table 1, and generally speaking, also for other 3d-metal SIMs reported so far.15,28 Such lowering of spin reversal barrier is usually ascribed to the rhombic term, which causes quantum-tunnelling of magnetization and indeed we found a large rhombicity in compound 1 (E/D = 0.24(5)). However, we must stress here that U reflects a thermally activated Orbach mechanism, and therefore limiting the analysis of AC susceptibility data only to the data having maxima in the Argand diagram, which means that data measured between T = 1.9 and 2.8 K, could be also the source of reported deviation in U, because non-zero out-of-phase AC susceptibility is already observed below 5 K. Therefore, AC susceptibility data were also analysed with the simplified model29 based on eqn (9):
| ln(χ′′/χ′) = ln(2πfτ0) + U/kT | (9) |
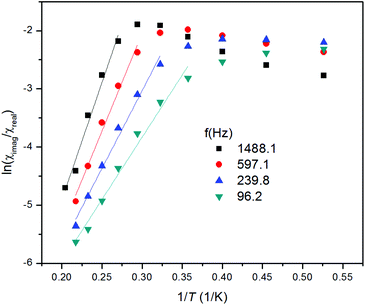 | ||
| Fig. 6 Analysis of in-phase χreal and out-of-phase χimag molar susceptibilities for 1 measured at the applied external field Bdc = 0.1 T according to eqn (9). Full points – experimental data, full lines – calculated data. | ||
| Experimental data | Ab initio calculationsa,b | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Compound {chromophore} | τ | g iso | D/cm−1 | E/D | U eff/cm−1 | t 0/s | D/cm−1 | E/D | g 1, g2, g3, giso | g eff,1, geff,2, geff,3 |
| a D, E and g1, g2, g3, giso correspond to the spin Hamiltonian with S = 3/2 (eqn (4)). It has to be noted that the first excited states are relatively close to the ground state – see Table S1 (ESI). b g eff,1, geff,2, geff,3 correspond to the Kramers doublet ground state with effective spin Seff = 1/2. c The parameters calculated using eqn (9). | ||||||||||
| 1 {CoN2Cl2O} | 0.54 | 2.44(1) | −17(1) | 0.24(5) | 7.2 | 5.69 × 10−9 | −17.7 | 0.31 | 2.176, 2.321, 2.461, 2.320 | 1.546, 2.178, 6.774 |
| 14.9–28.0c | 0.248–58.3 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|||||||||
| I {CoN5}10 | 0.27 | 2.07 | −28.1 | — | 11.1 | 3.6 × 10−6 | −45.1 | 0.18 | 2.078, 2.254, 2.713, 2.348 | 0.997, 1.284, 7.864 |
| II {CoN5}10 | 0.03 | 2.13 | −28.2 | — | 16.7 | 5.1 × 10−7 | −113.5 | 0.13 | 1.836, 2.104, 3.211, 2.383 | 0.718, 0.875, 9.194 |
| III {CoN3Cl2}16 | 0.01 | 2.85 | +151 | 0.08 | 6.4 | 3.1 × 10−9 | −120.2 | 0.11 | 1.718, 1.927, 3.304, 2.316 | 0.687, 0.771, 9.328 |
| IV {CoN3Cl2}16 | 0.05 | — | — | — | 19.5 | 1.1 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
−106.6 | 0.13 | 1.819, 2.072, 3.234, 2.375 | 0.859, 0.994, 9.163 |
| V {CoN5}17 | 0.43 | — | — | — | 11.8 | 5.9 × 10−6 | +40.3 | 0.23 | 1.990, 2.274, 2.478, 2.247 | 1.718, 2.952, 6.345 |
To conclude, the relaxation processes in Co(II) SIMs are generally very complex covering apart from the Orbach process, also Raman and direct relaxation processes, influenced also by electronuclear spin entanglement, which makes the analysis of these mechanisms non-trivial.30
Experimental
Synthesis
All reagents and solvents were purchased from commercial sources (Sigma Aldrich) and used as received. The synthesis of [Co(phen)2(μ-Cl)2CoCl2] was performed according to literature methods.18Synthesis of [Co(phen)(DMSO)Cl2]
0.5 g of [Co(phen)2(μ-Cl)2CoCl2] was dissolved in a minimal volume of dry DMSO and then the solution was filtered through filter paper. Then the dark blue-green solution was transferred to a 15 ml flask, which was sealed by a perforated plastic cap and it was left in a 500 ml closed flask with 50 ml of diethyl ether and with a beaker full of potassium hydroxide (drying agent). After one week, the blue crystalline solid was formed, which was filtered off, washed with diethyl ether and dried in a desiccator under a stream of nitrogen. The phase purity of the sample was verified by powder X-ray diffraction analysis (ESI, Fig. S2†). Elemental analysis: C14H14Cl2Co1N2O1S1, Mr = 388.2, found: C, 43.4; H, 3.6; N, 7.0; requires: C, 43.3; H, 3.6; N, 7.2.Physical methods
Elemental analysis (C, H, N) was performed on a Flash 2000 CHNO-S Analyzer (Thermo Scientific). Temperature dependence of the magnetization at B = 0.1 T from 1.9 to 300 K and the isothermal magnetizations at T = 2.0 and 5.0 K up to B = 5 T were measured using a MPMS XL-7 SQUID magnetometer (Quantum Design). The experimental data were corrected for diamagnetism. Measurements of AC susceptibility were carried out in a 3.8 Oe ac field oscillating at various frequencies from 1 to 1500 Hz and with various dc fields. The X-ray powder diffraction patterns of all solid samples were recorded on a MiniFlex600 (Rigaku) instrument equipped with the Bragg–Brentano geometry, and with iron-filtered Cu Kα 1,2 radiation.High-frequency EPR spectra were recorded on a home-built spectrometer. Its radiation source is a 0–20 GHz signal generator (Anritsu or VDI) in combination with an amplifier–multiplier chain (VDI) to obtain the required frequencies (80–1100 GHz). It features a quasi-optical bridge (Thomas Keating) and induction mode detection. The detector is a QMC Instruments magnetically tuned InSb hot electron bolometer. The sample is located in an Oxford Instruments 15/17 T cryomagnet equipped with a variable temperature insert (1.5–300 K). The spectrometer control programme was written in LabView.
Theoretical methods
All theoretical calculations were performed with the ORCA 3.0 computational package.31 All the calculations employed the scalar relativistic contracted version of def2-TZVP(-f) basis functions32 together with the zero order regular approximation (ZORA)33 and also utilized the chain-of-sphere (RIJCOSX) approximation to exact exchange.34 DFT calculations were based on the B3LYP functional.35 The ZFS and g tensors were calculated by using self-consistent field (SA-CASSCF) wave functions36 complemented by N-electron valence second order perturbation theory (NEVPT2).37 The active space of the CASSCF calculation was set to five d-orbitals of Co(II) (CAS(7,5)). The ZFS parameters, based on dominant spin–orbit coupling contributions from excited states, were calculated through quasi-degenerate perturbation theory (QDPT),38 in which approximations to the Breit–Pauli form of the spin–orbit coupling operator (SOMF approximation)39 and the effective Hamiltonian theory40 were utilized.Conclusions
In this article, we reported results of thorough structural and magnetic analyses of [Co(phen)(DMSO)Cl2] (1). It has been revealed that this compound has large and negative magnetic anisotropy (D = −17(1) cm−1) and a very large rhombicity (E/D = 0.24(5)) as derived from spin Hamiltonian analysis of temperature and field dependent magnetic data. These results were supported by the HF-EPR measurements; however, in the frequency range of 150–1000 GHz any resonance arising from an interdoublet transition was not observed. Thus we were not able to determine sign and magnitude of the zero-field splitting parameters, but a very large rhombicity was confirmed (E/DEPR = 0.33). Ab initio calculations are in agreement with the experimentally derived zero-field splitting parameters: Dcalc = −17.1 cm−1, E/Dcalc = 0.31.Dynamic magnetic properties revealed that 1 behaves as a field-induced single molecule magnet with either energy of spin reversal barrier (Ueff = 10.4 K) and fast relaxation time (τ0 = 5.69 × 10−9 s) according to analysis of the Argand diagram and the one-component Debye model (eqn (8)), or with Ueff = 21.4–40.3 K and τ0 = 0.248–58.3 × 10−9 s according to the simplified model (eqn (9)). To conclude, compound 1 represents a first example of a pentacoordinate Co(II) single-ion magnet with the {CoCl2N2O} chromophore and it must be stressed that this compound differs structurally from all the previously reported pentacoordinate Co(II) single-molecule magnets.10,16,17 Thus, this report deals with the magnetic properties of a new type of pentacoordinate Co(II) single-molecule magnet.
Acknowledgements
We acknowledge financial support from the Grant Agency of the Czech Republic (GAČR 13-27355P), the National Programme of Sustainability I (LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic, and the Czech-German FP6-Mobility-9 project 7AMB15DE002 and DFG SPP1601.Notes and references
- R. Boča, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef.
- (a) A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873–5874 CrossRef CAS; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- (a) O. Waldmann, Inorg. Chem., 2007, 46, 10035–10037 CrossRef CAS PubMed; (b) F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229–238 RSC.
- (a) J. M. Zadrozny, D. J. Xiao, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123–13131 CrossRef CAS PubMed; (b) J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- (a) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC; (b) C. Mathonière, H.-J. Lin, D. Siretanu, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2013, 135, 19083–19086 CrossRef PubMed; (c) X. Feng, C. Mathonière, I.-R. Jeon, M. Rouzières, A. Ozarowski, M. L. Aubrey, M. I. Gonzalez, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2013, 135, 15880–15884 CrossRef CAS PubMed; (d) W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126 CrossRef CAS PubMed; (e) D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed; (f) D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem. – Eur. J., 2011, 17, 4700–4704 CrossRef CAS PubMed.
- S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13651–13661 CrossRef CAS PubMed.
- R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. López, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, J. Am. Chem. Soc., 2013, 135, 13640–13643 CrossRef CAS PubMed.
-
(a) R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300–8302 CrossRef CAS PubMed;
(b) G. A. Craig, J. J. Marbey, S. Hill, O. Roubeau, S. Parsons and M. Murrie, Inorg. Chem., 2014, 54, 13–15 CrossRef PubMed;
(c) J. Vallejo, A. Pascual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef CAS PubMed.
Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef CAS PubMed. - T. Jurca, A. Farghal, P.-H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814–15817 CrossRef CAS PubMed.
- See e.g.: (a) R. Boča, J. Miklovič and J. Titiš, Inorg. Chem., 2014, 53, 2367–2369 CrossRef PubMed; (b) D.-K. Cao, J.-Q. Feng, M. Ren, Y.-W. Gu, Y. Song and M. D. Ward, Chem. Commun., 2013, 49, 8863–8865 RSC; (c) J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Chem. Commun., 2012, 48, 3927–3929 RSC; (d) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734 CrossRef CAS PubMed; (e) M. Idešicová and R. Boča, Inorg. Chim. Acta, 2013, 408, 162–171 CrossRef; (f) M. Idešicová, Ľ. Dlháň, J. Moncoľ, J. Titiš and R. Boča, Polyhedron, 2012, 36, 79–84 CrossRef; (g) M. Idešicová, J. Titiš, J. Krzystek and R. Boča, Inorg. Chem., 2013, 52, 9409–9417 CrossRef PubMed.
- See e.g.: (a) N. Nedelko, A. Kornowicz, I. Justyniak, P. Aleshkevych, D. Prochowicz, P. Krupiński, O. Dorosh, A. Ślawska-Waniewska and J. Lewiński, Inorg. Chem., 2014, 53, 12870–12876 CrossRef CAS PubMed; (b) R. Ruamps, L. J. Batchelor, R. Guillot, G. Zakhia, A.-L. Barra, W. Wernsdorfer, N. Guihery and T. Mallah, Chem. Sci., 2014, 5, 3418–3424 RSC; (c) D. M. Pinero Cruz, D. N. Woodruff, I.-R. Jeon, I. Bhowmick, M. Secu, E. A. Hillard, P. Dechambenoit and R. Clerac, New J. Chem., 2014, 38, 3443–3448 RSC; (d) C. Rajnák, J. Titiš, I. Šalitroš, R. Boča, O. Fuhr and M. Ruben, Polyhedron, 2013, 65, 122–128 CrossRef.
- (a) V. Chandrasekhar, A. Dey, A. J. Mota and E. Colacio, Inorg. Chem., 2013, 52, 4554–4561 CrossRef CAS PubMed; (b) Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806 RSC; (c) J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704–15707 CrossRef CAS PubMed; (d) J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704–15707 CrossRef CAS PubMed.
- (a) X.-C. Huang, C. Zhou, D. Shao and X.-Y. Wang, Inorg. Chem., 2014, 53, 12671–12673 CrossRef CAS PubMed.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC.
- C. Rajnák, J. Titiš, O. Fuhr, M. Ruben and R. Boča, Inorg. Chem., 2014, 53, 8200–8202 CrossRef PubMed.
- F. Habib, O. R. Luca, M. K. Takase, R. H. Crabtree and M. Murugesu, Angew. Chem., Int. Ed., 2013, 52, 11290 CrossRef CAS PubMed.
- B. Brewer, N. Brooks, S. Abdul-Halim and A. Sykes, J. Chem. Crystallogr., 2003, 33, 651–662 CrossRef CAS.
- A. W. Addison, T. N. Rao, J. Reedijk, J. Vanrijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356 RSC.
- (a) E. Pardo, M. Verdaguer, P. Herson, H. Rousseliere, J. Cano, M. Julve, F. Lloret and R. Lescouezec, Inorg. Chem., 2011, 50, 6250 CrossRef CAS PubMed; (b) I. Nemec, R. Herchel, I. Šalitroš, Z. Trávníček, J. Moncoľ, H. Fuess, M. Ruben and W. Linert, CrystEngComm, 2012, 14, 7015 RSC; (c) I. Nemec, R. Herchel, T. Silha and Z. Trávníček, Dalton Trans., 2014, 43, 15602–15616 RSC; (d) D. Valigura, J. Moncol, M. Korabik, Z. Pučekova, T. Lis, J. Mrozinski and M. Melnik, Eur. J. Inorg. Chem., 2006, 3813 CrossRef CAS; (e) Z. Vasková, J. Moncoľ, M. Korábik, D. Valigura, J. Švorec, T. Lis, M. Valko and M. Melník, Polyhedron, 2010, 29, 154–163 CrossRef; (f) J. S. Costa, N. A. G. Bandeira, B. Le Guennic, V. Robert, P. Gamez, G. Chastanet, L. Ortiz-Frade and L. Gasque, Inorg. Chem., 2011, 50, 5696–5705 CrossRef CAS PubMed.
- Y.-H. Chi, J.-M. Shi, H.-N. Li, W. Wei, E. Cottrill, N. Pan, H. Chen, Y. Liang, L. Yu, Y.-Q. Zhang and C. Hou, Dalton Trans., 2013, 42, 15559–15569 RSC.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS.
- E. Ruiz, A. Rodriguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed.
- R. Boča, A Handbook of Magnetochemical Formulae, Elsevier, Amsterdam, 2012 Search PubMed.
- The standard deviations were calculated as σi = (Pii−1·S/(N − k))−1/2, where Pij = Σ(δμn/δai·δμn/δaj) and S = ∑(μn − μexpn)2 with n = 1 to N; ai and aj are fitted parameters, N is the number of experimental points (a sum of temperature and field dependent data), μn and μexpn are the calculated and experimental effective magnetic moments for a given temperature and magnetic field. The σi was then multiplied by Student's t95% to provide confidence limits with 95% probabilities listed in the text.
- I. Nemec, R. Herchel and Z. Trávníček, Sci. Rep., 2015, 5, 10761 CrossRef CAS PubMed.
- R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896–5898 CrossRef CAS PubMed.
- S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392 CrossRef.
- (a) J. Bartolomé, G. FIloti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter, 2009, 80, 014430 CrossRef; (b) R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300–8302 CrossRef CAS PubMed.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2015, 5, 4300 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theor. Comput., 2008, 4, 908–919 CrossRef CAS.
- (a) E. Vanlenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS; (b) C. van Wullen, J. Chem. Phys., 1998, 109, 392–399 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS; (b) C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS; (d) C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043–4049 CrossRef CAS PubMed; (e) C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theor. Comput., 2009, 5, 2977–2984 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of CASSCF calculations, in-phase χreal and out-of-phase χimag molar susceptibilities for 1 at zero static magnetic field and in non-zero static field, and comparison between theoretical and experimental X-ray powder diffraction patterns for 1. See DOI: 10.1039/c5dt02162f |
| This journal is © The Royal Society of Chemistry 2015 |


