Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic and magnetocaloric properties of an unusual family of carbonate-panelled [LnIII6ZnII2] cages†
Waqas
Sethi
ab,
Sergio
Sanz
b,
Kasper S.
Pedersen
a,
Mikkel A.
Sørensen
a,
Gary S.
Nichol
b,
Giulia
Lorusso
c,
Marco
Evangelisti
*c,
Euan K.
Brechin
*a and
Stergios
Piligkos
*a
aDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, 2100, Denmark. E-mail: piligkos@kiku.dk
bEaStCHEM School of Chemistry, The University of Edinburgh, David Brewster Road, Edinburgh, Scotland EH9 3FJ, UK. E-mail: ebrechin@staffmail.ed.ac.uk
cInstituto de Ciencia de Materiales de Aragón and Departamento de Física de la Materia Condensada, CSIC-Universidad de Zaragoza, 50009 Zaragoza, Spain. E-mail: evange@unizar.es
First published on 8th May 2015
Abstract
The reaction of the pro-ligand H4L, which combines the complementary phenolic oxime and diethanolamine moieties within the same organic framework, with Zn(NO3)2·6H2O and Ln(NO3)3·6H2O in a basic methanolic solution generates a family of isostructural heterometallic coordination compounds of general formula [Ln6Zn2(CO3)5(OH)(H2L)4(H3L)2(H4L)]NO3·xMeOH [Ln = Gd, x = 30 (1), Ln = Dy, x = 32 (2), Ln = Sm, x = 31 (3), Ln = Eu, x = 29 (4), Ln = Tb, x = 30 (5)]. The octametallic skeleton of the cage describes a heavily distorted [GdIII6] octahedron capped on two faces by ZnII ions. The metal core is stabilised by a series of μ3- and μ4-CO32− ions, originating from the serendipitous fixation of atmospheric CO2. The magnetic properties of all family members were examined via SQUID magnetometry, with the χMT product and VTVB data of the Gd analogue (1) being independently fitted by numerical diagonalisation to afford the same best-fit parameter JGd–Gd = −0.004 cm−1. The MCE of complex 1 was elucidated from specific heat data, with the magnetic entropy change reaching a value of 22.6 J kg−1 K−1 at T = 1.7 K, close to the maximum entropy value per mole expected from six GdIII spins (SGd = 7/2), 23.7 J kg−1 K−1.
Introduction
The large value of their total angular momentum, their often strong magnetic anisotropy and the inherently weak magnetic exchange mediated via their contracted f-orbitals engender Ln-based molecular cages with some fascinating and potentially useful low temperature physics.1–5 In academia these have been much exploited for the construction of Single-Molecule Magnets (SMMs)6 and Molecular Coolers.7 The prospect of employing molecular cages in low temperature cooling applications is based upon the compounds magneto-caloric effect (MCE), as derived from the change in magnetic entropy upon application of a magnetic field.8 The design of such molecular materials therefore requires the control and optimisation of quantum properties at the molecular level (spin ground state, magnetic anisotropy, the presence of low-lying excited spin states), which in turn requires the synthetic chemist to follow a particular recipe that includes high spin, anisotropic metal ions and lightweight organic bridging ligands.9When a magnetic field is applied to a polynuclear molecular magnetic material in which the magnetic exchange interaction between constitutive metal centres and the local magnetic anisotropies are small, the magnetic moments of the constitutive paramagnetic centres become polarised by the magnetic field. When this magnetisation process is performed at constant temperature, the total magnetic entropy of the material is reduced. In a subsequent adiabatic demagnetisation process, the temperature of the material decreases, thereby cooling the material.10 This is a particularly attractive, and potentially technologically important phenomenon, since recent studies have shown that the MCE of some molecular clusters can be much larger than that found in the best intermetallic and lanthanide alloys, and magnetic nanoparticles employed commercially.11,12 The obvious metal ion of choice is GdIII since it possesses an isotropic S = 7/2, and its clusters will exhibit weak magnetic exchange courtesy of the contracted f-orbitals, resulting in the presence of field-accessible, low-lying excited states. Indeed the vast majority of clusters reported recently to display an enhanced MCE have contained multiple GdIII centres.13–18 We continue this trend by reporting the syntheses, structures, magnetic and magnetocaloric properties of a rather unusual set of complexes of general formula [Ln6Zn2(CO3)5(OH)(H2L)4(H3L)2(H4L)]NO3·xMeOH [Ln = Gd, x = 30 (1), Ln = Dy, x = 32 (2), Ln = Sm, x = 31 (3), Ln = Eu, x = 29 (4), Ln = Tb, x = 30 (5)] built with the ligand (Z)-1-(3-((bis(2-hydroxyethyl)aminomethyl)-2-hydroxy-5-methylphenyl)ethan-1-one oxime), [H4L], shown in Scheme 1. We have previously shown that this ligand is highly effective in forming transition metal cages with aesthetically pleasing structures and fascinating magnetic properties, and we now extend its coordination chemistry to the 4f elements.19
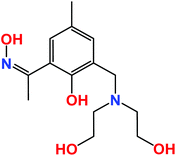 | ||
| Scheme 1 The structure of the ligand H4L which contains both phenolic oxime and diethanolamine moieties. | ||
Experimental
Materials and physical measurements
All manipulations were performed under aerobic conditions, using materials as received (reagent grade). (Z)-1-(3-((Bis(2-hydroxyethyl)aminomethyl)-2-hydroxy-5-methylphenyl)ethan-1-one oxime) [H4L] was synthesised as described in the literature.19 Magnetisation data were acquired on a MPMS-XL SQUID magnetometer equipped with a 5 T dc magnet. Freshly isolated crystalline material was covered immediately with hexadecane (MP = 18 °C) in order to suppress loss of co-crystallized solvent. Dc susceptibility data were obtained with Hdc = 1000 Oe in the temperature range 1.8–280 K and magnetisation data at Hdc ≤ 50 kOe at selected low temperatures. All data were corrected for diamagnetic contributions from the sample, hexadecane and the capsule by means of Pascals constants. Specific heat measurements were carried out at temperatures down to 0.3 K by using a Quantum Design 9T-PPMS, equipped with a 3He cryostat. The experiments were performed on thin pressed pellets (ca. 1 mg) of a polycrystalline sample, thermalised by ca. 0.2 mg of Apiezon N grease, whose contribution was subtracted using a phenomenological expression.Syntheses
General synthetic procedure for complexes 1–3: Ln(NO3)3·xH2O (0.25 mmol), Zn(NO3)2·6H2O (75 mg, 0.25 mmol), H4L (140 mg, 0.5 mmol), tBuONa (100 mg, 1 mmol) and Et3N (300 μL, 2.15 mmol) were stirred in 25 ml MeOH for 2 hours. The solution was then filtered and allowed to stand. X-ray quality crystals formed via slow evaporation of the mother liquor over a period of 5 days in ∼30–40% yield. Complex 4 was made in the same manner, but using 0.5 mmol (100 mg) tBuONa, whilst no tBuONa was added to the reaction mixture to make 5. Elemental analyses, calculated (found): 1: C 36.18 (36.24), H 4.27 (4.61), N 6.14 (6.19). 2: C 35.85 (34.97), H 4.24 (4.52), N 6.09 (5.81). 3: C 36.62 (35.40), H 4.33 (4.28), N 6.22 (5.92). 4: C 36.52 (35.36), H 4.31 (4.38), N 6.20 (5.73). 5: C 36.07 (34.91), H 4.26 (4.42), N 6.13 (5.95).X-ray crystallography
Diffraction data were collected on a Bruker Smart Apex CCD diffractometer equipped with an Oxford Cryosystems LT device, using Mo radiation. Data collection parameters and structure solution and refinement details are listed in Table S1.† Full details can be found in the CIF files provided in the ESI† and CCDC 1055091–1055095.Results and discussion
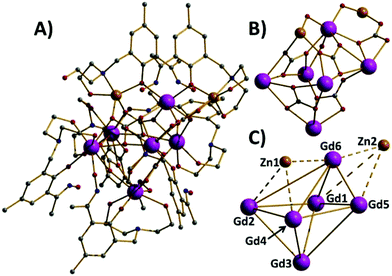
Compounds 1–5 are isostructural, and so for the sake of brevity we limit discussion to complex 1, [GdIII6ZnII2(CO3)5(OH) (H2L)4(H3L)2(H4L)]NO3·30MeOH (Fig. 1). The metallic skeleton of the cage describes a highly distorted [GdIII6] octahedron with the two ZnII ions each capping a triangular face. The core of the molecule is stabilised by the presence of five CO32− ions, originating from the serendipitous fixation of atmospheric CO2. These exhibit several different bonding modes [μ3-Gd3, μ3-Gd2Zn, μ3-Gd4, μ4-Gd4, μ4-Gd2Zn2] as shown in Fig. 1B. There is a single −OH ion which μ-bridges between Gd4 and Gd6 (Gd–O–Gd, 112°) and four H2L2−, two H3L− and one H4L ligands that adorn the outer periphery of the molecule. These ligands exhibit four different coordination modes as shown in Fig. 2: the majority bond in a μ-fashion along the edges of the Gd octahedron, or between a Gd vertex and a Zn cap. One ligand (H4L) chelates Gd5 through its phenolic and alkoxide O-atoms, with its oximic O- and N-atoms remaining non-coordinating, and H-bonding to the alkoxide O-atom on a neighbouring ligand (O⋯O, ∼2.6 Å). Indeed all of the organic ligands are involved in extensive intramolecular H-bonding interactions with their neighbouring ligands and to the MeOH molecules of crystallisation (Fig. S2 and 3†). All of the Gd ions are nine coordinate {GdO8N} and in capped square antiprismatic geometries, with the exception of Gd6 which is eight coordinate {GdO6N2} and square antiprismatic; the latter being the only Ln ion that is not chelated by the diethanolamine moieties. The Zn ions are both five coordinate {ZnO4N} and in distorted trigonal bipyramidal geometries.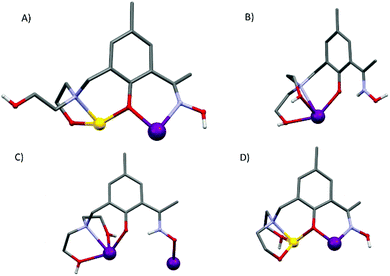 | ||
| Fig. 2 The different bonding modes of the H2L2−, H3L− and H4L ligands highlighting the diverse levels of protonation. | ||
There are several close intermolecular contacts. The diethanolamine O-atoms coordinated to Zn2 are H-bonding to the equivalent group on their nearest neighbour (O⋯O, 2.46 Å; Zn⋯Zn, 4.14 Å), and at the opposite end of the molecule the Ph rings of the organic ligands are involved in π⋯π stacking interactions (C⋯C, 3.58 Å). The result is the formation of a serpentine-like H-bonded chain of cationic cages (Fig. S3†). Closest contacts between these chains are through the Me-groups on the Ph rings of the organic ligand and between the same moiety and the –CH2 arms of the diethanolamine unit (Me⋯CH3/CH2, ∼4 Å). This produces 2D sheets of cations of 1 forming an overall layered structure in the crystal (Fig. S3†). The presence of the carbonate ligands is intriguing, and one that is becoming ever more prevalent with the increasing number of Ln-based cages being reported. Of the ∼130 entries in the CSD of metal cluster compounds containing carbonate anions approximately ∼25% are 4f complexes and ∼5% are heterometallic 3d–4f complexes.20 While the majority have been formed serendipitously, this observation has led some researchers to deliberately employ Na2CO3, NaHCO3 and CO2 as reaction ingredients.21 The CSD search also highlights the extraordinary coordinative flexibility of the CO32− ion demonstrating bridging modes ranging from bidentate to nonadentate – with the majority (65%) being tridentate and forming M3 triangles, a topology of inherent interest to the magnetochemist.22
Magnetic properties
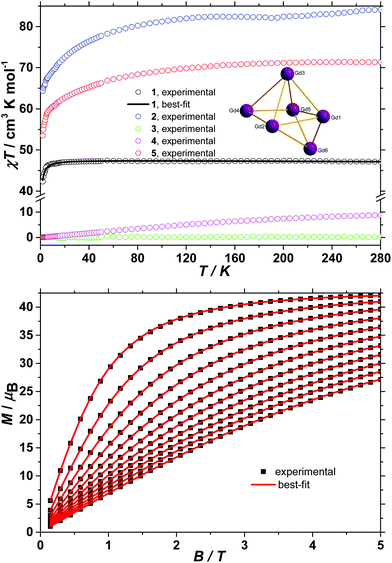
The d.c. molar magnetic susceptibility, χM, of polycrystalline samples of complexes 1–5 were measured in an applied magnetic field, B, of 0.1 T, over the 2–280 K temperature, T, range. The experimental results are shown in Fig. 3 in the form of χMT products, where χ = M/B, and M is the magnetisation of the sample. At room temperature, the χMT products of 1–5 have values of 47.2, 84.1, 0.3, 8.9 and 71.3 cm3 K mol−1, respectively. These are in good agreement with the sum of Curie constants for a [GdIII6] unit (47.3 cm3 K mol−1, gGd = 2.0) for 1, a [DyIII6] unit (85.0 cm3 K mol−1, gDy = 4/3) for 2, a [SmIII6] unit (0.5 cm3 K mol−1, gSm = 2/7) for 3, and a [TbIII6] unit (70.9 cm3 K mol−1, gTb = 3/2) for 5. In the case of 4, although the 7F0 ground state of EuIII possesses no magnetic moment and thus the [EuIII6] unit should be diamagnetic at low temperatures, a finite magnetic moment is observed at room temperature, due to the low-lying 7F1 first excited state that is partly populated at room temperature. Upon cooling, the χMT product of 1 remains essentially constant down to approximately 20 K, wherefrom it begins to decrease upon further cooling to reach 42.3 cm3 K mol−1 at 2 K. Given that the anisotropy of GdIII is negligible, this behaviour is consistent with the presence of weak intramolecular antiferromagnetic exchange interactions. The χMT products of 2 and 5 decrease continuously upon cooling, reaching 64.3 and 53.5 cm3 K mol−1, respectively, at 2 K. This behaviour can be ascribed to the large magnetic anisotropy of DyIII and TbIII and potentially to the presence of weak intramolecular magnetic exchange interactions. The χMT product of 3 remains essentially constant in the investigated temperature range, at the low, but finite value of 0.3 cm3 K mol−1, a consequence of the low Landé g-factor of the ground 6H5/2 term, indicating a splitting between the ground and first excited Kramers doublets of the 6H5/2 term larger than the thermal energy at 280 K. Finally, the χMT product of 4 decreases continuously upon cooling and reaches virtually zero at 2 K, reflecting the thermal depopulation of the 7F1 first excited state upon cooling, likely indicating mixing of the 7F0 ground state with excited states possessing a magnetic moment. To better define the low-temperature magnetic properties of complexes 1–5, low temperature variable-temperature-and-variable-field (VTVB) magnetisation data were measured in the temperature and magnetic field ranges 2 to 12 K and 0 to 5 T for 1 and 2, to 8 K and 0 to 5 T for the remaining complexes. The VTVB magnetisation data of 1 are shown in Fig. 3. At the highest investigated field (5 T) and the lowest investigated temperature (2 K), the magnetisation of 1 is 42.1μB (μB is the Bohr magneton), thus 7.0μB per GdIII and in good agreement with the expected (7.0μB, for gGd = 2.0). This is consistent with the presence of very weak exchange interactions operating in 1. Furthermore, when the VTVB data of 1 are plotted against the reduced quantity μBB/kT (Fig. S4†), no nesting of the VTVB data is observed. This indicates that the energy spectrum of 1 does not present significant splitting with respect to the temperature of measurement at zero magnetic field.The VTVB magnetisation data of 2 to 5 are shown in Fig. S5–S8,† respectively. At the highest investigated field (5 T) and the lowest investigated temperature (2 K), the magnetisation of 2 and 5 is 32.0 and 29.4μB, respectively, thus 5.3 and 4.9μB per DyIII and TbIII, respectively. These values are significantly lower than the expected magnetic moment of isolated DyIII (10.0μB) and TbIII (9.0μB) centres, for which the mJ = −15/2 projection of the 6H15/2 ground term or the mJ = −6 projection of the 7F6 ground term, respectively, is the lowest energy state. Furthermore, the VTVB data of 2 (Fig. S5†) and 5 (Fig. S8†) present nesting when plotted against μBB/kT. These observations indicate that the energy spectra of 2 and 5 present significant splittings with respect to the temperature of measurement, at zero magnetic field. The VTVB magnetisation data of 3 (Fig. S6†) present no nesting when plotted against the reduced quantity μBB/kT and are also linear with magnetic field. This behaviour is consistent with the presence of a thermally isolated Kramers doublet as the ground state of the 6H5/2 ground term, in agreement with the analysis of the temperature dependence of the χMT product. Finally, the VTVB magnetisation data of 4 (Fig. S7†) responds in a linear fashion with magnetic field and constant temperature, and are temperature independent at a constant field. This behaviour indicates a field-induced mixing of the 7F0 ground state with excited states possessing a magnetic moment, consistent with the analysis of the temperature dependence of the χMT product.
The hexanuclear nature of complexes 2–5, combined with the low symmetry of the local coordination sphere of the LnIII centres and the ensuing large number (twenty-seven) of associated ligand field parameters per LnIII ion, precludes any quantitative interpretation of the magnetic properties of these complexes. However, in the case of 1, given that the orbital angular moment for GdIII is quenched, a quantitative analysis is possible through the use of a spin-Hamiltonian parameterisation. Thus, we employed the general form of the isotropic spin-Hamiltonian (1)
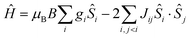 | (1) |
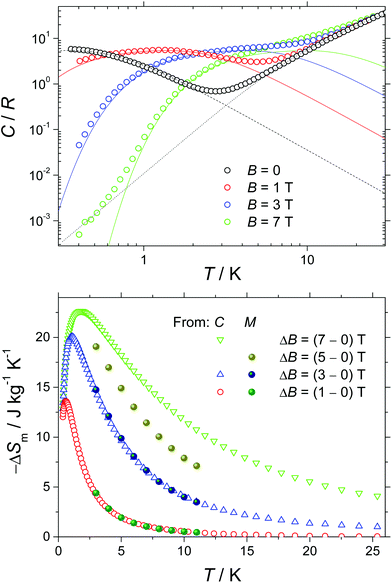
Next, we report the specific heat (C) data collected for a polycrystalline sample of 1 in the temperature range 0.3 to 30 K and in applied magnetic fields, B, of 0, 1, 3 and 7 T (Fig. 4). At the higher temperatures, the specific heat is dominated by a nonmagnetic contribution arising from thermal vibrations of the lattice, which can be modelled by the Debye–Einstein model (dotted line).8 The phonon specific heat simplifies to a C/R = aT3 dependence at the lowest temperatures, where R is the gas constant and a = 1.1 × 10−2 K−3. For B ≥ 1 T, we model the field-dependent specific heat as the sum of the Schottky curves arising from the field-split levels of GdIII independent spins (solid lines). Note the nice overall agreement agreement with the experimental data, suggesting that applied fields of B ≥ 1 T are nearly sufficient for fully decoupling the spin centres. The zero-applied-field specific heat can be described by the Schottky curve depicted in Fig. 4 as a dashed line. This curve is calculated by assuming that every spin centre is experiencing an effective field Beff = 0.25 T, as the result of the magnetic interactions involved. By making use of the specific heat data, we calculate the entropy (S) according to the expression S/R = ∫C/TdT, which we plot in Fig. S10† as a function of temperature and for the corresponding applied field values. The final step in the evaluation of the MCE of 1 consists of obtaining the magnetic entropy change –ΔSm(T), for selected applied field changes ΔB. The result is shown in Fig. 4. This calculation is straightforwardly obtained from the S(T) curves in Fig. S10† and also from the magnetisation data in Fig. 3 by employing the Maxwell relation, ΔSm = ∫∂M/∂TdB. As can be seen in Fig. 4, the nice agreement between the results obtained via both methods is validation of the approaches employed. For the largest applied field change (ΔB = 7 T), the magnetic entropy change, –ΔSm, reaches 22.6 J kg−1 K−1 at T = 1.7 K. Because of the very weak strength of the magnetic exchange interactions, this value of –ΔSm is close to the maximum entropy value per mole involved, corresponding to six GdIII spins (SGd = 7/2), calculated as 6R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2 SGd + 1) = 103.7 J mol−1 K−1, that is, 23.7 J kg−1 K−1. Thus, in 1, nearly the full magnetocaloric potential of GdIII is achieved.
ln(2 SGd + 1) = 103.7 J mol−1 K−1, that is, 23.7 J kg−1 K−1. Thus, in 1, nearly the full magnetocaloric potential of GdIII is achieved.
Conclusions
A highly unusual family of Ln6Zn2 cages whose structures are based on highly distorted bicapped octahedra can be constructed from the simple one-pot self-assembly reaction between the two metal salts and the ligand H4L in basic methanolic solutions. The ligand has been previously used in Mn coordination chemistry to produce dodecametallic wheels and truncated tetrahedra. Magnetic exchange between the GdIII ions in the octahedron is shown to be vanishingly small by independent fits of both susceptibility and magnetisation data. The MCE of complex 1 was elucidated from specific heat data, with the magnetic entropy change reaching a value of 22.6 J kg−1 K−1 at T = 1.7 K, close to the maximum entropy value per mole expected from six GdIII spins, 23.7 J kg−1 K−1.Acknowledgements
S.P. thanks the Danish Ministry of Science, Innovation and Higher Education for a Sapere Aude Fellowship (10-081659), M.E. acknowledges financial support from MINECO through grant MAT2012-38318-C03-01. EKB thanks the EPSRC.Notes and references
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed.
- R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328 CrossRef CAS PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092 RSC.
- Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley VCH, 2015 Search PubMed.
- E. K. Brechin and G. Aromí, Struct. Bonding, 2006, 1, 1 Search PubMed; C. J. Milios and R. E. P. Winpenny, Struct. Bonding, 2015, 164, 1 CrossRef.
- M. Evangelisti, in Molecular Magnets, NanoScience and Technology, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer, Berlin, 2014, pp. 365–387 Search PubMed.
- M. Evangelisti, F. Luis, L. J. de Jongh and M. Affronte, J. Mater. Chem., 2006, 16, 2534 RSC.
- M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672 RSC.
- J. W. Sharples and D. Collison, Polyhedron, 2013, 54, 91 CrossRef CAS PubMed.
- M. Evangelisti, A. Candini, A. Ghirri, M. Affronte, E. K. Brechin and E. J. L. McInnes, Appl. Phys. Lett., 2005, 87, 072504 CrossRef CAS PubMed; R. Shaw, R. H. Laye, L. F. Jones, D. M. Low, C. Talbot-Eeckelaers, Q. Wei, C. J. Milios, S. Teat, M. Helliwell, J. Raftery, M. Evangelisti, M. Affronte, D. Collison, E. K. Brechin and E. J. L. McInnes, Inorg. Chem., 2007, 46, 4968 CrossRef PubMed.
- M. Manoli, R. D. L. Johnstone, S. Parsons, M. Murrie, M. Affronte, M. Evangelisti and E. K. Brechin, Angew. Chem., Int. Ed., 2007, 46, 4456 CrossRef CAS PubMed; M. Manoli, A. Collins, S. Parsons, A. Candini, M. Evangelisti and E. K. Brechin, J. Am. Chem. Soc., 2008, 130, 11129 CrossRef PubMed.
- G. Karotsis, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 9928 CrossRef CAS PubMed; G. Karotsis, S. Kennedy, S. J. Teat, C. M. Beavers, D. A. Fowler, J. J. Morales, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, J. Am. Chem. Soc., 2010, 132, 12983 CrossRef PubMed.
- K. S. Pedersen, G. Lorusso, J. J. Morales, T. Weyhermüller, S. Piligkos, S. K. Singh, D. Larsen, M. Schau-Magnussen, G. Rajaraman, M. Evangelisti and J. Bendix, Angew. Chem., Int. Ed., 2014, 53, 2394 CrossRef CAS PubMed.
- M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606 CrossRef CAS PubMed.
- S. K. Langley, N. F. Chilton, B. Moubaraki, T. Hooper, E. K. Brechin, M. Evangelisti and K. S. Murray, Chem. Sci., 2011, 2, 1166 RSC.
- J. W. Sharples, D. Collison, E. J. L. McInnes, J. Schnack, E. Palacios and M. Evangelsiti, Nat. Commun., 2014, 5, 5321 CrossRef CAS PubMed; J. W. Sharples, Y.-Z. Zheng, F. Tuna, E. J. L. McInnes and D. Collison, Chem. Commun., 2011, 47, 7650 RSC.
- G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653 CrossRef CAS PubMed.
- S. Sanz, J. M. Frost, M. B. Pitak, S. J. Coles, S. Piligkos, P. J. Lusby and E. K. Brechin, Chem. Commun., 2014, 50, 3310 RSC; J. M. Frost, S. Sanz, T. Rajeshkumar, M. B. Pitak, S. J. Coles, G. Rajaraman, W. Wernsdorfer, J. Schnack, P. J. Lusby and E. K. Brechin, Dalton Trans., 2014, 43, 10690 RSC.
- See for example: J. B. Peng, Q. C. Zhang, X. J. Kong, Y. Z. Zheng, Y. P. Ren, L. S. Long, R. B. Huang, L. S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2012, 134, 3314 CrossRef CAS PubMed.
- See for example: Y. N. Guo, X. H. Chen, S. Xue and J. Tang, Inorg. Chem., 2012, 51, 4035 CrossRef CAS PubMed; T. N. Hooper, R. Inglis, M. A. Palacios, G. S. Nichol, M. B. Pitak, S. J. Coles, G. Lorusso, M. Evangelisti and E. K. Brechin, Chem. Commun., 2014, 50, 3498 RSC.
- J. Schnack, Dalton Trans., 2010, 39, 4677 RSC.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical recipes in C: The Art of Scientific Computing, Cambridge University Press, Cambridge, 2nd edn, 1992 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data in tabulated format, and additional structural and magnetic figures. CCDC 1055091–1055095. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt01240f |
| This journal is © The Royal Society of Chemistry 2015 |