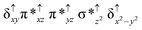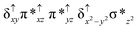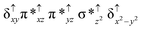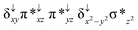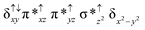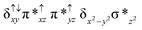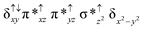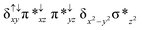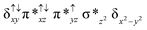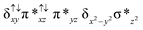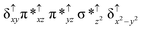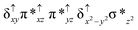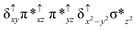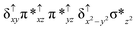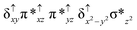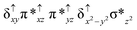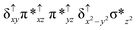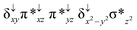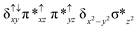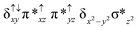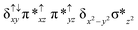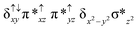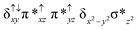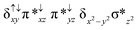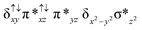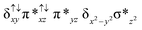Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oxidation of methane by an N-bridged high-valent diiron–oxo species: electronic structure implications on the reactivity†
Mursaleem
Ansari
,
Nidhi
Vyas
,
Azaj
Ansari
and
Gopalan
Rajaraman
*
Department of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai-400076, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 22nd April 2015
Abstract
High-valent iron–oxo species are key intermediates in C–H bond activation of several substrates including alkanes. The biomimic heme and non-heme mononuclear Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes are very popular in this area and have been thoroughly studied over the years. These species despite possessing aggressive catalytic ability, cannot easily activate inert C–H bonds such as those of methane. In this context dinuclear complexes have gained attention, particularly μ-nitrido dinuclear iron species [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− reported lately exhibits remarkable catalytic abilities towards substrates such as methane. Here using DFT methods, we have explored the electronic structure and complex spin-state energetics present in this species. To gain insights into the nature of bonding, we have computed the absorption, the EPR and the Mössbauer parameters and have probed the mechanism of methane oxidation by the dinuclear Fe(IV)
O complexes are very popular in this area and have been thoroughly studied over the years. These species despite possessing aggressive catalytic ability, cannot easily activate inert C–H bonds such as those of methane. In this context dinuclear complexes have gained attention, particularly μ-nitrido dinuclear iron species [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− reported lately exhibits remarkable catalytic abilities towards substrates such as methane. Here using DFT methods, we have explored the electronic structure and complex spin-state energetics present in this species. To gain insights into the nature of bonding, we have computed the absorption, the EPR and the Mössbauer parameters and have probed the mechanism of methane oxidation by the dinuclear Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species. Calculated results are in agreement with the experimental data and our calculations predict that in [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]−species, the two high-spin iron centres are antiferromagnetically coupled leading to a doublet ground state. Our calculations estimate an extremely low kinetic barrier of 26.6 kJ mol−1 (at doublet surface) for the C–H bond activation of methane by the dinuclear Fe(IV)
O species. Calculated results are in agreement with the experimental data and our calculations predict that in [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]−species, the two high-spin iron centres are antiferromagnetically coupled leading to a doublet ground state. Our calculations estimate an extremely low kinetic barrier of 26.6 kJ mol−1 (at doublet surface) for the C–H bond activation of methane by the dinuclear Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species. Besides these mechanistic studies on the methane activation reveal the unique electronic cooperativity present in this type of dinuclear complex and unravel the key question of why mononuclear analogues are unable to perform such reactions.
O species. Besides these mechanistic studies on the methane activation reveal the unique electronic cooperativity present in this type of dinuclear complex and unravel the key question of why mononuclear analogues are unable to perform such reactions.
Introduction
Selective oxidation of the thermodynamically strong and kinetically inert C–H bonds of hydrocarbon has been a subject of intensive study for the development of economical and sustainable global carbon management in the pursuit of alternating fuels, in particular methane to methanol conversion.1–3 A wide range of important chemical and biological reactions occur at high-valent metal centres embedded in the active sites of metalloenzymes such as methane monooxygenase (sMMO), cytochrome P450, and cytochrome c peroxidases.4–7 The function of these metalloenzymes and their significance has inspired numerous studies in the synthesis of model complexes mimicking the mechanism of these remarkable catalytic reactions.8–11 These efforts investigate ways to enhance efficiency and selectivity at will, as well as provide important tools for understanding these enzymatic processes.12–15 Over the past few decades a large body of the literature is available on non-heme Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes using polydentate chelating ligands such as TPA (tris(2-pyridylmethyl)amine), TMC (1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane), bispidines,16–21 salen, corrole and porphyrin.22–27 Both mono and dinuclear oxo complexes are explored in this area, however, the μ-oxo dimers are not completely stable under catalytic conditions and often decompose resulting in a decrease of selectivity of the oxidation process. The nitrogen bridged bimetallic systems possessing particularly the macrocyclic ligands are fascinating as they are very robust and are stable compared to the μ-oxo analogues.28 Ercolani and co-workers have reported29–35 several dinuclear complexes such as [(TPP)Fe]2N (TPP = tetraphenylporphyrin) and [(Pc)Fe]2N (Pc = phthalocyanine) and thoroughly characterized them using spectroscopic methods. Further progress has been made by Sorokin and co-workers in the preparation and characterization of a series of μ-nitrido bridged diiron phthalocyanines and their substituted complexes. With the aim to probe the electronic structure and nature of the species involved in the catalytic cycles36–41 these complexes are characterized thoroughly using EPR, absorption, Mössbauer, XANES and EXAFS techniques. Recently, X-ray absorption and emission spectroscopy, along with theoretical calculations on the Fe–X–Fe (X = C, N, O) core were investigated by Sorokin et al. revealing superiority of nitrogen bridged complexes over oxo analogues for oxidation reactions.42 Theoretical calculations on this set of complexes were recently performed to analyse the electronic structure and their catalytic potential.43
O complexes using polydentate chelating ligands such as TPA (tris(2-pyridylmethyl)amine), TMC (1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane), bispidines,16–21 salen, corrole and porphyrin.22–27 Both mono and dinuclear oxo complexes are explored in this area, however, the μ-oxo dimers are not completely stable under catalytic conditions and often decompose resulting in a decrease of selectivity of the oxidation process. The nitrogen bridged bimetallic systems possessing particularly the macrocyclic ligands are fascinating as they are very robust and are stable compared to the μ-oxo analogues.28 Ercolani and co-workers have reported29–35 several dinuclear complexes such as [(TPP)Fe]2N (TPP = tetraphenylporphyrin) and [(Pc)Fe]2N (Pc = phthalocyanine) and thoroughly characterized them using spectroscopic methods. Further progress has been made by Sorokin and co-workers in the preparation and characterization of a series of μ-nitrido bridged diiron phthalocyanines and their substituted complexes. With the aim to probe the electronic structure and nature of the species involved in the catalytic cycles36–41 these complexes are characterized thoroughly using EPR, absorption, Mössbauer, XANES and EXAFS techniques. Recently, X-ray absorption and emission spectroscopy, along with theoretical calculations on the Fe–X–Fe (X = C, N, O) core were investigated by Sorokin et al. revealing superiority of nitrogen bridged complexes over oxo analogues for oxidation reactions.42 Theoretical calculations on this set of complexes were recently performed to analyse the electronic structure and their catalytic potential.43
Notably Sorokin et al. have synthesised [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− dinuclear species and characterized them using EPR, UV/Vis and Mössbauer techniques. Examination of their catalytic ability reveals that these species can oxidize a variety of alkanes including the most difficult ones such as methane.41 Apart from the experimental studies, quantum chemical calculations were also extensively used in this area to gain insights into the electronic structure of the catalytically active species and to explore the mechanism of the catalytic reactions.44–46 In particular the potency of the nitride bridge over the O2− bridge in their catalytic abilities has been rationalized earlier using DFT calculations.43,47 Recently our group has reported comparative oxidative abilities of Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NTs with Fe(IV)
NTs with Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species and also explored the mechanism of ortho-hydroxylation of aromatic acids by an Fe(V)
O species and also explored the mechanism of ortho-hydroxylation of aromatic acids by an Fe(V)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxidant.48,49 Although there are several reports on the electronic structure and mechanistic studies of mononuclear high-valent iron–oxo species, studies on dinuclear iron–oxo species are rare due to the presence of several spin states arising from the exchange coupling between the two metal centres and it is often challenging to compute all these spin states in dinuclear species.43,47,50,51 In this regard, the report of [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− tetraphenylporphyrin cation radical species gained our attention as it possesses both nitrido and oxo groups which are reported to have diverse reactivity patterns.41 In this manuscript we aim to perform density functional theory calculations on an N-bridged non-heme dimer [(TPP)Fe(III)(μ-N)Fe(IV)(TPP)] in the formation of an oxo–diiron(IV) porphyrin cation radical complex and explore its reactivity for oxidation of methane. With this study, we aim to answer the following intriguing questions, (1) what is the nature of bonding in μ-nitrido dinuclear Fe species and what are the energetics of formation for the diiron(IV) analogues? (2) What is the nature of the ground state in these species and how does the calculation of ground state spectroscopic parameters (EPR, absorption and Mössbauer) compare with that of the experiments? (3) What are the mechanistic pathways by which the diiron(IV) activates the C–H bond of methane and what is the origin for its very high reactivity?
O oxidant.48,49 Although there are several reports on the electronic structure and mechanistic studies of mononuclear high-valent iron–oxo species, studies on dinuclear iron–oxo species are rare due to the presence of several spin states arising from the exchange coupling between the two metal centres and it is often challenging to compute all these spin states in dinuclear species.43,47,50,51 In this regard, the report of [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− tetraphenylporphyrin cation radical species gained our attention as it possesses both nitrido and oxo groups which are reported to have diverse reactivity patterns.41 In this manuscript we aim to perform density functional theory calculations on an N-bridged non-heme dimer [(TPP)Fe(III)(μ-N)Fe(IV)(TPP)] in the formation of an oxo–diiron(IV) porphyrin cation radical complex and explore its reactivity for oxidation of methane. With this study, we aim to answer the following intriguing questions, (1) what is the nature of bonding in μ-nitrido dinuclear Fe species and what are the energetics of formation for the diiron(IV) analogues? (2) What is the nature of the ground state in these species and how does the calculation of ground state spectroscopic parameters (EPR, absorption and Mössbauer) compare with that of the experiments? (3) What are the mechanistic pathways by which the diiron(IV) activates the C–H bond of methane and what is the origin for its very high reactivity?
Computational details
All calculations were performed using the Gaussian 09 suite of programs on a model complex of the TPP ligand where the bulky phenyl groups are modelled as the H-atom.52 The EPR, UV/Vis and Mössbauer spectral parameters of the species were computed using ORCA 2.9 software suite incorporating COSMO solvation effects.53 The geometries were optimized using the B3LYP-D2 functional, incorporating the dispersion correction proposed by Grimme et al.54 This functional has been employed by us and others earlier to predict the correct spin state energetic of several mononuclear metal–oxo/hydroxo/superoxo complexes.49,55 Two different basis sets were used: LanL2DZ, which encompasses a double-ζ quality basis set with the Los Alamos effective core potential for Fe and a 6-31G basis set for the other atoms (C, H, N, O and Cl).56–58 A single point calculation was performed using the TZVP basis set for all the atoms.59,60 Frequency calculation on the optimized structures was undertaken to confirm the minima on the potential-energy surface (PES) and also to obtain zero-point energy corrections. The quoted DFT energies are B3LYP-D2 solvation energy including free-energy corrections from the frequency calculations at a temperature of 298.15 K. The transition states were characterized by a single negative frequency which pertains to the desired motion as visualized in Chemcraft.61 The role of solvation in the structures and energetics was studied at the B3LYP-D2 level using the polarizable continuum solvent (PCM) model using acetonitrile as the solvent.62 The J values were computed from the energy differences between the high spin (EHS) state calculated using single determinant wave functions, and the low spin (EBS) state determined using the Broken Symmetry (BS) approach developed by Noodleman.63,64 Negative and positive values for J correspond to antiferromagnetic and ferromagnetic interactions respectively. Elaborate discussion of the computational methodology employed to compute the exchange interaction is discussed in detail elsewhere.65 The following notation M1(sFe1, sFe2) where superscript ‘M’ denotes the total multiplicities of the spin-coupled dimer and subscript ‘(sFe1, sFe2)’ denotes the spin multiplicity on Fe(1) and Fe(2) atoms is employed throughout the manuscript. All spectroscopic parameter calculations incorporate a relativistic effect via a zeroth-order regular approximation method (ZORA) as implemented in ORCA suite.66,67 The MB-isomer shifts (IS) were calculated based on the calibration constants reported by Römelt et al. and 0.16 barn was used for the calculation of quadruple moment of 57Fe nuclei.68 Calculation of g-anisotropy incorporates spin–orbit coupling using mean-field approximation and this methodology has been widely employed to compute the g-anisotropy.69 Time dependent density functional theory (TD-DFT) implemented in the ORCA program was used for the calculation of excitation energies. MO and NBO analyses were performed using G09 suite and visualizations are done using Chemcraft software.Results and discussion
Electronic structure of μ-nitrido dinuclear iron species
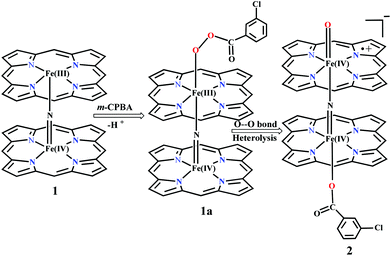
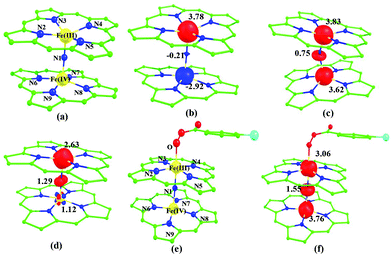
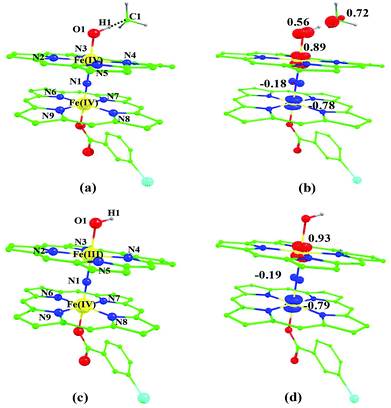
Sorokin and co-workers reported a dinuclear [(TPP)Fe(III)(μ-N)Fe(IV)(TPP)] (1) as the starting point which upon reaction with m-CPBA (m-CPBA = meta-chloroperbenzoic acid) yields m-CPBA coordinated [(TPP)(m-CPBA)Fe(III)(μ-N)Fe(IV)(TPP)] (1a) species. Species 1a undergoes heterolytic cleavage of the O–O bond of the m-CPBA leading to the formation of the catalytically active [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− (2) species (see Scheme 1).41Among the three spin states computed, the 21(hs, hs) is found to be the ground state followed by the 61(is, is) state by an energy margin of 25.7 kJ mol−1 and the 101(hs, hs) state is found to lie 64.7 kJ mol−1 higher in energy. Our calculations reveal that both the metal centres possess high-spin ground states and this is in line with the experimental observation for similar Fe(III) and Fe(IV) geometries reported earlier.41 The μ-nitrido bridge mediates a strong delocalization of spin leading to an antiferromagnetic coupling between the two metal centres. Optimized geometries and spin density computed are shown in Fig. 1. The Fe(III) centre has the following electronic configuration (δxy)1 (π*xz)1 (π*yz)1 (σ*z2)1 (δx2−y2)1 while the Fe(IV) centre has (δxy)1 (π*xz)1 (π*yz)1 (δx2−y2)1 (σ*z2)0 electronic configuration for the 21(hs, hs) species (see Fig. S1 of the ESI†). There is a significant π-type interaction between the dxz and dyz orbitals of the two Fe centres via the μ-nitrido bridges and this leads to a very strong antiferromagnetic coupling in this species. The magnetic coupling is estimated using the ground state structure employing the standard protocol69 and this yields a J value of −479.4 cm−1 (in Ĥ = −JS1·S2 formalism) and this observation corroborates with the J value expected for the dinuclear iron complexes possessing similar structural motifs.70–75 The doublet ground state predicted by the calculations is in agreement with the EPR data reported for complex 1.41 The Fe–N(1) distances of the 21(hs, hs) state are found to be 1.790 Å and 1.647 Å for the Fe(III) and Fe(IV) site, respectively. As expected the Fe(III)–N(1) distances are longer than the Fe(IV)–N(1) distance for antiferromagnetic coupled, valance localized states. Although the computed distances are in broad agreement with the X-ray structure reported at 120 K, the Fe(III)–N(1) and Fe(IV)–N(1) distances are predicted to be the same in the X-ray structure (1.679 Å). The Wiberg bond indexes computed for Fe(III)–N(1) and Fe(IV)–N(1) are 1.25 and 1.62 revealing a double bond between Fe and N(1) in case of the Fe(IV) centre.
The NBO analysis (see Fig. S2 of the ESI†) further reiterates the nature of Fe–N bonding between the two centres where the Fe(III)–N1 bond is found to be strongly σ in character with 30.6% donation from Fe(III) and 69.4% from the N(1) nitrogen atom. The Fe(IV)–N(1) bond on the other hand is found to be covalent in nature with 48.5% contribution from Fe and 51.5% from the N(1) nitrogen atom. For the Fe(IV)–N(1) π-bond, 67.1% and 32.9% donations from Fe and nitrogen atoms respectively have been detected. As expected from the electronic configuration given above, the Fe(IV) centre undergoes Jahn–Teller distortion (axial compression here) possessing longer Fe–N(prop) distances and shorter Fe(IV)–N(1) distances. Since the Fe(IV) centre is a Jahn–Teller ion, the structural distortion leads to a valence localization suggesting type I mixed-valence description. Computed spin density plots for all three spin states obtained are shown in Fig. 1(b–d). The spin density values on the Fe(III) and Fe(IV) of the 21(hs, hs) state are noted as 3.78 and −2.92 suggesting a valence localization of the spins. Significant reduction from the expected value of the spin density suggests that the spin density is delocalized to the coordinated atoms, particularly to the nitrido nitrogen atom (−0.21).
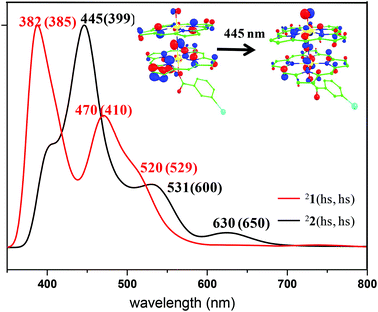
To probe the electronic structure further and to compare and contrast the computed electronic structure with the experimental values, we have computed the spectroscopic parameters of species 1. The vibrational frequency corresponding to the Fe–N–Fe vibrational mode was computed as 1010 cm−1 and this is in agreement with the experimental value of 910 cm−1 for the [(TPP)Fe(III)(μ-N)Fe(IV)(TPP)] species. The computed value is also in the range expected for other dinuclear complexes.36 The computed absorption spectra of the 21(hs, hs) state are shown in Fig. 2. Calculations reveal three intense peaks at 382, 470 and 520 nm and this agrees well with the experimental observation of the three features. The peak observed at 382 nm is found to be a metal (π*) to ligand charge transfer band. The peak at 470 nm, pertaining to the π* orbital of the metal to π* of the ligand orbitals and the peak at 520 nm are assigned as ligand to ligand charge transfer bands (see Fig. S3 in the ESI†).
The g tensor is an integral property of the complexes, and the molecular g tensor can be related to the site tensor values by a vector coupling approach where G is the molecular g tensor of the entire system while g1 and g2 are the site g-tensor values of the two Fe centres
| G = c1g1 + c2g2 |
Here c1 and c2 are the coefficients for the two sites. Calculations yield G1 = 2.1107 and G2 = 2.0117 for the 21(hs, hs) state (see Table 2 for individual tensor quantities. Note: to differentiate site g-tensor and molecular g-tensor, G notations are employed throughout) and this is broadly in agreement with the X-band EPR recorded at a power sample of 1 (G1 = 2.155 and G2 = 2.008).41,76
| Spin states | δ values (mm s−1) | ΔEQ values (mm s−1) | g-value | ||||
|---|---|---|---|---|---|---|---|
| Fe(III) | Fe(IV) | Fe(III) | Fe(IV) | G x | G y | G z | |
| a For this species the oxidation state of Fe is IV. | |||||||
| 10 1 (hs, hs) | 0.50 | 0.33 | 0.31 | 0.16 | 2.0055 | 2.0139 | 2.0164 |
| 2 1 (hs, hs) | 0.37 | 0.13 | 0.18 | 1.04 | 2.0116 | 2.1039 | 2.1174 |
| 6 1 (is, is) | 0.01 | 0.51 | 1.93 | −1.44 | 2.0033 | 2.0146 | 2.0361 |
| 10 1a (hs, hs) | 0.54 | 0.36 | −1.51 | 1.90 | 2.0128 | 2.0216 | 2.0231 |
| 10 2 (hs, hs) | 0.44a | 0.18 | 0.61a | −1.79 | 2.0068 | 2.0163 | 2.0179 |
| 2 2 (hs, hs) | 0.08a | 0.13 | −0.13a | −1.79 | 2.0132 | 2.1084 | 2.2627 |
| 8 2 (hs, hs) | 0.08a | 0.13 | −1.43a | −0.49 | 2.0092 | 2.0095 | 2.0183 |
| 6 2 (is, is) | 0.25a | 0.05 | −2.36a | 0.38 | 1.9995 | 2.0364 | 2.0465 |
Strong deviations from the free electron g-values and significant anisotropy on the estimate of the g-anisotropy reveal that the unpaired electrons are metal based and significant anisotropy computed in the g-tensors is likely due to the Fe(IV) metal centre possessing large spin–orbit coupling. The high-spin Fe(III) centre on the other hand is expected to be isotropic in nature and is unlikely to influence the G-tensor to this extent. The computed isomer shift and quadruple splitting values for the 21(hs, hs) state are given in Table 2. The isomer shift computed for the Fe(III) centre is larger than that found for the Fe(IV) centre and this is as expected based on the electron density of core electrons computed. The quadruple shift computed for the two centres is also different, with a concomitant larger ΔEQ for the Fe(IV) centre and a smaller one noted for the Fe(III) centre. Among the spin Hamiltonian parameters computed for all three spin states (see Table 2), a closer match to experiments41 was found for the 21(hs, hs) state reiterating the S = 1/2 ground state for this species with high-spin configurations on both metal centres coupled in an antiferromagnetic fashion.
Reaction of m-CPBA with species 1 is expected to yield [(TPP)Fe(III)(m-CPBA)(μ-N)Fe(IV)(TPP)] (1a) species (Fig. 1). The spin states expected for this species are similar to that of species 1. To estimate the energetics of formation of 1a from species 1, we have computed the structure and energetics of only the 101a(hs, hs) state. The computed geometry and the spin density plots are shown in Fig. 1e and f. The energetics of formation of 1a from 1 is computed to be slightly endothermic in nature (+10.9 kJ mol−1) revealing facile coordination of the m-CBPA to the Fe(III) site. Upon m-CPBA coordination, both the Fe–N(1) distances elongate and the μ-nitrido nitrogen gains significant spin density.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species upon heterolytic cleavage of the O⋯O bond in 1a. The optimized structure of the 22(hs, hs) state is shown in Fig. 3(a).
O species upon heterolytic cleavage of the O⋯O bond in 1a. The optimized structure of the 22(hs, hs) state is shown in Fig. 3(a).
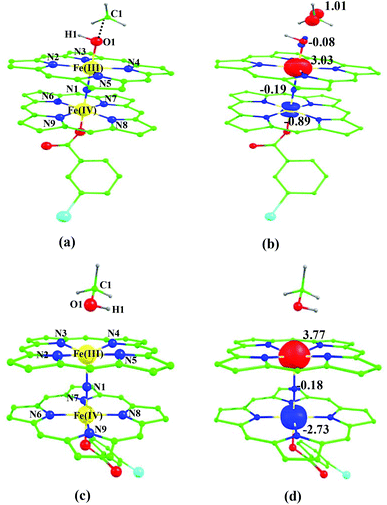
For the 22(hs, hs) state, the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance is computed to be 1.661 Å and this estimate is consistent with the experimental values reported for similar Fe(IV)
O bond distance is computed to be 1.661 Å and this estimate is consistent with the experimental values reported for similar Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species (note that the Fe(IV)
O species (note that the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances reported are in the range of 1.63–1.66 Å for different heme-Fe(IV)
O distances reported are in the range of 1.63–1.66 Å for different heme-Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species26,45,49,78). As a consequence of short Fe(IV)
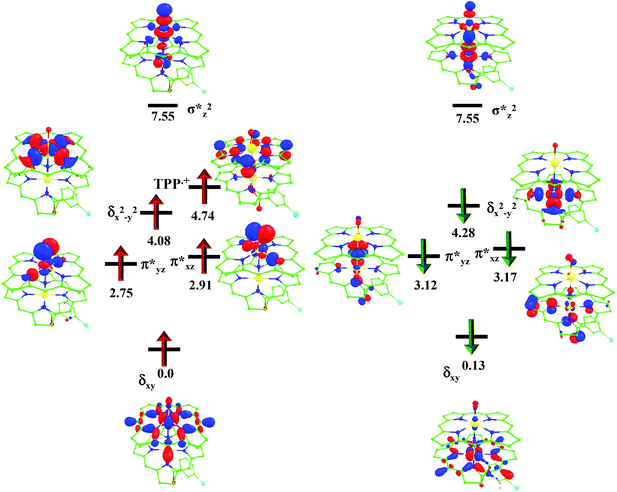
O species26,45,49,78). As a consequence of short Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, the bond distance between the bridged nitrogen atom and the Fe(IV) centre has become longer (1.974 Å) while Fe(IV)–N(1) of the second Fe(IV) centre where the meta-chlorobenzoate is coordinated has been shortened to 1.686 Å. The eigen-value plot computed for the 22(hs, hs) state is shown in Fig. 4 and here both the Fe(IV) centres have (δxy)1 (π*xz)1 (π*yz)1 (δx2−y2)1 (σ*z2)0 electronic configuration leading to Jahn–Teller distortion and longer Fe–N(porp) distances. In both the metal centres, the degeneracy of the π*xz and π*yz orbitals is lifted and the radical orbital is found to be significantly destabilized (higher in energy than the δx2−y2 orbital). The computed Wiberg bond indexes for the Fe–N bond in O
O bonds, the bond distance between the bridged nitrogen atom and the Fe(IV) centre has become longer (1.974 Å) while Fe(IV)–N(1) of the second Fe(IV) centre where the meta-chlorobenzoate is coordinated has been shortened to 1.686 Å. The eigen-value plot computed for the 22(hs, hs) state is shown in Fig. 4 and here both the Fe(IV) centres have (δxy)1 (π*xz)1 (π*yz)1 (δx2−y2)1 (σ*z2)0 electronic configuration leading to Jahn–Teller distortion and longer Fe–N(porp) distances. In both the metal centres, the degeneracy of the π*xz and π*yz orbitals is lifted and the radical orbital is found to be significantly destabilized (higher in energy than the δx2−y2 orbital). The computed Wiberg bond indexes for the Fe–N bond in O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe(IV)–N(1) and N(1)–Fe(IV)–m-CBA are 0.562 and 1.25, indicating single and double bonds, respectively. Furthermore, the observed WB index of Fe(IV) and ferryl oxygen (1.35) suggests the presence of a clear double bond between them. In addition, the computed NBO analysis reveals the intrinsic bonding scenario and how the electron distribution presents between the two metal ions. The σ Fe–N bond in the O
Fe(IV)–N(1) and N(1)–Fe(IV)–m-CBA are 0.562 and 1.25, indicating single and double bonds, respectively. Furthermore, the observed WB index of Fe(IV) and ferryl oxygen (1.35) suggests the presence of a clear double bond between them. In addition, the computed NBO analysis reveals the intrinsic bonding scenario and how the electron distribution presents between the two metal ions. The σ Fe–N bond in the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe(IV)–N(1) unit has 26.5% contribution from the Fe(IV) unit while N(1) contributes 73.5% (see Fig. S5 of the ESI†).
Fe(IV)–N(1) unit has 26.5% contribution from the Fe(IV) unit while N(1) contributes 73.5% (see Fig. S5 of the ESI†).
 | ||
| Fig. 4 B3LYP-D2 computed eigen-value plot incorporating energies computed for d-based orbitals for alpha and beta spin of 22(hs, hs) species (energies are given in eV). | ||
This unveils a fact that this bond is ionic in nature and has significant donation from the bridging nitrogen atom. On the other hand, the N(1)–Fe(IV) bond in the other unit is found to be covalent in nature with 54.5% contribution from Fe(IV) and 45.5% from N(1). This suggests that the electrons essentially flow from the Fe(IV)–m-CBA unit to the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe(IV) unit and such arrangement is likely to enhance the reactivity of the Fe(IV)
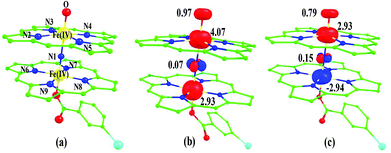
Fe(IV) unit and such arrangement is likely to enhance the reactivity of the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species compared to mononuclear analogues (see Fig. S4 of the ESI†). The computed spin densities for the complex 102(hs, hs) and 22(hs, hs) states are shown in Fig. 3 (see ESI Fig. S5 †for spin density plots of other spin states computed). For the 22(hs, hs) state, the spin density on the Fe(IV) centres is estimated to be ∼2.9 on both Fe centres while significant spin density (0.79) on the ferryl oxygen atom is noted. Although primarily, we expected a localized radical centre on the TPP ring, calculations reveal that electrons are completely delocalized to all the atoms including the ferryl oxygen atom, μ-nitrido nitrogen atom and the oxygen atom of the meta-chlorobenzoate derivatives with spin densities as high as ∼0.15 detected on the nitrogen atoms of the TPP ring.
O species compared to mononuclear analogues (see Fig. S4 of the ESI†). The computed spin densities for the complex 102(hs, hs) and 22(hs, hs) states are shown in Fig. 3 (see ESI Fig. S5 †for spin density plots of other spin states computed). For the 22(hs, hs) state, the spin density on the Fe(IV) centres is estimated to be ∼2.9 on both Fe centres while significant spin density (0.79) on the ferryl oxygen atom is noted. Although primarily, we expected a localized radical centre on the TPP ring, calculations reveal that electrons are completely delocalized to all the atoms including the ferryl oxygen atom, μ-nitrido nitrogen atom and the oxygen atom of the meta-chlorobenzoate derivatives with spin densities as high as ∼0.15 detected on the nitrogen atoms of the TPP ring.
The computed absorption spectra of the 22(hs, hs) state are shown in Fig. 2. The TD-DFT calculations yield four intense peaks at 396, 445, 531 and 630 nm. These peak positions corroborate well with the experimental absorption spectra (see Fig. 2). The most intense peak observed at 445 nm is found to be N (centred on μ-nitrido nitrogen) to π* (dxz–px) transition while the shoulder observed at 531 nm is assigned to π(Fe–O)* to π* TPP ligand transition (see Fig. S6 of the ESI†). The peak observed at 630 nm corresponds to transition from the π* TPP ligand to the π(Fe–N–Fe–O)* orbital. Magnetic coupling between the two Fe(IV) centres is estimated to be antiferromagnetic in nature with the estimate of J being −225 cm−1 (in Ĥ = −JS1·S2 formalism).
Experiments suggest very strong antiferromagnetic interaction between the two metal centres and the computed J supports this argument.41 The computed g-tensors for species 2 are given in Table 2. Calculations yield a rhombic set of G-values (Gx = 2.0132, Gy = 2.1084 and Gz = 2.2627) for the 22(hs, hs) state while for all other spin states, the computed G-values are nearly isotropic in nature. The frozen solution X-band EPR spectra recorded at 120 K for this species however yield an isotropic g-value (estimated G = 2.001).41,76 This suggests that apart from the ground state, other spin states might also have contributed to the observed experimental G-values. The computed isomer shift and quadruple splitting values for the 22(hs, hs) state are given in Table 2.
Calculations yield two distinct isomer shift values with a very small value for the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O centre and slightly larger value for the Fe(IV)–m-CBA centre. Similarly the ΔEQ values are noted to be distinctly different for both the sites with a smaller ΔEQ value for the Fe(IV)
O centre and slightly larger value for the Fe(IV)–m-CBA centre. Similarly the ΔEQ values are noted to be distinctly different for both the sites with a smaller ΔEQ value for the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O centre and a larger value for the Fe(IV)–m-CBA site. Experimental Mössbauer spectra recorded at 4.2 K for species 2 yield two satisfactory fits and these values are given in Table 2. The second set of the fit parameters is found to comply with the calculated data better than the first set.41 Although dissymmetry (different isomer shifts and ΔEQ for the two Fe centres) is observed in the experiments, due to a low signal-to-noise ratio of the recorded spectra, the individual values have not been extracted.
O centre and a larger value for the Fe(IV)–m-CBA site. Experimental Mössbauer spectra recorded at 4.2 K for species 2 yield two satisfactory fits and these values are given in Table 2. The second set of the fit parameters is found to comply with the calculated data better than the first set.41 Although dissymmetry (different isomer shifts and ΔEQ for the two Fe centres) is observed in the experiments, due to a low signal-to-noise ratio of the recorded spectra, the individual values have not been extracted.
Mechanism of C–H activation of methane by 2
The Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit present in species 2 is proposed as an active oxidant responsible for alkane hydroxylation to a variety of substrates such as cyclohexane, adamantane, ethylbenzene and methane.41,49,79 Methane oxidation under turnover conditions by 2 yields a turnover number as high as 13.7 revealing strong oxidizing ability of the species 2. Here we have attempted to explore the intrinsic mechanism of methane activation by this species as this is an extremely important reaction from both industrial and green chemistry perspectives. The schematic mechanism proposed based on the experimental evidence and earlier precedence on the cytochrome P450 and MMO reactivity is shown in Scheme 2.4,6,44,80,81
O unit present in species 2 is proposed as an active oxidant responsible for alkane hydroxylation to a variety of substrates such as cyclohexane, adamantane, ethylbenzene and methane.41,49,79 Methane oxidation under turnover conditions by 2 yields a turnover number as high as 13.7 revealing strong oxidizing ability of the species 2. Here we have attempted to explore the intrinsic mechanism of methane activation by this species as this is an extremely important reaction from both industrial and green chemistry perspectives. The schematic mechanism proposed based on the experimental evidence and earlier precedence on the cytochrome P450 and MMO reactivity is shown in Scheme 2.4,6,44,80,81
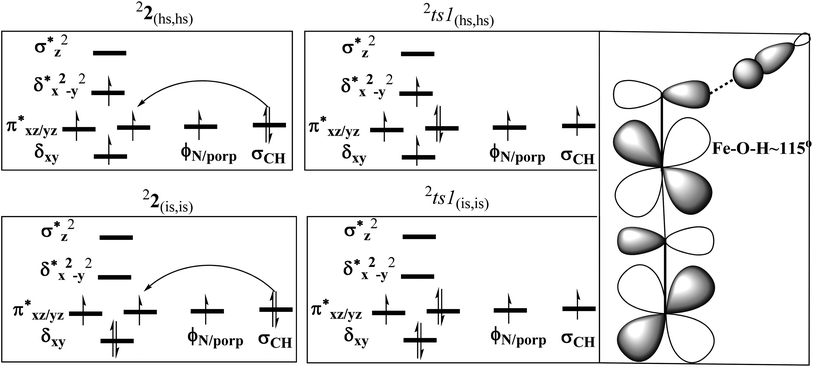
In the first step, the C–H activation of the methane by the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit is assumed via ts1. This is preceded by the formation of an Fe(III)–OH intermediate (int1). In the next step rebounding of the –OH group is assumed to take place via (ts2) leading to the formation of methanol. The rebound mechanism for the hydroxylation of alkanes and alkenes is thoroughly explored and significant experimental evidence for this mechanism has been accumulated.80–82 The five spin states computed for species 2 have been employed to construct the potential energy surface (PES) for the methane oxidation as described in the above scheme (see Fig. 5). Among five possible transition states, 10ts1(hs, hs), 2ts1(hs, hs) and 2ts1(is, is) transition states were successfully optimized. The 2ts1(hs, hs) is characterized by a single imaginary frequency (−1292 cm−1) and has a barrier height of 56.6 kJ mol−1. However this is not the lowest energy pathway as the 2ts1(is, is) transition state is found to have a barrier height of just 26.6 kJ mol−1 from the 22(hs, hs) surface. This certainly demands a mean energy crossing point (MECP)83 between the two spin surfaces and given the large anisotropy and spin–orbit coupling estimated for these states, we expect that this spin-crossover is likely to be facile. The orbital evolution diagram for the C–H bond activation for 2ts1(is, is) and 2ts1(hs, hs) is shown in Fig. 6. No significant exchange enhanced reactivity is expected for the high-spin state at the π-type pathway.84 Besides, as a significant spin density has been found at the μ-nitrido atom and it is strongly bound to the metal centre via the σ and π interaction, the electron delocalization to σ*z2 is presumably expected for this species. For these reasons, the C–H bond activation even at a high-spin state is found to occur via the π-channel. For the 2ts1(is, is) state as well, no gain in exchange enhanced reactivity is seen and significant reduction in the barrier height is primarily due to the orbital controlled nature of the reaction. In addition weak C–H⋯π interactions between methane and the TPP ring are expected to fix the methane on the TPP surface and thus activate π-type reactivity. The estimated barrier height of 26.6 kJ mol−1 for C–H bond activation of methane is remarkably low for species 2. For the cytochrome P450, earlier theoretical studies have estimated the barrier heights to be 110.8 kJ mol−1 while theoretical calculations performed on model systems of dinuclear MMO estimate the barrier height to be 81.6 kJ mol−1 (note that there are some minor deviations in the theoretical methodology employed here and the literature values quoted). Despite these higher barriers computed for these two enzymes, they are naturally superior to species 2 as enzymatic conditions are very different compared to the bio-mimic systems. This also highlights the fact that for the model systems, the kinetic barrier heights lower than that of enzymes are desired to demonstrate the oxidizing abilities under laboratory conditions.
O unit is assumed via ts1. This is preceded by the formation of an Fe(III)–OH intermediate (int1). In the next step rebounding of the –OH group is assumed to take place via (ts2) leading to the formation of methanol. The rebound mechanism for the hydroxylation of alkanes and alkenes is thoroughly explored and significant experimental evidence for this mechanism has been accumulated.80–82 The five spin states computed for species 2 have been employed to construct the potential energy surface (PES) for the methane oxidation as described in the above scheme (see Fig. 5). Among five possible transition states, 10ts1(hs, hs), 2ts1(hs, hs) and 2ts1(is, is) transition states were successfully optimized. The 2ts1(hs, hs) is characterized by a single imaginary frequency (−1292 cm−1) and has a barrier height of 56.6 kJ mol−1. However this is not the lowest energy pathway as the 2ts1(is, is) transition state is found to have a barrier height of just 26.6 kJ mol−1 from the 22(hs, hs) surface. This certainly demands a mean energy crossing point (MECP)83 between the two spin surfaces and given the large anisotropy and spin–orbit coupling estimated for these states, we expect that this spin-crossover is likely to be facile. The orbital evolution diagram for the C–H bond activation for 2ts1(is, is) and 2ts1(hs, hs) is shown in Fig. 6. No significant exchange enhanced reactivity is expected for the high-spin state at the π-type pathway.84 Besides, as a significant spin density has been found at the μ-nitrido atom and it is strongly bound to the metal centre via the σ and π interaction, the electron delocalization to σ*z2 is presumably expected for this species. For these reasons, the C–H bond activation even at a high-spin state is found to occur via the π-channel. For the 2ts1(is, is) state as well, no gain in exchange enhanced reactivity is seen and significant reduction in the barrier height is primarily due to the orbital controlled nature of the reaction. In addition weak C–H⋯π interactions between methane and the TPP ring are expected to fix the methane on the TPP surface and thus activate π-type reactivity. The estimated barrier height of 26.6 kJ mol−1 for C–H bond activation of methane is remarkably low for species 2. For the cytochrome P450, earlier theoretical studies have estimated the barrier heights to be 110.8 kJ mol−1 while theoretical calculations performed on model systems of dinuclear MMO estimate the barrier height to be 81.6 kJ mol−1 (note that there are some minor deviations in the theoretical methodology employed here and the literature values quoted). Despite these higher barriers computed for these two enzymes, they are naturally superior to species 2 as enzymatic conditions are very different compared to the bio-mimic systems. This also highlights the fact that for the model systems, the kinetic barrier heights lower than that of enzymes are desired to demonstrate the oxidizing abilities under laboratory conditions.
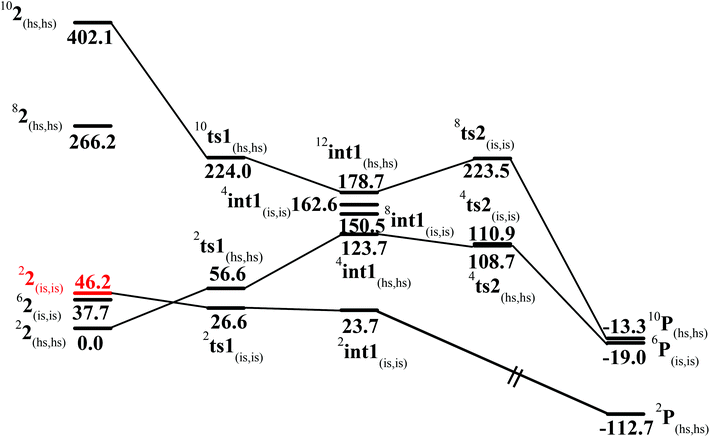 | ||
| Fig. 5 B3LYP-D2 computed potential energy surface for C–H bond activation of methane by species 2 (kJ mol−1). See ref. 77. | ||
The next question obviously arises is, what is the reason for lower barrier heights for the C–H bond activation compared to P450 models? Due to the dinuclear nature of the model system, the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species possesses stronger electron delocalization than the corresponding mononuclear analogues. Here the {Fe(IV)(O)(TPP˙+)} unit has a {(TPP)(m-CBA)Fe(IV)(N)} unit as the axial ligand and the μ-nitrido groups possessing a significant spin density and its accrual of electron from the {(TPP)(m-CBA)Fe(IV)} unit clearly reveals the cooperativity between two iron centres on the reactivity. The spin density plot (Fig. 3c) clearly reveals a spin polarization at the Fe(IV)
O species possesses stronger electron delocalization than the corresponding mononuclear analogues. Here the {Fe(IV)(O)(TPP˙+)} unit has a {(TPP)(m-CBA)Fe(IV)(N)} unit as the axial ligand and the μ-nitrido groups possessing a significant spin density and its accrual of electron from the {(TPP)(m-CBA)Fe(IV)} unit clearly reveals the cooperativity between two iron centres on the reactivity. The spin density plot (Fig. 3c) clearly reveals a spin polarization at the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O centre (gain of spin density on the Fe(IV)
O centre (gain of spin density on the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit at the transition state) and the existence of cooperative oxidizing ability of the combined unit. The second unit present also helps to stabilize the newly forming Fe(III)O–H bond thus enhancing the reactivity further. Earlier experimental and theoretical studies on the axial ligand effect on [Fe(IV)(O)(porp˙+)(X)] species clearly demonstrate that an electron donating group significantly increases the reactivity and this supports our observation.26
O unit at the transition state) and the existence of cooperative oxidizing ability of the combined unit. The second unit present also helps to stabilize the newly forming Fe(III)O–H bond thus enhancing the reactivity further. Earlier experimental and theoretical studies on the axial ligand effect on [Fe(IV)(O)(porp˙+)(X)] species clearly demonstrate that an electron donating group significantly increases the reactivity and this supports our observation.26
The ∠Fe–O⋯H angle is estimated to be 113.8 degrees revealing a rather π-type pathway for the hydrogen atom abstraction reaction.84,85 The optimized structure and the corresponding spin density plot of the 2ts1(is, is) are shown in Fig. 7 (see also Table S1 of the ESI†). The Fe–O bond in 2ts1(is, is) elongates to 1.844 Å compared to its bond length in the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O reactant (1.673 Å) and at the same time the Fe–N(1) bond length shortens. The newly forming O1⋯H1 bond in the transition states is computed to be 1.123 Å (see Fig. 7) suggesting that the O–H bond is fully formed at the transition state while the H1⋯C1 bond is nearly broken (1.418 Å). The computed energy profile diagram is depicted in Fig. 4. At the transition state as the H1⋯C1 bond is broken, this subsequently spurs the generation of radical character at the carbon atom suggesting a HAT type reaction.48,86
O reactant (1.673 Å) and at the same time the Fe–N(1) bond length shortens. The newly forming O1⋯H1 bond in the transition states is computed to be 1.123 Å (see Fig. 7) suggesting that the O–H bond is fully formed at the transition state while the H1⋯C1 bond is nearly broken (1.418 Å). The computed energy profile diagram is depicted in Fig. 4. At the transition state as the H1⋯C1 bond is broken, this subsequently spurs the generation of radical character at the carbon atom suggesting a HAT type reaction.48,86
In the next step, the Fe(III)–OH formation gets accomplished leading to the formation of int1. For the intermediate, we have computed 2int1(is, is), 4int1(hs, hs), 8int1(is, is),4int1(is, is) and 12int1(hs, hs) states (note that the spin state of the methyl radical is assumed to be in spin-up state and thus the spin multiplicity of all the species is raised by one more unpaired electron). Here the 2int1(is, is) is found to be low lying being just 3 kJ mol−1 lower than the transition state 2ts1(is, is), revealing the endothermic nature of the reaction. Other intermediates are computed to be much higher in energy with the 4int1(hs, hs) state lying 100 kJ mol−1 higher compared to the 2int1(is, is) state (see Fig. 4 for other state energies). Also for cytochrome P450, this step is computed to be endothermic in nature, revealing resemblance in the energetic landscape despite significant structural/electronic differences.80,82,87 In the 2int1(is, is) intermediate, the Fe–O and the O–H bonds are computed to be 1.865 Å and 0.981 Å revealing complete bond formation and also indicating the single bond nature of the Fe–OH bond. The Fe(III)–N(1) distance is computed to be 1.697 Å implying shortening of the Fe–N distance compared to the transition state and the reactant. The N(1)–Fe(IV) bond on the other hand remains almost similar throughout (here it is 1.651 Å). Shortening of the Fe(III)–N(1) distance delineates strong electron delocalization and in fact the spin density distribution further indicates a complete delocalization of spin with a +3.5 oxidation state on both the metal centres. This additional flexibility available enhances the reactivity. In the next step rebound of the O–H group to the methyl radical is expected to take place. Here we have calculated 4ts2(is, is), 8ts2(is, is) and 4ts2(hs, hs) transition states and 4ts2(hs, hs) is found to be the lowest in energy and its barrier height is found to be 85.0 kJ mol−1 followed by 87.2 and 199.8 kJ mol−1 for 4ts2(is, is) and 8ts2(is, is) respectively (from 2int1(is, is) state). Our attempt to obtain the 2ts2(is, is) transition state corresponding to the lowest lying intermediate was not successful and generally on the doublet surface the rebound step is barrier-less as it has been demonstrated earlier for both heme and non-heme Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O hydroxylation reactions.87 We believe that a similar barrier-less process is operational also for the second step leading to the formation of methanol. The optimized structure and spin density plot of the ground state of 4ts2(hs, hs) are shown in Fig. 8. For the 4ts2(hs, hs) transition state, the Fe–O bond is further elongated (1.901 Å) compared to the intermediate and the newly forming O1–C1 bond is computed to be 2.488 Å revealing a reactant like transition state with no significant bonding interaction between the ferryl oxygen and the carbon atom of the methyl radical. This also adds significance to our earlier statement on barrier-less reaction on the doublet surface as here the spin-up position on the radical centre leads to significant electron repulsion and thus very long O1⋯C1 bond distances in the transition state. A significant increase of spin density at the carbon atom (1.0) in the transition state reveals that the spin polarization is operational. The computed barrier height at this surface is very high compared to P450 models where the barrier height is computed to be 23 kJ mol−1. Clearly one of the reasons for a very large barrier height at this surface is the significant electron repulsion as delocalization of methyl radical spin is not seen and also the Fe(III)–OH bond being stronger adds up significant energy penalty (see Fig. 8).88
O hydroxylation reactions.87 We believe that a similar barrier-less process is operational also for the second step leading to the formation of methanol. The optimized structure and spin density plot of the ground state of 4ts2(hs, hs) are shown in Fig. 8. For the 4ts2(hs, hs) transition state, the Fe–O bond is further elongated (1.901 Å) compared to the intermediate and the newly forming O1–C1 bond is computed to be 2.488 Å revealing a reactant like transition state with no significant bonding interaction between the ferryl oxygen and the carbon atom of the methyl radical. This also adds significance to our earlier statement on barrier-less reaction on the doublet surface as here the spin-up position on the radical centre leads to significant electron repulsion and thus very long O1⋯C1 bond distances in the transition state. A significant increase of spin density at the carbon atom (1.0) in the transition state reveals that the spin polarization is operational. The computed barrier height at this surface is very high compared to P450 models where the barrier height is computed to be 23 kJ mol−1. Clearly one of the reasons for a very large barrier height at this surface is the significant electron repulsion as delocalization of methyl radical spin is not seen and also the Fe(III)–OH bond being stronger adds up significant energy penalty (see Fig. 8).88
Conclusions
Activation of inert C–H bonds such as that of methane has been a great challenge in the area of catalysis. Despite the fact that several enzymes perform oxidation of methane readily, a biomimic complex which could do this transformation efficiently is rare. Report of N-bridged high-valent diiron(IV)–oxo possessing additional cationic-radical character found to oxidize methane readily is a significant breakthrough in this area. Here using density functional methods we have explored the electronic structure and mechanism of methane activation by this species. Conclusions derived from our work are summarized below,(i) The dinuclear reactant species [(TPP)Fe(III)(μ-N)Fe(IV)(TPP)] (1) is found to possess a doublet valence localized ground state. Absorption spectra indicate low-energy ligand to ligand transition indicating possibility of ligand oxidation at lower potential, while computed g-anisotropy yields anisotropic G-tensors revealing significant spin–orbit coupling at the Fe(IV) centre.
(ii) Reaction of 1 with m-CPBA is found to be facile and yields an m-CPBA coordinated species by an endothermic reaction and this species quickly undergoes heterolytic cleavage of the O–O bond of the m-CPBA leading to the formation of the catalytically active [(TPP)(m-CBA)Fe(IV)(μ-N)Fe(IV)(O)(TPP˙+)]− (2) by an exothermic reaction. Calculations reveal that the two iron centres in species 2 are strongly antiferromagnetically coupled while the radical centres are found to significantly delocalize to many atoms including the μ-nitrido nitrogen atom of the porphyrin ring etc. Intricate bonding analysis reveals that the Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O centre accepts electrons from the μ-nitrido nitrogen atom which in turn accepts donation from the Fe(IV)–m-CBA unit. The computed spectroscopic parameters are broadly in agreement with the experiments.
O centre accepts electrons from the μ-nitrido nitrogen atom which in turn accepts donation from the Fe(IV)–m-CBA unit. The computed spectroscopic parameters are broadly in agreement with the experiments.
(iii) Extremely small activation energy for C–H bond activation of methane was detected for species 2 and the reaction was in fact found to proceed via the excited intermediate-spin state of the Fe(IV) centre rather than the high-spin ground state. Preferential π-type reactivity is observed in all spin states and the orbital control nature of the reaction was found to lead to a significant reduction in the barrier height in the intermediate-spin state of Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species. The formation of the radical intermediate is found to be endothermic in nature in all spin states while the rebound step is expected to be barrier-less at the doublet surface. The computed rebound step at other spin surfaces yields a very high barrier for the –OH rebound reaction.
O species. The formation of the radical intermediate is found to be endothermic in nature in all spin states while the rebound step is expected to be barrier-less at the doublet surface. The computed rebound step at other spin surfaces yields a very high barrier for the –OH rebound reaction.
(iv) Overall an electronic cooperativity between two metal centres throughout the catalytic reactions is witnessed and this leads to an extremely low barrier height, stronger Fe(III)–OH bond at the intermediate and lower barriers for the rebound step. All these lead to very high turnover numbers for methane oxidation per catalytically active species. A comparison of our calculated results with the earlier report on cytochrome P450 and MMO models reveals that biomimic models should possess a significantly lower barrier height than the enzymes to demonstrate catalytic abilities under the laboratory conditions.
To this end, here for the first time using DFT methods we have described a subtle electronic structure of a μ-nitrido bridged dinuclear iron(IV)–oxo species and have unravelled the oxidation of methane by this species. The idea of electronic cooperativity as presented here has the potential for wider application in other dinuclear models/enzymes.
Acknowledgements
GR would like to thank DST, INSA and DST Nanomission for funding. NV would like to thank the DST for fast track fellowship (CS-338/2011). MA and AA thanks CSIR/IIT Bombay for a fellowship.References
- D. A. Whittington, M. H. Sazinsky and S. J. Lippard, J. Am. Chem. Soc., 2001, 123, 1794–1795 CrossRef CAS PubMed.
- V. Guallar, B. F. Gherman, W. H. Miller, S. J. Lippard and R. A. Friesner, J. Am. Chem. Soc., 2002, 124, 3377–3384 CrossRef CAS PubMed.
- C. E. Tinberg and S. J. Lippard, Acc. Chem. Res., 2011, 44, 280–288 CrossRef CAS PubMed.
- G.-D. Roiban, R. Agudo and M. T. Reetz, Angew. Chem., Int. Ed., 2014, 53, 8659–8663 CrossRef CAS PubMed.
- A. F. W. Coulson and T. Yonetani, Biochemistry, 1975, 14, 2389–2396 CrossRef CAS PubMed.
- D. Hamdane, H. Zhang and P. Hollenberg, Photosynth. Res., 2008, 98, 657–666 CrossRef CAS PubMed.
- B. J. Wallar and J. D. Lipscomb, Chem. Rev., 1996, 96, 2625–2658 CrossRef CAS PubMed.
- X. Shan and L. Que Jr., J. Inorg. Biochem., 2006, 100, 421–433 CrossRef CAS PubMed.
- E. Y. Tshuva and S. J. Lippard, Chem. Rev., 2004, 104, 987–1012 CrossRef CAS PubMed.
- C. Kim, Y. Dong and L. Que, J. Am. Chem. Soc., 1997, 119, 3635–3636 CrossRef CAS.
- B. Modén, B.-Z. Zhan, J. Dakka, J. G. Santiesteban and E. Iglesia, J. Phys. Chem. C, 2006, 111, 1402–1411 CrossRef.
- X. Li, R. Fu, S. Lee, C. Krebs, V. L. Davidson and A. Liu, Proc. Natl. Acad. Sci., U. S. A., 2008, 105, 8597–8600 CrossRef CAS PubMed.
- J. T. Groves, J. Inorg. Biochem., 2006, 100, 434–447 CrossRef CAS PubMed.
- S. Hong, H. So, H. Yoon, K.-B. Cho, Y.-M. Lee, S. Fukuzumi and W. Nam, Dalton Trans., 2013, 42, 7842–7845 RSC.
- D. Lee, J. D. Bois, D. Petasis, M. P. Hendrich, C. Krebs, B. H. Huynh and S. J. Lippard, J. Am. Chem. Soc., 1999, 121, 9893–9894 CrossRef CAS.
- P. Comba, H. Wadepohl and S. Wunderlich, Eur. J. Inorg. Chem., 2011, 2011, 5242–5249 CrossRef CAS.
- P. Comba, H. Wadepohl and S. Wiesner, Eur. J. Inorg. Chem., 2011, 2011, 2610–2615 CrossRef.
- P. Comba, H. Wadepohl and A. Waleska, Aust. J. Chem., 2014, 67, 398–404 CrossRef CAS.
- P. Comba, M. Morgen and H. Wadepohl, Inorg. Chem., 2013, 52, 6481–6501 CrossRef CAS PubMed.
- P. Comba, Y.-M. Lee, W. Nam and A. Waleska, Chem. Commun., 2014, 50, 412–414 RSC.
- M. Jaccob, P. Comba, M. Maurer, P. Vadivelu and P. Venuvanalingam, Dalton Trans., 2011, 40, 11276–11281 RSC.
- S. Fukuzumi, Y. Morimoto, H. Kotani, P. Naumov, Y.-M. Lee and W. Nam, Nat. Chem., 2010, 2, 756–759 CrossRef CAS PubMed.
- A. J. McGown, W. D. Kerber, H. Fujii and D. P. Goldberg, J. Am. Chem. Soc., 2009, 131, 8040–8048 CrossRef CAS PubMed.
- A. R. McDonald and L. Que Jr., Coord. Chem. Rev., 2013, 257, 414–428 CrossRef CAS.
- M. H. Lim, J.-U. Rohde, A. Stubna, M. R. Bukowski, M. Costas, R. Y. N. Ho, E. Münck, W. Nam and L. Que, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3665–3670 CrossRef CAS PubMed.
- Y. Kang, H. Chen, Y. J. Jeong, W. Lai, E. H. Bae, S. Shaik and W. Nam, Chem. – Eur. J., 2009, 15, 10039–10046 CrossRef CAS PubMed.
- A. Takahashi, D. Yamaki, K. Ikemura, T. Kurahashi, T. Ogura, M. Hada and H. Fujii, Inorg. Chem., 2012, 51, 7296–7305 CrossRef CAS PubMed.
- A. B. Sorokin, S. Mangematin and C. Pergrale, J. Mol. Catal. A: Chem., 2002, 182–183, 267–281 CrossRef CAS.
- L. A. Bottomley, J. N. Gorce, V. L. Goedken and C. Ercolani, Inorg. Chem., 1985, 24, 3733–3737 CrossRef CAS.
- C. Ercolani, M. Gardini, G. Pennesi, G. Rossi and U. Russo, Inorg. Chem., 1988, 27, 422–424 CrossRef CAS.
- G. Rossi, M. Gardini, G. Pennesi, C. Ercolani and V. L. Goedken, J. Chem. Soc., Dalton Trans., 1989, 193–195 RSC.
- C. Ercolani, S. Hewage, R. Heucher and G. Rossi, Inorg. Chem., 1993, 32, 2975–2977 CrossRef CAS.
- C. Ercolani, J. Jubb, G. Pennesi, U. Russo and G. Trigiante, Inorg. Chem., 1995, 34, 2535–2541 CrossRef CAS.
- M. P. Donzello, C. Ercolani, K. M. Kadish, Z. Ou and U. Russo, Inorg. Chem., 1998, 37, 3682–3688 CrossRef CAS PubMed.
- M. P. Donzello, C. Ercolani, U. Russo, A. Chiesi-Villa and C. Rizzoli, Inorg. Chem., 2001, 40, 2963–2967 CrossRef CAS PubMed.
- A. B. Sorokin, Chem. Rev., 2013, 113, 8152–8191 CrossRef CAS PubMed.
- A. B. Sorokin, E. V. Kudrik and D. Bouchu, Chem. Commun., 2008, 2562–2564 RSC.
- A. B. Sorokin, E. V. Kudrik, L. X. Alvarez, P. Afanasiev, J. M. M. Millet and D. Bouchu, Catal. Today, 2010, 157, 149–154 CrossRef CAS.
- E. V. Kudrik and A. B. Sorokin, Chem. – Eur. J., 2008, 14, 7123–7126 CAS.
- U. Isci, P. Afanasiev, J.-M. M. Millet, E. V. Kudrik, V. Ahsen and A. B. Sorokin, Dalton Trans., 2009, 7410–7420 RSC.
- E. V. Kudrik, P. Afanasiev, L. X. Alvarez, P. Dubourdeaux, M. Clémancey, J.-M. Latour, G. Blondin, D. Bouchu, F. Albrieux, S. E. Nefedov and A. B. Sorokin, Nat. Chem., 2012, 4, 1024–1029 CrossRef CAS PubMed.
- P. Afanasiev, E. V. Kudrik, J.-M. M. Millet, D. Bouchu and A. B. Sorokin, Dalton Trans., 2011, 40, 701–710 RSC.
- C. Colomban, E. V. Kudrik, V. Briois, J. C. Shwarbrick, A. B. Sorokin and P. Afanasiev, Inorg. Chem., 2014, 53, 11517–11530 CrossRef CAS PubMed.
- H. Basch, K. Mogi, D. G. Musaev and K. Morokuma, J. Am. Chem. Soc., 1999, 121, 7249–7256 CrossRef CAS.
- P. E. M. Siegbahn and R. H. Crabtree, J. Am. Chem. Soc., 1997, 119, 3103–3113 CrossRef CAS.
- M.-H. Baik, M. Newcomb, R. A. Friesner and S. J. Lippard, Chem. Rev., 2003, 103, 2385–2420 CrossRef CAS PubMed.
- R. Silaghi-Dumitrescu, S. V. Makarov, M.-M. Uta, I. A. Dereven'kov and P. A. Stuzhin, New J. Chem., 2011, 35, 1140–1145 RSC.
- M. Jaccob, A. Ansari, B. Pandey and G. Rajaraman, Dalton Trans., 2013, 42, 16518–16526 RSC.
- A. Ansari, A. Kaushik and G. Rajaraman, J. Am. Chem. Soc., 2013, 135, 4235–4249 CrossRef CAS PubMed.
- S.-P. Huang, Y. Shiota and K. Yoshizawa, Dalton Trans., 2013, 42, 1011–1023 RSC.
- T. Saito, Y. Kataoka, Y. Nakanishi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Supramol. Chem., 2010, 23, 83–87 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Wallingford CT, 2009.
- F. Neese, WIRES, 2012, 2, 73–78 CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Pabis, I. Geronimo and P. Paneth, J. Phys. Chem. B, 2014, 118, 3245–3256 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- G. A. Zhurko, ChemCraft software, version 1.6, 2014 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef.
- E. J. B. a. J. G. S. E. van Lenthe, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- C. J. v. Wullen, Chem. Phys., 1998, 109, 392–399 Search PubMed.
- M. Radoul, M. Sundararajan, A. Potapov, C. Riplinger, F. Neese and D. Goldfarb, Phys. Chem. Chem. Phys., 2010, 12, 7276–7289 RSC.
- M. Römelt, S. Ye and F. Neese, Inorg. Chem., 2009, 48, 784–785 CrossRef PubMed.
- G. Rajaraman, E. Ruiz, J. Cano and S. Alvarez, Chem. Phys. Lett., 2005, 415, 6–9 CrossRef CAS.
- S. Tewary, I. A. Gass, K. S. Murray and G. Rajaraman, Eur. J. Inorg. Chem., 2013, 2013, 1024–1032 CrossRef CAS.
- N. Berg, T. Rajeshkumar, S. M. Taylor, E. K. Brechin, G. Rajaraman, L. F. Jones, N. Berg, T. Rajeshkumar, S. M. Taylor, E. K. Brechin, G. Rajaraman and L. F. Jones, Chem. – Eur. J., 2012, 18, 5906–5918 CrossRef CAS PubMed.
- P. Jayapal and G. Rajaraman, Phys. Chem. Chem. Phys., 2012, 14, 9050–9053 RSC.
- S. K. Singh, N. K. Tibrewal and G. Rajaraman, Dalton Trans., 2011, 40, 10897–10906 RSC.
- G. Rajaraman, M. Murugesu, E. C. Sañudo, M. Soler, W. Wernsdorfer, M. Helliwell, C. Muryn, J. Raftery, S. J. Teat, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2004, 126, 15445–15457 CrossRef CAS PubMed.
- P. Christian, G. Rajaraman, A. Harrison, J. J. W. McDouall, J. T. Raftery and R. E. P. Winpenny, Dalton Trans., 2004, 1511–1512 RSC.
- D. Gatteschi and A. Bencini, EPR of Exchange Coupled Systems, Springer-Verlag, Berlin, 1990 Search PubMed.
- Note here that since geometry optimization was not successful for this spin state, single point calculations on 62(is, is) geometry were utilized to compute the energy.
- J. T. Groves, R. C. Haushalter, M. Nakamura, T. E. Nemo and B. J. Evans, J. Am. Chem. Soc., 1981, 103, 2884–2886 CrossRef CAS.
- S. R. Bell and J. T. Groves, J. Am. Chem. Soc., 2009, 131, 9640–9641 CrossRef CAS PubMed.
- S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS PubMed.
- K.-B. Cho, X. Wu, Y.-M. Lee, Y. H. Kwon, S. Shaik and W. Nam, J. Am. Chem. Soc., 2012, 134, 20222–20225 CrossRef CAS PubMed.
- F. Ogliaro, N. Harris, S. Cohen, M. Filatov, S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2000, 122, 8977–8989 CrossRef CAS.
- J. N. Harvey and M. Aschi, Faraday Discuss., 2003, 124, 129–143 RSC.
- P. Barman, A. K. Vardhaman, B. Martin, S. J. Wörner, C. V. Sastri and P. Comba, Angew. Chem., Int. Ed., 2015, 54, 2095–2099 CrossRef CAS PubMed.
- S. Ye and F. Neese, Proc. Natl. Acad. Sci., U. S. A., 2011, 108, 1228–1233 CrossRef CAS PubMed.
- G. Schwarz, R. R. Mendel and M. W. Ribbe, Nature, 2009, 460, 839–847 CrossRef CAS PubMed.
- M. Filatov, N. Harris and S. Shaik, Angew. Chem., Int. Ed., 1999, 38, 3510–3512 CrossRef CAS.
- S. Shaik, S. P. de Visser, F. Ogliaro, H. Schwarz and D. Schröder, Curr. Opin. Chem. Biol., 2002, 6, 556–567 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Eigen value plots, NBO plots, table for energy, optimized parameters, spin density. See DOI: 10.1039/c5dt01060h |
| This journal is © The Royal Society of Chemistry 2015 |