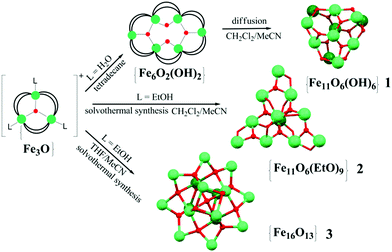
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Undecametallic and hexadecametallic ferric oxo–hydroxo/ethoxo pivalate clusters†
Svetlana G.
Baca
*ab,
Manfred
Speldrich
a,
Jan
van Leusen
a,
Arkady
Ellern
c and
Paul
Kögerler
*ad
aInstitute of Inorganic Chemistry, RWTH Aachen University, Aachen, Germany. E-mail: paul.koegerler@ac.rwth-aachen.de; Fax: +49-241-80-92642; Tel: +49-241-80-93642
bInstitute of Applied Physics, ASM, Chisinau, R. Moldova. E-mail: sbaca_md@yahoo.com; Fax: +373-22-738154; Tel: +373-22-725887
cAmes Laboratory, Iowa State University, Ames, Iowa, USA
dPeter Grünberg Institute-6, Research Centre Jülich, Jülich, Germany
First published on 27th March 2015
Abstract
Synthesis strategies for highly condensed {Fe11} and {Fe16} pivalate clusters have been developed based on archetypal geometrically frustrated triangular {Fe3(μ3-O)} motifs that are interlinked via oxo, hydroxo, ethoxo, and carboxylate groups.
High-nuclearity transition metal coordination clusters receive considerable attention due to their magnetic properties and their possible technological application in high-density magnetic storage devices, quantum computing and spintronics.1 In most cases the synthetic methods towards such high-nuclearity clusters are not straightforward and final products cannot be predicted. Following up on our work on the design of high-nuclearity iron oxo-carboxylates2 we have been interested in developing different synthetic approaches to this type of ferric clusters, including their similarities to concepts of molecular metal oxide cluster chemistry, and report here the synthesis, structure and magnetic properties of a series of undeca- and hexadecametallic FeIII pivalate clusters, namely the undecanuclear clusters [Fe11O6(OH)6(O2CCMe3)15] (1) and [Fe11O6(EtO)9(O2CCMe3)12] (2) [2·1.5CH2Cl2·MeCN], and hexadecanuclear clusters [Fe16O13(EtO)6(O2CCMe3)16] (3) [3·0.25thf and 3·3thf]. Over the past two decades several successful attempts have been made to prepare {Fe11}- and {Fe16}-type carboxylate clusters: Lippard et al.3a,b reported the first oxo–hydroxo benzoate-based {Fe11}, [Fe11O6(OH)6(O2CPh)15], in 1986 starting from simple iron salt, sodium benzoate and a defined amount of water present in the reaction mixture. Using other carboxylate bridging groups, 3-(4-methylbenzoyl)-propionic or tert-butylacetic acids, Winpenny et al.3c–e designed undecanuclear cages with a similar {Fe11O6(OH)6}15+ core: here again the synthetic procedure involved the employment of a simple hydrated iron nitrate salt or heating a trinuclear iron carboxylate starting material under an inert atmosphere at 300 °C. Moreover, the solid-state decomposition of pre-formed polynuclear species, in particular hexanuclear iron carboxylates, into [Fe11O6(OH)6(O2CR)15] (R = Ph, 2-MePh, 3-MePh) complexes has been further developed.3f Another successful approach for the synthesis of undecametallic ferric complexes that was used by several groups3g–i employs different chelating and bridging polyalcohol ligands together with carboxylates. This led to the formation of clusters with new metallic core topologies, some of which exhibit single-molecule magnet characteristics.3g,h The same strategy was used for preparation of {Fe16}-type compounds; previously reported examples feature: a wheel-shaped structure3j,k and a cluster with a {Fe16O10(OH)2}26+ metallic core.3l All these {Fe16} compounds were prepared by the reaction of FeIII precursors with polyalcohol ligands under ambient conditions. Herein, we demonstrate easy and convenient routes (Scheme 1) starting from μ3-oxo trinuclear species to yield a series of high-nuclearity, charge-neutral ferric clusters.
The oxo–hydroxo {Fe11} complex 1 was prepared in good yield (80%) by slow diffusion of MeCN in a CH2Cl2 solution of [Fe6O2(OH)2(O2CCMe3)12]. Direct solvothermal heating of a μ3-oxo trinuclear pivalate cluster compound, [Fe3O(O2CCMe3)6(EtOH)3]NO3·EtOH (4) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of CH2Cl2–MeCN at 120 °C for 4 hours yields the oxo–ethoxo {Fe11} cluster 2·1.5CH2Cl2·MeCN.
1 mixture of CH2Cl2–MeCN at 120 °C for 4 hours yields the oxo–ethoxo {Fe11} cluster 2·1.5CH2Cl2·MeCN.
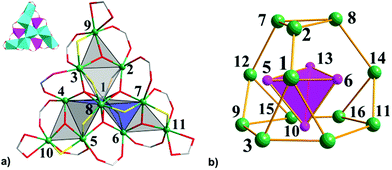
Single-crystal X-ray diffraction analysis showed that 1 crystallizes in the monoclinic space group P21/c and the unit cell contains two crystallographically independent neutral [Fe11O6(OH)6(O2CCMe3)15] clusters [structural units A and B] with a metallic {Fe11O6(OH)6}15+ core similar to mentioned-above {Fe11} clusters.3a–i Complex 2·1.5CH2Cl2·MeCN contains a neutral [Fe11O6(EtO)9(O2CCMe3)12] cluster and crystallizes with 1.5 molecules of CH2Cl2 and one molecule of MeCN per formula unit in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The geometry of the Fe11 substructure in the metallic core of 1 can be best described as a distorted pentacapped trigonal prism (Fig. 1). The two triangular faces of the prism, which are equilateral Fe3 triangles [A: Fe2, Fe6, Fe8 and Fe3, Fe5, Fe9; B: Fe19, Fe16, Fe22 and Fe18, Fe15, Fe13, Fig. 2], are twisted by an angle of 17.99(8), 19.16(8) and 18.22(8)° (average 18.46°, A), and 18.57(10), 17.93(9) and 18.77(9)° (average 18.42°, B). Two Fe centers [Fe11 and Fe10 (A), and Fe20 and Fe21 (B)] cap the triangular faces, whereas three other Fe atoms [Fe1, Fe4 and Fe7 (A); Fe12, Fe14 and Fe17 (B)] each cap one of the rectangular faces of the prism. Each Fe atom is in +3 oxidation state (BVS, 2.89–3.24, Table S3†), and has a distorted octahedral environment. The Fe atoms at the corners of the triangular faces of the prism [such as Fe2, Fe6 and Fe8 and Fe3, Fe5 and Fe9, etc.] are coordinated to one μ3-O, two μ3-OH and three O atoms from three pivalates. The Fe atoms which cap the rectangular faces [labelled as Fe1, Fe4, Fe7, etc.] each bind to two μ3-O, two μ3-OH and two O atoms from two carboxylates, whereas the central Fe atoms [Fe10 and Fe11 (A), and Fe20 and Fe21 (B)] are coordinated to three μ3-O atoms and three carboxylate O atoms (Fe–Ocarb, 1.922(1) to 2.126(1) Å). The Fe–μ3-O distances are in the 1.876(1)–1.944(1) Å range, which are significantly shorter then Fe–μ3-OH distances of 2.017(1)–2.168(1) Å (Table S2†).
. The geometry of the Fe11 substructure in the metallic core of 1 can be best described as a distorted pentacapped trigonal prism (Fig. 1). The two triangular faces of the prism, which are equilateral Fe3 triangles [A: Fe2, Fe6, Fe8 and Fe3, Fe5, Fe9; B: Fe19, Fe16, Fe22 and Fe18, Fe15, Fe13, Fig. 2], are twisted by an angle of 17.99(8), 19.16(8) and 18.22(8)° (average 18.46°, A), and 18.57(10), 17.93(9) and 18.77(9)° (average 18.42°, B). Two Fe centers [Fe11 and Fe10 (A), and Fe20 and Fe21 (B)] cap the triangular faces, whereas three other Fe atoms [Fe1, Fe4 and Fe7 (A); Fe12, Fe14 and Fe17 (B)] each cap one of the rectangular faces of the prism. Each Fe atom is in +3 oxidation state (BVS, 2.89–3.24, Table S3†), and has a distorted octahedral environment. The Fe atoms at the corners of the triangular faces of the prism [such as Fe2, Fe6 and Fe8 and Fe3, Fe5 and Fe9, etc.] are coordinated to one μ3-O, two μ3-OH and three O atoms from three pivalates. The Fe atoms which cap the rectangular faces [labelled as Fe1, Fe4, Fe7, etc.] each bind to two μ3-O, two μ3-OH and two O atoms from two carboxylates, whereas the central Fe atoms [Fe10 and Fe11 (A), and Fe20 and Fe21 (B)] are coordinated to three μ3-O atoms and three carboxylate O atoms (Fe–Ocarb, 1.922(1) to 2.126(1) Å). The Fe–μ3-O distances are in the 1.876(1)–1.944(1) Å range, which are significantly shorter then Fe–μ3-OH distances of 2.017(1)–2.168(1) Å (Table S2†).
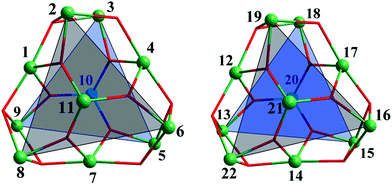 | ||
| Fig. 1 The distorted pentacapped trigonal prismatic arrangement of Fe atoms in the metallic core {Fe11O6(OH)6}15+ of 1 (left – unit A, right – unit B). | ||
In contrast to 1, the Fe11 substructure in 2·1.5CH2Cl2·MeCN, more resembles a three-blade propeller (Fig. 2a). Each blade consists of 5 Fe atoms: four of them form a Fe4 tetrahedron and a μ3-O atom further bridges the fifth peripheral Fe ion to the edge of the polyhedron with the formation of an almost planar {Fe3(μ3-O)} unit. The central μ3-O atoms in each Fe3 unit deviate only slightly out-of-plane: O4 and O5 by 0.034 Å, and O6 by 0.076 Å. The pairs of Fe atoms that form the external edges of this triangle unit are additionally bridged by carboxylate or by carboxylate and ethanolate ligands. As a result, the Fe⋯Fe distance (ca. 3.36 Å) between the Fe atoms bridged by only carboxylate is longer than the bond distance of ca. 2.96 Å between Fe atoms connected by pivalate and ethanolate ligands. Thus, the metallic core of 2·1.5CH2Cl2·MeCN includes three flattened polyhedra sharing the central Fe1−Fe8 axis of the core with a shortest Fe⋯Fe distance of 2.801(1) Å. The three μ4-O atoms (O1, O2, and O3) and three bridging pivalates link the blades of the propeller. BVS calculations revealed mean oxidation states of +III for all Fe atoms in 2·1.5CH2Cl2·MeCN [2.99–3.22, Table S3†]. Eight Fe centers from them adopt distorted octahedral coordination environment with an O6 donor set: the central Fe1 and Fe8 atoms are coordinated by three μ4-O atoms and three O atoms from three bridging ethanol ligands; Fe3, Fe5 and Fe7 centres are coordinated by one μ4-O and one μ3-O atoms, two carboxylate O atoms and two ethoxy O atoms, and finally, the coordination geometry of the peripheral Fe9, Fe10 and Fe11 atoms is completed by one μ3-O atom, one ethoxy O atom, two O atoms from bridging pivalates and two O atoms from the chelated carboxylate ligand (Fe–O, 1.881(6)–2.107(6) Å, Table S2†). The remaining three Fe atoms [Fe2, Fe4 and Fe6] are five-coordinated and all adopt a square pyramidal coordination environment with an O5 donor set and tau (τ) parameter4 being in the range of 0.04–0.09 (Fig. 2a). The equatorial positions are occupied by a μ4-O atom, an ethoxy O atom and two carboxylate O atoms (Fe–O, 1.943(6)–2.009(6) Å), while the axial position is ligated by a μ3-O atom [Fe–O, 1.812(6)–1.821(6) Å]. The deviation of the Fe atoms from the equatorial plane is 0.349 (Fe2), 0.367 (Fe4), and 0.380 Å (Fe6).
Solvothermal heating of μ-oxo trinuclear species in thf or thf–MeCN solution afforded the largest oxo–ethoxo FeIII pivalate cluster [Fe16O13(EtO)6(O2CCMe3)16] (3) in ca. 50% yield. In thf–MeCN solution, 3 crystallizes in the monoclinic space group P21/c with 0.25 molecules of thf per formula unit, while crystallization out of a MeCN solution leads to a product with three thf crystal solvent molecules per formula unit, crystallizing in the monoclinic space group C2/n. Single-crystal X-ray diffraction analysis revealed a similar arrangement of 16 Fe atoms in both complexes, so here we will discuss the structure of 3·3thf in detail. The metallic core in 3 consists of 16 FeIII atoms, whose oxidation states were confirmed by BVS (2.87–3.12, Table S3†), bridged by five μ4-O2− ions, eight μ3-O2− ions, six ethoxy EtO− groups and additionally linked by 16 bridging pivalate ligands. All FeIII atoms are six-coordinated with a distorted octahedral geometry except for Fe5, Fe6, Fe10, and Fe13 atoms which are five-coordinated with a distorted square pyramidal geometry (τ = 0.14–0.16).4 The coordination sphere of six-coordinated Fe atoms is completed by a μ3-O atom, a μ4-O atom, three carboxylate O atoms from three different pivalates and one O atom from ethanol ligand (Fe–O, 1.897(4)–2.180(4) Å, Table S2†). The Fe atoms with a square pyramidal environment are coordinated by three μ4-O atoms and one μ3-O atom of ethanol ligand, that form an equatorial plane [Fe–μ4-O, 1.962(3)–2.039(4) Å; Fe–μ3-O 2.053(4)–2.067(3) Å] and a μ3-O atom occupying the axial position (Fe–μ3-O, 1.796(4)–1.803(4) Å). Thus, the arrangement of Fe atoms in 3 can be approximated as assembly of a smaller inverted Fe4 tetrahedron defined by the square pyramidal Fe5, Fe6, Fe10 and Fe13 sites within a giant truncated tetrahedron forming by other 12 octahedral Fe sites with four triangular and four hexagonal faces (Fig. 2b). Note the structural similarity of the Fe12 substructure to the metal skeleton of the classical polyoxometalate {M12(XO4)} Keggin structure, also of Td symmetry. The internal inverted tetrahedron houses a central μ4-O atom (O13) and represents an irregular polyhedron with all triangular faces being isosceles [two shorter Fe⋯Fe separations of 3.017(1)–3.029(1) Å and one long separation of 3.567(1)–3.572(1) Å]. Moreover, the Fe–μ4-O–Fe angles within this tetrahedron range from 100.25(1)° to 130.19(1)°, deviating significantly from the ideal values of a tetrahedron (109.5°). The giant truncated tetrahedron also deviates from regular truncated tetrahedra: all its triangular faces are isosceles with two longer Fe⋯Fe distances (3.388(1)–3.423(1) Å) and one short Fe⋯Fe distance (3.081(1)–3.093(1) Å) [Fe3⋯Fe4, Fe7⋯Fe8, Fe9⋯Fe12, and Fe11⋯Fe12 edges]. The Fe⋯Fe separations around the hexagonal faces range from 2.713(1) to 3.543(1) Å.
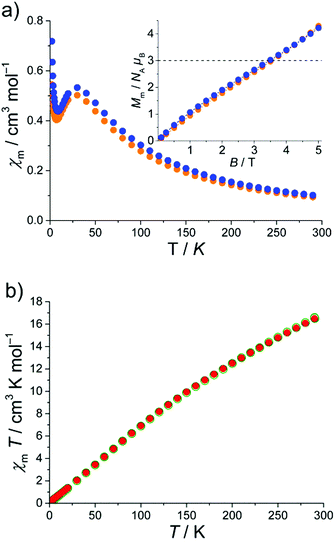
The magnetic susceptibilities of 1–3 were measured on microcrystalline samples in a 0.1 T field in the 2.0–290 K range. In addition, the field dependence of the molar magnetization B was determined for fields up to 5.0 T at T = 2 K. The χmvs. T plot and the Mmvs. B plot (as inset) for 1 and 2·1.5CH2Cl2·MeCN are shown in Fig. 3. The molar susceptibility curve reveals a broad maximum at 30.0 K (0.51 cm3 mol−1 (1) and 0.53 cm3 mol−1 (2·1.5CH2Cl2·MeCN)). In addition, χmT (not shown) exhibits a continuous decrease upon cooling starting at χmT = 27.1 cm3 mol−1 K (1) and 29.4 cm3 mol−1 K (2·1.5CH2Cl2·MeCN) at room temperature. These values are well below the spin-only (g = 2) value of 48.1 cm3 mol−1 K expected for eleven non-interacting high-spin (S = 5/2) FeIII ions. Such behavior is characteristic of {Fe3(μ3-O)-type compounds that often display strong antiferromagnetic exchange interactions.
Upon cooling, a second characteristic point appears in the χmvs. T plot for 1 and 2·1.5CH2Cl2·MeCN: a sharp minimum at 7 K, most likely due to a paramagnetic impurity, a change of the ground state under the influence of applied magnetic field or a mixture of both. In frustrated molecular rings Kozłowski et al. investigated the ground state of a {Cr9}-ring by analyzing their Mmvs. H and χmvs. T behavior.5 The investigated {Cr9}-ring shows a similar behavior as the Mmvs. B and χmvs. T plots for 1 and 2·1.5CH2Cl2·MeCN presented in Fig. 3a. If the ground state changes within the measured range of the magnetic field, an inflection (or intersection5) point appears in the Mmvs. B plot. Such a point is indeed revealed in the powder magnetization curve close to 3NAμB (see inset Fig. 3a). Thus, the upper limit of ground state is S = 3/2. In Fig. 3a, the dotted line corresponds to the theoretical magnetization plot (for T → 0) for a S = 3/2 ground state which intersects the Mmvs. B curve at B = 3.2 T. The intersection point is equal to the inflection point of the Mmvs. B plots of 1 and 2·1.5CH2Cl2·MeCN. On the basis of the Mmvs. B and χmvs. T behavior and adopting the work of Kozłowski et al.,5 we propose S = 3/2 ground states for 1 and 2·1.5CH2Cl2·MeCN.
In the case of 3·0.25thf and 3·3thf the situation is quite different because of the even number of magnetic centers. The obtained data are plotted as χmT vs. T in Fig. 3b. The χmT value for 3·0.25thf and 3·3thf decreases steadily with decreasing temperature from 16.5 cm3 mol−1 K at 290 K to 0.2 cm3 mol−1 K at 2.0 K, consistent with an S = 0 ground state. The χmT value at 290 K is well below the spin-only (g = 2) value of 70.0 cm3 mol−1 K expected for sixteen non-interacting high-spin (S = 5/2) FeIII ions. This behavior clearly indicates strong antiferromagnetic interactions between the FeIII centers supporting the assumption of an overall S = 0 ground state. This result is fully in agreement with those previously reported compounds for comparable even-nuclearity Fen compounds, which also have spin singlet ground state as a result of antiferromagnetic exchange interactions between adjacent FeIII ions and resulting antiparallel arrangement of spins in the cluster.6
Conclusions
The presented syntheses of {Fe11}- and {Fe16}-type coordination clusters highlight the role of co-ligands, solvent and reaction temperature in the described synthesis route that exploits the possibilities of {FeIII3(μ3-O)}-based condensation reactions. The facile syntheses produce starkly different high-nuclearity coordination cluster structures that are highly condensed yet still retain the archetypal triangular motif. Strong antiferromagnetic coupling and spin frustration effects dominate the magnetic properties, and both singlet (3) and S = 3/2 (1 and 2·1.5CH2Cl2·MeCN) ground states were predicted based on polycrystalline susceptibility measurements.Acknowledgements
Financial support from the EU (POLYMAG, IIF contract no. 252984; ERC Starting Grant MOLSPINTRON; COST Action CM1203, COST-STSM-CM1203-19097) is acknowledged.Notes and references
- Molecular Cluster Magnets, ed. R. Winpenny, World Scientific Books, Singapore, 2011 Search PubMed.
- (a) S. G. Baca, M. Speldrich, A. Ellern, S. G. Baca and P. Kögerler, Materials, 2011, 4, 300 CrossRef CAS PubMed; (b) S. G. Baca, O. Botezat, I. Filippova, M. Speldrich, E. Jeanneau and P. Kögerler, Z. Anorg. Allg. Chem., 2011, 637, 821 CrossRef CAS.
- (a) S. M. Gorun and S. J. Lippard, Nature, 1986, 319, 666 CrossRef CAS PubMed; (b) S. M. Gorun, G. C. Papaefthymiou, R. B. Frankel and S. J. Lippard, J. Am. Chem. Soc., 1987, 109, 3337 CrossRef CAS; (c) M. Frey, S. G. Harris, J. M. Holmes, D. A. Nation, S. Parson, P. A. Tasker, S. J. Teat and R. E. P. Winpenny, Angew. Chem., Int. Ed., 1998, 37(23), 3246 CrossRef CAS; (d) M. Frey, S. G. Harris, J. M. Holmes, D. A. Nation, S. Parson, P. A. Tasker and R. E. P. Winpenny, Chem. – Eur. J., 2000, 6(8), 1407 CrossRef CAS; (e) A. A. Smith, R. A. Coxall, A. Harrison, M. Helliwell, S. Parson and R. E. P. Winpenny, Polyhedron, 2004, 23, 1557 CrossRef CAS PubMed; (f) E. C. Sanudo, M. Font-Bardia, X. Solans and R. H. Laye, New J. Chem., 2011, 35, 842 RSC; (g) L. F. Jones, E. K. Brechin, D. Collison, M. Helliwell, T. Mallah, S. Piligkos, G. Rajaraman and W. Wernsdorfer, Inorg. Chem., 2003, 42, 6601 CrossRef CAS PubMed; (h) C. Boskovic, H. U. Güdel, G. Labat, A. Neels, W. Wernsdorfer, B. Moubaraki and K. S. Murray, Inorg. Chem., 2005, 44, 3181 CrossRef CAS PubMed; (i) A. M. Ako, V. Mereacre, Y. Lan, W. Wernsdorfer, R. Clerac, C. E. Anson and A. K. Powell, Inorg. Chem., 2010, 49, 1 CrossRef CAS PubMed; (j) L. F. Jones, A. Batsanov, E. K. Brechin, D. Collison, M. Helliwell, T. Mallah, E. J. L. McInnes and S. Piligkos, Angew. Chem., Int. Ed., 2002, 41, 4318 CrossRef CAS; (k) L. F. Jones, D. M. Low, M. Helliwell, J. Raftery, D. Collison, G. Aromi, J. Cano, T. Mallah, W. Wernsdorfer, E. K. Brechin and E. J. L. Mcinnes, Polyhedron, 2006, 25, 325 CrossRef CAS PubMed; (l) A. M. Ako, V. Mereacre, Y. Lan, C. E. Anson and A. K. Powell, Chem. – Eur. J., 2011, 17, 4366 CrossRef CAS PubMed.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349 RSC.
- (a) M. Antkowiak, P. Kozłowski, G. Kamieniarz, G. A. Timco, F. Tuna and R. E. P. Winpenny, Phys. Rev. B: Condens. Matter, 2013, 87, 184430 CrossRef; (b) P. Kozłowski and G. Kamieniarz, J. Nanosci. Nanotechnol., 2011, 11, 9175 CrossRef PubMed.
- M. Murugesu, K. A. Abboud and G. Christou, Dalton Trans., 2003, 4552 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Syntheses, crystallographic details and BVS calculations, TGA/DTA spectra. CCDC 875371 (1), 875369 (2), 875370 (3·0.25thf), 875373 (3·3thf) and 875372 (4). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt00665a |
| This journal is © The Royal Society of Chemistry 2015 |