Open Access Article
Open Access ArticleThe interaction of Eu(III) with organoborates – a further approach to understand the complexation in the An/Ln(III)–borate system†
Juliane
Schott
ab,
Jerome
Kretzschmar
a,
Satoru
Tsushima
 a,
Björn
Drobot
a,
Margret
Acker
*b,
Astrid
Barkleit
a,
Steffen
Taut
b,
Vinzenz
Brendler
a and
Thorsten
Stumpf
ac
a,
Björn
Drobot
a,
Margret
Acker
*b,
Astrid
Barkleit
a,
Steffen
Taut
b,
Vinzenz
Brendler
a and
Thorsten
Stumpf
ac
aHelmholtz-Zentrum Dresden-Rossendorf, Institute of Resource Ecology, Bautzner Landstraße 400, 01328 Dresden, Germany
bTechnische Universität Dresden, Central Radionuclide Laboratory, 01062 Dresden, Germany. E-mail: margret.acker@tu-dresden.de
cTechnische Universität Dresden, Division of Radiochemistry and Radioecology, 01062 Dresden, Germany
First published on 5th May 2015
Abstract
The formation equilibria of salicylatoborate, lactatoborate and 3-hydroxybutyratoborate were studied by means of 11B NMR spectroscopy. The smaller the pKa of the respective organic acid, the higher is the formation constant of the organoborate. The complexation of Eu(III) with salicylatoborate and lactatoborate was investigated by means of TRLFS (time-resolved laser-induced fluorescence spectroscopy) and 11B NMR spectroscopy, yielding complexation constants lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β011 = 2.6–3.2. A Eu(III)–3-hydroxybutyrate complex was characterized by TRLFS and 1H NMR spectroscopy (lg
β011 = 2.6–3.2. A Eu(III)–3-hydroxybutyrate complex was characterized by TRLFS and 1H NMR spectroscopy (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β011 = 2.89). DFT calculations of the investigated Eu(III)–organoborates and inorganic Eu(III)–(poly)borates provided information about the Eu(III) coordination (most likely chelate). They support the hypothesis that the complexation of Eu(III) with organic as well as inorganic borate structures containing the binding site “B(OR)4−” (R = H, threefold coordinated boron center(s), organic moiety) is comparable.
β011 = 2.89). DFT calculations of the investigated Eu(III)–organoborates and inorganic Eu(III)–(poly)borates provided information about the Eu(III) coordination (most likely chelate). They support the hypothesis that the complexation of Eu(III) with organic as well as inorganic borate structures containing the binding site “B(OR)4−” (R = H, threefold coordinated boron center(s), organic moiety) is comparable.
Introduction
Great efforts have been made worldwide to find suitable environments for the safe storage of high-level radioactive wastes. In many countries it is agreed that these wastes should be stored in deep geological formations (salt, argillaceous rock, crystalline rock). Safety and risk assessment of a nuclear waste repository has to consider the case of water ingress, which would initiate corrosion and dissolution processes of the stored inventory (container material, radioactive waste), the backfill and host rock components. Trivalent actinides such as americium, curium and, under reducing conditions, plutonium, will significantly contribute to the long-term radiotoxicity of the spent nuclear fuel.1 Any reliable estimation of their migration behavior in the near and far field of such a repository requires both process understanding and data to parameterize the respective reactive transport models. In the last few decades large amounts of data concerning the chemistry of trivalent actinides, like complexation with organic and inorganic ligands as well as solubility, have been generated. Several thermodynamic databases are summarizing them.2–5 However, only recently the actinide–borate system has attracted more attention6–10 though borates are ubiquitous. In the context of nuclear waste repositories they are obtained – naturally as well as technologically – from different sources, e.g., salt deposits and brines, and corroded glass coquilles in which the high-level radioactive waste is fused.6,9,11 So far, knowledge about the complexation of (poly)borates with trivalent actinides has been insufficient in order to estimate a possible mobilization of actinides by (poly)borates in a nuclear waste repository.Borkowski et al. investigated in their pioneering work the complexation of Nd(III) (as an analog for trivalent actinides) in borate solutions considering conditions typical for the Waste Isolation Pilot Plant (WIPP) near Carlsbad, New Mexico, USA.6 From solubility experiments they determined a Nd(III) borate complexation constant lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β011 = 4.55.6 This complex was considered to be a predominant actinide(III) species under the WIPP brine conditions (up to 160 mM borate, pHc = 8–9), also influencing the actinide–carbonate complexation.6,12 In a previous work, we demonstrated that the complexation constant of the trivalent europium (as another chemical analog for trivalent actinides) with (poly)borates is smaller (lg
β011 = 4.55.6 This complex was considered to be a predominant actinide(III) species under the WIPP brine conditions (up to 160 mM borate, pHc = 8–9), also influencing the actinide–carbonate complexation.6,12 In a previous work, we demonstrated that the complexation constant of the trivalent europium (as another chemical analog for trivalent actinides) with (poly)borates is smaller (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β011 ∼ 2.6) than expected.9 Several difficulties (precipitation of the metal borates, metal hydroxide complexation and precipitation at higher pH) made the investigation of this system very challenging. Therefore, approximations had to be made in order to obtain a complexation constant for the An/Ln(III)–(poly)borate system (An = actinide, Ln = lanthanide).9
β011 ∼ 2.6) than expected.9 Several difficulties (precipitation of the metal borates, metal hydroxide complexation and precipitation at higher pH) made the investigation of this system very challenging. Therefore, approximations had to be made in order to obtain a complexation constant for the An/Ln(III)–(poly)borate system (An = actinide, Ln = lanthanide).9
In the present work, a completely different approach was drafted to support the lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(0)11 values obtained previously for Eu(III)–(poly)borate complexes9 using organoborates as structural representatives for borate compounds.
β(0)11 values obtained previously for Eu(III)–(poly)borate complexes9 using organoborates as structural representatives for borate compounds.
The simplest form of a borate species is the monoborate anion. Due to the high dissociation constant of boric acid (pKa = 9.13, our data by potentiometric titration, see below) the monoborate anion exists in considerable amounts only in the high alkaline pH range. There, unfortunately, complexation studies with trivalent actinides or lanthanides are next to impossible, due to the formation of strong metal hydroxide complexes, which could even precipitate. Therefore, an alternative experimental approach under acidic conditions was devised. The binding site to the metal ion is the structural unit B(OR)4− containing a fourfold coordinated boron center with a negative charge. Our hypothesis is that all borates (inorganic, organic) containing this B(OR)4− unit (R = H, other threefold coordinated boron center(s), organic moieties, thereby including also the simple monoborate anion and inorganic polyborates with one binding site) exhibit a comparable complexation behavior concerning trivalent lanthanides or actinides.
Organoborates form a group of compounds containing such a B(OR)4− unit. The literature describes the formation of these organoborates by reactions of either boric acid with hydroxycarboxylates or the monoborate anion with polyols (Fig. 1).13,14 In contrast to the polyol based organoborates the ones based on hydroxycarboxylates are formed (and are stable) in the acidic pH range. Here, metal complexation studies can be carried out with good prospects. Hence, hydroxycarboxylate based organoborates were used to study the complexation with Eu(III).
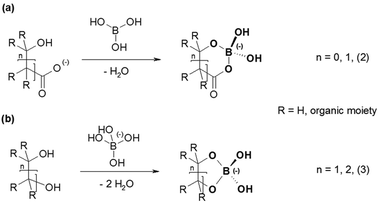 | ||
| Fig. 1 General structures of organoborates resulting from the reaction of (a) boric acid with hydroxycarboxylates and (b) the monoborate anion with polyols. | ||
Primarily, the objective of this work was to confirm our hypothesis experimentally investigating the complexation of Eu(III) with different organoborates. Namely, we wanted to know to what extent the ring size (five- and six-membered) of the respective organoborate and the nature of the organic moiety bound to the B(OR)4− unit influence the Eu(III) complexation. Consequently, for the first time different Eu(III)–organoborate complexes are described with specific thermodynamic values.
Salicylatoborate, lactatoborate and 3-hydroxybutyratoborate were chosen as complexing organic borate ligands (Fig. S1†). Because the complexation reactions of Eu(III) with the (pure) carboxylates have to be considered in the calculation of the Eu(III)–organoborate complex formation constants, it is of advantage that these reactions with the chosen carboxylates are well characterized.
By TRLFS (time-resolved laser-induced fluorescence spectroscopy) and 11B NMR (nuclear magnetic resonance) spectroscopy we were able to study the Eu(III)–organoborate complexation from two opposite perspectives: TRLFS probes the metal site, where changes in the Eu(III) speciation can be observed with high sensitivity and selectivity at low metal concentrations (∼10−5 M), whereas NMR provides a view of the ligand (organoborate) and its speciation changes in the presence of Eu(III). Due to the paramagnetism of Eu3+, the signals of molecules interacting with the europium ion are shifted considerably with only low signal broadening.15–17 The Eu(III) concentration dependent paramagnetic induced shift18 was used here to determine the complexation constant of the Eu(III)–salicylatoborate and Eu(III)–lactatoborate.
Density functional theory (DFT) calculations are useful to test the hypothesis that borates with the structural unit B(OR)4− have comparable complexation properties to An/Ln(III). Therefore, in this work different borate structures (inorganic (poly)borates, organoborates) and the respective Eu(III) complex structures were calculated. This also provided further insights into the coordination of Eu(III) with the borate structures.
One prerequisite for the Eu(III) organoborate complexation studies is the pKa values of the organic compounds used (salicylic, lactic and 3-hydroxybutyric acid) and boric acid. They were determined by potentiometric titration. Furthermore, the formation constants of the organoborates were obtained from 11B NMR experiments. The Eu(III)–salicylate and Eu(III)–lactate complexation constants were determined by TRLFS or obtained from the literature. A complexation constant for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Eu(III)–3-hydroxybutyrate complex was determined from TRLFS and 1H NMR spectroscopic data.
1 Eu(III)–3-hydroxybutyrate complex was determined from TRLFS and 1H NMR spectroscopic data.
Experimental section
Chemicals and materials
Solutions were prepared from chemicals of analytical grade and deionized water. Sodium salicylate (Sigma Aldrich), sodium L-lactate (Sigma Aldrich), sodium D/L-3-hydroxybutyrate (Fluka) and boric acid (Merck) were used without further purification. The total boron concentration (cB,total) was adjusted with boric acid. A Eu(III) stock solution (30 mM) was prepared by dissolving Eu2O3 (Aldrich) in 0.1 M HClO4. Its concentration was verified by ICP-MS (Elan 9000, Perkin Elmer). Solid EuCl3·6H2O (Aldrich) was used to adjust higher Eu(III) concentrations (up to 50 mM). All samples for potentiometric titration and TRLFS experiments were prepared at 0.1 M ionic strength (NaClO4 (Merck)). The pH measurements (adjustment, potentiometric titration) were carried out with glass electrodes (SCHOTT) calibrated with buffer solutions (NIST/PTB standard buffers). The pH of the solutions was adjusted with NaOH or HClO4 (Merck).Determination of pKa of boric, salicylic, lactic and 3-hydroxybutyric acid
Potentiometric titration series were carried out with solutions containing varying concentrations of boric acid, salicylate, lactate or 3-hydroxybutyrate prepared at ∼pH 2 under ambient conditions (T = 22 °C, pCO2 = 10−3.5 bar). 20 mL of each solution were automatically titrated (736 GP Titrino/TiNet 2.50, Metrohm) up to pH 12 under a N2-atmosphere in a temperature adjustable titration vessel at 22 °C by adding 0.1 M NaOH (carbonate-free). The dynamic titration procedure was used. 60 seconds after adding NaOH the pH measurements were initiated.Formation of organoborates
Solutions with varying total organic (salicylate/lactate/3-hydroxybutyrate) and total boron concentrations were prepared at pH 5 under ambient conditions one day prior to the 11B NMR measurements. The total boron concentration was used in large excess so that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 organoborate compound is formed exclusively. Any polyborate formation is negligible under these pH conditions in both the salicylatoborate and lactatoborate systems.9
1 organoborate compound is formed exclusively. Any polyborate formation is negligible under these pH conditions in both the salicylatoborate and lactatoborate systems.9
Eu(III) complexation by salicylate and 3-hydroxybutyrate (3-HB)
For the TRLFS studies solutions with varying total salicylate/3-HB concentrations were prepared at pH 5.5 under ambient conditions. 2 mL of each solution were transferred into a quartz cuvette. 2 μL of the 30 mM Eu(III) stock solution were added to this volume to set total Eu(III) concentration as 3 × 10−5 M. The samples were titrated from pH 5.5 down to around pH 2 by adding appropriate amounts of HClO4. After each titration step a stationary europium TRLFS spectrum was recorded.For the 1H NMR measurements solutions with a constant 5 mM total 3-HB concentration were prepared at pH 5.17 under ambient conditions before adding appropriate amounts of EuCl3·6H2O to adjust up to 50 mM total Eu(III) concentration.
Eu(III)–organoborate complexation studies
For the TRLFS studies solutions with varying total organic (salicylate/lactate) and total boron concentrations were prepared at pH 4.4 under ambient conditions. The total boron concentration was adjusted up to 0.4 M to provide high-level conversion of the organic compound into the respective organoborate. The formation of polyborates can be excluded under such experimental conditions.9 One day after the solution preparation, 2 mL of a solution with adjusted total organic and boron concentrations was transferred into a quartz cuvette. 2 μL of the 30 mM Eu(III) stock solution was added to this volume to adjust the total Eu(III) concentration to 3 × 10−5 M. The samples were titrated from pH 4.4 down to around pH 2 by adding appropriate amounts of HClO4. After each titration step the stationary and, in some cases, also the time-resolved europium luminescence spectra were recorded.For the 11B NMR measurements solutions with a constant total organic concentration (5 mM or 10 mM salicylate; 5 mM lactate) and a total boron concentration (200 mM) were prepared at pH 5 under ambient conditions one day prior to the addition of appropriate amounts of EuCl3·6H2O to adjust up to 50 mM total Eu(III) concentration.
Nuclear magnetic resonance (NMR) spectroscopy
The NMR spectra of the 10 mM salicylate solution series were recorded on a Varian Unity Inova 400 spectrometer with a field strength of 9.4 T, corresponding to a 11B resonance frequency of 128.4 MHz, using a 5 mm direct detection broadband probe. The spectra of the 5 mM salicylate, lactate, and 3-hydroxybutyrate series were recorded on an Agilent DD2-600 MHz NMR system, operating at 14.1 T with the corresponding 1H and 11B resonance frequencies of 599.8 and 192.4 MHz, respectively, using a 5 mm broadband (OneNMR™) probe and a quarter-wave switch for 11B. As an experimental setup the 5 mm NMR tube (quartz) containing the aqueous (H2O) solution was equipped with a D2O filled coaxial quartz insert for a deuterium lock. As the investigations were performed in H2O, suppression of the 1H water signal was mandatory, and achieved by a presaturation pulse sequence, applying a 2 s presaturation pulse with an offset on resonance of the water signal frequency (varying with the Eu(III) concentration) prior to the detection pulse. For 1H and 11B experiments the measurements were quantitatively obtained by application of π/6 and π/2 pulses, respectively, and relaxation delays ≥5 × T1, the latter being shortened with increasing Eu(III) concentration. 1H and 11B chemical shifts (δ) are referenced externally with respect to TMS (tetramethylsilane) in CDCl3 and BF3 etherate in CDCl3, respectively.Time-resolved laser-induced fluorescence spectroscopy (TRLFS)
A Nd:YAG-OPO laser system (Continuum) was used for the TRLFS measurements of the europium containing solutions. The solutions were stirred and stationary as well as time-resolved europium spectra were recorded with an excitation wavelength of 394 nm, a constant time window of 1 ms, a pulse energy of 2–3 mJ and an optical multichannel analyzer (spectrograph (Oriel MS 257) and ICCD camera (Andor iStar)). Stationary spectra were recorded under the following conditions: wavelength detection range 565–650 nm, 1200 lines per mm grating (0.2 nm resolution), and 3000 accumulations. Time-resolved spectra were recorded under the following conditions: wavelength detection range 440–780 nm, 300 lines per mm grating (0.7 nm resolution), 100 accumulations, and delay time steps 15–40 μs.Density functional theory (DFT) calculations
DFT calculations of organic and inorganic borate structures and respective Eu(III) complexes were performed using the Gaussian 0919 program. Geometries were optimized in the aqueous phase at the B3LYP level using the CPCM solvation model with UAHF radii.20 Two additional DFT functionals, namely TPSSh and PBE0, were tested for organic and inorganic borate complexes without europium. 11B NMR spectra were calculated using the optimized geometry. The large core effective core potential (LC-ECP) as well as the corresponding basis set suggested by Dolg et al.21 was used for europium. For O, C, B, and H, all-electron valence triple-ζ basis set plus polarization and diffuse functions22 have been used. More details of the DFT calculations are described in our previous publication.23Data analysis
The following chemical reactions were considered for the subsequent analysis procedures, eqn (1a)–(f):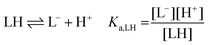 | (1a) |
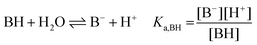 | (1b) |
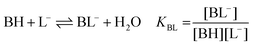 | (1c) |
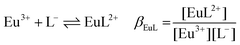 | (1d) |
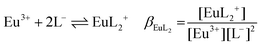 | (1e) |
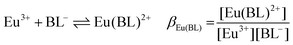 | (1f) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Eu(III)–organic complex (Eu(III)–salicylate (Eu–Sal), Eu(III)–lactate (Eu–Lac), Eu(III)–3-hydroxybutyrate (Eu–3-HB)), EuL2+ = 1
1 Eu(III)–organic complex (Eu(III)–salicylate (Eu–Sal), Eu(III)–lactate (Eu–Lac), Eu(III)–3-hydroxybutyrate (Eu–3-HB)), EuL2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Eu(III)–organic complex, Eu(BL)2+ = 1
2 Eu(III)–organic complex, Eu(BL)2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Eu(III)–organoborate complex (Eu(III)–salicylatoborate (Eu–BSal), Eu(III)–lactatoborate (Eu–BLac)), Ka = acid dissociation constant, KBL = formation constant of organoborate, β = complexation constant.
1 Eu(III)–organoborate complex (Eu(III)–salicylatoborate (Eu–BSal), Eu(III)–lactatoborate (Eu–BLac)), Ka = acid dissociation constant, KBL = formation constant of organoborate, β = complexation constant.
The pKa values of the organic acids and boric acid were calculated from the potentiometric titration data by means of the software Hyperquad2008.24 Applications of this software are demonstrated elsewhere.25–27
The organoborate formation constants KBL were calculated from 11B NMR data by means of the software HySS, version 4.0.31.28KBL were iteratively determined by varying the KBL value until the calculated free boric acid and organoborate concentrations were equal to those determined by 11B NMR spectroscopy (integrating the concentration proportional 11B signal areas).
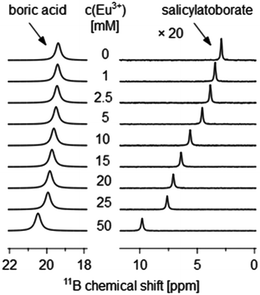
The complexation constants of the Eu(III)–organoborate complexes βEu(BL) were calculated from 11B NMR spectroscopic data by analyzing the Eu(III) concentration dependent chemical shift, δobs, of the organoborate (Fig. 2, and S2†).
The observed 11B chemical shift of the organoborate signal, δobs, is an average of the chemical shifts of the free and Eu(III) bound organoborate weighed by their respective molar fractions (fast exchange approximation). In addition, a contribution of the bulk susceptibility (Δδsusc) increasingly enhanced due to the rising Eu(III) concentration has to be considered, eqn (2a).
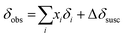 | (2a) |
It is assumed that the bulk susceptibility affects all components – organoborates, free boric acid and solvent – equally and isotropically. After subtraction of the bulk susceptibility contribution term, Δδsusc, the effective signal position, δ*obs, of the organoborate was obtained, eqn (2b.1) and (2b.2). Δδsusc can be estimated from chemical shift changes of signals of molecules that virtually do not interact with Eu(III), such as B(OH)3 and bulk H2O. These changes are due to the difference in the 11B and 1H chemical shifts of the B(OH)3 and H2O signals, respectively, in the respective Eu(III) containing systems (δB(OH)3 or δH2O) and the Eu(III) free system (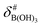 or
or 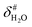 ).
).
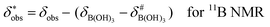 | (2b.1) |
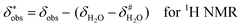 | (2b.2) |
In conclusion δ*obs is expressed as follows (eqn (2c)) according to eqn (2a):
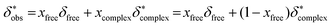 | (2c) |
The 11B chemical shift of the organoborate, δfree, was obtained from the 11B NMR spectrum of the Eu(III) free organoborate solution. The 11B chemical shift of the completely Eu(III) bound organoborate, δ*complex, was determined by fitting the corrected data points δ*obs by an asymptotic function of the Eu(III) concentration (Fig. 3 and S3†). The limit of this function at infinite Eu(III) concentrations represents δ*complex. An example for the determination of δ*complexvia the asymptotic fit is shown in Fig. 3. The values of δfree and δ*complex for BSal and BLac are summarized in Table 1. From the 11B NMR signal positions of the organoborate, δ*obs, the mole fraction x of free and Eu(III) bound organoborates was deduced, eqn (2d) and (2e).
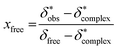 | (2d) |
| xcomplex = 1 − xfree | (2e) |
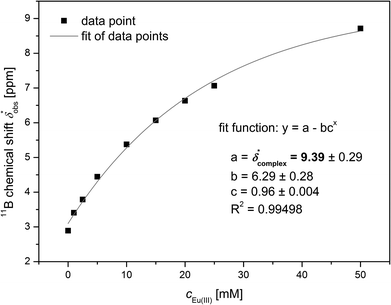 | ||
| Fig. 3 Determination of δ*complex of the Eu(III) salicylatoborate complex from 11B NMR spectroscopic data (5 mM salicylate, 200 mM total boron, varying Eu(III) concentrations). | ||
| Organoborate | c organic,total [mM] | c B,total [mM] | δ free [ppm] | δ *complex [ppm] |
|---|---|---|---|---|
| BSal | 5 | 200 | 2.9 | 9.4 (±0.3) |
| BSal | 10 | 200 | 2.9 | 9.2 (±0.4) |
| BLac | 5 | 200 | 6.3 | 26.3 (±4.8) |
With the information of the fractions of free (xfree) and Eu(III) bound organoborates (xcomplex) complexation constants were determined by the described iterative procedure using the speciation program HySS.28 The complexation constant of the Eu(III)–organoborate in the speciation model was varied until the calculated free and Eu(III) bound organoborate concentrations are equal to those determined by 11B NMR spectroscopy.
In a similar way βEu(3-HB) was determined from 1H NMR spectroscopic data (Fig. S4 and S5†). The 1H chemical shifts of 3-HB, δfree (CH–OH/CH2/CH3), were obtained from the Eu(III) free 3-HB solution (Fig. S4†). The 1H chemical shifts of the completely Eu(III) bound 3-HB, δ*complex (CH–OH/CH2/CH3), were determined by plotting δ*obs (CH–OH/CH2/CH3) vs. the Eu(III) concentration (Fig. S5†). δ*obs (CH–OH/CH2/CH3) was obtained by correcting δobs (CH–OH/CH2/CH3) with Δδsusc of bulk water (eqn (2b.2)). The corrected data points were fitted by an asymptotic function (Fig. S5†). The values of δfree (CH–OH/CH2/CH3) and δ*complex (CH–OH/CH2/CH3) for 3-HB are summarized in Table S1.† With the information of the fractions of free (xfree (CH–OH/CH2/CH3)) and Eu(III) bound 3-HB (xcomplex (CH–OH/CH2/CH3)), Table S1,† a complexation constant for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Eu(III)–3-hydroxybutyrate complex was determined by the described iterative procedure (see above) using the program HySS.28
1 Eu(III)–3-hydroxybutyrate complex was determined by the described iterative procedure (see above) using the program HySS.28
Usually, europium luminescence spectra are analyzed in terms of 5D0 → 7F0 (at ∼578 nm; forbidden for the europium aqua ion (Eu(III)aq)), 5D0 → 7F1 (at ∼592 nm) and 5D0 → 7F2 (at ∼616 nm) transition bands. The analysis of the TRLFS spectra was carried out using the software Origin™ (version 7.5G, OriginLab Corporation). Stationary and time-resolved raw spectra were baseline corrected. In addition, the stationary spectra were normalized to the 5D0 → 7F1 transition, because the luminescence intensity caused by this transition is independent of the chemical environment of europium.29 The time-resolved luminescence spectra of the Eu(III)–organoborate complexation systems were analyzed by parallel factor analysis (PARAFAC),30 successfully applied before in a broad variety of research fields,31–34 and in the inorganic Eu(III)–(poly)borate complexation system.9 From PARAFAC the luminescence lifetimes of pure Eu(III) species and Eu(III) species distributions were obtained. The Eu(III) speciation serves as a basis to calculate the complexation constant for the Eu(III)–organoborate complexes. The complexation constant was determined by the described iterative procedure (see above) using the program HySS.28 The stationary TRLFS data from the pH titration series to determine the complexation constants of the Eu–Sal complex βEuSal and Eu–3-HB complex βEu(3-HB) as well as the complexation constants of the Eu–BSal complex βEu(BSal) were analyzed using the software HypSpec.35 Applications of this software can be found in various studies.36–39
Our determined values of pKa, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBL and lg
KBL and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β were extrapolated to infinite dilution, following the extended Debye–Hückel approach as published by Davies, 1962.40
β were extrapolated to infinite dilution, following the extended Debye–Hückel approach as published by Davies, 1962.40
Throughout the paper all given uncertainties correspond to 2σ, i.e., the 95% confidence level.
Results and discussion
Determination of pKa of organic acids and boric acid
The determined pKa values of salicylic, lactic, 3-hydroxybutyric and boric acid are summarized in Table 2, showing good agreement with the literature data (Table 2). The pKa values are required for the calculation of βEuL, KBL and βEu(BL) as described in the subsequent sections.| LH | pKa (I = 0.1 M) | pK0a (I = 0)a |
|---|---|---|
| a Extrapolation to infinite dilution according to the Davies approach.40 | ||
| Salicylic acid | 2.83 ± 0.04 | 3.04 ± 0.04 |
| 2.77,41 2.81,42 2.8243 | ||
| Lactic acid | 3.73 ± 0.01 | 3.94 ± 0.01 |
| 3.6244, 3.6945, 3.7746 | ||
| 3-Hydroxybutyric acid | 4.39 ± 0.02 | 4.60 ± 0.02 |
| 4.3447 | ||
| Boric acid | 9.13 ± 0.04 | 9.34 ± 0.04 |
| 8.9848, 9.0549 | ||
Formation of organoborates
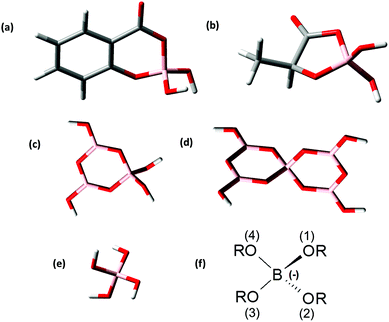
For the theoretical considerations the solution structures of BSal and BLac were optimized at the B3LYP level and are presented in Fig. 4a and b. For comparison of the B(OR)4− unit in different borate compounds (inorganic, organic), and discussion of the hypothesis later on, the solution structures of triborate (B3O3(OH)4−), pentaborate (B5O6(OH)4−) and monoborate (B(OH)4−) were also calculated and are shown in Fig. 4c–e.The general borate structure (B(OR)4− unit) occurring in all the considered borates is shown in Fig. 4f. For the attribution of the structural parameters from DFT calculations (bond lengths, angles) the atoms are numbered in the general B(OR)4− unit (Fig. 4f).
The B(OR)4− units in all calculated borate structures exhibit only slight deviations concerning the determined B–O bond lengths and O–B–O angles (Table 3). In the BLac structure the O(3)–B–O(4) angle is smaller than in other borate structures due to the formation of a five-membered ring. The structural parameters of BLac are in good agreement with the calculated glycolatoborate structure (five-membered ring).50 Furthermore, in the organoborate structures the B–O(4) bond is somewhat longer (on average ∼0.07 Å) than the B–O(1/2/3) bond. This is not the case in the inorganic borate structures. The bond B–O(4) is longer in the organoborates, because the electrons of O(4) are involved in the mesomerism of the ester group. Nevertheless, in all calculated borate structures the structural parameters of the B(OR)4− unit are almost identical, thus, allowing the conclusion that these borate structures should have a comparable complexation behavior to An/Ln(III), as expected in our hypothesis (see the Introduction section).
| BSal | BLac | Glycolatoborateb | B(OH)4− | B3O3(OH)4− | B5O6(OH)4− | |
|---|---|---|---|---|---|---|
| a Oxygen atom bound to the carbonyl-carbon atom. b Ref. 50. | ||||||
| B–O(1) | 1.455 | 1.447 | 1.39 | 1.495 | 1.466 | 1.477 |
| B–O(2) | 1.443 | 1.462 | 1.474 | 1.466 | 1.477 | |
| B–O(3) | 1.494 | 1.471 | 1.50 | 1.484 | 1.493 | 1.480 |
| B–O(4) | 1.520a | 1.552a | 1.58a | 1.482 | 1.497 | 1.477 |
| O(1)–B–O(2) | 115 | 113 | 112 | 113 | 113 | 111 |
| O(2)–B–O(3) | 111 | 115 | 110 | 106 | 109 | |
| O(3)–B–O(4) | 109 | 102 | 102 | 113 | 110 | 111 |
| O(1)–B–O(4) | 111 | 112 | 111 | 106 | 109 | |
The formation of BSal, BLac and B–3-HB was studied by means of 11B NMR spectroscopy.
The existence of organoborates can be clearly verified by specific 11B NMR signals. In the 11B NMR spectrum of the organic–boron system two characteristic signals were found. A signal at 19.3 ppm appears in every 11B NMR spectrum. It can be assigned to boric acid.9,51 According to DFT calculations at the B3LYP level, the 11B chemical shift of boric acid appears at 19.8 ppm (relative to BF3 etherate), Table S2,† which is in agreement with the NMR experiments. Furthermore 11B chemical shifts at 2.9, 6.3, and 1.1 ppm for the salicylate–boron, lactate–boron and 3-hydroxybutyrate–boron systems, respectively, were observed (Fig. S6†). The former two chemical shifts are assigned to BSal and BLac, respectively, being in very good agreement with the DFT calculated 11B chemical shifts of 2.5 ppm and 6.1 ppm (Table S2†). The 11B chemical shift of BSal is also in good agreement with the literature.52
To evaluate the reliability of the B3LYP functional for the borate system, we additionally tested the TPSSh and PBE0 functionals for several organic and inorganic borate complexes. Structural parameters as well as NMR chemical shifts from these calculations are shown in Table S2.† The deviation of B–O bond distances among different theories never exceeds 0.01 Å and the structural agreement is excellent. The accuracy of the 11B NMR chemical shift using these three different functionals is at a comparable level. For the sake of consistency with our previous studies on Eu complexes,23 we decided to use the B3LYP functional in this study.
Difficulties arose in the 3-HB–boron system. DFT calculations at the B3LYP level predicted 11B chemical shifts for B–3-HB at 2.2 ppm and 2.5 ppm for L- and D-isomers, respectively (Table S2†). However, no chemical shift at 2.2 ppm (±0.5 ppm) was observed in the NMR spectrum, and only an unexpected signal at 1.1 ppm occurred. The DFT calculations for all but this organoborate compound predicted the positions of the NMR signals very precisely. Thus, the missing 2.2 ppm signal means that there is no or only a very weak formation of B–3-HB (at least below the detection limit of the NMR spectrometer).
The signal at 1.1 ppm has most likely to be assigned to another borate species. Two possible explanations of this signal exist. A first explanation can be derived from the literature. Miyazaki et al. described a 11B NMR signal at 1.8 ppm in the ethane-1,2-diol/propane-1,3-diol-borate system assigned to an organoborate ester, where the fourfold coordinated boron center is maintained but no ring structure is formed.53 Therefore, the 11B NMR signal of this non-chelate monodentate organoborate ester is comparable to the free monoborate anion (1.7 ppm54). The formation of such an organoborate structure could also be the case in the 3-HB–boron system. The DFT calculated chemical shift of this organoborate species would be 2.1 ppm. The second explanation is derived from the experimental conditions. The total boron concentration used in this system was 0.6 M and 0.7 M (at pH 5), i.e., higher than in the other two investigated organic–boron systems. Thus, the signal could be attributed to the pentaborate anion (1.2 ppm). At concentrations above 0.5 M cB,total and pH 5 a slight polyborate formation was observed by 11B NMR spectroscopy in a previous work.9 Because of the high signal position similarity the occurrence of pentaborate is the most likely explanation for the discrepancy between the calculated and measured signal position of the supposed B–3-HB. As a result the formation of this species is very weak and is not measureable by NMR.
It seems that the ring size of the formed organoborate has a stronger influence on the 11B chemical shift than the nature of the organic moiety (e.g., inductive effect) bound to the B(OR)4− unit. The 11B chemical shift of BLac (6.3 ppm), possessing a five-membered ring, is remarkably more downfield shifted than that of BSal (2.9 ppm) or B–3-HB (chemical shift not observed, but calculated to be ∼2.2 ppm), where six-membered rings are formed. The ring size effect on the 11B chemical shift of organoborates and, therefore, the differentiation of five-membered and six-membered organoborates is also known from the literature.53,55,56 The 11B chemical shifts from our DFT calculations based on the optimized organoborate structure for BLac (6.1 ppm) and BSal (2.5 ppm) support the formation of such rings.
The nature of the organic moiety in the B(OR)4− unit has only a slight influence on the 11B chemical shift of the organoborate compared to the impact of the ring size. Regardless of the ring size, the carbonyl group typically induces downfield shifts of about 1–2 ppm:
BLac (five-membered ring, carbonyl group): δobs = 6.3 ppm,
ethane-1,2-diol borate (five-membered ring, no carbonyl group): δobs = 5.6 ppm,53
BSal (six-membered ring, carbonyl group): δobs = 2.9 ppm,
propane-1,3-diol borate (six-membered ring, no carbonyl group): δobs = 1.0 ppm.53
Regarding the initial hypothesis, from theoretical calculations and NMR studies of organoborates it can be stated that the Eu(III) complexation with organoborates should be not significantly influenced by the nature of the organic moieties at the B(OR)4− unit. The possible effect of organoborate ring size on the reactivity of the B(OR)4− unit concerning Eu(III) is not assessable and remains to be seen in the following described complexation studies.
The formation constants KBL, according to eqn (1c), of BSal and BLac were determined from 11B NMR spectroscopic data. A detailed listing of the lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBL values of the investigated organoborates for different composed solutions is shown in Table S3,† and the average values are summarized in Table 4. For BSal and BLac the averaged formation constants, lg
KBL values of the investigated organoborates for different composed solutions is shown in Table S3,† and the average values are summarized in Table 4. For BSal and BLac the averaged formation constants, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBL = 1.10 ± 0.14 and 0.57 ± 0.22, respectively, were obtained. These values are comparable to literature data.42,44,50,52,57–62 As discussed above, the formation of B–3-HB is not detectable by 11B NMR spectroscopy. A KBL for this species cannot be obtained from NMR experiments. No literature data are available for lg
KBL = 1.10 ± 0.14 and 0.57 ± 0.22, respectively, were obtained. These values are comparable to literature data.42,44,50,52,57–62 As discussed above, the formation of B–3-HB is not detectable by 11B NMR spectroscopy. A KBL for this species cannot be obtained from NMR experiments. No literature data are available for lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBL of B–3-HB.
KBL of B–3-HB.
| L | lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBL KBL |
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuL βEuL |
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuL2 βEuL2 |
||
|---|---|---|---|---|---|
| I = 0.1 M | I = 0 Ma | I = 0.1 M | I = 0 Ma | I = 0.1 M | |
| a Extrapolation to infinite dilution according to the Davies approach.40 b NMR spectroscopy. c TRLFS. d Photometry. e Potentiometry. f Average of both methods. g Dy(III) instead of Eu(III). | |||||
| Salicylate | 1.10 ± 0.14 | 1.10 ± 0.14 | 2.10 ± 0.26 | 2.74 ± 0.26 | |
1.04,42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d 1.05,52 d 1.05,52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b 1.03,57 b 1.03,57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d 1.23,59 d 1.23,59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e 1.2860 e 1.2860![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
1.8425![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
3.5625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|||
2.0263![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
3.8463![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
||||
| Lactate | 0.57 ± 0.22 | 0.57 ± 0.22 | |||
0.60,44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e 0.96,61 e 0.96,61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e 0.5264 e 0.5264![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
2.5165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
4.4565![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|||
3.0966![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e,g e,g |
5.3866![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e,g e,g |
||||
| 3-Hydroxybutyrate | 2.24 ± 0.16 | 2.89 ± 0.17 | |||
| 2.26 ± 0.10 | |||||
Taking into account the very weak formation of B–3-HB, it can be stated that the formation constant of the organoborate increases with decreasing pKa of its corresponding organic acid.
It is noteworthy that the reaction according to eqn (1c) is isocoulombic, i.e., the extrapolation to infinite dilution by following the Davies approach40 does not change the value of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBL determined at I = 0.1 M.
KBL determined at I = 0.1 M.
An example for a speciation calculation for the investigated organic–boron systems is shown in Fig. 5 (calculated using HySS28). In all systems the amount of the respective organoborate reaches its maximum at pH 5–6. At pH > 8 the content of organoborate distinctly decreases, because the concentration of available boric acid decreases (eqn (1b)). Thus, the optimum pH for the existence of organoborates is in the range pKa(organic acid) < pH < pKa(boric acid) (also found by Van Duin et al.67).
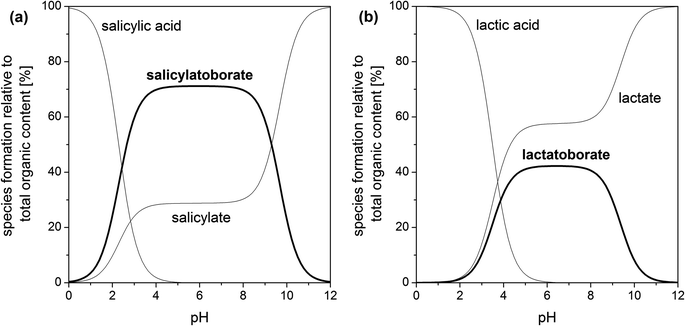 | ||
| Fig. 5 Speciation of different organic–boron systems for solutions with 5 mM total organic and 200 mM total boron concentration, I = 0.1 M, T = 22 °C (our data for pKa and KBL taken from Tables 2 and 4): (a) salicylate–boron system and (b) lactate–boron system. | ||
The very weak formation of B–3-HB made valid complexation experiments with Eu(III) impossible. Nevertheless, a Eu–3-HB complex (βEu(3-HB)) was determined from TRLFS and 1H NMR spectroscopic investigations (see the next subsection).
Eu(III) complexation with 3-hydroxybutyrate (3-HB), salicylate (Sal) and lactate (Lac)
The Eu–3-HB complexation constant βEu(3-HB) (Table 4) was determined from TRLFS and 1H NMR spectroscopic data (Fig. S4, S5, and Table S1†) processed as described in the section “Data analysis”. Both spectroscopic methods delivered very similar complexation constants, yielding an average lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(3-HB) = 2.25 ± 0.17 (lg
βEu(3-HB) = 2.25 ± 0.17 (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0Eu(3-HB) = 2.89 ± 0.17). This value is comparable to the complexation constant for the Pr–3-HB complex (lg
β0Eu(3-HB) = 2.89 ± 0.17). This value is comparable to the complexation constant for the Pr–3-HB complex (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βPr(3-HB) = 2.0847 (potentiometry), the only comparable system found in the literature).
βPr(3-HB) = 2.0847 (potentiometry), the only comparable system found in the literature).
The complexation constant βEuSal (Table 4) was determined from TRLFS data. The analysis yielded an average lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuSal = 2.10 ± 0.26 (lg
βEuSal = 2.10 ± 0.26 (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0EuSal = 2.74 ± 0.26). This value, together with the obtained (pure) stationary luminescence spectrum of the 1
β0EuSal = 2.74 ± 0.26). This value, together with the obtained (pure) stationary luminescence spectrum of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Eu–Sal complex was used to derive the complexation constant βEu(BSal) from TRLFS data (see below).
1 Eu–Sal complex was used to derive the complexation constant βEu(BSal) from TRLFS data (see below).
Table 4 summarizes lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuL for L = Sal/Lac/3-HB and lg
βEuL for L = Sal/Lac/3-HB and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuL2 for L = Sal/Lac both from this work and the literature. These Eu(III)–organic complexation constants are involved in the determination of βEu(BL). In particular for the lactate system, the 1
βEuL2 for L = Sal/Lac both from this work and the literature. These Eu(III)–organic complexation constants are involved in the determination of βEu(BL). In particular for the lactate system, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Eu(III) complex is required.
2 Eu(III) complex is required.
Obviously, the βEuLac and βEuLac2 determined by different experimental methods deviate significantly from each other.68 Therefore, the upper and lower limits for βEuLac and βEuLac2 were used to determine the upper and lower limits of βEu(BLac).
Eu(III)–organoborate complexation studies
The complexation of Eu(III) with BSal and BLac was studied by means of TRLFS and 11B NMR spectroscopy as well as by DFT calculations.At first the results of TRLFS studies are presented.
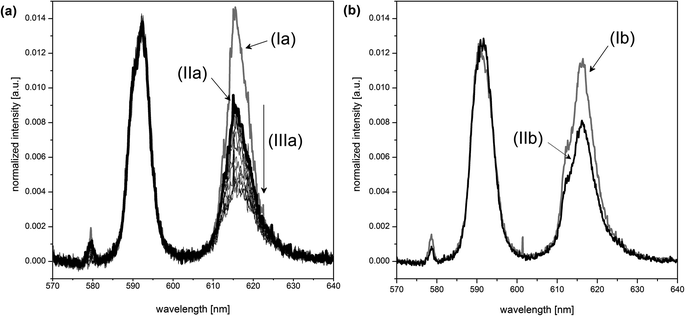
The presence of boric acid as the boron source influences the Eu(III)–organic speciation. This can be shown by comparing the europium luminescence spectra (Fig. 6). The spectra for the Eu(III)–salicylate (Fig. 6, Ia) and Eu(III)–lactate systems (Fig. 6, Ib) clearly differ from the spectra in the presence of boric acid under the same conditions (Fig. 6, IIa and IIb, respectively). There are two explanations for the observed intensity decrease of the 5D0 → 7F0 transition at ∼578 nm and 5D0 → 7F2 transition at ∼616 nm: (1) removal of free salicylate/lactate (complexing the europium) due to the formation of the respective organoborate, and, (2) different luminescence properties of the Eu(III)–organoborate complex in comparison with the Eu(III)–salicylate/lactate complexes.
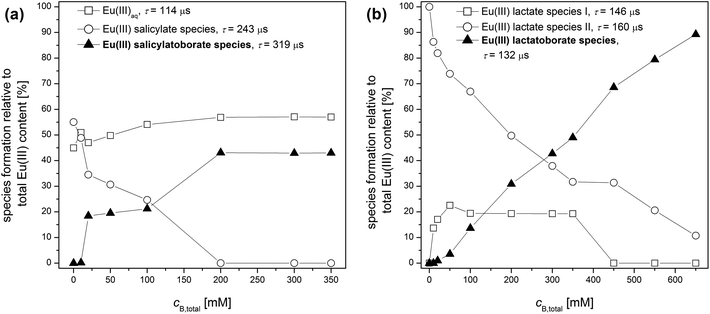
The time-resolved luminescence spectra of a series of solutions containing varying concentrations of total boron and constant concentrations of Eu(III) (3 × 10−5 M) and of the organic compound (10 mM) were analyzed by PARAFAC. This provided the Eu(III) speciation for the respective system as shown in Fig. 7. In the Eu(III)–salicylate–boron system as well as in the Eu(III)–lactate–boron system the amount of the Eu(III)–organoborate complex increases with increasing total boron concentration due to the increasing formation of the respective organoborate. Parallel to that a decrease in the formation of the Eu(III)–organic complex(es) can be observed. This is explainable with the decrease of free available organic content for the Eu(III) complexation due to the increasing formation of the organoborate.
From PARAFAC the luminescence lifetimes of Eu(III) species were extracted (summarized in Fig. 7). The luminescence lifetimes for the Eu–BSal complex and Eu–BLac complex were determined to be 319 μs and 132 μs, respectively. The luminescence lifetime of the Eu–BLac is comparable to that of the Eu(III)–polyborate complex exhibiting a lifetime of ∼150 μs.9 This is a first support of our hypothesis that borates with the general B(OR)4− unit show a comparable complexation behavior concerning trivalent lanthanides (and actinides). The luminescence lifetime of the Eu–BSal complex calculated with PARAFAC is strongly increased in comparison with the Eu–BLac and –polyborate complex. However, we expect a similar Eu(III) complexation with BSal as with the other described borate ligands (see the hypothesis).
The BSal system was the most suitable system to study the Eu(III) complexation at a low metal concentration (3 × 10−5 M) by TRLFS, because of the high formation yield of BSal and the well characterized Eu(III)–salicylate complexation as the secondary reaction system. Unfortunately, the Eu–BLac TRLFS titration series were very difficult to analyse. Due to the stronger Eu(III)–lactate complexation and more pronounced formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex already at low lactate concentrations (in comparison with the salicylate system; see Eu(III) organic speciations in Fig. S7†) a separation of the Eu–BLac complex from the stationary TRLFS titration data was not possible. Only the analysis of the Eu(III) speciation in the Eu(III)–lactate–boron system (Fig. 7b) determined by PARAFAC of the time-resolved spectra gave a hint of the Eu–BLac complexation (see below).
2 complex already at low lactate concentrations (in comparison with the salicylate system; see Eu(III) organic speciations in Fig. S7†) a separation of the Eu–BLac complex from the stationary TRLFS titration data was not possible. Only the analysis of the Eu(III) speciation in the Eu(III)–lactate–boron system (Fig. 7b) determined by PARAFAC of the time-resolved spectra gave a hint of the Eu–BLac complexation (see below).
The Eu–BSal complexation constant was determined from TRLFS pH titration series of solutions containing Eu(III) and varying total concentrations of both salicylate and boron (e.g., Fig. 6, IIIa). In Table 5 the resulting lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BSal) (average) according to eqn (1f) is shown. Several values of lg
βEu(BSal) (average) according to eqn (1f) is shown. Several values of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BSal) are shown in Table S4.† For the Eu–BSal complex an average of lg
βEu(BSal) are shown in Table S4.† For the Eu–BSal complex an average of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BSal) = 1.93 ± 0.48 was determined.
βEu(BSal) = 1.93 ± 0.48 was determined.
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BL) βEu(BL) |
Method and parameters for data analysis | |
|---|---|---|
| I = 0.1 M | I = 0 Ma | |
a Extrapolation to infinite dilution according to the Davies approach.40
b Fixed parameters for data analysis: pKa,Sal = 2.83, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBSal = 1.10, lg KBSal = 1.10, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuSal = 2.10.
c Fixed parameters for data analysis: pKa,Lac = 3.73, lg βEuSal = 2.10.
c Fixed parameters for data analysis: pKa,Lac = 3.73, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBLac = 0.57, lg KBLac = 0.57, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLac = 2.5165, lg βEuLac = 2.5165, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLac2 = 4.45.65
d Fixed parameters for data analysis: pKa,Lac = 3.73, lg βEuLac2 = 4.45.65
d Fixed parameters for data analysis: pKa,Lac = 3.73, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBLac = 0.57, lg KBLac = 0.57, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βDyLac = 3.0966, lg βDyLac = 3.0966, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βDyLac2 = 5.38.66 βDyLac2 = 5.38.66
|
||
| Eu(III)–salicylatoborate | ||
| 1.93 ± 0.48 | 2.57 ± 0.48 | TRLFSb |
| 1.95 ± 0.32 | 2.59 ± 0.32 | 11B NMR (5 mM salicylate, 200 mM total boron), δfree = 2.9 ppm, δ*complex = 9.4 ppmb |
| 2.12 ± 0.28 | 2.76 ± 0.28 | 11B NMR (10 mM salicylate, 200 mM total boron), δfree = 2.9 ppm, δ*complex = 9.2 ppmb |
| 2.11 ± 0.32 | 2.75 ± 0.32 | PARAFAC (10 mM salicylate, varying total boron)b |
| Eu(III)–lactatoborate | ||
| 1.94 ± 0.22 to 2.18 ± 0.26 | 2.58 ± 0.22 to 2.82 ± 0.26 | 11B NMR (5 mM lactate, 200 mM boron) δfree = 6.3 ppm, δ*complex = 21.5 (lower limit) to 31.2 ppm (upper limit)c |
| 2.37 ± 0.26 to 2.61 ± 0.15 | 3.01 ± 0.26 to 3.25 ± 0.15 | 11B NMR (5 mM lactate, 200 mM boron) δfree = 6.3 ppm, δ*complex = 21.5 (lower limit) to 31.2 ppm (upper limit)d |
| 2.68 ± 0.92 | 3.32 ± 0.92 | PARAFAC (10 mM lactate, varying total boron)c |
A complexation constant lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BSal) = 2.11 ± 0.32 was deduced (Table 5) from PARAFAC of time-resolved luminescence spectra and analysis of the obtained Eu(III) speciation (Fig. 7a). For the Eu(III)–lactate–boron system a complexation constant with a high uncertainty (lg
βEu(BSal) = 2.11 ± 0.32 was deduced (Table 5) from PARAFAC of time-resolved luminescence spectra and analysis of the obtained Eu(III) speciation (Fig. 7a). For the Eu(III)–lactate–boron system a complexation constant with a high uncertainty (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BLac) = 2.68 ± 0.92, Table 5) was determined similarly. However, the Eu(III) complexation with BLac seems to be somewhat stronger (around half order of magnitude) than that with BSal.
βEu(BLac) = 2.68 ± 0.92, Table 5) was determined similarly. However, the Eu(III) complexation with BLac seems to be somewhat stronger (around half order of magnitude) than that with BSal.
In the following section the results of 11B NMR spectroscopic studies are presented and discussed.
It has already been shown above (in the section Eu(III) complexation with 3-hydroxybutyrate (3-HB), salicylate (Sal) and lactate (Lac)) that complexation constants can be derived from NMR spectroscopic data. The Eu(III) induced 11B NMR signal shift of the organoborates (Fig. S2, S3, and Table S5†) was used to determine the complexation constants βEu(BSal) and βEu(BLac) according to eqn (1f). The procedure is described in the “Experimental section”. The resulting lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BL) (averages) are summarized in Table 5.
βEu(BL) (averages) are summarized in Table 5.
The complexation constant for the Eu–BSal complex from TRLFS and 11B NMR spectroscopic data agree very well (Table 5) and βEu(BSal) can be reproduced by both methods. Eventually, this gave lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BSal) = 2.05 ± 0.17 (averaged over all lg
βEu(BSal) = 2.05 ± 0.17 (averaged over all lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BSal) values (TRLFS, NMR and PARAFAC) of Table 5). Extrapolation to infinite dilution yielded lg
βEu(BSal) values (TRLFS, NMR and PARAFAC) of Table 5). Extrapolation to infinite dilution yielded lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0Eu(BSal) = 2.69 ± 0.17.
β0Eu(BSal) = 2.69 ± 0.17.
Unfortunately, the literature values of both lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLac and lg
βEuLac and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLac2 differ considerably (see Table 4). Furthermore, the uncertainty of δ*complex of BLac is much higher than that of BSal (see Table 1). This large uncertainty stems from the overlapping of the 11B NMR signals of BLac and B(OH)3 with increasing Eu(III) concentration (Fig. S2b†). Even our attempt to replace Eu(III) by Pr(III) or Dy(III) did not succeed. The expected upfield shift of the organoborate 11B NMR signal as in the case of 1H NMR signals16 did not occur. The separation of BLac and B(OH)311B chemical shifts is possible only up to 15 mM Eu(III), see Fig. S2b.† Here, only around one half of BLac binds to the Eu(III). Therefore, a higher uncertainty in the asymptotic fit to determine δ*complex is unavoidable.
βEuLac2 differ considerably (see Table 4). Furthermore, the uncertainty of δ*complex of BLac is much higher than that of BSal (see Table 1). This large uncertainty stems from the overlapping of the 11B NMR signals of BLac and B(OH)3 with increasing Eu(III) concentration (Fig. S2b†). Even our attempt to replace Eu(III) by Pr(III) or Dy(III) did not succeed. The expected upfield shift of the organoborate 11B NMR signal as in the case of 1H NMR signals16 did not occur. The separation of BLac and B(OH)311B chemical shifts is possible only up to 15 mM Eu(III), see Fig. S2b.† Here, only around one half of BLac binds to the Eu(III). Therefore, a higher uncertainty in the asymptotic fit to determine δ*complex is unavoidable.
In the frame of both these uncertainties (deviation in literature data for βEuLac and βEuLac2, upper and lower limits of δ*complex) a more extended data analysis was carried out to determine βEu(BLac). All possible variations of the upper and lower limits of the input data βEuLac, βEuLac2, and δ*complex of BLac were used (Tables 5, and S6†) to calculate the upper and lower limits of βEu(BLac).
Assuming that the lower limits of the Eu(III)–lactate complex constants are valid (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLac = 2.51 and lg
βEuLac = 2.51 and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEuLac2 = 4.45)65 we obtained the following range of the complexation constant for the Eu–BLac complex: lg
βEuLac2 = 4.45)65 we obtained the following range of the complexation constant for the Eu–BLac complex: lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BLac) = 1.94 ± 0.22 to 2.18 ± 0.26. If, in contrast, the upper limits of the Eu(III)–lactate complex constants are taken to be (lg
βEu(BLac) = 1.94 ± 0.22 to 2.18 ± 0.26. If, in contrast, the upper limits of the Eu(III)–lactate complex constants are taken to be (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βDyLac = 3.09 and lg
βDyLac = 3.09 and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βDyLac2 = 5.38; Dy(III) as an Eu(III) analog)66 lg
βDyLac2 = 5.38; Dy(III) as an Eu(III) analog)66 lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BLac) ranges from 2.37 ± 0.26 to 2.61 ± 0.15. These results are summarized in Table 5. Extrapolation to infinite dilution for the lower limit of lg
βEu(BLac) ranges from 2.37 ± 0.26 to 2.61 ± 0.15. These results are summarized in Table 5. Extrapolation to infinite dilution for the lower limit of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BLac) yielded lg
βEu(BLac) yielded lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0Eu(BLac) = 2.58 ± 0.22 to 2.82 ± 0.26 and for the upper limit of lg
β0Eu(BLac) = 2.58 ± 0.22 to 2.82 ± 0.26 and for the upper limit of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BLac) lg
βEu(BLac) lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0Eu(BLac) = 3.01 ± 0.26 to 3.25 ± 0.15.
β0Eu(BLac) = 3.01 ± 0.26 to 3.25 ± 0.15.
Taking into account the uncertainties, the complexation constants of both BSal and BLac are in the range lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BL) 2.0–2.6 (lg
βEu(BL) 2.0–2.6 (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0Eu(BL) 2.6–3.2) and, hence, are comparable and quite weak. The differences result from the high complexity of the equilibrium systems combined with the uncertainties of all involved constants. Though differences in the 11B NMR signals of both organoborate ligands indicate differences in the electronic structure of the boron atom, both the ring size of the organoborate and the electronic nature of the organic moieties bound to the B(OR)4− unit seems to have only a small influence on lg
β0Eu(BL) 2.6–3.2) and, hence, are comparable and quite weak. The differences result from the high complexity of the equilibrium systems combined with the uncertainties of all involved constants. Though differences in the 11B NMR signals of both organoborate ligands indicate differences in the electronic structure of the boron atom, both the ring size of the organoborate and the electronic nature of the organic moieties bound to the B(OR)4− unit seems to have only a small influence on lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βEu(BL).
βEu(BL).
Furthermore, the complexation constants of the Eu(III)–organoborate complexes are well comparable to the complexation constant (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β011 = 2.66 ± 0.16)9 of Eu(III)–polyborates (i.e., tri- and pentaborate) with one binding site. This is an important corroboration of the initial hypothesis that borates with the general structural unit B(OR)4− – regardless if R is organic or inorganic – show a comparable complexation behavior concerning trivalent lanthanides (and actinides).
β011 = 2.66 ± 0.16)9 of Eu(III)–polyborates (i.e., tri- and pentaborate) with one binding site. This is an important corroboration of the initial hypothesis that borates with the general structural unit B(OR)4− – regardless if R is organic or inorganic – show a comparable complexation behavior concerning trivalent lanthanides (and actinides).
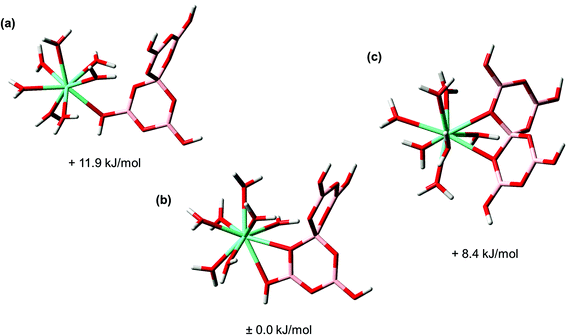
Finally, the structures of the Eu–BSal and Eu–BLac complex were calculated by DFT. For the sake of comparison and to test the hypothesis that all borate structures show a comparable complexation behavior concerning An/Ln(III), Eu(III) inorganic borate structures were also studied. In order to understand the general tendency of possible binding/coordination modes between Eu(III) and borates (inorganic as well as organic) an example is shown in Fig. 8, presenting the most likely Eu(III)–pentaborate complexes (structures and relative Gibbs energies).
Three different binding modes were calculated for the Eu(III)–pentaborate complex including one monodentate coordination mode (–B–O(H)–Eu) where a threefold coordinated boron atom is involved (Fig. 8a), and two complexes with a chelate coordination mode (Fig. 8b and c). In one of these chelate complexes a threefold and fourfold coordinated boron unit is involved (Eu–O(H)–B–O–(Eu)), Fig. 8b, and in the other chelate the fourfold coordinated boron unit of the pentaborate is involved (Eu–O–B–O–(Eu)), Fig. 8c. The calculated relative Gibbs energies of these complexes are very similar. The energy difference between the most and least stable structures is only 12 kJ mol−1. From this, one cannot decide, whether there is a preferred structure in reality. However, we know from TRLFS studies that an interaction between Eu(III) and boron compounds with a threefold coordinated boron unit, e.g., boric acid, does not occur. This is a hint regarding the preference of the chelate of the Eu(III)–pentaborate complex shown in Fig. 8c. Moreover, in the crystal structures of Ln(III)– and An(III)–polyborates, reported in the literature,69,70 4-membered chelate rings are found, supporting the chelate motif as shown in Fig. 8c rather than as in Fig. 8b.
In the case of Eu–BSal, Eu–BLac, Eu(III)–monoborate, and Eu(III)–triborate complexes, chelate and monodentate Eu(III) coordination modes by the fourfold coordinated boron unit were calculated as well. Both coordination modes are also energetically very similar and, thus, not distinguishable. However, in analogy with Eu(III) coordination to pentaborate, the chelate Eu(III) coordination in these complexes is more likely. It is also conceivable that the monodentate and chelate complexes are in equilibrium.
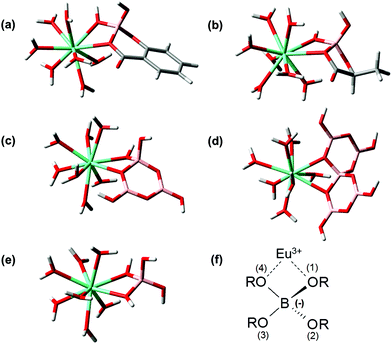
As a summary of the DFT section the structures (in chelate coordination mode, assuming coordination number 9) of Eu–BSal, Eu–BLac, Eu(III)––monoborate, Eu(III)–triborate and Eu(III)–pentaborate optimized at the B3LYP level are presented in Fig. 9.
The structural parameters of the optimized organic and inorganic Eu(III)–borate complexes are shown in Fig. S8–S12, and Tables S7–S11.†
For comparison the structural parameters of the Eu(III)–B(OR)4− unit in the complexes are summarized in Table 6 (referring to Fig. 9f). It turns out that the structural parameters of the considered Eu(III)–borate complexes (Table 6) are comparable. The Eu–O(1) and Eu–B distances in the considered Eu(III)–borate complexes, Table 6, have a maximum deviation of 0.1 Å. The deviation in the Eu–O(4) bond distance is somewhat higher (maximum 0.2 Å). Because the difference in the Eu–O(4) bond lengths is independent of the nature of the borate ligand (organic or inorganic) this higher deviation in the case of the Eu–O(4) bonding could be a consequence of the steric flexibility of the borate structures (BLac and pentaborate might be less flexible than the other borate structures). The bond angles in the EuB(OR)42+ complex are also comparable. In particular the (B–)O–Eu–O(–B) bond angle only deviates within 1.1°. Due to the Eu(III) binding the O(1)–B–O(4) angles become smaller in comparison with the free borate structures (comparing O(1)–B–O(4) in Tables 3 and 6).
| Eu–BSal | Eu–BLac | Eu(B(OH)4)2+ | Eu(B3O3(OH)4)2+ | Eu(B5O6(OH)4)2+ | |
|---|---|---|---|---|---|
| Eu–O(1) | 2.438 | 2.405 | 2.392 | 2.448 | 2.498 |
| Eu–O(4) | 2.536 | 2.698 | 2.465 | 2.533 | 2.641 |
| Eu–B | 3.186 | 3.249 | 3.113 | 3.129 | 3.193 |
| O(1)–B–O(4) | 98.4 | 98.8 | 96.0 | 99.2 | 103.2 |
| O(3)–B–O(4) | 106.0 | 100.4 | 117.1 | 111.6 | 112.7 |
| Eu–O(1)–B | 106.6 | 111.2 | 103.3 | 102.6 | 103.0 |
| Eu–O(4)–B | 99.4 | 95.1 | 100.4 | 97.8 | 97.5 |
| O(1)–Eu–O(4) | 54.9 | 54.0 | 55.1 | 54.8 | 54.2 |
The listed structural similarities indicate the comparable bonding of Eu(III) to the B(OR)4− unit in the considered borates. This supports the experimental data (TRLFS, 11B NMR) of all investigated inorganic (poly)borates as well as different organoborates in which the same order of magnitude (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0 = 2.6–3.2) for the complexation was determined. The observed differences in a few structural parameters (due to the ring size of the organoborates, moieties at the B(OR)4− unit or flexibility of borate molecules) have only a small effect on the Eu(III)–B(OR)4− complexation. The complexation in the Eu(III)–B(OR)4− system is comparable within the obtained uncertainty limits.
β0 = 2.6–3.2) for the complexation was determined. The observed differences in a few structural parameters (due to the ring size of the organoborates, moieties at the B(OR)4− unit or flexibility of borate molecules) have only a small effect on the Eu(III)–B(OR)4− complexation. The complexation in the Eu(III)–B(OR)4− system is comparable within the obtained uncertainty limits.
Conclusion
This work was started with the hypothesis that borate structures with one general B(OR)4− unit show comparable complexation behavior concerning trivalent lanthanides and actinides. This hypothesis was confirmed both by experimental Eu(III)–borate complexation studies using the complementary methods TRLFS and 11B NMR, and theoretical DFT calculations. Borates (organic or inorganic) with the structural unit B(OR)4− show a weak complexation with Eu(III) as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with lg
1 complex with lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0 = 2.6–3.2 (lg
β0 = 2.6–3.2 (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 2.0–2.6, I = 0.1 M). The influence of the moiety R on the B(OR)4− unit binding Eu(III) is secondary.
β = 2.0–2.6, I = 0.1 M). The influence of the moiety R on the B(OR)4− unit binding Eu(III) is secondary.
The application of different experimental approaches (Eu(III) complexation with inorganic and organic borates) and complementary spectroscopic methods provide a well secured range for the Eu(III)–borate complexation.
Thus, our approach to use polyborates (Schott et al.9) and organoborates (this work) to determine Eu(III) complexation data allows for the conclusion that the Eu(III)–monoborate also, which is not accessible for investigation directly, has a comparable complexation constant of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0 = 2.6–3.2.
β0 = 2.6–3.2.
In the context of deep geological disposal of radioactive wastes, the presence of dissolved borate compounds in a future nuclear waste repository should only slightly enhance the mobility of trivalent actinides and lanthanides in comparison with the much stronger complexing agents like hydroxide and carbonate.
Acknowledgements
This work was funded by the Federal Ministry of Economics and Energy (BMWi) under contract number 02E11021. The authors would like to thank A. Ritter (HZDR) for ICP-MS analyses. All the quantum chemical calculations were performed using PC-Farm Atlas at the “Zentrum für Informationsdienste und Hochleistungsrechnen” (ZIH) at the Technische Universität Dresden, Germany.References
- OECD/NEA, Physics and Safety of Transmutation Systems – A Status Report, Paris, 2006.
- W. Hummel, U. Berner, E. Curti, F. J. Pearson and T. Thoenen, Nagra/PSI Chemical Thermodynamic Data Base 01/01, NAGRA, Wettingen/Switzerland, 2002 Search PubMed.
- R. J. Silva, G. Bidoglio, M. H. Rand, P. B. Robouch, H. Wanner and I. Puigdomènech (OECD, NEA-TDB), Chemical Thermodynamics of Americium, North Holland, Amsterdam, 1995 Search PubMed.
- R. Guillaumont, T. Fanghänel, J. Fuger, I. Grenthe, V. Neck, D. A. Palmer and M. H. Rand (OECD, NEA-TDB), Update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium and Technetium, Elsevier, Amsterdam, 2003 Search PubMed.
- W. Hummel, G. Anderegg, I. Puigdomènech, L. Rao and O. Tochiyama (OECD, NEA-TDB), Chemical Thermodynamics of Compounds and Complexes of U, Np, Pu, Am, Tc, Se, Ni and Zr with Selected Organic Ligands, Elsevier, Amsterdam, 2005 Search PubMed.
- M. Borkowski, M. Richmann, D. T. Reed and Y. Xiong, Radiochim. Acta, 2010, 98, 577–582 CrossRef CAS.
- M. Altmaier, X. Gaona and T. Fanghänel, Chem. Rev., 2013, 113, 901–943 CrossRef CAS PubMed.
- M. J. Polinski, E. M. Villa and T. E. Albrecht-Schmitt, Coord. Chem. Rev., 2014, 266–267, 16–27 CrossRef CAS PubMed.
- J. Schott, J. Kretzschmar, M. Acker, S. Eidner, M. U. Kumke, B. Drobot, A. Barkleit, S. Taut, V. Brendler and T. Stumpf, Dalton Trans., 2014, 43, 11516–11528 RSC.
- K. Hinz, M. Altmaier, X. Gaona, T. Rabung, D. Schild, M. Richmann, D. T. Reed, E. V. Alekseev and H. Geckeis, New J. Chem., 2015, 39, 849–859 RSC.
- W. G. Woods, Environ. Health Perspect., 1994, 102(Suppl. 7), 5–11 CrossRef CAS.
- J. F. Lucchini, M. Borkowski, M. K. Richmann, S. Ballard and D. T. Reed, J. Alloys Compd., 2007, 444/445, 506–511 CrossRef PubMed.
- D. A. Köse, B. Zümreoglu-Karan, T. Hökelek and E. Sahin, Inorg. Chim. Acta, 2010, 363, 4031–4037 CrossRef PubMed.
- T. Oi, T. Takeda and H. Kakihana, Bull. Chem. Soc. Jpn., 1992, 65, 1903–1909 CrossRef CAS.
- C. C. Hinckley, J. Am. Chem. Soc., 1969, 91, 5160–5162 CrossRef CAS.
- B. C. Mayo, Chem. Soc. Rev., 1973, 2, 49–74 RSC.
- J. D. Roberts, G. E. Hawkes, J. Husar, A. W. Roberts and D. W. Roberts, Tetrahedron, 1974, 30, 1833–1844 CrossRef CAS.
- A. F. Cockerill, G. L. O. Davies, R. C. Harden and D. M. Rackham, Chem. Rev., 1973, 73, 553–588 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS PubMed.
- A. Barkleit, S. Tsushima, O. Savchuk, J. Philipp, K. Heim, M. Acker, S. Taut and K. Fahmy, Inorg. Chem., 2011, 50, 5451–5459 CrossRef CAS PubMed.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753 CrossRef CAS.
- A. Barkleit, M. Acker and G. Bernhard, Inorg. Chim. Acta, 2013, 394, 535–541 CrossRef CAS PubMed.
- G. Tian, L. R. Martin and L. Rao, Inorg. Chem., 2010, 49, 10598–10605 CrossRef CAS PubMed.
- N. Rawat, R. S. Sharma, B. S. Tomar and V. K. Manchanda, Thermochim. Acta, 2010, 501, 13–18 CrossRef CAS PubMed.
- P. Gans, A. Sabatini and A. Vacca, Hyperquad Simulation and Speciation, Protonic Software, Leeds, 2009 Search PubMed.
- Lanthanide Probes in Life, Chemical and Earth Sciences Theory and Practice, ed. J.-C. G. Bünzli and G. R. Choppin, Elsevier Science B. V., Amsterdam, 1989 Search PubMed.
- C. A. Andersson and R. Bro, Chemom. Intell. Lab. Syst., 2000, 52, 1–4 CrossRef CAS.
- B. Drobot, R. Steudtner, J. Raff, G. Geipel, V. Brendler and S. Tsushima, Chem. Sci., 2015, 6, 964–972 RSC.
- T. Saito, H. Sao, K. Ishida, N. Aoyagi, T. Kimura, S. Nagasaki and S. Tanaka, Environ. Sci. Technol., 2010, 44, 5055–5060 CrossRef CAS PubMed.
- R. M. Callejón, J. M. Amigo, E. Pairo, S. Garmón, J. A. Ocana and M. L. Morales, Talanta, 2012, 88, 456–462 CrossRef PubMed.
- K. Ishida, T. Saito, N. Aoyagi, T. Kimura, R. Nagaishi, S. Nagasaki and S. Tanaka, J. Colloid Interface Sci., 2012, 374, 258–266 CrossRef CAS PubMed.
- P. Gans, A. Sabatini and A. Vacca, Hyperquad suite of programs, Protonic Software, Leeds, 2008 Search PubMed.
- A. Heller, A. Barkleit, H. Foerstendorf, S. Tsushima, K. Heim and G. Bernhard, Dalton Trans., 2012, 41, 13969–13983 RSC.
- A. Shokrollahi, M. Montazerozohori, T. Mehrpour, H. Tavallali, B. Z. Khafri and Z. Montaseri, Quim. Nova, 2013, 36, 1354–1359 CrossRef CAS PubMed.
- L. E. Santos-Figueroa, M. E. Moragues, M. M. M. Raposo, R. M. F. Batista, R. C. M. Ferreira, S. P. G. Costa, F. Sancenon, R. Martinez-Manez, J. Soto and J. V. Ros-Lis, Tetrahedron, 2012, 68, 7179–7186 CrossRef CAS PubMed.
- A. Günther and G. Bernhard, HZDR-IRE Annual Report 2012, Dresden, 2013, HZDR-030, ISSN 2191-8716.
- C. W. Davies, Ion Association, Butterworths, London, 1962 Search PubMed.
- R. Corigli, F. Secco and M. Venturini, Inorg. Chem., 1982, 21, 2992–2998 CrossRef CAS.
- O. Lukkari and J. Tamminen, Finn. Chem. Lett., 1988, 15, 13–17 CAS.
- M. L. S. Goncalves and A. M. Mota, Talanta, 1987, 34, 839–847 CrossRef CAS.
- T. Paal and M. Mate, Magy. Kem. Foly., 1988, 94, 143–144 CAS.
- S. Friedman, B. Pace and R. Pizer, J. Am. Chem. Soc., 1974, 96, 5381–5384 CrossRef CAS.
- S. H. Eberle and J. B. Schaefer, J. Inorg. Nucl. Chem., 1969, 31, 1523–1527 CrossRef CAS.
- S. Giroux, S. Aury, B. Henry and P. Rubini, Eur. J. Inorg. Chem., 2002, 5, 1162–1168 CrossRef.
- N. Ingri, Acta Chem. Scand., 1962, 16, 439–448 CrossRef CAS PubMed.
- K. Yoshimura, Y. Miyazaki, F. Ota, S. Matsuoka and H. Sakashita, J. Chem. Soc., Faraday Trans., 1998, 94, 683–689 RSC.
- R. Pizer and P. J. Ricatto, Inorg. Chem., 1995, 34, 1007–1008 CrossRef CAS.
- A. Hertam, Diploma thesis, Freiberg University of Mining and Technology, 2011.
- Y. Miyazaki, H. Matsuo, T. Fujimori, H. Takemura, S. Matsuoka, T. Okobira, K. Uezu and K. Yoshimura, Polyhedron, 2008, 27, 2785–2790 CrossRef CAS PubMed.
- Y. Miyazaki, T. Fujimori, H. Okita, T. Hirano and K. Yoshimura, Dalton Trans., 2013, 42, 10473–10486 RSC.
- J. M. Coddington and M. J. Taylor, J. Coord. Chem., 1989, 20, 27–38 CrossRef CAS PubMed.
- Y. Miyazaki, K. Yoshimura, Y. Miura, H. Sakashita and K. Ishimaru, Polyhedron, 2003, 22, 909–916 CrossRef CAS.
- M. Van Duin, J. A. Peters, A. P. G. Kieboom and H. Van Bekkum, Tetrahedron, 1985, 41, 3411–3421 CrossRef CAS.
- A. Queen, Can. J. Chem., 1977, 55, 3035–3039 CrossRef CAS.
- R. Larsson and G. Nunziata, Acta Chem. Scand., 1972, 26, 1503–1509 CrossRef CAS PubMed.
- M. Mikesova and M. Bartusek, Chem. Zvesti, 1978, 32, 472–477 CAS.
- T. Paal and M. Mate, Magy. Kem. Foly., 1985, 91, 569–570 CAS.
- R. Pizer and R. Selzer, Inorg. Chem., 1984, 23, 3023–3026 CrossRef CAS.
- R. Larsson and G. Nunziata, Acta Chem. Scand., 1970, 24, 2156–2168 CrossRef CAS PubMed.
- Y. Hasegawa, Y. Morita, M. Hase and M. Nagata, Bull. Chem. Soc. Jpn., 1989, 62, 1486–1491 CrossRef CAS.
- R. Pizer and P. J. Ricatto, Inorg. Chem., 1994, 33, 2402–2406 CrossRef CAS.
- A. Barkleit, J. Kretzschmar, S. Tsushima and M. Acker, Dalton Trans., 2014, 43, 11221–11232 RSC.
- M. A. Gouveia and R. Guedes de Carvalho, J. Inorg. Nucl. Chem., 1966, 28, 1683–1688 CrossRef CAS.
- M. Van Duin, J. A. Peters, A. P. G. Kieboom and H. Van Bekkum, Tetrahedron, 1984, 40, 2901–2911 CrossRef CAS.
- R. Portanova, L. H. J. Lajunen, M. Tolazzi and J. Piispanen, Pure Appl. Chem., 2003, 75, 495–540 CrossRef CAS.
- M. J. Polinski, E. B. Garner, R. Maurice, N. Planas, J. T. Stritzinger, T. G. Parker, J. N. Cross, T. D. Green, E. V. Alekseev, S. M. Van Cleve, W. Depmeier, L. Gagliardi, M. Shatruk, K. L. Knappenberger, G. Liu, S. Skanthakumar, L. Soderholm, D. A. Dixon and T. E. Albrecht-Schmitt, Nat. Chem., 2014, 6, 387–392 CrossRef CAS PubMed.
- M. J. Polinski, S. Wang, J. N. Cross, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2012, 51, 7859–7866 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5dt00213c |
| This journal is © The Royal Society of Chemistry 2015 |