The nature of the bonding in symmetrical pincer palladacycles

Abstract

The accuracy of DFT-optimised geometries of the symmetrical pincer palladacycles PdNCN and PdSCS, [ClPd{2,6-(Me₂NCH₂)₂C₆H₃}] and [ClPd{2,6-(MeSCH₂)₂C₆H₃}] respectively, has been evaluated by investigating the performance of eight commonly used density functionals with four combinations of basis set, in reproducing their X-ray crystal structures. It was found that whilst the ωB97XD functional performed best over all, the PBE and TPSS functionals performed best when considering the palladium coordination geometry. The role of the donor atom in the stability and reactivity of the symmetric palladacycles, PdYCY, Y = N, S, or P, has been determined using Bader's Atoms in Molecules method to elucidate the nature of the bonding, and using a model formation reaction, which involves the C–H activation of the pincer ligand YCY by PdCl₂. The calculations reveal distinct differences in the bond strength and nature of the interaction of Pd with the donor atoms Y, which support differences in the thermodynamic stability of the palladacycles.

---

Introduction

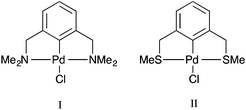
Palladacycles, where a Pd–C bond is intramolecularly stabilised by donor atoms typically from a sulfur, nitrogen or phosphorus donor, are an interesting class of compound. The discovery that they could display extremely high catalytic activity in Suzuki–Miyaura coupling and Heck olefination by Herrmann and Beller et al.^1,2 developed the field into a vibrant research area, with several reviews showing the recent developments.^3–6 Pincer complexes are a type of palladacycle whereby two intramolecular donor atoms chelate to the palladium along with the Pd–C bond. These pincers can be symmetrical with identical side arms, such as PdNCN (e.g. [ClPd{2,6-(Me₂NCH₂)₂C₆H₃}]) and PdSCS (e.g. [ClPd{2,6-(MeSCH₂)₂C₆H₃}] examples (Fig. 1), or more seldom, unsymmetric with different donor atoms or groups such as SCN or PCN types.^7,8 Reports have suggested interesting catalytic properties of the unsymmetrical examples, often showing greater activity than their symmetrical analogues.^9,10 The ability to fine-tune the properties of the ligand, and combine hard and soft Lewis bases with palladium results in hemilability.¹¹ Thus, determining the nature of the bonding in symmetrical pincer palladacycles is a vital first step to understanding the bonding and reactivity of unsymmetric pincer palladacycles.

Fig. 1 Symmetrical PdNCN (I)¹² and PdSCS (II)¹³ pincer palladacycles.

The structure and bonding of palladacycles can be investigated using density functional theory (DFT), however an appropriate choice of functional, basis set, and relativistic effective core potential (ECP) for Pd, is essential for obtaining accurate structures, and hence thermodynamic and kinetic data.¹⁴ Several papers provide useful benchmarking studies of DFT geometries compared to experimental data including the recent study by Minenkov et al.¹⁵ The authors compared DFT-optimised geometries with experimental crystal structures for 18 ruthenium complexes, and a further 10 transition metal complexes. The results showed that the use of functionals that account for dispersion decrease the statistical error between experiment and theory compared to those that do not include dispersion corrections, with the ωB97XD functional providing the best overall results. However for accuracy around the metal centre the PBE and TPSS functionals also performed very well, and for organic ligands B3LYP performed very well. Waller et al.¹⁶ investigated the ability of 15 functionals to describe the optimised geometries of 19 second-row transition metal complexes compared to experimental gas-phase data, showing that hybrid functionals such as the PBE hybrid, B3PW91 and B3P86 provide the most accurate geometries. Clearly the choice of functional is dependent on the chemical nature of the structures studied.

The purpose of this paper is two-fold. First, to determine an optimum DFT methodology for the study of pincer palladacycles that combines accuracy with computational speed. This will be achieved by evaluating the performance of a range of functionals in their ability to reproduce the structural features of two experimentally characterised symmetric pincer palladacycles (Fig. 1). Second, to determine the role of the donor atoms, Y = N, S or P, in the symmetric palladacycles, PdYCY. To compare stability and reactivity, the steps involved in a simple formation reaction, which involves the C–H activation of the pincer ligand YCY by PdCl₂, will be calculated, and the strength and nature of the Pd–L bonding in PdYCY, where L = Y, C, Cl, evaluated.

Computational details

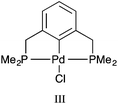
All calculations were performed with the Gaussian 09 package.¹⁷ The neutral spin singlet complexes were studied. The geometry and electronic structure of PdNCN and PdSCS (Fig. 1) were calculated using the same eight density functionals considered by Minenkov et al.¹⁵ The set of density functionals investigated were three generalized gradient approximation (GGA) functionals: BP86,¹⁸ PBE,^19,20 and B97D,²¹ a hybrid-GGA functional: B3LYP,^18,22 two meta-GGA functionals: TPSS²³ and M06L,²⁴ and two hybrid meta-GGA functionals: ωB97XD²⁵ and M06.²⁶ The basis sets tested were 6-31G(d) and 6-31+G(d,p) for all atoms except Pd for which the two relativistic ECPs, LanL2DZ^27,28 and SDD,²⁹ were considered. All optimised structures were compared with the X-ray crystal structures^12,13 (Fig. 1) obtained from the Cambridge Structural Database (CSD number 720256 for PdNCN and 725124 for PdSCS).³⁰ The root mean square (RMS) errors between the calculated and experimental structures were calculated using the Quatfit program.³¹

The optimum methodology for geometry optimisation in the present work was found to be PBE/6-31+G(d,p)[SDD] and was therefore used to calculate the stationary points along the formation reaction pathway of PdNCN and PdSCS (Fig. 1) along with the phosphorus analogue PdPCP ([ClPd{2,6-(Me₂PCH₂)₂C₆H₃}]) (Fig. 2).

Fig. 2 PdPCP pincer palladacycle (III).

All minima and transition states were verified by, respectively, the absence or presence of a single imaginary mode. Single point energy calculations were performed at the ωB97XD/6-311++G(2df,2p)[SDD] level of theory, as the ωB97XD functional²⁵ includes important non-covalent interactions and has been shown to provide accurate energetics.^32–35 The zero-point energy or the Gibbs free energy corrections obtained at PBE/6-31+G(d,p)[SDD] level of theory were applied to the single point energy calculations unscaled.

A topological analysis of the electron density was performed using the Atoms in Molecules (AIM) method,^36,37 as implemented in the Multiwfn program,³⁸ to analyse the bonding using the ωB97XD/6-311++G(2df,2p)[DGDZVP]//PBE/6-31+G(d,p)[SDD] model chemistry. The use of ECPs are not recommended for AIM analysis as bond paths cannot be traced,³⁹ hence the relativistic DGDZVP all electron basis set was used to treat palladium.⁴⁰

Results and discussion

Method validation

To determine an optimum model chemistry the X-ray crystal structures were optimised using a range of functionals and basis sets, and differences between the calculated and observed structural data compared using the Quatfit program.³¹ This provides quantitative root mean square (RMS) errors between the experimental and theoretical structures by analysing the difference between the Cartesian coordinates of each atom pair. Hydrogen atoms were excluded due to the known difficulty in accurately determining their position from X-ray crystallography.¹⁵ Two calculations were performed: (i) with equal weighting given to every atom (except hydrogens which are excluded), and (ii) with zero weighting given to atoms that were not directly bonded to palladium to obtain the accuracy of reproduction of the Pd–L environment. In both cases the results of the PdNCN and PdSCS error analysis were combined to give an overall assessment.

The results from the Quatfit analysis when all atoms have equal weighting show that there is very little difference between the performances of the functionals (Fig. 3), with the RMS values ranging from 0.067 to 0.080 Å.

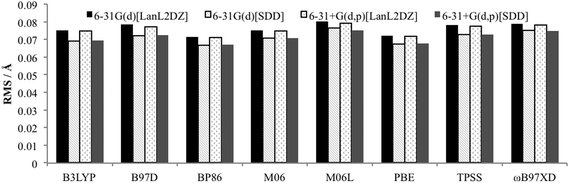Fig. 3 RMS error for optimised PdNCN and PdSCS structures compared to X-ray crystal structures using Quatfit program with equal weighting for all non-hydrogen atoms.

The Quatfit analysis using only palladium and directly bound atoms (Fig. 4), shows that these bonds are better reproduced and show a slightly greater variation in the errors, with the GGAs PBE and BP86, along with the meta-GGA TPSS performing best. However, the difference between the best and worst performing functional is just 0.019 Å.

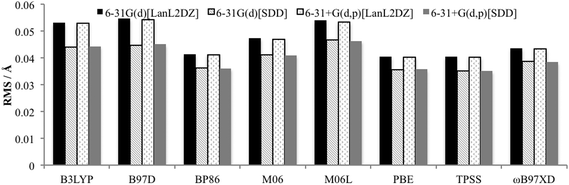Fig. 4 RMS error for optimised PdNCN and PdSCS structures compared to X-ray crystal structures using Quatfit program for Pd–L bonds.

When the basis set choice is studied, it is very clear that the SDD ECP outperforms LanL2DZ (Fig. 3 and 4). There is negligible difference between the 6-31G(d) and 6-31+G(d,p) basis sets, however the inclusion of the diffuse functions is desirable because this provides greater flexibility without a substantial increase in computational time. Therefore, the 6-31+G(d,p)[SDD] basis set was chosen as the optimum basis set for geometry optimisation.

Minenkov et al. showed that functionals that do not account for dispersion interactions systematically overestimated internuclear distances, whereas when dispersion was included these overestimations were matched with underestimates, resulting in very small mean signed errors (MSE).¹⁵ In the study by Waller et al. it was also found that standard DFT functionals overestimated bond distances.¹⁶ Therefore complementary to the Cartesian coordinate approach utilised by the Quatfit analysis, in order to gain an insight into any systematic over or underestimation of bond distances and interatomic distances, a total of 422 interatomic distances and 34 chemically bonded distances calculated using the 6-31+G(d,p)[SDD] basis set and the eight density functionals were compared with the experimentally determined distances. The mean unsigned error (MUE): the average of the absolute deviation between calculation and experiment, and the mean signed error (MSE): the average deviation, were calculated (Fig. 5). The MSE results indicate functionals containing dispersion: M06, M06L and ωB97XD, with the exception of B97D, experience a greater degree of fortuitous cancellation of errors by the cancellation of some of the overestimated distances with underestimated bond distances as reported by Minenkov et al.,¹⁵ for both the bonded and interatomic distances. There are also slightly lower MUE values for functionals accounting for dispersion (except B97D), however once again the differences between all the functionals were relatively small with MUE values for bonded distances between 0.011 and 0.022 Å, and for all interatomic distances slightly larger between 0.022 and 0.046 Å.

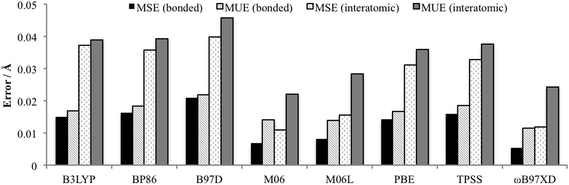Fig. 5 Average bond and interatomic distance MSE and MUE (excluding hydrogens) for PdNCN and PdSCS compared to their X-ray crystal structures using 6-31+G(d,p)[SDD] basis set.

Of key importance is the Pd–L bonding environment. Fig. 6 depicts the MUE and MSE values for the eight Pd–L distances of the PdNCN and PdSCS structures. It is clear that, as per the Quatfit data, the PBE and TPSS functionals reproduce the metal ligand environment extremely well.

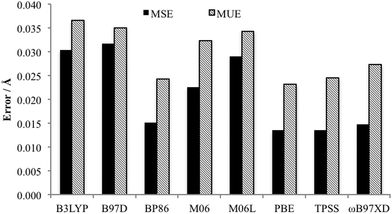Fig. 6 Comparison MUE and MSE of Pd–L bonds of both PdNCN and PdSCS using the 6-31+G(d,p)[SDD] basis set.

Taking into account the data from the MUE and MSE of all bond and interatomic distances, all the DFT functionals considered predict expanded structures, but the errors are reasonably small with ωB97XD having the smallest error. The non-hybrid functionals PBE, BP86 and TPSS provide the best results for the Pd–L environment, and provide advantageous calculation time compared to the other functionals which appear higher on Jacob's ladder.⁴¹ The importance of the Pd–L environment, and the desire for an accurate but computationally efficient method for optimisation of large molecular structures led to the choice of the PBE functional, although the use of TPSS or ωB97XD would be equally appropriate. To confirm this, the Gibbs free energy of formation of the palladacycles via PdCl₂ using both the PBE- and ωB97XD-optimised geometries were compared and found to differ by less than 2 kJ mol⁻¹ (see Table 1). Therefore the methodology of choice for optimisation in the proceeding section is PBE/6-31+G(d,p)[SDD]. Single point energies using ωB97XD/6-311++G(2df,2p)[SDD] at the optimised geometry were performed to ensure accurate energetics as it has been shown that the inclusion of non-covalent interactions is essential for accurate thermodynamics and kinetics, for example, it has been shown that they constitute a significant proportion of the binding energy in various transition metal phosphine complexes.^32,33

Table 1 Gibbs free energies of formation, ΔG⁰, of PdNCN, PdSCS and PdPCP calculated using ωB97XD/6-311++G(2df,2p)[SDD] with either the PBE/6-31+G(d,p)[SDD] or ωB97XD/6-31+G(d,p)[SDD] optimised geometry

Complex	ΔG^0/kJ mol^−1
	PBE	ωB97XD
PdNCN	−207.3	−206.6
PdSCS	−213.2	−214.9
PdPCP	−318.7	−320.4

---

Energy and mechanism of formation of PdYCY

The Gibbs free energy of formation was calculated for PdNCN and PdSCS palladacycles, (Fig. 1) and their phosphorous analogue PdPCP (Fig. 2) from PdCl₂ and the pincer ligand (Scheme 1). This simple formation reaction provides a model for investigating the thermodynamic and kinetic properties as a function of the donor atom Y, i.e. N, S or P. The ωB97XD single point energies were determined using both the PBE and ωB97XD optimised geometries (Table 1), and show that for these systems there is negligible difference (<2 kJ mol⁻¹) between the two datasets. The calculation time using PBE and ωB97XD, starting from the same PdNCN structure and with the same number of iterations, differed by almost a factor of 2. Therefore as the results are comparable, the PBE functional was preferred for geometry optimisation due to its lower computation time.

Scheme 1 Model formation reaction of palladacycles from PdCl₂.

The data in Table 1 show that the PdPCP complex is the most thermodynamically stable, and that the formation of all three complexes is spontaneous (ΔG⁰ < 0).

The simplest concerted formation reaction,^42,43 was studied for PdNCN, PdSCS and PdPCP (Scheme 2) with the energy profile for each reaction provided in Fig. 7. The purpose of this study was to gain insight into the reactivity of the pincer ligands and to provide a reference point when comparing symmetrical and unsymmetrical pincer palladacycle structures. This mechanism involves several steps. Initially the metal coordinates to one of the donor atoms of the pincer ligand and then inserts via a concerted C–H bond activation to form a coordinately-unsaturated Pd centre weakly bound to HCl which is eliminated before the second donor atom of the ligand coordinates to the metal centre to form the PdYCY palladacycle.

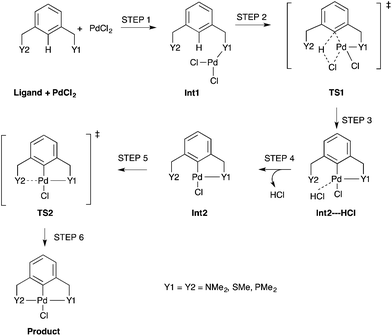Scheme 2 An unassisted formation reaction pathway for PdNCN, PdSCS and PdPCP using monomeric PdCl₂. Int = Intermediate and TS = Transition State.

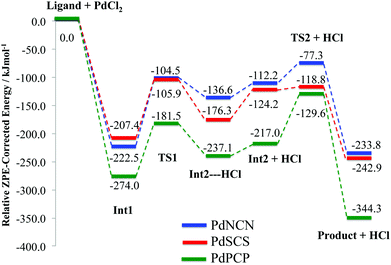Fig. 7 ZPE corrected energy profiles for the formation reaction pathway (Scheme 2) of PdNCN, PdSCS and PdPCP.

The concerted C–H bond activation step proceeds viaTS1. C–H activation is one of the most widely studied and important topics in organometallic chemistry due to its importance in catalysis.^44,45 The C–H bond activation energies for PdNCN, PdSCS, and PdPCP are 118.0, 101.5 and 92.5 kJ mol⁻¹, respectively (Fig. 7). The observation that the barrier to C–H activation in this concerted activation pathway is lowest for PdPCP is in agreement with a similar investigation into the C–H activation of CH₄ by late transition metal pincer complexes.⁴⁵ This step has the highest activation energy barrier in the mechanism and thus constitutes the rate-determining step. The second activation step consists of the coordination of the second donor atom to the palladium centre viaTS2. This occurs via the inversion of the second donor atom into the position to begin coordination to the metal centre for PdNCN and PdPCP, and the rotation of the ligand arm for PdSCS. Due to the different mechanisms, the TS2 barrier for PdNCN and PdPCP is considerably larger (34.9 and 87.4 kJ mol⁻¹, respectively) than that of PdSCS (5.4 kJ mol⁻¹). Decoordination of one of the donor atoms from the Pd centre is likely to be a key step in the catalyst activation.⁴⁶

Nature of the bonding in PdYCY

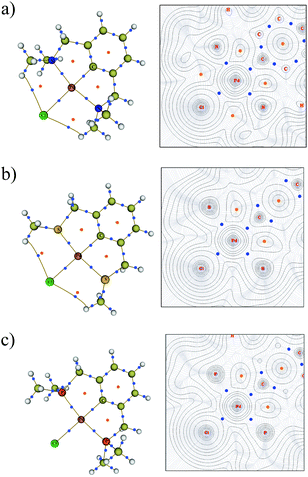
To elucidate the bonding in the symmetrical PdNCN, PdSCS and PdPCP structures, Bader's AIM method was used.^36,37 A bond critical point (BCP) corresponds to the point where the electron density becomes a minimum along the bond path between interacting atoms. The molecular graphs and contour maps for each PdYCY structure (Fig. 8) show the presence of BCPs (blue dots) and ring critical points (orange dots). The data show the presence of BCPs between the palladium atom and the donor atoms, carbon and chlorine as expected. Fig. 8 also shows the presence of an unexpected BCP between the Cl atom and H atom of the YCH₃ arm for the PdSCS and PdNCN complexes, which is absent in the PdPCP complex. These interactions are significantly weaker (ρ(r) ≤ 0.010 a.u.) than those of the Pd–L bonds (see below). The absence of a BCP in the PdPCP is attributed to the considerably longer Cl–H distance (3.33 Å) compared to that in PdNCN (2.76 Å) and PdSCS (2.95 Å).

Fig. 8 Molecular graph (left) and the contour map of electron densities (right) for (a) PdNCN, (b) PdSCS and (c) PdPCP. The BCPs are shown as small blue dots and RCPs are shown as orange dots. For contour map: the N, Cl and N plane for PdNCN, the S, Cl and S plane for PdSCS and the P, Cl and P plane for PdPCP is shown.

The AIM parameters at the key BCPs are provided in Table 2. The magnitude of the electron density ρ(r) at the BCP indicates the strength of the interaction. The Laplacian of the electron density ∇²ρ(r) indicates the nature of the interaction; ∇²ρ(r) < 0 indicates regions of local electronic charge concentration corresponding to a covalent-type interaction, whereas ∇²ρ(r) > 0 indicates density depletion corresponding to an ionic or closed-shell interaction.³⁹ Additionally, the sum of the gradient kinetic electron density G(r) and the potential energy density V(r), provides the total electron energy density H(r), which further elucidates the nature of the bond.

Table 2 AIM parameters (electron density ρ(r), Laplacian of the electron density ∇²ρ(r), total energy H(r), ellipticity ε, and delocalisation index δ(Pd–L)) of the Pd–L bond critical points in PdNCN, PdSCS (Fig. 1) and PdPCP (Fig. 2). All values are in atomic units

Structure	Bond type	ρ(r)	∇^2ρ(r)	H(r)	ε	δ(Pd–L)
PdNCN	Pd–N1	0.087	0.383	−0.014	0.033	0.908
	Pd–N2	0.086	0.383	−0.014	0.033	0.908
	Pd–C	0.156	0.236	−0.070	0.081	1.126
	Pd–Cl	0.064	0.238	−0.011	0.198	1.219
PdSCS	Pd–S1	0.091	0.257	−0.025	0.040	1.157
	Pd–S2	0.091	0.257	−0.025	0.040	1.157
	Pd–C	0.137	0.223	−0.055	0.061	1.051
	Pd–Cl	0.068	0.237	−0.013	0.114	1.234
PdPCP	Pd–P1	0.101	0.183	−0.036	0.022	1.124
	Pd–P2	0.101	0.183	−0.036	0.022	1.124
	Pd–C	0.126	0.224	−0.047	0.050	1.029
	Pd–Cl	0.069	0.232	−0.013	0.085	1.258

---

The data in Table 2 indicate that, for all PdYCY complexes the Pd–C bond is the strongest, indicated by the largest ρ(r), and the Pd–Cl bond is the weakest. Furthermore, the Pd–P bonds are stronger than the analogous Pd–S and Pd–N bonds at the BCP. This is corroborated by the fact that PdPCP is the most thermodynamically stable (Table 1), and the comparatively larger energetic gains of coordination of P to Pd in the formation of Int1 and Product (Fig. 7). The bond strengths of the Pd–N and Pd–S bonds in PdNCN and PdSCS respectively are similar, with slightly stronger Pd–S interactions.

In Suzuki–Miyaura catalysis,⁴⁷ and other types of catalysis where the active species are Pd(0) species, the active species must be generated from the palladacycle precatalysts. A necessary step in this activation is the reductive elimination of Pd from the Pd–C bond.⁴⁶ In an investigation into the reductive elimination of ethane from Pd(PR₃)₂(Me)₂ by Sajith and Suresh it was found that the nature of the bond to be eliminated is more important than their strengths.⁴⁰ They found that a more ionic bond results in a higher activation barrier for the reductive elimination whereas a more covalent bond is easier to cleave. Therefore in the present work the nature of the bonds present in PdNCN, PdSCS and PdPCP, is determined, as this may prove important in fine-tuning the reactivity of pincer palladacycles.

Using the combination of ∇²ρ(r), H(r)^40,48 and the delocalisation index δ(Pd–L) which determines the degree of covalency,^49,50 the nature of the bonding between palladium and the donor atoms can be determined. All the Pd–L bonds exhibit partial ionic and covalent character, the former indicated by the positive ∇²ρ(r) and the latter by the negative H(r). This type of character has been described as “transit closed shell” bonding, with some covalent contribution.^51,52 These transit closed shell interactions are typical in many transition metal donor atom bonds.^{40,50,53–55} The extent of sharing of electrons between the bonds, δ(Pd–L), provides an independent measure of the degree of covalency. The δ(Pd–L) values range from 0.9–1.3 indicating that all of the Pd–L bonds have significant covalent character.

The Pd–N bonds have most ionic character, demonstrated by the largest ∇²ρ(r) and H(r), and smallest δ(Pd–L). The values of ∇²ρ(r) and H(r) at the BCPs indicate that the Pd–P bonds have the most covalent character, however the Pd–S bonds have slightly larger delocalisation indices (Table 2). The bond degree parameter |H(r)/ρ(r)|, which can be interpreted as the total pressure per electron density unit,⁵¹ also indicates that the Pd–P bond is the strongest (|H(r)/ρ(r)| = 0.356) and the Pd–N the weakest (|H(r)/ρ(r)| = 0.161).

The bond ellipticity, ε, can be used to determine the degree of σ and π character in the Pd–L bonds. It measures the extent to which the electron density is unequally distorted away from the bond axis.⁵⁶ The low ε of all the Pd–L bonds reflect their predominant σ character, with the Pd–Cl interactions exhibiting a greater π character contribution.

It is clear from this analysis that all of the Pd–L bonds are characterised by low ρ(r), positive ∇²ρ(r) and negative H(r) indicating partial ionic and covalent character. However, it is also clear that there are subtle differences between the Pd–L interactions; the relative magnitude of the parameters indicates that the Pd–P bond is most covalent and the Pd–N bond most ionic. This varying nature of the bonds in each palladacycle could potentially have implications in reactivity.

Conclusions

The importance of securing an appropriate DFT methodology for the particular system of interest is now well established. Therefore, the experimentally-characterised PdNCN and PdSCS complexes (Fig. 1) were used to test the accuracy of a number of DFT functionals. It was found that the GGA's PBE and BP86 and the meta-GGA TPSS provided the most accurate and reliable geometries around the Pd centre, and that the SDD ECP on Pd proved more effective than LanL2DZ in all cases. Functionals containing dispersion were shown to provide slightly better MUEs and fortuitous cancellation of errors resulting in lower MSEs, with the ωB97XD exhibiting the smallest errors. Overall PBE, TPSS and ωB97XD performed best. The faster computational times and focus on the Pd–L environment led to the choice of PBE as the functional of choice for geometry optimisation.

The role of the donor atoms in the stability and reactivity of the symmetric pincer palladacycles, PdYCY, Y = N, S or P, was evaluated. The simple formation reaction of the YCY pincer ligand with PdCl₂, via C–H activation, was determined in order to give a measure of the relative stability and reactivity as a function of the donor atom in the absence of other effects (such as intra- or inter-molecular assisted formation and solvent effects). It was found that both thermodynamically and kinetically PdPCP was the most stable and PdNCN was the least stable. This was supported by a topological analysis of the electron density in the PdYCY complexes. The data suggested that Pd–P bonds were the strongest and the Pd–N bonds the weakest. Furthermore, it was found that the Pd–P bond had more covalent character than the Pd–S and that the Pd–N bond had the most ionic character.

The calculations clearly revealed distinct differences in the bond strength and nature of the interaction of Pd with the donor atoms N, S and P, which supported the differences in the stability, namely that the PdPCP was the most thermodynamically stable (in the absence of external effects). The varying nature of the bonds in each palladacycle could potentially have implications in their reactivity. Exploitation of these differences by considering unsymmetric YCY’ complexes, both experimentally and theoretically, are underway.

Acknowledgements

We would like to thank the Thai Government and the University of Sussex for fully-funded scholarships (SB and GWR, respectively). The authors would also like to acknowledge the use of the EPSRC UK National Service for Computational Chemistry Software (NSCCS) at Imperial College London in carrying out this work.

References

1. M. Beller, H. Fisher, W. A. Herrmann, K. Öfele and C. Brossmer, Angew. Chem., Int. Ed. Engl., 1995, 34, 1848–1849.
2. W. A. Herrmann, C. Brossmer, K. Öfele, C.-P. Reisinger, T. Priermeier, M. Beller and H. Fisher, Angew. Chem., Int. Ed. Engl., 1995, 34, 1844–1848.
3. Palladacycles: Synthesis, Characterization and Applications, ed. J. Dupont and M. Pfeffer, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2008.
4. J. Dupont, C. S. Consorti and J. Spencer, Chem. Rev., 2005, 105, 2527–2571.
5. N. Selander and K. J. Szabó, Chem. Rev., 2011, 111, 2048–2076.
6. V. Farina, Adv. Synth. Catal., 2004, 346, 1553–1582.
7. M. Gagliardo, N. Selander, N. C. Mehendale, G. van Koten, R. J. M. Klein Gebbink and K. J. Szabó, Chem. – Eur. J., 2008, 14, 4800–4809.
8. G. Ebeling, M. R. Meneghetti, F. Rominger and J. Dupont, Organometallics, 2002, 21, 3221–3227.
9. I. Moreno, R. SanMartin, B. Ines, M. T. Herrero and E. Dominguez, Curr. Org. Chem., 2009, 13, 878–895.
10. J.-L. Niu, X.-Q. Hao, J.-F. Gong and M.-P. Song, Dalton Trans., 2011, 40, 5135–5150.
11. P. Braunstein and F. Naud, Angew. Chem., Int. Ed., 2001, 40, 680–699.
12. B.-B. Liu, X.-R. Wang, Z.-F. Guo and Z.-L. Lu, Inorg. Chem. Commun., 2010, 13, 814–817.
13. C. A. Kruithof, H. P. Dijkstra, M. Lutz, A. L. Spek, R. J. M. Klein Gebbink and G. van Koten, Organometallics, 2008, 27, 4928–4937.
14. M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2, 1282–1290.
15. Y. Minenkov, Å. Singstad, G. Occhipinti and V. R. Jensen, Dalton Trans., 2012, 41, 5526–5541.
16. M. P. Waller, H. Braun, N. Hojdis and M. Bühl, J. Chem. Theory Comput., 2007, 3, 2234–2242.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision B), Gaussian, Inc., Wallingford CT, 2009.
18. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
19. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
21. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
22. A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046.
23. J. Tao, J. Perdew, V. Staroverov and G. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
24. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
25. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
26. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
27. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
28. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
29. D. Andrae, U. Häuβermann, M. Dolg, H. Stoll and H. Preuβ, Theor. Chim. Acta, 1990, 77, 123–141.
30. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 . http://www.ccdc.cam.ac.uk/pages/Home.aspx.
31. D. J. Heisterberg, The Quatfit Program, the CCL archive, 1990. http://www.ccl.net/cca/software/SOURCES/C/quaternion-mol-fit/quatfit.txt.shtml.
32. Y. Minenkov, G. Occhipinti and V. R. Jensen, J. Phys. Chem. A, 2009, 113, 11833–11844.
33. N. Sieffert and M. Bühl, Inorg. Chem., 2009, 48, 4622–4624.
34. M. L. Laury and A. K. Wilson, J. Chem. Theory Comput., 2013, 9, 3939–3946.
35. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 669–676.
36. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15.
37. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990.
38. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 . http://multiwfn.codeplex.com.
39. The Quantum Theory of Atoms in Molecules, ed. C. F. Matta and R. J. Boyd, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2007, pp. 1–34.
40. P. K. Sajith and C. H. Suresh, Inorg. Chem., 2011, 50, 8085–8093.
41. J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20.
42. S. Pascual, P. de Mendoza, A. A. C. Braga, F. Maseras and A. M. Echavarren, Tetrahedron, 2008, 64, 6021–6029.
43. D. García-Cuadrado, P. de Mendoza, A. A. C. Braga, F. Maseras and A. M. Echavarren, J. Am. Chem. Soc., 2007, 129, 6880–6886.
44. A. D. Ryabov, Chem. Rev., 1990, 90, 403–424.
45. W. Lai, J. Yao, S. Shaik and H. Chen, J. Chem. Theory Comput., 2012, 8, 2991–2996.
46. D. V. Aleksanyan, V. A. Kozlov, N. E. Shevchenko, V. G. Nenajdenko, A. A. Vasil'ev, Y. V. Nelyubina, I. V. Ananyev, P. V. Petrovskii and I. L. Odinets, J. Organomet. Chem., 2012, 711, 52–61.
47. N. Miyaura, T. Yanagi and A. Suzuki, Synth. Commun., 1981, 11, 513–519.
48. W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181–197.
49. P. Macchi and A. Sironi, Coord. Chem. Rev., 2003, 238–239, 383–412.
50. M. Montag, I. Efremenko, G. Leitus, Y. Ben-David, J. M. L. Martin and D. Milstein, Organometallics, 2013, 32, 7163–7180.
51. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
52. M. Niskanen, P. Hirva and M. Haukka, J. Chem. Theory Comput., 2009, 5, 1084–1090.
53. S. K. Brayshaw, J. C. Green, G. Kociok-Köhn, E. L. Sceats and A. S. Weller, Angew. Chem., Int. Ed., 2006, 45, 452–456.
54. X. Li, J. Sun, Z. Sun, Y. Zeng, S. Zheng and L. Meng, Organometallics, 2012, 31, 6582–6588.
55. J. A. Cabeza, J. F. Van der Maelen and S. García-Granda, Organometallics, 2009, 28, 3666–3672.
56. C. Silva López, O. Nieto Faza, F. P. Cossió, D. M. York and A. R. de Lera, Chem. – Eur. J., 2005, 11, 1734–1738.

---

Footnote

† Electronic supplementary information (ESI) available: Energies and Cartesian coordinates of the stationary points along the formation reaction pathway are provided. See DOI: 10.1039/c5dt00031a

---