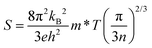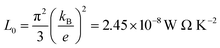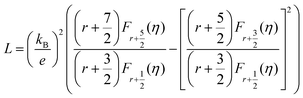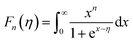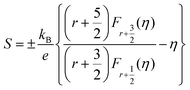Thermoelectric properties and chlorine doping effect of In₄Pb_0.01Sn_0.03Se_2.9Cl_x polycrystalline compounds

Abstract

We investigated the thermoelectric properties of Cl-doped polycrystalline compounds In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.02, 0.04, and 0.06). X-ray diffraction measurement shows a gradual change in lattice volume for x ≤ 0.04 without any impurity phases indicating a systemic change in Cl doping. The Cl doping in the compounds has the effect of increasing carrier concentration and the effective mass of carriers, resulting in an increase in power factor at a high temperature (∼700 K). Because of the increased electrical conductivity at a high temperature, the dimensionless thermoelectric figure of merit ZT reaches 1.25 at 723 K for the x = 0.04 Cl-doped compound, which is a relatively high value for n-type polycrystalline materials.

---

1. Introduction

The global energy crisis makes a case for not only the development of new eco-friendly energy sources but also efficient consumption of the energy currently in use. Thermoelectric research is one of the efforts made to promote energy efficiency. Thermoelectric performance can be defined by the dimensionless figure of merit ZT = S²σT/κ, where S, σ, κ, and T are the Seebeck coefficient, electrical conductivity, thermal conductivity, and absolute temperature, respectively.

State-of-the-art thermoelectric materials have reported high ZT values of 2.6 at 923 K (SnSe)¹ and 2.2 at 915 K (SrTe-doped PbTe).² However, the materials with high recorded ZT values are mostly based on p-type materials. We need counterpart n-type materials with high thermoelectric performance in order to make thermoelectric devices.

One class of promising n-type thermoelectric materials is In₄Se₃-based compounds. Single-crystalline In₄Se_3−x (x = 0.65) reported a high ZT value of 1.48 at 705 K using the Peierls distortion.³

Basically, because the Peierls distortion is based on quasi-one-dimensional electron transport, the effect of the Peierls distortion is averaged out in polycrystalline materials. Therefore, compared with single-crystalline materials, polycrystalline In₄Se_3−x compounds show decreased ZT values of 0.63 at 710 K and 0.97 at 698 K, synthesized by spark plasma sintering (SPS) and ball milling-hot press sintering methods, respectively.^4,5

Recently, Pb and Sn co-doping of In₄Se₃-based compounds produced greatly increased values of thermoelectric performances in spite of polycrystalline compounds. For example, Pb/Sn-co-doped In₄Pb_xSn_ySe₃ and Se-deficient In₄Pb_0.01Sn_0.03Se_3−x compounds exhibit relatively high ZT values of 1.4 at 733 K and 1.2 (x = 0.1) at 723 K, respectively.^6,7

The other promising route to improve thermoelectric properties in In₄Se₃ compounds is halogen doping of the compounds In₄Se_3−xH_y (H = F, Cl, Br, and I).⁸ The Hall mobilities of single-crystalline In₄Se_3−xH_0.03 are significantly increased by halogen doping. It was found that Cl doping is the most effective for increasing Hall mobility. Cl-doped single-crystalline In₄Se_3−xCl_0.03 (x = 0.33) exhibits high ZT values, with a maximum ZT of 1.53 at 698 K, over a wide temperature range compared with In₄Se_3−x.⁹ The critical issue with In₄Se₃-based compounds is the increase in chemical potential because the materials have far from the optimum chemical potential from a Boltzmann transport calculation.^3,9 It has been reported that multiple cation doping and halogen doping on a Se-deficient site can increase the chemical potential resulting in enhancement of thermoelectric performance.^6,10,11

Here, we investigate the Cl doping effect on Pb/Sn-co-doped In₄Pb_0.01Sn_0.03Se_2.9Cl_x compounds. In the previous study, we successfully synthesized polycrystalline In₄Pb_0.01Sn_0.03Se_2.9 compounds without any impurities which exhibited a maximum ZT value of 1.2 at 723 K.⁷ However, the power factor of the In₄Pb_0.01Sn_0.03Se_2.9 compound can increase further, because it is still far from the optimized chemical potential of 0.8 eV from a Boltzmann transport calculation.^3,9 The chemical potential of the In₄Se₃ phase can be further increased by electron doping. Cl doping is believed to be a good candidate for increasing thermoelectric performance in multiple elements-doped In₄Pb_0.01Sn_0.03Se_2.9Cl_x compounds.

2. Experimental

Polycrystalline ingots of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.02, 0.04, and 0.06) were synthesized by melting, quenching, and annealing processes. The elements In, Pb, Sn, and Se, and InCl₃ compound were sealed in evacuated quartz tubes under high vacuum with respect to their stoichiometric molar ratios. The quartz ampoules were heated at 1123 K for 24 h with subsequent water quenching.

The ingots were pulverized and sintered under an argon atmosphere by hot press at about 730 K for 1 h under uniaxial pressure of 70 MPa. In order to increase their thermal stability, the pellets were annealed at 753 K for 5 days. The relative densities of the annealed samples were above 95% (5.82–5.93 g cm⁻³) of the theoretical density.

The crystal structure and phase of the annealed samples were identified by powder X-ray diffraction (XRD) using Cu Kα radiation (D8 Advance, Bruker). Rietveld refinement was carried out using FullProf software. The electrical resistivity ρ and Seebeck coefficient S were measured under an argon atmosphere by a four-probe method using a thermoelectric properties measurement system (ZEM-3, ULVAC-RIKO, Japan). The carrier concentration was calculated by the relation n_H = −1/(R_He) where R_H is the Hall coefficient. The Hall coefficient R_H (R_H = ρ_xy/H) and Hall resistivity ρ_xy were measured by a four-probe contact method with sweeping magnetic fields from −5 T to +5 T using a physical property measurement system (PPMS, Quantum Design, USA). We obtained the thermal conductivity from the relation κ = λρ_sC_p, where λ, ρ_s, and C_p are the thermal diffusivity, sample density, and specific heat, respectively. The thermal diffusivity λ and specific heat C_p were measured by a laser flash method (LFA-457, NETZSCH) and physical property measurement system, respectively.

3. Results and discussion

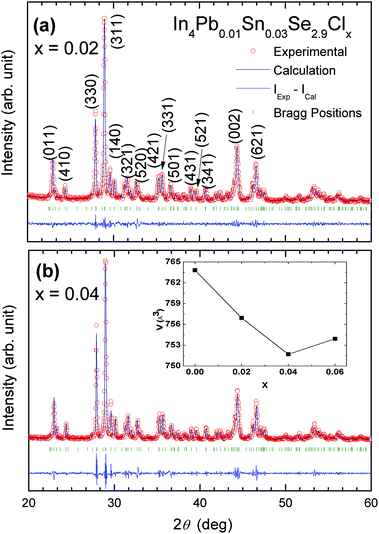
Fig. 1 shows Rietveld refinement analysis on powder X-ray diffraction (XRD) patterns of the prepared samples (x = 0.02 and x = 0.04) based on the orthorhombic Pnnm space group, respectively. The XRD patterns show a single phase of In₄Se₃ with no noticeable impurity peaks except for x = 0.06. Because of the impurity phase of InSe (hexagonal, no. 194), we cannot analyse the XRD pattern by Rietveld refinement for the x = 0.06 compound. This indicates that the x = 0.06 compound is at the solubility limit of chlorine which induces the phase separation from In₄Se₃ to the InSe phase. The lattice parameter was calculated as shown in Table 1. In the previous investigation of Se-deficient Pb/Sn-co-doped compounds In₄Pb_0.01Sn_0.03Se_3−x (x = 0.1, 0.2, 0.3, 0.4, and 0.5), the lattice parameters were systematically changed.⁷ However, the lattice parameters of the Cl-doped samples In₄Pb_0.01Sn_0.03Se_2.9Cl_x do not exhibit systematic changes but show a decrease in lattice volume (inset of Fig. 1b) with increasing chlorine concentration up to the x = 0.04 compound. Because the compound with x = 0.06 has an InSe impurity phase, the lattice volume of this compound does not exhibit systematic change.

Fig. 1 Powder X-ray diffraction profiles of In₄Pb_0.01Sn_0.03Se_2.9Cl_x compounds (a) x = 0.02 and (b) x = 0.04. Reliability factors (R-factors) obtained from the fitting are as follows. x = 0.02: R_p = 6.75, R_wp = 8.78, R_exp = 7.30; x = 0.04: R_p = 9.10, R_wp = 11.3, R_exp = 7.34. The inset of (b) shows the lattice volume with respect to Cl concentration of the compounds.

Table 1 Lattice parameters of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06)

x	a (Å)	b (Å)	c (Å)	V (Å^3)
a Ref. 7.
0.00^a	15.29	12.24	4.08	764
0.02	15.19	12.29	4.06	757
0.04	15.20	12.19	4.06	752
0.06	15.22	12.20	4.06	754

---

From the formation energy calculations of halogen-substituted In₄Se_3−xH_0.03 compounds, substitution and vacancy occupation at a Se3 site by Cl doping is the most stable state in In₄Se_3−x.⁸ The decrease in lattice volume by Cl doping can be understood by the strong Coulomb interaction from the electronegativity of Cl and the Cl substitution at a Se3 site.¹²

The temperature-dependent electrical resistivity of polycrystalline In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.02, 0.04, and 0.06) compounds and the x = 0.0 compound⁷ is presented in Fig. 2(a). The electrical resistivity of the Cl-doped compounds exhibits semiconducting behaviour in the measured temperature range. The increasing electrical resistivity with increasing Cl doping shows similar behaviour to In₄Se_2.7Cl_x.¹⁰

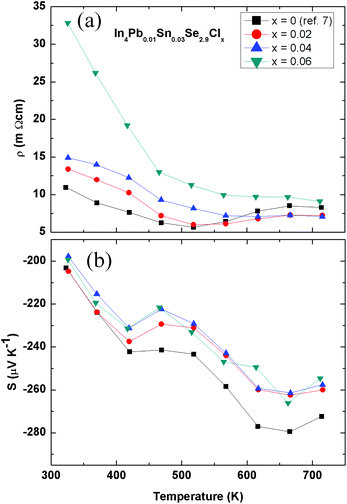Fig. 2 Temperature-dependent electrical resistivity ρ(T) (a) and Seebeck coefficient S(T) (b) of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) compounds.

The electrical resistivity is given by the relation ρ = neμ, where n, e, and μ are the Hall carrier concentration, electric charge, and Hall mobility of the carrier. From Hall resistivity ρ_xy and electrical resistivity ρ measurements, we obtain the effective carrier concentration n_H and Hall mobility μ_H, which are listed in Table 2. The carrier concentration of the In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.02) compound shows a value 1.58 times higher than that of the pristine In₄Pb_0.01Sn_0.03Se_2.9 compound. The carrier concentration does not increase with Cl doping for x = 0.04 and 0.06, implying a solubility limit of the compounds as in the case of polycrystalline In₄Se_2.7Cl_x compounds (x = 0–0.05).¹⁰

Table 2 Hall carrier concentration n_H, electrical resistivity ρ, Hall mobility μ_H, negative Seebeck coefficient −S, and effective mass of the carriers m* of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0, 0.02, 0.04, and 0.06) compounds at 320 K

x	n H (×10^18 cm^−3)	ρ (mΩ cm)	μ H (cm^2 V^−1 s^−1)	−S (μV K^−1)	m* (me)
0.00	2.67	10.9	214	203	0.18
0.02	4.22	13.4	111	205	0.25
0.04	4.09	14.9	103	198	0.24
0.06	3.99	32.9	48	199	0.23

---

The Hall mobilities of In₄Pb_0.01Sn_0.03Se_2.9Cl_x compounds decrease with increasing Cl doping. In contrast with the result for an In₄Se_3−xCl_0.03 single crystal,⁹ the polycrystalline compounds In₄Se_2.7Cl_x¹⁰ and In₄Pb_0.01Sn_0.03Se_2.9Cl_x exhibited a decreased Hall mobility by increasing the Cl doping. This implies that the Hall mobility of polycrystalline In₄Se₃ is decreased by excess Cl impurity scattering at the grain boundary. However, a CuBr-doped In₄Se_2.5 polycrystal shows an increased Hall mobility.¹³

The increase in Hall mobility in bulk crystalline materials is caused by an enhancement of crystallinity, e.g. in a chlorine-doped In₄Se_3−xCl_0.03 single crystal.⁹ For example, X-ray diffraction patterns for the cross-sectional planes of crystalline ingots show well-aligned crystal orientation. However, for polycrystalline materials, the Hall mobility of chlorine-doped samples decreases with increasing chlorine doping concentration.¹⁰ This implies that the chlorine itself acts as a scattering centre of carriers but helps to enhance crystallinity during crystal growth. Doped chlorine can increase the Hall carrier density, but excess chlorine can precipitate at grain boundaries, resulting in a decrease in Hall mobility. On the other hand, single-crystalline materials have less effect on grain boundaries, and thereby the enhanced crystallinity can increase the Hall mobility of carriers.

The temperature-dependent Seebeck coefficient S(T) of polycrystalline In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.02, 0.04, and 0.06) compounds decreases with Cl doping as compared with the x = 0.0 compound, as shown in Fig. 2(b). The Seebeck coefficient of degenerate semiconductors can be expressed by the following equation:

where m* and n are the effective mass of the carrier and the carrier concentration, respectively.¹⁴ From the Hall carrier concentration and the measured Seebeck coefficient, the calculated effective mass of the carrier is listed in Table 2. The effective mass of the carrier of the x = 0.02 sample has obviously increased compared with that of the x = 0.0 sample, even though the Cl doping dependence is not clear. The increased effective mass of the carrier indicates a less dispersive electron band than in the non-Cl-doped sample. From the effective thermal band gap relation, E_g = 2eS_maxT_max,¹⁵ we can estimate the band gap as 0.372 eV (x = 0.0)⁷ and 0.347 eV (x = 0.04). The Cl doping in In₄Pb_0.01Sn_0.03Se_2.9Cl_x compounds induces a less dispersive and decreased band gap than that of the In₄Pb_0.01Sn_0.03Se_2.9 compound.

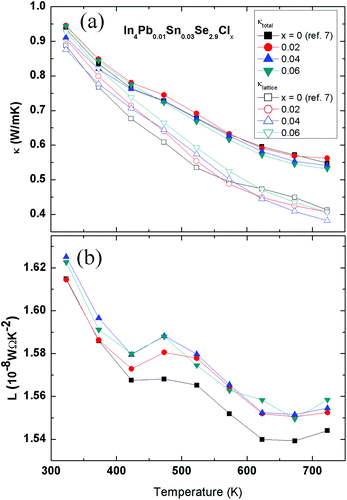
The total thermal conductivities of the polycrystalline In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0, 0.02, 0.04 and 0.06) compounds are shown in Fig. 3(a). The thermal conductivities of the x = 0.0, 0.02, 0.04, and 0.06 compounds decrease with increasing temperature. This conventional 1/T behaviour is mainly caused by an acoustic phonon contribution to thermal transport. There is no systematic change in κ(T) with respect to the Cl doping concentration.

Fig. 3 Temperature-dependent total thermal conductivity κ_tot (closed symbols), lattice thermal conductivity κ_ph (a), and Lorenz number L(T) (b) of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) compounds.

In general, the total thermal conductivity κ is composed of electronic κ_el and lattice thermal conductivity κ_ph. The electronic thermal conductivity κ_el can be calculated by the Wiedemann–Franz law κ_el = L₀σT, where L₀, σ, and T are the Lorenz number, electrical conductivity, and absolute temperature, respectively. In usual cases, the Lorenz number is written as:

However, the Lorenz number is incorrect in correlated metals and many degenerate semiconductors. In order to obtain a more reliable Lorenz number, we calculated the Lorenz number using the following equation:⁷

where r is the scattering parameter, η = E_F/k_BT is the reduced Fermi energy, and F_n(η) is the nth order Fermi integral given by

In most cases, the scattering parameter for acoustic phonon scattering is r = −1/2. When we fit the measured Seebeck coefficient to the following equation with a free parameter η, we can obtain the Fermi integral η:

Using the Fermi integral, the calculated temperature-dependent Lorenz numbers of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) are shown in Fig. 3(b). The calculated temperature-dependent Lorenz number is lower than the conventional Lorenz number L₀ = 2.45 × 10⁻⁸ W Ω K⁻². The low Lorenz numbers indicate that the electronic contribution to thermal transport is lower than in conventional metals. Using the calculated Lorenz number and electrical resistivity, we can obtain the lattice thermal conductivity by subtracting the electronic thermal conductivity from the total thermal conductivity as shown in Fig. 3(a) (open symbols). The change in lattice thermal conductivity with respect to the chlorine doping concentration of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) is not obvious. The similar thermal conductivity can be explained by the similarity of the crystal structure and phonon dispersion relation between In₄Se₃ and InSe.¹⁶

Fig. 4(a) shows the temperature-dependent power factor S²σ of polycrystalline In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) compounds. The decreased power factor with increasing Cl doping is mainly caused by decreased Hall mobility in the room- and mid-temperature range. On the other hand, slightly increased power factors for the x = 0.02 and 0.04 compounds are obtained near 723 K. The x = 0.06 compound exhibits a decreased power factor from that of the other samples (x = 0.0, 0.02, and 0.04) implying that InSe phase separation is ineffective in increasing the power factor in the In₄Se₃ phase.

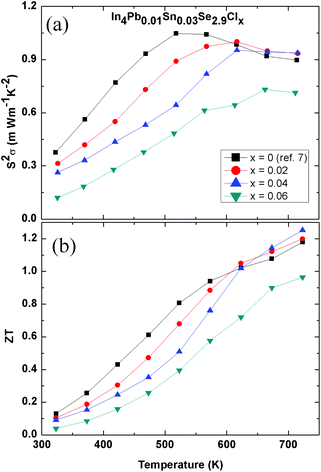Fig. 4 Temperature-dependent power factor S²σ (a) and ZT values (b) of In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04 and 0.06) compounds.

The ZT values of polycrystalline In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) compounds are presented in Fig. 4(b). The maximum ZT, when x = 0.04, reaches 1.25 at 723 K, which is a slightly increased value compared with that of the pristine compound x = 0.0 (ZT = 1.2). The high ZT value over a wide temperature range in bulk crystals of In₄Se_3−xCl_0.03 (1.53) is caused by a significant increase in Hall mobility which is attributed to an enhancement of crystallinity by chlorine doping.⁹ Because the polycrystalline In₄Se_2.7Cl_x samples exhibit a decreased ZT value (0.67) with increasing chlorine doping concentration, we believe that a further enhancement of ZT is possible in In₄Pb_0.01Sn_0.03Se_2.9Cl_x compounds in single-crystalline form. Therefore we should investigate the thermoelectric properties of the single-crystalline compounds as further research.

4. Conclusions

Cl-doped polycrystalline In₄Pb_0.01Sn_0.03Se_2.9Cl_x (x = 0.0, 0.02, 0.04, and 0.06) compounds are synthesized well by melting and solid-state reactions with a systematic change in lattice volume. Because of chlorine impurity scattering, the electrical resistivities of the Cl-doped samples (x = 0.02, 0.04, and 0.06) are increased as compared with the non-Cl-doped sample (x = 0.0) near room temperature, which is mainly caused by a decrease in Hall mobility by chlorine doping. However, the electrical resistivities of the x = 0.02 and 0.04 compounds are decreased at high temperature accompanied by smearing out of the broad shoulder near 670 K.

Consequently, they exhibit a relatively low thermal conductivity and high power factor over a wide temperature range. The power factor and ZT values of the Cl-doped compounds (x = 0.02 and 0.04) increased as compared with the non-Cl-doped compound (x = 0.0) near 700 K. The maximum ZT value of 1.25 is relatively high for polycrystalline In₄Se₃-based compounds. Further enhancement of thermoelectric performance can be expected in single-crystalline compounds by promoting crystallinity of the samples.

Acknowledgements

This research was supported by Mid-career Research Program (Strategy) (no. 2012R1A2A1A03005174) and Nano-Material Technology Development Program (2011-0030147) through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology and Energy Efficiency & Resources program of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government Ministry of Knowledge Economy (no. 20112010100100), and SK Innovation.

Notes and references

1. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373.
2. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414.
3. J.-S. Rhyee, K. H. Lee, S. M. Lee, E. Cho, S. I. Kim, E. Lee, Y. S. Kwon, J. H. Shim and G. Kotliar, Nature, 2009, 459, 965.
4. J.-S. Rhyee, E. Cho, K. H. Lee, S. M. Lee, S. I. Kim, H.-S. Kim, Y. S. Kwon and S. J. Kim, Appl. Phys. Lett., 2009, 95, 212106.
5. G. H. Zhu, Y. C. Lan, H. Wang, G. Joshi, Q. Chen and Z. F. Ren, Phys. Rev. B: Condens. Matter, 2011, 83, 115201.
6. Z.-S. Lin, L. Chen, L.-M. Wang, J.-T. Zhao and L.-M. Wu, Adv. Mater., 2013, 25, 4800.
7. J. H. Kim, M. J. Kim, S. Oh and J.-S. Rhyee, J. Alloys Compd., 2014, 615, 933.
8. K. Ahn, E. Cho, J.-S. Rhyee, S. I. Kim, S. Hwang, H.-S. Kim, S. M. Lee and K. H. Lee, J. Mater. Chem., 2012, 22, 5730.
9. J.-S. Rhyee, K. Ahn, K. H. Lee, H. S. Ji and J.-H. Shim, Adv. Mater., 2011, 23, 2191.
10. J.-S. Rhyee and D. Choi, J. Appl. Phys., 2011, 110, 083706.
11. K. Ahn, E. Cho, J.-S. Rhyee, S. I. Kim, S. M. Lee and K. H. Lee, Appl. Phys. Lett., 2011, 99, 102110.
12. R. T. Sanderson, J. Am. Chem. Soc., 1983, 105, 2259.
13. Y. Luo, J. Yang, G. Liu, Y. Xiao, L. Fu, W. Li, P. Zhu, J. Peng, S. Gao and J. Zhang, Adv. Energy Mater., 2014, 4, 1300599.
14. A. F. Ioffe, Semiconductor Thermoelements and Thermoelectric Cooling, Infosearch, 1957.
15. H. J. Goldsmid and J. W. Sharp, J. Electron. Mater., 1999, 28, 869.
16. M. Sznajder, K. Z. Rushchanskii, L. Y. Kharkhalis and D. M. Bercha, Phys. Status Solidi B, 2006, 243, 592.

---