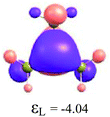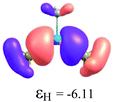Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Feasibility of novel (H3C)nX(SiH3)3−n compounds (X = B, Al, Ga, In): structure, stability, reactivity, and Raman characterization from ab initio calculations†
Renato B.
dos Santos
*ab,
R.
Rivelino
*a,
F. de Brito
Mota
a,
A.
Kakanakova-Georgieva
b and
G. K.
Gueorguiev
*b
aInstituto de Física, Universidade Federal da Bahia, 40210-340 Salvador, Bahia, Brazil. E-mail: renatobs@ufba.br; rivelino@ufba.br
bDepartment of Physics, Chemistry and Biology (IFM), Linköping University, 581 83 Linköping, Sweden. E-mail: gekos@ifm.liu.se
First published on 6th January 2015
Abstract
We employ ab initio calculations to predict the equilibrium structure, stability, reactivity, and Raman scattering properties of sixteen different (H3C)nX(SiH3)3−n compounds (X = B, Al, Ga, In) with n = 0–3. Among this methylsilylmetal family, only the (H3C)3X members, i.e., trimethylboron (TMB), trimethylaluminum (TMA), trimethylgallium (TMG), and trimethylindium (TMI), are currently well-studied. The remaining twelve compounds proposed here open up a two-dimensional array of new possibilities for precursors in various deposition processes, and evoke potential applications in the chemical synthesis of other compounds. We infer that within the (H3C)nX(SiH3)3−n family, the compounds with fewer silyl groups (and consequently with more methyl groups) are less reactive and more stable. This trend is verified from the calculated cohesive energy, Gibbs free energy of formation, bond strength, and global chemical indices. Furthermore, we propose sequential reaction routes for the synthesis of (H3C)nX(SiH3)3−n by substitution of methyl by silyl groups, where the silicon source is the silane gas. The corresponding reaction barriers for these chemical transformations lie in the usual energy range typical for MOCVD processes. We also report the Raman spectra and light scattering properties of the newly proposed (H3C)nX(SiH3)3−n compounds, in comparison with available data of known members of this family. Thus, our computational experiment provides useful information for a systematic understanding of the stability/reactivity and for the identification of these compounds.
Introduction
The gas-phase chemistry of metalorganic molecules, where the metal belongs to group 13 of the periodic table and, particularly, concerning the trimethylmetal compounds (H3C)3X (X = B, Al, Ga, In) – suitable as precursors for the synthesis of III–V semiconductors – has been extensively studied.1,2 Examples include trimethylaluminum (TMA), trimethylgallium (TMG), and trimethylindium (TMI). All of them are widely used as precursors, together with ammonia, in metalorganic chemical vapour deposition (MOCVD) processes of AlN, GaN, InN, and their alloys.3–5 Some of these metalorganic precursors are also employed for synthesizing other materials, such as trimethylboron (TMB), which is used as a precursor for growing boron doped diamond (BDD)6 and also for carbon-doped MgB2 films.7Recently, we have addressed the implication of the silane gas in the MOCVD growth of AlN. Our preliminary results point out viable reactions of silane molecules with (H3C)3Al, yielding a variety of intrinsic precursor molecules. In this context, the possibility for other reactions of the silane gas with (H3C)3Al, leading to the formation of stable methylsilylaluminum compounds, of the type (H3C)nAl(SiH3)3−n (n = 0–3), certainly deserves to be exploited both due to possible implications in MOCVD processes8 and due to possible applications in general chemical syntheses.9–11
A natural generalization of the concept of mixed methylsilylaluminum molecules envisages the family of metallic methylsilyl molecules (H3C)nX(SiH3)3−n, where the metal atom X belongs to the triels (B, Al, Ga, In). All these molecules are natural candidates for independent precursors in general organic synthesis. Thus, the stability, structure, reaction routes, and spectral fingerprints (e.g., Raman spectra) of (H3C)nX(SiH3)3−n are useful for their identification.
Chemical compounds similar to (H3C)nX(SiH3)3−n have been studied and their properties have been reported earlier in the context of the organometallic derivative chemistry.12,13 Complementary to our study, the (H3C)3X compounds (X = B, Al, Ga, In) are standard, commercially available, precursors for the MOCVD growth of III-nitrides.2 Similarly to the trimethylmetal precursors, their trisilyl analogues X(SiH3)3 are also known14–17 for X = B, Al, Ga, and In. Another similar compound is tris(trimethylsilyl)borate, B(OSiCH3)3, which can be seen as an analogue of B(SiH3)3 and has also been synthesized from the reaction of trimethylacetoxysilane (C5H12O2Si) and powdered boric acid (H3BO3) of chemically pure grade at 110 °C.14 Tris(trimethylsilyl)borate has diversified applications, e.g., as a catalyst for polymerization processes, as a half-product in chemical synthesis, and as boron-doped silicon dioxide in microelectronics technology.14
Tris(trimethylsilyl)aluminum, Al[Si(CH3)3], an analogue of Al(SiH3)3, has also been long known, being synthesizable from a mixture of Hg[Si(CH3)3]2 and aluminum powder.15 The reaction of tris(trimethylsilyl)aluminum with ammonia leads to a series of adducts with a pronounced tendency to elimination reactions which are of interest from the point of view of finding new and more efficient (more controllable reactions) precursors for the growth of solid solutions of AlN and even SiC.18 Other tris(trimethylsilyl)triels have also been synthesized,15,16,19,20 although they are not widely used in chemical synthesis. Similarly, tris(trimethylsilyl)gallium, Ga(SiMe3)3, an analogue of Ga(SiH3)3, is synthesizable from the reactants GaCl3, Li, and Me3SiCl.16 Even the corresponding In-containing molecule, tris(trimethylsilyl)indium, In(SiMe3)3, a counterpart of In(SiH3)3, is obtainable using the reactants InCl3, Me3SiCl, and Li.17 This is a chemically metastable compound, which forms greenish-yellow crystals and decomposes at 0 °C.17
In this work, we employ the Møller–Plesset perturbation theory, at the second-order level of approximation (MP2),21,22 to address the stability, structure, reaction routes, and Raman fingerprints of sixteen different (H3C)nX(SiH3)3−n compounds (X = B, Al, Ga, In). For comparison, we also perform some calculations within the framework of the density functional theory (DFT), employing the Perdew and Wang (PW91)23 approach, which is also useful for calculating chemical reactivity indices through the Kohn–Sham orbital eigenvalues.24 As discussed above, among these compounds, only the pure methylmetal (H3C)3X members are currently well-studied.25–29 The remaining twelve molecules proposed here open up a two-dimensional array of new possibilities for precursors in various deposition processes and the chemical synthesis of other compounds. For this reason, the present study is timely and of great interest for epitaxial growth of two-dimensional materials containing the triels B, Al, Ga, and In, as well as their mixed phases.
Methods and computational details
The Møller–Plesset perturbation theory at the second-order level of approximation (MP2)21,22 was utilized to optimize all the (H3C)nX(SiH3)3−n structures proposed in this study, together with harmonic vibrational frequency calculations, as implemented in the Gaussian09 program.30 For the metal atoms X = B, Al, and Ga, the frozen-core MP2 option for defining inner-shells to be excluded from the correlation calculations was combined with the usual aug-cc-pVDZ basis set. In the case of X = In, the MP2 method was combined with an electron-core potential (ECP)31 for the core electrons and the aug-cc-pV5Z-pp basis set32 was utilized for the remaining electrons, as recommended in the literature.33 For C, Si, and H atoms in each (H3C)nX(SiH3)3−n compound, the MP2 calculations were carried out with the 6-311G(d,p) basis set.In order to address possible synthesis routes of the (H3C)nX(SiH3)3−n compounds, we have considered the reaction paths for their formation, by substitution of the methyl by silyl groups, in the commercially available metalorganic precursor molecules (H3C)3X, when these interact with silane. The connecting first-order saddle points (transition states, TS) between two equilibrium geometries were obtained using the synchronous transit-guided quasi-Newton (STQN) method34,35 as implemented in the Gaussian09 program.30 Thus, for the purposes of this work, TS and reaction barriers were calculated at the MP2 level of theory. Furthermore, to evaluate the stability of the resulting (H3C)nX(SiH3)3−n products, cohesive energies (Ecoh/at)36 and Gibbs free energies of formation37 (ΔfG0) were also calculated. A fragmentation scheme has also been proposed to investigate the bond strength of these compounds.
For assessing and comparing the structural and energetic features of the (H3C)nX(SiH3)3−n compounds, the exchange-correlation density-functional of Perdew and Wang,23 PW91, was also employed in the calculations. We notice that both MP2 and PW91 are methods successfully applied to related systems.25,38 For each optimized structure, the frontier molecular orbitals, HOMO (the highest occupied molecular orbital), and LUMO (the lowest unoccupied molecular orbital) were evaluated at the PW91 level of DFT. In order to perceive an ionic or covalent character in these compounds, the Bader charge analysis39 was also performed employing PW91 and MP2 methods.
The calculated HOMO and LUMO energies were further employed to analyse the reactivity of all (H3C)nX(SiH3)3−n compounds by computing the electronic chemical potential (μ) and chemical hardness (η), in the context of the Kohn–Sham molecular orbitals (KS-MO), according to the following definitions:24
| μ = (εL + εH)/2 | (1) |
| η = (εL − εH) | (2) |
| ω = μ2/2η | (3) |
Raman scattering properties were calculated at the MP2 level of theory to analyse important vibrational modes, characteristic of these compounds. In this description, the differential cross sections of depolarized Raman scattering observed at right angles to the incident beam are determined by the activities,43 whereas depolarization ratios for both natural (ρn) and plane-polarized (ρp) light are, respectively, given by
 | (4) |
 | (5) |
In eqn (4) and (5), 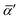 and Δα′ are the derivatives of the average and anisotropic dipole polarizabilities. As is well known in Raman light-scattering theory, the largest values of the depolarization ratios arise for the most depolarized band, varying in the
and Δα′ are the derivatives of the average and anisotropic dipole polarizabilities. As is well known in Raman light-scattering theory, the largest values of the depolarization ratios arise for the most depolarized band, varying in the  and
and 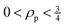 ranges. These are useful properties to characterize possible fingerprints in the vibrational modes due to the molecular formation.
ranges. These are useful properties to characterize possible fingerprints in the vibrational modes due to the molecular formation.
Results and discussion
A. Structure, stability, and reactivity of (H3C)nX(SiH3)3−n
The optimized molecular structures of the sixteen (H3C)nX(SiH3)3−n compounds are displayed in Fig. 1. We observe that all calculated vibrational modes give real-frequency values (indicating that the novel compounds are also true energy minima). The lowest vibrational frequencies, as well as the dipole moments, of each compound are given in the ESI in Table S1.† In general, the calculated bond lengths (X–CH3 and X–SiH3, with X = B, Al, Ga, or In) do not depend on the relative numbers of silyl/methyl groups bonded to the corresponding metal centre. For example, in the cases of Al–SiH3 (n = 0–2) and H3C–Al (n = 1–3), the bond lengths are almost constant, i.e., 2.48 and 1.98 Å, respectively, as indicated in Fig. 1. Moreover, the calculated bond lengths of the (H3C)nX(SiH3)3−n compounds are similar to the bond lengths found for other types of molecules containing the triels. For instance, the Si–B bond length in all (H3C)nB(SiH3)3−n compounds is between 2.01 and 2.04 Å, exhibiting a similar value to the corresponding bond length in H3SiBH2 (2.03 Å).44 Our calculated Si–B bond lengths are also in line with other chemically different compounds containing Si–B bonds, such as [{(Me3Si)3Si}B-(NiPr2)] (Me = CH3, iPr = (CH3)2CH, and Ph = C6H5),20 with a bond length of 2.06 Å, or silylborazine [{(Me3Si)Si}(Me)2B3N3(Me)3],45 with a bond length of 2.10 Å. In a theoretical and experimental study by Gaetrner et al.46 the Al–Si and Ga–Si bond lengths in HAlSiH3 and HGaSiH3 molecules are 2.48 and 2.43 Å, respectively. For comparison, we found essentially values of 2.48 and 2.44 Å for the same type of Al–Si and Ga–Si bond lengths in (H3C)nAl(SiH3)3−n and (H3C)nGa(SiH3)3−n, respectively. Regarding the (H3C)nIn(SiH3)3−n compounds, we obtain In–Si bond lengths of 2.61 Å, which are quite similar to the corresponding value of 2.57 Å predicted for tris(trimethylsilyl)silylindium [In{Si(SiMe3)3}2].47 The B–C, Al–C, Ga–C, and In–C bond lengths (1.58, 1.98, 1.99, and 2.18 Å, respectively) calculated for the (H3C)3X compounds are also in good agreement with the experimental values (1.578, 1.957, 1.967, and 2.093 Å, respectively) found for the corresponding compounds studied by others.5,25,26,48 Accordingly, the calculated X–C bond lengths are in agreement with, theoretically or experimentally, values determined for H3CBH2, H3CAlH2,44 Aryl2GaSi(SiMe3)3,49 Al(But)3, and Ga(But)3.50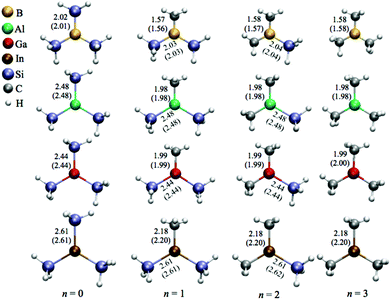 | ||
| Fig. 1 Optimized structures including bond lengths (in Å) for the (H3C)nX(SiH3)3−n compounds at both MP2 and PW91 (values in parentheses) levels of theory. | ||
The cohesive energy per atom (Ecoh/at) calculated for all sixteen (H3C)nX(SiH3)3−n compounds displayed in Fig. 1 is listed in Table 1. In all cases, values obtained with PW91 are larger than the values calculated with MP2. By considering an X(SiH3)3 series, we find that the cohesive energy values slightly decrease from B to In. The cohesive energies for Al(SiH3)3 and Ga(SiH3)3 are very close: 221.0 and 220.3 kcal mol−1 (MP2) and 230.0 and 228.0 kcal mol−1 (PW91), respectively. A similar behaviour is also observed for all the (H3C)nX(SiH3)3−n family (n = 1–3). In a previous study by Kakanakova-Georgieva et al.,36 it was found that the decrease of stability in the (H3C)3M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH3 (M = Al, Ga, In) adducts follows the same order, i.e., from Al to In.
NH3 (M = Al, Ga, In) adducts follows the same order, i.e., from Al to In.
| E coh/at | ΔfG0 | E coh/at | ΔfG0 | E coh/at | ΔfG0 | E coh/at | ΔfG0 | |
|---|---|---|---|---|---|---|---|---|
| n | B | Al | Ga | In | ||||
| 0 | 236.4 | −71.89 | 221.0 | −67.97 | 220.3 | −78.93 | 217.8 | −74.76 |
| (245.0) | (−105.45) | (230.0) | (−101.55) | (228.0) | (−108.90) | (224.3) | (−99.07) | |
| 1 | 264.6 | −115.34 | 248.0 | −106.33 | 246.4 | −113.62 | 242.7 | −104.76 |
| (275.4) | (−158.13) | (258.7) | (−148.27) | (255.7) | (−149.84) | (250.7) | (−136.02) | |
| 2 | 293.6 | −161.34 | 275.3 | −146.27 | 272.7 | −149.37 | 267.7 | −135.23 |
| (306.5) | (−213.09) | (287.6) | (−194.83) | (283.4) | (−191.63) | (277.2) | (−173.17) | |
| 3 | 322.9 | −206.52 | 302.6 | −187.69 | 299.1 | −187.06 | 292.8 | −167.25 |
| (337.8) | (−268.42) | (316.5) | (−242.40) | (311.2) | (−216.85) | (303.6) | (−208.95) | |
Other trend illustrated by the values reported in Table 1 is that when the value of n increases (i.e., less silyl and more methyl groups are bonded to the central metal atom), the stability of the compound also increases. This indicates that the compounds with more methyl groups and fewer silyl groups are expected to be more stable. For example, in the case of (H3C)3Al (n = 3), which is a well-known MOCVD precursor, its Ecoh/at is higher by 81.6 kcal mol−1 (MP2) or by 86.5 kcal mol−1 (PW91) than Ecoh/at for Al(SiH3)3 (n = 0). According to this analysis, TMB is the most stable and trisilylindium is the least stable compound. As we shall see in the following, this stability trend is related to the type of interaction and bond strength involved in each compound.
In Table 1, we also list the calculated Gibbs free energy of formation (ΔfG0) for all sixteen (H3C)nX(SiH3)3−n compounds under their standard conditions37 (1 bar and 298.15 K). As the value of n in (H3C)nX(SiH3)3−n increases, the ΔfG0 values become more negative, indicating that the formation of methyl-rich compounds may be a more spontaneous process. Thus, (H3C)3B is not only the most stable (i.e., exhibiting the highest Ecoh/at), but also the easiest to be formed (i.e., exhibiting the most negative value of ΔfG0). Interestingly, in the X(SiH3)3 series, Ga(SiH3)3 seems to be the easiest to be formed, both with MP2 and PW91 methods. In contrast, In(SiH3)3 appears to be the least stable (exhibiting the lowest Ecoh/at), although its ΔfG0 = –74.76 kcal mol−1 is lower than the ΔfG0 = –67.97 kcal mol−1 for Al(SiH)3 or even a little lower than ΔfG0 = –71.89 kcal mol−1 for B(SiH)3, as obtained with MP2. However, the expected trend in obtaining the favourable compounds comes up when we take into account the PW91 results for which In(SiH3)3 also exhibits the highest ΔfG0. Nonetheless, this difference between the calculated Gibbs free energies of In(SiH3)3 with both methods may be an artifact, since the calculations carried out for the In-containing compounds took into account the ECP combined with the aug-cc-pV5Z-pp basis set. In contrast, considering the metal atoms calculated by including all electrons, described by the aug-cc-pVDZ basis set, as is the case for B, Al and Ga, we observe that the Ga-containing compounds may exhibit lower ΔfG0 than the B- or Al-containing compounds, at both the levels of calculations considered here.
The free energy trend observed for the (H3C)nX(SiH3)3−n compound may be related to the type of pair interaction in each of them. To provide an additional description of the stability of these compounds, we have considered their fragmentation per silyl and methyl group. The calculated average bond strengths between each group and the central metal atom, BS(X), are reported in Table 2. This quantity is defined here as the difference between the total energy of a (H3C)nX(SiH3)3−n compound and the sum of the energies of all (H3C)iX(SiH3)2−i fragments (i = 0–2) and the corresponding methyl or silyl group removed during the fragmentation. To simplify the notation, the (H3C)n–X(SiH3)3−n and (H3C)nX–(SiH3)3−n bonds are represented as X–C (bond of the CH3 group to the central atom X) or X–Si (bond of the SiH3 group to the central atom X). In all cases, the bond strengths corresponding to the X–C bonds are higher than those associated with the X–Si bonds, as expected for these types of compounds. From this analysis, the average bond strength of the Ga–Si pair (n = 0–2) is higher than the corresponding value for the Al–Si pair by 0.7 kcal mol−1, on average, in line with the calculated Gibbs free energies. However, considering BS(In) in In(SiH3)3, in comparison with BS(Al) in Al(SiH3)3, or even BS(B) in B(SiH3)3, there is no systematic trend (especially when the Gibbs free energies are calculated with MP2).
| Bond | BS(B) | BS(Al) | BS(Ga) | BS(In) |
|---|---|---|---|---|
| X–Si | 82.07 | 64.45 | 65.25 | 59.15 |
| (n = 0) | (80.11) | (62.09) | (63.80) | (57.84) |
| X–Si | 82.02 | 65.60 | 66.25 | 59.74 |
| (n = 1) | (79.80) | (66.09) | (65.18) | (58.64) |
| X–C | 100.73 | 78.43 | 75.27 | 64.70 |
| (n = 1) | (99.54) | (77.02) | (72.11) | (61.28) |
| X–Si | 84.15 | 67.18 | 67.91 | 60.77 |
| (n = 2) | (81.99) | (67.93) | (67.18) | (59.77) |
| X–C | 103.78 | 80.48 | 77.25 | 65.69 |
| (n = 2) | (101.86) | (79.15) | (73.94) | (62.10) |
| X–C | 107.02 | 82.39 | 79.41 | 66.84 |
| (n = 3) | (104.84) | (81.14) | (76.02) | (63.05) |
The X–C (X–Si) bond strengths exhibit small and moderate variations for different n (see Table 2). For example, the MP2 average bond strength of the B–C bond is 100.73 kcal mol−1 for n = 1, 103.78 kcal mol−1 for n = 2, and 107.02 kcal mol−1 for n = 3. Even smaller variations are exhibited by the MP2 average bond strengths of the B–Si bond: 82.07 kcal mol−1 for n = 0, 82.02 kcal mol−1 for n = 1, and 84.15 kcal mol−1 for n = 2. A similar behaviour is observed for X = Al, Ga, and In by changing n; the smallest variation of the average bond strengths was found in the case of the (H3C)nIn(SiH3)3−n compounds. In general, the BS(X) trend is very similar independently of the level of theory employed. Not surprisingly, TMB (the most stable compound obtained in this study) also exhibits the highest average bond strength, while In(SiH3)3 (the least stable compound obtained here) exhibits the lowest average bond strength.
To understand the reactivity of the (H3C)nX(SiH3)3−n compounds, we analyse their frontier molecular orbitals HOMO and LUMO, in the context of the KS-MO, of all optimized structures. These orbitals are arranged in a two-dimensional array for all compounds in Table 3. Additionally, the electronic chemical potential (μ), chemical hardness (η), and electrophilicity (ω) were properly24 calculated with the PW91 method (see Table 4). In general, a look at the μ, η and ω values for the Al-containing (H3C)nAl(SiH3)3−n and Ga-containing (H3C)nGa(SiH3)3−n compounds indicates a similar reactivity profile of these compounds. Furthermore, for the In-containing (H3C)nIn(SiH3)3−n compounds, all reactivity indices yield quite similar values to the values of the Al- and Ga-containing compounds. Indeed, the greatest differences observed for the μ, η and ω values appear for the B(SiH3)3 compound.
| μ | η | ω | μ | η | ω | μ | η | ω | μ | η | ω | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | B | Al | Ga | In | ||||||||
| 0 | −5.48 | 2.90 | 5.19 | −4.89 | 3.02 | 3.96 | −4.87 | 2.98 | 3.98 | −4.71 | 2.92 | 3.82 |
| 1 | −4.82 | 3.19 | 3.64 | −4.49 | 3.31 | 3.05 | −4.48 | 3.25 | 3.08 | −4.41 | 3.14 | 3.10 |
| 2 | −4.40 | 4.16 | 2.32 | −4.16 | 3.92 | 2.21 | −4.17 | 3.83 | 2.26 | −4.13 | 3.56 | 2.40 |
| 3 | −4.20 | 5.93 | 1.50 | −3.82 | 4.97 | 1.47 | −3.85 | 4.78 | 1.55 | −3.83 | 4.17 | 1.76 |
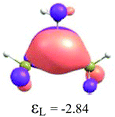
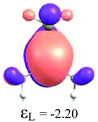
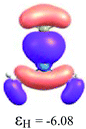
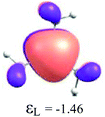
By considering the optimized structures of the (H3C)nX(SiH3)3−n compounds, it is expected that the metal atom X is in an sp2 hybridization, giving rise to triangular systems (see Fig. 1). Nevertheless, spatial distortions do appear due to rotations and combinations of the methyl (silyl) groups attached to the metal atom. These structures are supposed to be totally symmetric for (H3C)3X and X(SiH3)3 (except the preferential orientations of the terminal hydrogen atoms in each functional group). In fact, this type of hybridization is expected to be more stable for (H3C)3B and less stable for B(SiH3)3.51,52 However, in the case of the (H3C)3X and X(SiH3)3 compounds, the HOMO is doubly degenerate, as displayed in Table S2 in the ESI.† The small distortions of the attached group to the central atom can almost break this degeneracy. In one of these degenerate HOMOs there is a preferential orientation of the electronic distribution along only one X–C or X–Si bond (as displayed in Table 3), whereas the other degenerate HOMO exhibits an electronic distribution along two X–C or two X–Si bond (see Table S2†). In the case of the intermediate (H3C)nX(SiH3)3−n compounds (n = 1 and 2), there is no degenerate HOMO, provided the spatial symmetry of these compounds is lowered with respect to the most symmetric one. In all these compounds, the LUMOs are delocalized involving the central atom and exhibit a typical π-electron density involving the central atom.
Despite similar spatial symmetry observed for the X(SiH3)3 compounds, most symmetric HOMO and LUMO do occur for B(SiH3)3. However, the latter compound exhibits the highest reactivity, with an electrophilicity index ω = 5.19 eV, as reported in Table 4. As displayed in Fig. 2, the lower the stability of each compound, the higher its reactivity. Still considering the less stable X(SiH3)3 compounds, from X = Al, Ga, and In, we notice a small reduction in their electrophilicity; i.e., ω = 3.96 eV for Al(SiH3)3, ω = 3.98 eV for Ga(SiH3)3, and ω = 3.82 eV for In(SiH3)3. Correspondingly, only a small reduction is observed in their cohesive energies (Fig. 2a). In contrast, fixing the central atom in (H3C)nX(SiH3)3−n and increasing n, we observe a stronger reduction in ω (see Fig. 2b) as well as an increase in the stability. For example, this reactivity index is 3.64 eV in (H3C)B(SiH3)2, 2.32 eV in (H3C)2B(SiH3), and 1.50 eV in (H3C)3B, indicating that TMB is one of the less reactive (and the most stable) compounds in this family. The purpose of Fig. 2 is to illustrate together the reactivity and stability trends for all compounds. In summary, we notice that while Ecoh/at linearly increases with the value of n for each of the different metals X, the corresponding electrophilicity linearly decreases with n, except in the case of X = B, in which case for n = 0 and n = 1, ω sharply deviates from the linearity.
 | ||
| Fig. 2 (a) Cohesive energy per atom and (b) electrophilicity index as a function of n for all (H3C)nX(SiH3)3−n compounds calculated at the PW91 level of DFT. | ||
Complementing the study of the global reactivity indices, the charge transfers between the central metal atom and the silyl or methyl groups were also calculated employing the Bader method.39 Table S3 in ESI† displays the Bader analysis for all (H3C)nX(SiH3)3−n compounds. In general, the calculated Bader charges indicate that the metal centre (X) loses electrons, with the exception of X = B for n = 0 and n = 1, in which case the central B atom gains electrons. This may be related to the electronegativity difference between B and Si, leading to a higher reactivity of the compounds B(SiH3)3 and (H3C)B(SiH3)2 (see Fig. 2b). As can be seen in Table 4, the electrophilicity of these two compounds differs significantly from the electrophilicity of the remaining (H3C)nX(SiH3)3−n compounds.
B. Reaction paths for obtaining the (H3C)nX(SiH3)3−n compounds
In order to address possible synthesis routes for obtaining the (H3C)nX(SiH3)3−n compounds, we consider the reactions of substitution of methyl by silyl groups in the metalorganic precursor molecules (H3C)3X, when they interact with silane. We propose the following reaction steps:(1) (H3C)3X + SiH4 → (H3C)2X(SiH3) + CH4
(2) (H3C)2X(SiH3) + SiH4 → (H3C)X(SiH3)2 + CH4
(3) (H3C)X(SiH3)2 + SiH4 → X(SiH3)3 + CH4
We notice that, considering all the sequential steps (1)–(3), only in the case of the B-containing compounds the products are less energetically favourable than the reactants (see Fig. S2–S5 in ESI†). For example, in step (1) the calculated relative energy between reactants and products is 5.25 kcal mol−1, in step (2) this difference is 4.61 kcal mol−1, and in step (3) this difference increases to 12.84 kcal mol−1. Conversely, in all other cases (X = Al–In) the products are more energetically favourable than the reactants. In Fig. 3, the sequential steps (1)–(3) are illustrated for the case of (H3C)nAl(SiH3)3−n, obtained via STQN at the MP2 level of theory. More interestingly, the absolute values of the relative energy between reactants and products increase when going from X = Al to X = In (Fig. S3–S5†). The calculated barriers for these reactions are listed in Table 5, together with the barriers corresponding to the analogous reactions involving X = B, Ga, and In.
| X | Reaction | ΔEa |
|---|---|---|
| B | Ia → IIa | 78.83 |
| IIIa → IVa | 20.10 | |
| Va → VIa | 21.19 | |
| Al | Ib → IIb | 75.88 |
| IIIb → IVb | 37.83 | |
| Vb → VIb | 35.93 | |
| Ga | Ic → IIc | 40.95 |
| IIIc → IVc | 38.44 | |
| Vc → VIc | 35.76 | |
| In | Id → IId | 68.63 |
| IIId → IVd | 68.24 | |
| Vd → VId | 34.58 | |
In general, reaction (1) (I → II, as described in Table 5) for all metal atoms (X = B, Al, Ga, and In) yields higher energy barriers; the highest one was calculated in the case of B (78.83 kcal mol−1) and the lowest one was calculated in the case of Ga (40.95 kcal mol−1). These results are in agreement with our predictions for stability/reactivity as obtained from our calculated ΔfG0, Ecoh/at, and chemical indices. The SiH4 molecule reacts with these molecules to form the (H3C)2X(SiH3) compounds by necessarily breaking a CH3–X bond which is the strongest bond (see Table 2) for all (H3C)nAl(SiH3)3−n compounds (see Table 5). In the case of reactions (2) and (3) (III → IV and V → VI, as described in Table 5), they exhibit a lower energy barrier (20.10–68.24 kcal mol−1). For these types of reactions, the lowest energy barrier occurs for X = B (20.10 kcal mol−1 for the reaction IIIa → IVa, as given in Table 5) and the highest energy barrier occurs for X = In (68.24 kcal mol−1 for the reaction IIId → IVd, as given in Table 5).
In the specific case of reaction (3) for X = B (described as Va → VIa in Table 5 and displayed in Fig. S2(c)†), an intermediate adduct, (H3C)B(SiH3)3H (νmin = 91.1 cm−1), is formed due to the higher reactivity of the (H3C)B(SiH3)2 compound in the presence of silane. The (H3C)B(SiH3)2 compound interacts with silane to form one additional bonding B–SiH3, while an H atom is detached from SiH4 and temporarily occupies a site between the two silyl groups (see reactants and the adduct formation in Fig. S2(c)†). This adduct gives rise to a first-order TS (νi = 807.9i cm−1), leading to the formation of the reaction products B(SiH3)3 + CH4 by overcoming an energy barrier of 21.19 kcal mol−1.
In all reactions studied in this work (involving the triels), the calculated heights of the energy barriers (20.10–78.83 kcal mol−1) are in agreement with the energy barriers calculated in other similar studies.53–55 Moreover, these barriers are in line with those calculated for the kinetics of the group 13 trihydrides.56 This finding may indicate the feasibility of the chemical synthesis for these compounds, under typical MOCVD conditions of high temperatures and general thermodynamic disequilibrium. Moreover, the mechanisms of all these reactions appear to proceed in a similar manner, except in the last step of B(SiH3)3 formation, for which an adduct precedes the transition state formation.
C. Raman spectra and scattering properties of (H3C)nX(SiH3)3−n
For the identification of the structural features of these compounds, it is useful to analyse their vibrational properties, since experimental infrared and Raman spectroscopies may be very suitable for this purpose.26,57,58 Hence, we have calculated the Raman spectra and depolarized light-scattering properties of all (H3C)nX(SiH3)3−n compounds at the MP2 level of theory. The calculated Raman spectra are displayed in Fig. 4–6. In Fig. 4, we display Raman spectra for two borderline cases: (i) pure silyl-containing entities (n = 0) or X(SiH3)3 and (ii) pure methyl-containing molecules (n = 3) or (H3C)3X. The most typical features of X(SiH3)3 appear in the 2260–2300 cm−1 spectral range, while the spectra of (H3C)3X exhibit their most prominent peaks in the 3050–3180 cm−1 spectral range. The vibrational modes responsible for these peaks correspond to the symmetric Si–H stretching in X(SiH3)3 and to the symmetric C–H stretching in (H3C)3X. Our results are in agreement with the experimental data available for the Si–H stretching modes in the HCSiH3 molecule (2139.1 cm−1)59 and the C–H stretching modes in TMB (2958 and 2875 cm−1),26 TMA (2919 and 2925 cm−1),27 TMG (2990 and 2916 cm−1),28 and TMI (2925 cm−1).29 It is worth emphasizing that the Raman intensities of the Si–H stretching in the X(SiH3)3 compounds are much more pronounced and localized than the intensities of the C–H stretching in the (H3C)3X compounds. Also, a small blue-shift is noticed in these peaks when going from X = B–In.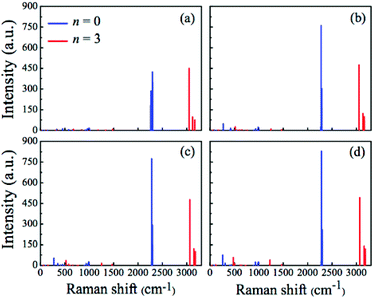 | ||
| Fig. 4 Raman spectra for the (H3C)nX(SiH3)3−n compounds X(SiH3)3 (blue line) and (H3C)3X (red line), calculated at the MP2 level. (a) X = B, (b) X = Al, (c) X = Ga, and (d) X = In. | ||
 | ||
| Fig. 5 Raman spectra for the (H3C)X(SiH3)2 compounds, calculated at the MP2 level. (a) X = B, (b) X = Al, (c) X = Ga, and (d) X = In. | ||
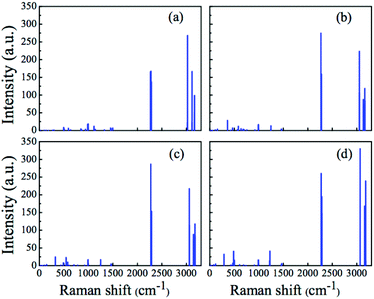 | ||
| Fig. 6 Raman spectra for the (H3C)2X(SiH3) compounds, calculated at the MP2 level. (a) X = B, (b) X = Al, (c) X = Ga, and (d) X = In. | ||
Regarding the X–Si stretching modes in the X(SiH3)3 compounds, we notice very small Raman activities with frequencies at 334, 271, 277, and 259 cm−1 for X = B, Al, Ga, and In, respectively. Similarly, the X–C stretching modes in (H3C)3X exhibit small Raman activities, although at higher frequencies: 675, 517, 525, and 478 cm−1 for X = B, Al, Ga, and In, respectively. For comparison, the X–C stretching is experimentally observed for TMB26 at around 675 cm−1, for TMA60 at around 530 cm−1, for TMG28 at around 570 cm−1, and for TMI29,58 at around 478 cm−1, which are in good agreement with our theoretical results obtained with the MP2 method.
Considering now the mixed methylsilyl compounds [(H3C)nX(SiH3)3−n], with n = 1 and n = 2, we still note the typical features (symmetric Si–H and C–H stretching) in the Raman spectra, as observed for the compounds with n = 0 and n = 3. Essentially, these stretching modes are in the same frequency range (see Fig. 5 and 6). Furthermore, in the mixed compounds, both X–Si and X–C modes do appear with very low Raman activities. In the case of (H3C)X(SiH3)2 (see Fig. 5), the X–Si stretching modes appear at 403, 310, 300, and 273 cm−1 for X = B, Al, Ga, and In, respectively. Yet, the X–C stretching mode appears only for X = Al (642 cm−1), X = Ga (561 cm−1), and X = In (493 cm−1), whereas it is strongly coupled in the case of X = B. For the (H3C)2X(SiH3) compound (see Fig. 6), the X–Si stretching modes are shifted to higher frequencies (as compared to (H3C)X(SiH3)2), appearing at 496, 582, 544, and 587 cm−1 for X = B, Al, Ga, and In, respectively. Again, in this compound the B–C stretching mode is not clearly resolved in its vibrational spectrum, whereas the other X–C stretching modes appear at 360, 427, and 289 cm−1 for X = Al, Ga, and In, respectively.
As a complementary study to the Raman shift, it is worth analysing the Raman light scattering properties of the most intense vibrational modes. Tables 6 and 7 report the calculated values of Raman intensities and depolarization ratios for the (H3C)nX(SiH3)3−n compounds with MP2. In Table 6, for each active vibrational mode (υ), we provide the corresponding intensity (An) and degrees of depolarization of plane-polarized and natural light (ρn and ρp). As can be seen in Table 6, the symmetric stretching modes exhibit large intensities and are the most depolarized, when compared to the maximum depolarization ratio value. Among this class of vibrational modes, the lowest depolarization ratio is found for the symmetric Si–H stretching in (H3C)2B(SiH3), i.e., ρn = 0.27 (ρp = 0.43); for the asymmetric Si–H stretching in (H3C)Al(SiH3)2, i.e., ρn = 0.47 (ρp = 0.64); and for the asymmetric Si–H in (H3C)Ga(SiH3)2, i.e., ρn = 0.58 (ρp = 0.73). In Table 7, we show that all the symmetric stretching modes exhibit (in general) larger intensities than the asymmetric modes, although they are the least depolarized modes when compared to the minimum depolarization ratio value.
| υ | A n | ρ p | ρ n | υ | A n | ρ p | ρ n | υ | A n | ρ p | ρ n | υ | A n | ρ p | ρ n | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | B | Al | Ga | In | ||||||||||||
| a Si–H asymmetric stretching. b C–H asymmetric stretching. c Si–H symmetric stretching. | ||||||||||||||||
| 0 | 2298a | 121.6 | 0.75 | 0.86 | 2279a | 193.2 | 0.75 | 0.86 | 2285a | 184.7 | 0.75 | 0.86 | 2287a | 205.9 | 0.75 | 0.86 |
| 1 | 2286a | 95.2 | 0.73 | 0.85 | 2287a | 147.9 | 0.47 | 0.64 | 2293a | 137.0 | 0.58 | 0.73 | 2293a | 158.1 | 0.74 | 0.85 |
| 3168b | 87.0 | 0.75 | 0.86 | 3135b | 78.7 | 0.75 | 0.86 | 3145b | 77.1 | 0.75 | 0.86 | 3159b | 89.0 | 0.75 | 0.86 | |
| 2 | 2285c | 137.1 | 0.27 | 0.43 | 2270a | 126.9 | 0.75 | 0.86 | 2278a | 121.9 | 0.75 | 0.86 | 2289a | 147.9 | 0.75 | 0.86 |
| 3167b | 98.6 | 0.75 | 0.86 | 3167b | 73.6 | 0.75 | 0.86 | 3144b | 88.2 | 0.75 | 0.86 | 3160b | 167.9 | 0.75 | 0.86 | |
| 3 | 3119b | 96.8 | 0.75 | 0.86 | 3134b | 122.2 | 0.75 | 0.86 | 3146b | 121.2 | 0.75 | 0.86 | 3159b | 139.8 | 0.75 | 0.86 |
| υ | A n | ρ p | ρ n | υ | A n | ρ p | ρ n | υ | A n | ρ p | ρ n | υ | A n | ρ p | ρ n | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | B | Al | Ga | In | ||||||||||||
| a Si–H symmetric stretching. b C–H symmetric stretching. | ||||||||||||||||
| 0 | 2295a | 423.5 | 0.07 | 0.13 | 2276a | 761.3 | 0.01 | 0.02 | 2281a | 775.1 | 0.01 | 0.02 | 2282a | 830.8 | 0.00 | 0.01 |
| 1 | 2284a | 379.0 | 0.09 | 0.17 | 2270a | 349.8 | 0.10 | 0.18 | 2275a | 365.2 | 0.09 | 0.16 | 2277a | 463.7 | 0.06 | 0.11 |
| 2996b | 137.5 | 0.06 | 0.12 | 3053b | 161.7 | 0.01 | 0.02 | 3062b | 162.6 | 0.01 | 0.02 | 3070b | 170.2 | 0.01 | 0.03 | |
| 2 | 2277a | 167.1 | 0.17 | 0.30 | 2267a | 274.8 | 0.04 | 0.07 | 2274a | 286.4 | 0.03 | 0.05 | 2273a | 260.4 | 0.08 | 0.14 |
| 3023b | 268.0 | 0.02 | 0.04 | 3053b | 106.6 | 0.00 | 0.01 | 3062b | 114.1 | 0.00 | 0.01 | 3069b | 330.0 | 0.00 | 0.00 | |
| 3 | 3047b | 450.0 | 0.00 | 0.00 | 3054b | 475.3 | 0.00 | 0.00 | 3063b | 478.6 | 0.00 | 0.00 | 3069b | 493.0 | 0.00 | 0.00 |
The Raman spectra of the mixed (H3C)nX(SiH3)3−n compounds (n = 1, 2) differ sufficiently from the extreme cases (n = 0, 3). This ensures that every single compound may be successfully identified by applying Raman spectroscopic techniques. Our theoretical results not only justify the simulation of the Raman spectra provided here, but encourage experimental attempts for the synthesis and identification of the (H3C)nX(SiH3)3−n compounds.
Conclusions
We have employed high-level ab initio calculations, at the MP2 levels of theory, to predict the equilibrium structure, stability, reactivity, and Raman scattering properties of novel (H3C)nX(SiH3)3−n compounds (X = B, Al, Ga, In). For a methodological comparison, we have also employed DFT calculations within the PW91 approach and additionally addressed the chemical reactivity indices of the systems. Most of these compounds may serve as templates for building/synthesizing new materials. Currently, only the pure (H3C)3X members of the triels, namely TMB, TMA, TMG, and TMI, are well-known and commercially available, while the remaining twelve (H3C)nX(SiH3)3−n compounds (n = 0–2) are a novelty. By increasing n (i.e., fewer silyl groups and more methyl groups) for all metal elements, the (H3C)nX(SiH3)3−n molecules become less reactive and more stable. Thus, it may be more demanding to synthesize the silyl saturated (H3C)nX(SiH3)3−n counterparts. On the other hand, being more reactive, the silyl saturated (H3C)nX(SiH3)3−n may be of more interest as highly reactive intrinsic/intermediate precursors, playing a role in certain deposition processes.We have proposed sequential reaction routes for the synthesis of all the (H3C)nX(SiH3)3−n compounds, by the substitution of methyl by silyl groups, where the Si source is the silane gas. Our calculations performed at the MP2/STQN level demonstrate that, except in the case of the B-containing compounds, all other products are energetically more favourable than the reactants. The corresponding reaction barriers for these chemical transformations remain in the energy range typical for MOCVD processes involving the corresponding precursors. We have also calculated the Raman spectra and depolarization ratios of all (H3C)nX(SiH3)3−n compounds, thus providing useful data for their identification.
Acknowledgements
This work was supported by the Swedish Foundation for International Cooperation in Research and Higher Education (STINT) (project YR2009-7017) and the Swedish Research Council (VR) (Swedish Research Links project 348-2014-4249). G.K.G. and A.K.-G. gratefully acknowledge support by the Linköping Linnaeus Initiative on Novel Functionalized Materials (VR). G.K.G. gratefully acknowledges support by the Swedish Foundation for Strategic Research (SSF) Synergy grant #RMA11-0029 on Functional Carbides and Advanced Surface Engineering (FUNCASE). A.K.-G. gratefully acknowledges support by the Swedish Governmental Agency for Innovation Systems (VINNOVA) and the Swedish Research Council (VR). R.R., R.B.S., and F.deB.M. acknowledge Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundação de Amparo à Pesquisa do Estado da Bahia (FAPESB) for partial support. R.B.S. acknowledges support by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES).Notes and references
- A. Y. Timoshkin and H. F. Schaefer, J. Phys. Chem. C, 2008, 112, 13816–13836 CAS.
- I. N. Przhevalskii, S. Y. Karpov and Y. N. Makarov, MRS Internet J. Nitride Semicond. Res., 1998, 3, 30 Search PubMed.
- A. Kakanakova-Georgieva, R. R. Ciechonski, U. Forsberg, A. Lundskog and E. Janzén, Cryst. Growth Des., 2009, 9, 880–884 CAS.
- I. M. Watson, Coord. Chem. Rev., 2013, 257, 2120–2141 CrossRef CAS PubMed.
- M. Fikri, A. Makeich, G. Rollmann, C. Schulz and P. Entel, J. Phys. Chem. A, 2008, 112, 6330–6337 CrossRef CAS PubMed.
- P.-N. Volpe, J.-C. Arnault, N. Tranchant, G. Chicot, J. Pernot, F. Jomard and P. Bergonzo, Diamond Relat. Mater., 2012, 22, 136–141 CrossRef CAS PubMed.
- W. Dai, V. Ferrando, a V. Pogrebnyakov, R. H. T. Wilke, K. Chen, X. Weng, J. Redwing, C. W. Bark, C.-B. Eom, Y. Zhu, P. M. Voyles, D. Rickel, J. B. Betts, C. H. Mielke, a Gurevich, D. C. Larbalestier, Q. Li and X. X. Xi, Supercond. Sci. Technol., 2011, 24, 125014 CrossRef.
- D. Nilsson, E. Janzén and A. Kakanakova-Georgieva, Appl. Phys. Lett., 2014, 105, 082106 CrossRef PubMed.
- J. Liu and H. Ma, Dalton Trans., 2014, 43, 9098–9110 RSC.
- B. L. Korbad and S.-H. Lee, Chem. Commun., 2014, 50, 8985–8988 RSC.
- B. Gong and G. N. Parsons, J. Mater. Chem., 2012, 22, 15672 RSC.
- C. A. López, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2009, 105, 98 RSC.
- R. A. Kresinski, Annu Rep. Prog. Chem., Sect. A: Inorg. Chem., 2006, 102, 88 RSC.
- M. G. Voronkov, S. V. Basenko, R. G. Mirskov and S. N. Adamovich, Russ. J. Appl. Chem., 2006, 79, 1721–1722 CrossRef CAS.
- L. Rösch, Angew. Chem., Int. Ed., 1977, 16, 480–480 CrossRef.
- L. Rösch and H. Neumann, Angew. Chem., Int. Ed., 1980, 19, 55–56 CrossRef.
- A. John Downs, Chemistry of Aluminium, Gallium, Indium, and Thallium, Springer Science & Business Media, 1993, vol. 04 Search PubMed.
- J. F. Janik, E. N. Duesler and R. T. Paine, Inorg. Chem., 1987, 26, 4341–4345 CrossRef CAS.
- M. Fan, E. Duesler, H. Nöth and R. Paine, Main Group Chem., 2011, 10, 37–50 CAS.
- M. Fan, R. T. Paine, E. N. Duesler and H. Nöth, Z. Anorg. Allg. Chem., 2006, 632, 2443–2446 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- J. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter, 1996, 54, 16533–16539 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS PubMed.
- P. Raghunath and M. C. Lin, J. Phys. Chem. A, 2007, 111, 6481–6488 CrossRef CAS PubMed.
- C. Manzanares, V. M. Blunt and J. Peng, J. Chem. Phys., 1993, 99, 9412 CrossRef PubMed.
- G. T. Wang and J. R. Creighton, J. Phys. Chem. A, 2006, 110, 1094–1099 CrossRef CAS PubMed.
- J. O. Jensen, J. Mol. Struct. (THEOCHEM), 2004, 673, 173–179 CrossRef CAS PubMed.
- C. Park, W. Jung, Z. Huang and T. J. Anderson, J. Mater. Chem., 2002, 12, 356–360 RSC.
- M. J. Frisch and et al., Gaussian 09, Revision A.02, 2009 Search PubMed.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563 CrossRef CAS PubMed.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099 CrossRef CAS PubMed.
- C. Estarellas, X. Lucas, A. Frontera, D. Quiñonero and P. M. Deyà, Chem. Phys. Lett., 2010, 489, 254–258 CrossRef CAS PubMed.
- C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49–56 CrossRef CAS.
- A. Kakanakova-Georgieva, G. K. Gueorguiev, S. Stafström, L. Hultman and E. Janzén, Chem. Phys. Lett., 2006, 431, 346–351 CrossRef CAS PubMed.
- J. W. Ochterski, Thermochemistry in Gaussian, Gaussian, Inc., 2000, http://www.gaussian.com/g_whitepap/thermo.htm Search PubMed.
- H. Zhang, G. Zhang, J.-Y. Liu, M. Sun, B. Liu and Z. Li, J. Comput. Chem., 2009, 30, 236–242 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- G. Makov, J. Phys. Chem., 1995, 99, 9337–9339 CrossRef CAS.
- R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- H. Szymanski, Raman spectroscopy: theory and practice, Plenum Press, New York, 1967 Search PubMed.
- B. T. Luke, J. A. Pople, M. B. Krogh-Jespersen, Y. Apeloig, J. Chandrasekhar and P. V. R. Schleyer, J. Am. Chem. Soc., 1986, 108, 260–269 CrossRef CAS.
- D. Srivastava, E. N. Duesler and R. T. Paine, Eur. J. Inorg. Chem., 1998, 1998, 855–859 CrossRef.
- B. Gaertner, H.-J. Himmel, V. A. Macrae, A. J. Downs and T. M. Greene, Chem. – Eur. J., 2004, 10, 3430–3443 CrossRef CAS PubMed.
- M. Bühler and G. Linti, Z. Anorg. Allg. Chem., 2006, 632, 2453–2460 CrossRef.
- D. Berthomieu, Y. Bacquet, L. Pedocchi and A. Goursot, J. Phys. Chem. A, 1998, 102, 7821–7827 CrossRef CAS.
- N. L. Pickett, O. Just, X. Li, D. G. Vanderveer and W. S. Rees, J. Organomet. Chem., 1999, 582, 119–125 CrossRef CAS.
- A. Keys, P. T. Brain, C. A. Morrison, R. L. Callender, B. a. Smart, D. A. Wann, H. E. Robertson, D. W. H. Rankin and A. R. Barron, Dalton Trans., 2008, 404 RSC.
- A. Hansson, F. de Brito Mota and R. Rivelino, Phys. Rev. B: Condens. Matter, 2012, 86, 195416 CrossRef.
- Y. Ding and Y. Wang, J. Phys. Chem. C, 2013, 117, 18266–18278 CAS.
- S. A. Macgregor, G. W. Neave and C. Smith, Faraday Discuss., 2003, 124, 111 RSC.
- R. R. Q. Freitas, G. K. Gueorguiev, F. de Brito Mota, C. M. C. de Castilho, S. Stafström and A. Kakanakova-Georgieva, Chem. Phys. Lett., 2013, 583, 119–124 CrossRef CAS PubMed.
- L. Baptista and E. F. da Silveira, Phys. Chem. Chem. Phys., 2014, 16, 21867–21875 RSC.
- B. Vest, K. Klinkhammer, C. Thierfelder, M. Lein and P. Schwerdtfeger, Inorg. Chem., 2009, 48, 7953–7961 CrossRef CAS PubMed.
- G. A. Atiya, A. S. Grady, D. K. Russell and T. A. Claxton, Spectrochim. Acta A: Mol. Spectrosc., 1991, 47, 467–476 CrossRef.
- A. P. Kurbakova, S. S. Bukalov, L. A. Leites, L. M. Golubinskaya and V. I. Bregadze, J. Organomet. Chem., 1997, 536–537, 519–529 CrossRef.
- P. R. Schreiner, H. P. Reisenauer, K. W. Sattelmeyer and W. D. Allen, J. Am. Chem. Soc., 2005, 127, 12156–12157 CrossRef CAS PubMed.
- R. J. O'Brien and G. A. Ozin, J. Chem. Soc. A, 1971, 1136 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the lowest frequencies, molecular dipole moments, optimized structures, frontier orbitals, Bader analysis, and reaction paths for all (CH3)nX(SiH3)3−n compounds. See DOI: 10.1039/c4dt03406f |
| This journal is © The Royal Society of Chemistry 2015 |