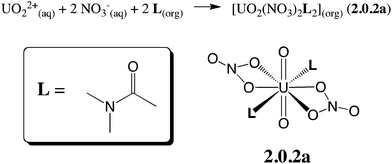
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Uranyl extraction by N,N-dialkylamide ligands studied using static and dynamic DFT simulations†
Nicolas
Sieffert
*ab and
Georges
Wipff
c
aUniv. Grenoble Alpes, DCM, F-38000 Grenoble, France
bCNRS, DCM, F-38000, Grenoble, France. E-mail: nicolas.sieffert@ujf-grenoble.fr
cUMR 7177 CNRS, Laboratoire MSM, Institut de Chimie, Université de Strasbourg, 1 rue Blaise Pascal, 67000 Strasbourg, France
First published on 20th November 2014
Abstract
We report DFT static and dynamic studies on uranyl complexes [UO2(NO3)x(H2O)yLz]2−x involved in the uranyl extraction from water to an “oil” phase (hexane) by an amide ligand L (N,N-dimethylacetamide). Static DFT results “in solution” (continuum SMD models for water and hexane) predict that the stepwise formation of [UO2(NO3)2L2] from the UO2(H2O)52+ species is energetically favourable, and allow us to compare cis/trans isomers of penta- and hexa-coordinated complexes and key intermediates in the two solvents. DFT-MD simulations of [UO2(NO3)2L2], [UO2(NO3)2(H2O)L2], and [UO2(NO3)(H2O)L2]+ species in explicit solvent environments (water, hexane, or the water/hexane interface) represented at the MM or full-DFT level reveal a versatile solvent dependent binding mode of nitrates, also evidenced by metadynamics simulations. In water and at the interface, the latter exchange from bi- to monodentate, via in plane rotational motions in some cases. Remarkably, structures of complexes at the interface are more “water-like” than gas phase- or hexane-like. Thus, the order of U–ONO3/U–OL bond distances observed in the gas phase (U–Onit < U–OL) is inverted at the interface and in water. Overall, the results are consistent with the experimental observation of uranyl extraction from nitric acid solutions by amide analogues (bearing “fatty” substituents), and allow us to propose possible extraction mechanisms, involving complexation of L “right at the interface”. They also point to the importance of the solvent environment and the dynamics on the structure and stability of the complexes.
1. Introduction
Oil-soluble N,N-dialkylamide ligands bearing hydrophobic alkyl chains represent an interesting alternative to tri-n-butylphosphate (TBP) for the reprocessing of nuclear waste solutions by liquid–liquid extraction. Like TBP, they selectively extract UO22+ from concentrated nitric acid solutions, and share most of its assets (e.g. stability towards radiolysis, etc.).1 In solution, they also form a neutral complex of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry,2 namely UO2(NO3)2(L)2, where U is hexacoordinated in the equatorial plane by two trans ligands L and two bidentate nitrates (see Scheme 1), as in X-ray structure analogues.3 Additionally, being free of phosphorus atoms they are fully incinerable and are thus “greener” than TBP. In the source phase (water) UO22+ is solubilized as (nitrato)aquo complexes [UO2(NO3)x(H2O)y]2−x. Transfer to the organic phase therefore requires displacement of the coordinated water by lipophilic ligands while co-extracting nitrates to keep the complex neutral. The intimate complexation and extraction mechanism is unknown and intriguing since L partitions to the organic phase, immiscible with the aqueous source phase, while the uncomplexed cation is insoluble in the oil phase. Understanding where and how uranyl complexation takes place in biphasic solutions is crucial from a fundamental and an industrial point of view. In practice, ion extraction is not a simple process, since the two phases are agitated and involve heterogeneous mixtures (like salts and concentrated acids in the source phase and aggregates, micelles or microemulsions in the oil phase).1c,4 Early kinetic studies on uranyl extraction pointed to the importance of interfacial complexation reactions,5 without affording microscopic characterization of the interface, though. Microscopic views stem from classical molecular dynamics “MD” simulations on explicitly represented nanosized oil/water solutions of ions,6 extractants and their complexes.7 The interface is generally found to be quite sharp and abrupt, a few nanometers wide, and to fluctuate with time, without local intersolvent mixing. Extractants like TBP7c,8 or fatty amides9 are amphiphilic and adsorb at the aqueous interface, as suggested by surface tension,10 kinetic or surface spectroscopy11 studies, hinting at a complexation mechanism occurring “at the interface”, without defining its characteristics (size, composition, inter-solvent miscibility, electrostatic properties) though.
2 stoichiometry,2 namely UO2(NO3)2(L)2, where U is hexacoordinated in the equatorial plane by two trans ligands L and two bidentate nitrates (see Scheme 1), as in X-ray structure analogues.3 Additionally, being free of phosphorus atoms they are fully incinerable and are thus “greener” than TBP. In the source phase (water) UO22+ is solubilized as (nitrato)aquo complexes [UO2(NO3)x(H2O)y]2−x. Transfer to the organic phase therefore requires displacement of the coordinated water by lipophilic ligands while co-extracting nitrates to keep the complex neutral. The intimate complexation and extraction mechanism is unknown and intriguing since L partitions to the organic phase, immiscible with the aqueous source phase, while the uncomplexed cation is insoluble in the oil phase. Understanding where and how uranyl complexation takes place in biphasic solutions is crucial from a fundamental and an industrial point of view. In practice, ion extraction is not a simple process, since the two phases are agitated and involve heterogeneous mixtures (like salts and concentrated acids in the source phase and aggregates, micelles or microemulsions in the oil phase).1c,4 Early kinetic studies on uranyl extraction pointed to the importance of interfacial complexation reactions,5 without affording microscopic characterization of the interface, though. Microscopic views stem from classical molecular dynamics “MD” simulations on explicitly represented nanosized oil/water solutions of ions,6 extractants and their complexes.7 The interface is generally found to be quite sharp and abrupt, a few nanometers wide, and to fluctuate with time, without local intersolvent mixing. Extractants like TBP7c,8 or fatty amides9 are amphiphilic and adsorb at the aqueous interface, as suggested by surface tension,10 kinetic or surface spectroscopy11 studies, hinting at a complexation mechanism occurring “at the interface”, without defining its characteristics (size, composition, inter-solvent miscibility, electrostatic properties) though.
Regarding the accurate description of the evolution of ion coordination features with time and solvent environment, classical MD results are limited, however, by the empirical energy representation. In principle, quantum mechanical QM approaches with an explicit account of solvation effects are more suitable. Two QM approaches are used here, focusing on the uranyl speciation at different key stages of the extraction reaction. First, ab initio Molecular Dynamics (AIMD) simulations have been undertaken in explicitly represented solvent(s) to gain insights into the uranyl speciation and complexation features, and to obtain relevant structural, thermodynamics and kinetics data on chemically relevant model systems in the source phase (water), the receiving phase (hexane), and at their interface. The simulated times (30–40 ps) are long enough to relax and solvate a given structure in its environment and to test its (in)stability, but are far too short to observe spontaneous complexation/decomplexation processes of the ligands. In the second approach, the solute is described at the DFT level, while the solvent is treated by a simple continuum, allowing us to energetically compare different species “in bulk solutions”, namely the water and oil phases. Our DFT and AIMD studies aim at better understanding the nature of [UO2(NO3)x(H2O)y(L)z]2−x species, and the gradual formation of UO2(NO3)2(L)2 complexes. To investigate whether the structure of these species at the interface is rather “water-like” or “oil-like”, they will be simulated in the three environments using our recently developed DFT/MM protocol12 combining a DFT representation of the solute and, at a lower level, a molecular mechanics model for the solvent. These results will allow us to better understand “what happens at the interface”13 during uranyl extraction.
2. Methods
2.1. Static DFT calculations
| δEG = ΔGBLYP-D3/SDD − ΔEBLYP-D3/SDD | (1) |
The entropic contributions have been evaluated at a pressure of 1354 atm in order to model the changes in entropy for a condensed phase.18
Energies have been corrected for the basis set superposition error (BSSE) using the counterpoise method.23 The BSSE energy corrections are denoted δEBSSE in the rest of the paper.
Estimates of the solvation effects were computed using the SMD model24 where the solute is immersed in a shape adapted isotropic polarizable continuum, with a dielectric constant ε = 78.3553 for water and ε = 1.8819 for hexane. The corresponding media will be denoted hereafter SMD-water and SMD-hexane, respectively. The δEsolv energy correction is defined as the difference between the reaction energy in the continuum (denoted ΔESMD) and in the gas phase (ΔEgas), at the M06-2X/SDD+ level:
| δEsolv = ΔESMD(M06-2X) − ΔEgas(M06-2X) | (2) |
| ΔG = ΔEgas + δEsolv + δEBSSE + δEG. | (3) |
All DFT calculations have been performed with the Gaussian09 software (rev. D.01),25 and CCSD(T) single points were obtained with NWChem (version 6.1.1).26
2.2. Molecular dynamics simulations
3. Results and discussion
The paper is organized as follows: we first present a benchmark of density functionals to validate our models in the gas phase. Then, we tackle the question of the speciation of mixed UO22+/NO3−/H2O/L complexes in SMD-water. Finally, we investigate the structure and the dynamics of selected complexes by DFT/MM-MD and DFT-MD simulations in explicit hexane, water and at the hexane/water interface. Based on these results, we propose two reaction pathways for the extraction process of UO22+ by L in hexane/water binary systems.3.1. Influence of the density functional and validation of the computational protocol in the gas phase
We first screened selected density functionals to account for the relative stability of three isomers of the [UO2(NO3)(H2O)4]+ complex (see Scheme 2). The latter have been studied in detail previously (see ref. 44) by static calculations in the gas phase (BLYP level) and represent a good test case to investigate the relative stability of hexa- vs. penta-coordinated complexes and H2O dissociation vs. partial decoordination of NO3−, which are relevant to the speciation study undertaken herein. We first computed the relative energies of the three isomers at the CCSD(T) level (the “gold standard” in quantum chemistry) and then considered different density functionals (see relative energies in Table 1). | ||
| Scheme 2 Isomers of the [UO2(NO3)(H2O)4]+ complex considered for the benchmark of density functionals (see Table 1 for relative energies at various computational levels). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| 1.4.0a → 1.4.0b | 1.4.0a → 1.3.0…H2O | |||
|---|---|---|---|---|
| ΔEgas | ΔEgasc (cor.) | ΔEgas | ΔEgasc (cor.) | |
| a The basis set is aug-cc-pVTZ everywhere. b Car–Parrinello optimizations from ref. 44. c Gas phase energies including a correction for the BSSE (counterpoise method). | ||||
| Single point energies on BLYP optimized geometriesb | ||||
| CCSD(T)/SDD+ | 6.2 | [5.5] | −2.4 | [−3.8] |
| BLYP (CP-opt)b | 1.6 | −8.7 | ||
| BLYP/SDD+ | 2.0 | [1.9] | −6.7 | [−6.8] |
| BLYP-D3/SDD+ | 2.5 | [2.5] | −4.0 | [−4.1] |
| BLYP-D3 (CP2K) | 3.3 | −2.3 | ||
| PBE0-D3/SDD+ | 4.6 | [4.5] | −4.1 | [−4.3] |
| M06/SDD+ | 6.1 | [6.1] | −1.3 | [−1.5] |
| M06-2X/SDD+ | 6.6 | [6.6] | −0.7 | [−0.8] |
| B3LYP/SDD+ | 3.4 | [3.3] | −5.8 | [−5.9] |
| MP2/SDD+ | 11.8 | [11.9] | 0.0 | [−0.3] |
| Single point energies on BLYP-D3/SDD optimized geometries | ||||
| BLYP-D3/SDD+ | 2.8 | [2.7] | −3.5 | [−3.6] |
| PBE0-D3/SDD+ | 5.6 | [5.6] | −3.1 | [−3.2] |
| M06-2X/SDD+ | 7.7 | [7.7] | 0.0 | [−0.1] |
In ref. 44, BLYP calculations showed that the penta-coordinated isomer “1.3.0…H2O” is the most stable (by 8.7 kcal mol−1), while 1.4.0a and 1.4.0b are very close in energy, the latter being slightly more stable than the former (by 1.6 kcal mol−1). Repeating these calculations at the BLYP/SDD+ level, we obtain similar values (6.8 kcal mol−1 and 1.9 kcal mol−1, respectively). Comparing these results with our CCSD(T)/SDD+ reference,45 it is found that BLYP predicts the correct sequence of stability among the series but underestimates both the binding of the sixth aquo ligand and the bidentate coordination mode of the nitrate, making the hexacoordinated complex 1.4.0a artificially too unstable. This feature is (at least partially) due to the lack of an explicit description of van der Waals interactions, and more accurate values can be obtained after addition of the “–D3” correction, i.e. at the BLYP-D3 level. At this level, the relative stability of “1.3.0…H2O” vs. 1.4.0a is well described, but 1.4.0a is not stabilized enough compared to 1.4.0b (by ca. 3 instead of 5.5 kcal mol−1). PBE0-D3 appears to give more satisfactory results, since it allows for a good description of the H2O binding in 1.4.0a and better describe the relative stability of 1.4.0avs. 1.4.0b. Interestingly, M06 and M06-2X, which have been recommended for actinide complexes elsewhere,46 slightly overestimate the stability of 1.4.0avs. 1.4.0b and significantly underestimate the H2O binding in 1.4.0a. The popular B3LYP functional, which we employed in previous studies,47 gives more balanced results but still underestimates the stability of the hexacoordinated species 1.4.0a compared to the two pentacoordinated species. We also considered the MP2 level that has been widely employed in the literature to study uranyl compounds48 and we found significant deviations compared to the CCSD(T) reference (see Table 1). The hybrid functionals considered herein (M06, M06-2X and PBE0-D3) provide more satisfying results.
Given the good performance of PBE0-D3 compared to CCSD(T), we therefore calculated ΔEgas at this level in the rest of the paper. Results with BLYP-D3 and M06-2X are also provided in the ESI (see Table S2†). For consistency with AIMD simulations (vide infra), the geometries of all complexes have been optimized at the BLYP-D3/SDD level. We note that our conclusions on the relative performances of BLYP-D3, PBE0-D3 and M06-2X single point calculations remain the same on these BLYP-D3/SDD optimized geometries (see Table 1), so that PBE0-D3/SDD+ still appears as the most satisfying model among those tested herein.
3.2. Speciation of [UO2(NO3)x(H2O)yLz]2−x complexes (x = 0,…, 2, y = 0,…, 5 and z = 0,…, 2) from “static” DFT calculations in SMD-water
We investigated the relative stabilities of [UO2(NO3)x(H2O)yLz]2−x complexes (x = 0,…, 2, y = 0,…, 5 and z = 0,…, 2) in water relative to the dicationic uranyl pentahydrate [UO2(H2O)5]2+ (0.5.0) and free nitrates and L ligands, i.e. according to eqn (4):| [UO2(H2O)5]2+(aq) + xNO3−(aq) + zL(aq) → [UO2(NO3)x(H2O)yLz]2−x(aq) + (5 − y)H2O(aq) | (4) |
Given the large number of possible stereoisomers, we first focused on a consistent series of complexes where nitrates and/or L are in trans position, as in 2.0.2a and found in the solid state structures3 (see Scheme 3). Selected “isomers” (including some with ligands in cis position) have also been considered (see Scheme 4), as the latter should be more polar and possibly more stable in polar or asymmetrical environments such as bulk water or the interface. Reaction free energies in SMD-water are gathered in Table 2.
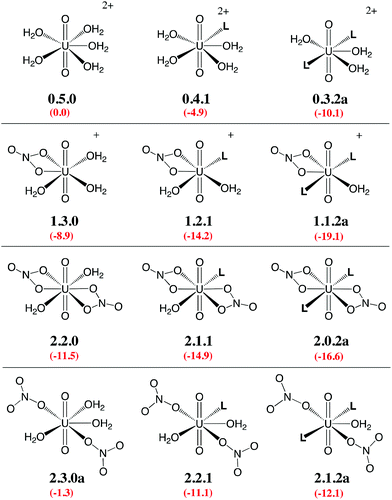 | ||
| Scheme 3 Investigated complexes labelled according to the number of nitrate (first digit), aquo (second digit), and L ligands (third digit). The “a” label corresponds to trans isomers (other isomers are shown in Scheme 4). Reaction free energies in SMD-water according to eqn (4) are given in red (see Table 2 for details). | ||
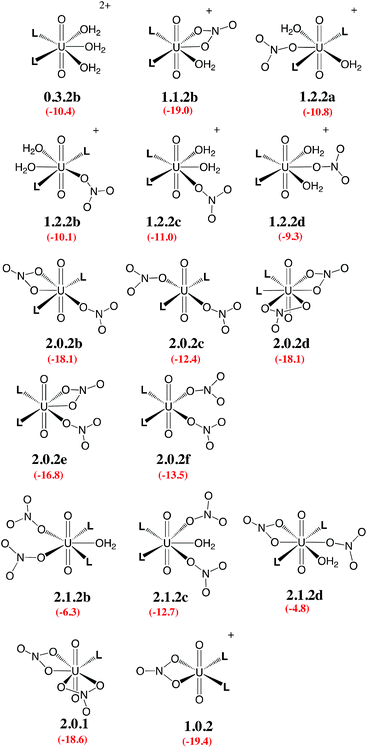 | ||
| Scheme 4 Investigated isomers. See Scheme 3 for the legend. | ||
| ΔEgas | δEBSSE | δEsolv | δEG | ΔG | |
|---|---|---|---|---|---|
| a ΔG = ΔEgas + δEBSSE + δESolv + δEG where ΔEgas and δEBSSE are computed at the PBE0-D3/SDD+ level, δESolv is computed at the M06-2X/SDD+ level with water as the solvent, and δEG is computed at the BLYP-D3/SDD level. BSSE corrections are 0.3, 0.5 and 0.5 kcal mol−1 for the dissociation of H2O, NO3− and L, respectively. | |||||
| 0.5.0 + L → 0.4.1 + H2O | −35.2 | 0.2 | 27.3 | 2.8 | −4.9 |
| 0.5.0 + 2L → 0.3.2a + 2H2O | −63.8 | 0.4 | 49.1 | 4.2 | −10.1 |
| 0.5.0 + 2L → 0.3.2b + 2H2O | −62.1 | 0.4 | 46.8 | 4.6 | −10.4 |
| 0.5.0 + NO3− → 1.4.0a + H2O | −191.9 | 0.2 | 186.0 | 4.6 | −1.1 |
| 0.5.0 + NO3− → 1.4.0b + H2O | −186.3 | 0.2 | 181.6 | 2.6 | −1.9 |
| 0.5.0 + NO3− → 1.3.0…H2O + H2O | −195.0 | 0.2 | 184.1 | 3.1 | −7.6 |
| 0.5.0 + NO3− → 1.3.0 + 2H2O | −177.4 | −0.1 | 173.1 | −4.5 | −8.9 |
| 0.5.0 + L + NO3− → 1.2.1 + 3H2O | −200.8 | 0.1 | 189.3 | −2.8 | −14.2 |
| 0.5.0 + 2L + NO3− → 1.1.2a + 4H2O | −219.6 | 0.3 | 201.3 | −1.1 | −19.1 |
| 0.5.0 + 2L + NO3− → 1.1.2b + 4H2O | −219.1 | 0.3 | 199.4 | 0.5 | −19.0 |
| 0.5.0 + 2L + NO3− → 1.2.2a + 3H2O | −229.3 | 0.6 | 208.1 | 9.8 | −10.8 |
| 0.5.0 + 2L + NO3− → 1.2.2b + 3H2O | −226.6 | 0.6 | 207.6 | 8.3 | −10.1 |
| 0.5.0 + 2L + NO3− → 1.2.2c + 3H2O | −228.8 | 0.6 | 207.6 | 9.6 | −11.0 |
| 0.5.0 + 2L + NO3− → 1.2.2d + 3H2O | −225.8 | 0.6 | 205.8 | 10.1 | −9.3 |
| 0.5.0 + 2NO3− → 2.2.0 + 3H2O | −301.7 | 0.1 | 291.6 | −1.5 | −11.5 |
| 0.5.0 + L + 2NO3− → 2.1.1 + 4H2O | −311.0 | 0.3 | 294.9 | 1.0 | −14.9 |
| 0.5.0 + 2L + 2NO3− → 2.0.2a + 5H2O | −316.0 | 0.5 | 296.7 | 2.3 | −16.6 |
| 0.5.0 + 2L + 2NO3− → 2.0.2b + 5H2O | −316.6 | 0.5 | 294.4 | 3.7 | −18.1 |
| 0.5.0 + 2L + 2NO3− → 2.0.2c + 5H2O | −307.3 | 0.5 | 290.4 | 4.0 | −12.4 |
| 0.5.0 + 2L + 2NO3− → 2.0.2d + 5H2O | −315.0 | 0.5 | 294.5 | 1.8 | −18.1 |
| 0.5.0 + 2L + 2NO3− → 2.0.2e + 5H2O | −308.6 | 0.5 | 290.1 | 1.3 | −16.8 |
| 0.5.0 + 2L + 2NO3− → 2.0.2f + 5H2O | −302.9 | 0.5 | 287.6 | 1.3 | −13.5 |
| 0.5.0 + 2L + 2NO3− → TS2.0.2a–2.0.2b + 5H2O | −313.0 | 0.5 | 293.4 | 4.2 | −15.0 |
| 0.5.0 + 2L + 2NO3− → TS2.0.2b–2.0.2c + 5H2O | −306.2 | 0.5 | 288.6 | 3.2 | −13.9 |
| 0.5.0 + L + 2NO3− → 2.0.1 + 5H2O | −295.4 | 0.0 | 284.0 | −7.2 | −18.6 |
| 0.5.0 + 2L + 2NO3− → 2.1.2a + 4H2O | −320.6 | 0.8 | 297.5 | 10.2 | −12.1 |
| 0.5.0 + 2L + 2NO3− → 2.1.2b + 4H2O | −311.3 | 0.8 | 292.7 | 11.6 | −6.3 |
| 0.5.0 + 2L + 2NO3− → 2.1.2c + 4H2O | −322.8 | 0.8 | 296.5 | 12.8 | −12.7 |
| 0.5.0 + 2L + 2NO3− → 2.1.2d + 4H2O | −317.4 | 0.8 | 298.4 | 13.3 | −4.8 |
| 0.5.0 + 2L + 2NO3− → 1.1.2a…NO3− + 4H2O | −321.9 | 0.8 | 297.1 | 15.0 | −8.9 |
| 0.5.0 + 2L + NO3− → 2.0.2b…H2O + 4H2O | −323.1 | 0.8 | 299.2 | 11.4 | −11.7 |
| 0.5.0 + 2NO3− → 2.3.0a + 2H2O | −303.5 | 0.4 | 293.8 | 8.0 | −1.3 |
| 0.5.0 + L + 2NO3− → 2.2.1 + 3H2O | −315.5 | 0.9 | 297.7 | 5.7 | −11.1 |
| 0.5.0 + L + 2NO3− → 2.0.1 + 5H2O | −295.4 | 0.0 | 284.0 | −7.2 | −18.6 |
| 0.5.0 + 2L + NO3− → 1.0.2 + 5H2O | −197.5 | 0.0 | 186.7 | −8.6 | −19.4 |
Interestingly, in water, both nitrates and L displace water from 0.5.0. The driving force for complexation of a first nitrate is relatively weak when only one water is displaced from 0.5.0, leading either to 1.4.0a (−1.1 kcal mol−1) or 1.4.0b (−1.9 kcal mol−1, see Table 2). However, the displacement of two aquo ligands by a nitrate is more favourable and affords 1.3.0 with a significant free energy gain of 8.9 kcal mol−1. A similar value is obtained when considering the formation of the microsolvated complex “1.3.0…H2O” (−7.6 kcal mol−1; see Scheme 2). These results therefore suggest that, in bulk water, the mono-nitrate complex should preferably exist as a penta-coordinated species possessing three aquo ligands. The complexation of a second nitrate is also thermodynamically favourable but to a lesser extent, especially when the hexa-coordinated 2.2.0a complex is afforded (ΔG = −11.5 kcal mol−1). Similarly, the displacement of water by amides is thermodynamically favourable in water, regardless of the number of coordinated nitrates. In the dicationic series (0.5.0, 0.4.1 and 0.3.2a/b), every H2O/L exchange releases ca. 5 kcal mol−1, yielding a highly negative free energy of formation of 0.3.2a (−10.1 kcal mol−1). This feature is observed regardless of the isomer that is considered since the cis isomer (0.3.2b) is found to be isoenergetic with the trans one (0.3.2a). A similar behaviour is observed in the monocationic series (1.3.0, 1.2.1 and 1.1.2a), where the free energy of formation of 1.1.2a amounts to −19.1 kcal mol−1, making this complex one of the most stable among those considered in this study. Monocationic complexes featuring a monodentate nitrate and two aquo ligands (affording a penta-coordination) are higher in free energy by ca. 9 kcal mol−1 (see 1.2.2a–d in Table 2).
When neutral complexes are considered, H2O → L exchanges are still favourable: complexes with two L ligands (2.0.2a and 2.1.2a) are more stable than those with one or zero. As a result, the formation of 2.0.2a is exergonic in water, by −16.6 kcal mol−1. Neutral complexes possessing two monodentate nitrates and an additional aquo ligand to afford a penta-coordinated uranyl are less stable regardless of the isomer considered (2.1.2a–c, see Schemes 3 and 4): water should thus decoordinate from 2.1.2a to afford 2.0.2a/b. Similarly, a spontaneous release of water from 2.1.2c to afford 2.0.2d/e is predicted.
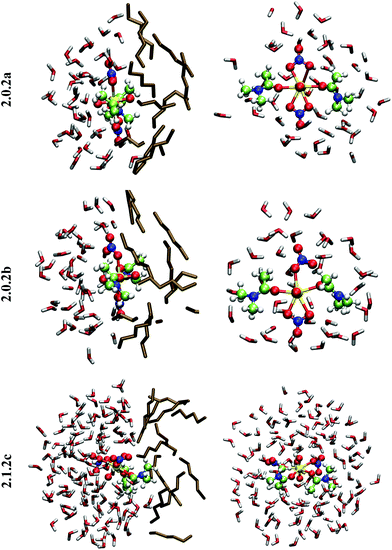
3.3. Structure, dynamics and solvation patterns of [UO2(NO3)2L2] (2.0.2) in hexane, water and at the hexane/water interface
We investigated six “isomers” of the [UO2(NO3)2L2] complex (2.0.2a–f; see Schemes 3 and 4) in the three different environments relevant for the extraction process: bulk hexane, bulk water and the hexane/water interface.| Gasb | Hexanec | Waterd | |
|---|---|---|---|
| a Values reported in the table are calculated as: ΔG = ΔEgas + δEBSSE + δESolv + δEG, where ΔEgas and δEBSSE are computed at the PBE0-D3/SDD+ level. b δEsolv = 0. c δEsolv evaluated using parameters of hexane (SMD model). d δEsolv evaluated using parameters of water (SMD model). | |||
| [UO2(NO3)2L2] complexes | |||
| 2.0.2a | 0.0 | 0.0 | 0.0 |
| 2.0.2b | 0.8 | 1.9 | −1.5 |
| 2.0.2c | 10.4 | 11.1 | 4.2 |
| 2.0.2d | 0.6 | 0.8 | −1.6 |
| 2.0.2e | 6.4 | 5.7 | −0.2 |
| 2.0.2f | 12.2 | 12.2 | 3.1 |
| TS2.0.2a–2.0.2b | 4.9 | 5.1 | 1.6 |
| TS2.0.2b–2.0.2c | 10.7 | 11.2 | 2.6 |
| 2.0.1 + L | 10.7 | 9.1 | −2.0 |
| 1.0.2 + NO3− | 107.1 | 63.5 | −2.9 |
| [UO2(NO3)2(H2O)L2] complexes | |||
| 2.1.2a | −0.3 | 0.2 | 0.7 |
| 2.1.2b | 10.3 | 10.6 | 6.5 |
| 2.1.2c | 0.0 | 0.0 | 0.0 |
| 2.1.2d | 6.0 | 7.0 | 7.9 |
| 1.1.2a + NO3− | 89.3 | 47.0 | −5.8 |
In bulk hexane, the complex retains its hexa-coordination for ca. 22 ps of MD, and then one nitrate becomes monodentate to afford 2.0.2b for the remaining 10 ps of MD. In bulk water, the nitrates exhibit a fluxional behaviour, where one quickly moves from a bidentate to a monodentate coordination mode to afford 2.0.2b, with transient recoordinations to afford 2.0.2a. Interestingly, the identity of the bound Onit atom can change in the process, namely: “nitrate-1” is bound via Ob during the first 20 ps of MD and via Oc for the remaining 12 ps (see the crossing of the blue and green curves on Fig. 1 at t = 20 ps). The exchange occurs with an associative process, via2.0.2a. A similar behaviour is observed by full DFT-MD simulations, where “nitrate-1” remains bidentate for the whole 32 ps of MD, whereas “nitrate-2” is monodentate (as in 2.0.2b) most of the time, but exhibits a rotational motion: during the first 9 ps, it is originally bound by its Oa atom, then a transient bidentate coordination mode is achieved (for 0.5 ps) and Oa decoordinates (i.e. the anion remains bound by its Ob atom). After 4.5 ps of MD, another rotation is observed, where Oc coordinates to UO22+ while Ob decoordinates (see Scheme 5). Such a dynamics points to a rather weakened binding of the nitrate to the complex in water, in accord with the result of static calculations shown in Table 3 and with the systematic increase of average U–Onit distances when moving from hexane (or gas phase) to water (see Table 4).
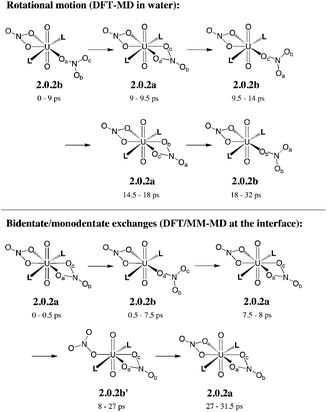 | ||
| Scheme 5 Fluxional coordination of nitrate in 2.0.2a/b: rotational motion and bidentate/monodentate exchanges, as observed from DFT-MD in explicit water and DFT/MM-MD at the interface (over 32 ps). See the time evolution of U–Onit distances in Fig. 1. | ||
| OPT | MD | |||||
|---|---|---|---|---|---|---|
| G09 | CP2K | DFT/MM-MD | DFT-MD | |||
| Gasb | Gas | Hexane | Interface | Water | Water | |
| a The BLYP-D3 functional has been employed throughout. b SDD basis set. c Not reported because the lifetime of the hexacoordinated complex (with two bidentate nitrates) is too short; see Fig. 1. d No DFT/MM-MD simulations have been performed on this species. | ||||||
| 2.0.2a | ||||||
d(U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
1.81 | 1.81 | 1.81(5) | 1.82(4) | ||
| d(U–Onit) | 2.54 | 2.55 | 2.57(13) | 2.59(10) | ||
| d(U–OL) | 2.44 | 2.43 | 2.46(10) | 2.37(9) | ||
| 2.0.2b | ||||||
d(U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
1.81 | 1.81 | 1.81(4) | 1.81(5) | 1.81(7) | 1.82(3) |
| d(U–Onit) | 2.50 | 2.50 | 2.52(7) | 2.57(14) | 2.57(15) | 2.56(8) |
| d(U–O′nit) | 2.37 | 2.38 | 2.35(7) | 2.40(11) | 2.45(14) | 2.41(9) |
| d(U–OL) | 2.38 | 2.37 | 2.40(8) | 2.36(10) | 2.33(12) | 2.33(7) |
| 2.1.2c | ||||||
d(U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
1.81 | 1.81 | 1.81(4) | 1.81(8) | 1.81(5) | 1.82(3) |
| d(U–Onit) | 2.37 | 2.38 | 2.40(10) | 2.49(15) | 2.48(14) | 2.51(12) |
| d(U–OL) | 2.47 | 2.46 | 2.45(10) | 2.39(12) | 2.38(10) | 2.36(7) |
| d(U–Owat) | 2.50 | 2.52 | 2.55(10) | 2.54(15) | 2.56(12) | 2.47(9) |
| 1.1.2a…NO3− | ||||||
d(U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
1.81 | 1.81 | 1.82(3) | |||
| d(U–Onit) | 2.50 | 2.50 | 2.57(10) | |||
| d(U–OL) | 2.37 | 2.36 | 2.33(7) | |||
| d(U–Owat) | 2.39 | 2.42 | 2.45(9) | |||
| d(U–Nnit) | 4.69 | 4.81 | 5.22(53) | |||
We note that such an elongation of U–Onit distances when going from the gas phase to water has already been observed in the cases of 2.2.050 and 1.4.0a/b.44 However, no spontaneous nitrate dissociation is observed in the course of our DFT/MM-MD and DFT-MD simulations (over 32 ps). Regarding the L ligand, its strengthened coordination to uranyl in a water environment is a particularly noteworthy and important feature for the extraction mechanism.
When simulated at the hexane/water interface, the complex does not diffuse toward any of the bulk phase, but remains located in the interfacial domain over the 32 ps of DFT/MM-MD. On average, its O–U–O axis sits perpendicular to the interfacial plane, with the amide and nitrate ligands being co-planar to the interface (see Fig. 2). Interestingly, the complex behaves similarly as in water, since 2.0.2b is afforded most of the time with transient formation of 2.0.2a. However, no rotational motion of NO3− is observed at the interface. Instead, a dynamical exchange occurs between two “isomers” of 2.0.2b: during the first 8 ps of MD, “nitrate-1” is monodentate and “nitrate-2” is bidentate, then an exchange occurs (via2.0.2a) to obtain the reverse situation where “nitrate-1” is bidentate and “nitrate-2” monodentate (see 2.0.2bvs. 2.0.2b′ in Scheme 5).
As discussed above, we should emphasise that the bidentate binding mode of the nitrates may be underestimated by the BLYP-D3 functional that is employed in the DFT/MM-MD simulations (compare CCSD(T)/SDD+ and BLYP-D3(CP2K) in Table 1, where the η2-coordination of NO3− in 1.4.0avs. η1-1.4.0b is underestimated by 2.2 kcal mol−1). We therefore expect a larger difference in stabilities between 2.0.2a, 2.0.2b and 2.0.2c, making the tetra-coordinated complex 2.0.2c in reality less stable. Also, the free energy surfaces could be refined by performing longer metadynamics simulations with smaller hills (see Fig. S2†). However, taken together, these metadynamics results point to the solvent-dependent versatility of binding mode of the nitrate that is beneficial for changes in coordination number and for ligand exchange processes occurring along the extraction process.
3.4. Structure, dynamics and solvation patterns of [UO2(NO3)2(H2O)L2] (2.1.2c) in hexane, water and at the hexane/water interface
We now consider the hydrated [UO2(NO3)2(H2O)L2] complex as a possible precursor of the extracted [UO2(NO3)2L2] species, by losing its aquo ligand. We decided to start with the cis isomer (2.1.2c) that might be afforded at the interface upon complexation by L via a least motion pathway. This cis isomer being almost isoenergetic with the trans one (2.1.2a) in hexane or in water (see Table 3), the two complexes are expected to be in equilibrium at the interface. Again, DFT/MM-MD simulations have been performed in hexane, water and at the interface for 32 ps along with a full DFT-MD simulation in water. Time evolution of (U,O) coordination numbers around uranyl shows that the complex retains its five ligands for the whole 32 ps of MD, in the three environments (see Fig. 4). Again, nitrates essentially remain monodentate but sometimes display transient bidentate coordinations. Rotational motions are also observed, as depicted in Scheme 5 in the case of 2.0.2b. Average interatomic distances reported in Table 4 show that, intrinsically (i.e., in the gas phase), the three metal–ligand distances follow the order: d(U–Onit) < d(U–OL) < d(U–Owat). NO3− is the most strongly bound because of its negative charge, while L is intrinsically a better ligand than H2O (vide supra). In hexane, average metal–ligand distances are almost identical to those found in the gas phase, and thus follow the same order. In water, U–Onit is elongated by ca. 0.13 Å whereas U–OL distances are shortened by ca. 0.10 Å, yielding a reverse sequence: d(U–OL) < d(U–Owat) < d(U–Onit). This result points to a weaker binding of monodentate nitrates in water that should stem from their attraction by water, as in the case of 2.0.2a/b discussed below. We note that the weak binding of nitrates in water evidenced by these MD simulations is consistent with the static calculations in the continuum (see Table 3), where the full dissociation of NO3− from 2.1.2a is found to be favoured by 7 kcal mol−1. However, the process should be associated with a significant kinetic barrier, as no spontaneous nitrate dissociation is observed in the course of DFT-MD and DFT/MM-MD simulations in water. Conversely, the shortening of the U–OL distances suggests that amides are more strongly bound to the metal in water than in hexane. Interestingly, the U–Owat distance remains similar in the two environments but a closer look at the average structures in the two media reveals a marked difference: in hexane, the water ligand forms intramolecular hydrogen bonds with the two neighbouring nitrates (as in the gas phase), whereas, in water, it mainly forms intermolecular hydrogen bonds with the solvent. A similar competition between intramolecular and intermolecular hydrogen bonds has been observed in the cases of [UO2(NO3)2(H2O)2]50 and LaClx complexes (x = 1,…, 3).55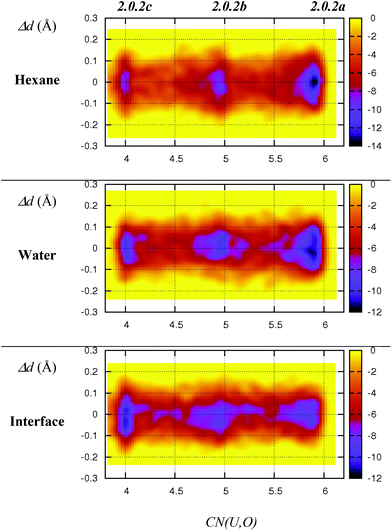 | ||
| Fig. 3 Free energy surfaces (colour coded in kcal mol−1) of 2.0.2a–c as obtained from DFT/MM metadynamics simulations in hexane, water and at the interface. X-axis: equatorial coordination number around uranyl. Y-axis: differences between the two U–Nnit distances (in Å). The time evolution of the collective variables is given in Fig. S1 in ESI.† | ||
When simulated in the hexane/water biphasic system, 2.1.2c remains adsorbed at the interface for the whole 32 ps of MD. The snapshot of the complex at the interface presented in Fig. 2 shows that its orientation clearly differs from that of 2.0.2a/b, as the O–U–O axis of 2.1.2c does not sit perpendicular to the interface anymore but is rather tilted, and the equatorial plane of the complex is no longer co-planar with the interface. It tends to adopt an amphiphilic orientation with the two L ligands on the hexane side of the interface and the nitrates and aquo ligands on the water side. Interestingly, metal–ligand distances follow the same sequence as in water (see Table 4). Visual inspection of the trajectories shows that intermolecular hydrogen bonds with (interfacial) water molecules are also predominant over intramolecular hydrogen bonds, in keeping with the fact that the polar [UO2(NO3)2(H2O)] moiety of the complex is essentially solubilized on the water side of the interface. As a result, the uranyl–nitrate bond appears to be significantly weakened at the interface to a similar extent as in bulk water. Concomitantly, the uranyl–L bond is strengthened at the interface.
3.5. Structure and dynamics of the [UO2(NO3)(H2O)L2]+ complex (1.1.2) in water
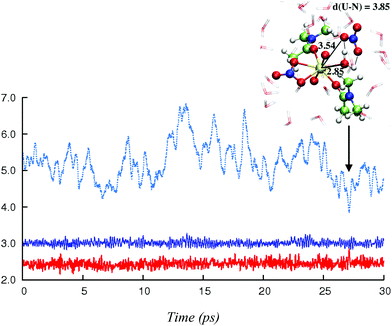
In this section, we explore by MD simulations the stability and structure of another potential precursor of the extracted complex, namely the cationic [UO2(NO3)(H2O)L2]+ species for which a H2O/NO3− exchange leads to 2.0.2. As seen above, the 1.1.2a complex, a possible intermediate between the +2 charged 0.5.0 and neutral 2.0.2 species, is also one of the most stable in the studied series in SMD-water. We thus decided to study by DFT-MD its dynamics in the presence of a second shell nitrate ligand. Because the “free” nitrate salt is insoluble in the oil phase, water was chosen as the explicit solvent environment, as a first approach. The complex more likely forms at the interface, but its structure should be similar in the two environments, as seen above. The DFT-MD on the “1.1.2a…NO3−” complex was thus started with the second sphere nitrate constrained to be hydrogen-bonded to the H2O ligand, for 2.5 ps (by fixing the U–Nnit at 5.5 Å). We then released the constraint for an extra 30 ps of MD. Time evolution of the uranium–nitrogen distance (denoted d(U–Nnit)) shown in Fig. 5 reveals that the free nitrate is quite mobile, with d(U–Nnit) oscillating from 3.85 Å to 6.80 Å. At longer distances, the hydrogen bond with 1.1.2a is disrupted and nitrate is fully surrounded by solvent water molecules. The free anion does not diffuse further into the “bulk” water phase, but essentially remains in the second shell, forming a contact ion pair, on average. This feature is favourable for its further complexation to afford the extracted species 2.0.2a/b. However, neither spontaneous coordination of NO3− nor full dissociation of H2O is observed in the course of the DFT-MD (over 30 ps). Interestingly, at some stage of the dynamics (ca. 27 ps), NO3− approaches the metal and this process is accompanied by an elongation of U–Owat (see the structure extracted from the DFT-MD in Fig. 3) to reach 2.85 Å. This value is larger than the typical U–Owat distance in mixed UO22+/NO3−/H2O/L complexes (see e.g.2.1.2c in Table 4, where U–Owat = 2.48(9) Å) and likely corresponds to a structure close to the transition state for a concerted H2O/NO3− ligand exchange. However, it is apparent from the structure that the nitrate does not point any of its oxygen toward the metal but remains hydrogen bonded to the solvent and to the coordinated H2O. As a result, the closest U–Onit distance remains quite long (namely 3.54 Å), suggesting that the structure afforded during the DFT-MD is still far from the transition structure and that the associated kinetic barrier should be rather high. In order to estimate this barrier, we performed a transition state search by static calculations (PBE0-D3 energies in SMD-water on the gas phase BLYP-D3/SDD geometries, optimized with a single imaginary frequency) using the structure extracted from the DFT-MD as the starting structure (after removing all solvent molecules). Interestingly, no transition state could be located directly from that structure, but we needed to slightly rotate the free nitrate to approach its closest oxygen atom slightly closer to the metal. The search led, in fact, to a (late) transition state for an associative process, where the nitrate coordinates while the U–Owat bond is retained, i.e. to afford 2.1.2d. The activation barrier from “1.1.2a…NO3−” (as depicted in Fig. 6) is found to be small (+3.7 kcal mol−1) and therefore potentially accessible. Searching for the full pathway connecting the “1.1.2a…NO3−” complex to “2.0.2b…H2O” in solution is beyond the scope of this study. However, taken together, these DFT-MD results in water and the small difference in their free energies of formation in SMD-water (−8.9 and −11.7 kcal mol−1, respectively, see Table 2) suggest that 1.1.2a can be a potential intermediate along the 0.5.0 to 2.0.2 transformation.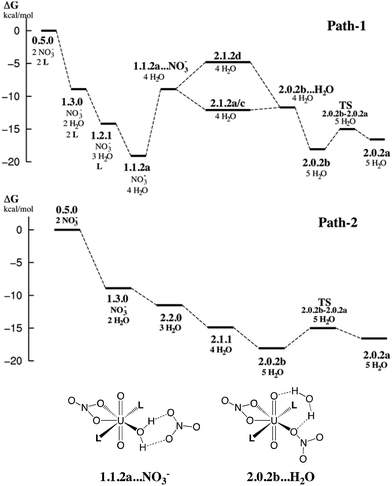 | ||
| Fig. 6 Possible free energy profiles path-1 and path-2 (kcal mol−1) for the stepwise complexation of NO3− and L by 0.5.0 to afford the extracted complex 2.0.2. Energies estimated from static calculations in SMD-water (top). Bottom: schematic representation of selected intermediates. Other intermediates are depicted in Schemes 3 and 4. | ||
3.6. Proposed extraction mechanism
The results on the relative stabilities of [UO2(NO3)x(H2O)yLz]2−x complexes and mechanistic considerations allow us to propose reasonable sequences of reactions involved in the uranyl extraction by the amide ligand, starting from 0.5.0 solubilized in water and ending up with 2.0.2a in hexane (see Scheme 1). Two possible routes are schematized in Fig. 6, with relative free energies calculated “in SMD-water”. These are only indicative because of the limitations of the continuum SMD solvation model (lack of explicit H-bond interactions with the solute, for instance). The changes in solvation energies cannot pretend to be accurate, especially for the complexation of charged species in a given medium. See for instance the recently reported case of actinide and lanthanide ion extraction.56 When compared to experimental conditions where uranyl is extracted by amide ligands,1e,57 two important features must be noted. First, the N,N-dimethylacetamide ligand L used here for convenience is soluble in water and thus does not extract uranyl. Its coordination features to uranyl should be similar, however, to those of more hydrophobic oil-soluble amide ligands.58 The latter are more bulky and polarizable than L, and thus form stronger bonds with uranyl.59 A second important simplification concerns the pH conditions. Experimentally, uranyl extraction occurs from highly acidic media (≈3 M nitric acid solutions where irradiated nuclear fuel is usually dissolved), and increases with the acid concentration.1e,57 Without acid, uranyl is not extracted. Experimentally, some nitric acid in its HNO3 form and some water are also co-extracted with the extracted 2.0.2 complex, presumably forming hydrogen bonds with its external nitrate oxygens.The two proposed routes start by the coordination of one nitrate (path-1) or two nitrates (path-2), respectively, in “bulk water”. The corresponding calculated free energies are overestimated, if one refers to the low stability of the UO2(NO3)(H2O)x+1 cation in water,60 but are consistent with the experimental61 and computational62 evidence of increased nitrate coordination to uranyl when nitric acid is added to the solution. Coordination of nitrate(s) (by exchange with two aquo ligands from 0.5.0 affords 1.3.0 (one nitrate) or 2.2.0 (two nitrates)). Both 1.3.0 and 2.2.0 species are less hydrophilic than the dicationic 0.5.0 species and are thus expected to approach the interface,63 close enough to interact with the carbonyl group of L that displaces H2O from the complex, affording 1.1.2a in path-1. This complex should sit “right at the interface” in an amphiphilic manner, i.e. with the alkyl groups of the amide on the oil side and the water and nitrate ligands on the water side. As surface active species, such positively charged complexes concentrate at the interface and thus attract free nitrate counterions to afford contact ion pairs as in “1.1.2a…NO3−” via electrostatic interactions. Then, H2O/NO3− ligand exchange occurs at the interface to afford the neutral 2.1.2d species, from which water decoordinates, yielding the more hydrophobic 2.0.2b and 2.0.2a complexes. These finally diffuse from the interface to bulk hexane.
In path-2, the first neutral species formed is 2.2.0. From there, displacement of H2O ligands by L at the interface successively yields the more hydrophobic 2.1.1 and 2.0.2b or 2.0.2a complexes. Interestingly, comparing these two structures, we note that 2.0.2b with a monodentate nitrate is calculated to be slightly more stable in SMD-water, while 2.0.2a with two bidentate nitrates is preferred in SMD-hexane. 2.0.2a should also interact less than 2.0.2b with water at the interface. Thus, the migration of 2.0.2 from the interface to the oil phase is likely correlated with a switch in the η1 to η2 nitrate coordination mode. The free energy profiles provided in Fig. 6 show that both path-1 and path-2 processes are favourable in SMD-water, and are also likely to be so at the interface where interfacial charged species mostly interact with water (see for instance an energy component analysis in recent classical MD simulations).9 Interestingly, path-2 that requires more acidic conditions than path-1 mainly corresponds to a regular downhill process, while path-1 involves higher energy intermediates and might thus be kinetically less favourable. In path-1, we located a transition state involved in the key H2O/NO3− exchange process and found that the height of the kinetic barrier is rather small, indicating that associative ligand exchange should be entirely plausible, though. It should be noted that in reality, the extraction kinetics not only depends on barriers for ligand coordination/decoordination, but is also generally limited by the diffusion rates, hardly accessible from calculations.
4. Discussion and conclusions
We report DFT studies on selected uranyl complexes involved in the uranyl extraction from water to an “oil” phase (hexane) by an amide ligand L, using two complementary approaches: static DFT results “in SMD-solution” and MD studies in explicit solvent environments (water, hexane, or the water/hexane interface) represented at the MM or full-DFT level. In the following, we summarize the related strengths and weaknesses, as well as the most important results regarding the studied uranyl complexation and extraction processes.On the methodological side, our “static” results were obtained from high-level DFT calculations, involving a small-core ECP on U and large basis sets including many polarisation and diffuse functions. The PBE0-D3 functional has been employed to compute refined energies, after validation against CCSD(T) calculations. This functional includes a correction for dispersion interactions that are generally lacking in GGA and hybrid functionals. The latter have been recognized to be important to properly describe metal–ligand interactions in several organometallic,64 and actinide65 complexes, and turn out to be also important to model mono- vs. bidentate coordination or H2O dissociation in uranyl nitrate complexes herein (see Table 1). As a result, gas phase reaction energies (ΔEgas) should be quite well predicted. The estimation of changes in solvation free energies remains the most difficult task for present-day DFT modelling, and we tackled this issue by two different approaches of increasing accuracy. First, we employed the recently developed SMD model that is recognized to perform particularly well to compute absolute free energy of solvation and free energies of transfer from water to an organic phase, especially when neutral solutes are considered.24 Solvation of ions still remains a challenging task,24 especially when “strong” explicit interactions with the solvent are involved (namely, hydrogen bonding with water). As a result, the solvation of the nitrates is a difficult case for the SMD model and the latter uncomplexed appears to be not enough solvated, making their complexation in water somewhat too favourable.66 However, free energies for exchange of neutral ligands are expected to be better accounted for. In particular, the clear-cut preference for L over H2O binding in SMD-water and SMD-hexane should be realistic, and is a key feature for the extraction process: L displaces water from uranyl, whatever be the number of coordinated nitrates. In our second approach, the solvent molecules are represented explicitly, and their motions and interactions with the uranyl complexes have been described by performing ab initio MD simulations. Our mixed DFT/MM-MD protocol12 allowed us to consider systems containing one complex and few thousands of solvent molecules, at a similar computational expense as in fully DFT-MD simulations on small boxes (containing one complex and 89 water molecules only). With the DFT/MM-MD protocol, one can thus simulate “DFT solutes” in quite large solvent boxes, as involved in biphasic systems and their interfaces. Despite a lower accuracy compared to fully DFT-MD (e.g. the lack of back polarization of the first solvation shell by the solute), our DFT/MM model captures most of the solvation effects. For instance, the polarisation of the solute by the solvent12 and the influence of aqueous solvation on the structure of a uranyl peroxo complex67 have been qualitatively well described elsewhere. Herein, for instance, the shortening/elongation of metal-distances in water vs. gas phase (see Table 4) and the fluxional coordination of the nitrates (see Scheme 5) are described satisfactorily when compared to full DFT-MD at the same DFT level. Our simulations of uranyl complexes at the hexane/water interface reveal that their structure in this peculiar nano-domain is more “water-like” than “oil-like”. The binding of L is thus reinforced compared to the gas phase, a feature particularly important in the context of a complexation process occurring “right at the interface”. Another important feature concerns the cis/trans forms of the complexes. DFT/MM-MD simulations, supported by static DFT calculations, reveal that the formation of cis isomers is competitive to that of trans isomers, in the bulk solvents as well as at the interface. Interestingly, the former can be afforded via a least motion pathway upon complexation with interfacial L ligands (oriented in an amphiphilic manner),9a and then rearrange to less amphiphilic and less surface active trans isomers when diffusing to the organic phase. Taken together, our results allowed us to propose possible paths for the overall extraction process of UO22+ by N,N-dialkylamide ligands, and shed new light on the key role of the interface in the process. Similar features are expected by other ligands like TBP.9 To the best of our knowledge, our study reports the first DFT/MM-MD simulations of a uranyl liquid–liquid extraction system. Further work will focus on improving our hybrid DFT/MM model by considering the actual oil-soluble amide ligand (with long alkyl chains on L, e.g. described at an MM level), and by taking into account the high concentration of L in the organic phase, the ionic strength and the acidic pH of the aqueous phase, thus approaching the complexity of “real” extraction systems. Beyond the case of uranyl extraction, the results have a bearing on biphasic processes in chemistry and biology, involving ion separation or transport or phase transfer catalysis processes.68
Acknowledgements
N. S. thanks Univ. Grenoble Alpes, CNRS and ICMG FR 2607 for financial support. MD simulations were performed using the Cecic and Froggy platforms of the CIMENT infrastructure, which is supported by the Rhône-Alpes region (grant CPER07_13 CIRA) and the Equip@Meso project (reference ANR-10-EQPX-29-01) of the programme Investissements d'Avenir supervised by the Agence Nationale pour la Recherche (project “liqsim”). NWChem calculations made use of the facilities of HECToR, the U.K. national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc., and NAG Ltd and funded by the Office of Science and Technology through EPSRC's High End Computing Programme. Support from the ANR ILLA is also acknowledged (G. W.). The authors also thank all the participants of the “Dalton Discussion 14: Advancing the Chemistry of the f-elements” meeting for fruitful discussions.Notes and references
- (a) T. H. I. Siddal, J. Phys. Chem., 1960, 64, 1863 CrossRef; (b) G. M. Gasparini and G. Grossi, Sep. Sci. Technol., 1980, 15, 825 CrossRef CAS; (c) C. Musikas and W. W. Schulz, in Principles and Practices of Solvent Extraction, ed. J. Rydberg, C. Musikas and G. R. Choppin, M. Dekker, Inc., New York, 1992, ch. 11, p. 413 Search PubMed; (d) C. Musikas, N. Condamines and C. Cuillerdier, Anal. Sci., 1991, 7(Suppl.), 11 CrossRef CAS; (e) P. N. Pathak, D. R. Prabhu, P. B. Ruikar and V. K. Mancha, Solvent Extr. Ion Exch., 2002, 20, 293 CrossRef CAS; (f) M. Miguirditchian, C. Sorel, B. Cames, I. Bisel and P. Baron, in Global 2009, Paris, France, 2009, p. 1032 Search PubMed.
- F. Rodrigues, G. Ferru, L. Berthon, N. Boubals, P. Guilbaud, C. Sorel, O. Diat, P. Bauduin, J. P. Simonin, J. P. Morel, N. Morel-Desrosiers and M. C. Charbonnel, Mol. Phys., 2014, 112, 1362 CrossRef CAS.
- For X-ray structures of UO2(NO3)2(RCONR′2)2 complexes, see for instance Refcodes DOGZOO (R = C11H23, R′ = C4H9) and NOGTAF (R = iPrCH2, R′ = iPr) in the Cambridge Crystallographic Database. DOGZOO: P. Charpin, M. Lance, M. Nierlich, D. Vigner, N. Descouls and C. Musikas, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 560 CrossRef CAS NOGTAF: S. Kannan, S. B. Deb, J. S. Gamare and M. G. B. Drew, Polyhedron, 2008, 27, 2557 CrossRef.
- Y. Meridiano, L. Berthon, X. Crozes, C. Sorel, P. Dannus, M. R. Antonio, R. Chiarizia and T. Zemb, Solvent Extr. Ion Exch., 2009, 27, 607 CrossRef CAS.
- (a) J. B. Lewis, Nature, 1956, 178, 274 CrossRef CAS; (b) H. T. Hahn, J. Am. Chem. Soc., 1957, 79, 4625 CrossRef CAS; (c) F. Baumgärtner and L. Finsterwalder, J. Phys. Chem., 1970, 74, 108 CrossRef; (d) W. Nitsch, Faraday Discuss. Chem. Soc., 1984, 77, 85 RSC.
- (a) P. Jungwirth and B. Winter, Annu. Rev. Phys. Chem., 2008, 59, 343 CrossRef CAS PubMed; (b) F. Berny, R. Schurhammer and G. Wipff, Inorg. Chim. Acta, 2000, 300–302, 384 CrossRef CAS; (c) I. Benjamin, Chem. Rev., 1996, 96, 1449 CrossRef CAS PubMed; (d) T.-M. Chang and L. X. Dang, Chem. Rev., 2005, 106, 1305 CrossRef PubMed.
- (a) G. Wipff, E. Engler, P. Guilbaud, M. Lauterbach, L. Troxler and A. Varnek, New J. Chem., 1996, 20, 403 CAS; (b) F. Berny, N. Muzet, R. Schurhammer, L. Troxler and G. Wipff, in Current Challenges in Supramolecular Assemblies, NATO ARW Athens, ed. G. Tsoucaris, Kluwer Acad. Pub., Dordrecht, 1998, p. 221 Search PubMed; (c) M. Baaden, R. Schurhammer and G. Wipff, J. Phys. Chem. B, 2002, 106, 434 CrossRef CAS.
- (a) M. Baaden, M. Burgard and G. Wipff, J. Phys. Chem. B, 2001, 105, 11131 CrossRef CAS; (b) M. Jayasinghe and T. L. Beck, J. Phys. Chem. B, 2009, 113, 11662 CrossRef CAS PubMed.
- (a) G. Benay and G. Wipff, J. Phys. Chem. B, 2013, 117, 7399 CrossRef CAS PubMed; (b) G. Benay and G. Wipff, J. Phys. Chem. B, 2014, 118, 3133–3149 CrossRef CAS PubMed.
- N. H. Sagert and M. J. Quinn, J. Colloid Interface Sci., 1987, 115, 283 CrossRef CAS.
- G. Martin-Gassin, P. M. Gassin, L. Couston, O. Diat, E. Benichou and P. F. Brevet, Phys. Chem. Chem. Phys., 2011, 13, 19580 RSC.
- N. Sieffert, M. Bühl, M.-P. Gaigeot and C. A. Morrison, J. Chem. Theory Comput., 2013, 9, 106 CrossRef CAS.
- H. Watarai, Trends Anal. Chem., 1993, 12, 313 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535 CrossRef.
- Generated automatically according to the procedure implemented in Gaussian 09.
- Following the argument in R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565–3573 CrossRef CAS , where this simple procedure has been proposed as adjustment for the concentration of water molecules in the liquid, and where the necessary value for the pressure has been derived from the experimental density of liquid water. Such an elevated pressure is designed to model the change in entropy existing in the condensed phase when the number of particles varies during a given reaction.
- (a) T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS; (b) R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- (a) For the PBE0 functional see: C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS; (b) For the “–D3” correction see: S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- J. A. Pople, et al.Gaussian 09, Revision D.01, Gaussian, Inc., Pittsburgh, PA, 2009 Search PubMed (the full reference is given in ESI†).
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477 CrossRef CAS.
- D. A. Pearlman, D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham Iii, S. DeBolt, D. Ferguson, G. Seibel and P. Kollman, Comput. Phys. Commun., 1995, 91, 1 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- P. Guilbaud and G. Wipff, J. Mol. Struct. (THEOCHEM), 1996, 366, 55 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179 CrossRef CAS.
- (a) T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS; (b) U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS; (c) P. P. Ewald, Annalen der Physik, 1921, 369, 253 CrossRef; (d) T. Laino and J. Hutter, J. Chem. Phys., 2008, 129, 074102 CrossRef PubMed; (e) A. Y. Toukmaji and J. A. Board, Comput. Phys. Commun., 1996, 95, 73 CrossRef CAS.
- D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, M. Crowley, R. C. Walker, W. Zhang, K. M. Merz, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin and P. A. Kollman, AMBER 10, University of California, San Francisco, 2008 Search PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103 CrossRef CAS.
- For more information on CP2K, see: http://www.cp2k.org (last accessed: November 2014).
- A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- (a) S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter, 1996, 54, 1703 CrossRef CAS; (b) C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter, 1998, 58, 3641 CrossRef CAS; (c) M. Krack, Theor. Chem. Acc., 2005, 114, 145 CrossRef CAS.
- J. Rabone and M. Krack, Comput. Mater. Sci., 2013, 71, 157 CrossRef CAS.
- O. Hollóczki, Inorg. Chem., 2014, 53, 835 CrossRef PubMed.
- R. Jonchiere, A. P. Seitsonen, G. Ferlat, A. M. Saitta and R. Vuilleumier, J. Chem. Phys., 2011, 135, 154503 CrossRef PubMed.
- (a) S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef; (b) G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635 CrossRef; (c) W. G. Hoover, Phys. Rev. A, 1985, 31, 1695 CrossRef PubMed.
- (a) T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2005, 1, 1176 CrossRef CAS; (b) T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2006, 2, 1370 CrossRef CAS.
- (a) L. Genovese, T. Deutsch, A. Neelov, S. Goedecker and G. Beylkin, J. Chem. Phys., 2006, 125, 074105 CrossRef PubMed; (b) L. Genovese, T. Deutsch and S. Goedecker, J. Chem. Phys., 2007, 127, 054704 CrossRef PubMed.
- M. Bühl, R. Diss and G. Wipff, Inorg. Chem., 2007, 46, 5196 CrossRef PubMed.
- Due to program limitations, the so-called T1-diagnostic (J. T. Lee and P. R. Taylor, Int. J. Quantum Chem. Symp., 1989, 23, 199–207) could not be printed after the CCSD calculations with NWChem. This property is an indication of possible shortcomings of the Hartree–Fock single-reference wavefunction. With a smaller basis set (no g-functions on U, aug-cc-pVDZ on O, C and N, cc-pVDZ on H), this diagnostic could be computed with Gaussian 09, where it amounted to 0.025 for 1a, 1b and 1c. This number is somewhat above the commonly used threshold for the need for a multi-determinantal ansatz (0.02), but similar to those computed for uranyl hydrate (ref. 48), for cis- and trans-uranyl complexes involved in the yl-exchange (ref. 65c) or uranyl peroxo complexes (ref. 67). Note that transition-metal complexes with T1-values up to 0.05 have been classified as single-reference cases (W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theor. Comput., 2012, 8, 460–468).
- J. P. Austin, N. A. Burton, I. H. Hillier, M. Sundararajan and M. A. Vincent, Phys. Chem. Chem. Phys., 2009, 11, 1143 RSC.
- (a) M. Buhl, N. Sieffert, V. Golubnychiy and G. Wipff, J. Phys. Chem. A, 2008, 112, 2428 CrossRef PubMed; (b) M. Bühl, N. Sieffert and G. Wipff, Chem. Phys. Lett., 2009, 467, 287 CrossRef; (c) M. Bühl, N. Sieffert, A. Chaumont and G. Wipff, Inorg. Chem., 2011, 50, 299 CrossRef PubMed; (d) M. Bühl, N. Sieffert, A. Chaumont and G. Wipff, Inorg. Chem., 2012, 51, 1943 CrossRef PubMed.
- P. Wahlin, C. Danilo, V. Vallet, F. Réal, J.-P. Flament and U. Wahlgren, J. Chem. Theory Comput., 2008, 4, 569 CrossRef CAS.
- The total equatorial coordination number is defined here as a continuous function of metal–ligand distances: CN = ∑Nwat(1 − (dNwatU–Owat/2.80)25)/(1 − (dNwatU–Owat/2.80)50) + ∑Nnit(1 − (dNnitU–Onit/3.10)25)/(1 − (dNnitU–Onit/3.10)50) + ∑NL(1 − (dNLU–OL/2.90)25)/(1 − (dNLU–OL/2.90)50) where Nwat, Nnit and NL are the numbers of water, nitrate, and amide oxygens, respectively. Nwat = 0 (in 2.0.2a/b) or 1 (in 2.1.2c), Nnit = 6 and NL = 2. Similarly, dNwatU–Owat, dNnitU–Onit and dNLU–OL are the Nth metal–water, metal–nitrate and metal–amide U–O distances, respectively (in angstrom).
- M. Bühl, H. Kabrede, R. Diss and G. Wipff, J. Am. Chem. Soc., 2006, 128, 6357 CrossRef PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562 CrossRef CAS PubMed.
- Time evolution of the collective variables and results of additional metadynamics simulations are provided in ESI (see Fig. S1 and S2†).
- Experimental EXAFS data on 2.0.2a are available in the literature: in the case of more hydrophobic amide ligands, U–Onit is 2.52 Å (see: T. Yaita, S. Suzuki, H. Narita, S. Tachimori, K. Takai, H. Motohashi and K. Kobayashi, Proccedings of the Workshop on Speciation, Techniques and Facilities for Radioactive Materials at Synchrotron Light Sources. 4–6 October 1998, Grenoble, France. pp. 325–330). EXAFS data are also available for a series of 2.0.2a analogues with several phosphate ligands (instead of amides) where U–Onit distances range from 2.51 to 2.54 Å, depending on the ligand that is considered (see: C. Den Auwer, C. Lecouteux, M. C. Charbonnel, C. Madic and R. Guillaumont, Polyhedron, 1997, 16, 2233 and C. D. Auwer, M. C. Charbonnel, M. T. Presson, C. Madic and R. Guillaumont, Polyhedron, 1998, 17, 4507). These values are in good accord with the average calculated for 2.0.2a in bulk hexane (U–Onit = 2.57(13) Å, see Table 4).
- We note that the free energy difference of ca. 2 kcal mol−1 between 2.0.2a and 2.0.2b obtained from metadynamics correlates well with the results of the unconstrained MDs presented in Fig. 1, from which the relative free energy between the two structures can be calculated from their relative populations (denoted P2.0.2a/P2.0.2b). We used the coordination number (CN) to discriminate between 2.0.2a and 2.0.2b, considering that 2.0.2a is populated when CN > 5.5 and 2.0.2b when CN ≤ 5.5. The relative free energy is computed as ΔG2.0.2a→2.0.2b = −RT
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln(P2.0.2b/P2.0.2a) at T = 320 K. We found −1.7 kcal mol−1 in DFT/MM-MD water, −1.1 kcal mol−1 in DFT-MD water and −1.2 kcal mol−1 at the interface.
Ln(P2.0.2b/P2.0.2a) at T = 320 K. We found −1.7 kcal mol−1 in DFT/MM-MD water, −1.1 kcal mol−1 in DFT-MD water and −1.2 kcal mol−1 at the interface. - M. Bühl, N. Sieffert, A. Partouche, A. Chaumont and G. Wipff, Inorg. Chem., 2012, 51, 13396 CrossRef PubMed.
- V. Vallet and I. Grenthe, Solvent Extr. Ion Exch., 2013, 31, 358 CrossRef CAS.
- P. N. Pathak, L. B. Kumbhare and V. K. Manchanda, Solvent. Extr. Ion Exch., 2001, 19, 105 CrossRef CAS.
- Previous simulations of 2.0.2 complexes including the more hydrophobic “DEHiBA” ligands showed that the complexes are afforded at the interface and tend to spontaneously transfer to the bulk hexane phase. When at the interface, the solvation pattern of the 2.0.2 complexes with DEHiBA and with L are very similar: the amide groups sit “flat” on the water surface and the long alkyl chains are solubilized at the hexane side of the interface (see ref. 9a). As a result, our conclusions obtained with the simplified L ligand are expected to be transferable to real systems.
- A. Prestianni, L. Joubert, A. Chagnes, G. Cote and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 19371 RSC.
- A value of log10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β01 = 0.30 ± 0.15 has been estimated for the equilibrium constant in the aqueous system UO22+ + NO3− → UO2NO3+, see
(a)
I. Grenthe, J. Fuger, R. J. M. Konings, R. J. Lemire, A. B. Muller, C. Nguyen-trung and H. Wanner, in Chemical Thermodynamics Vol. 1: Chemical Thermodynamics of Uranium, ed. H. Wanner and I. Forest, Elsevier, Amsterdam, 1992 Search PubMed. Formation constants for uranyl dinitrate complexes are shown to be smaller than those for the mononitrate by roughly one order of magnitude; for results from an extraction-based method see:
(b) H. Lahr and W. Knoch, Radiochim. Acta, 1970, 13, 1 CrossRef CAS; for results from a 1H NMR spectroscopic study in water–acetone mixtures see:
(c) A. Fratiello, V. Kubo, R. E. Lee and R. E. Schuster, J. Phys. Chem., 1970, 74, 3726 CrossRef CAS.
β01 = 0.30 ± 0.15 has been estimated for the equilibrium constant in the aqueous system UO22+ + NO3− → UO2NO3+, see
(a)
I. Grenthe, J. Fuger, R. J. M. Konings, R. J. Lemire, A. B. Muller, C. Nguyen-trung and H. Wanner, in Chemical Thermodynamics Vol. 1: Chemical Thermodynamics of Uranium, ed. H. Wanner and I. Forest, Elsevier, Amsterdam, 1992 Search PubMed. Formation constants for uranyl dinitrate complexes are shown to be smaller than those for the mononitrate by roughly one order of magnitude; for results from an extraction-based method see:
(b) H. Lahr and W. Knoch, Radiochim. Acta, 1970, 13, 1 CrossRef CAS; for results from a 1H NMR spectroscopic study in water–acetone mixtures see:
(c) A. Fratiello, V. Kubo, R. E. Lee and R. E. Schuster, J. Phys. Chem., 1970, 74, 3726 CrossRef CAS. - S. de Houwer and C. Gorller-Walrand, J. Alloys Compd., 2001, 323, 683 CrossRef.
- X. Ye, R. B. Smith, S. Cui, V. deAlmeida and B. Khomami, Solvent Extr. Ion Exch., 2010, 28, 1 CrossRef CAS.
- Recent classical MD simulations indeed indicate a driving force for the approach of 2.2.0 to the hexane/water interface in the presence of TBP (see Fig. 10 in ref. 9b).
- See e.g.: (a) Y. Zhao and D. G. Truhlar, Org. Lett., 2007, 9, 1967 CrossRef CAS PubMed; (b) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 324 CrossRef CAS; (c) N. Sieffert and M. Bühl, Inorg. Chem., 2009, 48, 4622 CrossRef CAS PubMed; (d) Y. Minenkov, G. Occhipinti and V. R. Jensen, J. Phys. Chem. A, 2009, 113, 11833 CrossRef CAS PubMed.
- For comparisons of density functionals to model actinyl complexes, see e.g. (a) J. P. Austin, N. A. Burton, I. H. Hillier, M. Sundararajan and M. A. Vincent, Phys. Chem. Chem. Phys., 2009, 11, 1143 RSC; (b) F. P. Rotzinger, Chem. – Eur. J., 2007, 13, 800 CrossRef CAS PubMed; (c) M. Bühl and G. Schreckenbach, Inorg. Chem., 2010, 49, 3821 CrossRef PubMed; (d) See also ref. 67.
- The free energy of hydration of NO3− “in SMD-water” can be estimated as: ΔG°hyd(NO3−) = ESMD-water − Egas = −61.3 kcal mol−1 at the M06-2X/SDD+ level. This should be compared with the experimental value of −73.2 kcal mol−1 reported in: Y. Marcus, Ion Solvation, Wiley-Interscience, Chichester, U.K., 1985 CrossRef CAS PubMed. This result correlates with a tendency of the SMD model to undersolvate anions (see ref. 24), a feature that can lead to overestimated equilibrium constants compared to the experiment. For instance, the calculated free energy of reaction for 0.5.0 + 2NO3− → 2.2.0 + 3H2O appears unreasonably large (−11.5 kcal mol−1), presumably because the two nitrates are undersolvated in our SMD model. However, under extraction conditions, the aqueous phase contains a large amount of nitric acid (at ca. 3 M) in such a way that 2.2.0 should still be significantly populated. As a result, the path-2 depicted in Fig. 6 should be realistic. We also note that modelling the free energy of hydration of uranyl–hydrate complexes (such as 0.5.0) by implicit solvation models is also particularly challenging, as shown e.g. in: K. E. Gutowski and D. A. Dixon, J. Phys. Chem. A, 2006, 110, 8840 CrossRef CAS PubMed , and ideally requires the addition of several second-shell water molecules. All these issues justify the use of more elaborate approaches, such as the DFT/MM-MD and DFT-MD simulations undertaken herein, in which the presence of the solvent and the dynamics of the systems are explicitly accounted for.
- M. Bühl, N. Sieffert and G. Wipff, Dalton Trans., 2014, 43, 11129 RSC.
- (a) I. Benjamin, J. Phys. Chem. B, 2013, 117, 4325 CrossRef CAS PubMed; (b) A. G. Volkov, D. W. Deamer, D. L. Tanelian and V. S. Markin, Liquid Interfaces in Chemistry and Biology, John Wiley & Sons, Inc., New York, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Atomic charges on L (Table S1), reaction free energies at the BLYP-D3/SDD+ and M06-2X/SDD+ levels (Table S2), time of evolution of the collective variable in metadynamics simulations (Fig. S1), additional free energy surfaces obtained from longer metadynamics simulations (Fig. S2 and S3) and Cartesian coordinates of all complexes optimized at the BLYP-D3/SDD level. See DOI: 10.1039/c4dt02443e |
| This journal is © The Royal Society of Chemistry 2015 |