Open Access Article
Open Access ArticleUsing structural diversity to tune the catalytic performance of Pt nanoparticle ensembles
Hector
Barron
and
Amanda S.
Barnard
*
CSIRO Virtual Nanoscience Laboratory, 343 Royal Parade, Parkville, Victoria 3052, Australia. E-mail: amanda.barnard@csiro.au; Tel: +61 3 9662 7356
First published on 23rd March 2015
Abstract
Recent developments of metallic nanoparticle catalysts have been largely based on the assumption and evidence that exquisite control over the size or shape (or both) is critically important to the economic efficiency of future products. However, the cost associated with reducing polydispersivity on the industrial scale is also a limiting factor, and at this stage it is unclear if samples that are monodispersed in size or shape are more desirable. In this study we use a combination of thermodynamic and statistical models to explore how restricting different types of structural polydispersivity impacts the performance of platinum electrocatalysts, characterized by the molar density of surface defects, and their respective degree of under-coordination. We find that a combination of simultaneous size and shape control is advantageous, but attention and resources should be directed toward producing shape control. More specifically, a sample containing particles entirely enclosed by {111} facets, regardless of the geometric shape, will always outperform samples where other crystallographic facets are present; but perfect monodispersivity is unnecessary. Distributions in both size and shape are acceptable (and can even be useful), provided they are predictable and reproducible.
1. Introduction
The size, shape, and morphology control of nanostructures has become a central priority in nanoparticles production, principally due to the tunability of their physical and chemical properties,1–4 and the promise of applications in catalysis, sensors, photochemistry, optoelectronics.5–7 Catalysis is arguably the most important area where this topic prevails, since it has been shown that structures with controlled size and shape, characterized by specific surface areas and crystallographic facets, can be used to tune the selectivity and reactivity of many major catalytic reactions.8,9 In particular, platinum and palladium are ideal for numerous catalytic reactions,10 such as hydrogenation and dehydrogenation,11 and CO oxidation in catalytic convertors.12The predominant mechanism for the full electroreduction of oxygen to water (the oxygen reduction reaction, ORR, which is critical to the efficiency of fuel cells13 and metal–air batteries14,15) involves an adsorbed hydrogen peroxide intermediate that may convert and adsorb as H2O2, before undergoing further reduction. The formation of hydrogen peroxide is undesired as it reduces the effective cathodic current, contaminates the surroundings of the catalyst, and corrodes the polymer membrane present in fuel cells. Platinum is the superior monometallic electrode material for the ORR because the oxygen–oxygen bond can be efficiently broken on platinum surfaces, with relatively little interference from the formation of an irreversible oxide. Likewise, the hydrogen oxidation reaction (HOR, which consumes fuel in fuel cells) and the hydrogen evolution reaction (HER, which produce hydrogens via cathodic reaction in electrolyzers) are both characterized by extremely fast kinetics on platinum electrodes16 with almost perfect reversibility. Platinum is key to the development of fuel cells and batteries, electrolyzers, and electrosynthetic methods, as well as electrochemical sensing systems, provided the particles are decorated with Miller index facets that improve the catalytic activity, and a high density of atomic edges, steps, and kinks that serve as the active sites for bond breaking and bond making.
While significant achievements in the size-controlled synthesis of quasi-spherical nanostructures have been recently made,17–26 the formation of non-spherical nanostructures with precise shape control is still very challenging.27–30 Among the new techniques under development around the world, solution-phase methods have emerged as a highly versatile synthesis to control the size and the shape of nanoparticles of different materials.31–34 Solution-phase synthesis of platinum nanoparticles consists in the reduction and decomposition of a metal precursor in the presence of a surfactant.35–41 A variation in the type and concentration of the precursor as well as the reducing agent and stabilizer with temperature and time, leads to the formation of different shapes and sizes. Other variables that also influence the final shape and growth stages is the introduction of seeds or foreign species42 and the introduction of twin planes.43,44
The investment in this area has been largely driven by both assumption and evidence that exquisite control (of both size and shape, or size or shape) is central to future technology advancements.45 For example, reliable performance in many applications requires consistent properties, which are only possible when samples are monodispersed.2,17,46–48 However, most samples are not perfectly monodispersed, and contain distributions of sizes and mixtures of shapes;49,50 many of which are very difficult to distinguish when the particles are small. At this stage it is unclear if future efforts should strive for samples that are monodispersed in size, shape, or both.
Based on these recent studies it is easy to see that a better understanding of how this persistent polydispersivity impacts the performance of platinum electrocatalysts will aid in development. This can be done in a straightforward manner using a large and diverse virtual sample of platinum nanoparticles, where it is a simple matter to accurately determine the density of under-coordinated surface atoms that activate the reactions. This includes the atoms located at surfaces, edges and corners; the coordination of which varies depending on the crystallographic orientation of each surface feature. Once the density of active sites is known for a large statistical ensemble of morphologies, we can combine this with the size-, shape- and temperature-dependent probability of observation, and explore how restricting the diversity of the ensemble improves or degrades the molar density of active sizes; to enhance or retard the efficiency of different reactions, as a measure of catalytic performance.
2. Methods
While it is possible to generate a virtual samples containing a large set of individual structures (that contain considerable variety of shapes and sizes) and study metal nanoparticle ensembles using explicit computer simulations, this represents a very large undertaking, and considerable time and resources will be spent describing structures that have a very low probability of observation; contributing little to the properties of the ensemble. It is more efficient to use an analytical model to generate the sample, rather than to attempt to simulate thousands of individual nanoparticles.Previously it has been established that a phenomenological nanomorphology model, designed to compare the thermodynamic stability of isolated (unsupported) nanoparticles,51 is ideally suited to this task. The model used here provides the geometric summation of the Gibbs free energy with contributions from the particle bulk and surfaces:
 | (1) |
 , and
, and  (to be consistent with the Laplace–Young formalism). While it has been shown in previous works that the contributions to the free energy from the edges and corners are minor, and that (over this critical size) they do not drive the formation of alterative shapes, they are important to the catalytic activity and are included explicitly in the proceeding analysis.
(to be consistent with the Laplace–Young formalism). While it has been shown in previous works that the contributions to the free energy from the edges and corners are minor, and that (over this critical size) they do not drive the formation of alterative shapes, they are important to the catalytic activity and are included explicitly in the proceeding analysis.
The temperature-dependent free energy ΔG(T) may be determined by parameterizing with γi(T) and σi(T). This may be done using any suitable computational method, such as density functional theory (DFT),52,53 provided that it is used consistently (to avoid uncertainties associated with the mixing methods) and has sufficient accuracy to distinguish between different facets and provide the right energetic ordering. A detailed account of this model, with a parameterization for platinum, is provided elsewhere.52 From experiment, it is usually known that defects, such as edges and corners, make up the majority of the active sites for catalysis, and that the activity of an atomic site is related to the inter-atomic coordination number of the site. A 3-fold coordinated corner atom has a different activity to a 9-fold coordinated surface atom, and will be instrumental in different reactions.
Once parameterized, the models above can be used to compare the relative stability of each shape (n), and predict their probability of observation (p) as a function of T.54 The latter can be easily obtained using a Boltzmann distribution:
| p(n) = e−Gn(T)β | (2) |
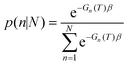 | (3) |
Using the size- and shape-dependent relative stability Gn(T) we can compute the probabilities pn∀n ∈ N, and then determine the populations for a range of equilibrium and non-equilibrium (metastable) geometries. Irrespective of the sizes and shapes included in the ensemble, the populations for non-equilibrium shapes are always non-zero at finite temperatures, though they are, of course, low for the least stable morphologies. The ensemble average of the density of different classes of active sites (Xc) can then be computed for any ensemble containing N particles using:
 | (4) |
where xc,n is the density of active sites of class c, on a given particle n.
Our classification scheme is based on the degree of under-coordination of each surface atoms, and the similarity with respect to known surface features that share characteristics. These classes include: surface defects, which include all adatoms in configurations (“top”, “bridge” and “hollow”) where the Pt-coordination number can be 1, 2 or 3; surface microstructures, which include surface “kinks” and “steps”, where the Pt coordination number can be 4, 5, 6 or 7; and surface facets, which include planar configurations (in any hkl orientation) where the Pt coordination number can be 8, 9, 10 or 11. The coordination number of Pt atom in the bulk is 12. In each case the individual values of xc,n have been estimated using a linear fit to the exact number of under-coordinated sites of a range of explicit structures with between 300 and 6600 atoms. As we will see, these classification become useful when we relate the results to different types of catalytic reactions.
Note that while there is some evidence for metals such as palladium55–57 that the efficiency of these different classes of surface features may vary with the over all size of the particle, due to some predicted size-dependence of the density of electronic states,58 the present study does not include this phenomenon. The reason for this is 3-fold; firstly, as it only pertains to structures that are below the size range considered here; secondly, that it is a simple matter for Readers to include this effects as a size-dependent weighting function to the final results; and finally, we are dealing with distributions of sizes (and shapes), rather than comparisons between individual particles, and minor variations in the size-dependent activity of specific types of surface structures will be indistinguishable. Explicitly inclusion of the size-dependent shift in the electronic states is only relevant when considering individual nanoparticles, or perfectly monodispersed samples, which we are not.
3. Results and discussion
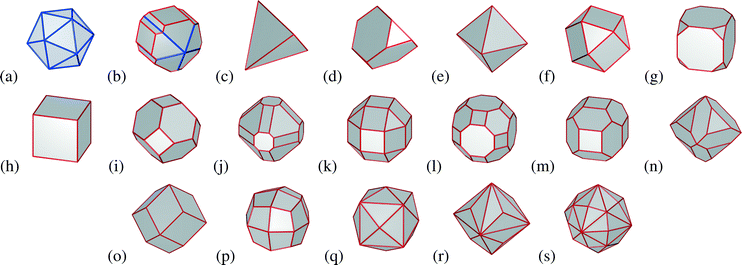
In this study a virtual sample of 3705 nanoparticles from 5 nm to 55 nm in average diameter has been developed theoretically, including a range of facetted and quasi-spherical morphologies, with unique geometric shapes. These include the icosahedron, Marks decahedron, tetrahedron, truncated tetrahedron, octahedron, cuboctahedron, truncated cube, cube, truncated octahedron, doubly-truncated octahedron, small rhombicuboctahedron, great rhombicuboctahedron, rhombi-truncated cube, rhombi-truncated octahedron, rhombic dodecahedron, trapezohedron, tetrahexahedron, trisoctahedron and the hexoctahedron; as shown in Fig. 1. This virtual sample is an ensemble, because every one of the 3705 particles is unique. The size range chosen here extends beyond the range that is typically targeted by researchers (usually under 10 nm in size59) but is sufficiently large to cover the range of sizes present in industrial samples60 (where value is place on cost reduction, as opposed to efficiency gains and monodispersivity). It is also sufficiently large to capture the impact of more complex nanoparticle shapes that are typically produced at the upper end of this size range.61–65 As we will see however, the properties are still dominated by the small nanoparticles, and the inclusion of large particles does nothing more than establish a more commercially relevant frame of reference. Choosing a different frame of reference would shift numerical results, but not alter the general trends.Computationally many studies have been carried out on metallic nanoparticles in order to find energetically stable structures using different approaches. The energetic stability of platinum clusters has been addressed by different studies,66–69 finding icosahedral structures are stable at small sizes, followed by decahedral and truncated octahedral structural motifs as the size increases. This is consistent with the relevant regions of the phase diagram of platinum at low temperatures,52 as well as the statistical probabilities of observations predicted using consistent methods.54
This is not to say, however, that other shapes may not be present. A mixture of different species is commonly present following solution-phase synthesis, based on the precursor,28,39,70–75 solvent, stabilizer and reducing agent,28,39,76–78 or the foreign ions70,79–82 and seeds.83 In addition to this reaction temperatures may affect the decomposition or reduction rate of the metal precursor, as well as moderating the growth kinetics by shifting the equilibrium established between the different species that co-exist in the solution. By varying the reaction temperature, different morphologies of platinum nanoparticles have been reported.79,84–86 For example, truncated cubic and cubic morphologies could be obtained at temperatures of 180 °C, 160 °C and 120 °C.79
Given that platinum nanoparticles can have a range of morphologies (some deliberatively encouraged, and others appearing adventurously) regardless of how carefully they are prepared, it is more realistic to model distributions and mixtures of particles, than to assume all samples are adequately represented by the ground state structure. Attempts to improve the degree of monodispersivity can be costly, and may not be amenable to industrial level production, so in addition to this it is highly desirable to ascertain how detrimental persistent polydispersivity is to performance, and whether perfect monodispersivity is as advantageous as has previously been assumed.
Using our virtual sample of 3705 particles, the relative stability, density of active sites, and the Boltzmann population at 160 °C was calculated as described above. Setting aside for a moment the classification of surface sites, we can first predict the total number of under-coordinated surface atoms for each structure, and obtain an ensemble average of 196.9 sites per mmol, where polydispersivity is entirely unrestricted (in both size and shape). This is a crude measure of performance, but we can see that it changes very little with temperature, as shown in Fig. 2, though the additive contribution from particles of different sizes varies. In Fig. 3 we can see a histogram of the change in performance (relative to the entire ensemble) if sub-samples of particles were extracted with near perfect monodispersivity in size, but retaining the natural polydispersivity in shape. In this figure the difference in size is equivalent to one atomic layer, and we can see that for each class of surface site a clear trend emerges. There is a significant advantage in growing or selecting small sizes (as we would expect), but this advantage depends on what type of feature one seeks to promote. The relative increase in the number of surface defects sites is extreme (see Fig. 3a); over 2000% increase if we were to extract only 5 nm particles from the 5–55 nm distribution. Over ~20.3 nm the millimolar fraction of surface defects sites decreases, and we would be better off retaining the unrestricted distribution. A similar trend is observed for the surface facet sites (Fig. 3c), though the maximum increase (29.8% for 5 nm monodispersed samples) is significantly less, and threshold is slightly higher (~28.3 nm).
 | ||
| Fig. 2 Ensemble average of the number of under-coordinated surface sites per millimolar volume as a function of temperature, for an ensemble of 3705 particles between 5 nm to 55 nm in size, and with the shapes displayed in Fig. 1 (with each structure weighted by the size- and shape-dependent probability of observation). | ||
 | ||
| Fig. 3 The performance change, in %, attributed to the number of surface defect sites, surface microstructure sites, and surface facet sites, relative to the entire unrestricted ensemble. The results are predicted for samples of platinum nanoparticle catalysts that are perfectly monodispersed in size, with a resolution of one atomic layer, but with the natural mixture of the shapes displayed in Fig. 1 (with each structure weighted by the size- and shape-dependent probability of observation). Note the dramatically different scale in the case of surface defects, characterized by adatoms in “top”, “bridge” and “hollow” configurations. | ||
The results for the surface microstructure sites, however, are different (Fig. 3b). If we were to extract monodispersed samples of small nanoparticles we would expect to see an increase in performance (relative to the entire ensemble), due to the larger surface-to-volume ratio. This supports the reasons why researchers target these sizes. However, we also see an increase in performance (relative to the unrestricted sample) if we extract the larger particles as well, due to the larger overall surface area. In contrast, particles between ~8.6 nm and ~33.7 nm are predicted to have fewer surface microstructure sites per mmol, and an unrestricted polydispersed sample will likely perform better than a monodispersed sample in this range.
This is hugely significant, since it has been clearly demonstrated in the literature that surface defects are important in the second stage of CO oxidation reactions, where it has been shown than CO oxidation initiated at step on (111) facets rapidly diffuse to adatom sites where the atomic coordination numbers are 1, 2 or 3.87,88 Surface microstructures are important in the first stage of CO reactions,87,88 and oxygen reduction reactions (ORR), since electrolyte anions adsorb more strongly on steps and kinks with coordination numbers of 4, 5 and 6, where oxygen–oxygen bonds can be more readily broken.88 Surface facets, in turn are responsible for H oxidation (HOR) and evolution (HER) reactions, with the desorption/adsorption of hydrogen increasing on surfaces with atoms with coordination numbers of 7, 8 and 9.89
While this prediction is instructive, it is not particularly practical, since achieving this degree of monodispersivity is still beyond most experimental capabilities. In Table 1 we can see the performance change that could be achieved if a range of smaller size distributions were made or extracted (while retaining the natural mixture of shapes). Here we can see that, relative to the entire unrestricted ensemble of shapes between 5–55 nm, it is possible to achieve a significant increase in performance while still tolerating a reasonable size distribution. Irrespective of the class of surface site that is required, we can see that targeting a smaller distribution between 5 nm to 10 nm will still yield a measurable improvement. The surface defects site and surface facet sites decrease logarithmical with the expanding size distribution, and the surface microstructures exhibit a polynomial relationship to the size distribution (for the reasons mentioned above).
| Shape | Surface defects | Surface microstructures | Surface facets |
|---|---|---|---|
| 5–10 nm | +631.81 | +2.80 | +12.63 |
| 5–15 nm | +272.20 | −0.56 | +7.26 |
| 5–20 nm | +139.02 | −1.17 | +4.64 |
| 5–25 nm | +81.51 | −1.14 | +3.21 |
| 5–30 nm | +49.05 | −0.95 | +2.22 |
| 5–35 nm | +30.70 | −0.74 | +1.54 |
| 5–40 nm | +18.78 | −0.53 | +1.03 |
| 5–45 nm | +10.23 | −0.33 | +0.61 |
| 5–50 nm | +4.47 | −0.16 | +0.28 |
| 5–55 nm | 0.00 | 0.00 | 0.00 |
Rather than attempting to restrict or segregate the particle sizes, an alternative way of improving the performance of platinum nanocatalysts is to control the shape. If we modify the mixture of shapes in the virtual sample, targeting specific morphologies instead of restricting the size distribution of the ensemble, then we can also predict ways to improve performance. Taking a coarse-grained approach we could target simple polyhedra (Platonic and Archimedean solids) over more complex polyhedra (zonohedrons) that appear quasi-spherical. In this case we find that the simple polyhedra, decorated with distinct edges and corners, may increase in density of surface facets sites over the unrestricted mixture; while the quasi-spherical particles will increase the density of surface defects and surface microstructures (see Table 2). This is because there are a greater number of edges and corners on the quasi-spherical particles and even the atoms of the high-index facets tend to have a lower coordination number (being more step-like or kink-like).
| Surface defects | Surface microstructures | Surface facets | |
|---|---|---|---|
| Coarse-grained | |||
| Simple polyhedra | −58.82 | −13.25 | +18.4 |
| Quasi-spherical | +71.24 | +9.88 | −22.42 |
| Fine-grained | |||
| (111)-Enriched | +631.81 | +2.80 | +12.63 |
| (100)-Enriched | +272.20 | −0.56 | +7.26 |
| (110)-Enriched | +81.51 | −1.14 | +3.21 |
| Edge-enriched | +49.05 | −0.95 | +2.22 |
If we take a more fine-grained approach we may begin to ask which types of shapes are most suitable for different reactions, and how monodispersed do the samples need to be? By creating some more restrictive ensembles we find that shapes with >50% {111} surface are the ones responsible for the enhancement of surface facets sites that are useful for HER and HOR reactions. In contrast, the shapes >50% {110} surface area provide a greater density of surface microstructure sites for ORR reactions (more than 64% over the mixed ensemble). Surface defects sites are enriched if we targeting shapes with a high edge-to-volume ratio, such as a trapezohedron, tetrahexahedron, hexaoctahedron, trisoctahedron or icosahedron. This is also reflected in the performance changes for perfectly shape-selected samples (see Table 3); assuming that this degree of shape control were possible.
| Shape | Surface defects | Surface microstructures | Surface facets | Fig. |
|---|---|---|---|---|
| Icosahedron | −100.00 | −99.94 | +42.55 | 1(a) |
| Marks decahedron | −100.00 | −44.62 | +65.50 | 1(b) |
| Tetrahedron | +122.70 | −61.35 | +119.87 | 1(c) |
| Truncated tetrahedron | −100.00 | −67.81 | +75.25 | 1(d) |
| Octahedron | −100.00 | −56.59 | +60.55 | 1(e) |
| Cuboctahedron | −100.00 | −49.88 | +32.48 | 1(f) |
| Truncated cube | −100.00 | −63.04 | +47.19 | 1(g) |
| Cube | −100.00 | −73.81 | +60.28 | 1(h) |
| Truncated octahedron | −100.00 | −58.85 | +36.54 | 1(i) |
| Doubly-truncated octahedron | −100.00 | +50.37 | −22.07 | 1(j) |
| Small rhombicuboctahedron | −100.00 | +17.91 | −29.86 | 1(k) |
| Great rhombicuboctahedron | −100.00 | +13.72 | −33.87 | 1(l) |
| Rhombi-truncated cube | −0.34 | +49.38 | −67.67 | 1(m) |
| Rhombi-truncated octahedron | −100.00 | +100.96 | −91.07 | 1(n) |
| Rhombic dodecahedron | −5.44 | +158.58 | −100.00 | 1(o) |
| Trapezohedron | −100.00 | +96.84 | −92.07 | 1(p) |
| Tetrahexahedron | +1577.42 | +88.69 | −92.80 | 1(q) |
| Trisoctahedron | +42.28 | +41.74 | −21.44 | 1(r) |
| Hexoctahedron | −100.00 | +20.05 | −50.73 | 1(s) |
By comparing the results in Table 3 we can see that there is a delicate balance between the number of facets, edges and corners, the orientation of the facets, and the angle subtended at the edges and corners. Some facets, edges and corners have atoms with a lower degree of under-coordination than others. The un-twinned shapes that have exclusively {111} facets (the tetrahedron, truncated tetrahedron and octahedron) all show a marked increase in surface facets sites; the shapes that have structurally very similar the rhombic dodecahedron (rhombic dodecahedron, rhombi-hexahedron, rhombi-octahedron, trapezohedron and trisoctahedron) show an increase in surface microstructure sites; and the tetrahedron and tetrahexahedron significantly increase the density of surface defects sites—even when we make no attempt to control the size.
The culmination of this systematic investigation, is the combination of simultaneous size and shape control. We have shown that, depending on the type of surface structure that are required (with particular reactions in mind), targeting some generalized morphologies and a range of sizes distributed between 5 nm to 10 nm are both advantageous. Combining this knowledge we now find that a 5–10 nm {111}-rich sample of tetrahedra, truncated tetrahedra and octahedra is predicted to offer +90.53% more surface facet sites than the polydispersed sample. Similarly, a 5–10 nm sample of rhombic dodecahedron-like shapes (rhombic dodecahedron, rhombi-hexahedron, rhombi-octahedron, trapezohedron and trisoctahedron) is predicted to provide +87.73% more surface microstructure sites than the polydispersed sample. And finally, a 5–10 nm sample of tetrahedra and tetrahexahedra is predicted to exhibit a staggering 4594% more surface defect sites than the polydispersed sample. In each case, one could argue that this increase in performance is certainly worth the investment, particularly given that a significant degree of polydispersivity is still permitted.
At this point it is prudent to remind Readers that the results use Boltzmann distributions, based on the relative stability of the individual structures in the ensemble. If we were to use a different distribution, such as normal or Gaussian distribution, we would expect some differences in the numerical values. However, as we have reported relative changes in all cases (comparing only like-distributions) we would not expect the trends to be significantly different. This would be, of course, an interesting topic for further research.
Before concluding it is also worthwhile to briefly discuss what one may expect from particles smaller than 5 nm, which were deliberately excluded from this work. Particles in this size range are significantly more complicated than the idealized polyhedra included here, and often present as amorphous structures with significant geometric heterogeneity. An assumption inherent in the model used in this study is that the nanoparticles are symmetric, crystalline, and sufficiently large that their surface features can be related to those observed in the bulk. For these reasons it is better to undertake explicit computer simulations on a large ensemble of small platinum nanocatalysts (rather than building theoretical models), to ensure than this complexity is captured effectively. It would then be possible to undertake a similar statistical study, and compare smaller structures to the results presented herein.
4. Conclusions
Although it is well known that engineering the size or shape of electrocatalysts will enhance performance, a fact that is certainly supported by these results, the outcome of the comparisons presented here indicate that there is not one strategy that will suit all situations. Reducing the size of Pt nanocatalysts will increase the density of surface defect sites (such as adatoms in “top”, “bridge” and “hollow” configurations) and benefit CO oxidation reactions; irrespective of the shape. In contrast, the traditional approach of targeting morphologies with exclusively {111} facets will succeed in improving HER and HOR efficiency, regardless of the size. In the case of ORR reactions however, the promotion of more Surface Microstructure sites (such as “kinks” and “steps”) is more complicated, and will require trade-offs to be made in terms of size- and/or shape-selectivity. However, given the time and cost associated with controlling size, shape, and the degree of polydispersivity in both, it is reassuring to find that achieving perfect monodispersivity is unnecessary. Distributions in both size and shape are acceptable (and can even be useful), provided they are predictable and reproducible.Further work is currently underway to include defective particles with surface steps, corners and concave surfaces;90 with the ultimate objective of treating more sophisticated branched nanostructures.72
Acknowledgements
Computational resources for this project were supplied by the National Computing Infrastructure national facility under Mass Allocation Scheme, grant p00.References
- X. G. Peng, L. Manna, W. Yang, J. Wickham, E. Scher, A. Kadavanich and A. P. Alivisatos, Nature, 2000, 404, 59–61 CrossRef CAS PubMed.
- C. Burda, X. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025–1102 CrossRef CAS PubMed.
- J. R. Morones, J. L. Elechigeurra, A. Camacho, K. Holt, J. B. Kouri, J. T. Ramirez and M. J. Yacaman, Nanotechnology, 2005, 16, 2346–2453 CrossRef CAS PubMed.
- S. Berchmans, P. J. Thomas and C. N. R. Rao, J. Phys. Chem. B, 2002, 106, 4647–4651 CrossRef CAS.
- R. Narayanan and M. A. El-Sayed, J. Am. Chem. Soc., 2004, 126, 7194–7195 CrossRef CAS PubMed.
- N. L. Rosi and C. A. Mirkin, Chem. Rev., 2005, 105, 1547–1562 CrossRef CAS PubMed.
- L. M. Liz-Marzan and P. Mulvaney, New J. Chem., 1998, 22, 1285–1288 RSC.
- A. Wieckowski, E. R. Savinova and C. G. Vayenas, Catalysis and Electrocatalysis at Nanoparticle Surfaces, Marcel Dekker, Inc., New York, 2003 Search PubMed.
- M. S. Chen and D. W. Goodman, Catal. Today, 2006, 111, 22–33 CrossRef CAS PubMed.
- V. Mazumder, Y. Lee and S. Sun, Adv. Funct. Mater., 2010, 20, 1224–1231 CrossRef CAS.
- P. Kačer and L. Cerveny, Appl. Catal., A, 2002, 229, 193–216 CrossRef.
- R. Burch, Catal. Rev.: Sci. Eng., 2004, 46, 271–334 CAS.
- M. K. Debe, Nature, 2012, 486, 43–51 CrossRef CAS PubMed.
- G. Girishkumar, B. McCloskey, A. C. Luntz, S. Swanson and W. Wilcke, J. Phys. Chem. Lett., 2010, 1, 2193–2203 CrossRef CAS.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- S. Chen and A. Kucernak, J. Phys. Chem. B, 2004, 108, 13984–13994 CrossRef CAS.
- J. Park, J. Joo, S. G. Kwon, Y. Jang and T. Hyeon, Angew. Chem., Int. Ed., 2007, 46, 4630–4660 CrossRef CAS PubMed.
- S. I. Stoeva, B. L. V. Prasad, S. Uma, P. K. Stoimenov, V. Zaikovski, C. M. Sorensen and K. J. Klabunde, J. Phys. Chem. B, 2003, 107, 7441–7448 CrossRef CAS.
- V. Germain and M.-P. Pileni, Adv. Mater., 2005, 17, 1424–1429 CrossRef CAS.
- B. L. V. Prasad, S. I. Stoeva, C. M. Sorensen and K. J. Klabunde, Chem. Mater., 2003, 15, 935–942 CrossRef CAS.
- S. Stoeva, K. J. Klabunde, C. M. Sorensen and I. Dragieva, J. Am. Chem. Soc., 2002, 124, 2305–2311 CrossRef CAS PubMed.
- M. J. Hostetler, J. E. Wingate, C. J. Zhong, J. E. Harris, R. W. Vachet, M. R. Clark, J. D. Londono, S. J. Green, J. J. Stokes and G. D. Wignall, et al. , Langmuir, 1998, 14, 17–30 CrossRef CAS.
- D. Lee, R. L. Donkers, J. M. DeSimone and R. W. Murray, J. Am. Chem. Soc., 2003, 125, 1182–1183 CrossRef CAS PubMed.
- N. K. Chaki, P. Singh, C. V. Dharmadhikari and V. K. Pillai, Langmuir, 2004, 20, 10208–10217 CrossRef CAS PubMed.
- Z. Liu, S. Li, Y. Yang, Z. Hu, S. Peng, J. Liang and Y. Qian, New J. Chem., 2003, 27, 1748–1752 RSC.
- N. S. Ramgir, I. S. Mulla and V. K. Pillai, J. Phys. Chem. B, 2006, 110, 3995–4001 CrossRef CAS PubMed.
- L. Gou and C. J. Murphy, Chem. Mater., 2005, 17, 3668–3672 CrossRef CAS.
- B. Wiley, Y. Sun and Y. Xia, Acc. Chem. Res., 2007, 40, 1067–1076 CrossRef CAS PubMed.
- C. Xu, H. Wang, P. K. Shen and S. P. Jiang, Adv. Mater., 2007, 19, 4256–4259 CrossRef CAS.
- Y. Song, Y. Yang, C. J. Medforth, E. Pereira, A. K. Singh, H. Xu, Y. Jiang, C. J. Brinker, F. V. Swol and J. A. Shelnutt, J. Am. Chem. Soc., 2004, 126, 635–645 CrossRef CAS PubMed.
- V. F. Puntes, K. M. Krishnan and A. P. Alivisatos, Science, 2001, 291, 2115–2117 CrossRef CAS PubMed.
- J. Zhang and J. A. Fang, J. Am. Chem. Soc., 2009, 131, 18543–18547 CrossRef CAS PubMed.
- Y.-W. Jun, J.-H. Lee, J.-S. Choi and J. Cheon, J. Phys. Chem. B, 2005, 109, 14795–14806 CrossRef CAS PubMed.
- S. Kumar and T. Nann, Small, 2006, 2, 316–329 CrossRef CAS PubMed.
- T. Teranishi, M. Hosoe, T. Tanaka and M. Miyake, J. Phys. Chem. B, 1999, 103, 3818–3827 CrossRef CAS.
- Y. Xiong and Y. Xia, Adv. Mater., 2007, 19, 3385–3391 CrossRef CAS.
- T. S. Ahmandi, Z. L. Wang, T. C. Green, A. Henglein and M. A. El-Sayed, Science, 1996, 272, 1924–1926 Search PubMed.
- J. Chen, T. Herricks and Y. Xia, Angew. Chem., Int. Ed., 2005, 44, 2589–2592 CrossRef CAS PubMed.
- H. Lee, S. E. Habas, S. Kweskin, D. Butcher, G. A. Somorjai and P. Yang, Angew. Chem., Int. Ed., 2006, 45, 7824–7828 CrossRef CAS PubMed.
- S. W. Kim, J. Park, Y. Jang, Y. Chung, S. Hwang and T. Hyeon, Nano Lett., 2003, 3, 1289–1291 CrossRef CAS.
- V. Mazumder and S. Sun, J. Am. Chem. Soc., 2009, 131, 4588–4589 CrossRef CAS PubMed.
- E. E. Finney and R. G. Finke, J. Colloid Interface Sci., 2008, 317, 351–374 CrossRef CAS PubMed.
- J. L. Elechiguerra, J. Reyes-Gasga and M. José-Yacamán, J. Mater. Chem., 2006, 16, 3906–3919 RSC.
- S. Maksimuk, X. Teng and H. Yang, J. Phys. Chem. C, 2007, 111, 14312–14319 CAS.
- B. Zhang, D. Wang, Y. Hou, S. Yang, X. Hua Yang, J. Hua Zhong, J. Liu, H. Feng Wang, P. Hu and H. Jun Zhao, et al. , Sci. Rep., 2013, 3, 1836 Search PubMed.
- Y. Yin and A. P. Alivisatos, Nature, 2005, 437, 664–670 CrossRef CAS PubMed.
- A. C. Templeton, M. P. Wuelfing and R. W. Murray, Acc. Chem. Res., 2000, 33, 27–36 CrossRef CAS PubMed.
- C. B. Murray, C. R. Kagan and M. G. Bawendi, Annu. Rev. Mater. Sci., 2000, 30, 545–610 CrossRef CAS.
- M. Anand, M. C. McLeod, P. W. Bell and C. B. Roberts, J. Phys. Chem. B, 2005, 109, 22852–22859 CrossRef CAS PubMed.
- Y. Li, O. Zaluzhna and Y. J. Tong, Chem. Commun., 2011, 47, 6033–6035 RSC.
- A. S. Barnard, J. Phys. Chem. B, 2006, 110, 24498–24504 CrossRef CAS PubMed.
- A. S. Barnard, H. Konishi and H. Xu, Catal. Sci. Technol., 2011, 1, 1440–1488 CAS.
- A. S. Barnard, Catal. Sci. Technol., 2012, 2, 1485–1492 CAS.
- A. S. Barnard, Nanoscale, 2014, 8, 9985–9990 Search PubMed.
- I. V. Yudanov, M. Metzner, A. Genest and N. Rösch, J. Phys. Chem. C, 2008, 118, 20269–20275 Search PubMed.
- I. V. Yudanov, A. Genest and N. Rösch, J. Cluster Sci., 2011, 22, 433–448 CrossRef CAS PubMed.
- I. V. Yudanov, A. Genest, S. Schauermann, H.-J. Freund and N. Rösch, Nano Lett., 2012, 12, 2134–2139 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- S. Mostafa, F. Behafarid, J. R. Croy, L. K. Ono, L. Li, J. C. Yang, A. I. Frenkel and B. R. Cuenya, J. Am. Chem. Soc., 2010, 132, 15714–15719 CrossRef CAS PubMed.
- S. H. Joo, S. J. Choi, I. Oh, J. Kwak, Z. Liu, O. Terasaki and R. Ryoo, Nature, 2001, 412, 169–172 CrossRef CAS PubMed.
- Y. Li, Y. Jiang, M. Chen, H. Liao, R. Huang, Z. Zhou, N. Tian, S. Chen and S. Sun, Chem. Commun., 2012, 48, 9531–9533 RSC.
- N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Science, 2007, 316, 732–735 CrossRef CAS PubMed.
- Y. Ding, Y. Gao, Z. L. Wang, N. Tian, Z.-Y. Zhou and S.-G. Sun, Appl. Phys. Lett., 2007, 91, 121901 CrossRef PubMed.
- Z.-Y. Zhou, N. Tian, Z.-Z. Huang, D.-J. Chen and S.-G. Sun, Faraday Discuss., 2008, 140, 81–92 RSC.
- J. Xiao, S. Liu, N. Tian, Z.-Y. Zhou, H.-X. Liu, B.-B. Xu and S.-G. Sun, J. Am. Chem. Soc., 2013, 135, 18754–18757 CrossRef CAS PubMed.
- J. P. K. Doye and D. J. Wales, New J. Chem., 1998, 22, 733–744 RSC.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- C. Massen, T. V. Mortimer-Jones and R. L. Johnston, J. Chem. Soc., Dalton Trans., 2002, 4375–4388 RSC.
- A. Sebetci and Z. B. Güvenç, Surf. Sci., 2003, 525, 66–84 CrossRef CAS.
- X. Teng and H. Yang, Nano Lett., 2005, 5, 885–891 CrossRef CAS PubMed.
- Y. Piao, Y. Jang, M. Shokouhimehr, I. S. Lee and T. Hyeon, Small, 2007, 3, 255–260 CrossRef CAS PubMed.
- J. Ren and R. D. Tilley, Small, 2007, 3, 1508–1512 CrossRef CAS PubMed.
- J. Ren and R. D. Tilley, J. Am. Chem. Soc., 2007, 129, 3287–3291 CrossRef CAS PubMed.
- M. Nogami, R. Koike, R. Jalem, G. Kawamura, Y. Yang and Y. Sasaki, J. Phys. Chem. Lett., 2010, 1, 568–571 CrossRef CAS.
- S. I. Lim, I. Ojea-Jimenez, M. Varon, E. Casals, J. Arbiol and V. Puntes, Nano Lett., 2010, 10, 964–973 CrossRef CAS PubMed.
- S. Maksimuk, X. Teng and H. Yang, Phys. Chem. Chem. Phys., 2006, 8, 4660–4663 RSC.
- Y. Xiong, H. Cai, B. J. Wiley, J. Wang, M. J. Kim and Y. Xia, J. Am. Chem. Soc., 2007, 129, 3665–3675 CrossRef CAS PubMed.
- J. Watt, N. Young, S. Haigh, A. Kirkland and R. D. Tilley, Adv. Mater., 2009, 21, 2288–2293 CrossRef CAS.
- C. Wang, H. Daimon, O. Onodera, T. Koda and S. Sun, Angew. Chem., Int. Ed., 2008, 47, 3588–3591 CrossRef CAS PubMed.
- B. Lim, X. Lu, M. Jiang, P. H. C. Camargo, E. C. Cho, E. P. Lee and Y. Xia, Nano Lett., 2008, 8, 4043–4047 CrossRef CAS PubMed.
- H. Song, F. Kim, S. Connor, G. A. Somorjai and P. Yang, J. Phys. Chem. B, 2005, 109, 188–193 CrossRef CAS PubMed.
- C. Wang, H. Daimon, Y. Lee, J. Kim and S. Sun, J. Am. Chem. Soc., 2007, 129, 6974–6975 CrossRef CAS PubMed.
- H. Yu, P. C. Gibbons, K. F. Kelton and W. E. Buhro, J. Am. Chem. Soc., 2001, 123, 9198–9199 CrossRef CAS.
- C.-K. Tsung, J. N. Kuhn, W. Huang, C. Aliaga, L.-I. Hung, G. A. Somorjai and P. Yang, J. Am. Chem. Soc., 2009, 131, 5816–5822 CrossRef CAS PubMed.
- H.-T. Zhang, J. Ding and G.-M. Chow, Langmuir, 2008, 24, 375–378 CrossRef CAS PubMed.
- X. Zhong, Y. Feng, I. Lieberwirth and W. Knoll, Chem. Mater., 2006, 18, 2468–2471 CrossRef CAS.
- J. S. Spendelow, Q. Xu, J. D. Goodpaster, P. J. A. Kenis and A. Wieckowski, J. Electrochem. Soc., 2007, 154, F238–F242 CrossRef CAS PubMed.
- N. Tian, Z.-Y. Zhou and S.-G. Sun, J. Phys. Chem. C, 2008, 112, 19801–19817 CAS.
- Q.-S. Chen, F. J. Vidal-Iglesias, J. Solla-Gullón, S.-G. Sun and J. M. Feliu, Chem. Sci., 2012, 3, 136–147 RSC.
- A. S. Barnard and L. Y. Chang, ACS Catal., 2011, 1, 76–81 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |