Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Improving mass-transfer in controlled pore glasses as supports for the platinum-catalyzed aromatics hydrogenation†
M.
Goepel
a,
H.
Kabir
a,
C.
Küster
a,
E.
Saraçi
a,
P.
Zeigermann
b,
R.
Valiullin
b,
C.
Chmelik
b,
D.
Enke
a,
J.
Kärger
b and
R.
Gläser
*a
aInstitute of Chemical Technology, Universität Leipzig, Germany. E-mail: roger.glaeser@uni-leipzig.de
bInstitute of Experimental Physics I, Universität Leipzig, Germany
First published on 13th April 2015
Abstract
The liquid-phase hydrogenation of toluene and other alkyl substituted benzene derivatives with different critical diameters was investigated over Pt-catalysts supported on spherical controlled pore glasses (CPGs) as model supports at 373 K in the batch mode. The effect of mass-transfer within the catalyst pores was studied by varying the pore width (4, 10, and 80 nm) and average grain size (18–150 μm) of the Pt/CPG catalysts. For toluene hydrogenation, internal mass-transfer limitations were absent (effectiveness factor >90%) only for catalysts with particle sizes below 25 μm and pore widths ≤10 nm or with a pore width of 80 nm and particle sizes around 75 μm, respectively. Effective diffusion coefficients obtained from initial reaction rates via the Thiele concept, e.g., 2.8 × 10−10 m2 s−1 for toluene over the catalyst with 10 nm pore width, were an order of magnitude lower than when determined by PFG-NMR. This difference was explained in terms of transport resistances such as surface barriers affecting the diffusivity assessment via the Thiele concept, while PFG-NMR measures intraparticle diffusion only.
1 Introduction
Hydrogenation reactions play an important role in many industrial heterogeneously catalyzed reactions such as the removal of hetero atoms from crude oil fractions,1 the transformation of unsaturated to saturated (cyclic) hydrocarbons2,3 the defunctionalization of biomass,4 the reduction of carbonyl5 and nitro groups in organic subtrates6 as well as the production of pharmaceuticals, fine and bulk chemicals.7 Metal-catalyzed hydrogenation reactions are known to occur with high intrinsic reaction rates. Thus, the overall reaction rate is often limited by mass-transfer.8 Therefore, the improvement of solid hydrogenation catalysts often depends on an understanding of the mass-transfer processes with respect to the catalytic conversion.Generally, internal and external mass-transfer are distinguished. Internal mass-transfer refers to the transport of a reactant inside the catalyst pores. External mass transfer relates to reactant transport through the boundary layer around a catalyst particle, within the bulk phase surrounding the catalyst particles or across phase boundaries in multiphase reaction systems. Although a wealth of theoretical work was conducted in this field,9–11 systematic experimental catalytic investigations are less common. Most of the reported work was devoted to gas phase conversions,12 especially involving zeolite catalysts within which mass-transfer limitations may pose a crucial restriction for the reaction rates.13
In recent years, materials with hierarchically structured pore systems (often zeolite-based) generated interest due to their potential of overcoming mass-transfer limitations in heterogeneously catalyzed conversions.14–16 These materials are most attractive due to the combination of the zeolitic micropores, providing a high surface area, and the larger pores (typically mesopores, d = 2–50 nm) providing improved accessibility to the micropores containing the majority of the catalytically active sites. Thus, the mesopores mainly act to supply mass transfer routes within the catalyst particles resulting in an increased effectiveness factor. Several reports in this field attribute the higher catalytic activity to improved mass-transport in hierarchically structured pore systems.17–19 It is, however, noteworthy that experimental data on the mass-transport in these catalytic systems are rarely presented. Moreover, knowledge about the required pore width for unhindered mass-transfer in the larger (meso)pores is needed to arrive at a rational design of hierarchically structured catalysts.
Particularly few experimental work is available on mass-transfer limitations of liquid-phase conversions. This is surprising in view of their industrial relevance, especially of catalytic liquid-phase hydrogenations,20 on the one hand, and in view of the fact that mass-transfer limitations are generally more likely to occur because of reduced diffusion rates in liquid compared to gaseous reaction phases, on the other hand. Although mass-transfer limitations were observed for catalytic liquid-phase conversions,20–22 systematic experimental investigations on how to overcome them are scarce. Recently, Foley et al.23,24 conducted two studies on platinum supported on nanoporous carbon as a catalyst for the liquid-phase hydrogenation of different alkenes. Based on a study of the influence of mass-transfer, the catalyst design, i.e., grain size and porosity, was optimized to overcome internal mass-transfer limitations. However, in these carbon-based systems, the pore width cannot be readily adjusted. This results in broad or less-defined pore width distributions making correlations of mass-transfer behavior and pore width difficult.
In the present study, catalysts based on controlled pore glass (CPG) are presented as interesting alternative supports for metal-based hydrogenation catalysts. Controlled pore glasses are versatile catalyst support materials with tunable surface area, pore volume and narrow pore width distributions between 1–1000 nm.25 They were already successfully used as catalyst supports22,26 and are available as monoliths with different shapes including spheres.27 They are, thus, interesting model supports for mass-transfer investigations.
Consequently, the aim of this study was to systematically investigate the influence of pore width and grain size of CPG-supported noble metal catalysts on the initial reaction rate in the hydrogenation of alkylated benzene derivatives as a model hydrogenation reaction. In particular, the mass-transfer properties and, ultimately, the pore width needed for unhindered mass-transfer during noble metal-catalyzed liquid-phase hydrogenations were determined. Thus, CPG spheres with pore widths between 4 and 100 nm were applied as supports for platinum as the catalytically active hydrogenation component.
Furthermore, the effective diffusion coefficients Deff of the alkyl benzene reactants were determined from the effectiveness factor based on the Thiele concept. The thus obtained Deff values were, then, compared to an effective diffusion coefficient obtained by pulsed field gradient nuclear magnetic resonance (PFG-NMR) spectroscopy for a selected catalytic system. PFG-NMR is a well-established tool to directly measure effective diffusion coefficients,28–31 also applied for the selective measurement of the diffusivities of the individual components during catalytic reactions.32,33 However, studies conducted under conditions similar to those of catalytic experiments (temperatures ≥ 373 K) are rare.34 Thus, another aim of this study was to directly compare the diffusion coefficient obtained via PFG-NMR with the diffusion coefficient calculated using the Thiele concept applied to a catalytic conversion. This presents an attempt to experimentally verify the validity of the Thiele concept for determining effective diffusion coefficients under conditions of catalytic conversions.
2 Experimental section
2.1 Synthesis and characterization of the controlled pore glasses and supported Pt-catalysts
The spherical controlled pore glasses (CPGs) were synthesized according to the VYCOR-Process.25 Therefore, non-porous glass beads (Biosearch Inc. Steinach, grain sizes 100–200 μm) with a composition of 70 wt.-% SiO2, 23 wt.-% B2O3 and 7 wt.-% Na2O were used to prepare CPGs with average pore widths of 4 (CPG(4)) and 10 nm (CPG(10)), respectively. To obtain a CPG with an average pore width of 80 nm (CPG(80)), an initial glass with a different composition, i.e., 62 wt.-% SiO2, 30 wt.-% B2O3 and 7 wt.-% Na2O and 1 wt.-% Al2O3, was used. First, an annealing (heating rate 10 K min−1) was carried out for 24 h at different temperatures according to the desired pore widths, i.e., at 793 K for CPG(4), at 803 K for CPG(10), and at 863 K for CPG(80). Then, the solids were extracted, first with aqueous 3 N hydrochloric acid for 15 h at 363 K followed by treatment with an aqueous sodium hydroxide solution. While the extraction for CPG(4) and CPG(10) was carried out with 0.5 N sodium hydroxide solution for 1 h at room temperature, a three-step extraction was applied for CPG(80), i.e., first for 4 h with 0.6 N, then twice with 0.4 N sodium hydroxide solution at 303 K for 2 h, respectively.The CPG beads were loaded with platinum via electrostatic adsorption (EA). For that purpose, 10 g of the CPG beads were suspended in 50 cm3 deionized water. This suspension was kept at a pH of 10 via addition of 1 M aqueous ammonia solution (prepared using 32 wt.-% aqueous ammonia solution (≥30 wt.-% NH3 content, Merck)) for 2 h under stirring. Afterwards, an aqueous solution of 0.1 M Pt(NH3)4Cl2·2H2O (3.52 g Pt(NH3)4Cl2·2H2O (99.0 Ma.-%, ABCR) dissolved in 100 cm3 deionized water) was added dropwise under stirring. After stirring for an additional hour, the solid was separated by filtration and washed three times with 20 cm3 deionized water. The complete removal of excess Pt(NH3)4Cl2 from the support was proven by the absence of chloride ions in the washing water by addition of AgNO3-solution. Finally, the solid was dried at 353 K overnight under an air atmosphere and reduced at 623 K for 4 h in a stream of 20 vol.-% H2 in N2 (10 cm3 min−1). The resulting catalysts were labelled Pt/CPG(4), Pt/CPG(10), and Pt/CPG(80), respectively, according to their average pore width. For the investigation of internal mass-transfer, the catalyst beads of Pt/CPG(4) and Pt/CPG(10) were crushed and sieved to obtain the grain size fractions of 0–50 μm, 51–71 μm and 72–100 μm for Pt/CPG(4) and of 0–36 μm, 37–50 μm, 51–71 μm, 72–100 and 101–200 μm for Pt/CPG(10), respectively.
The characterization via N2-sorption was conducted at 77 K using a micromeritics ASAP 2010 (for the catalysts Pt/CPG(4) and Pt/CPG(10)) and a Quantachrome Autosorb iQ (for the catalyst Pt/CPG(80)). Hg-intrusion was carried out using a Thermo Scientific, Pascal 440 Series instrument. Elemental analysis was achieved via optical emission spectrometry with inductively coupled plasma (ICP-OES, after microwave-assisted digestion of the samples in a mixture of 2.0 cm3 HF (48%, Roth), 3.0 cm3 HNO3 (69%, Roth) and 3.0 cm3 HCl (35%, Roth)) using a Perkin Elmer Optima 8000 instrument. Scanning electron microscopy (SEM) images of the catalysts were recorded on an E-O-GmbH CamScan CS44. Transmission electron microscopy (TEM) images were taken on a Philips CM-200 with an acceleration voltage of 200 kV. The detection limit for Pt-crystallites of the TEM instrument used is about 1 nm. The catalyst density was determined using a micromeritics multivolume pycnometer 1305. X-ray powder diffraction (XRD) patterns were recorded on a Siemens D5000 diffractometer operating with Cu-Kα radiation (0.154 nm). The scanning range was 5–80° (2θ) using a step scan mode with the step of 0.05° (2θ). Hydrogen (Air Liquide, 99.999%) chemisorption experiments were conducted using a Quantachrome Autosorb iQ in the vacuum volumetric mode at 313 K. The isotherms for the dispersion calculation are given in the ESI,† Fig. S5 and S6.
2.2 Catalytic experiments
The catalytic hydrogenation of aromatics was carried out in the batch mode using a stainless steel autoclave (Berghof, BR-200, volume = 200 cm3, tetrafluoroethylene-coated) at 373 K, 1300 min−1 stirring speed and a static hydrogen pressure of 50 bar. As a reactant solution, a mixture of the aromatic (1.60 mol l−1) and n-octane (0.19 mol l−1, as internal standard for GC analysis, ≥98%, Sigma-Aldrich) dissolved in n-hexane (≥95%, VWR) was used. As aromatic reactants, toluene (≥99.5%, Sigma Aldrich), m-xylene (99%, Sigma-Aldrich), mesitylene (≥98.0, Merck Schuchardt) and 1,3,5-triisopropylbenzene (TIPB, 95% Sigma-Aldrich) were used without further purification. The catalysts were reduced prior to use in an H2/N2 flow as described above. A typical catalytic experiment was performed by heating up the reactant solution (75 cm3) and the suspended catalyst (150 mg) in the reaction autoclave up to 373 K. The reaction was, then, started by applying a static hydrogen pressure of 50 bar. Samples (0.5 cm3) were taken periodically from the liquid reaction mixture through a sampling tube and the catalyst was separated by filtration. The product composition was analyzed using a GC (Shimadzu, 14 A) equipped with an FID (separation column: Macherey-Nagel, Optima 5, length: 30 m, inner diameter: 0.25 mm, film thickness: 0.25 μm).The conversion of the aromatic reactants Xaromatic was calculated based on the aromatics concentration at time t (caromatic,t) and the initial aromatics concentration at time 0 (caromatic,0) using the equation
 | (1) |
The experimental accuracy of the conversion data is ±8% of the reported value. The carbon balance was closed within 98%. No coke formation or side products were observed.
2.3 Pulsed field gradient nuclear magnetic resonance measurements
For the pulsed field gradient nuclear magnetic resonance (PFG-NMR) experiments, a solution of 1.60 mol l−1 toluene dissolved in d-14 n-hexane (Merck Millipore, >99% deuterated) was added to the reduced Pt/CPG(10) in a glass ampule. The amount of the liquid (d-14 n-hexane and toluene) was chosen to provide complete filling with the capillary-condensed liquid of the mesopore space only. Therefore, an excess amount of the d-14 n-hexane–toluene mixture was added to Pt/CPG(10) into the glass ampule. The ampule was then shaken and left to equilibrate for 5 min. Afterwards, the excess solution was removed using a syringe. The interparticle space remained filled with the vapor phase. Thereafter, the glass tube was sealed keeping the bottom part of the tube containing the catalyst particles at liquid nitrogen temperature.The 1H diffusion measurements were performed with an NMR spectrometer operating at a proton resonance frequency of 400 MHz, equipped with a home-built pulsed field gradient unit with field gradient amplitudes up to 35 T m−1.35 This means that only toluene molecules were traced in the experiments. For minimizing disturbing effects due to internal field gradients and eddy currents, the 13-interval stimulated-echo pulse sequence with bipolar gradients was applied.36
Typical experimental parameters were δ = 400 μs for the gradient pulse width, 1.2 ms for the pulse separations within a pair of bipolar gradient pulses. The observation time, i.e., the separation td between the two gradient pulse pairs, was varied between 10 and 100 ms. The primarily measured spin-echo diffusion attenuation functions, which were obtained by varying the gradient strength g2 keeping all other parameters constant, were found to have exponential shape. In addition, when plotted versus (γδg)2td, where γ is the gyromagnetic ratio for protons, the echo attenuations were found to be independent of the observation time td. These two facts revealed that, in this way, no disturbing boundary effects were present during measurements and the genuine intraparticle diffusivities were measured.
3 Results and discussion
3.1 Pt catalysts supported on CPG beads
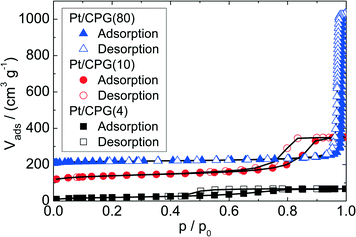
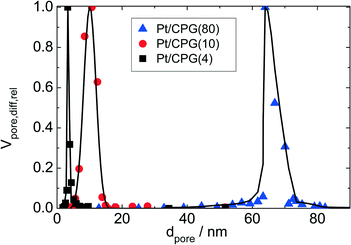
Three catalysts containing comparable Pt contents on controlled pore glasses (CPGs) were prepared. The three catalysts possess comparable specific surface areas, but different pore widths and, thus, different specific pore volumes as can be seen from the nitrogen sorption isotherms (Fig. 1). A relatively narrow pore width distribution with a maximum at 4 nm and 10 nm was found for the catalysts Pt/CPG(4) and Pt/CPG(10), respectively (Fig. 2). The pore width distribution of the catalyst Pt/CPG(80) as determined via Hg-intrusion is broader with a well pronounced maximum at ca. 80 nm (Fig. 3). The pore width maximum calculated from the nitrogen sorption isotherm is, however, somewhat lower, i.e., around 70 nm (Fig. 2). Inaccuracies of the pore size characterization of macroporous solids via nitrogen sorption are well known and are mostly attributed to the capillary condensation occurring close to the saturation pressure of nitrogen. To ensure comparability of the textural data obtained, Hg-intrusion measurements were also conducted on the catalysts Pt/CPG(4) and Pt/CPG(10) (ESI,† Fig. S1 and S2). The data obtained via Hg-intrusion agree reasonably well with those from N2-sorption. The textural properties of the catalysts are summarized in Table 1. The materials exhibit a spherical macroscopic shape with a narrow size distributions around 150–200 μm for the catalysts Pt/CPG(4) and Pt/CPG(10) and 50–100 μm for the catalyst Pt/CPG(80), respectively (Fig. 4).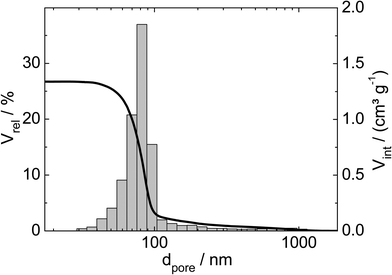 | ||
| Fig. 3 Relative volume (Vrel) and volume intruded (Vint) as a function of pore width (dpore) for the Hg-intrusion profile and pore width distribution histogram of Pt/CPG(80). | ||
 | ||
| Fig. 4 SEM-micrographs of the catalysts Pt/CPG(4) (top), Pt/CPG(10) (middle) and Pt/CPG(80) (bottom). | ||
Furthermore, all catalysts possess a similar Pt-loading of around 2.2 wt.-% (Table 1). No Pt reflections are observed in the XRD patterns for all catalysts investigated (ESI,† Fig. S3). Assuming a detection limit of 5 nm for XRD, a Pt dispersion of >25% is calculated.22,37 In addition, TEM analysis was conducted for the catalyst Pt/CPG(10) (SEM overview: ESI,† Fig. S4). However, no Pt particles can be detected by TEM. Considering the detection limit for Pt-crystallites of the TEM instrument used (ca. 1 nm), the Pt dispersion is >85% assuming ideally spherical particles.37 These findings are further supported by the results from hydrogen chemisorption for the catalysts Pt/CPG(10) and Pt/CPG(80) (for isotherms see ESI,† Fig. S5 and S6). Accordingly, a Pt dispersion of 91% and 87% was determined for Pt/CPG(10) and Pt/CPG(80), respectively. These values correspond to the same Pt dispersion within experimental accuracy of hydrogen chemisorption.
3.2 Toluene hydrogenation
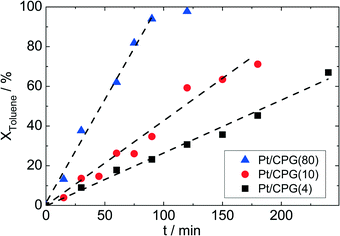
To investigate for possible mass-transfer limitations, the CPG-supported Pt catalysts were used in the liquid-phase hydrogenation of toluene. A clear correlation between the average pore width (dpore) and the conversion as a function of time can be seen for the three catalysts (Fig. 5). Thus, the catalyst with the largest average pore width (Pt/CPG(80)) shows the fastest toluene conversion. For the catalysts with the smaller pore widths, the toluene conversion is slower. As a measure for the catalyst performance in the hydrogenation reactions, the initial reaction rate, determined as the slope of the linear part of the dependence of conversion on time at the beginning of the experiments, was used. As the linear dependence of conversion over reaction time extends over the whole reaction duration studied (up to 200 min, or until complete conversion was reached), a deactivation of the catalyst during the experiment can be excluded. Since the Pt loading and dispersion are comparable, the higher initial reaction rate for the catalysts with larger pore widths (Pt/CPG(4): 0.032 mmol g−1 s−1, Pt/CPG(10) 0.060 mmol g−1 s−1 and Pt/CPG(80): 0.144 mmol g−1 s−1) is an indication for higher internal mass-transfer rates within the respective catalyst pore systems.The reaction rate for Pt/CPG(10) can be calculated on basis of the reaction rate of Pt/CPG(4) using the Thiele concept and assuming internal mass-transfer limitation and Knudsen diffusion (for detailed calculation see ESI†). This calculated reaction rate value for Pt/CPG(10) (0.051 mmol g−1 s−1) is in good agreement with the one determined experimentally (0.060 mmol g−1 s−1). Evidently, the assumption of mass-transfer limitation in case of Pt/CPG(4) and Pt/CPG(10) for the toluene hydrogenation is valid. Note, however, that Knudsen diffusion is usually related to mass-transfer in porous solids with a surrounding gas-phase. It apparently describes the diffusion under the liquid-phase conditions of the present reaction systems equally well.
The absence of external mass-transfer limitations, i.e., hindered mass-transfer of hydrogen from the gas into the liquid phase, inside the bulk liquid phase and from the liquid phase through the boundary layer to the outer catalyst surface, was investigated in a separate series of experiments varying the stirring speed (see ESI,† Fig. S7). At values above 600 min−1, the initial reaction rate of toluene was independent of the stirring rate proving the absence of external mass-transfer limitations. Consequently, all further conversions were carried out at a stirring speed of 1300 min−1 to exclude limitations by external mass transfer.
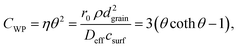 | (2) |
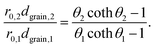 | (3) |
Note that the terms csurf, ρ, Deff cancel because they are assumed to be identical for two catalytic experiments under the same conditions. According to the literature,38 the Thiele modulus (with rint as the intrinsic, i.e., not mass-transfer limited reaction rate) can be defined as
 | (4) |
Thus, for the ratio of the Thiele moduli for the two experiments, we obtain
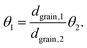 | (5) |
Substituting eqn (5) in eqn (3) results in
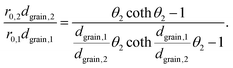 | (6) |
This equation can be numerically solved to obtain the Thiele modulus θ2. θ1 can then be calculated from eqn (5). The effectiveness factor η and the effective diffusion coefficient Deff are calculated using eqn (2) (ρ = 2.1 g cm−3).
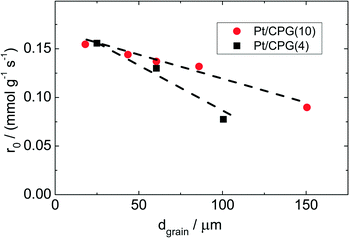
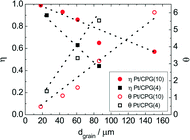
As Fig. 7 shows, an effectiveness factor of about 90% is reached for both catalysts Pt/CPG(4) and Pt/CPG(10), when the average grain size is below 25 μm. The differently strong influence of the mass-transfer limitation on the conversion over the catalysts Pt/CPG(4) and Pt/CPG(10) is indicated by the different slopes of the decrease of the effectiveness factor with average grain size. This decrease is more pronounced for Pt/CPG(4) than for Pt/CPG(10), consistent with the earlier conclusion drawn from the dependence of the initial reaction rate of average grain size (see Fig. 6). Consequently, the effective diffusion coefficients calculated for Pt/CPG(4) (Deff = 0.8 × 10−10 m2 s−1) is about three times lower than that of Pt/CPG(10) (Deff = 2.8 × 10−10 m2 s−1).
3.3 Hydrogenation of alkyl substituted benzene derivatives
As another important parameter of the mass-transport inside a pore network, the dimension (size) of the reactant molecule needs to be considered. Therefore, the catalytic hydrogenation of alkyl substituted benzene derivatives with different critical diameters dcrit was studied, i.e., methyl-benzene (toluene, dcrit = 0.67 nm39), 1,3-dimethylbenzene (m-xylene, dcrit = 0.74 nm39), 1,3,5-trimethylbenzene (mesitylene, dcrit = 0.82 nm40) and 1,3,5-triisopropylbenzene (TIPB, dcrit = 0.95 nm41) (reaction scheme: Fig. 8). The critical diameter dcrit is defined as the smallest cylindrical orifice through which a molecule can pass.42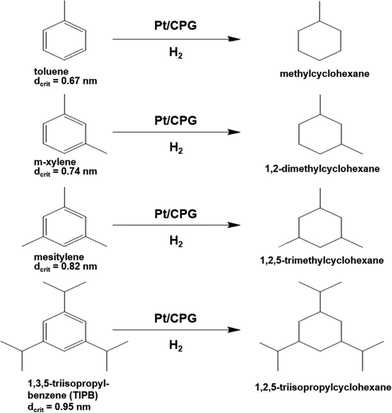 | ||
| Fig. 8 Reaction scheme for the hydrogenation of alkyl substituted benzenes over Pt supported on controlled pore glasses (Pt/CPG). | ||
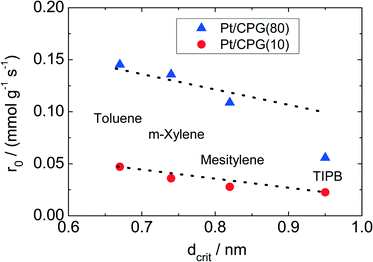
The results of the hydrogenation of these reactants using the catalysts Pt/CPG(10) and Pt/CPG(80) are displayed in Fig. 9. As already discussed above (cf.Fig. 5), the hydrogenation of toluene proceeds with an about three-fold higher initial reaction rate when using the catalyst with the larger average pore width of 80 nm (Pt/CPG(80)) instead of the one with 10 nm pore width (Pt/CPG(10)). This higher initial reaction rate was attributed to faster internal mass transfer within the Pt/CPG(80) catalyst compared to the catalyst Pt/CPG(10). Moreover, the initial reaction rate for toluene hydrogenation over Pt/CPG(80) is essentially the same as that for the catalysts with the smaller pore widths, i.e., Pt/CPG(10) and Pt/CPG(4), and an average grain size of 25 μm (Fig. 6, ca. 0.15 mmol g−1 s−1). This indicates that the reaction rate of toluene is not limited by internal mass transfer on Pt/CPG(80). As mentioned above, the similar reaction rates provide further evidence for a comparable local distribution of the Pt-particles inside the catalyst grains. Also for the other alkyl substituted benzenes, the initial reaction rate is generally higher by a factor of 2 to 4 over Pt/CPG(80) than over Pt/CPG(10). Note, however, that the pore width of both catalysts is larger by at least on order of magnitude than the critical molecule diameter of all reactants studied.
The decrease in initial reaction rate with increasing critical molecule diameter of the reactant is almost linear for both catalysts, with the initial rate for TIPB conversion over Pt/CPG(80) being the only exception. This clearly reflects the growing impact of mass transfer on the observed reaction rate with increasing critical molecule diameter. For toluene and m-xylene no, or only small mass-transfer limitations are expected. With increasing critical molecule diameter, the influence of mass transfer becomes more pronounced, severely limiting the initial reaction rate. Interestingly, the slopes for the linear decrease of the initial reaction rate with increasing critical molecule diameter is similar for both catalysts (Fig. 9). This indicates that the same mode of mass transfer takes place in the pores of both catalysts. It is, however, surprising that the slope is not steeper for the catalyst with the smaller pores (Pt/CPG(10)) which might be expected for stronger limitations of the mass transfer within the grains of this catalyst. A possible explanation for this finding is that the initial reaction rates for Pt/CPG(10) are closer to the threshold reaction rate for an effectiveness factor (η) → 0 corresponding to the conversion taking place at the outer surface of the catalyst only. Thus, the reaction rate is less strongly affected by slower mass-transport of the bulkier molecules.
When considering the decrease of the initial reaction rate of the alkyl substituted benzenes with increasing critical diameter of the reactant molecules, the intrinsic reaction rate needs to be taken into account. The adsorption of aromatics on noble metal surfaces is known to occur via π-bonding involving electron transfer from the aromatic ring to the unoccupied d-orbitals of the noble metal atoms.43 Since the π-electron density in aromatics increases with increasing degree of alkyl-substitution, the aromatic reactants are expected to bind more strongly. This was confirmed by Gallezot et al.44 for the adsorption of benzene and toluene on Pt(111) surfaces. Smith et al.45 observed similar reaction rates for the hydrogenation of toluene, m-xylene and mesitylene using a platinum catalysts under similar reaction conditions (liquid phase, solvent: acetic acid, aromatics concentration 0.2 mol l−1, 303 K). However, it is to be expected that a higher reaction rate results for more electron rich aromatics, i.e., with higher degree of alkylation. Thus, the decreasing reaction rates with increasing molecular diameter of the aromatic reactants as observed here (Fig. 8) are in line with an increasing mass-transfer limitation within the catalysts pores.
3.4 Pulsed field gradient nuclear magnetic resonance
For the catalyst Pt/CPG(10), the effective diffusion coefficient was determined using PFG-NMR at temperatures between 313 K and 373 K (Fig. 10). For 373 K, the temperature of the catalytic experiments (cf. above), the effective diffusion coefficient Deff determined via PFG-NMR amounts to 35 × 10−10 m2 s−1. This is about one order of magnitude larger than the effective diffusion coefficient calculated using the Thiele concept from the initial catalytic reaction rates (2.9 × 10−10 m2 s−1). The difference in Deff may be attributed to the fact, that the PFG-NMR measurement was, due to experimental reasons, not conducted under a static hydrogen pressure of 50 bar as applied in the catalytic experiments. Because of the low solubility of hydrogen in n-hexane,46 the static pressure of 50 bar mainly results in a compression and, thus, a density increase of the liquid n-hexane. However, the density of toluene increases only by 1% upon a pressure increase of 50 bar.47 In addition, toluene can be assumed to be a hard sphere fluid,48 the diffusivity and density of which are indirectly proportional. Thus, a tenfold decrease of Deff cannot be explained by the increased pressure.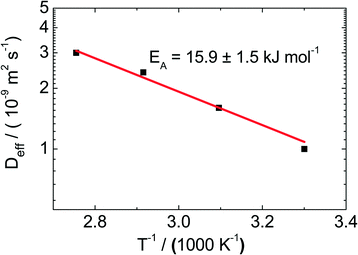 | ||
| Fig. 10 Effective diffusion coefficients (Deff) determined using PFG-NMR for the catalyst Pt/CPG(10) at temperatures (T) between 313 and 373 K. | ||
Consequently, the higher values of the effective diffusivities determined by PFG-NMR might be related to the existence of an additional transport resistance at the particle surface (“surface barriers”), giving rise to a finite surface permeability. The surface permeability is defined as the factor of proportionality between the flux through the surface and the concentration difference between actual concentration in the genuine pore space close to the surface and the pore space concentration in equilibrium with the bulk liquid-phase reactant concentration.49 The relevance of these surface permeabilities concerning mass-transfer processes was proven in different studies50,51 and was recently summarized in a review.49
When Deff is determined on the basis of the Thiele concept, it is assumed, that the deviation of the observed initial reaction rate from the intrinsic reaction rate is only based on the slower rate of mass-transfer through the pore system with respect to the reaction at the catalytically active sites. If, however, the surface permeability of the investigated system is low, i.e., if mass transfer through the surface (not the external boundary layer, cf. section 3.2 and ESI,† Fig. S7) is hindered, the observed reaction rate will also be decreased. The Thiele concept does not take into account surface permeabilities, and, thus, the decrease in the initial reaction rate observed is only attributed to a slower mass-transfer inside the pore system. This results in an underestimation of the diffusion coefficient. However, in PFG-NMR, the experimental conditions (observation time and grain size) are chosen so that the diffusion of the molecules of interest are only observed within the pore system and not entering or leaving the pore system. As a consequence, the Deff determined by PFG-NMR will not be falsified by surface permeability effects. It can furthermore be concluded that, although the Thiele modulus can be applied to obtain an estimate of Deff, even if the surface permeability of an investigated catalyst is low, the Deff calculated using the Thiele concept will always be lower than the real value.
4 Conclusions
Mass-transfer effects in liquid-phase hydrogenation reactions of alkyl substituted aromatics were investigated over Pt catalysts supported on controlled pore glasses (CPGs) as suitable model supports. These supports are available as monoliths with adjustable pore widths in the range of 1–1000 nm. For three different CPGs with spherical particles of 80 and 200 μm diameter and pore widths between 4 and 80 nm as well as a Pt-loading of 2 wt.-%, it was shown that aromatics hydrogenation under typical conditions can be mass-transfer limited, even for larger mesopores around 80 nm.While for catalyst particles with 25 μm diameter (and for 80 nm pore width), toluene conversion occurrs with the intrinsic (kinetic) reaction rate, the conversion of reactants with bulkier molecules such as m-xylene or mesitylene, is evidently hindered by internal mass-transfer within the catalyst mesopores. Evidently, an average pore width of at least 80 nm is needed to overcome internal mass-transfer limitations in the liquid-phase hydrogenation of toluene (dcrit = 0.61 nm), corresponding to a ratio of average pore width to critical molecule diameter of about 130. This knowledge may serve as a guide for a rational design of mass-transfer optimized hierarchical hydrogenation catalysts in the future.
Moreover, a particle size reduction may be applied to avoid mass-transfer limitations. Thus, for catalysts with mesopores of 10 nm, to achieve effectiveness factors ≥0.9 in toluene hydrogenation, the particle size would have to be below 25 μm, which is in the range of fine powders. If catalyst particles of larger diameters are to be applied, the only option for prohibiting mass-transfer-limited conditions for liquid-phase hydrogenations is, thus, to introduce sufficiently large pores, ideally with widths of 100 nm or beyond.
The effective diffusion coefficient of toluene for the catalysts with 4 and 10 nm pore width was determined from the initial reaction rates using the Thiele concept. The diffusion coefficient obtained from PFG-NMR is, however, an order of magnitude larger. Apparently, the Thiele concept is too simplified to assess the intraparticle transport of the reactants only. Rather, additional transport hindrances such as surface barriers may affect the diffusivity determination via the Thiele concept. It presents a challenge for further studies to identify more precisely these additional phenomena influencing diffusivity determination under conditions of catalytic reactions.
Acknowledgements
The authors would like to thank the “Deutsche Forschungsgemeinschaft” for funding within the International Research Training Group GRK 1056 “Diffusion in Porous Materials”.References
- C. S. Song, Catal. Today, 2003, 86, 211 CrossRef CAS.
- H. U. Blaser, C. Malan, B. Pugin, F. Spindler, H. Steiner and M. Studer, Adv. Synth. Catal., 2003, 345, 103 CrossRef CAS PubMed.
- M. C. Willis, Chem. Rev., 2010, 110, 725 CrossRef CAS PubMed.
- A. D. Sutton, F. D. Waldie, R. L. Wu, M. Schlaf, L. A. Silks and J. C. Gordon, Nat. Chem., 2013, 5, 544 CrossRef.
- H. Bonnemann, W. Brijoux, A. S. Tilling and K. Siepen, Top. Catal., 1997, 4, 217 CrossRef.
- X. B. Lou, L. He, Y. Qian, Y. M. Liu, Y. Cao and K. N. Fan, Adv. Synth. Catal., 2011, 353, 281 CrossRef CAS PubMed.
- B. Chen, U. Dingerdissen, J. G. E. Krauter, H. G. J. L. Rotgerink, K. Mobus, D. J. Ostgard, P. Panster, T. H. Riermeier, S. Seebald, T. Tacke and H. Trauthwein, Appl. Catal., A, 2005, 280, 17 CrossRef CAS PubMed.
- S. Tadepalli and A. Lawal, Int. J. Chem. React. Eng., 2008, 6 Search PubMed.
- S. M. Rao and M. O. Coppens, J. Phys. Chem. C, 2012, 116, 26816 CAS.
- G. Wang and M. O. Coppens, Ind. Eng. Chem. Res., 2008, 47, 3847 CrossRef CAS.
- G. Wang, E. Johannessen, C. R. Kleijn, S. W. de Leeuwa and M. O. Coppens, Chem. Eng. Sci., 2007, 62, 5110 CrossRef CAS PubMed.
- T. D. Tang, C. Y. Yin, L. F. Wang, Y. Y. Ji and F. S. Xiao, J. Catal., 2007, 249, 111 CrossRef CAS PubMed.
- C. H. Christensen, K. Johannsen, I. Schmidt and C. H. Christensen, J. Am. Chem. Soc., 2003, 125, 13370 CrossRef CAS PubMed.
- C. H. Christensen, K. Johannsen, E. Toernqvist, I. Schmidt, H. Topsoe and C. H. Christensen, Catal. Today, 2007, 128, 117 CrossRef CAS PubMed.
- M. S. Holm, E. Taarning, K. Egeblad and C. H. Christensen, Catal. Today, 2011, 168, 3 CrossRef CAS PubMed.
- J. Perez-Ramirez, C. H. Christensen, K. Egeblad, C. H. Christensen and J. C. Groen, Chem. Soc. Rev., 2008, 37, 2530 RSC.
- B. Y. Liu, L. M. Zheng, Z. H. Zhu, C. Li, H. X. Xi and Y. Qian, Appl. Catal., A, 2014, 470, 412 CrossRef CAS PubMed.
- J. J. Zheng, Q. H. Zeng, Y. M. Yi, Y. Wang, J. H. Ma, B. Qin, X. W. Zhang, W. F. Sun and R. F. Li, Catal. Today, 2011, 168, 124 CrossRef CAS PubMed.
- D. J. Wang, Z. N. Liu, H. Wang, Z. K. Xie and Y. Tang, Microporous Mesoporous Mater., 2010, 132, 428 CrossRef CAS PubMed.
- P. A. Rautanen, J. R. Aittamaa and K. O. I. Krause, Ind. Eng. Chem. Res., 2000, 39, 4032 CrossRef CAS.
- N. Wilde, C. Worch, W. Suprun and R. Gläser, Microporous Mesoporous Mater., 2012, 164, 182 CrossRef CAS PubMed.
- M. Goepel, M. Al-Naji, P. With, G. Wagner, O. Oeckler, D. Enke and R. Gläser, Chem. Eng. Technol., 2014, 37, 551 CrossRef CAS PubMed.
- M. Peer, A. Qajar, B. P. M. Holbrook, R. Rajagopalan and H. C. Foley, Carbon, 2013, 57, 485 CrossRef CAS PubMed.
- B. P. M. Holbrook, R. Rajagopalan, K. Dronvajjala, Y. K. Choudhary and H. C. Foley, J. Mol. Catal. A: Chem., 2013, 367, 61 CrossRef CAS PubMed.
- D. Enke, F. Janowski and W. Schwieger, Microporous Mesoporous Mater., 2003, 60, 19 CrossRef CAS.
- A. Stolle, C. Schmoger, B. Ondruschka, W. Bonrath, T. F. Keller and K. D. Jandt, Cuihua Xuebao, 2011, 32, 1312 CAS.
- T. Munkelt, C. Kuster, C. Hamel, D. Enke and A. Seidel-Morgenstern, Chem. Ing. Tech., 2013, 85, 1686 CrossRef CAS PubMed.
- D. Mehlhorn, R. Valiullin, J. Kärger, K. Cho and R. Ryoo, Materials, 2012, 5, 699 CrossRef CAS PubMed.
- C. Chmelik and J. Karger, Chem. Soc. Rev., 2010, 39, 4864 RSC.
- J. Kärger, D. M. Ruthven and D. N. Theodorou, Diffusion in Nanoporous Materials, Wiley - VCH, Weinheim, 2012 Search PubMed.
- J. Kärger and R. Valiullin, Chem. Soc. Rev., 2013, 42, 4172 RSC.
- U. Hong, J. Kärger, B. Hunger, N. N. Feoktistova and S. P. Zhdanov, J. Catal., 1992, 137, 243 CrossRef CAS.
- H. B. Schwarz, S. Ernst, J. Kärger, B. Knorr, G. Seiffert, R. Q. Snurr, B. Staudte and J. Weitkamp, J. Catal., 1997, 167, 248 CrossRef CAS.
- W. Heink, J. Karger, H. Pfeifer, K. P. Datema and A. K. Nowak, J. Chem. Soc., Faraday Trans., 1992, 88, 3505 RSC.
- P. Galvosas, F. Stallmach, G. Seiffert, J. Kärger, U. Kaess and G. Majer, J. Magn. Reson., 2001, 151, 260 CrossRef CAS.
- D. H. Wu, A. D. Chen and C. S. Johnson, J. Magn. Reson., Ser. A, 1995, 115, 260 CrossRef CAS.
- P. Gallezot and G. Bergeret, in Handbook of Heterogenous Catalysis, ed. G. Ertl, H. Knözinger, F. Schüth and J. Weitkamp, Wiley-VCH, Weinheim, Germany, 2008 Search PubMed.
- Elements of Chemical Reaction Engineering, ed. H. S. Fogler, Prentice Hall PTR, Westford, 2006, 4th edn Search PubMed.
- V. R. Choudhary, V. S. Nayak and T. V. Choudhary, Ind. Eng. Chem. Res., 1997, 36, 1812 CrossRef CAS.
- C. E. Webster, R. S. Drago and M. C. Zerner, J. Phys. Chem. B, 1999, 103, 1242 CrossRef CAS.
- S. Al-Khattaf and H. de Lasa, Appl. Catal., A, 2002, 226, 139 CrossRef CAS.
- S. F. Zaman, K. F. Loughlin and S. S. Al-Khattaf, Ind. Eng. Chem. Res., 2005, 44, 2027 CrossRef CAS.
- J. J. Rooney, J. Mol. Catal., 1985, 31, 147 CrossRef CAS.
- J. Massardier, J. C. Bertolini, T. M. Tri, P. Gallezot and B. Imelik, Bull. Soc. Chim. Fr., 1985, 333 CAS.
- C. P. Rader and H. A. Smith, J. Am. Chem. Soc., 1962, 84, 1443 CrossRef.
- W. Z. Gao, R. L. Robinson and K. A. M. Gasem, J. Chem. Eng. Data, 2001, 46, 609 CrossRef CAS.
- M. O. McLinden and J. D. Splett, J. Res. Natl. Inst. Stand. Technol., 2008, 113, 29 CrossRef CAS.
- C. K. J. Sun and S. H. Chen, AIChE J., 1985, 31, 1510 CrossRef CAS PubMed.
- J. Kärger, Microporous Mesoporous Mater., 2014, 189, 126 CrossRef PubMed.
- D. Tzoulaki, L. Heinke, H. Lim, J. Li, D. Olson, J. Caro, R. Krishna, C. Chmelik and J. Kärger, Angew. Chem., Int. Ed., 2009, 48, 3525 CrossRef CAS PubMed.
- F. Hibbe, J. Caro, C. Chmelik, A. S. Huang, T. Kirchner, D. Ruthven, R. Valiullin and J. Kärger, J. Am. Chem. Soc., 2012, 134, 7725 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI:10.1039/c4cy01665c |
| This journal is © The Royal Society of Chemistry 2015 |