Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Block copolymer self-assembly for nanophotonics
Morgan
Stefik
*a,
Stefan
Guldin
*b,
Silvia
Vignolini
c,
Ulrich
Wiesner
d and
Ullrich
Steiner
 e
e
aDepartment of Chemistry and Biochemistry, University of South Carolina, Columbia, South Carolina 29208, USA. E-mail: morgan@stefikgroup.com
bDepartment of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK. E-mail: s.guldin@ucl.ac.uk
cDepartment of Chemistry, University of Cambridge, Lensfield Rd., Cambridge, CB21EW, UK
dDepartment of Materials Science & Engineering, Cornell University, Ithaca, New York 14853, USA
eAdolphe Merkle Institute, Chemin des Verdiers, 1700 Fribourg, CH, Switzerland
First published on 9th April 2015
Abstract
The ability to control and modulate the interaction of light with matter is crucial to achieve desired optical properties including reflection, transmission, and selective polarization. Photonic materials rely upon precise control over the composition and morphology to establish periodic interactions with light on the wavelength and sub-wavelength length scales. Supramolecular assembly provides a natural solution allowing the encoding of a desired 3D architecture into the chemical building blocks and assembly conditions. The compatibility with solution processing and low-overhead manufacturing is a significant advantage over more complex approaches such as lithography or colloidal assembly. Here we review recent advances on photonic architectures derived from block copolymers and highlight the influence and complexity of processing pathways. Notable examples that have emerged from this unique synthesis platform include Bragg reflectors, antireflective coatings, and chiral metamaterials. We further predict expanded photonic capabilities and limits of these approaches in light of future developments of the field.
1 Introduction
From informatics to alternative energy, the ability to control light–matter interactions on the nanoscale is crucial to a wide gamut of applications. Whether the goal is to trap or guide light within photonic bandgap materials, enhance certain reflections (e.g. for structural color), prevent reflections for enhanced light harvesting, or the polarization of light, the ability to control on the nanoscale the spatial organization of materials has progressed from a fundamental question to a technological need. With the promise of widespread benefits from this new generation of nanostructured materials, the main question today is: “How can we fabricate functional nanomaterials in a truly scalable fashion?”. Historically materials science has focused on top-down lithographic approaches and on colloidal self-assembly to gain access to periodic material arrangements on the length scale of visible light. Supramolecular assembly provides a powerful alternative, where the structure formation is controllable on a smaller sub-wavelength 5–100 nm length scale that opens the possibility of mesoporous structures and metamaterials that are active at visible wavelengths. Such material architectures have a wide range of tunable symmetries and a remarkable range of accessible compositions.Here we review promising block copolymer pathways for nanophotonics, covering a wide spectrum of processing conditions and morphologies as well as a range of optical constants and anisotropies. Despite the nuanced processing complexity, such block copolymer based nanophotonics remain in principle compatible with solution processing such as spin coating, dip coating, or roll-to-roll fabrication. Most polymers are commodity materials where the constituent monomers cost only pennies per gram and the controlled chain-growth synthesis techniques needed to make block copolymers are routinely deployed at the industrial scale.1
2 Nanostructures for photonics
For a photonic bandgap or antireflective properties, the periodic spatial modulation of the refractive index has to be comparable to the incident wavelength. The scattering of photons occurs at interfaces of differing refractive index and the resulting constructive or destructive interference arises from the particular nanostructure geometry. The modulation of visible photons with 400–700 nm wavelengths is thus rarely accommodated directly by block copolymers due to the challenges of forming such large unit cells (Section 3.1.3) as well as the typically low refractive index contrast between the polymer blocks (Section 4). However, inorganic nanostructures generated from block copolymers enable access to larger refractive indices and higher refractive index contrasts. The tunability of refractive index with porous inorganic layers thus enables the modulation of refractive index with controlled layer thickness on the length scale of visible wavelengths (Section 3.2).Although the typical 5–100 nm block copolymer unit cell dimensions are not suitable for visible photonic bandgaps, they are ideal scaffolds for the fabrication of metamaterials. The relevant optical parameters for metamaterials require spatial modulation on a sub-wavelength regime. In non-resonant dielectrics, light propagates across the material, averaging over its morphology, yielding a medium with designable permittivity and permeability. This behavior is no longer determined by macroscopic structural parameters of material assemblies, but from their composition and geometries that act as “artificial atoms.” This effect, also termed “optical crowding,” is particularly useful for the creation of materials with very low refractive indices. Materials in which the electron system is resonant with respect to the incident light, such as in metals, the propagating resonant electronic modes (plasmon-polaritons) determine the optical properties of sub-micrometer structured materials. For example, efficient wave guide design requires sufficient propagating modes and limited energy dissipation, both of which may be improved by decreasing the local thickness of metallic nanostructures. Based on predictions by Pendry et al. in 1999,2,3 numerous examples of metamaterials have emerged with fascinating and unusual optical properties based upon the precise spatial arrangement of conventional materials into suitable architectures. The possibility of achieving a negative refractive index and super-lensing has intrigued many groups and caused a flurry of activity in this field.
The production of nanophotonics is often accomplished with complex and costly photolithographic techniques. Here, block copolymers are an ideal platform to develop tuned nanomaterials with a wide range of accessible structures and length scales. The reliance on self-assembly approaches considerably reduces overhead costs since they are widely based on solution processing and are thus directly compatible with future industrial upscaling. Below we outline how the particular block copolymer processing methodologies result in different types of nanostructure symmetries for particular photonic properties.
2.1 Fabrication and function
The assembly of pure block copolymers in the condensed matter state allows access to a range of highly ordered materials with unique nanostructure symmetries. The resulting assemblies may be directly used as photonic materials, or may be used as templates to produce complimenting inorganic nanostructures. The coassembly of inorganic nanoparticles with block copolymers provides a different pathway to generate highly ordered inorganic nanostructures in a more direct fashion. These approaches are based upon well-equilibrated assemblies (Section 3.1) resulting from the thermodynamics underlying supramolecular assembly. Equilibrated block copolymer derived materials uniquely yield a combination of uniform patterns with tunable symmetries that are amenable towards interactions with visible light, including photonic crystals and metamaterials. While this extent of 3D structure control is intriguing, the widespread adoption is somewhat challenged by the need to master polymer synthesis and processing conditions at which ordered phase separation occurs. Often equilibration is promoted through thermal or solvent annealing. Many photonic applications crucially depend on reliable morphology generation in thin films, where the bulk thermodynamic equilibrium is further perturbed by additional interfacial interactions and solvent evaporation kinetics as elaborated in Sections 3.1.1 and 4.Subtly different solution processing routes result in non-equilibrated nanostructures with remarkably different characteristics and photonic applications. Although pure polymer films are also processed from solutions, their equilibrium assembly in the condensed state is determined by the block copolymer thermodynamics alone, which is conceptually different from the assembly of solution structures. Polymer solution morphologies are often spherical micelles where the thermodynamics are additionally influenced by solvent interactions4,5 and the reorganization kinetics vary over many orders of magnitude.6–9 In the case of block copolymer coassembly with inorganic nanoparticles, the reorganization kinetics may be hampered by the presence of water to lead to kinetically trapped structures (Section 3.2). The resulting morphologies from this approach are uniform and usually have limited symmetries related to packed spheres. Porous inorganic materials are readily generated from such assemblies where the porosity serves to modulate the refractive index and may provide further advantages such as photocatalytic self-cleaning. Such non-equilibrium assemblies have been successfully demonstrated both for photonic band-gaps and anti-reflective properties.
3 Exploring the tool box of block copolymer self-assembly
Supramolecular assembly is the spontaneous aggregation of molecules towards an equilibrium condition, yielding well-defined assemblies based upon non-covalent interactions. The emergence of ordered and periodic structures indicates that the overall free energy change is often dominated by enthalpic terms such as the interaction strength of the different molecular segments. This free energy contribution is in concert with entropic terms, which are related to the molecular conformations induced by reorganization. Such assemblies are ubiquitous in biology, giving rise to highly ordered structures over many length scales.10 The direct evolution of assembled morphologies from the molecular structures affords a high level of control by adjusting molecular parameters during synthesis. Biological molecules such as DNA and the proteins derived therefrom are complex sequences of molecular segments that change motif frequently and without a simple pattern. While DNA sequences contain up to millions of repeated segments in a seemingly chaotic pattern, block copolymers are a much simpler molecular analog that also undergoes supramolecular assembly.3.1 Block copolymer assembly near the thermodynamic equilibrium
Block copolymers are macromolecules with the different monomer segments organized into continuous blocks. Typical block copolymers are linear and contain two or three unique monomer chemistries organized into two to three blocks: AB, ABA, ABC. Although these provide idealized models for morphology studies, much more complex molecular structures are accessible, including non-linear polymers with various types of branches (star, H-shaped, comb, dendrimers) and more than three blocks.11 The equilibrium self-assembly of pure AB diblock copolymers is well understood and leads to just four classes of morphologies with spherical micelle packing (FCC or BCC), hexagonally packed cylinders, a 3D continuous double gyroid (GD, space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d), and a lamellar phase.12 Notably, other morphologies are stabilized near the very limited region of phase space associated with the order-to-disorder transition. The prediction of the equilibrium phase morphologies of AB diblock copolymers is largely based on the volume fractions of the blocks and the product of their Flory–Huggins interaction parameter, χ, with the chain length, N, although further parameters contribute in non-ideal systems. Here, control over the chain length, and thus molecular weight, directly governs the periodic length-scale of the resulting assembly with an approximate relationship of d ∝ N2/3χ1/6 for the strong-segregation regime.13
d), and a lamellar phase.12 Notably, other morphologies are stabilized near the very limited region of phase space associated with the order-to-disorder transition. The prediction of the equilibrium phase morphologies of AB diblock copolymers is largely based on the volume fractions of the blocks and the product of their Flory–Huggins interaction parameter, χ, with the chain length, N, although further parameters contribute in non-ideal systems. Here, control over the chain length, and thus molecular weight, directly governs the periodic length-scale of the resulting assembly with an approximate relationship of d ∝ N2/3χ1/6 for the strong-segregation regime.13
The addition of a single additional block to form an ABC triblock terpolymer significantly expands the parameter space and complexity of the accessible morphologies with more than 30 reported so far.11,14–25 The use of ABC triblock terpolymers also enables access to several different 3D continuous network morphologies, including the chiral alternating gyroid network (GA, space group I4132) (Fig. 1).22 Chiral assemblies have important ramifications for optical metamaterials, vide infra. Although still significantly less complex than biological DNA and proteins, the further extension to block copolymers with four or more blocks opens a “Pandora's box” of parameter space,26 the exploration of which is only beginning.
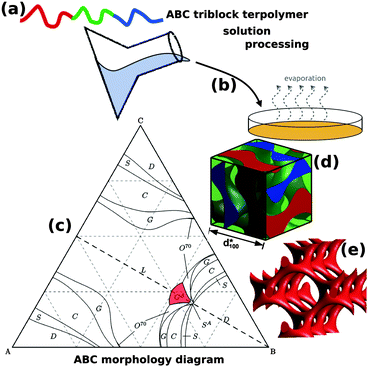 | ||
| Fig. 1 Block copolymer self-assembled nanostructures for photonic applications. Block copolymers (a) are solution processable (b) to form self-assembled nanostructures. While AB diblock copolymers only form centrosymmetryic morphologies, ABC triblock terpolymers (c) can enable non-centrosymmetric morphologies such as the alternating gyroid, GA (d). The GA contains two single gyroid networks that contain several helical axes, formed by the A and C blocks (e). (c) Adapted with permission from ref. 156. Copyright 2012 American Chemical Society. (d, e) Adapted from ref. 64 with permission from The Royal Society of Chemistry. | ||
The equilibration of block copolymers onto a substrate alters self-assembly in a way that may either be beneficial or detrimental for photonic applications. For a lamellar morphology, preferential interactions of one of the blocks with the substrate interface and/or the film surface typically orients the lamellae parallel to the surfaces,27 which greatly facilitates the manufacture of Bragg reflectors (see Fig. 2). Care must however be taken to design the film thickness to be commensurate with the lamellar spacing. Otherwise the free surface may reconstruct into islands or troughs.28 Sandwiched between two solid surfaces, the interplay of surface interactions and confinement controls the orientation of the lamellar structure.29 Surface roughness also has an effect on the interfacial block copolymer morphology.30
Beyond the mere reorientation of the self-assembled bulk phase, preferential block interactions are able to alter the phase morphologies near surfaces, for example from hexagonal to lamellar.31 For photonic applications, this change in symmetry may be significant, particularly because changes in surface morphology may affect the in- and out-coupling for light from the film. In extremely thin films, surface effects often lead to a rich block copolymer phase diagram that by far exceeds the complexity of the bulk phase space.32,33
In cases where self-assembled morphologies are used as templates for electrochemical material synthesis, surface-induced polymer reorientation or surface reconstruction is often undesired, since this leads to morphologies that cannot be electrochemically replicated. The in-plane orientation of the lamellar or cylindrical phases cannot be accessed via either of the surfaces, but this can be overcome, e.g. by reorienting the phase morphology in an electric field.34 The control over domain alignment in thin films has indeed been a subject of intense study. Meanwhile a number of effective and less complex methods have been developed, including the utilisation of solvent casting,35 thermal and solvent annealing methods,36,37 photo-induced alignment,38 as well as chemical templating,39–42 chemoepitaxy,43,44 and graphoepitaxy.45,46
With gyroid-forming block copolymers, surface reconstruction into the lamellar phase is common, and causes a significant barrier to electrochemical replication. At the free film surface, plasma or ion etching may be necessary to expose the buried gyroid phase. At the substrate interface, typically a combination of surface and chemical modification by a self-assembled monolayer can be used to prevent the formation of a surface-induced lamellar phase.47 Note that the successful replication of an interpenetrating network phase requires that all block copolymer phases make contact with a conducting substrate; while a lack of surface connectivity of the sacrificial phase will inhibit electrochemical processes, the preferential segregation of this material to the substrate will cause the film to float-off the surface during immersion into the electrolyte. The formation of sparse pore-interconnects at the surface leads to only localized replication.48
With coassembly, an amphiphilic block copolymer and inorganic nanoparticles are combined in solution.51 Coassembly relies on the selective interaction of the inorganic components with a single block of the copolymer via attractive intermolecular forces such as hydrogen bonding. The selective association of the inorganic component with one of the polymer blocks changes their relative volume fractions, thereby significantly altering the self-assembled morphologies.52 Coassembly strategies have been developed for highly ordered silicate,53,54 transition metal oxide,55 and metal56 nanostructures. Successful coassembly relies upon careful tuning of key enthalpic,52,57,58 entropic,59 and kinetic60 considerations. Although there are numerous reported coassemblies based on AB and ABA block copolymers, only very few reports have emerged on the coassembly of inorganic components with ABC polymers.61–65 Coassembled hybrids also have challenges associated with the shrinkage and cracking of amorphous assemblies during formation and crystallization. The use of thin films provides support from the substrate and may allow partial stress relaxation. Multiple coatings with subsequent crystallization cycles significantly lower the film strain and enable device-relevant film thicknesses up to several micrometers.66 Bulk films typically detach from the casting container and can be processed as films or powders without a substrate. A method (termed “CASH”) was developed to crystallize bulk films by utilizing the in situ generation of carbon as a hard-template to preserve the nanostructure during crystallization at temperatures up to 1000 °C.67 An elegant alternative is the direct coassembly of crystalline nanoparticles and block copolymers.68–72 While relatively new, the additional key parameter for this coassembly is the particle surface coverage by ligands.73 Recent calculations suggest that under certain conditions the nanoparticles in coassemblies may form superlattices for novel photonic applications.58,74 Many block copolymer approaches to synthesize controlled inorganic nanostructures have been successfully applied towards a wide array of photonic materials.
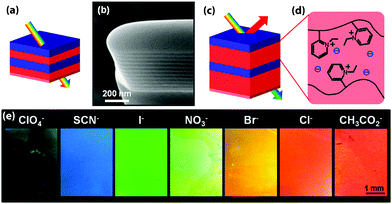 | ||
| Fig. 2 Schematic representation of a color change mechanism in a photonic block copolymer multilayer modulated by an exchange of counterions (a). In the dry film, the modulation is too small to create an optical effect in the visible range as can be seen in the cross-sectional SEM image of the lamellar film (b). Schematic of the modified photonic response due to swelling (c and d). Depending on the hydration characteristics of the counteranions, the selective swelling of the block copolymer lamellae can be controlled, causing a change in the optical response (e). Adapted with permission from ref. 89. Copyright 2012 American Chemical Society. | ||
Increasing the unit cell size in two and three dimensionally continuous morphologies poses new challenges for block copolymer assembled photonic crystals. A photonic response in the visible requires reliable phase separation and a high degree of long-range order in very high molecular weight block copolymers. Although several 3D continuous block copolymer network morphologies were predicted to exhibit complete photonic bandgaps,91 their demonstration at visible wavelengths has been hampered by slow relaxation kinetics of the required high molecular weight polymers. To the best of our knowledge, the largest 3D structure assembled from a block copolymer had a double gyroid morphology with a lattice parameter of 258 nm, requiring a 2 week casting process of a ∼750 kg mol−1 poly(styrene-b-isoprene).81 Please note that this unit cell dimension corresponds to a 129 nm spacing from strut-to-strut. High molecular weight polymers are highly entangled and suffer from ever decreasing reptation rates as the molecular weight increases. This example demonstrates routes to reduce kinetic limitations by starting the structure formation process in the presence of a solvent.81 The solvent plays two roles: it plasticizes the glassy polystyrene block and swells the chains to reduce entanglements and facilitate reorganization by polymer reptation. The equilibration of networked morphologies from ABC triblock terpolymers are additionally limited by a bridging B-block conformation with limited reorganization pathways.92 Similarly, solution processing was shown as a viable route to also circumvent such kinetic challenges for network forming ABC polymers.93 The additional challenge of inducing such long-range order with predictable alignment and on a macroscopic scale is discussed in Section 4.
A recent review highlights the use of soft materials for photonic crystal fabrication.94 Although a strong candidate approach for the scalable production of nanoscale materials, the manufacture of photonic crystals by block copolymer self-assembly, in particular of ordered 3D geometries from molecular weights larger than 100 kg mol−1, remains challenging. Examples are mostly limited to one-dimensional structures although there were recently several advances with photonic architectures based on block copolymer assembly within the confinements of both opal and inverse-opal templates.95,96 Block copolymer approaches have yet to demonstrate a complete photonic band-gap in the visible range.
While AB diblock copolymers can generate double gyroid morphologies that are achiral and centrosymmetric, the use of ABC triblock terpolymers has a greatly expanded the range of accessible morphologies and space groups. In particular, the alternating gyroid (GA, space group I4132) is one of the most attractive ABC morphologies because it has chiral spirals along six axes, 〈100〉 and 〈111〉 (Fig. 1e) and is predicted to exhibit a complete photonic bandgap for a sufficiently high refractive index contrasts and filling fractions.81,91,99,105,106 These non-centrosymmetric features are not found in more common double gyroid morphologies because the inversion center of symmetry provides equivalent helixes of opposite chirality leading to an overall achiral structure (space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d). ABC triblock terpolymers have been shown to form the GA both in the neat melt16,107 and when coassembled with nanoparticles.64 The use of compositions with similar A and C block fractions (near the dashed line in Fig. 1c) are crucial for the symmetry breaking that places the A and C blocks separately into a similar topology that alternates in composition. In the GA, the A and C blocks each form a single gyroid that interweave each other without intersecting and have opposite chiralities.
d). ABC triblock terpolymers have been shown to form the GA both in the neat melt16,107 and when coassembled with nanoparticles.64 The use of compositions with similar A and C block fractions (near the dashed line in Fig. 1c) are crucial for the symmetry breaking that places the A and C blocks separately into a similar topology that alternates in composition. In the GA, the A and C blocks each form a single gyroid that interweave each other without intersecting and have opposite chiralities.
GA polymer templates were recently used to produce the first 3D chiral metamaterials made by self-assembly.100 The template was a GA-forming poly(isoprene-b-styrene-b-ethylene oxide) that was self-assembled onto a conductive substrate (Fig. 3). The polyisoprene was selectively removed by UV ozone etching, followed by a rinse. The resulting pores were filled by electrodeposition of gold into the voided template. A subsequent plasma etch was used to selectively remove the surrounding polymer template, leaving behind a free-standing single gyroid network of gold that replicated the original structure of the minority polyisoprene block. Because of the “polycrystalline” self-assembly of poly(isoprene-b-styrene-b-ethylene oxide), the resulting GA domains had a random distribution of handedness. Measurements of individual GA domains showed evidence of the internal chirality by exhibiting an anisotropic gyrotopic transmission. Along one of the chiral axes, either left or right circularly polarized light was preferentially transmitted, depending to the chirality of the morphology.100 A follow up study, showed that these structures are highly tunable with several easily adjusted parameters.101 Control over the d100* unit cell dimension from 35 to 50 nm was demonstrated by changing the molecular weight of the block copolymer from 33 to 53 kg mol−1. The increasing d100* unit cell dimension allowed a systematic variation of the transmission and reflection spectral response (Fig. 4a–c). Remarkably, about 20% of the incident light transmitted through a 300 nm thick film with 30 vol% gold, clearly indicating that the optical energy flux was transmitted by plasmon resonances propagating along the gold struts, confirming the well established fact that plasmon resonance frequencies are tunable by varying the structural dimensions. This allows the tuning of the metamaterial characteristics of a given GA unit cell by changing the diameter of its gold struts. This was demonstrated by the electrodeposition of gold radially around the conductive struts of an initially replicated gold gyroid (Fig. 4d–f). The resulting filling fraction of gold in the GA unit cell was tuned in this fashion from the initial value of 30% up to 90%, yielding systematic control over the blue shift of the plasma edge.101 Correspondingly, the strength of linear dichroism decreased monotonically, reaching 0 at 60 vol% gold.
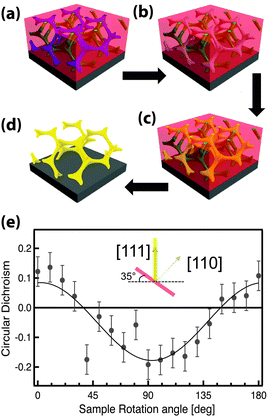 | ||
| Fig. 3 Self-assembly of a 3D chiral metamaterial using a block copolymer template. An ISO polymer was assembled into a GA morphology (a) followed by selective UV etching of polyisoprene (b). The resulting pores were backfilled by electrodeposition of gold (c). Subsequent removal of the polymer template by plasma etching (d) resulted in a free-standing single-gyroid network of gold. The anisotropic sample exhibited gyrotropic transmission that selectively allowed the passing of circularly polarized light corresponding to the structural chirality (e). Adapted with permission from ref. 104 and 100. Copyright John Wiley and Sons. | ||
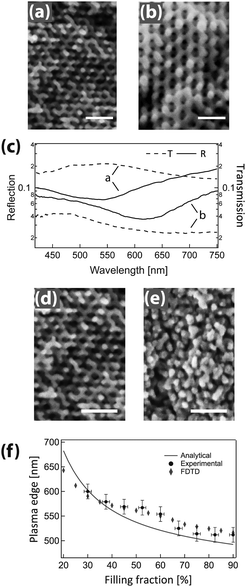 | ||
| Fig. 4 Tunable chiral metamaterials. The GA unit cell size is adjustable by changing the molecular weight of the poly(isoprene-b-styrene-b-ethylene oxide) template (a, b) to modulate the spectral wavelength dependence (c). After gold replication of the isoprene phase and template removal, the strut width of the replicated GA network was increased by further Au electrodeposition (d, e). This modified the unit cell filling fraction, causing a variation of the plasma edge wavelength (f). Adapted with permission from ref. 101. Copyright John Wiley and Sons. | ||
Although this approach has not yet demonstrated a negative refractive index, gold gyroid metamaterials strongly affect light propagation beyond standard dichroism. For example, the nonlinear optical response of these structures provides an enhancement larger than ten fold when compared to all other metallic nanomaterials, including bulk gold. This remarkable increase of nonlinearity can be attributed to the metamaterial effect.102 The interconnected nanostructured network confines light, making the nonlinear response dominant. The fact that the structures are truly three dimensional and easily tunable makes this type of metamaterial the perfect platform for a new sensing principle as well as nonlinear and active devices.
Additional flexibility in the optical response can also be introduced by fabricating coaxial geometries (Fig. 5).103 Here, similar to the discussion above, the porous scaffold after polyisoprene removal was backfilled with nickel by electrodeposition. The remaining polymers were subsequently removed by plasma etching, resulting in a freestanding Ni single gyroid. This structure was then used as the working electrode for the electrodeposition of coaxial gold. Finally, the inner nickel core was etched away by immersion in FeCl3, providing a hollow single gyroid morphology (Fig. 5c and e). This metamaterial design provides a substantial transmission enhancement by nearly a factor of 3 when compared to the solid alternating Au gyroid with the same amount of gold per unit cell. The presence of a hollow guide geometry increases the number of propagating modes across the wave-guide structure. At the same time, the hollow geometry increases the efficiency of light in-coupling while also reducing the dissipation by decreasing the Au-volume involved in plasmon mode propagation to values much below the Au skin-depth. These conclusions are probably valid not only for hollow gyroid structures but also for the diamond or column morphologies. These findings are likely to pave the way for novel designs of metamaterials with low losses.
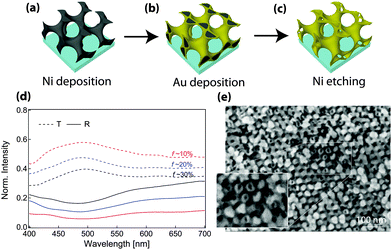 | ||
| Fig. 5 Hollow alternating gyroid. Hollow GA structures were templated from poly(isoprene-b-styrene-b-ethylene oxide) by first electroplating nickel into the free-volume generated by etching polyisoprene (a). The polymer template was removed and the resulting nickel network was used as the working electrode for the deposition of a coaxial gold layer (b), followed by selectively etching the nickel (c). The final hollow single gyroid structure (e) exhibited a 3-fold enhancement of photonic transmission compared to a structure consisting of solid struts with the same filling fraction (d). Adapted from ref. 103 with permission from The Royal Society of Chemistry. | ||
Recent simulations suggest that simpler manufacturing routes based on polymer coassembly with ligated metallic nanoparticles may directly form 3D chiral structures involving fewer processing steps.74 Following this prediction, the coassembly of metallic nanoparticles with a different ABC polymer, poly(isoprene-b-styrene-b-dimethylaminoethyl methacrylate), led to the direct fabrication of GA structures with platinum and gold nanoparticles.108 The use of a different hydrophilic block, PDMAEMA, is key to provide for sufficiently enthalpic interactions with the metal nanoparticles. These advances lay a path to the broader development of optical metamaterials prepared by block copolymer self-assembly.
3.2 Block copolymer assembly away from equilibrium
The use of block copolymers for photonic applications can also be powerful from persistent solution morphologies under robust and simple fabrication conditions. Most solution processing routes for block copolymers are at least partially selective for one of the polymer blocks thereby inducing micellisation. Depending on the processing kinetics and conditions, these micelles may be translated into the final morphology rather than transitioning to the classical condensed matter state behavior of pure block copolymers. Please note that in the strictest sense, solution phases can exist in equilibrium with a reversible dependence on thermodynamic parameters,4,5 however the kinetics for the rearrangement of highly amphiphilic block copolymers are often extremely slow,6,7 with few exceptions.9 In recent years, protocols that allow the use of block copolymer coassembly in thin films have been developed. It has been demonstrated that the spontaneous dense packing of copolymer micelles allows detailed control over porosity71,109,110 and pore sizes71 in a fully interconnected and accessible porous network.109,111 The architecture closely resembles an inverse opal morphology, well known on 10 times larger length scales and typically created by colloidal self-assembly. While inverse opal architectures by colloidal assembly have become a well studied and widely used materials route, a similar architecture on the 10 nm length scale opens up a number of potential applications in optical coatings, photocatalysis, water cleaning or photovoltaic devices.As schematically shown in Fig. 6a, the polymer acts as a structure-directing agent for the inorganic material. With proper chemical design, the inorganic guest can preferentially interact and coordinate with the hydrophilic block and thereby participate in the supramolecular coassembly process. In selective solvents, amphiphilic block copolymers form micelles in solution with cores that consist of the solvophobic block. Film processing, solvent evaporation, annealing of the inorganic material and subsequent removal of the organic host gives rise to a nanoscopic inverse opal-type structure of densely packed pores in an inorganic matrix. It is important to note that the effectiveness of this approach relies on the nature of the block copolymer. Poly(isoprene-b-ethylene oxide) (PI-b-PEO) was employed, which differs largely from the widely established Pluronic structure-directing agent (PEO-b-PPO-b-PEO) that acts like a surfactant, forming small ∼10 nm structures that often collapse during high temperature processing.114,115 The high Flory–Huggins interaction parameter of the isoprene and ethylene oxide blocks,116 their low glass-transition temperatures, and the ability to synthesize high molecular weights with low polydispersities117 enable fast microphase separation, high polymer mobility during processing, and uniform structure control, respectively.
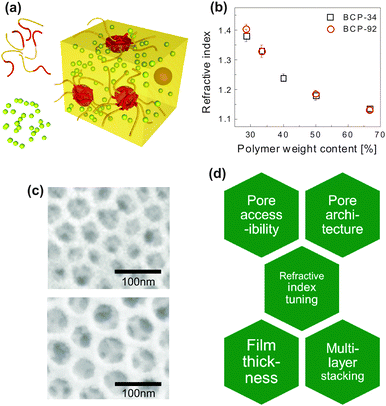 | ||
| Fig. 6 Inorganic photonic nanoarchitectures by block copolymer coassembly. Schematic of block copolymer coassembly (a). The block copolymer (indicated as yellow and red chain strands) acts as a host for the inorganic material (yellow-green spheres) during block copolymer self-assembly. Film processing, solvent evaporation, annealing of the inorganic material and subsequent removal of the organic host gives rise to a nanoscopic inverse opal-type structure of densely packed pores in an inorganic matrix. Dependence of the refractive index of the resulting porous film as a function of polymer weight content in the initial mixture for two different block copolymers (b). Resulting pore size in silica-type films is dependent on the molecular weight of the polymer (c). A molecular weight Mn of 24.8 kg mol−1 led to a pore size distribution of 33 ± 6 nm, while Mn = 63.2 kg mol−1 resulted in 52 ± 6 nm. Overview of key requirements for porous thin film architectures with tunable photonic responsive (d). (a) Adapted with permission from ref. 112. Copyright 2010 American Chemical Society. (b, c) Adapted with permission from ref. 71. Copyright 2013 American Chemical Society. (d) Adapted with permission from ref. 113. Copyright 2014 Society of Photo Optical Instrumentation Engineers. | ||
The coassembly route enables the manipulation of the refractive index of porous film over a wide range. Fig. 6b shows this variation as a function of the organic-to-inorganic mixing ratio in the initial solution. The refractive index window of 1.4 > n > 1.13 corresponds to porosity values ranging from 20% to 73%. The resulting porous architectures in Fig. 6c are highly ordered and well interconnected. Their average pore size is a direct consequence of the molecular weight of the PI block in the organic host and can thus be finely controlled. In the example of Fig. 6c, a molecular weight Mn of 24.8 kg mol−1 led to a mean pore size of 33 ± 6 nm, while Mn = 63.2 kg mol−1 resulted in a pore size distribution of 52 ± 6 nm. This is in good agreement with scaling laws for the radius of gyration of the polyisoprene block in the melt.
One core challenge in a coassembly route to porous thin films is the material shrinkage that occurs during the processing, mostly due to the evaporation of the solvents and the condensation of the inorganic network. Processing protocols have however been developed to accommodate material shrinkage. This involves layer-by-layer processing combined with a specific annealing protocol which prevents the formation of cracks even in several μm thick films.66
Adsorption and desorption of gas molecules in the pores results in reversible changes of the refractive index of the porous layers and thus in a modification of the characteristic optical properties.114,120 When functionalized to bind specific molecules, MDBRs have been successfully used as biosensors to detect pico- to femtomolar concentrations of small organic molecules, DNA oligomers and proteins.121,122 2D principal component analysis123 or the coupling of MDBRs to surface layers124 and resonance cavities125 facilitates sensing with even greater accuracy. The ability to manipulate and control the flow of light in one dimension make MDBRs a powerful component in optoelectronic devices. When infiltrated with light emitting polymers, MDBRs have been successfully used for distributed feedback lasing.126,127 Incorporated into excitonic solar cells, MDBRs can lead to the localization of light in specific parts of the spectrum, while retaining the cell's transparency in others.119,128–131
There are numerous material routes towards MDBRs. Initial attempts were based on porous silicon where the etching conditions were periodically changed to realize a dielectric 1D lattice with alternating porosity. A first block copolymer-based route to coassemble alternative layers of porous TiO2 and SiO2 was introduced by Ozin and coworkers.114 This approach provided a greatly improved structure control of the porous networks. Yet, due to the slow phase separation and very limited thermal tolerance of the Pluronic surfactant, processing was extremely time consuming with fabrication times up to several days for each individual layer of the stack.115 A less complex route to form inorganic porous networks in thin films is the random packing of nanoparticles.132,133 While the optical properties of the stack can be tuned by film thickness and choice of the materials used in the individual layers (e.g. TiO2 and SiO2), control over other key parameters as discussed in Fig. 6d remains difficult. The random-close packing of somewhat polydisperse nanoparticles results in a rather random pore size distribution and allows only limited control over the porosity by changing the nanoparticle size and the addition of sacrificial fillers.134,135
A fabrication route to MDBRs that makes use of solution-based block copolymer assembly far from equilibrium is illustrated in Fig. 7. The coassembly interplay between the structure-directing polymer and inorganic particles allows the fine tuning of porosity and thus the refractive index in the porous material by simply changing the ratio between organic and inorganic components in the initial solution. As shown in Fig. 7a, sequential film deposition and annealing enables multilayer stacking and the build-up of a MDBR. A cross-section of the multilayer stack after removal of the organic material by high temperature calcination imaged by TEM is shown in Fig. 7b. Note that the contrast in electron density within the TiO2 stack is caused exclusively by the alternating porosity. Experimental results of MDBR performance are shown in Fig. 7c–e.
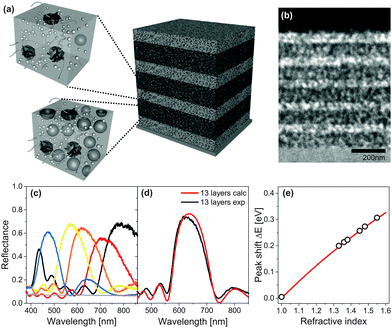 | ||
| Fig. 7 Mesoporous Bragg reflectors based on block copolymer coassembly. Two stock solutions with a different TiO2 to polymer weight ratio serve for the fabrication of high and low porosity layers in a multilayer architecture (a). Stacks are built-up by the alternating deposition and annealing of layers, followed by a final calcination step to reveal the mesopores. Cross-sectional view of a 11-layer TiO2 stack by transmission electron microscopy (TEM) (b). Reflectance of 9-layer MDBRs, where the thickness of the five high refractive layers was kept constant while the thickness of the low refractive layers was varied to manipulate the optical response across the visible spectrum (c). Comparison of experimental reflectance (black) with calculations of an ideally regular stack comprised of 13 layers (red) (d). Corresponding shift of the Bragg peak position after pore infiltration with a variety of different liquids (e). The grey line corresponds to the theoretical shift of the Bragg peak calculated by a Bruggeman effective medium approximation. (a, d) Adapted with permission from ref. 136 and 110. Copyright 2011 Society of Photo Optical Instrumentation Engineers. (b, c, e) Adapted with permission from ref. 109. Copyright John Wiley and Sons. | ||
The block copolymer coassembly route presented here offers several advantages over the state-of-the-art. It decouples important parameters in MDBR stack design, porosity and pore size, and allows the tuning of both properties in a wide parameter range. Furthermore the pore size distribution is narrow and controllable in comparison to random networks of nanoparticles. The control of the molecular weight of the pore-forming polymer block directly determines the resulting pore size.71 As previously discussed, the refractive index lattice in the nanoparticle-based MDBRs is realized by the sequential deposition of TiO2 and SiO2 nanoparticle layers.133 The use of SiO2 as the low refractive building block makes the stack non-conducting and thus prevents contributions to light absorption and conversion in photovoltaic devices. While certain nanoparticle-based routes allow the fabrication of conducting MDBRs,134,137 the lack of control over pore size and pore accessibility limits mass transport through the porous network and infiltration for solid state dye-sensitized solar cells.138 This is covered in more detail in recent reviews on MDBRs119 and on the bottom-up assembly of photonic crystals in general.94,139
Critical parameters for the manufacture of antireflective coatings are the porosity and to a smaller extent the pore size, both of which may be controlled by block copolymer coassembly far from thermodynamic equilibrium as described above, yielding a simple and scalable approach. The block copolymer acts as a porogen which is typically combined with sol–gel chemistry.142 Mild conditions (i.e. through wet chemical etching or plasma etching) to remove the organic hosts allow to process antireflective coatings on plastic-based flexible substrates.143
Block copolymer routes to antireflective coatings are diverse. Appealing concepts include the use block copolymer-functionalized gold nanoparticles or block copolymer patterns as lithographic masks in a reactive ion etching process, resulting in gradient refractive index surfaces that resemble the moth eye.144,145 Gradient refractive index antireflective coatings may also be achieved by exploiting domain rearrangement through surface reconstruction by block copolymer deposition on surface treated substrates followed by annealing.146 Block copolymer assembly near the thermodynamic equilibrium and subsequent use as a sacrificial template for gyroid-structured thin inorganic films is also a successful strategy for the manufacture of optical coatings with exceptionally low refractive indices.147
While numerous material routes lead to high performance optical coatings under laboratory conditions, commercial implementation is held up by their susceptibility to contamination and thus decay in functionality. This could be prevented by photocatalytic self-cleaning, i.e. the decomposition of organic contaminants by light-induced redox-reactions.148 The inclusion of photocatalytic hot spots is challenged by their high refractive index (nTiO2 > 2.5149), which limits the amount of photocatalytic material that can be included in a self-cleaning antireflective coating while still reaching sufficiently low values of nARC.
A simple method for the manufacture of robust antireflective coatings with greatly improved self-cleaning properties was recently reported.71 As shown in Fig. 8a, the process relies on the block copolymer coassembly of a mixture of silica-based sol and preformed TiO2 nanocrystals. The spontaneous dense packing of copolymer micelles during the film formation process, followed by condensation of the silica-based matrix during film annealing and subsequent removal of the organic host, results in an inverse opal-type silica morphology that is loaded with TiO2 photocatalytic hot-spots. The arrangement of micelles represents the densest packing of sacrificial material, i.e. pores. The resulting ultra low volume fraction of the inorganic material (down to 27%) enables a high loading of the network with TiO2 nanocrystals and thus a simultaneous matching of the requirements for self-cleaning and antireflection. This method requires only moderate annealing temperatures (<150 °C) and processing can therefore be accomplished onto plastic substrates. The resulting optical properties are shown in Fig. 8b, where the reflectance of an uncoated PET foil (PET-0s) is compared to a sample that was coated on one side with a self-cleaning antireflective coating (PET-1s). By simple interfacial analysis with RPET-0s = A + ((1 − A)A) and RPET-1s = B + ((1 − B)A), one can derive the reflectance R of an uncoated (A) and a coated PET interface (B). The spectral traces suggest a near ideal broad-band antireflective response with up to ≈5.2% reduction in reflectance for each coated interface. The photocatalytic self-cleaning efficiency can be studied by the decomposition of stearic acid as a function of irradiation time under simulated sunlight (AM1.5). Stearic acid is a widely used model molecule which assembles as a monolayer onto the coating and can be monitored by Fourier transform infrared spectroscopy (FTIR), shown in Fig. 8c for an antireflective coating with 50 wt% TiO2. The role of TiO2 loading is further evidenced in Fig. 8d, where the decay in normalized absorbance is compared for antireflective coatings containing 25–50 wt% TiO2. Interestingly, these coatings clearly outperform commercially available self-cleaning glass that is not antireflective and thus less constrained in coating composition.
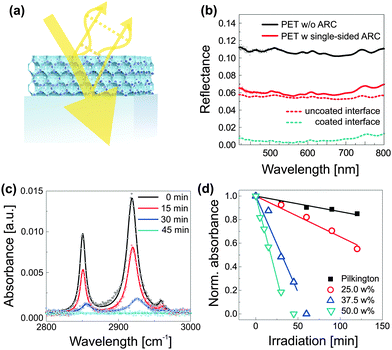 | ||
| Fig. 8 Self-cleaning antireflective optical coatings. Compatibilized photocatalytic TiO2 nanocrystals are coassembled with PI-b-PEO block copolymer and silica-based sol (a). Phase and amplitude matching of the optical coating results in destructive interference of reflected light, i.e. enhanced transmission, while the embedded photocatalytic hot spots prevent contamination of the antireflective coating. The low temperature fabrication route (<130 °C) allows film processing onto flexible and low-cost PET substrates with near optimum optical properties (b). FTIR spectra, illustrating the decomposition of stearic acid as a function of irradiation time under simulated sunlight (AM1.5) (c). Decay of the integrated peak area with time for different TiO2 loadings (d). The decay of the commercially available self-cleaning Pilkington active glass (not antireflective) is shown for comparison. (a–d) Adapted with permission from ref. 71. Copyright 2013 American Chemical Society. | ||
4 Outlook for block copolymer nanophotonics
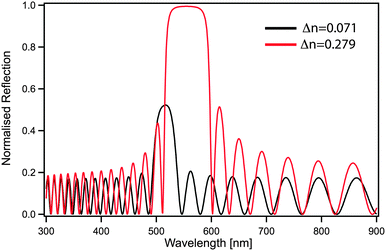
Although the control of multiple length scales and structures by block copolymer self-assembly has been demonstrated, a number of important challenges remain, preventing the exploitation of their full potential as a nanophotonics platform. In the case of photonic crystals, an increase in refractive index contrast between blocks would be beneficial not only to shift the optical response to larger wavelengths but also to increase the bandgap width. A second benefit of an improved contrast is the reduced amount of material needed to effectively reflect the desired wavelength. For a one-dimensional periodic stack, a simple transfer matrix calculation directly shows that only 20 layers (overall thickness of less than 3 μm) are sufficient to achieve 100% reflection when using refractive index contrast of Δn = 0.279, while with lower contrast Δn = 0.071 the reflectivity blue-shifts and is reduced to 50% (Fig. 9).Since the dimension of the unit cell is defined by the block copolymer molecular weight, longer blocks with higher refractive indices are also beneficial in the 3D case, where continuous morphologies such as the alternating gyroid or alternating diamond are predicted to provide a full phonic band-gap.150,151 The production of ever increasing molecular weights comes however with a significant kinetic penalty from increasing polymer entanglements. It is important to note that continuous morphologies such as the gyroid phases are mechanically self-supporting and therefore enable templating to further increase in refractive contrast through the complete removal of the organic template, thus replacing the organic matrix by air. In the case of the alternating gyroid, a refractive index of about 2.5 is large enough to open up a complete photonic band gap with a filling fraction of 50%, while for the alternating diamond a refractive index of only 2 would suffice. The optimization of geometry and refractive index are however not sufficient. The precise control of the filling fraction is required through a careful design of polymer self-assembly.104 Polymer materials exhibit a somewhat narrow range of refractive indices. Common building blocks, such as polystyrene, polyisoprene, poly(ethylene oxide) or poly(methyl methacrylate) all lie in the range of 1.4–1.6, see Table 1. Organic materials with higher refractive indices are often crystalline and thus pose a major challenge when included into a self-assembling system. The coassembly or templating of higher refractive index inorganic nanoparticles such as SiO2 or TiO2 is one viable route towards increasing the refractive index contrast.152,153 Many successful block copolymer derived photonic architectures thus rely on a partial or complete removal of the organic block copolymer. Thus the ability to derive novel nanophotonics from block copolymers is significantly aided by creative materials chemistry to facilitate novel functional architectures.
| Material | Refractive index (at 589.3 nm) |
|---|---|
| Poly(ethylene oxide), (PEO) | 1.4539 |
| Silicon dioxide | 1.458 |
| Poly(methyl methacrylate), (PMMA) | 1.481 |
| Indium oxide | 1.487 |
| Cellulose | 1.46–1.55 |
| Polyisoprene, (PI) | 1.521 |
| Chitin | 1.56 |
| Polycarbonate, (PC) | 1.586 |
| Polystyrene, (PS) | 1.592 |
| Tin oxide | 1.82 |
| Guanine | 1.83 |
| Zirconia | 2.1588 |
| Niobia | 2.316 |
| Titanium dioxide | 2.890 |
The use of block copolymer self-assembled structures as uniform templates for large scale production remains challenging. Typical grain sizes before unit cell reorientation are often just tens of micrometers, whereas practical devices would be greatly simplified by access to more uniform and larger block copolymer grains. This goes beyond the previously discussed challenges of unit cell dimension and compositional control. The upscaling of block copolymer nanostructures with precise structural control over unit cell orientation remains challenging to form centimeter-scale macroscopic materials with homogeneously oriented nanostructures. Block copolymer thin films are readily oriented via directed self-assembly,154e.g. employing chemoepitaxy43,44 or graphoepitaxy.45,46 Such approaches have limited spatial effects several unit cells away from the substrate, imposing a significant limitation on film thickness. Thus several combinations of block copolymer phase separation and guided patterns has enabled wafer-sized unidirectional alignment with a low defect density. On the other hand, the orientation of thicker bulk polymer films has been explored using shear forces, electric and magnetic fields. Lamellar structures, for example, have been demonstrated to be uniform over centimeters after shear alignment.155 Adapting block copolymer alignment procedures to emerging morphologies of interest for nanophotonics is an ongoing development. The extension of block copolymer morphologies through clever post synthesis materials chemistry also remains an open avenue of development.
5 Conclusions
Block copolymers provide an ideal platform to control and modulate the interaction of visible light with matter on the nanoscale. At sub-wavelength length scales, equilibrated block copolymer assemblies led to the first self-assembled 3D metamaterials with unprecedented control over the structural features. These alternating gyroid based gold structures were demonstrated to have tunable gyrotropic transmission as a function of the unit cell dimension, the gold strut diameter, and the gold morphology (solid vs. hollow). The photonic response varies strongly in terms of wavelength response, transmission, and in-coupling efficiency with tunable geometric parameters. Significant challenges include the capability to produce novel morphologies, control the replication of the polymer structure into novel inorganic nanoarchitectures, and the ability to form nanostructures with macroscopically uniform alignment and orientation.At the wavelength scale, block copolymers have been widely applied to 1D photonic crystals, Bragg reflectors, and antireflection coatings, including the capability to include features such as photocatalytic self-cleaning. The additional use of micellar solution-based morphologies enables the facile coassembly of inorganic materials with inverse opal-type structures with tunable refractive index, porosity, and film thickness. Growing larger 100–500 nm feature sizes for visible wavelength scale interactions poses additional challenges, particularly for photonic crystals. The transition from 1D to 3D photonic crystals made from block copolymers has remained elusive, where increasing the molecular weight slows the structure formation process. Though large unit cells have been demonstrated with ∼1 Mg mol−1 AB diblock copolymers, no morphologies that are predicted to exhibit a 3D photonic bandgap have been produced. The realization of additional morphologies requires the transition to ABC triblock terpolymers, or yet more complex systems, that introduce additional kinetic constraints. For example, the B-block of an ABC terpolymer has no free ends thereby significantly impeding its relaxation. Novel approaches need to overcome these fundamental physical limitations. For many of the discussed block copolymer nanophotonic examples, the block copolymer was used to structure inorganic materials with desirable optical constants. Here new developments in materials chemistry will not only produce new solid materials, but also coaxial, hollow, or localized islands. These post-block copolymer modifications expand upon the architectures available from polymers alone. The low-cost synthesis of block copolymers and solution-processability provide an ideal platform for the large-scale production of precision nanophotonics.
Acknowledgements
M.S. acknowledges startup funds from the University of South Carolina. S.G. is grateful for support by the German National Academy of Sciences Leopoldina, Fellowship LPDS2012-13 and startup funds from University College London, Department for Chemical Engineering. U.W. would like to thank the National Science Foundation (NSF) Single Investigator award (DMR-1409105) for financial support. U.S. acknowledges the EPSRC EP/G060649/1 for funding.References
- H. L. Hsieh, Industrial Applications of Anionic Polymerization: An Introduction, American Chemical Society, 1998, ch. 3, pp. 28–33 Search PubMed.
- J. Pendry, A. Holden, D. Robbins and W. Stewart, IEEE Trans. Microwave Theory Tech., 1999, 47, 2075–2084 CrossRef.
- J. Pendry, Science, 1999, 285, 1687–1688 CrossRef CAS.
- L. Luo and A. Eisenberg, Langmuir, 2001, 17, 6804–6811 CrossRef CAS.
- A. Choucair and A. Eisenberg, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 10, 37–44 CrossRef CAS PubMed.
- S.-H. Choi, T. P. Lodge and F. S. Bates, Phys. Rev. Lett., 2010, 104, 047802 CrossRef.
- T. Nicolai, O. Colombani and C. Chassenieux, Soft Matter, 2010, 6, 3111–3118 RSC.
- A. G. Denkova, E. Mendes and M.-O. Coppens, Soft Matter, 2010, 6, 2351–2357 RSC.
- E. G. Kelley, R. P. Murphy, J. E. Seppala, T. P. Smart, S. D. Hann, M. O. Sullivan and T. H. Epps, Nat. Commun., 2014, 5, 3599 Search PubMed.
- J. Aizenberg, J. Weaver, M. Thanawala, V. Sundar, D. Morse and P. Fratzl, Science, 2005, 309, 275–278 CrossRef CAS PubMed.
- F. Bates and G. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS PubMed.
- E. Cochran, C. Garcia-Cervera and G. Fredrickson, Macromolecules, 2006, 39, 2449–2451 CrossRef CAS.
- A. Semenov, Zhurnal Eksperimentalnoi I Teoreticheskoi Fiziki, 1985, 88, 1242–1256 CAS.
- R. Stadler, C. Auschra, J. Beckmann, U. Krappe, I. Voigtmartin and L. Leibler, Macromolecules, 1995, 28, 3080–3097 CrossRef CAS.
- U. Krappe, R. Stadler and I. Voigtmartin, Macromolecules, 1995, 28, 4558–4561 CrossRef CAS.
- Y. Matsushita, J. Suzuki and M. Seki, Physica B, 1998, 248, 238–242 CrossRef CAS.
- S. Ludwigs, A. Boker, A. Voronov, N. Rehse, R. Magerle and G. Krausch, Nat. Mater., 2003, 2, 744–747 CrossRef CAS PubMed.
- S. Ludwigs, K. Schmidt, C. Stafford, E. Amis, M. Fasolka, A. Karim, R. Magerle and G. Krausch, Macromolecules, 2005, 38, 1850–1858 CrossRef CAS.
- C. Tang, J. Bang, G. E. Stein, G. H. Fredrickson, C. J. Hawker, E. J. Kramer, M. Sprung and J. Wang, Macromolecules, 2008, 41, 4328–4339 CrossRef CAS.
- I. W. Hamley, Prog. Polym. Sci., 2009, 34, 1161–1210 CrossRef CAS PubMed.
- H. Jinnai, T. Kaneko, K. Matsunaga, C. Abetz and V. Abetz, Soft Matter, 2009, 5, 2042–2046 RSC.
- A. J. Meuler, M. A. Hillmyer and F. S. Bates, Macromolecules, 2009, 42, 7221–7250 CrossRef CAS.
- H.-C. Kim, S.-M. Park and W. D. Hinsberg, Chem. Rev., 2010, 110, 146–177 CrossRef CAS PubMed.
- C. G. Hardy and C. Tang, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 2–15 CrossRef CAS.
- M. J. Barthel, F. H. Schacher and U. S. Schubert, Polym. Chem., 2014, 5, 2647–2662 RSC.
- F. S. Bates, M. A. Hillmyer, T. P. Lodge, C. M. Bates, K. T. Delaney and G. H. Fredrickson, Science, 2012, 336, 434–440 CrossRef CAS PubMed.
- S. Anastasiadis, T. Russell, S. Satija and C. Majkrzak, Phys. Rev. Lett., 1989, 62, 1852–1855 CrossRef CAS.
- G. Coulon, T. P. Russell, V. R. Deline and P. F. Green, Macromolecules, 1989, 22, 2581–2589 CrossRef CAS.
- G. T. Pickett and A. C. Balazs, Macromol. Theory Simul., 1998, 7, 249–255 CrossRef CAS.
- Y. Tsori, E. Sivaniah, D. Andelman and T. Hashimoto, Macromolecules, 2005, 38, 7193–7196 CrossRef CAS.
- M. S. Turner, M. Rubinstein and C. M. Marques, Macromolecules, 1994, 27, 4986–4992 CrossRef CAS.
- N. Rehse, A. Knoll, M. Konrad, R. Magerle and G. Krausch, Phys. Rev. Lett., 2001, 87, 035505 CrossRef CAS.
- A. Knoll, A. Horvat, K. Lyakhova, G. Krausch, G. Sevink, A. Zvelindovsky and R. Magerle, Phys. Rev. Lett., 2002, 89, 035501 CrossRef CAS.
- T. Thurn-Albrecht, J. Schotter, G. A. Kästle, N. Emley, T. Shibauchi, L. Krusin-Elbaum, K. Guarini, C. T. Black, M. T. Tuominen and T. P. Russell, Science, 2000, 290, 2126–2129 CrossRef CAS.
- S. Kim, M. Misner, T. Xu, M. Kimura and T. Russell, Adv. Mater., 2004, 16, 226–231 CrossRef CAS.
- R. Olayo-Valles, S. Guo, M. Lund, C. Leighton and M. Hillmyer, Macromolecules, 2005, 38, 10101–10108 CrossRef CAS.
- G. Cui, S. Ohya, T. Matsutani, S. Nagano, T. Dohi, S. Nakamura, S. Sakurai, T. Miyazaki and K. Yamamoto, Nanoscale, 2013, 5, 6713–6719 RSC.
- H. Yu, T. Iyoda and T. Ikeda, J. Am. Chem. Soc., 2006, 128, 11010–11011 CrossRef CAS PubMed.
- R. Segalman, H. Yokoyama and E. Kramer, Adv. Mater., 2001, 13, 1152–1155 CrossRef CAS.
- S.-M. Park, M. P. Stoykovich, R. Ruiz, Y. Zhang, C. T. Black and P. E. Nealey, Adv. Mater., 2007, 19, 607–611 CrossRef CAS.
- A. M. Welander, H. Kang, K. O. Stuen, H. H. Solak, M. Mueller, J. J. de Pablo and P. F. Nealey, Macromolecules, 2008, 41, 2759–2761 CrossRef CAS.
- C. M. Bates, T. Seshimo, M. J. Maher, W. J. Durand, J. D. Cushen, L. M. Dean, G. Blachut, C. J. Ellison and C. G. Willson, Science, 2012, 338, 775–779 CrossRef CAS PubMed.
- J. Heier, E. Kramer, S. Walheim and G. Krausch, Macromolecules, 1997, 30, 6610–6614 CrossRef CAS.
- S. Kim, H. Solak, M. Stoykovich, N. Ferrier, J. de Pablo and P. Nealey, Nature, 2003, 424, 411–414 CrossRef CAS PubMed.
- I. Bita, J. K. W. Yang, Y. S. Jung, C. A. Ross, E. L. Thomas and K. K. Berggren, Science, 2008, 321, 939–943 CrossRef CAS PubMed.
- J.-B. Chang, H. K. Choi, A. F. Hannon, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Nat. Commun., 2014, 5, 3305 Search PubMed.
- E. J. W. Crossland, S. Ludwigs, M. A. Hillmyer and U. Steiner, Soft Matter, 2010, 6, 670–676 RSC.
- M. R. J. Scherer, P. M. S. Cunha and U. Steiner, Adv. Mater., 2014, 26, 2403–2407 CrossRef CAS PubMed.
- E. Kim, Y. Vaynzof, A. Sepe, S. Guldin, M. Scherer, P. Cunha, S. V. Roth and U. Steiner, Adv. Funct. Mater., 2014, 24, 863–872 CrossRef CAS.
- E. J. W. Crossland, M. Kamperman, M. Nedelcu, C. Ducati, U. Wiesner, D. M. Smilgies, G. E. S. Toombes, M. A. Hillmyer, S. Ludwigs, U. Steiner and H. J. Snaith, Nano Lett., 2009, 9, 2807–2812 CrossRef CAS PubMed.
- T. Hoheisel, K. Hur and U. Wiesner, Prog. Polym. Sci., 2015, 40, 3–32 CrossRef CAS PubMed.
- B. C. Garcia, M. Kamperman, R. Ulrich, A. Jain, S. M. Gruner and U. Wiesner, Chem. Mater., 2009, 21, 5397–5405 CrossRef CAS.
- D. Zhao, J. Feng, Q. Huo, N. Melosh, G. Fredrickson, B. Chmelka and G. Stucky, Science, 1998, 279, 548–552 CrossRef CAS.
- M. Templin, A. Franck, A. Duchesne, H. Leist, Y. Zhang, R. Ulrich, V. Schadler and U. Wiesner, Science, 1997, 278, 1795–1798 CrossRef CAS.
- P. Yang, D. Zhao, D. Margolese, B. Chmelka and G. Stucky, Nature, 1998, 396, 152–155 CrossRef CAS PubMed.
- S. C. Warren, L. C. Messina, L. S. Slaughter, M. Kamperman, Q. Zhou, S. M. Gruner, F. J. Disalvo and U. Wiesner, Science, 2008, 320, 1748–1752 CrossRef CAS PubMed.
- G. Soler-Illia and C. Sanchez, New J. Chem., 2000, 24, 493–499 RSC.
- Z. Li, H. Sai, S. C. Warren, M. Kamperman, H. Arora, S. M. Gruner and U. Wiesner, Chem. Mater., 2009, 21, 5578–5584 CrossRef CAS PubMed.
- S. C. Warren, F. J. Disalvo and U. Wiesner, Nat. Mater., 2007, 6, 156–161 CrossRef CAS PubMed.
- E. Crepaldi, G. Soler-Illia, D. Grosso, F. Cagnol, F. Ribot and C. Sanchez, J. Am. Chem. Soc., 2003, 125, 9770–9786 CrossRef CAS PubMed.
- G. E. S. Toombes, S. Mahajan, M. Weyland, A. Jain, P. Du, M. Kamperman, S. M. Gruner, D. A. Muller and U. Wiesner, Macromolecules, 2008, 41, 852–859 CrossRef CAS.
- G. E. S. Toombes, S. Mahajan, M. Thomas, P. Du, M. W. Tate, S. M. Gruner and U. Wiesner, Chem. Mater., 2008, 20, 3278–3287 CrossRef CAS.
- M. Stefik, S. Mahajan, H. Sai, T. H. Epps, III, F. S. Bates, S. M. Gruner, F. J. Disalvo and U. Wiesner, Chem. Mater., 2009, 21, 5466–5473 CrossRef CAS PubMed.
- M. Stefik, S. Wang, R. Hovden, H. Sai, M. W. Tate, D. A. Muller, U. Steiner, S. M. Gruner and U. Wiesner, J. Mater. Chem., 2012, 22, 1078–1087 RSC.
- P. Docampo, M. Stefik, S. Guldin, R. Gunning, N. A. Yufa, N. Cai, P. Wang, U. Steiner, U. Wiesner and H. J. Snaith, Adv. Energy Mater., 2012, 2, 676–682 CrossRef CAS.
- S. Guldin, P. Docampo, M. Stefik, G. Kamita, U. Wiesner, H. J. Snaith and U. Steiner, Small, 2012, 8, 432–440 CrossRef CAS PubMed.
- J. Lee, M. C. Orilall, S. C. Warren, M. Kamperman, F. J. Disalvo and U. Wiesner, Nat. Mater., 2008, 7, 222–228 CrossRef CAS PubMed.
- V. Mueller, M. Rasp, J. Rathousky, B. Schuetz, M. Niederberger and D. Fattakhova-Rohlfing, Small, 2010, 6, 633–637 CrossRef CAS PubMed.
- J. M. Szeifert, D. Fattakhova-Rohlfing, D. Georgiadou, V. Kalousek, J. Rathousky, D. Kuang, S. Wenger, S. M. Zakeeruddin, M. Graetzel and T. Bein, Chem. Mater., 2009, 21, 1260–1265 CrossRef CAS.
- T. Brezesinski, J. Wang, J. Polleux, B. Dunn and S. H. Tolbert, J. Am. Chem. Soc., 2009, 131, 1802–1809 CrossRef CAS PubMed.
- S. Guldin, P. Kohn, M. Stefik, J. Song, G. Divitini, F. Ecarla, C. Ducati, U. Wiesner and U. Steiner, Nano Lett., 2013, 13, 5329–5335 CrossRef CAS PubMed.
- P. Kohn, S. Pathak, M. Stefik, C. Ducati, U. Wiesner, U. Steiner and S. Guldin, Nanoscale, 2013, 5, 10518–10524 RSC.
- I. E. Rauda, R. Buonsanti, L. C. Saldarriaga-Lopez, K. Benjauthrit, L. T. Schelhas, M. Stefik, V. Augustyn, J. Ko, B. Dunn, U. Wiesner, D. J. Milliron and S. H. Tolbert, ACS Nano, 2012, 6, 6386–6399 CrossRef CAS PubMed.
- K. Hur, R. G. Hennig, F. A. Escobedo and U. Wiesner, Nano Lett., 2012, 12, 3218–3223 CrossRef CAS PubMed.
- A. Urbas, Y. Fink and E. Thomas, Macromolecules, 1999, 32, 4748–4750 CrossRef CAS.
- A. Urbas, R. Sharp, Y. Fink, E. Thomas, M. Xenidou and L. Fetters, Adv. Mater., 2000, 12, 812–814 CrossRef CAS.
- C. Osuji, C. Chao, I. Bita, C. Ober and E. Thomas, Adv. Funct. Mater., 2002, 12, 753–758 CrossRef CAS.
- J. Yoon, R. Mathers, G. Coates and E. Thomas, Macromolecules, 2006, 39, 1913–1919 CrossRef CAS.
- B. R. Sveinbjoernsson, R. A. Weitekamp, G. M. Miyake, Y. Xia, H. A. Atwater and R. H. Grubbs, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14332–14336 CrossRef CAS PubMed.
- G. M. Miyake, R. A. Weitekamp, V. A. Piunova and R. H. Grubbs, J. Am. Chem. Soc., 2012, 134, 14249–14254 CrossRef CAS PubMed.
- A. Urbas, M. Maldovan, P. DeRege and E. Thomas, Adv. Mater., 2002, 14, 1850–1853 CrossRef CAS.
- T. Deng, C. Chen, C. Honeker and E. Thomas, Polymer, 2003, 44, 6549–6553 CrossRef CAS PubMed.
- M. Bockstaller, R. Kolb and E. Thomas, Adv. Mater., 2001, 13, 1783–1786 CrossRef CAS.
- M. Bockstaller and E. Thomas, J. Phys. Chem. B, 2003, 107, 10017–10024 CrossRef CAS.
- A. Urbas, R. Sharp, Y. Fink, E. Thomas, M. Xenidou and L. Fetters, Adv. Mater., 2000, 12, 812–814 CrossRef CAS.
- S. Valkama, H. Kosonen, J. Ruokolainen, T. Haatainen, M. Torkkeli, R. Serimaa, G. Ten Brinke and O. Ikkala, Nat. Mater., 2004, 3, 872–876 CrossRef CAS PubMed.
- Y. Kang, J. J. Walish, T. Gorishnyy and E. L. Thomas, Nat. Mater., 2007, 6, 957–960 CrossRef CAS PubMed.
- J. J. Walish, Y. Kang, R. A. Mickiewicz and E. L. Thomas, Adv. Mater., 2009, 21, 3078–3081 CrossRef CAS.
- H. S. Lim, J.-H. Lee, J. J. Walish and E. L. Thomas, ACS Nano, 2012, 6, 8933–8939 CrossRef CAS PubMed.
- A. Noro, Y. Tomita, Y. Shinohara, Y. Sageshima, J. J. Walish, Y. Matsushita and E. L. Thomas, Macromolecules, 2014, 47, 4103–4109 CrossRef CAS.
- M. Maldovan, A. Urbas, N. Yufa, W. Carter and E. Thomas, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165123 CrossRef.
- T. Epps and F. Bates, Macromolecules, 2006, 39, 2676–2682 CrossRef CAS.
- J. Suzuki, K. Nakane, A. Takano and Y. Matsushita, Polymer, 2004, 45, 8989–8997 CrossRef CAS PubMed.
- J.-H. Lee, C. Y. Koh, J. P. Singer, S.-J. Jeon, M. Maldovan, O. Stein and E. L. Thomas, Adv. Mater., 2014, 26, 532–569 CrossRef CAS PubMed.
- D. A. Rider, J. I. L. Chen, J.-C. Eloi, A. C. Arsenault, T. P. Russell, G. A. Ozin and I. Manners, Macromolecules, 2008, 41, 2250–2259 CrossRef CAS.
- H. Yabu, T. Jinno, K. Koike, T. Higuchi and M. Shimomura, Macromolecules, 2011, 44, 5868–5873 CrossRef CAS.
- A. Demetriadou, S. S. Oh, S. Wuestner and O. Hess, New J. Phys., 2012, 14, 083032 CrossRef.
- S. S. Oh, A. Demetriadou, S. Wuestner and O. Hess, Adv. Mater., 2013, 25, 612–617 CrossRef CAS PubMed.
- K. Hur, Y. Francescato, V. Giannini, S. A. Maier, R. G. Hennig and U. Wiesner, Angew. Chem., Int. Ed., 2011, 50, 11985–11989 CrossRef CAS PubMed.
- S. Vignolini, N. A. Yufa, P. S. Cunha, S. Guldin, I. Rushkin, M. Stefik, K. Hur, U. Wiesner, J. J. Baumberg and U. Steiner, Adv. Mater., 2012, 24, Op23–Op27 CrossRef CAS PubMed.
- S. Salvatore, A. Demetriadou, S. Vignolini, S. S. Oh, S. Wuestner, N. A. Yufa, M. Stefik, U. Wiesner, J. J. Baumberg, O. Hess and U. Steiner, Adv. Mater., 2013, 25, 2713–2716 CrossRef CAS PubMed.
- P. Farah, A. Demetriadou, S. Salvatore, S. Vignolini, M. Stefik, U. Wiesner, O. Hess, U. Steiner, V. K. Valev and J. J. Baumberg, Phys. Rev. Appl., 2014, 2, 044002 CrossRef.
- S. Salvatore, S. Vignolini, J. Philpott, M. Stefik, U. Wiesner, J. J. Baumberg and U. Steiner, Nanoscale, 2015, 7, 1032–1036 RSC.
- J. A. Dolan, B. D. Wilts, S. Vignolini, J. J. Baumberg, U. Steiner and T. D. Wilkinson, Adv. Opt. Mater., 2015, 3, 12–32 CrossRef CAS.
- V. Babin, P. Garstecki and R. Holyst, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 235120 CrossRef.
- V. Saranathan, C. O. Osuji, S. G. J. Mochrie, H. Noh, S. Narayanan, A. Sandy, E. R. Dufresne and R. O. Prum, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11676–11681 CrossRef CAS PubMed.
- J. Chatterjee, S. Jain and F. S. Bates, Macromolecules, 2007, 40, 2882–2896 CrossRef CAS.
- Z. Li, K. Hur, H. Sai, T. Higuchi, A. Takahara, H. Jinnai, S. M. Gruner and U. Wiesner, Nat. Commun., 2014, 5, 3247 Search PubMed.
- S. Guldin, M. Kolle, M. Stefik, R. Langford, D. Eder, U. Wiesner and U. Steiner, Adv. Mater., 2011, 23, 3664–3668 CrossRef CAS PubMed.
- S. Guldin, M. Kolle, M. Stefik, U. Wiesner and U. Steiner, Proc. SPIE, 2011, 8095, 80951G CrossRef PubMed.
- S. Guldin, P. Docampo, M. Stefik, G. Kamita, U. Wiesner, H. Snaith and U. Steiner, Small, 2012, 8, 432–440 CrossRef CAS PubMed.
- S. Guldin, S. Hüttner, M. Kolle, M. Welland, P. Müller-Buschbaum, R. Friend, U. Steiner and N. Tetreault, Nano Lett., 2010, 10, 2303–2309 CrossRef CAS PubMed.
- S. Guldin and U. Steiner, Proc. SPIE, 2014, 9083, 908320 CrossRef PubMed.
- S. Choi, M. Mamak, G. von Freymann, N. Chopra and G. Ozin, Nano Lett., 2006, 6, 2456–2461 CrossRef CAS PubMed.
- M. C. Fuertes, F. J. Lopez-Alcaraz, M. C. Marchi, H. E. Troiani, V. Luca, H. Míguez and G. J. d. A. Arturo Soler-Illia, Adv. Funct. Mater., 2007, 17, 1247–1254 CrossRef CAS.
- G. Floudas, R. Ulrich and U. Wiesner, J. Chem. Phys., 1999, 110, 652–663 CrossRef CAS PubMed.
- J. Allgaier, A. Poppe, L. Willner and D. Richter, Macromolecules, 1997, 30, 1582–1586 CrossRef CAS.
- L. Bonifacio, B. Lotsch, D. Puzzo, F. Scotognella and G. Ozin, Adv. Mater., 2009, 21, 1641–1646 CrossRef CAS.
- M. Calvo, S. Colodrero, N. Hidalgo, G. Lozano, C. Lopez-Lopez, O. Sanchez-Sobrado and H. Míguez, Energy Environ. Sci., 2011, 4, 4800–4812 Search PubMed.
- C. Fuertes, S. Colodrero, G. Lozano, A. González-Elipe, D. Grosso, C. Boissière, C. Sánchez, G. J. d. A. Soler-Illia and H. Míguez, J. Phys. Chem. C, 2008, 106, 3157–3163 Search PubMed.
- V. Lin, K. Motesharei, K. Dancil, M. Sailor and M. Ghadiri, Science, 1997, 278, 840–843 CrossRef CAS.
- L. D. Bonifacio, D. P. Puzzo, S. Breslav, B. M. Willey, A. McGeer and G. A. Ozin, Adv. Mater., 2010, 22, 1351–1354 CrossRef CAS PubMed.
- I. Jolliffe, Principal Component Analysis, Springer, 2nd edn, 2002 Search PubMed.
- N. Hidalgo, M. E. Calvo and H. Míguez, Small, 2009, 5, 2309–2315 CrossRef CAS PubMed.
- O. Sánchez-Sobrado, M. E. Calvo, N. Núñez, M. Ocaña, G. Lozano and H. Míguez, Nanoscale, 2010, 2, 936 RSC.
- D. Puzzo, F. Scotognella, M. Zavelani-Rossi, M. Sebastian, A. Lough, I. Manners, G. Lanzani, R. Tubino and G. Ozin, Nano Lett., 2009, 9, 4273–4278 CrossRef CAS PubMed.
- F. Scotognella, D. P. Puzzo, M. Zavelani-Rossi, J. Clark, M. Sebastian, G. A. Ozin and G. Lanzani, Chem. Mater., 2011, 23, 805–809 CrossRef CAS.
- A. Mihi and H. Míguez, J. Phys. Chem. B, 2005, 109, 15968–15976 CrossRef CAS PubMed.
- S. Colodrero, A. Mihi, J. A. Anta, M. Ocaña and H. Míguez, J. Phys. Chem. C, 2009, 113, 1150–1154 CAS.
- S. Colodrero, A. Mihi, L. Haggman, M. Ocaña, G. Boschloo, A. Hagfeldt and H. Míguez, Adv. Mater., 2009, 21, 764–770 CrossRef CAS.
- D. Colonna, S. Colodrero, H. Lindstrom, A. Di Carlo and H. Miguez, Energy Environ. Sci., 2012, 5, 8238–8243 CAS.
- Z. Wu, D. Lee, M. F. Rubner and R. E. Cohen, Small, 2007, 3, 1445–1451 CrossRef CAS PubMed.
- S. Colodrero, M. Ocana and H. Míguez, Langmuir, 2008, 24, 4430–4434 CrossRef CAS PubMed.
- M. E. Calvo, S. Colodrero, T. C. Rojas, J. A. Anta, M. Ocana and H. Míguez, Adv. Funct. Mater., 2008, 18, 2708–2715 CrossRef CAS.
- C. Lopez-Lopez, S. Colodrero, S. R. Raga, H. Lindstrom, F. Fabregat-Santiago, J. Bisquert and H. Miguez, J. Mater. Chem., 2012, 22, 1751–1757 RSC.
- S. Guldin, P. Docampo, S. Hütner, P. Kohn, M. Stefik, H. J. Snaith, U. Wiesner and U. Steiner, Proc. SPIE, 2011, 8111, 811108 CrossRef PubMed.
- M. Anaya, M. E. Calvo, J. M. Luque-Raigon and H. Miguez, J. Am. Chem. Soc., 2013, 135, 7803–7806 CrossRef CAS PubMed.
- P. Docampo, S. Guldin, T. Leijtens, N. K. Noel, U. Steiner and H. J. Snaith, Adv. Mater., 2014, 26, 4013–4030 CrossRef CAS PubMed.
- G. von Freymann, V. Kitaev, B. V. Lotsch and G. A. Ozin, Chem. Soc. Rev., 2013, 42, 2528–2554 RSC.
- H. Macleod, Thin film optical filters, Institute of Physics Publishing, 3rd edn, 2001 Search PubMed.
- W. Joo, H. J. Kim and J. K. Kim, Langmuir, 2010, 26, 5110–5114 CrossRef CAS PubMed.
- S. Kim, J. Cho and K. Char, Langmuir, 2007, 23, 6737–6743 CrossRef CAS PubMed.
- B. G. Kum, Y. C. Park, Y. J. Chang, J. Y. Jeon and H. M. Jang, Thin Solid Films, 2011, 519, 3778–3781 CrossRef CAS PubMed.
- T. Lohmueller, M. Helgert, M. Sundermann, R. Brunner and J. P. Spatz, Nano Lett., 2008, 8, 1429–1433 CrossRef PubMed.
- B. Paeivaenranta, P. K. Sahoo, E. Tocce, V. Auzelyte, Y. Ekinci, H. H. Solak, C.-C. Liu, K. O. Stuen, P. F. Nealey and C. David, ACS Nano, 2011, 5, 1860–1864 CrossRef PubMed.
- X. Li, J. Gao, L. Xue and Y. Han, Adv. Funct. Mater., 2010, 20, 259–265 CrossRef CAS.
- H.-Y. Hsueh, H.-Y. Chen, M.-S. She, C.-K. Chen, R.-M. Ho, S. Gwo, H. Hasegawa and E. L. Thomas, Nano Lett., 2010, 10, 4994–5000 CrossRef CAS PubMed.
- I. P. Parkin and R. G. Palgrave, J. Mater. Chem., 2005, 15, 1689–1695 RSC.
- H. Tang, H. Berger, P. Schmid and F. Lévy, Solid State Commun., 1994, 92, 267–271 CrossRef CAS.
- V. Babin, P. Garstecki and R. Hoyst, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 235120 CrossRef.
- C. T. Chan, K. M. Ho and C. M. Soukoulis, EPL, 1991, 16, 563 CrossRef CAS.
- K. Krogman, T. Druffel and M. Sunkara, Nanotechnology, 2005, 16, S338–S343 CrossRef PubMed.
- C. Lu and B. Yang, J. Mater. Chem., 2009, 19, 2884–2901 RSC.
- J. Y. Cheng, C. A. Ross, H. I. Smith and E. L. Thomas, Adv. Mater., 2006, 18, 2505–2521 CrossRef CAS.
- N. Houbenov, R. Milani, M. Poutanen, J. Haataja, V. Dichiarante, J. Sainio, J. Ruokolainen, G. Resnati, P. Metrangolo and O. Ikkala, Nat. Commun., 2014, 5, 4043 CAS.
- C. A. Tyler, J. Qin, F. S. Bates and D. C. Morse, Macromolecules, 2007, 40, 4654–4668 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |