 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correction: “On-the-fly” coupled cluster path-integral molecular dynamics: impact of nuclear quantum effects on the protonated water dimer
Thomas
Spura
a,
Hossam
Elgabarty
a and
Thomas D.
Kühne
*ab
aDynamics of Condensed Matter, Department of Chemistry, University of Paderborn, Warburger Str. 100, D-33098 Paderborn, Germany. E-mail: tdkuehne@mail.upb.de
bPaderborn Center for Parallel Computing and Institute for Lightweight Design with Hybrid Systems, University of Paderborn, Warburger Str. 100, D-33098 Paderborn, Germany
First published on 7th July 2015
Abstract
Correction for “On-the-fly” coupled cluster path-integral molecular dynamics: impact of nuclear quantum effects on the protonated water dimer` by Thomas Spura et al., Phys. Chem. Chem. Phys., 2015, 17, 14355–14359.
In our calculations of the NMR chemical shifts,1 the nuclear geometries have been erroneously assumed to be in Bohr instead of Angstrom. Even though the conclusions of this work are not affected, the scale on the y-axis of Fig. 3–5 differ quantitatively and the absolute values of the computed chemical shifts are substantially reduced. We would like to apologize for any inconveniences this mistake may have caused.
In the following, the corrected Fig. 3–5 are shown. Moreover, on page 14358 it should read “Including NQE, the average isotropic nuclear shielding increases by 0.23 ppm (was: 3 ppm),… using classical nuclei the differences in the isotropic nuclear shielding of the proton between HF and CC is 0.64 ppm (was: 7.4 ppm), while including nuclear NQE reduces the difference to −0.31 ppm (was: 1.5 ppm) only.” and “As a consequence, the NQE induced change of our vapor-to-liquid chemical shift estimate is −0.67 ppm (was: −3.7 ppm),… The corresponding value at the HF level of theory is 0.25 ppm (was: 2.2 ppm),… the difference between the largest and smallest eigenvalues of the shielding tensor (the span) decreases by 1.7 ppm (was: 8 ppm) in case of the CC-PIMD simulation including NQE”.
 | ||
| Fig. 3 Isotropic nuclear magnetic shielding of the proton in units of ppm as a function of the proton reaction coordinate ν. | ||
 | ||
| Fig. 4 Isotropic nuclear magnetic shielding of the four hydrogens in units of ppm as a function of the hydrogen–oxygen distance rOH. | ||
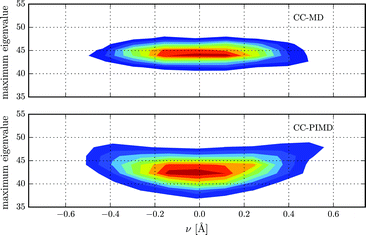 | ||
| Fig. 5 Distribution of the maximum eigenvalue of the proton magnetic shielding tensor in units of ppm with respect to the proton reaction coordinate ν. | ||
References
- T. Spura, H. Elgabarty and T. D. Kühne, Phys. Chem. Chem. Phys., 2015, 17, 14355–14359 RSC.
| This journal is © the Owner Societies 2015 |
