Influence of additives on the structure of surfactant-free microemulsions

Abstract

We study the addition of electrolytes to surfactant-free microemulsions in the domain where polydisperse pre-Ouzo aggregates are present. As in previous studies, the microemulsion is the ternary system water/ethanol/1-octanol, where ethanol acts as co-solvent. Addition of electrolytes modifies the static X-ray and neutron scattering, and dynamic light scattering patterns, as well as the position of the miscibility gap, where spontaneous emulsification occurs upon dilution with water. All observations can be rationalized considering that electrolytes are either “salting out” the ethanol, which is the main component of the interface stabilizing the aggregates, or producing charge separation via the antagonistic ion effect discovered by Onuki et al. Amphiphilic electrolytes, such as sodium dodecylsulfate or sodium dietheylhexylphosphate, induce a gradual transition towards monodisperse ionic micelles with their characteristic broad scattering “peak”. In these micelles the ethanol plays then the role of a cosurfactant. Dynamic light scattering can only be understood by combination of fluctuations of aggregate concentration due to the vicinity of a critical point and in-out fluctuations of ethanol.

---

1. Introduction

The so-called Ouzo effect is characterized by the formation of remarkably fine and time-stable emulsions when water is added in appropriate amounts to a mixture of ethanol and a hydrophobic component.¹ The name comes from the Greek drink Ouzo, in which the hydrophobic molecule trans-anethole is dissolved in the water-miscible solvent ethanol. The necessary condition for the Ouzo effect to occur is the addition of a solvent A (e.g. water) to a second solvent B, which is highly or entirely miscible with solvent A (e.g. ethanol), and a third component, which is highly soluble in solvent B, but not in solvent A (e.g. trans-anethole).² The Ouzo effect allows producing nano-capsules loaded with active components or to functionalize a hydrophobic surface with polymeric nano-lenses.³ Whereas the Ouzo effect had been known for a long time, the fact that well-defined aggregates of typical size similar to small surfactant-based micelles occur in the pre-Ouzo region has been demonstrated only recently, via detailed contrast variation neutron scattering experiments.⁴ All other scattering techniques may be ambiguous since there is always a critical point at compositions close to such systems and the presence of well-defined aggregates with defined size is difficult to distinguish from the occurrence of critical fluctuations. The important point is that, in a defined region close to the phase boundary, ethanol plays the role of the surfactant, an effect independent of critical fluctuations.⁵ For the sake of comprehension, we call the pre-Ouzo region this domain in the monophasic and clear phase, close to the phase separation border. In other words, the pre-Ouzo effect occurs before enough water is added to reach the Ouzo region, where the visible Ouzo effect takes place. Conductivity experiments help identifying three types of structures: pre-Ouzo aggregates, bicontinuous phases, and reverse micelles morphology. To all these structures correspond characteristic scattering patterns.⁶

The presence of a nano-ordering was also observed by Klossek et al. with dynamic (DLS) combined to static light scattering (SLS) in the system water/ethanol/1-octanol, which fulfills the conditions of the Ouzo effect, as explained before.² They proved the existence of well-defined domains composed of swollen micellar aggregates, which can be called surfactant-free microemulsions. Similar results were also found for the systems water/benzyl alcohol/ethanol or ethyl lactate or γ-valerolactone as oil phase.⁷ It is worth pointing out that surfactant-free microemulsions seem to occur always in the pre-Ouzo region as long as the studied system does exhibit an Ouzo region. This pre-Ouzo effect was then investigated in more details. Using molecular dynamics simulations, Schöttl et al. characterized the system water/ethanol/1-octanol.⁸ The first experimental observations were confirmed and micelle-like structures were indeed found for compositions in the pre-Ouzo region. Further, the authors showed that ethanol is distributed over both pseudo-phases and gave a clear molecular view of the system: according to their work, 1-octanol forms aggregates that are swollen by ethanol. A slight accumulation of ethanol is observed at the interface. Ethanol is also present in the water pseudo-phase. As expected, the surfactant-free aggregates disappear progressively when more and more ethanol is added. Diat et al. also studied the system water/ethanol/1-octanol by combining contrast-variation small-angle neutron scattering (SANS) and small- and wide-angle X-ray scattering (SWAXS).⁴ Their results are in agreement with the previously described work. They proved the existence of oil-rich aggregates of well defined size around 2 nm in radius. Ternary solutions in the pre-Ouzo region already showed their capability to be excellent solubilizers in the field of formulation. Zoumpanioti et al. showed that lipases from Rhizomucor miehei and Candida antartica could be entrapped in surfactant-free microemulsions and still have catalytic activities at 30 °C.⁹ The stability of enzymes is also higher than that observed in surfactant-based microemulsions. Introducing the term “lipotrope”, Bauduin et al. showed that polar compounds could be solubilize in dodecane by adding alcohols.¹⁰ Marcus et al. investigated mosquito repellent formulations using natural and synthetic mosquito repellent molecules used on the market.¹¹ They demonstrated that nano-structures with generally an organic continuum were present in such surfactant-free formulations. This nano-ordering may have an impact on the behavior of the mosquito repellent on the skin, and the outer pseudo-phase can play a role on the mosquito receptors. The same authors also found that such fluctuations can be predicted in Eau de Toilette, Eau de Parfum, and possibly in perfumes with very hydrophobic fragrance molecules.¹² The nano-ordering may have a significant influence on the vapour pressures of the different components. Tchakalova et al. proved these assumptions with the evaporation of ethanol-containing fragrance solutions, which reveals that the liquid and thus the vapour composition transformed from an unstructured ethanol-rich solution to a structured water-rich solution, affecting the fragrance performance.¹³ The fragrance evaporation was also accelerated in the pre-Ouzo region. Hankel et al. also investigated the possibility to dissolve hydrophobic compounds in surfactant-free microemulsions using a gas. They studied the dissolution of ibuprofen in presence of large amounts of water in the pressurized system water/acetone/CO₂.¹⁴

The aim of this work is now to understand how additives influence the weakly associated surfactant-free microemulsions. To this purpose, we study here the effect of salts and surfactants on it.

Beyond “simple” electrolytes, we consider in the same methodology amphiphilic molecules, i.e. sodium dodecylsulfate (SDS) and diethylhexylphosphate, as well in its acidic as in the sodium balanced form (HDEHP and NaDEHP, respectively). SDS and NaDEHP are water-soluble surfactants, while HDEHP is only soluble in non-polar solvents. These are the most used surfactants industrially for detergency and selective extraction. Finally, we consider also a so-called antagonistic salt, namely sodium tetraphenylborate (NaBPh₄).

Usually, the addition of a simple salt to a binary mixture of water and an organic solvent changes the phase behavior of this mixture. Cations and anions of simple salts are sometimes labeled as hydrophilic: this means that their water hydration enthalpy as well as entropy are much larger than kT or respectively kT/K and the corresponding values are tabulated for pure water.¹⁵ To our knowledge, enthalpy and its entropic compensation¹⁶ are not available in water/ethanol binary mixtures. However, it is known that the solubility of salts decreases when adding ethanol, an effect used in organic synthesis.¹⁷ By attracting water molecules for their solvation shell, some salts decrease the miscibility of water and the organic solvent when the salt concentration is high. The two-phase region is then enhanced. But this is not the case for all salts. Sadakane et al. observed the opposite behavior when adding a salt formed by antagonistic ions such as NaBPh₄ to the binary mixture of deuterated water (D₂O) and 3-methylpyridine (3MP).^18,19 NaBPh₄ is called an antagonistic salt, because it is composed of a chaotropic anion and a kosmotropic cation. The chaotropic ion is adsorbed to the water/oil (w/o) interface in all emulsions or micellar systems investigated so far. Is this local charge separation also true in the case of pre-Ouzo aggregates? Using SANS, Sadakane et al. showed even the emergence of surfactant-free lamellar lyotropic phases upon addition of NaBPh₄. They also observed for the first time an ordered lamellar structure as a consequence of the local charge separation due to preferential solvation of an antagonistic salt.²⁰ With the binary system D₂O/3MP, they also investigated the effects of an inversely antagonistic salt, tetraphenylphosphonium chloride. The solvation effects were the same as the normally antagonistic salt NaBPh₄, i.e. the presence of a long-range periodic structure and a shrinking of the two-phase region were observed. These behaviors and the preferential solvation phenomenon have been quantified and explained by Onuki et al.²¹ Chaotropic anions have a higher tendency to adsorb onto the interface between water and the organic solvent, thus forming an electric double layer without initial charge of the interface. Thus, electrostatic forces can drive to a minimum in free energy if a lamellar phase is formed. In other words, chaotropic ions act as “sticky” disrupting ions at soft interfaces and kosmotropic ions form a diffuse layer.²² As a consequence, it is most interesting to test the effect of the antagonistic electrolytes NaBPh₄ on surfactant-free microemulsions.

Our reference system is the ternary mixture water/ethanol/1-octanol in the pre-Ouzo region, i.e. in the region where initially polydisperse pre-Ouzo aggregates of correlation length around 2 nm are observed. Further, the partition coefficient of ethanol between octanol-rich aggregates and the water-rich external medium, a water/ethanol mixture that constitutes the solvent, is close to one. Since the sample is in the single-phase region, both pseudo-phases are in dynamic equilibrium.²³

2. Experimental

2.1. Materials

Ethanol (purity ≥99.8%), NaSCN (purity ≥98%), and dietheylhexylphophoric acid (HDEHP, purity ≥97%) were purchased from Sigma-Aldrich Chemie GmbH (Steinheim, Germany). 1-Octanol (purity ≥99%), LiCl (purity ≥99%), KCl (purity ≥99.5%), NaBr (purity ≥99%), NaNO₃ (purity ≥99%), and NaOH (purity ≥99%) were purchased from Merck Schuchardt OHG (Hohenbrunn, Germany). CH₃COONa (purity ≥99%), CaCl₂ (purity ≥96%), and NH₄Cl (purity ≥99.8%) were purchased from Merck (Darmstadt, Germany). NaCl (purity ≥99.6%) was purchased from VWR (Leuven, Belgium). CsCl (purity ≥99%) and NaBPh₄ (purity ≥99.5%) were purchased from Alfa Aesar GmbH & CoKG (Karlsruhe, Germany). NaClO₄ (purity ≥88%) was from Fluka AG (Buchs, Switzerland). Sodium dodecylsulfate (SDS, ultrapure) was from AppliChem GmbH (Darmstadt, Germany). All solutions were prepared using deionized water with a resistivity of 18.2 MΩ cm. All other chemicals were used without further purification.

2.2. Dynamic light scattering

Solutions were prepared by mixing the adequate amounts of each constituent in a test tube. The prepared solution was then filtered with a 0.2 μm PTFE membrane filter into a cylindrical light-scattering cell of 10 mm outer diameter. The cell was placed in a temperature controlled bath of toluene, at 25 °C. The measurements were carried out with a CGS-3 goniometer system from ALV (Langen, Germany) equipped with an ALV-7004/FAST Multiple Tau digital correlator and a vertical-polarized 22 mW HeNe laser (wavelength λ = 632.8 nm). The homodyne correlation functions 〈I(0)I(τ)〉 (or G¹(τ), τ being the correlator delay time) were recorded for 300 s at an angle of 90°.

As discussed elsewhere, the correlation functions reflect fluctuations of nano-clusters and not molecular critical fluctuations near a critical point.^2,8,11,12 However, in ternary systems, dynamic light scattering is the time-convolution of two different possible fluctuations, with two (dn/dc) and constant chemical potential of pseudo-component 1 and of pseudo-component 2.²⁴ It is the choice of the experimentalist to choose convenient pseudo-components. In the study here, we choose as for classical micelles the pseudo-component to be an aggregate with its typical diffusion time.

According to the general theory of Aniansson et al.,²⁵ the in-out fluctuation of the most labile component induces one type of refractive index increment (dn/dc). The “rapid component” is in our case the ethanol molecules fluctuating with a short time-scale between octanol-rich aggregates and water-rich “solvent”. The chemical potential of ethanol is equal in both pseudo-phases and the transfer energy of ethanol between those phases remains much smaller than kT. The contribution of ethanol convolutes with the slower one, which is attributed to the fluctuations of aggregates in the solvent with constant partition of the cosolvent. These two orthogonal fluctuations are shown in Fig. 1 and induce two distinct contributions in the correlation.²⁶ In our case, slow and rapid components can be considered as independent and therefore additive in intensity. These two contributions combine also in binary systems without existence of a well-defined interface.²⁷ In the case of binary solutions near a critical point, the intense light scattering has also to be decomposed in monomer-micelle and micelle-micelle fluctuations, with all the consequences: DLS and SLS near a phase separation line is always observed, and is not the proof of existence of surfactant-free microemulsions in a given sample. One consequence is that the correlation sizes deduced from light scattering are typical of slowly fluctuating aggregates or quickly fluctuating cosolvent molecules. The apparent exponents measured in the situation of two combined fluctuations between pseudo-phases, as defined by C. Tanford, are distinct from exponents measured in binary solutions, when only one type of fluctuations can occur. To our knowledge, this has been proved experimentally for the first time by adding traces of electrolytes, quenching one of the fluctuations to a solution of non-ionic micelles.

Fig. 1 (a) Ternary phase diagram in weight fractions of the system water/ethanol/1-octanol, at 25 °C; (b) ternary phase diagram in mole fractions of the same system, at 25 °C. The clear and homogeneous phase is represented in white, the multiphasic domain in gray. Positions corresponding to the octanol-rich and water-rich pseudo-phases are shown as points respectively labeled O and W. Direction of fluctuations considered in dynamic studies are shown with the arrows: the black arrows represent the local fluctuation of aggregates concentration, the gray arrows represent the in-out fluctuation of ethanol between both pseudo-phases.

2.3. Small-angle X-ray scattering (SAXS)

2.3.1. Apparatus. A bench built by Xenocs and an X-ray radiation generated by a sealed molybdenum tube (wavelength λ = 0.71 Å) were used to carry out the SAXS measurements. The large on-line detector (MAR 345, MAR Research, diameter = 345 mm) was located at 750 mm from the sample stage. Off-centre detection allowed small and wide angles to be measured simultaneously. The scattering vector q has a magnitude of:ϑ being the scattering angle. The attainable q-region was 0.2–30 nm⁻¹ with an experimental resolution of Δq/q = 0.05. Collimation was applied using a 12: ∞ multilayer Xenocs mirror coupled to two sets of Forvis scatterless slits providing a 0.8 × 0.8 mm² X-ray beam at the sample position. Absolute intensities were obtained by using a 2.36 mm thick high-density polyethylene sample (from Goodfellow) as a calibration standard. The software FIT2D was used to integrate the two-dimensional spectra. The electronic background of the detector, transmission measurements and empty cell subtraction were taken into account during the integration. The acquisition time was 3600 s per sample.

2.3.2. Fits of the experimental data. The scattering by fluctuations with no defined interface can be generally expressed as an Ornstein–Zernike-type inverse quadratic function (OZ):where ξ_X is the correlation length in Å. We set I(0) = (Δρ)²Φ (1 − Φ), where Δρ is the difference of electronic densities between the oil-rich and water-rich domains in Å⁻², Φ the volume fraction of the oil-rich phase including the volume fractions of ethanol and additive which may be found in that phase. The electronic densities used can be found in the ESI,† Section A.

As the addition of salts into the surfactant-free microemulsion has an influence on its structure, we propose an empirical function to fit the data showing the phenomenon known as “correlation hole” for charged polymers and that cannot be fitted with an Ornstein–Zernike function:

V_object is the volume of the scattered object in ų, and is equal to:where R_mv is the mean radius of an object in Å, i.e. the hypothetical radius that would have the fluctuations or nano-droplets if their geometry were a sphere. V_object and Φ can be used to calculate the object density in a micelle volume n_d expressed in Å⁻³ (see eqn (5)).In eqn (3), (1 − Φ) is introduced to account to a first-order for repulsive interactions lowering the intensity (decrease of the compressibility). The physical meaning of q₀ is the scattering vector corresponding to the most probable distance between centres of scattering objects D*. In the case of repulsive objects, the number of objects can be deduced from the position of the maximum of the structure factor S(q), that is usually very close to the maximum of the intensity:It is very important to notice that n_d′ and n_d, determined by two independent measurements, may differ. When both values are close, this is a proof of self-consistency.²⁸ If these two densities differ, this may come from anisotropy of the object or attraction of the objects instead of repulsion.

2.4. Small-angle neutron scattering (SANS)

Small-angle neutron scattering (SANS) experiments were performed at the Institut Laue Langevin (ILL, France) on the D16 spectrometer. The neutron wavelength was fixed at 4.51 Å using a monochromator. A 2D gas-filled detector settled at 953 mm from the sample position (1 mm pathway quartz cell) was moved at two different angles (γ) on a goniometer arm in order to cover a q-vector range respectively between 0.025 < q (Å⁻¹) < 0.3 (position 1, γ = 0°) and 0.06 < q (Å⁻¹) < 0.6 (position 2, γ = 16°) with a reasonable overlap that allows a good concatenation of the scattering data. A standard H₂O normalization, detector noise, empty cell and incoherent scattering corrections were applied to display the scattering intensity I(q) in absolute units, the cm⁻¹.

In a first approximation, the data were also fitted using an OZ function, as described by eqn (2). The correlation length obtained from these fits is noted ξ_N. The neutron scattering length densities used can be found in the ESI,† Section A.

2.5. The formulation investigated

The ternary phase diagram water/ethanol/1-octanol was already published in another study² and is reproduced here for the sake of clarity, see Fig. 1. The investigated formulation corresponds to point α on the phase diagrams. Its composition as well as the compositions of both octanol-rich and water-rich pseudo-phases are summed up in Table 1 in weight and mole fractions.

Table 1 Composition of the reference formulation α and the water-rich and octanol-rich pseudo-phases in weight and mole fraction, the latter being inferred from the scattering experiments

Point	Weight fraction			Mole fraction
	Water	Ethanol	1-Octanol	Water	Ethanol	1-Octanol
α	0.375	0.4375	0.1875	0.6558	0.2989	0.0453
W	0.606	0.391	0.002	0.798	0.202	0
O	0.098	0.493	0.409	0.283	0.555	0.163

---

As already mentioned before and explained in details in previous papers, the fluctuations found in that surfactant-free microemulsion can be interpreted as nano-structuring or fluctuating nano-clusters. How to distinguish them from bicontinuous structures will be discussed in another paper in preparation.

Different amounts of salts were added to the formulation α and SAXS, SANS, and DLS were measured. In the case of NaDEHP, the same amount of sodium hydroxide was also added to the investigated formulations to ensure the ionisation of HDEHP.

3. Results

3.1. Influence of the addition of different anions on the nano-structures of the ternary composition α

In order to investigate the influence of anions on the structures of the surfactant-free microemulsion, SAXS were performed with increasing amounts of sodium salts. In the following, molarities (mol of solute per kg of solution) are used. The investigated formulation corresponded to formulation α, whose composition can be found in Fig. 1. As it can be seen in Fig. 2, the curves of the absolute intensity against the scattering vector q obtained for the anions CH₃COO⁻, Cl⁻, and NO₃⁻ exhibit the same behaviours, i.e. the absolute intensity at low q-values increases with increasing concentration of the different salts. The increase of the intensity at q → 0 is a bit more pronounced for NO₃⁻ than for the two other salts. The obtained curves for those three salts were all fitted using an Ornstein–Zernike function. The correlation lengths ξ_X obtained from these fits increase and are equal to 40.6 Å for 1.50 mol kg⁻¹ CH₃COO⁻, 27.7 Å for 0.68 mol kg⁻¹ Cl⁻, and 46.2 Å for 1.17 mol kg⁻¹ NO₃⁻ (see Fig. 3a).

Fig. 2 SAXS spectra on a log–log scale and in absolute units for the system water/ethanol/1-octanol in presence of (a) CH₃COONa; (b) NaSCN; (c) NaCl; and (d) NaNO₃. The dotted lines are the fits done with the Ornstein–Zernike equation or with eqn (3) in the case of NaSCN.

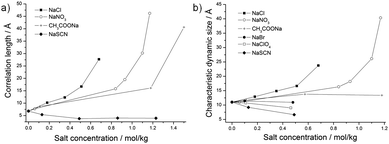Fig. 3 (a) Correlation lengths ξ_X in Å obtained from SAXS; and (b) characteristic dynamic size ξ_D in Å obtained from DLS plotted against the anion concentration in mol kg⁻¹.

For SCN⁻, the absolute intensity decreases at low q-values when the concentration increases from 0 to 1.23 mol kg⁻¹, see Fig. 2b. Further, a peak is observed at medium q-values, whose intensity increases with increasing SCN⁻ concentrations. It should be also mentioned that the peak is shifted to higher q-values with increasing concentrations. The first two concentrations, i.e. 0.13 and 0.49 mol kg⁻¹ of NaSCN, were fitted using an Ornstein–Zernike function, whereas the last two ones, i.e. 0.86 and 1.23 mol kg⁻¹ of NaSCN, were fitted using the model developed for this work (see the Experimental section, eqn (3)). A jump in the correlation length values is observed due to the use of two different models. However, it can be clearly seen that the correlation length tends to decrease, as shown in Fig. 3a.

SANS measurements were also carried out on the reference system without additives and with 0.35 mol kg⁻¹ of NaCl and 0.46 mol kg⁻¹ of NaClO₄, see Fig. 4. Three different contrasts were measured for each sample and the correlation lengths were obtained from the OZ fits. The octanol-rich contrast allows us to visualize the octanol-rich micro-domains, and the water-rich contrast allows us to visualize the water-rich micro-domains “containing” the organic-rich aggregates. It is consistent that the correlation lengths obtained from both fits differ only slightly. On the contrary, the ethanol-rich contrast allows us to directly visualize the typical size of aggregates. Ethanol is distributed in both phases, with an accumulation at the emerging interface. If there were no accumulation at the interface, i.e. as critical fluctuations in a ternary fluid only, the three contrasts would give the same size. Here, it is clear that the ethanol-rich contrast gives a smaller apparent size: this is a direct proof of the existence of an interface, rich in cosolvent. Another proof is the fact that in all samples measured by SANS, the correlation length obtained from the water-rich domain is higher than the one for the octanol-rich domain. This shows that the octanol-rich domains do not “fit” perfectly in the holes present in the water-rich domain and, thus, a diffuse interface must be present. The micro-structure in the pre-Ouzo region corresponds to two immiscible fluids separated by an interface: this corresponds to the definition of a microemulsion where the ethanol plays the role of a “weak” surfactant. High absolute intensities are observed for the octanol-rich and water-rich contrasts for the reference system (see Fig. 4). This observation is valid for the reference sample and remains true in the case of added salt.²⁹

Fig. 4 SANS curves on a log–log scale and in absolute units of the formulation corresponding to point α with (a) 0.35 mol kg⁻¹ NaCl, and (b) 0.46 mol kg⁻¹ NaClO₄. For NaCl, the correlation length ξ_N increases from 16.3 to 18.8 Å for the octanol-rich contrast, from 16.0 to 22.0 Å for the water-rich contrast, and decreases from 6.3 to 5.1 Å for the ethanol-rich contrast. For NaClO₄, the correlation length ξ_N decreases from 16.3 to 8.6 Å for the octanol-rich contrast, from 16.0 to 9.4 Å for the water-rich contrast, and from 6.3 to 5.8 Å for the ethanol-rich contrast.

In presence of Cl⁻, the intensities of the curves at low q-values for the octanol-rich and water-rich contrasts are higher and the curvature changes accordingly (see Fig. 4a). The correlation length values ξ_N found for the octanol-rich and water-rich contrasts are higher than ξ_N of the reference. For ClO₄⁻, the absolute intensities at low q-values are smaller than the reference and a saturation of the signal is observed more rapidly, as represented in Fig. 4b. ξ_N also decreases with 0.46 mol kg⁻¹ NaClO₄. However, no significant change is observed regarding the ethanol-rich contrast for Cl⁻ and ClO₄⁻. All correlation lengths, sizes, and other useful data can be found in the ESI,† Section B and Table S1.

DLS was also measured for the composition α with increasing salt concentrations. The autocorrelation functions for each salt can be found in the ESI,† Section C. The characteristic dynamic sizes ξ_D as obtained from DLS are plotted against the anion concentrations, see Fig. 3b. ξ_D increases and diverges at a given concentration for NaCl and NaNO₃. Regarding CH₃COONa, ξ_D is constant. It decreases for NaSCN, NaBr, and NaClO₄.

3.2. Influence of the addition of different cations on the nano-structures of the ternary composition α

SAXS measurements were also performed with increasing concentration of cations, keeping chloride as a common anion. The investigated formulation corresponded to formulation α, cf.Fig. 1.

The SAXS curves for all cations exhibit the same behaviour. As presented in Fig. 5, the absolute intensity increases at low q-values when increasing the salt concentrations. It can be noted that the intensity at q → 0 is the highest for Cs⁺ and the smallest for Li⁺. All the curves were fitted using an Ornstein–Zernike equation. The correlation lengths obtained from these fits increase for NH₄⁺, Cs⁺, K⁺, and Na⁺ and are equal to 45.8 Å for 1.47 mol kg⁻¹ NH₄⁺, 45.9 Å for 0.62 mol kg⁻¹ Cs⁺, 24.1 Å for 0.53 mol kg⁻¹ K⁺, and 27.7 Å for 0.68 mol kg⁻¹ Na⁺ (see Fig. 6a). The trend is less evident for the most kosmotropic cations Li⁺ and Ca²⁺.

Fig. 5 SAXS spectra on a log–log scale and in absolute units for the system water/ethanol/1-octanol in presence of (a) NH₄Cl; (b) CsCl; (c) KCl; (d) NaCl; (e) LiCl; and (f) CaCl₂. The dotted lines are the fits done with the Ornstein–Zernike equation.

Fig. 6 (a) Correlation length ξ_X in Å obtained from SAXS; (b) characteristic dynamic size ξ_D in Å obtained from DLS plotted against the cation concentration in mol kg⁻¹.

SANS measurements were also carried out on the reference system without additives and with 0.50 mol kg⁻¹ of LiCl (see Fig. 7). The same three contrasts were measured for each sample. As already described for the reference, high absolute intensities are observed for the octanol-rich and water-rich contrasts contrary to the ethanol-rich contrast which exhibits a lower absolute intensity. The curvature of the octanol-rich and water-rich contrasts curves is the same. In presence of Li⁺, the intensities of those curves at low q-values are higher and the curvature changes accordingly. This is in agreement with the slight increase of ξ_N for the octanol-rich and water-rich contrasts. No significant change is observed regarding the ethanol-rich contrast.

Fig. 7 SANS curves on a log–log scale and in absolute units of the formulation corresponding to point α with 0.5 mol kg⁻¹ LiCl. The correlation length ξ_N stays almost the same for the octanol-rich contrast and is equal to 16 Å. ξ_N increases from 6.3 to 6.6 Å for the ethanol-rich contrast and from 16.0 to 19.0 Å for the water-rich contrast.

As for the anions, DLS was also performed for the composition α with increasing cation concentrations. The autocorrelation functions for each salt can be found in the ESI,† Section D. The characteristic dynamic size ξ_D was also plotted against the cation concentration, see Fig. 6b. It increases and diverges at a given concentration of CsCl, KCl, NaCl and NH₄Cl. Note that NH₄Cl diverge at much higher concentration than the other three salts. For LiCl and CaCl₂, ξ_D exhibits a slight increase at low concentration and stays more or less the same at higher concentrations.

3.3. Influence of “special” electrolytes on the nano-structures of the ternary composition α

SAXS experiments were also performed with increasing concentrations of NaBPh₄, SDS, HDEHP, and NaDEHP in the composition α. NaBPh₄ is a typical antagonistic salt since sodium is a kosmotropic ion and BPh₄⁻ is extremely chaotropic, hence expelled from the water-rich domains. As a consequence, it must be adsorbed on the octanol-rich domain: charge separation of antagonistic salts should produce a net electrostatic repulsion. Extreme cases are investigated with anionic surfactants, where the amphiphilic anion is expected to be mixed with the octanol-rich aggregate and stabilize them. We use HDEHP, the oil-soluble acidic form of the diethylhexylphosphoric acid, as a counter-example, since it should increase the volume of octanol-rich aggregates without inducing negative charge-stabilization.

The absolute intensity decreases for NaBPh₄ and SDS at low q-values when their concentrations increase respectively from 0 to 0.26 and 0.55 mol kg⁻¹ (see Fig. 8a and b). The decrease of the intensity at q → 0 is more significant for the surfactant SDS. Further, the emergence of the classical broad peak associated to repulsive aggregates³⁰ or disordered-open-connected structures³¹ are observed for the two additives at medium q-values. Its intensity increases with increasing additive concentrations. The maximal intensity is observed for the highest SDS concentration. It should be also mentioned that the peak is shifted to higher q-values with increasing concentrations, a direct hint that distance between the centers of neighboring aggregates decreases, hence there are more smaller aggregates, consistent with the general idea of charge distribution. For NaBPh₄, the first four concentrations, i.e. from 0.03 to 0.12 mol kg⁻¹, were fitted using an Ornstein–Zernike function, whereas the last four ones, i.e. from 0.15 to 0.23 mol kg⁻¹, were fitted using the model developed for this work (see the Experimental section, eqn (3)). It can be seen that the correlation length stays more or less constant. Regarding SDS, all the curves were fitted using the model developed for this work (see the Experimental section, eqn (3)). The correlation length ξ_X obtained from these fits increases from 3.95 Å for 0.07 mol kg⁻¹ SDS to 12.8 Å for 0.69 mol kg⁻¹ SDS.

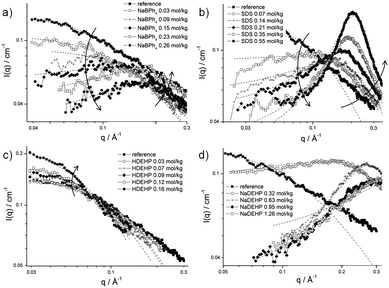Fig. 8 SAXS spectra on a log–log scale and in absolute units for the system water/ethanol/1-octanol in presence of (a) NaBPh₄; (b) SDS; (c) HDEHP; and (d) NaDEHP. The dotted lines are the fits corresponding to the Ornstein–Zernike equation or to eqn (3).

For the uncharged HDEHP, the absolute intensity slightly increases when increasing its concentration in the surfactant-free microemulsion and no peak appears. The correlation length ξ_X obtained from these fits also increases and reaches 12.9 Å with 0.16 mol kg⁻¹ HDEHP. Regarding the ionized HDEHP, called NaDEHP, the absolute intensity decreases at low q-values and a broad peak is obtained when increasing the concentration. Due to the use of two different models to fit the curves, the evolution of the correlation length ξ_X is not clear.

The measured DLS autocorrelation functions for NaBPh₄ and SDS can be found in the ESI,† Section E.

4. Discussion

The addition of salt on the structuring of ternary surfactant-free microemulsions has two main effects:

1. A salting-out effect towards ethanol: ethanol molecules are driven to the interface or inside the octanol-rich aggregates upon addition of the electrolyte. Consequently, the size of the nano-structures increases and ξ_D, ξ_X, and ξ_N increase.

2. Charging of the interface via the antagonistic ion effect (see Introduction): the chaotropic ion is partly adsorbed onto the o/w interface and charges it, according to the charge regulation equilibrium.³² As the electrostatic repulsion between the structures is enhanced, the compressibility decreases and I(0) from SAXS decreases. Further, the Ornstein–Zernike behaviour should disappear in favour of a correlation peak.

To each of these effects we can infer opposite consequences on the surfactant-free microemulsion. The consequences 1 and 2 are related respectively to the effects 1 and 2:

1. It leads to an increase of the dynamic scattering, with effects equivalent to a decrease of the initial ethanol concentration, i.e. the experimental point is getting closer to the demixing line upon addition of electrolyte.

2. It leads to a decrease of the dynamic scattering, with effects equivalent to an increase of the initial ethanol concentration, i.e. the experimental point is getting away from the demixing line upon addition of electrolyte. The pre-Ouzo aggregates are disappearing. The sample composition crosses the so-called Lifshitz line³³ for which noticeable scattering at vanishing q-values disappears and the microstructure is better described as a weakly correlated ternary molecular solution and the associated transition towards a ternary unstructured fluid. If a critical point is present in the vicinity, only critical fluctuations are present. In this case, there is no pre-Ouzo region near the miscibility gap. There is no enrichment of ethanol at the interface between aggregates and there are no aggregates of a preferred size.

Regarding the SAXS measurements, the interactions between the aggregates (“nano-clusters”) present in the solutions can also be observed at q-values higher than 0.1 Å⁻¹ by the emergence of a peak, whereas the Ornstein–Zernike-like fluctuations of weakly interacting clusters can be observed at low q-values. Concerning SANS, a saturation of the absolute intensity at low q-values hints at repulsive interactions between the nano-structures.

4.1. Static scattering

4.1.1. Anions. NaCl, NaNO₃, CH₃COONa (mechanism 1): considering the SANS spectrum of the reference formulation, the correlation length obtained from the fits of the octanol-rich and water-rich contrasts is almost the same, whereas the correlation length for the ethanol-rich contrast is much smaller. As already pointed out, this result proves that the observed intensity comes from nano-structures inside the surfactant-free microemulsion and not from critical molecular fluctuations near a critical point.

Considering now the SANS spectrum of NaCl, the difference between the correlation length obtained from the fits for the octanol-rich and water-rich contrasts is more important, indicating a change at the interface or in the aggregates. The apparent size increases: it can be deduced that the salt has a salting-out effect and pushes the ethanol molecules inside the aggregates, thus increasing their size, or at least the interface. This is seen by the difference in size as seen with octanol and ethanol contrast. However, as the SANS curves of the reference and NaCl overlap for the octanol-rich and water-rich contrasts at high q-values, the total water-rich to octanol-rich interface per unit volume remains constant.

From both these results, we suppose that the primary result is that the presence of salt induces maximum stability of larger aggregates in the microemulsion. In a first order approximation of hydration force competing with entropy, the secondary hydration force comes into play, favouring larger aggregates.³⁴ The increase of the correlation length ξ_X and the increase of the absolute intensity in SAXS with increasing salt concentration, meaning that the compressibility increases and the repulsions between the nano-structures decrease, are in agreement with an increase of ethanol concentration in the aggregates. Further, Schöttl's and Horinek's simulations show that the ethanol concentration inside the aggregates and at the interface is enhanced upon addition of salts.³⁵ Consequently, this leads to an apparent decrease of ethanol concentration and the formulation is getting closer to the demixing boundary upon addition of NaCl: getting closer to the boundary increases the fluctuations that should be detected with light scattering at lower q-value, as will be discussed below.

NaNO₃ and CH₃COONa exhibit the same effect as NaCl. The same trend is indeed observed in SAXS and ξ_X also increases when increasing the salt concentration. However, the salting-out effect of CH₃COO⁻ is weaker than that of NO₃⁻, which is weaker than Cl⁻ as the correlation length ξ_X starts diverging at higher concentrations, following the order Cl⁻, NO₃⁻, and CH₃COO⁻. It is also interesting to note that, usually, the carboxylate ion –COO⁻ is harder than Cl⁻. However, the acetate ion is less efficient than NaCl due to the presence of the hydrotropic group –CH₃.

NaSCN, NaBr, NaClO₄ (mechanism 2): the thiocyanate anion SCN⁻ exhibits a very different behaviour, as it is chaotropic; thus the sodium salt is antagonistic and easily separated. The decrease of the absolute intensity in SAXS at low q-values means that the repulsive interactions between the nano-structures increase. That increase is also confirmed by the presence of a peak at higher q-values coming from a structure factor. The Ornstein–Zernike behavior disappears and the spectra have to be fitted using another equation, as indicated in the methods and in Section 3.1. The anion SCN⁻ goes onto the interface, leading to an increase of the repulsions and to a stabilization of smaller microemulsion domains. The addition of NaSCN should also increase the monodispersity of the surfactant-free microemulsion as ξ_X tends to decrease, indicating that smaller aggregates are formed. It can be noted that both anions and ethanol participate in forming the interfacial film. The addition of NaSCN leads to an apparent increase of ethanol concentration and the formulation is moving away from the demixing boundary.

Considering the SANS spectrum of NaClO₄, the intensity shows no divergence at low q-values compared with the intensity of the reference: this is due to low osmotic compressibility, indicating the presence of repulsive interactions. Like in the case of SCN⁻, the anion ClO₄⁻ goes onto the interface and charges it, leading also to repulsive interactions. The size of the aggregates is also smaller, as the correlation length ξ_N decreases for the three contrasts with 0.46 mol kg⁻¹ NaClO₄. Further, as the octanol-rich and water-rich curves of the reference and NaClO₄ overlap at high q-values, the interface per unit volume remains the same. This means that the presence of antagonistic salt induces smaller and a larger number of aggregates inside the surfactant-free microemulsion. We are here in a situation very similar to the case first described by Onuki et al. when concentrated antagonistic salts, by themselves and without even a co-solute, induce stability of spontaneous emulsions. Instead of two macroscopically separated phases, droplets of 100 nm are observed in the system water/3-methylpentane and NaBr, used as antagonistic salt.³⁶

It is worth stressing the main result here: an antagonistic salt, such as NaSCN, NaClO₄, and probably NaBr (as its behavior is the same as the perchlorate and thiocyanate ion in DLS) behaves like a surfactant in presence of ethanol.

4.1.2. Cations. NaCl, KCl, CsCl, NH₄Cl, LiCl, CaCl₂ (mechanism 1): regarding the SANS spectrum of LiCl and the correlation lengths obtained from the fits of the three contrasts, it is again confirmed that the obtained intensities originate from nano-structures inside the solution and not from critical fluctuations. Like in the case of NaCl, the facts that (i) the difference between the sizes of the octanol-rich and water-rich contrasts is more important than the one for the reference and (ii) the absolute intensity in SAXS increases, indicate that LiCl “pushes” the ethanol molecules inside the octanol-rich aggregates. However, as the correlation length ξ_X stays almost the same and the increase of ξ_N is smaller than the increase for NaCl, the salting-out effect of Li⁺ is much weaker that the one of Na⁺. This is also in agreement with the work of Schöttl and Horinek, who showed that the increase of the concentration of ethanol inside the organic-rich phase and at the interface upon addition of LiCl is smaller compared to CsCl (which behaves like NaCl, see next paragraph).³⁵ Further, they also showed that the aggregates with LiCl are a bit broader. Ca²⁺ should behave like Li⁺ as they exhibit the same behavior in DLS.

K⁺, Cs⁺, and NH₄⁺ exhibit a behavior similar to the one of NaCl in SAXS and thus have a salting-out effect towards ethanol. When the ethanol content of the water-rich “solvent” decreases from 40% to 0%, the free energy of transfer of the ethanol molecules inside the aggregates increases from 0.25 kT/mole to 1 kT/mole (2.5 kJ), as can be derived from measured partition coefficient.^4,37 This induces a size increase as shown by the measured correlation lengths ξ_X. Na⁺, K⁺, and Cs⁺ behave approximately alike, whereas NH₄⁺ has a much weaker salting-out effect when considering the divergence of the correlation length with increasing salt concentration. The addition of those salts leads to an apparent decrease of the ethanol concentration, i.e. the studied formulation comes closer to the demixing line.

4.1.3. Special sodium salts. NaBPh₄ (mechanism 2): the strong decrease of the SAXS absolute intensity of BPh₄⁻ at low q-values shows that the electrostatic repulsions between the nano-structures increase upon addition of the antagonistic salt. Further, the emergence of a slight peak at around 0.17 Å⁻¹ corroborates the increased interactions between the clusters. That can be explained by the strong propensity of the bulky organic and hydrophobic anion to the interface. The small sodium ion must follow to ensure local electro-neutrality. Since the structures are charged and repulsive, the Ornstein–Zernike fluctuations vanish and a correlation peak appears. As explained by Sadanake et al. and Onuki et al. (see Introduction), the antagonistic salt acts as a significant surface active agent, but due to its bulky structure, it cannot form a well-ordered film or a sharp interface, as observed by the presence of a small broad peak in the SAXS spectra. Another type of microemulsions is observed here. It is neither stabilized by surfactants nor by any hydration forces due to the ordering of alcohol groups at the interface. The structuring is mainly (or even purely) due to electrostatic interactions. Using eqn (5) and (6), one charged aggregate has a volume of approximately 11 100 ų. Assuming that (i) the volume fraction of the octanol-rich phase is 0.4,⁴ and (ii) half of the octanol-rich phase is ethanol and the other half is 1-octanol, one aggregate has approximately 21 octanol molecules and 58 ethanol molecules. In our case, the correlation lengths and the volume of one aggregate are much smaller than the ones found by Sadakane et al., who studied a similar system with other chemicals.¹⁹ Like NaSCN or NaClO₄, NaBPh₄ can play the role of a surfactant in presence of ethanol. Further, as ξ_X stays constant, there is no strong variation of the free energy of transfer of ethanol from water-rich to oil-rich domains and no changes in the size of aggregates is induced. The latter are now simply stabilized by the antagonistic salt and ethanol molecules, which render the interface more “visible”.

SDS: the decrease of the absolute intensity observed upon addition of SDS at low q-values coupled with the apparition of a peak at medium q-values with increasing SDS concentrations are proofs that true surfactant micelles appear progressively.³⁰ The same effect occurs in light scattering when the osmotic compressibility increases when aggregates become charged, see ESI,† Section E. This effect is known and related to non-electrostatic effects in “normal” micelles. It cannot be excluded that the addition of SDS destroys first (meaning upon addition of very small amounts of SDS) the surfactant-free clusters. Qualitatively, this would lead to a decrease of intensity at low q-values similar to the measured one and cannot be distinguished from the intensity decrease because of increasing repulsions between charged micelles. But at least at low SDS concentrations, ethanol might prevent the formation of classical micelles, whereas at higher SDS concentrations, SDS micelles stabilized by octanol acting as cosurfactant can be expected.³⁸ At such high SDS concentrations, the characteristic peak of classical surfactant micelles is observed. The latter becomes narrower, its intensity higher with increasing concentrations of SDS, and polydispersity decreases. The correlation length ξ_X increases, meaning the size of the micelles also increases. We suppose that ethanol molecules are partitioned between both pseudo-phases and also participate in the interface, together with the surfactant.³⁹

HDEHP, NaDEHP: HDEHP can be considered as an oil. As such, the HDEHP molecules go inside the micelles and swell them, which is in agreement with the increase of the correlation length ξ_X from 6.8 Å without additive to 12.9 Å with 0.16 mol kg⁻¹ HDEHP.

The behavior of NaDEHP is comparable with the one of SDS, as the absolute intensity at low q-values decreases and the emergence of a broad peak is observed, both results leading to an increase of the electrostatic repulsions. In that case, a surfactant is formed in situ by deprotonating the HDEHP oil with sodium hydroxide.

To sum up, anions have either a salting-out effect where the ethanol molecules are pushed inside the nano-structures (the formulation is closer to the demixing boundary), or behave like a surfactant by stabilizing the interface with electrostatic effects (the formulation is farther away from the boundary). Cations mainly induce an increase of the size by salting-out. All antagonistic salts produce a transformation from pre-Ouzo aggregates into smaller charged repulsive micelles. We now examine if this global unified picture is consistent with what is observed by dynamic light scattering at lower-q.

4.2. Dynamic scattering

We consider here the Rayleigh ratios obtained from DLS to see if the results obtained with this method are in agreement with the static methods previously explained.

As it can be seen in Fig. 3b, 6b, 9a and b, the characteristic dynamic size ξ_D and the Rayleigh ratios of NaCl, NaNO₃, KCl, CsCl, and NH₄Cl increase with increasing salt concentration. The Rayleigh ratios are equal to 2.97, 4.45, 2.93, 3.92, and 2.70 mm⁻¹ with respectively 0.68 mol kg⁻¹ NaCl, 1.17 mol kg⁻¹ NaNO₃, 0.53 mol kg⁻¹ KCl, 0.62 mol kg⁻¹ CsCl, and 1.47 mol kg⁻¹ NH₄Cl. This, together with the increase of the characteristic time obtained from DLS (see the ESI,† Section B and Table S1), is in agreement with the SAXS and SANS results and confirms that the formulation comes closer to the demixing line. For NaClO₄, NaBr, and NaSCN the Rayleigh ratios decrease to 0.68, 0.49, and 0.52 mm⁻¹ with respectively 1.60 mol kg⁻¹ NaClO₄, 2.00 mol kg⁻¹ NaBr, and 1.23 mol kg⁻¹ NaSCN. The fact that ξ_D, the characteristic time, and the Rayleigh ratios decrease for those three anions upon increasing the salt concentration is in agreement with the Onuki's behavior previously explained: the line of the phase boundary moves away from the position of the sample, meaning that critical fluctuations of local density of octanol-rich pre-Ouzo aggregate (as shown by the black arrows in Fig. 1) and/or the fluctuations of local ethanol concentrations (as shown by the gray arrows in Fig. 1) decrease. Thus, the amplitude of the correlation functions obtained by DLS and the Rayleigh ratios decrease.

However, the Rayleigh ratios of CH₃COONa, LiCl, and CaCl₂ exhibit an opposite behaviour and decrease, although the formulation gets closer to demixing boundary upon addition of salt (Fig. 9a and b).

Fig. 9 (a) Rayleigh ratio in mm⁻¹ obtained from DLS plotted against the anion concentration in mol kg⁻¹; and (b) Rayleigh ratio in mm⁻¹ obtained from DLS plotted against the cation concentration in mol kg⁻¹.

In surfactant-free systems, two different types of fluctuations occur: (i) the fluctuations of the organic-rich phase in the water-rich phase and vice versa, and (ii) the fluctuations of the ethanol distribution between those pseudo-phases. Those fluctuations are represented in the ternary phase diagram in Fig. 1 by respectively the black and gray arrows. The scattered intensity in DLS in such system is caused by the convoluted contributions of those two fluctuations. In the case of those three salts made of kosmotropic ions, we may suppose that the ethanol fluctuation is perturbed and that the exchange dynamics of ethanol between both pseudo-phases is slowed down upon addition of salts. This would lead to a decrease of the Rayleigh ratios. The interactions acetate–ethanol, lithium–ethanol, and calcium–ethanol may be stronger than the corresponding interactions for the other salts.

5. Conclusions

Pre-Ouzo aggregates are a general type of weak aggregation that is very sensitive to addition of electrolytes. The pre-Ouzo domain sizes increase as soon as the presence of salt in the water-rich pseudo-phase induces a salting-out of the ethanol. In the case of antagonistic salts containing one chaotropic ion, the charge separation at the interface produces an electrostatic stabilization of the aggregates, which gradually transform to micelles similar to classical surfactant-co-surfactant micelles with an excess of anionic surfactant. This means that ethanol/chaotropic ion combinations may serve as an alternative to surfactants for the formulation of microemulsions.

When true surfactants are added to surfactant-free microemulsions, the main constituent at the interface is ethanol at low concentrations of additives, moving towards octanol-surfactant interfaces at higher additive concentrations, where, as expected, classical mixed micelles are formed. The variations of these molecular interactions are also at the origin of the variation of the phase boundary line. The light scattering is more sensitive to fluctuations, while SAXS/SANS patterns transform from pure Ornstein–Zernike behavior to a structured pattern with a broad peak. For the latter, we propose in this work a general formula for a convenient fitting of the data, introducing two quantities: the correlation size and a distance between centers at 2π/q₀ (eqn (3)).

Acknowledgements

Authors want to thank the Labex Chemisyst for providing invited Professorship. Prof. Thomas Zemb acknowledges the ERC for the support of project “REE-CYCLE” for rare earth separation and the COST Network CM1011. All authors acknowledge very helpful discussions with Prof. Dominik Horinek. We also thank Isabelle Grillo and Bruno Demé from the Institut Laue Langevin (Grenoble, France) for their help during the SANS experiments for the proposal 9-10-1395, and Bruno Corso for the in-house SAXS bench alignment and calibration.

References

1. N. L. Sitnikova, R. Sprik and G. Wegdam, Langmuir, 2005, 21, 7083–7089; R. Botet, J. Phys.: Conf. Ser., 2012, 352, 012047; J. Aubry, F. Ganachaud, J.-P. Cohen Addad and B. Cabane, Langmuir, 2009, 25, 1970–1979; S. A. Vitale and J. L. Katz, Langmuir, 2003, 19, 4105–4110; D. Carteau, I. Pianet, P. Brunerie, B. Guillemat and D. M. Bassani, Langmuir, 2007, 23, 3561–3565.
2. M. L. Klossek, D. Touraud, T. Zemb and W. Kunz, ChemPhysChem, 2012, 13, 4116–4119.
3. X. Yan, M. Delgado, A. Fu, P. Alcouffe, S. G. Gouin, E. Fleury, J. L. Katz, F. Ganachaud and J. Bernard, Angew. Chem., Int. Ed., 2014, 53, 6910–6913; S. Peng, C. Xu, T. C. Hughes and X. Zhang, Langmuir, 2014, 30, 12270–12277.
4. O. Diat, M. L. Klossek, D. Touraud, B. Deme, I. Grillo, W. Kunz and T. Zemb, J. Appl. Crystallogr., 2013, 46, 1665–1669.
5. S. Schöttl, D. Touraud, W. Kunz, T. Zemb and D. Horinek, Colloids Surf., A, 2015, 480, 222–227.
6. M. Duvail, L. Arleth, T. Zemb and J.-F. Dufreche, J. Chem. Phys., 2014, 140, 164711.
7. M. L. Klossek, D. Touraud and W. Kunz, Phys. Chem. Chem. Phys., 2013, 15, 10971–10977.
8. S. Schöttl, J. Marcus, O. Diat, D. Touraud, W. Kunz, T. Zemb and D. Horinek, Chem. Sci., 2014, 5, 2949–2954.
9. M. Zoumpanioti, M. Karali, A. Xenakis and H. Stamatis, Enzyme Microb. Technol., 2006, 39, 531–539.
10. P. Bauduin, F. Testard and T. Zemb, J. Phys. Chem. B, 2008, 112, 12354–12360.
11. J. Marcus, M. Müller, J. Nistler, D. Touraud and W. Kunz, Colloids Surf., A, 2014, 458, 3–9.
12. J. Marcus, M. L. Klossek, D. Touraud and W. Kunz, Flavour Fragrance J., 2013, 28, 294–299.
13. V. Tchakalova, T. Zemb and D. Benczédi, Colloids Surf., A, 2014, 460, 414–421.
14. R. F. Hankel, P. E. Rojas, M. Cano-Sarabia, S. Sala, J. Veciana, A. Braeuer and N. Ventosa, Chem. Commun., 2014, 50, 8215–8218.
15. Y. Marcus, Ion properties, Marcel Dekker, Inc., New York, 1997.
16. S. Subenik, L. Sapir and D. Harries, Curr. Opin. Colloid Interface Sci., 2013, 18, 495–501.
17. C. J. Rizzo, J. Org. Chem., 1992, 57, 6382–6384.
18. K. Sadakane, H. Seto, H. Endo and M. Shibayama, J. Phys. Soc. Jpn., 2007, 76, 113602.
19. K. Sadakane, N. Iguchi, M. Nagao, H. Endo, Y. B. Melnichenko and H. Seto, Soft Matter, 2011, 7, 1334.
20. K. Sadakane, A. Onuki, S. Koizumi and H. Seto, Phys. Rev. Lett., 2009, 103.
21. A. Onuki, J. Chem. Phys., 2008, 128, 224704; A. Onuki, T. Araki and R. Okamoto, J. Phys.: Condens. Matter, 2011, 23, 284113; A. Onuki and H. Kitamura, J. Chem. Phys., 2004, 121, 3143–3151; A. Onuki, R. Okamoto and T. Araki, Bull. Chem. Soc. Jpn., 2011, 84, 569–587; T. Araki and A. Onuki, J. Phys.: Condens. Matter, 2009, 21, 424116.
22. E. Leontidis, M. Christoforou, C. Georgiou and T. Delclos, Curr. Opin. Colloid Interface Sci., 2014, 19, 2–8.
23. C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, John Wiley & Sons Inc., New York, 1973.
24. M. Corti and V. Degiorgio, Chem. Phys. Lett., 1977, 49, 141–144.
25. E. A. G. Aniansson, S. N. Wall, M. Almgren, H. Hoffmann, I. Kielmann, W. Ulbricht, R. Zana, J. Lang and C. Tondre, J. Phys. Chem., 1976, 80, 905–922.
26. A. Arce, A. Blanco, A. Soto and I. Vidal, J. Chem. Eng. Data, 1993, 38, 336–340.
27. L. Cantù, M. Corti, V. Degiorgio, H. Hoffmann and W. Ulbricht, J. Colloid Interface Sci., 1987, 116, 384–389; L. Cantù, M. Corti, V. Degiorgio, C. Minero and R. Piazza, J. Colloid Interface Sci., 1985, 105, 628–634.
28. J. B. Hayter and J. Penfold, Colloid Polym. Sci., 1983, 261, 1022–1030; P. Lindner and T. Zemb, Neutrons, X-rays and light scattering methods applied to soft condensed matter, Elsevier, 2002.
29. T. Zemb, M. L. Klossek, T. Lopian, J. Marcus, D. Horinek, S. Schöttl, S. Prevost, D. Touraud, O. Diat, S. Marčelja and W. Kunz, Proc. Natl. Acad. Sci. U. S. A., 2015 , submitted.
30. J. B. Hayter, Langmuir, 1992, 8, 2873–2876.
31. T. Zemb, Colloids Surf., A, 1997, 129–130, 435–454.
32. B. W. Ninham and V. A. Parsegian, J. Theor. Biol., 1971, 31, 405–428.
33. K. V. Schubert and R. Strey, J. Chem. Phys., 1991, 95, 8532–8545; K. V. Schubert, R. Strey, S. R. Kline and E. W. Kaler, J. Chem. Phys., 1994, 101, 5343–5355.
34. S. Marčelja, Nature, 1997, 385, 689–690.
35. S. Schöttl, D. Horinek, 2015, in preparation.
36. R. Okamoto and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 1–20.
37. A. Arce, A. Blanco, P. Souza and I. Vidal, J. Chem. Eng. Data, 1994, 39, 378–380.
38. R. Zana, Adv. Colloid Interface Sci., 1995, 57, 1–64.
39. M. L. Klossek, J. Marcus, D. Touraud and W. Kunz, Colloids Surf., A, 2014, 442, 105–110; M. L. Klossek, J. Marcus, D. Touraud and W. Kunz, Colloids Surf., A, 2013, 427, 95–100.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp06364g

---