Hydrogen bond mediated stabilization of the salt bridge structure for the glycine dimer anion

Abstract

The formation of a salt bridge in deprotonated glycine dimer anions in a solvent-free environment is investigated using both infrared multiple photon dissociation spectroscopy between 600 and 1800 cm⁻¹ and theory. The zwitterionic and nonzwitterionic forms of glycine in this complex are computed to be nearly iso-energetic, yet predominantly the zwitterionic form is observed experimentally. The zwitterion stability is attributed to both the Coulombic attraction and the high stabilization from intramolecular hydrogen bonding that drives the energetic cost of proton transfer in a solvent free environment. These results show that there is a fine balance between the stabilities of these two forms of the anion. Elucidating the role of intrinsic factors, such as hydrogen bonding, can lead to a better understanding of the stabilities of salt bridges in the interiors of large proteins or at protein interfaces.

---

Introduction

Proteins are the workhorse molecules of life as they carry out much of the function in cells and organisms. Understanding what roles various proteins perform and how they function on a molecular level requires a detailed understanding of both intramolecular interactions and the interactions of the proteins with their environments. Basic and acidic residues with ionized side chains play an important role in the functionality and structure of proteins owing to long-range Coulombic interactions.^1–3 Charged groups can reside on the surface of a protein or can be buried in the interior, and are important for the reactivities of active sites and protein solubility. Charged groups can be distant from each other, or can form salt bridges (SBs)^1–4 in which protonated and deprotonated residues interact directly. SBs are stabilized by a number of non-covalent interactions and solvation, but predicting SB stabilities remains challenging.

In order to gain a better understanding of intrinsic factors that affect SB and zwitterion formation, amino acid and peptide model systems have been studied in the gas phase. All neutral isolated amino acids^5–7 and many peptides^8,9 exist only in their canonical, non-zwitterionic (NZ) form when isolated. The stabilities of the zwitterionic (ZW) forms of these gas-phase biomolecules are influenced by the addition of protons,¹⁰ electrons,¹¹ anions,¹² cations,^13–16 solvent molecules^17–19 and by molecular size.²⁰ Small complexes, including proton bound homo- and hetero-dimers of amino acids^21–24 and amino acid-HNR₃^+ 25–27 complexes have served as model systems for SBs or the formation of zwitterions that can lead to a better understanding of SBs in larger biological molecules. Whereas the electrostatic interaction of amino acids with small cations can favour the formation of NZ structures, large alkali or alkaline earth metal ions,^16,19 or the formation of hydrogen bonds either to solvent¹⁹/complexing^21,25–27 molecules or within these complexes,²⁰ can stabilize the ZW over the NZ isomers. Most of these investigations, which were focused on mainly neutral or cationized model systems,^{5–10,13–16,21–28} indicate that there is a fine balance between the relative stabilities of the ZW and NZ forms. The energetic separation between ZW and NZ forms of amino acids and small peptides are typically on the order of 0–5 kcal mol^{−1 19,25,27} but in some rare cases can go up to ∼15 kcal mol⁻¹.¹⁶ Understanding factors that stabilize the ZW or NZ form is important for developing more accurate models for SB interactions in more complex biomolecules.

The formation of zwitterions in anions has so far scarcely been studied,^11,18 even though most proteins under physiological conditions have more negative than positive groups and consequently carry an overall negative charge.¹ The simplest biomolecular model system for the formation of a –NH₃⁺⋯⁻O₂C SB is the glycine dimer which has so far only been studied in the neutral and cationic, [Gly₂ + H]⁺ or [Gly₂ + Na]⁺, forms.^21–24,29 For the neutral glycine dimer, ab initio calculations indicate that the SB form is 14 kcal mol⁻¹ higher in energy than the lowest energy NZ isomer but that the SB form is preferred in aqueous solution.²⁹ Protonated glycine dimers consist of neutral glycine molecules that share a proton.^21–24

Herein, we present both experimental infrared multiple photon dissociation (IRMPD) and theoretical results on the structures of sodiated and deprotonated anionic glycine dimers, [Gly₂–2H + Na]⁻ and [Gly₂–H]⁻. The former is a SB, but is used as reference system for NZ glycine and the latter is used to investigate whether the SB form, in which one glycine molecule is zwitterionic, is more stable than the NZ form in a solvent deficient environment.

Experimental section

Mass spectrometry and IRMPD spectroscopy

Experiments were performed using a 4.7 T Fourier-transform ion cyclotron resonance (FT-ICR) mass spectrometer equipped with an electrospray ionization source (ESI) and coupled to the free electron laser for infrared experiments (FELIX).³⁰ Ions were generated by ESI from methanol/water (∼80/20) solutions with 2–5 mM of glycine (Sigma-Aldrich) with 1% NH₄OH or 1 M NaOH added to generate [Gly₂–H]⁻ or [Gly₂–2H + Na]⁻, respectively. For the isotopic labelling experiments, the corresponding deuterated solvents were used and the ESI source was purged with dry nitrogen gas to prevent back exchange. A spray voltage of −2.5 kV and a solution flow rate of 5–10 μL min⁻¹ were used. Ions were accumulated for ∼5 s in a hexapole ion trap before they were guided into and trapped in the cell of the FT-ICR instrument. The ion of interest was isolated by stored waveform inverse Fourier transform, and subsequently irradiated by IR light from the FELIX light source for 2–3 s. The laser, operating at a macropulse rate of 5 Hz and with an energy of ∼40 mJ per pulse was attenuated by 0 dB for [Gly₂–2H + Na]⁻ and 3 dB for [Gly₂–H]⁻ and [Gly₂–6H + 5D]⁻ to avoid saturation of the dissociation signal on the strongest bands. Loss of neutral glycine was the only dissociation pathway observed. FELIX was scanned from 600 to 1800 cm⁻¹ in steps of 5 cm⁻¹ and at every frequency step, four mass spectra were summed. IR spectra were obtained by plotting the normalized IRMPD rate constant, k = −ln(I/I₀)/t, where I, I₀ and t are the precursor ion abundance, the summed precursor and product ion abundances and the irradiation time, respectively, as a function of photon energy and these values were corrected for the laser power.

Computational chemistry

Low-energy structures were identified using conformational searches using Macromodel 9.1 (Schrödinger Inc., Portland, OR, U.S.A.) and the OPLS2005 force field. All candidate structures were geometry optimized with the corresponding quantum chemical methods. The xyz coordinates for three isomers at the B3LYP/6-311++G** level of theory are given in the ESI.† The geometries of these isomers do not change significantly with other functionals, MP2 methods or basis sets. All quantum chemical calculations were performed in QChem.³¹ The method of Truhlar was used to extrapolate aug-cc-pVXZ calculations to the basis set limit.³² For MP2 with aug-cc-pVXZ basis sets, the resolution of identity (RI) approximation was employed.³³ Electronic energies, unscaled harmonic vibrations and rotational constants were used to calculate the relative thermodynamic stability as a function of temperature (0–350 K). An example of one of these curves is shown Fig. S1 (ESI†). Only the values at 0 and 298 K are reported in Table 1. Binding energies for the SB and NZ form were computed at the MP2/6-311++G** level of theory using the counterpoise correction method to account for the basis set superposition error.³⁴ Harmonic vibrational spectra were convolved with Gaussian functions of 50 cm⁻¹ fwhm and scaled with a uniform scaling factor in order to compare the predicted to experimental results. Vibrational frequency computations for [Gly₂–6H + 5D]⁻ were done using the corresponding [Gly₂–H]⁻ isomer geometries and substituting all exchangeable protons for deuterium. Unless otherwise stated, the computational results discussed in the text are obtained from B3LYP/6-311++G** computations.

Table 1 Comparison of the most intense experimental IRMPD transitions with the computed (B3LYP/6-311++G**) most intense harmonic vibrations scaled by 0.985 for [Gly₂–H]⁻ (H) and [Gly₂–6H + 5D]⁻ (D) and the corresponding peak assignment. “Free” ν_antisymm and ν_symm correspond to the vibrations of the carboxylate group of the SB isomer that is not involved in hydrogen-bonding to the second glycine molecule

	Exp./cm^−1	Vib. (SB)	Theo./cm^−1	Vib. (NZ)	Theo./cm^−1
H	1704	“Free” νantisymm	1697	COOH νantisymm	1782
H	1622	ν antisymm, NH3^+	1624, 1579, 1508	COO^−νantisymm	1685
H	1404	ν isymm	1379	COO^−νisymm	1397
H	1345	“Free” νsymm	1316	COOH νsymm	1339
H	1000–1300	Wagging	1146	O⋯H–O	1157, 1137, 1091
D	1703	“Free” νantisymm	1688	COOH νantisymm	1710
D	1632	ν antisymm	1579	COO^−νantisymm	1676
D	1401–1484	ν isymm	1382
D	1349	“Free” νsymm	1320	COO^−νisymm	1360
D	1270	NH3^+	1196	COOH νsymm	1285

---

Results and discussion

Reference ion [Gly₂–2H + Na]⁻

The IRMPD spectrum and the vibrational spectrum calculated from the lowest-energy structure of [Gly₂–2H + Na]⁻ are shown in Fig. 1. The experimental spectrum (Fig. 1a) has three well-resolved features at 1594, 1380 and 866 cm⁻¹, a small shoulder at 1303 cm⁻¹, and a broad band at 946 cm⁻¹. Only one stable isomer within an energy range of ∼12 kcal mol⁻¹ was identified. The sodium ion in this structure is tetrahedrally coordinated to the two deprotonated carboxylic acid groups of the glycine anions. The two most intense experimental bands at 1594 and 1380 cm⁻¹ are in very good agreement with the theoretically predicted antisymmetric and symmetric sodium bound carboxylate stretches ν_antisymm and ν_symm at 1597 and 1387 cm⁻¹, respectively, consistent with previous results for isolated carboxylate groups.³⁵

Fig. 1 Comparison of (a) the experimental IRMPD spectrum of [Gly₂–2H + Na]⁻ with (b) the calculated harmonic vibrational spectrum of the lowest energy isomer (structure inset). The theoretical IR spectra were computed at the B3LYP/6-311++G** level of theory and a uniform scaling factor of 0.985 was used to correct for the systematic errors of harmonic vibrational frequency calculations.

The other three calculated bands at 1301, 964 and 874 cm⁻¹ are combinations of NH₂ and CH₂ wagging vibrations differing mainly in the relative phases of the stretching motions. The close agreement between theory and experiment indicates that this is the predominant structure (Fig. 1b, inset). All of the features in the spectrum of [Gly₂–2H + Na]⁻ are assignable to specific vibrations and serve as reference values to evaluate the extent of hydrogen bonding in corresponding vibrations of the [Gly₂–H]⁻ complex.

Structure and IRMPD spectrum of [Gly₂–H]⁻

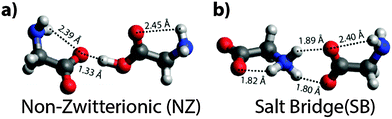
The IRMPD spectrum of [Gly₂–H]⁻ is significantly different from that of [Gly₂–2H + Na]⁻ (Fig. 2a). There are at least six resolved features (1704, 1622, 1404, 1345, 940 and 835 cm⁻¹) and a broad band between 1000 and 1300 cm⁻¹. Only two potential global minimum structures that are nearly iso-energetic were identified for [Gly₂–H]⁻ (Fig. 3). The third lowest-energy structure is 9.9 kcal mol⁻¹ higher in energy (see Fig. S1–S3, ESI†). The structure shown in Fig. 3a is the NZ form of the deprotonated glycine dimer in which the neutral glycine has an O–H bond distance of 1.12 Å. The anionic glycine binds non-covalently to the carboxylic acid proton (d_O⋯H = 1.33 Å) to form an O⋯H–O angle of 177° indicating a strong ionic H-bond. One N–H bond of each NH₂ group is directed towards an oxygen atom of a carboxyl/carbonyl group (d_O⋯H–N = 2.39/2.45 Å) indicating a hydrogen bond between these groups. In the SB form of [Gly₂–H]⁻ (Fig. 3b), the proton attaches to the NH₂ group of one glycine, forming a zwitterionic glycine with an NH₃⁺ (d_N–H = 1.04 Å) and a CO₂⁻ group. Each oxygen atom of the carboxylate group on the anionic glycine binds to one proton of the NH₃⁺ group (d_O⋯H = 1.80 and 1.89 Å) resulting in the formation of a SB. The remaining NH₂ group reorients with the N–H bonds towards the carboxylate group indicating the formation of one hydrogen bond (d_O⋯H–N = 2.40 Å). The calculated vibrational spectra for the NZ and SB isomers are significantly different (Fig. 2b and c, respectively). The most characteristic vibrational frequencies and their assignments are given in Table 1.

Fig. 2 Comparison of (a) the experimental IRMPD spectrum of [Gly₂–H]⁻ with calculated harmonic vibrational spectra for (b) NZ and (c) SB isomers. The theoretical IR spectra were computed at the B3LYP/6-311++G** level of theory and a uniform scaling factor of 0.985 was used to correct for the systematic errors of harmonic vibrational frequency calculations.

Fig. 3 Structural isomers for [Gly₂–H]⁻ with (a) a non-zwitterionic (NZ) and (b) a salt bridge structure (SB) computed at the B3LYP/6-311++G** level of theory. The hydrogen bonds are indicated by dashed lines and the corresponding bond lengths are included. Oxygen, nitrogen, carbon and hydrogen atoms are represented by red, blue, grey and white spheres, respectively.

These data (Fig. 2 and Table 1 and Table S1, ESI†) show that the SB structure and the corresponding IR spectrum are in much better agreement with the experimental spectrum than that for the NZ structure, indicating the presence of mostly SB structures. A similar conclusion is deduced from comparisons to spectra calculated using other levels of theory (Fig. S2–S4, ESI†). In particular, there is good agreement between the coupled antisymmetric stretching motion of the “free” carboxylate (“free” ν_antisymm and ν_symm in Table 1) and NH₃⁺ groups calculated to occur at 1697 cm⁻¹ and the relatively sharp experimental band centered at 1704 cm⁻¹, whereas the IR spectrum for the NZ isomer cannot explain this feature. The three resonances corresponding to NH₃⁺ umbrella and stretching modes are calculated to occur between 1508 and 1624 cm⁻¹ and there is a broad band in this region of the experimental spectrum. The very broad feature between 1000–1300 cm⁻¹ could indicate some contributions from a NZ structure but can also be attributed to anharmonic vibrations, a fluxional hydrogen bond, combination bands or tunnelling motions.

Energetics and hydrogen bond mediated SB formation

The SB and the NZ isomers differ in energy by less than 2 kcal mol⁻¹ and results using different levels of theory are given in Table 2. When only the electronic energy is taken into account, the SB is more stable than the NZ. However, the energetic contributions from the vibrations and rotations at 0 and 298 K destabilize the ZW compared to the NZ isomer. For some levels of theory, this makes the NZ structure the most stable structure at the experimental temperature of 298 K. Using the resolution of identity approximation for MP2,³³ extrapolating the energy to the basis set limit for aug-cc-pVXZ type basis sets³² and using the harmonic vibrations from B3LYP/aug-cc-pVTZ calculations, results in the stabilization of the SB over the NZ isomer by 0.6 kcal mol⁻¹ at 298 K. Even though the highest level of theory employed in this study favours the SB over the NZ at the experimental conditions, the energy differences are so small that an unambiguous theoretical assignment of the lowest-energy isomer is not possible. The absence of significant signal for the NZ isomer deduced from the IRMPD results compared to the similar energetics predicted by theory is likely due to the fact that the energetics of the theoretical methods used are not sufficiently accurate. It is also possible that a higher energy isomer may be kinetically trapped³⁶ as a result of solvent evaporation during ESI. This may favor formation of the SB isomer which has a higher number of intramolecular hydrogen bonds.

Table 2 Relative energy (ΔE = E_SB − E_NZ) of the SB isomer (E_SB) of [Gly₂–H]⁻ with respect to the energy of the NZ structure (E_NZ) and the corresponding Gibbs free energies for 0 and 298 K at different levels of theory (in kcal mol⁻¹)

Level of theory	ΔE/kcal mol^−1	ΔG (0 K)/kcal mol^−1^a	ΔG (298 K)/kcal mol^−1
a Equivalent to correcting the electronic energy for the zero-point vibrational energy. b Extrapolation method developed by Truhlar.^32 c 6-311++G**. d aug-cc-pVTZ.
B3LYP/^c	−1.84	0.38	1.01
TPSSh/^c	−4.05	−1.94	−0.80
ωB97-D/^c	−2.52	−0.38	1.11
MP2/^c	−0.99	0.93	1.65
RIMP2/^d//B3LYP/^d	−3.26	−0.99	−0.60
RIMP2/^b//B3LYP/^d	−3.27	−1.00	−0.61

---

A phenomenological explanation for the extraordinary stability of the SB over the NZ form for the negative glycine dimer can be deduced by comparing the isomeric structures in Fig. 3 with those for the neutral²⁹ and positive^21–24 glycine dimers. A zwitterion in the gas-phase without additional ions or solvent molecules attached can be stabilized both by the attractive Coulomb interaction between opposite charges and by enhanced hydrogen bonding networks that can outweigh the energetic cost associated with proton transfer.³⁷ Hydrogen bonds (HBs) can be divided into three general categories: HBs between two neutral groups that have bond strengths on the order of ∼5 kcal mol⁻¹,^38,39 ionic hydrogen bonds (IHB) between a neutral and charged group that have bond strengths typically between 5–35 kcal mol^−1 39 and zwitterionic hydrogen bonds (ZHB) between two oppositely charged groups. For the latter, there is no experimental reference data, but computations for [Gly₂–H]⁻ at the MP2/6-311++G** level of theory give a bond strength of 24.9 kcal mol⁻¹ per ZHB. Therefore, the bond strength should follow the ranking HB < IHB ≤ ZHB. For Gly₂, there are a maximum of two ZHB and two IHB for a double ZW isomer,²⁹ for [Gly₂ + H]⁺, there is only one each of ZHB, IHB and HB.²⁵ For the anionic glycine dimer, the SB form has three ZHB and one IHB (Fig. 3), corresponding to one of the two NH₂ hydrogen atoms and three NH₃⁺ hydrogen atoms bonding to the oxygen of the COO⁻ groups. A comparison can also be made between the NZ and SB isomers of [Gly₂–H]⁻. The NZ isomer has only one IHB with an unusually high bond energy of 48.7 kcal mol⁻¹ (MP2/6-311++G**), a weak IHB and weak HB. Therefore, the close energetic competition between SB and NZ isomers for only [Gly₂–H]⁻ is due to the high stabilization energy of the hydrogen bond network in the corresponding SB structure compared to that for Gly₂, [Gly₂ + H]⁺ and for the NZ isomer of [Gly₂–H]⁻.

Deuterated glycine dimer anion

Room temperature IRMPD spectra often resemble linear IR spectra and this method has been used to characterize many different gas-phase molecules of biological importance.⁴⁰ The structures of weakly bound complexes can be fluxional and vibrational anharmonicities become more important at elevated temperatures.⁴¹ For such systems, low temperature predissociation spectroscopy can produce linear IR spectra with sharp bands that can aid in spectral interpretation. However, the presence of a tagging atom/molecule that are often used can shift IR bands and even influence the structure of the complex.⁴² The computed binding energy between the two subunits in [Gly₂–H]⁻ is ∼50 kcal mol⁻¹. For ions with high dissociation energies, both spectroscopic methods yield spectra with comparable band positions and intensities, only differing in the width of the spectral bands as long as there are no weak HBs.⁴³

Because of broad bands obtained by IRMPD, the experimental assignment of the SB isomer was confirmed by measuring an IRMPD spectrum of the isotopically labelled deprotonated glycine dimer anion (Fig. 4a). Four intense bands at 1703, 1632, 1349 and 1270 cm⁻¹, two small features at 1049 and 948 cm⁻¹ and a broad band at 748 cm⁻¹ are observed. The peaks at 1349 and 1270 cm⁻¹ have broad shoulders on their high and low energy sides, respectively. The broad band between 1100 and 1300 cm⁻¹ for [Gly₂–H]⁻ (Fig. 2a) is not observed for [Gly₂ + 5D-6H]⁻. This is consistent with this feature in the [Gly₂–H]⁻ spectrum originating from either anharmonic vibrations, a fluxional hydrogen bond, or a tunnelling motion because deuterated vibrations are more harmonic and the tunnelling probability as well as the deuterium mobility are significantly reduced.⁴⁴ The calculated IR spectrum of the deuterated SB isomer (Fig. 4c) is in much better agreement with the IRMPD spectrum than the calculated spectrum of the deuterated NZ structure (Fig. 4b). A comparison of the experimental and theoretical results at the MP2/6-311++G** level of theory, shown in Fig. S5 (ESI†), supports this conclusion. Every peak in the experimental spectrum (Fig. 4a) is explainable by the SB isomer (Fig. 4c). Even the relative intensities match except for the lower intensity of the peak at 1703 cm⁻¹ in the experimental spectrum. A few computed frequencies are compared to the experimental features in Table 1 and a more complete comparison is found in Table S2 (ESI†). The two distinct features in the experimental spectrum at 1703 (“free” ν_antisymmTable 1) and 1632 cm⁻¹ can be assigned to the two well separated stretches involving the COO⁻ groups of the SB isomer at 1688 and 1579 cm⁻¹, whereas the corresponding COO⁻/COOD stretches of the NZ isomer only give one broad feature around 1697 cm⁻¹. This assignment is also consistent with the fact that these two features only shift by −1 and +10 cm⁻¹ due to the isotopic substitution comparable to the small predicted isotopic shift of −9 and 0 cm⁻¹ for the SB isomer (Table 1). The isotopic shift for the NZ structure is calculated to be −72 and −9 cm⁻¹.

Fig. 4 Comparison of (a) the experimental IRMPD spectrum of [Gly₂–6H + 5D]⁻ with calculated harmonic vibrational spectra for (b) NZ and (c) SB isomers. The theoretical IR spectra were computed at the B3LYP/6-311++G** level of theory and a uniform scaling factor of 0.985 was used to correct for the systematic errors of harmonic vibrational frequency calculations.

Conclusion

In conclusion, we have demonstrated that the glycine dimer anion predominantly forms a SB structure in the gas-phase in which one glycine molecule is zwitterionic. Computational results indicate that the energy difference between the SB structure and the NZ isomer is small. In contrast, neutral and protonated glycine dimers are NZ structures.^21–24,29 The extraordinary preference for the SB structure of the glycine dimer anion can be understood in terms of the optimized hydrogen bond network that is formed in this structure. These results show that there is a fine balance between the different intrinsic interactions that can stabilize SBs in a solvent-free environment even for amino acids as simple as glycine. Thus, this simple system can serve as a benchmark for theory that can be used to evaluate the accuracy of theoretical methods for predicting the formation of SBs and the stabilizing effect of inter-residue hydrogen bonding in the presence of excess negative charge. Although glycine is not involved in SBs in proteins, these results provide compelling evidence about the role of hydrogen bonding in stabilizing SB interactions that should lead to new insights into the stabilities of SBs in solvent-inaccessible environments, such as the interior of proteins and at protein–protein interfaces. Future work will focus on more complex amino acid and peptide systems in order to rationalize the principles of hydrogen bond mediated SB formation in peptides and proteins.

Acknowledgements

The authors thank the National Science Foundation (grant CHE-1306720) for generous financial support of this research and are grateful to the German National Academy of Sciences Leopoldina (LPDS 2012–15 and LPDR 2014–01) for a postdoctoral scholarship and financial support (SH). The authors thank Dr. Britta Redlich and others at the FELIX staff for excellent support. JO acknowledges support by the Stichting Physica and thanks NWO for a vici grant.

Notes and references

1. I. Gitlin, J. D. Carbeck and G. M. Whitesides, Angew. Chem., Int. Ed. Engl., 2006, 45, 3022–3060.
2. M. P. Williamson, A. M. Hounslow, J. Ford, K. Fowler, M. Hebditch and P. E. Hansen, Chem. Commun., 2013, 49, 9824–9826.
3. F. O. Tzul, K. L. Schweiker and G. I. Makhatadze, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E259–66.
4. (a) H. R. Bosshard, D. N. Marti and I. Jelesarov, J. Mol. Recognit., 2004, 17, 1–16; (b) K. Takano, K. Tsuchimori, Y. Yamagata and K. Yutani, Biochemistry, 2000, 39, 12375–12381.
5. R. D. Suenram and F. J. Lovas, J. Mol. Spectrosc., 1978, 72, 372–382.
6. C. J. Chapo, J. B. Paul, R. A. Provencal, K. Roth and R. J. Saykally, J. Am. Chem. Soc., 1998, 120, 12956–12957.
7. Y. Ding and K. Krogh-Jespersen, Chem. Phys. Lett., 1992, 199, 261–266.
8. R. Antoine, M. Broyer, P. Dugourd, G. Breaux, F. C. Hagemeister, D. Pippen, R. R. Hudgins and M. F. Jarrold, J. Am. Chem. Soc., 2003, 125, 8996–8997.
9. S. Jaeqx, J. Oomens, A. Cimas, M.-P. Gaigeot and A. M. Rijs, Angew. Chem., Int. Ed. Engl., 2014, 53, 3663–3666.
10. P. D. Schnier, W. D. Price, R. A. Jockusch and E. R. Williams, J. Am. Chem. Soc., 1996, 118, 7178–7189.
11. M. Gutowski, P. Skurski and J. Simons, J. Am. Chem. Soc., 2000, 122, 10159–10162.
12. J. T. O'Brien, J. S. Prell, G. Berden, J. Oomens and E. R. Williams, Int. J. Mass Spectrom., 2010, 297, 116–123.
13. J. M. Talley, B. A. Cerda, G. Ohanessian and C. Wesdemiotis, Chem. – Eur. J., 2002, 8, 1377–1388.
14. T. Wyttenbach, M. Witt and M. T. Bowers, J. Am. Chem. Soc., 2000, 122, 3458–3464.
15. C. Kapota, J. Lemaire, P. Maître and G. Ohanessian, J. Am. Chem. Soc., 2004, 126, 1836–1842.
16. M. F. Bush, J. Oomens, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 6463–6471.
17. J. H. Jensen and M. S. Gordon, J. Am. Chem. Soc., 1995, 117, 8159–8170.
18. S. Xu, J. M. Nilles and K. H. Bowen, J. Chem. Phys., 2003, 119, 10696.
19. M. F. Bush, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 13544–13553.
20. A. M. Rijs, G. Ohanessian, J. Oomens, G. Meijer, G. von Helden and I. Compagnon, Angew. Chem., Int. Ed. Engl., 2010, 49, 2332–2335.
21. R. Wu and T. B. McMahon, J. Am. Chem. Soc., 2007, 129, 4864–4865.
22. W. D. Price, P. D. Schnier and E. R. Williams, J. Phys. Chem. B, 1997, 101, 664–673.
23. C. G. Atkins, K. Rajabi, E. A. L. Gillis and T. D. Fridgen, J. Phys. Chem. A, 2008, 112, 10220–10225.
24. W. D. Price, R. A. Jockusch and E. R. Williams, J. Am. Chem. Soc., 1997, 119, 11988–11989.
25. R. Wu and T. B. McMahon, Angew. Chem., Int. Ed. Engl., 2007, 46, 3668–3671.
26. R. Wu and T. B. McMahon, J. Am. Chem. Soc., 2008, 130, 3065–3078.
27. J. T. O'Brien, J. S. Prell, J. D. Steill, J. Oomens and E. R. Williams, J. Am. Chem. Soc., 2009, 131, 3905–3912.
28. S. Jaeqx, J. Oomens and A. M. Rijs, Phys. Chem. Chem. Phys., 2013, 15, 16341–16352.
29. P. Friant-Michel and M. F. Ruiz-López, ChemPhysChem, 2010, 11, 3499–3504.
30. J. J. Valle, J. R. Eyler, J. Oomens, D. T. Moore, A. F. G. van der Meer, G. von Helden, G. Meijer, C. L. Hendrickson, A. G. Marshall and G. T. Blakney, Rev. Sci. Instrum., 2005, 76, 023103.
31. Y. Shao, et al. , Phys. Chem. Chem. Phys., 2006, 8, 3172–3191.
32. D. G. Truhlar, Chem. Phys. Lett., 1998, 294, 45–48.
33. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175.
34. F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885.
35. J. Oomens and J. D. Steill, J. Phys. Chem. A, 2008, 112, 3281–3283.
36. G. Papadopoulos, A. Svendsen, O. V. Boyarkin and T. R. Rizzo, J. Am. Soc. Mass Spectrom., 2012, 23, 1173–1181.
37. (a) E. F. Strittmatter, R. L. Wong and E. R. Williams, J. Phys. Chem. A, 2000, 104, 10271–10279; (b) E. F. Strittmatter and E. R. Williams, Int. J. Mass Spectrom., 2001, 212, 287–300.
38. C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511–544.
39. M. Meot-Ner Mautner, Chem. Rev., 2012, 112, PR22–PR103.
40. N. C. Polfer and J. Oomens, Mass Spectrom. Rev., 2009, 28, 468–494.
41. C. T. Wolke, et al. , J. Phys. Chem. A, 2015, 119, 1859–1866.
42. (a) J. Jašík and J. Roithová, Int. J. Mass Spectrom., 2015, 377, 109–115; (b) A. Masson, E. R. Williams and T. R. Rizzo, J. Chem. Phys., 2015, 143, 104313.
43. (a) N. S. Nagornova, T. R. Rizzo and O. V. Boyarkin, J. Am. Chem. Soc., 2010, 132, 4040–4041; (b) P. Kupser, K. Pagel, J. Oomens, N. Polfer, B. Koksch, G. Meijer and G. von Helden, J. Am. Chem. Soc., 2010, 132, 2085–2093; (c) J. Oomens, J. D. Steill and B. Redlich, J. Am. Chem. Soc., 2009, 131, 4310–4319; (d) A. F. DeBlase, S. R. Kass and M. A. Johnson, Phys. Chem. Chem. Phys., 2014, 16, 4569–4575.
44. P. R. Schreiner, H. P. Reisenauer, D. Ley, D. Gerbig, C.-H. Wu and W. D. Allen, Science, 2011, 332, 1300–1303.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed description of the experimental and theoretical methods, relative stability of the isomers as a function of temperature, detailed band assignment, harmonic spectra for other isomer and other levels of theory, xyz coordinates of isomers. See DOI: 10.1039/c5cp06120b

‡ Current address: Institute of Inorganic and Analytical Chemistry, Justus-Liebig-University Giessen, 35392 Giessen, Germany.

---