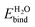Solvation effects on the band edge positions of photocatalysts from first principles

Abstract

The band edge positions of photocatalysts relative to the redox potentials of water play an important role in determining the efficiency of photoelectrochemical cells. These band positions depend on the structure of the solid–liquid interface, but direct ab initio molecular dynamics calculations of these interfaces, while expected to be accurate, are too computationally demanding for high-throughput materials screening. Thus rapid theoretical screening of new photocatalyst materials requires simplified continuum solvation models that are suitable for treating solid–liquid interfaces. In this paper, we evaluate the accuracy of the recently developed CANDLE and SaLSA continuum solvation models for predicting solvation effects on the band positions of several well-studied surfaces [Si(111), TiO₂(110), IrO₂(110) and WO₃(001)] in water. We find that the solvation effects vary considerably, ranging from <0.5 eV for hydrophobic surfaces, 0.5–1 eV for many hydrophilic oxide surfaces, to ∼2 eV for oxygen-deficient surfaces. The solvation model predictions are in excellent agreement (within ∼0.1 eV) with ab initio molecular dynamics results where available, and in good agreement (within ∼0.2–0.3 eV) with experimental measurements. We also predict the energetics for surface oxygen vacancies and their effect on the band positions of the hydrated WO₃(001) surface, leading to an explanation for why the solvation shift observed experimentally is substantially larger than predicted for the ideal surface. Based on the correlation between solvation shift and the type of surface and solvent, we suggest approaches to engineer the band positions of surfaces in aqueous and non-aqueous solutions.

---

Introduction

Artificial photosynthesis, the reduction of water to H₂ or CO₂ to carbon-based fuels using the energy from sunlight in a photoelectrochemical cell (PEC), provides a promising path towards clean renewable energy while reducing CO₂ emissions.^1,2 In addition to high catalytic activity for the reaction of interest, the reliability and efficiency of photocatalysts in a PEC depend critically on the alignment of their band edges, for example, with the redox potentials of water for water splitting solar cells.³

The discovery of new stable and efficient photocatalysts is the target of considerable recent theoretical and experimental effort.^4–8 However, most theoretical predictions are based on electronic structure calculations in vacuum^5,9,10 which neglect the substantial solvation effects on the electronic states of the photocatalysts. Depending on the interaction between water and the photocatalyst surfaces, the shift of electronic states due to solvation can be as large as 1–2 eV.¹¹ Consequently, neglecting solvation effects can qualitatively change predictions for certain materials.

In fact, ab initio molecular dynamics (AIMD) calculations of explicit liquid water/photocatalyst interfaces have been validated to provide accurate estimates of the band positions.¹¹ Unfortunately, these calculations are highly computationally expensive, requiring long simulation times to obtain statistically meaningful results. Evaluating reaction mechanisms at the solid/liquid interface introduces additional challenges and computational cost in such AIMD calculations, making it impractical today as a systematic tool for rapid theoretical screening of new photocatalysts.

Continuum solvation models directly abstract the thermodynamically-averaged effect of the liquid in an electronic structure calculation of the solute alone, and potentially provide an accurate but computationally affordable way of including solvent effects in the rapid theoretical screening of photocatalyst materials. However, these models are parameterized primarily to describe the solvated free energies of organic molecules,^12–14 and do not extrapolate well to strongly ionic surfaces.¹⁵ The absence of unambiguous thermodynamic data for transition metal oxide surfaces, analogous to the solvation energies available for molecules, precludes the direct parameterization of empirical solvation models for these systems. Consequently, band offsets in solvated ionic surfaces have not yet been validated, requiring the development of reliable non-empirical methods.

Here, we evaluate the accuracy of the recently-developed non-empirical SaLSA solvation model,¹⁶ and the empirical CANDLE solvation model¹⁷ derived from SaLSA, for the prediction of band positions in solution. We find good agreement for both models with available experimental measurements and with AIMD simulations of well-studied photocatalysts, such as Si, TiO₂ and WO₃. We also explore the effect of surface oxygen vacancies on the solvated band edge positions of WO₃, which is known to exhibit highly oxygen-deficient surfaces.^18,19 Our study compares solvation effects on various surfaces, including hydrophobic, hydrophilic, ionic and non-ionic in order to provide a general understanding of the magnitude of solvation shifts for different types of surfaces and to guide discovery of new materials.

We start with a brief description of solvation models and our protocol for calculating the solvation shift on the electronic states in the Methods section. The Results section begins with a comparison of solvation models with AIMD predictions for functionalized Si surfaces, and presents comparisons between theoretical predictions and experimental measurements on the solvation shift of the band positions of the stable TiO₂, IrO₂ and WO₃ surfaces. We also discuss the effect of oxygen vacancies on the WO₃ band positions and conclude the Results section with the trends of solvation shifts for surfaces in different solvents. The final two sections summarize these results, point out the general trends in solvation shifts that are relevant for ab initio photocatalyst design, and suggest future approaches to engineer band positions in solution.

Methods

We performed first principles calculations of Si, TiO₂, IrO₂ and WO₃ slabs in vacuum and solution using the open-source plane-wave density functional theory software, JDFTx.²⁰ This software is designed specifically for electronic structure calculations of systems in solution within the framework of joint density functional theory,²¹ and enables the rapid development of solvation models (such as SaLSA¹⁶ and CANDLE¹⁷) using the algebraic formulations for electronic and classical density functional theories.^22,23 We used the PBE²⁴ generalized gradient approximation (GGA) along with DFT-D2 pair-potential dispersion corrections,²⁵ and GBRV ultrasoft pseudopotentials.²⁶ See the ESI,† for further computational details of the DFT calculations and detailed structures of all calculations presented below.

Density functional predictions for the band gaps and absolute positions of the valence band maximum (VBM) and conduction band minimum (CBM) are inaccurate in comparison to experiment,²⁷ especially for semi-local exchange–correlation functionals such as the PBE GGA. Consequently, we calculate the shift of the electronic states due to solvation which is mainly an electrostatic effect; and compare it to the experimental solvation shift deduced from vacuum and electrochemical measurements, as detailed below. Specifically, we calculate the theoretical solvation shift by subtracting the planar-averaged electrostatic potential obtained from solvated and vacuum calculations. This electrostatic potential difference is insensitive to the choice of exchange–correlation approximation with differences only ∼0.1 eV between PBE, hybrid functionals and even many-body perturbation theory (GW approximation) calculations,^28–31 and can be reliably compared to experiment.

We constructed inversion-symmetric slab models for each material with sufficient number of layers (4 to 6) to converge the electrostatic potential in vacuum as well as solution, and optimized all ionic positions self-consistently both in vacuum and solvent. Inversion symmetry ensures identical top and bottom surface configurations of the slab with zero net dipole in the unit cell in all directions. We employ truncated Coulomb potentials^32–34 to eliminate spurious interactions between periodic images and accelerate the convergence with respect to the thickness of the vacuum or solvent region. The electrostatic potential decays to zero away from the slab in all cases, because of the truncation in vacuum calculations and the Debye screening due to the electrolyte in the solvated ones.³⁵ This establishes a well-defined vacuum reference (zero potential at infinity) in solvent as well as vacuum, thereby enabling reliable electrostatic potential difference calculations.

Solvation models replace the thermodynamically-averaged effect of the liquid by the electrostatic response of a continuum dielectric cavity along with corrections for cavity formation and dispersion energies.¹² The distance of the cavity surface from the solute atoms determines the strength of the electrostatic response and hence the solvation shift in the electronic states. This distance is conventionally fit to reproduce the solvation energies of organic solutes but such models are often unreliable for application to the ionic inorganic surfaces of interest here.¹⁵ The SaLSA solvation model¹⁶ directly captures the nonlocal response of the solvent and accurately captures its electrostatic response without any fit parameters,§ and is therefore ideal for applications to photocatalyst surfaces which are far removed from the fit sets of conventional solvation models.

However, SaLSA systematically underestimates the solvation energies of organic anions which, although unimportant for the present study, might be relevant for future studies of reaction mechanisms on these catalyst surfaces. The CANDLE solvation model¹⁷ is an empirical solvation model derived from SaLSA which adds two empirical parameters: one to capture the nonlocal response with an effective local response and another parameter to correct for the asymmetric error in anion solvation. CANDLE is systematically more accurate for solvation free energies with a mean absolute error of 1.8 kcal mol⁻¹ on an extensive set of 240 neutral molecules, 51 cations and 55 anions, and 3.5 kcal mol⁻¹ for the anions alone,¹⁷ compared to 4.5 kcal mol⁻¹ and 20 kcal mol⁻¹ respectively for SaLSA on the same set.¹⁶ However, the accuracy of neither SaLSA nor CANDLE has been tested previously for ionic surfaces, so we evaluate the accuracy of both models for predicting the solvation shift on the band positions of several photocatalyst surfaces.

Continuum solvation models can describe electrostatic solvent–solute interactions, but ignore stronger chemical bonding effects of the solvent molecules with the surface. In order to investigate these effects, we apply the solvation model both to the bare surface in solution and to the case in which we include a single layer of explicit water molecules adsorbed or chemisorbed on the surface. The solvent monolayer describes chemical bonding well, but without AIMD, it may not accurately describe the solvation shift due to liquid water because fluctuations between numerous low-energy configurations may introduce fluctuations in the interfacial dipoles. To estimate this error, we also consider multiple low-energy configurations of the explicit solvent layer.

Experimentally, the band edge positions in liquid are estimated from the flat-band potential U_fb, the applied potential at which the band bending of the semiconductor at the solid–liquid interface disappears. The flat-band potential measured relative to a reference electrode, such as the normal hydrogen electrode (NHE), satisfies

U^(NHE)_fb = A + ΔE_F + E^NHE₀ + V_pH + V_dip (1)

where A is the band edge positions of the majority carrier referenced to vacuum; which equals to the electron affinity (conduction band minimum E_c) for an n-type semiconductor and the ionization potential (valence band maximum E_v) for a p-type semiconductor. ΔE_F is the difference between the Fermi energy and A, and E^NHE₀ = 4.44 eV³⁷ is the absolute position of the reference NHE potential below vacuum.¶V_pH captures the variation of the flat-band potential with pH and is defined to be zero at the pH of zero charge (pH_PZC). Our calculations do not account for explicit adsorption of ions on the surface; thus they correspond to the pH_PZC condition where the net charge of adsorbed ions at the surface is zero. V_dip includes only the potential drop across the solid–liquid interface due to the effect of interfacial dipoles. This is exactly what the solvation model captures, and so we can compare V_dip directly with its theoretical counterpart: the difference between the electrostatic potential in vacuum and solvated calculations. Note that some studies assume V_H ≡ V_dip + V_pH = 0 at pH_PZCi.e. V_dip = 0,⁴⁰ which completely neglects the effect of dipoles at the solid–liquid interface in direct contrast to our findings.

Experimentally, A in eqn (1) is obtained from photoemission spectra in vacuum. Many body perturbation theory within the GW approximation well describes the one-particle excitation involved in the photoemission process,^41,42 and predicts ionization energies and electron affinities in good agreement with experiment.^43–45 We could therefore make theoretical predictions for the absolute band positions in liquid based on eqn (1), but as discussed above, we focus on the solvation shifts (V_dip), since they are insensitive to the choice of the electronic structure method.

Finally, we need to account for the effect of pH on the band edge positions in order to extract the interfacial dipole contribution V_dip from experimental data. Fortunately, the band edge positions in an electrolyte follow the Nernst equation for many oxides³ including TiO₂⁴⁶ and WO₃,⁴⁷ because H⁺ and OH⁻ are the only charge-determining ions on these surfaces. Consequently,

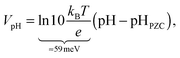since we defined V_pH to be zero at pH_PZC. We can now calculate V_dip using (1) and (2) from photoemission measurements of band positions in vacuum and electrochemical measurements of band positions in liquid relative to NHE (typically at pH = 0).^1–3

In summary, we calculate the solvation shift from the electrostatic potential difference between vacuum and solvated calculations, and compare it to the experimental difference in band edge positions from photoemission and electrochemical flat-band potential measurements referenced to pH_PZCvia the Nernst equation.

Results

Functionalized Si(111) surfaces

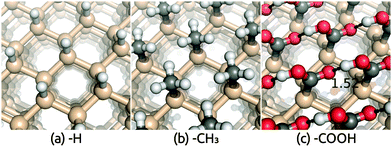
Crystalline silicon is an efficient and popular semiconductor for PEC applications because of its suitable band gap and band edge positions relative to water redox potentials. The stability of silicon against corrosion in electrolyte environments depends on its surface termination, and hence different terminations of Si(111) surfaces have been investigated both theoretically and experimentally.^31,48–52 Of particular interest is the recent AIMD study of band edge positions and electrostatic potentials in functionalized Si(111)/liquid H₂O interfaces.¹¹ As discussed previously, although computationally expensive, AIMD describes the dynamical interaction between H₂O and solid surfaces fairly accurately and serves as an ideal benchmark for our solvation approach before comparison to experiment for more complicated surfaces.

Table 1 compares the solvation shift in the band edge positions, V_dip, predicted using the SaLSA and CANDLE solvation models with the AIMD results from ref. 11, for the functionalized Si(111) surfaces shown in Fig. 1. AIMD predicts a small solvation shift ∼0.2–0.3 eV towards the vacuum level for the hydrophobic H and CH₃ terminated surfaces which interact weakly with liquid water. The SaLSA model predictions agree perfectly with AIMD for these surfaces and the CANDLE predictions agree reasonably well with AIMD with a small systematic error ∼−0.08 eV (i.e. further from the vacuum level) compared with the SaLSA results.

Table 1 Predicted solvation shifts (V_dip) of functionalized Si(111) surfaces, compared to ab initio molecular dynamics (AIMD) results.¹¹ Positive V_dip shifts up the bands towards the vacuum level (lower electron affinity). The final column, –COOH_x, presents solvation model results for a partially deprotonated (x = 0.92) surface using snapshots from the AIMD trajectory. The agreement with AIMD for H and CH₃ terminated surfaces validates the solvation models, while the COOH and COOH_x cases underscore the importance of identifying the correct surface composition

Termination	–H	–CH3	–COOH	–COOHx
SaLSA	0.29	0.25	0.31	1.78
CANDLE	0.20	0.17	0.23	1.41
AIMD	0.27	0.34	1.63

---

Fig. 1 Geometry of (a) hydrogen, (b) methyl and (c) carboxylic acid terminated Si(111) surfaces. Calculations used an inversion-symmetric (1 × 1) surface unit cell with four layers and atom positions optimized self-consistently in both vacuum and solution.

The hydrophilic COOH-terminated Si(111) surface, on the other hand, exhibits a large solvation shift >1.5 eV in AIMD and a much smaller shift in the solvation model predictions. However, the AIMD calculations for this surface find significant deprotonation of the COOH group, which implies that the surface is charged on average. Therefore, the AIMD simulation does not correspond to pH_PZC, while the solvation model predictions are for the neutral surface at pH_PZC, causing the discrepancy.

To verify this hypothesis for the discrepancy between AIMD and the solvation model results for the COOH-terminated surface, we applied the solvation model to partially deprotonated surface configurations extracted from the AIMD trajectory.¹¹ In the 20 configurations including explicit water molecules used in the band position calculations of the hydrated COOH surface in ref. 11, we separate the surface by removing all the water molecules and any H atoms not bound to the surface carboxylate groups.|| For each H atom that we remove, we add an electron to the calculation, so that the surface nominally consists of COOH and COO– anions. We find that the COOH terminations are deprotonated approximately 8% on average, and we refer to this surface as COOH_x (with x ≈ 0.92).** We then calculate band positions using the solvation models on these charged configurations, and find results in much better agreement with the AIMD results: SaLSA predicts a shift 0.15 eV more positive than AIMD while CANDLE predicts a 0.2 eV smaller shift (see Table 1).

We note that our solvation model is capable of explicitly dealing with charged systems in solution, e.g. Si–COOH_x (x ≈ 0.92) surface, because Debye screening in the electrolyte automatically produces a physically-meaningful counter-charge in the liquid that keeps the unit cell neutral and makes absolute potentials well-defined.³⁵ (We do not need to deal with charged surfaces in vacuum because the Si–COOH surface does not deprotonate in vacuum and remains neutral.)

The above analysis shows that our solvation model treats the effect of liquid water with remarkable accuracy once we determine the composition of the surface. We show below with comparisons to experimental data that this remains true even for strongly hydrophilic oxide surfaces.

Rutile TiO₂(110) surface

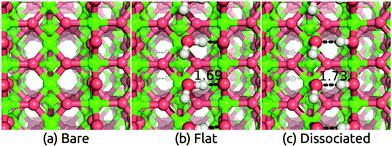
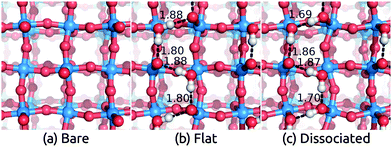
Having benchmarked our solvation approach against AIMD for functionalized Si surfaces, we proceed with comparisons to experimental data for ionic metal oxide surfaces to demonstrate the generality of our method. Rutile TiO₂ is one of the most well-studied and widely used photoelectrode materials because of its in operando stability, the proper alignment of its band edge positions with the H₂O redox potentials, and its capability to act as a conductive protective layer for higher efficiency photoelectrodes such as Si.^2,53,54 In particular, the most stable (110) surface, which has a coordination number of 5 for surface Ti atoms and 2 for surface O atoms, has been characterized extensively theoretically and experimentally.^55–58

We apply the solvation models to the TiO₂(110) surface both directly and with a single layer of explicit water molecules in order to account for any strong bonding effects. We find two distinct classes of stable H₂O configurations with comparable energy: the ‘flat’ configuration with intact water molecules and the ‘dissociated’ configuration with hydroxides and protons as shown in Fig. 2. In both cases, the additional O binds to the 5-coordinated surface Ti and the H atoms in such positions form a hydrogen bonding network parallel to the surface.††Table 2 shows that water binds strongly to the surface, with a binding energy of 1.39 eV and 1.24 eV per water molecule in vacuum respectively for the flat and dissociated configurations. The binding energies in solution are smaller because solvation stabilizes isolated water molecules more than adsorbed ones, but note that the binding energy difference between the two configurations is identical in the vacuum, SaLSA and CANDLE calculations. (See ESI,† for details of the binding energy calculations.) The higher binding energy in the flat configuration suggests that the first layer of liquid water would be dominated by the flat motif. Indeed the calculated V_dip for this configuration best matches the experimental estimates below.

Fig. 2 Geometry of (a) bare TiO₂(110) surface and surfaces with (b) flat adsorbed water molecules and (c) dissociated adsorbed water molecules. Calculations used an inversion-symmetric (1 × 1) surface unit cell with six layers and atom positions optimized self-consistently both in vacuum and solution.

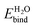Table 2 Predicted solvation shifts (V_dip) of the TiO₂(110) surface with and without explicit H₂O molecules, compared to experimental shift of the VBM due to liquid H₂O,^1,2,58,59 and the binding energies of explicit water molecules to the surface (per molecule), , in vacuum as well as with solvation models. ‘Vacuum’ represents DFT calculations that include a single layer of adsorbed explicit water molecules without any solvation model

Configuration		Bare	Flat	Dissociated
V dip [eV]	SaLSA	0.69	1.25	0.57
	CANDLE	0.54	1.07	0.47
	Vacuum	—	0.93	0.32
	Experiment	0.93–1.11
[eV]	SaLSA	—	0.79	0.63
	CANDLE	—	0.71	0.55
	Vacuum	—	1.39	1.24

---

We calculate the experimental solvation shift as the difference between band positions obtained from photoemission and from electrochemical measurements, as discussed earlier. Ultraviolet photoemission (UPS) measurements⁵⁸ find the work function to be 5.2 eV, which is the position of the CBM below the vacuum level since TiO₂ is naturally n-type. Flat-band potential measurements⁶⁰ find the CBM at 0.0–0.1 eV relative to NHE, which corresponds to an absolute position of 4.44–4.54 eV below the vacuum level. Therefore, using eqn (1) and (2) and the experimental pH_PZC of 4.5–6.0,⁵⁹ we find that the experimental estimate of V_dip ranges from 5.2–4.54 + 0.059 × 4.5 = 0.93 eV to 5.2–4.44 + 0.059 × 6 = 1.11 eV. Additionally, two-photon photoemission measurements⁵⁷ find that the work function shift of the TiO₂(110) surface due to adsorbed water molecules saturates to 0.9–1.0 eV after five layers of water molecules, in agreement with the above electrochemical estimates.

Table 2 compares these experimental estimates to the solvation shifts predicted using the solvation model with and without explicit water molecules. The flat configuration of water molecules is the most stable one, and the corresponding calculated shifts lie in the experimental range for the CANDLE model and is overestimated by 0.1 eV for the SaLSA. The calculated shifts for the less stable dissociated configuration disagree with the experimental estimates suggesting that the first water layer in experiment is indeed dominated by the intact water configurations. The solvation shifts due to a monolayer of explicit water molecules alone without the solvation models are smaller by ∼0.15 eV (0.30 eV) compared to those with CANDLE (SaLSA). In general, fluctuations of the water structure between multiple configurations under room temperature could render predictions from individual minimized structures unreliable, but this is apparently not an issue for TiO₂ because the water binds strongly forming a reasonably rigid structure. A direct application of the solvation models without any explicit water layers, which should in principle directly capture the statistical average of all water configurations, underestimates the experimental shift by 0.2 eV. As in the previous case of functionalized Si surfaces, the CANDLE predictions are systematically 0.1 eV smaller than the SaLSA predictions.

IrO₂(110) surface

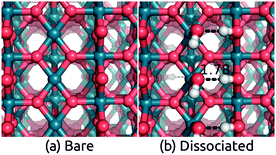
Next, we consider IrO₂ another rutile oxide, which is a highly active and the only known acid-stable catalyst for the oxygen evolution reaction (OER).^61,62 IrO₂ is metallic⁶³ and it is critical to understand the effect of solvation on its work function, since that determines the interfacial energetics and charge transfer between IrO₂ catalysts and semiconductor photoelectrodes.⁶⁴ We now apply our solvation protocol to estimate the work function shift for the most stable (110) surface⁶⁴ of IrO₂.

Table 3 shows the solvation shifts of the IrO₂(110) surface with and without a layer of the explicit water molecules. In this case, the water molecules on the surface dissociate to produce OH bound to the surface Ir and H to the surface O. The intact ‘flat’ configuration is not even meta-stable in this case because it dissociates without a barrier (comparing Fig. 3 to Fig. 2). Additionally, water binds more strongly to IrO₂ than to TiO₂(110) surfaces, with a binding energy in vacuum of 2.1 eV per water molecule compared to 1.4 eV. (The same is true for binding energies in solution: compare Tables 2 and 3.) The dissociation of H₂O to form OH groups at the surface of IrO₂ is likely related to its high catalytic activity for OER.

Table 3 Predicted solvation shifts (V_dip) of the IrO₂(110) surface with and without one layer of explicit water molecules, and binding energies per explicit water molecule,

Configuration		Bare	Dissociated
V dip [eV]	SaLSA	0.61	0.79
	CANDLE	0.60	0.75
	Vacuum	—	0.55
[eV]	SaLSA	—	1.79
	CANDLE	—	1.70
	Vacuum	—	2.13

---

Fig. 3 Geometry of (a) bare IrO₂(110) surface and surface with (b) dissociated adsorbed water molecules. The intact flat configuration is unstable and dissociates spontaneously to configuration (b). Calculations used an inversion-symmetric (1 × 1) surface unit cell with six layers and atom positions optimized self-consistently in both vacuum and solution.

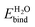
The work function of IrO₂ in liquid has not yet been measured but photoemission measurements in UHV have been reported.⁶⁵ We predict a solvation shift of 0.6 eV by directly applying both solvation models to the bare surface, and 0.75 eV for CANDLE (0.79 eV for SaLSA) after including an explicit water layer in the ‘dissociated’ configuration. These shifts are within 0.2 eV of the similar dissociated configuration for TiO₂. The solvation shifts due to a monolayer of explicit water molecules alone without solvation models are smaller by ∼0.20 eV (∼0.24 eV) compared to CANDLE (SaLSA). The stability of the intact configuration leads to a 0.4 eV larger shift in TiO₂, and since that configuration is unstable in IrO₂, we predict a lower solvation shift ≈0.75 eV for the IrO₂(110) surface, as shown in Table 3.

γ-WO₃(001) surface

Stoichiometric WO₃ surface. 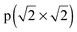Finally, we study the effect of solvation on the surface of γ-WO₃ (the room temperature phase), another important photoanode material for PEC, which is earth abundant, acid stable, and has a suitable optical gap of 2.6 eV (which is 0.4 eV smaller than that of rutile TiO₂).^8,66,67 At room temperature, WO₃ adopts a monoclinic phase and its (001) surface with the c(2 × 2) (or − R45°) reconstruction has the lowest surface energy.⁶⁴ This surface structure has been observed in STM and LEED experiments.^18,68–70

We apply the solvation models with and without a layer of explicit water molecules to the stable WO₃(001) surface. As before, we calculate the intact ‘flat’ and ‘dissociated’ water configurations shown in Fig. 4. Their binding energies (in vacuum and in solution) are comparable to those on TiO₂ but much smaller than those on IrO₂ (compare Tables 2–4), which indicates that WO₃ surfaces are not very reactive with H₂O. In this case, the intact configuration is more stable by 0.23 eV per water molecule than the dissociated one, which is expected since the reconstruction leaves each surface W with two short W=O bonds and two normal W–O bonds, leaving a Lewis acid site for binding an intact H₂O. Regardless, the solvation shifts for the two configurations, also shown in Table 4, differ only by 0.2 eV and the predictions without explicit water also agree within 0.2 eV. The solvation shifts due to a monolayer of explicit water molecules alone without solvation models are smaller by ∼0.2 eV (∼0.3 eV) compared to CANDLE (SaLSA). Overall, we find theoretical solvation shifts for WO₃ to be ∼1.0 eV.

Fig. 4 Geometry of (a) bare WO₃(001) surface and surfaces with (b) flat adsorbed water molecules and (c) dissociated adsorbed water molecules. Calculations used an inversion-symmetric (1 × 1) four layer surface unit cell with self-consistent atom positions in solution.

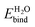Table 4 Predicted solvation shifts (V_dip) of the stoichiometric WO₃(001) surface with and without explicit H₂O molecules, compared to experimental shift of the VBM due to liquid H₂O,^1,71,72 and binding energies per explicit water molecule, . The large discrepancy between our theoretical predictions ≈1 eV and experimental measurements >2 eV suggest that the experimental surfaces may not be the stoichiometric defect-free surface we studied

Configuration		Bare	Flat	Dissociated
V dip [eV]	SaLSA	0.68	1.04	0.86
	CANDLE	0.58	0.98	0.76
	Vacuum	—	0.77	0.55
	Experiment	2.06–2.42
[eV]	SaLSA	—	0.93	0.71
	CANDLE	—	0.84	0.62
	Vacuum	—	1.24	1.01

---

Experimentally, pristine WO₃ surfaces have very high ionization energies ∼9.6–9.8 eV,^71,72 which can decrease dramatically by ∼2 eV due to adsorption of molecules such as water when the sample is exposed to air.⁷³ Electrochemical flat-band measurements find the VBM at ∼−3.0 to −3.1 eV relative to NHE (7.44–7.54 eV below vacuum).¹ Therefore, the above experimental results combined with eqn (1) and (2), as well as pH_PZC = 0–1⁵⁹ indicate that the experimental estimate of V_dip ranges from 9.6–7.54 + 0.059 × 0 = 2.06 eV to 9.8–7.44 + 0.059 × 1 = 2.42 eV, which is more than twice that of the theoretical predictions! Based on our findings for Si and TiO₂, we do not expect such large discrepancies. Additionally, our predictions conform with the 0.5–1.0 eV range of solvation shifts observed for most oxides in literature,^10,57,74 but the experimental estimates of the solvation shift of WO₃ do not fall in this range. This indicates the possibility that additional phenomena are at play in the solvation of WO₃ surfaces.

WO₃ surface with oxygen vacancies

WO₃ is intrinsically n-type due to oxygen deficiencies, which sets its Fermi level close to (0.2–0.3 eV below) its CBM in photoemission measurements.^71,72 STEM and LEED studies also observed O-deficient surfaces, such as a p(2 × 2) reconstruction¹⁸ with O atoms on top of 1/4 surface W atoms (compared to 1/2 at the most stable c(2 × 2) surface (Fig. 5)), or a p(1 × 1) reconstruction with no on-top O atoms.‡‡⁷⁰ Next to a liquid electrolyte, surface O vacancies could be further stabilized by bonding with water molecules. These bonds could contribute additional dipoles to the interface and influence the solvation shift. Direct experimental measurements of O vacancies on solvated surfaces would be extremely challenging and have not yet been reported. Consequently, in the remainder of this section, we discuss the formation energies of surface O vacancies in vacuum and solution, and their effect on the band positions, to explore this possibility.

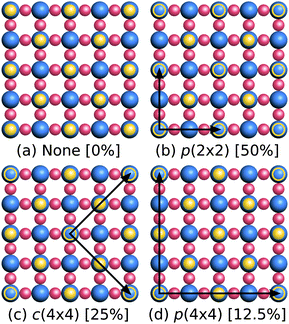Fig. 5 Schematic top view of configurations of O vacancies on the WO₃(001) surface ((a) 0%, (b) 50%, (c) 25%, (d) 12.5%). The solid yellow circles are the surface O atoms, empty yellow circles mark the O vacancies and black arrows indicate the lattice vectors of the supercell. For clarity, the monoclinic distortions (see Fig. 4) have been omitted in this illustration.

Table 5 compares the formation energy of O vacancies in bulk WO₃ as well as on the (001) surfaces in vacuum and solution at different O vacancy concentrations. The formation energies are presented for two limits: the O-rich limit where molecular oxygen provides O and the O-poor limit where the oxide (or water, when available) provides it. (See ESI,† for details on the vacancy formation energy calculations and additional discussions.) The formation energies of bulk O vacancies in WO₃ are positive and ≳1 eV over the entire range of O-rich to O-poor conditions. In comparison, the formation energies of surface vacancies in vacuum are much smaller than the bulk case (by ∼2 eV) and even become negative in the O-poor limit, indicating that O deficiency could be thermodynamically favorable in this limit.⁷⁵ Interestingly, the formation energy of O vacancies on WO₃(001) surfaces in solution are further stabilized by 0.1–0.4 eV compared to those in vacuum, which indicates higher concentrations of O vacancies on the solvated surfaces.

Table 5 Formation energies of various concentrations of oxygen vacancies in bulk WO₃ and WO₃(001) surfaces in vacuum and solution (explicit water layer + CANDLE solvation model). The O-rich limit corresponds to deriving O from molecular oxygen whereas the O-poor limit derives O from WO₃ or H₂O (when present)

Configuration		Formation energy [eV]
		O-rich	O-poor
Bulk	4%	4.75	1.90
	0.5%	3.77	0.93
Vacuum (001)	p(2 × 2) [50%]	2.60	−0.24
	c(4 × 4) [25%]	2.22	−0.62
	p(4 × 4) [13%]	1.99	−0.85
Solvated (001)	p(2 × 2) [50%]	2.15	−0.36
	c(4 × 4) [25%]	1.45	−1.06

---

Now that we have established the plausibility of high concentrations of O vacancies on solvated WO₃ surfaces, we explore the effect of these vacancies on the band edge positions in solution. Table 6 and Fig. 6 show the total band position shift due to interfacial dipoles, including the effect of vacancies and solvation (when present), for various concentrations of vacancies on the WO₃(001) surface in vacuum and in solution. As expected, the potential shift varies linearly with vacancy concentration because the surface dipole per vacancy approaches a constant in the dilute limit, and the potential shift is proportional to the induced surface dipole per unit area. (Zero vacancy concentration corresponds to the ideal surface calculations from the previous section.)

Table 6 Total shift of the band positions of WO₃(001) due to interfacial dipoles, V_dip+vacancy including contributions due to O vacancies and/or solvation, for various configurations of surface O vacancies in vacuum and solution. The H₂O-ML calculations include a monolayer of explicit water molecules without any solvation model, whereas the CANDLE calculations include the CANDLE solvation model in addition to the explicit monolayer

Vacancy configuration	V dip+vacancy [eV]
	Vacuum	CANDLE	H2O-ML
p(2 × 2) [50%]	0.76	3.14	2.34
c(4 × 4) [25%]	0.33	2.13	1.79
p(4 × 4) [13%]	0.16	—	—
None [0%]	0.00	0.98	0.77

---

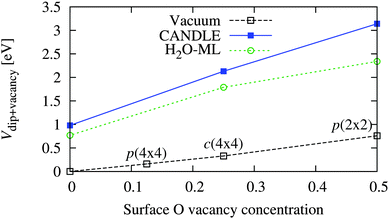Fig. 6 Variation of band position shift of WO₃(001) surfaces due to vacancies and/or solvation as a function of vacancy concentration (per surface O atom of the stoichiometric surface) in vacuum and solution (see Table 6). Vacancy concentrations of 0.125, 0.25 and 0.5 correspond to the p(4 × 4), c(4 × 4) and p(2 × 2) configurations respectively.

The surface dipole per vacancy, and hence the shift at identical vacancy configurations, is much larger in solution than vacuum because water molecules bind at the vacancy site and the extra H atoms (relative to the surface without vacancies) provide a large positive dipole and shift the bands towards the vacuum level. In this case, the shifts predicted using explicit water molecules alone underestimate those including the solvation model by up to 0.8 eV, unlike the previous underestimation ∼0.2 eV for the stoichiometric surfaces. This shows the importance of accounting for the effect of the liquid beyond the first layer using solvation models, especially for complicated surface structures including vacancies.

The total shift with the c(4 × 4) surface vacancy configuration in solution of 2.1 eV (Table 6) matches the experimental solvation shift of ∼2.0–2.4 eV (Table 4). This configuration corresponds to a surface vacancy concentration of 25%, which is high, but plausible as discussed above: the surface vacancy formation energies of WO₃ in solution are lower than in vacuum, and such high surface vacancy concentrations of WO₃ have been observed even in UHV STM and LEED experiments.^18,19 Experimental characterization of the WO₃ surface structure in the electrochemical environment is necessary to confirm our predictions.

Optimum alignment of WO₃ band edge positions with the water redox potentials requires shifting both the VBM and CBM further towards the vacuum level. Based on the above results, this could potentially be achieved by increasing the O vacancy concentration at the surface. Several surface preparation techniques lead to highly O deficient WO₃ surfaces in vacuum.^18,70 It may be possible to retain this O deficiency in the aqueous environment, especially under acidic conditions where WO₃ is stable.

Band position shifts in non-aqueous solvents

The previous section indicates the possibility of adjusting band positions by controlling surface preparation. Alternately, band positions would also vary with solvent, which could be particularly important for carbon dioxide reduction (CO2RR) in non-aqueous solvents. Here, we present a preliminary study of the variation of band positions with solvent, which has not been previously studied either experimentally or theoretically. For simplicity, we focus on the hydrophilic IrO₂(110) surface since it has a non-negligible solvation shift in water that could be described by the solvation models accurately without including explicit solvent molecules. We include a range of non-polar to polar solvents for which the SaLSA or CANDLE solvation models have been previously constructed: carbon tetrachloride (SaLSA), chloroform (SaLSA) and acetonitrile (CANDLE).

We expect intuitively that the effect should increase with the dielectric constant, ε, of the solvent and decrease with the distance, d, of the solute charge from the dielectric surface. In fact, for a point charge in a dielectric cavity of radius d, the solvent shift in the potential is proportional to (1 − ε⁻¹)d⁻¹. The solvation shift V_dip for a surface depends on its charge distribution in a complicated manner, but we can use the above spherical-cavity form to examine the correlations, with the solvent vdW radius⁷⁶ as an estimate of the distance d.

Fig. 7 shows the solvation shifts in the band positions of the IrO₂(110) surface. Indeed the shifts correlate well with the solvent dielectric function and solvent molecule size in the form (1 − ε⁻¹)R_vdW⁻¹, as discussed above. It also shows that the shift does not correlate well with dielectric constant alone, neither linearly nor inversely. Water sets the upper bound on solvation shifts, since it has a high dielectric constant and a small molecule size; increasing the dielectric constant further does not have an appreciable effect due to the (1 − ε⁻¹) dependence. However, it is possible to reduce the solvation shifts by selecting solvents with either larger molecules or smaller dielectric constants.

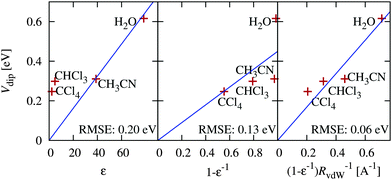Fig. 7 Correlation of the predicted solvation shift of IrO₂(110) band positions in various solvents with various combinations of solvent dielectric constant ε and vdW radius R_vdW.

Discussion

The effect of solvation on band positions is an important consideration in determining the alignment of semiconductor band edges with redox potentials across the solid–electrolyte interface. The magnitude of the solvation shift varies tremendously from one system to another, but our results indicate that it is possible to estimate them based on the nature of the surface (specifically its hydrophobicity).

Non-ionic hydrophobic surfaces, such as the hydrogen and methyl-terminated silicon surfaces in our study, interact weakly with water and exhibit small solvation shifts less than 0.5 eV. Vacuum calculations might suffice for such surfaces, especially for qualitative estimates seeking an accuracy ∼0.5 eV, as discussed in ref. 11.

Ionic hydrophilic surfaces interact strongly with water, and especially for oxides, the solvation shift of the band edge positions tends to fall in the 0.5–1.0 eV range. In general, predictions using vacuum calculations alone can be qualitatively incorrect for these surfaces and therefore the effect of H₂O should be included.

In some cases, defects on the surface can lead to larger solvation shifts, as we found for oxygen vacancies at the surface of WO₃. In this case, water molecules bind to the oxygen vacancy sites with the hydrogen atoms pointing outwards, which contributes a large positive dipole that can shift the electronic states by as much as 2 eV. Such surfaces require particular care, and calculations should account for restructuring of the surface and should analyze concentrations of possible surface defects, in addition to accounting for direct solvation effects.

In terms of the performance of the solvation models for predicting the solvation effects of the band positions of various surfaces, we find that the CANDLE and SaLSA continuum solvation models can accurately describe the solvation shifts for hydrophobic surfaces, when applied directly to the surface with no explicit water molecules. They agree qualitatively with experimental results for hydrophilic surfaces, but miss the stronger bonds of the surface with water and consistently underestimate the solvation shift by ∼0.2 eV. The agreement is considerably improved by including a layer of explicit water molecules, where these strong interactions are now handled by electronic density functional theory instead, but this introduces the complexity of dealing with many possible water configurations. The solvation models are adequate to describe the effect of subsequent layers of water, which keeps the number of water configurations manageable and mitigates the need for explicit statistical sampling via molecular dynamics. Additionally, we could also reparametrize empirical solvation models such as CANDLE to remove this underestimate: this could be useful for accurate high-throughput theoretical screening of PEC materials.

In addition, we also find that the results of the empirical CANDLE solvation model agree very well with the non-empirical and more computationally-expensive SaLSA model. This is particularly important for studies of reaction mechanisms with charged species, since CANDLE corrects the systematic under-solvation of anions in SaLSA (and most other solvation models). We also note that SaLSA and CANDLE show a systematic offset of ∼0.1 eV in the predicted solvation shifts. In fact, correlating theoretical and experimental potentials of zero charge of single crystalline metal surfaces predicts E^NHE₀ = 4.55 eV for the SaLSA model and 4.66 eV for the CANDLE model,¹⁷ which also differ by ∼0.1 eV (and agree well with the experimental estimate ∼4.44 eV³⁷). This is, therefore, a systematic difference in the dipole layer of the liquid at the interface, independent of the solid surface.

Finally, our results indicate two avenues for engineering band positions of surfaces in solution. First, surface preparation techniques that produce oxygen-deficient surfaces may be used to shift band positions of oxides e.g. WO₃ further towards the vacuum level. An experimental investigation of whether such surfaces remain stable in water is necessary to determine the feasibility of this approach in order to optimize band alignment with water redox potentials. Second, solvents consisting of larger molecules with lower dielectric constants may be used to reduce the solvation shift. This is particularly relevant for carbon dioxide reduction, which may be carried out in non-aqueous solvents. Additionally, solvent effects can modify the interface energetics and charge transfer between photoelectrodes and catalysts by introducing a porous structure of the catalysts, where the water can penetrate the catalyst layer and be in contact with photoelectrodes, e.g. in WO₃/IrO₂ interfaces.⁶² Such effects have been successfully predicted using atomistic models of the interface combined with solvation models,⁶⁴ and can be systematically exploited to improve the efficiency of the PEC.

Conclusions

We studied the solvation shifts of the electronic states of various surfaces using recently-developed continuum solvation models suitable for such systems. This computationally-efficient approach agrees well with much more expensive AIMD simulations of explicit solid–liquid interfaces, and is far more accurate than vacuum calculations alone while requiring minimal computational overhead.§§ Accounting for strong surface-liquid interactions such as formation of chemical bonds by using a single layer of explicit water molecules, we found good agreement with experimental band positions for highly ionic TiO₂ and WO₃ surfaces, and predicted the as-yet unmeasured Fermi level position of IrO₂ in liquid water. The solvation shifts vary considerably depending on the nature of the surface and the solvation model predictions are typically accurate to within ∼0.2 eV, as summarized in Table 7. Most importantly, we correlated the magnitude of the solvation shift with the surface type, the dielectric constant and molecule size of the solvent, and the strength of their mutual interaction, which provides valuable guidance for the discovery of new efficient photocatalyst materials.

Table 7 Summary of solvation shifts [eV] in band positions of various systems: solvation model predictions compared to experiment and AIMD results. Here, SM refers to solvation models alone (range includes SaLSA and CANDLE predictions), ML is monolayer of explicit water alone and ML + SM is solvation models in addition to explicit monolayer. See Tables 1–4 and 6 for more details

System	Expt/AIMD	SM	ML + SM	ML
Si(111)–H	0.3	0.2–0.3	—	—
Si(111)–CH3	0.3	0.2–0.3	—	—
Si(111)–COOH	1.6	1.4–1.8	—	—
TiO2(110)	0.9–1.1	0.5–0.7	1.1–1.2	0.9
IrO2(110)	—	0.6	0.8	0.6
WO3(001) (+vacancy)	2.1–2.4	0.6–0.7	1.0–1.1	0.8
		—	2.1	1.8

---

Acknowledgements

We thank Giulia Galli and Tuan Anh Pham for many useful discussions. This publication is based upon work performed by the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award Number DE-SC0004993.

References

1. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110(11), 6446–6473.
2. M. Grätzel, Nature, 2001, 414, 338–344.
3. R. van de Krol, Principles of Photoelectrochemical Cells, Springer, 2011.
4. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. a. Persson, APL Mater., 2013, 1(1), 011002.
5. M. C. Toroker, D. K. Kanan, N. Alidoust, L. Y. Isseroff, P. Liao and E. A. Carter, Phys. Chem. Chem. Phys., 2011, 13, 16644–16654.
6. Y. Ping, Y. Li, F. Gygi and G. Galli, Chem. Mater., 2012, 24(21), 4252–4260.
7. J. C. Hill, Y. Ping, G. A. Galli and K.-S. Choi, Energy Environ. Sci., 2013, 6, 2440–2446.
8. Q. Mi, Y. Ping, Y. Li, B. Cao, B. S. Brunschwig, P. G. Khalifah, G. A. Galli, H. B. Gray and N. S. Lewis, J. Am. Chem. Soc., 2012, 134(44), 18318–18324.
9. H. Jiang, J. Phys. Chem. C, 2012, 116(14), 7664–7671.
10. V. Stevanovic, S. Lany, D. S. Ginley, W. Tumas and A. Zunger, Phys. Chem. Chem. Phys., 2014, 16, 3706–3714.
11. T. A. Pham, D. Lee, E. Schwegler and G. Galli, J. Am. Chem. Soc., 2014, 136(49), 17071–17077.
12. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
13. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
14. O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 064102.
15. D. Gunceler, K. Letchworth-Weaver, R. Sundararaman, K. Schwarz and T. Arias, Modell. Simul. Mater. Sci. Eng., 2013, 21, 074005.
16. R. Sundararaman, K. Schwarz, K. Letchworth-Weaver and T. A. Arias, J. Chem. Phys., 2015, 142, 054102.
17. R. Sundararaman and W. A. Goddard, J. Chem. Phys., 2015, 142, 064107.
18. F. Jones, K. Rawlings, J. Foord, R. Egdell, J. Pethica, B. Wanklyn, S. Parker and P. Oliver, Surf. Sci., 1996, 359(1–3), 107–121.
19. R. Dixon, J. Williams, D. Morris, J. Rebane, F. Jones, R. Egdell and S. Downes, Surf. Sci., 1998, 399(2–3), 199–211.
20. R. Sundararaman, K. Schwarz, D. Gunceler, K. Letchworth-Weaver and T. A. Arias, JDFTx http://jdftx.sourceforge.net, 2012.
21. S. A. Petrosyan, J.-F. Briere, D. Roundy and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205105.
22. S. Ismail-Beigi and T. A. Arias, Comput. Phys. Commun., 2000, 128, 1.
23. R. Sundararaman and T. Arias, Comput. Phys. Commun., 2014, 185, 818.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
25. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
26. K. F. Garrity, J. W. Bennett, K. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446.
27. T. Le Bahers, M. Rérat and P. Sautet, J. Phys. Chem. C, 2014, 118(12), 5997–6008.
28. W. Chen and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(15), 165133.
29. K. Steiner, W. Chen and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205309.
30. A. Alkauskas, P. Broqvist, F. Devynck and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 106802.
31. Y. Li, L. E. OLeary, N. S. Lewis and G. Galli, J. Phys. Chem. C, 2013, 117(10), 5188–5194.
32. G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810.
33. C. A. Rozzi, D. Varsano, A. Marini, E. K. U. Gross and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 205119.
34. R. Sundararaman and T. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165122.
35. K. Letchworth-Weaver and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075140.
36. R. Sundararaman, D. Gunceler and T. A. Arias, J. Chem. Phys., 2014, 141, 134105.
37. S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966.
38. A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894.
39. J. Cheng and M. Sprik, Phys. Chem. Chem. Phys., 2012, 14, 11245.
40. Y. Xu and M. A. Schoonen, Am. Mineral., 2000, 85(3–4), 543–556.
41. Y. Ping, D. Rocca and G. Galli, Chem. Soc. Rev., 2013, 42, 2437–2469.
42. G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74(2), 601–659.
43. Y. Ping, D. Rocca and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165203.
44. W. Kang and M. S. Hybertsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 085203.
45. T. A. Pham, H.-V. Nguyen, D. Rocca and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155148.
46. E. C. Dutoit, F. Cardon and W. P. Gomes, Ber. Bunsenges. Phys. Chem., 1976, 80(6), 475–481.
47. M. Butler, R. Nasby and R. K. Quinn, Solid State Commun., 1976, 19(10), 1011–1014.
48. A. Aliano, Y. Li, G. Cicero and G. Galli, J. Phys. Chem. C, 2010, 114(27), 11898–11902.
49. B. Jaeckel, R. Hunger, L. J. Webb, W. Jaegermann and N. S. Lewis, J. Phys. Chem. C, 2007, 111(49), 18204–18213.
50. R. Hunger, R. Fritsche, B. Jaeckel, W. Jaegermann, L. J. Webb and N. S. Lewis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045317.
51. S. Maldonado, K. E. Plass, D. Knapp and N. S. Lewis, J. Phys. Chem. C, 2007, 111(48), 17690–17699.
52. L. E. OLeary, E. Johansson, B. S. Brunschwig and N. S. Lewis, J. Phys. Chem. B, 2010, 114(45), 14298–14302.
53. S. Hu, M. R. Shaner, J. A. Beardslee, M. Lichterman, B. S. Brunschwig and N. S. Lewis, Science, 2014, 344(6187), 1005–1009.
54. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
55. O. Bikondoa, C. L. Pang, R. Ithnin, C. A. Muryn, H. Onishi and G. Thornton, Nat. Mater., 2006, 5, 189–192.
56. K. J. Hameeuw, G. Cantele, D. Ninno, F. Trani and G. Iadonisi, J. Chem. Phys., 2006, 124(2), 024708.
57. K. Onda, B. Li and H. Petek, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045415.
58. K. Schierbaum, S. Fischer, M. Torquemada, J. de Segovia, E. Romn and J. Martn-Gago, Surf. Sci., 1996, 345(3), 261–273.
59. G. M. Veith, A. R. Lupini, S. J. Pennycook, A. Villa, L. Prati and N. J. Dudney, Catal. Today, 2007, 122(3–4), 248–253.
60. A. J. Nozik and R. Memming, J. Phys. Chem., 1996, 100(31), 13061–13078.
61. C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135(45), 16977–16987.
62. J. M. Spurgeon, J. M. Velazquez and M. T. McDowell, Phys. Chem. Chem. Phys., 2014, 16, 3623–3631.
63. Y. Ping, G. Galli and W. A. Goddard, J. Phys. Chem. C, 2015, 119(21), 11570–11577.
64. Y. Ping, W. A. Goddard and G. A. Galli, J. Am. Chem. Soc., 2015, 137(16), 5264–5267.
65. B. R. Chalamala, Y. Wei, R. H. Reuss, S. Aggarwal, B. E. Gnade, R. Ramesh, J. M. Bernhard, E. D. Sosa and D. E. Golden, Appl. Phys. Lett., 1999, 74(10), 1394–1396.
66. A. Tanaka, K. Hashimoto and H. Kominami, J. Am. Chem. Soc., 2014, 136(2), 586–589.
67. M. A. Butler, J. Appl. Phys., 1977, 48(5), 1914–1920.
68. F. H. Jones, K. Rawlings, J. S. Foord, P. A. Cox, R. G. Egdell, J. B. Pethica and B. M. R. Wanklyn, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R14392.
69. F. Jones, R. Dixon and A. Brown, Surf. Sci., 1996, 369(1–3), 343–350.
70. R. Dixon, J. Williams, D. Morris, J. Rebane, F. H. Jones, R. Egdell and S. Downes, Surf. Sci., 1998, 399(2–3), 199–211.
71. J. Meyer, M. Krger, S. Hamwi, F. Gnam, T. Riedl, W. Kowalsky and A. Kahn, Appl. Phys. Lett., 2010, 96(19), 193302.
72. M. Krger, S. Hamwi, J. Meyer, T. Riedl, W. Kowalsky and A. Kahn, Appl. Phys. Lett., 2009, 95(12), 123301.
73. L. Weinhardt, M. Blum, M. Br, C. Heske, B. Cole, B. Marsen and E. L. Miller, J. Phys. Chem. C, 2008, 112(8), 3078–3082.
74. T. Mayer, A. Klein, O. Lang, C. Pettenkofer and W. Jaegermann, Surf. Sci., 1992, 269–270, 909–914.
75. C. Lambert-Mauriat, V. Oison, L. Saadi and K. Aguir, Surf. Sci., 2012, 606(1–2), 40–45.
76. D. Ben-Amotz and K. G. Willis, J. Phys. Chem., 1993, 97, 7736.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05740j

‡ These authors contributed equally.

§ The SaLSA model contains a single parameter for the dispersion correction,³⁶ but this does not affect the electrostatic response and hence the solvation shifts in the band positions.

¶ The recommended absolute NHE potential is 4.281 eV below vacuum for calculating electron transfer energies in quantum chemistry methods,³⁸ whereas it is 4.44 eV below vacuum when comparing electrochemical measurements with work functions from photoemission measurements,³⁷ as we do here. See ref. 39 for a detailed discussion of the distinction between these two absolute scales of electrochemical potential.

|| We use an O–H threshold distance of 1.4 Å, which corresponds to the transition state in the deprotonation of carboxylic acids, to distinguish protons bound to the surface from those in solution.

** These calculations use a (4 × 3) surface unit cell with a total of 24 COOH/COO– groups per unit cell (including top and bottom surfaces). The number of deprotonated COO– groups in each of the twenty snapshots range from 0 to 3 and average to 1.85.

†† There is a unique configuration in each class that is commensurate with the smallest surface unit cell. We focus on such commensurate configurations for simplicity and computational expediency.

‡‡ Note that this standard notation for surface reconstructions, somewhat counter-intuitively, labels the underlying cubic lattice rather than the reduced-periodicity surface unit cell for monoclinic structure as primitive. Therefore, the stable surface is c(2 × 2) while the surface with all surface O absent is marked primitive i.e. p(1 × 1).

§§ The solvation models scale linearly with system size. Thus, the solvated DFT calculations asymptotically cost the same as vacuum DFT calculations for large numbers of electrons, and cost less than twice the vacuum DFT calculations for the typical surface unit cells in this work.

---