Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Counterintuitive issues in the charge transport through molecular junctions
Ioan
Bâldea†
*
Theoretische Chemie, Universität Heidelberg, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany. E-mail: ioan.baldea@pci.uni-heidelberg.de
First published on 30th October 2015
Abstract
Whether at phenomenological or microscopic levels, most theoretical approaches to charge transport through molecular junctions postulate or attempt to justify microscopically the existence of a dominant molecular orbital (MO). Within such single level descriptions, experimental current–voltage I–V curves are sometimes/often analyzed by using analytical formulas expressing the current as a cubic expansion in terms of the applied voltage V, and the possible V-driven shifts of the level energy offset relative to the metallic Fermi energy ε0 are related to the asymmetry of molecule–electrode couplings or an asymmetric location of the “center of gravity” of the MO with respect to electrodes. In this paper, we present results demonstrating the failure of these intuitive expectations. For example, we show how typical data processing based on cubic expansions yields a value of ε0 underestimated by a typical factor of about two. When compared to theoretical results of DFT approaches, which typically underestimate the HOMO–LUMO gap by a similar factor, this may create the false impression of “agreement” with experiments in situations where this is actually not the case. Furthermore, such cubic expansions yield model parameter values dependent on the bias range width employed for fitting, which is unacceptable physically. Finally, we present an example demonstrating that, counter-intuitively, the bias-induced change in the energy of an MO located much closer to an electrode can occur in a direction that is opposite to the change in the Fermi energy of that electrode. This is contrary to what one expects based on a “lever rule” argument, according to which the MO “feels” the local value of the electric potential, which is assumed to vary linearly across the junction and is closer to the potential of the closer electrode. This example emphasizes the fact that screening effects in molecular junctions can have a subtle character, contradicting common intuition.
1 Introduction
In spite of significant advances,1–13 charge transport across molecular junctions continues to remain a nonequilibrium problem difficult to understand.14,15 Resorting to a single (Newns–Anderson) model12,16–27 to describe the transport within a picture assuming the existence of a dominant molecular orbital is a common procedure in the field, also allowing one to rationalize more sophisticated microscopic transport calculations.28 In fact, this single-level picture turned out to excellently explain a series of transport measurements beyond the ohmic bias range29–31 and back the model parameters extracted from fitting the experimental data with high-level quantum chemical calculations.25,27,32 In the present work, we consider two issues related to the analysis of the transport data within this framework:(i) Typical current–voltage I–V characteristics measured in molecular junctions are featureless curves. An example is depicted in Fig. 1. Due to their general appearance, although a general analytic formula I = I(V) is available from the literature,18,23,28,33,34 using third-order expansions instead of the exact expression (see eqn (2)) appears to be a convenient and reasonable simplification and was used in earlier studies.12,24
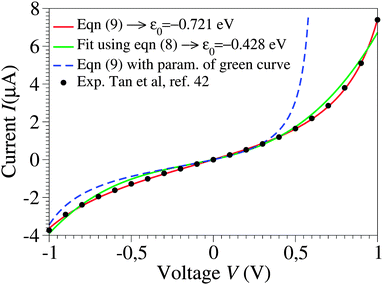 | ||
| Fig. 1 Raw experimental current–voltage data (courtesy of Pramod Reddy)43 fitted with eqn (9) (red curve) and with the third-order approximation of eqn (8) (green curve). The parameter values are ε0 = −0.721 eV, γ = 0.065, and G = 2.575 μS for the red curve and ε0 = −0.428 eV, γ = 0.165, and G = 1.922 μS for the green curve. As visible in the figure, the blue dashed line, obtained by using eqn (9) and the parameters corresponding to the green line, substantially deviates from the green curve, which would not be the case if the cubic approximation of eqn (8) was justified. The red curve could hardly be distinguished within the drawing accuracy from that obtained using eqn (1) or (2), because of the small values Γs ≈ Γt ∼ 10−2|ε0| deduced from eqn (3) with N ≈ 100.43 The negative ε0-values reflect the HOMO-mediated conduction in the junctions considered.43 | ||
Such third-order expansions are inspired by studies on a variety of macroscopic and mesoscopic junctions up to biases of current experimental interest, wherein it was considered a prominent characteristic of transport via tunneling.35–40
(ii) Like those shown in Fig. 1, experimental I–V curves may exhibit a more or less pronounced asymmetry upon bias polarity reversal I(−V) ≠ −I(V), which is particularly desirable for achieving current rectification using molecular devices.13 The most common way to embody this asymmetry in analytic transport approaches is either to relate it to asymmetric molecule–electrode couplings24,28 or to assume that the (“center of gravity” of the) dominant molecular orbital is located asymmetrically relative to the two (say, “substrate” s and “tip” t) electrodes.21,33
The analysis presented below will demonstrate that, although the aforementioned assumptions seem to be justified intuitively, they are in fact of rather limited applicability. Examples will be presented showing cases where the opposite is true.
2 Results and discussion
To provide the reader with a convenient reference when reading the text that follows, the definition of the variables utilized below is given in Table 1.| Symbol | Meaning |
|---|---|
| MO | (Dominant) molecular orbital |
| ε 0(V) | MO energy offset under an applied bias (V ≠ 0) |
| ε 0 ≡ |ε0(V)|V=0 | MO energy offset without an applied bias or for junctions with symmetric I–V curves |
| γ | (Dimensionless) Stark effect strength (−1/2 ≤ γ ≤ 1/2) |
| Γ s,t | MO broadening functions due to coupling to electrodes s (“substrate”) and t (“tip”) |
| Γ a | Arithmetic average of Γs and Γt |
| Γ g | Geometric average of Γs and Γt |
| Γ h | Harmonic average of Γs and Γt |
| V t(≡Vp) | Transition voltage (alias peak voltage, cf.ref. 15 and 41) for junctions with symmetric I–V curves |
| I t ≡ I(Vt) | Current at V = Vt |
| V t,±(≡Vp,±) | Transition (peak) voltages for positive/negative biases |
| V j t(j = 1, 2) | Transition voltage for positive/negative biases; V1,2t = Vt,± sign ε0 |
| N | Number of molecules in the junction |
| I 3 | Current within the cubic expansion (approx.) |
| V j t,3(j = 1, 2) | Transition voltage for positive or negative bias within the cubic approximation |
| δ | Asymmetry of the MO–electrode couplings (0 < δ < 1) |
| G | Low bias conductance |
| G 0 | Conductance quantum |
| μ s,t | Electrodes' Fermi energy |
| G fit, εfit0 | Conductance and MO energy offset deduced by fitting using cubic expansions I vs. V |
| V b | Bias range used for fitting |
| ε fit0(Vb) | MO energy offset deduced by fitting I–V curves obtained experimentally viaeqn (9) using cubic expansions in the bias range −Vb < V < Vb |
| δε0 | Bias-driven MO shift |
| z | Molecular axis |
| d | Molecular length |
| z 0 | MO “center of gravity” location |
| E z | Electric field along the molecular axis |
| δε0(z) | Bias-driven MO shift expected according to the “lever rule” (cf.ref. 20) |
2.1 Basic working equations
By assuming electrode bandwidths much larger than all other characteristic energies (wide band limit), the current mediated by a single, possibly bias-dependent energy level having an energy offset ε0(V) relative to the equilibrium Fermi energy of the electrodes can be written in a compact form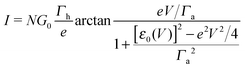 | (1) |
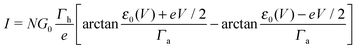 | (2) |
Above, the biased (“substrate” s and “tip” t) electrodes are assumed to have Fermi energies μs,t = ±eV/2, where N is the effective number of molecules in junctions, and G0 = 2e2/h is the conductance quantum. Γh,a,g stand for the harmonic, arithmetic, and geometric averages of the level broadening functions Γs,t arising from the couplings between molecules and electrodes. In the zero-bias limit (V → 0), the conductance G has the form
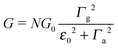 | (3) |
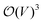 in terms of V of eqn (2) or (1) reads
in terms of V of eqn (2) or (1) reads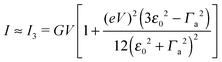 | (4) |
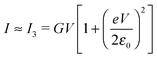 | (5) |
An applied bias V can shift the energy of the dominant orbital, ε0 → ε0(V). By assuming a linear dependence
| ε0(V) = ε0 + γeV | (6) |
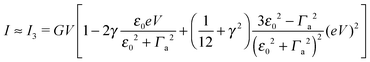 | (7) |
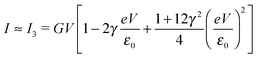 | (8) |
In off-resonance cases (Γa ≪ |ε0 ± eV/2|), an expression for the current not limited to low-order expansions in V can be deduced from eqn (2)29
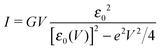 | (9) |
To end this section, we briefly refer to a quantity useful for the subsequent analysis, namely the transition voltage Vt, defined as the bias at the minimum of the Fowler–Nordheim quantity log(|I|/V2), or the equivalent peak voltage Vp(≡Vt), defined as the bias at the maximum of V2/|I|. The latter has been recently introduced15,41 to emphasize that no mechanistic transition (e.g., from direct tunneling to field-emission tunneling, as initially claimed42) occurs at V = Vt ≡ Vp.
In off-resonance situations described by eqn (9) and (5) or (8), simple expressions for the transition (peak) voltages for both polarities (Vt1Vt2 < 0) can be derived analytically15,29
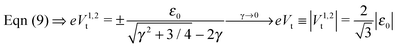 | (10) |
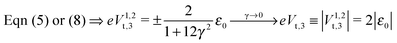 | (11) |
2.2 Exact Newns–Anderson description versus cubic expansion
By fitting experimental I–V curves using eqn (9) and (8), the values of the fitting parameters ε0, γ, and G entering these equations can be deduced. The analysis presented in this subsection will reveal surprising differences between the values estimated with the aid of these equations.The black symbols of Fig. 1 depict a typical, moderately asymmetric (I(−V) ≠ −I(V)) curve measured in molecular junctions.43 Fitting the experimental data shown in Fig. 1 with the aid of eqn (9) yields a curve (red line in Fig. 1) in virtually perfect agreement with the experiment. Although not so “perfect” as the red line, the green curve, obtained by fitting the experimental data using eqn (8), is in fact quite satisfactory. Still, much more importantly than the quality of the two fits, the two fitting procedures yield substantially different parameter values (see the caption of Fig. 1). Particularly noteworthy is the fact that the cubic approximation drastically underestimates the HOMO-energy offset ε0, which represents ∼60% of the exact estimate. (Let us mention that in the junctions considered conduction is mediated by the highest occupied molecular orbital (HOMO)43).
What is wrong with the green curve of Fig. 1 is the fact that the cubic expansion leading to eqn (8) is a legitimate approximation of eqn (2) or (1) or (9) (because in the present off-resonance limit (Γa ≪ |ε0|, see the caption of Fig. 1) eqn (2) or (1) reduces to eqn (9)) only at sufficiently low biases. If this were the case, the differences between the I–V curves computed using eqn (8) (green curve in Fig. 1) and eqn (9) (blue curve in Fig. 1) at the same parameter values would be negligible. However, the inspection of Fig. 1 clearly reveals that this is not the case. The cubic expansion does not hold in the whole experimental V-range; it is legitimate only up to biases |V| ∼ 0.3 V, wherein the differences between the green and blue curves are small.
Using experimental transport data from ref. 43, Fig. 2 emphasizes another important drawback of the cubic approximation, namely its inability to account for the experimental fact that the transition (Fig. 2a) or, alternatively, the peak (Fig. 2b) voltage spectra have minima or maxima located asymmetrically (Vt,+ ≠ −Vt,−). This result, based on experimental measurements, further supports a similar finding emerging from a theoretical simulation presented recently.15
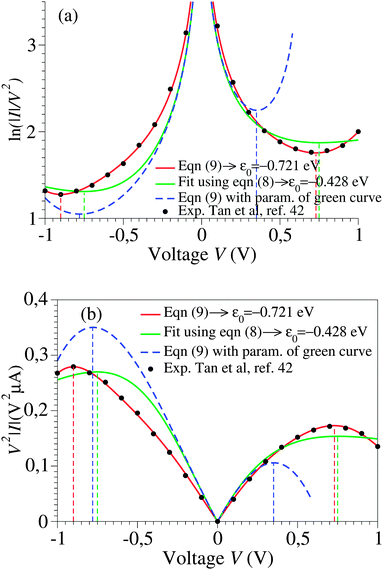 | ||
| Fig. 2 The I–V curves depicted in Fig. 1 recast as transition (TVS, panel a) and peak (PVS, panel b) voltage spectra. Notice the inability of the cubic approximation (green curves) to account for the experimental fact (cf. black symbols) that transition (peak) voltages (Vt,± = Vp,±) of opposite polarity—which specify the location of the minima (maxima) in panel a (panel b) can have different magnitudes. | ||
Typical transport measurements on molecular junction sample bias ranges slightly exceed the transition voltage (V ≳ Vt).42,44–46 In Fig. 3 we present the results of a numerical simulation. There, the (red) curve has been computed using eqn (9) at γ = 0 (i.e., for a curve I(−V) = −I(V) symmetric about origin V = 0) for such a bias range (−1.25Vt < V < 1.25Vt) along with the (green) curve obtained by fitting the red curve by means of eqn (5). Similar to Fig. 1, the quality of the fit is very good; nevertheless, the fitting parameter εfit0 (63% of the actual value ε0) is drastically underestimated. For convenience, the results presented in Fig. 3 are presented in dimensionless variables obtained by using the “natural” bias and current units Vt and It ≡ I(Vt) introduced recently.41
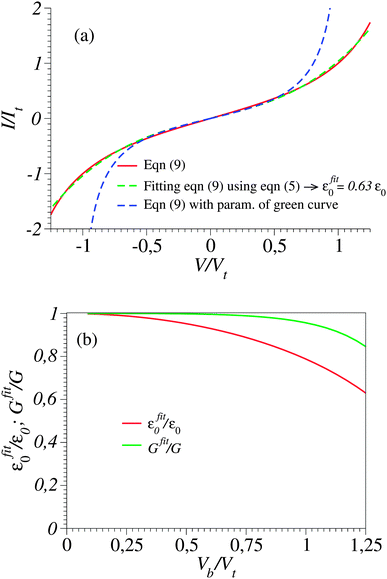 | ||
Fig. 3 (a) The current–voltage curve computed for γ = 0 using eqn (9) (red line) and fitted (green line) with the aid of eqn (5) in the bias range shown (0 < V < 1.25Vt). Notice that in spite of the very good quality of the fit, this procedure substantially underestimates the ε0-value (given in the legend). (b) Values of Gfit and εfit0 obtained by fitting with the aid of eqn (5) the current computed using eqn (9) in bias ranges −Vb < V < Vb. Vb is the variable entering the abscissa. The reduced variables I/It and Vb/Vt are expressed using the units 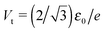 of eqn (10) and of eqn (10) and  .41 .41 | ||
An important pragmatic merit of the transition voltage is its reproducibility:31,47–49 in contrast to the very broad conductance (or current50) histograms, Vt-histograms are considerably narrower. Therefore, estimating the energy offset ε0 from Vt in cases where the existence of a single dominant level can be justified microscopically for the junction(s) in question (e.g., ref. 25, 27 and 32) may appear preferable to fitting the I–V data. From the experimental values Vt = 1.15 ± 0.15; 1.0 ± 0.07; and 0.87 ± 0.07 V for molecular junctions of phenyldithiol and Ag- Au- and Pt-electrodes, eqn (10), which follows from eqn (9),29 yields the (HO)MO energy offset values |ε0| = 1.0 ± 0.1; 0.88 ± 0.05; and 0.75 ± 0.04 eV, respectively, (γ = 0).27 These values agree well with those deduced via ultraviolet photoelectron spectroscopy (UPS): |ε0| = 1.1 ± 0.1; 0.9 ± 0.1; and 0.8 ± 0.1 eV, respectively.47 By contrast, the values obtained viaeqn (11), which follows from eqn (5), namely, |ε0| = 0.57; 0.50; and 0.43 eV, respectively, are underestimated by a factor of ∼58%. It is noteworthy that the value of this factor is very close to those of the two aforementioned cases (namely, ∼60% and ∼63%).
Like those presented in Fig. 1, the results presented in Fig. 3a reemphasize why attempting to fit the transport data in bias ranges sampled in typical experiments by using the cubic approximation represents an inadequate procedure: this V-range is beyond the applicability of the cubic expansion. If the cubic expansion was legitimate, differences between curves computed viaeqn (5) or (8) and the (practically) exact eqn (9) using the same parameters deduced via cubic fitting would be negligible. (In Fig. 1 the differences between the red curve and the experimental data43 are insignificant, so here we could refer to the results computed viaeqn (9) as the “experimental” results.) The comparison between solid green lines (cubic fitting) and blue dashed lines (exact equation + parameters from cubic fitting) of Fig. 1 and 3a, which depict the two aforementioned curves, shows that the opposite is true. These differences are small at low biases only; the contributions of the higher order terms neglected in eqn (5) and (8) are witnessed as significant differences between the green and blue curves at higher biases.
In this vein, one can attempt to employ cubic expansions for data fitting in narrower bias ranges, where higher order terms are indeed negligible. Simulations of these kinds are presented in Fig. 3b, 4a and b. For simplicity, in these figures we have chosen the case γ = 0 (I(−V) = −I(V)), so fittings in the bias ranges −Vb < V < Vb and 0 < V < Vb yield identical results. In Fig. 4a and b, we present results obtained from fitting by means of the cubic approximation of eqn (5) the symmetric I–V curves (corresponding to γ = 0) computed using the “exact” eqn (9) (which mimic the “experimental” curves in these simulations) within bias ranges |V| < 0.6Vt and |V| < 0.8Vt, respectively. The differences (∼5% and 10%, respectively) between the exact values of MO energy offsets (ε0) and those (εfit0) estimated in this way (εfit0 ≃ 0.95ε0 and εfit0 ≃ 0.90ε0, respectively) are reasonable and comparable to experimental inaccuracies (e.g., ref. 27). The examples depicted in Fig. 4a and b pass the self-consistency test: the differences between the fitting curves (green curves, cubic expansions) and the (blue) curves computed via the exact eqn (9) with the parameter values deduced by fitting (parameters of the green curves) are reasonably small in the whole bias range |V| < 1.25Vt shown (which mimics the bias range of experimental interest).
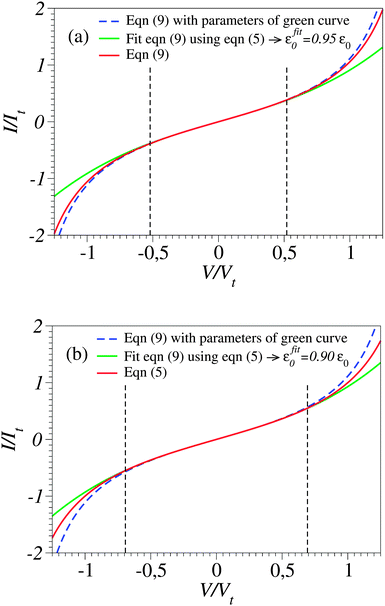 | ||
Fig. 4 The current–voltage curve computed for γ = 0 using eqn (9) (red line), which mimics a symmetric “experimental” curve, fitted with the aid of eqn (5) in the bias range delimited by the vertical dashed lines (−0.520 < V/Vt < 0.520 in panel a and −0.693 < V/Vt < 0.693 in panel b). The reduced variables I/It and V/Vt are expressed using the units  of eqn (10) and of eqn (10) and  .41 These results show that the level energy offset εfit0 deduced via fitting using cubic expansions restricted to sufficiently narrow bias ranges may represent the acceptable estimates of the exact value ε0. However, as explained in the main text, this procedure of restricting the bias range used for fitting cannot be applied for noisy curves. .41 These results show that the level energy offset εfit0 deduced via fitting using cubic expansions restricted to sufficiently narrow bias ranges may represent the acceptable estimates of the exact value ε0. However, as explained in the main text, this procedure of restricting the bias range used for fitting cannot be applied for noisy curves. | ||
Fig. 3b depicts the energy offset values εfit0 = εfit0(Vb) obtained by fitting the I–V curve computed viaeqn (9) up to biases Vb indicated on the x-axis. As is visible there, the fitting parameter εfit0 significantly depends on the bias range. To get reasonably accurate estimates (i.e., εfit0 ≈ ε0), the bias range employed for fitting (Vb) should be sufficiently narrow (as is the case in Fig. 4). This may seem unexpected: in principle, a better fit may be expected when more data are sampled. In fact, this is surprising only at the first sight; the data to be fitted here are ideal data resulting from computations viaeqn (9) that mimic (and actually very accurately reproduce) measurements (as visible in Fig. 1 and 2, or elsewhere25,27,29,30,51), but are not affected by (statistical or measurement41) errors. The accuracy of the εfit0-estimates obtained by choosing small Vb-values as visible in Fig. 3b is related to the possibility to accurately “detect” slight deviations from linearity in the data to be fitted. This poses no problem in cases where “ideal” data not affected by errors are used (like those utilized to generate Fig. 3b). However accurate eqn (9) is, in contrast to the situation analyzed in Fig. 3b, real I–V measurements are affected by inherent experimental errors, and data in a sufficiently broad Vb-range are needed for reliable fitting. The noise of experimental I–V curves, which is the typical situation for STM setups,12,24,48 acts detrimentally when too narrow bias ranges are employed for fitting.
The unacceptably strong dependence of the fitting parameters on the bias range encountered above for cases where γ = 0 becomes even more problematic in the case of asymmetric curves (I(−V) ≠ −I(V), γ ≠ 0). To illustrate this fact, in Fig. 5 we depict the results showing the dependence on the bias range (Vb) of the γ-parameter obtained by fitting the experimental I–V curve43 with the aid of the “exact” eqn (9) and the cubic approximation, eqn (8). They are shown as green and blue symbols, respectively. The difference between the two sets is obvious; while the Vb-dependence of γ-values obtained viaeqn (9) is insignificant, γ-values obtained viaeqn (8) vary by a factor of ∼3. It is worth noting in this context that accurate estimates of the parameter γ are needed to adequately describe the current asymmetry upon bias polarity reversal (“current rectification”). Fig. 1 presents a situation where the cubic approximation seems reasonable for one bias polarity (small differences between the green and blue curves for V < 0) but is totally unsatisfactory for the other bias polarity (V > 0). Cases of (inadequate) methods able to describe one bias polarity while failing for the opposite bias polarity have been presented earlier; see Fig. 5 of ref. 29 and the discussion related to it.
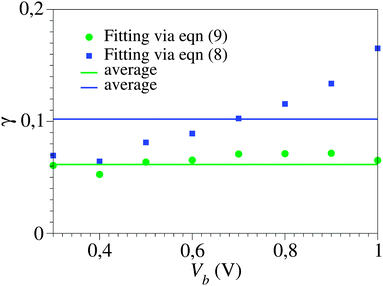 | ||
| Fig. 5 The Vb dependence of the γ-values obtained by fitting the experimental I–V curve43 of Fig. 1viaeqn (8) and (9) (blue and green symbols, respectively) within bias ranges (−Vb, Vb), where Vb is the variable on the abscissa. Notice the scattering of the blue symbols around average (much more pronounced than those of the green symbols, which are within experimental errors), which reflects the fact that the cubic approximation, eqn (8), represents an unsatisfactory description: model parameter values should not depend on how broad is the bias range employed for fitting. | ||
Strong dependence of the model parameters obtained by fitting using cubic expansions similar to eqn (7) has been found earlier in ref. 24 and ascribed to a limited applicability of the single-level model. Certainly, such limitations cannot be ruled out in some cases. However, the present investigation suggests a different possibility: the single-level description may apply (eqn (2) or (9)) while the related cubic approximations (eqn (7) or (8)) fail because they are employed for too broad V-ranges where terms beyond the third order are important.
2.3 Bias-driven molecular orbital energy shift – (I). State of the art
The most common view of current rectification is that the applied bias yields an energy shift of the dominant molecular orbital according to eqn (6).To describe this bias-driven shift, a series of studies resort to simplification;24,28,52 namely, they relate the asymmetric shift of the molecular orbital energy γ to the molecule–electrode couplings Γs,t
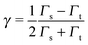 | (12) |
If eqn (12) is applied, the parameter δ, where
| δ ≡ Γt/Γa, | (13) |
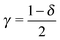 | (14) |
For further illustration, we present here another example. If eqn (12) is applied, the value δ = 0.0151 deduced in ref. 56 would correspond to γ = 0.49245. For typical low bias conductance values for single-molecule junctions G/G0 ∼ 10−3 to 10−4 and biases eV/|ε0| ≈ 1 (typical |ε0|-estimates are ∼0.5–1 eV12,24,25,27,29), current rectifications of ∼15–49 would result, which are considerably larger not only than that achieved in the experimental case considered56 but also in general.13
Another category of work ascribed the bias-driven shift of the energy level to an asymmetric location of the relevant molecular orbital in the space between electrodes. In this picture, the potential V(z) is assumed to drop linearly between electrodes. By assuming that the left contact located at z = −d/2 has the potential V(−d/2) = +V/2 and the right contact located at z = +d/2 has the potential V(+d/2) = −V/2 (Fig. 6b), the potential profile across the junction can be expressed as
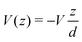 | (15) |
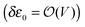 the energy correction for an MO having its “center of gravity” at z = z0 is
the energy correction for an MO having its “center of gravity” at z = z0 is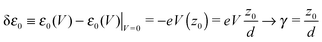 | (16) |
2.4 Bias-driven molecular orbital energy shift – (II). A counterintuitive example backed by quantum chemical calculations
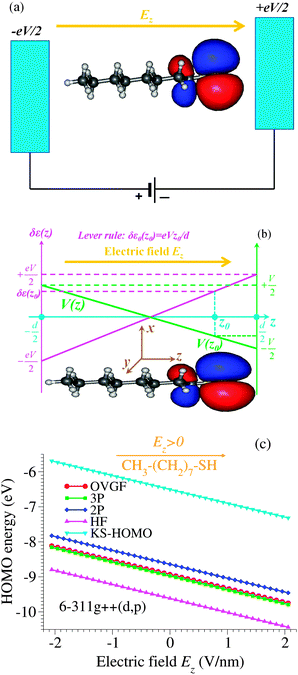
It is worth emphasizing that the “lever rule” (schematically depicted in Fig. 6b), which justifies the term of potential profile asymmetry or voltage division factor21 used for the parameter γ, assumes a linear potential drop across the junction. In some cases, data could be quantitatively analyzed within this picture validated by inserting spacers in a controlled way into the molecules embedded in junctions.10However, by assuming a linear potential profile, screening effects are neglected. To demonstrate that a negligible screening is a fact that can by no means be taken for granted, we present in Fig. 6 the results regarding the HOMO energy of the alkanethiol molecule CH3(CH2)7SH placed in an external field Ez along the (z-)molecular axis.
These results have been obtained via genuine ab initio quantum chemical calculations (OVGF and CCSD, vide infra). Our aim is to bring surprising aspects to experimentalists' attention when they process molecular transport data. Therefore, to make this subsection accessible to a broader audience some relevant details will be given below in order to justify why such ab initio quantum chemical calculations beyond the widely employed density functional theory (DFT) are needed and how they are performed.
DFT calculations are very useful to obtain a variety of ground state properties. For geometry optimization, such calculations based on the B3LYP functional as implemented in Gaussian 0959 have also been performed in this paper. However, as is well documented,60,61 the Kohn–Sham (KS) “orbitals” utilized in DFT calculations are not physical molecular orbitals. Less problematic conceptually is the HOMO. If one knew the exact exchange–correlation functional (the key DFT quantity), the KS–HOMO energy would correspond to the lowest ionization energy.62 However, for typical molecules that are used to fabricate molecular junctions this is not the case; even the HOMO energy is poorly described within the DFT.14
To avoid this issue, here we present results regarding the HOMO energies obtained via genuine ab initio quantum chemical calculations based on the outer valence Green's function (OVGF) method.63,64 The OVGF method is a diagrammatic many-body approach,65 wherein the self-energy entering the electronic Dyson equation includes full (i) second- and (ii) third-order terms of electron–electron interaction. Moreover, (iii) it is augmented by a geometrical approximation (physically associated to a screening factor) to also partially include fourth- and higher-order corrections.66 The ionization energies are determined from the poles of the Green's function computed in this way. In Fig. 6c the labels 2P, 3P, and OVGF refer to the lowest ionization energy with reversed sign (HOMO energy) corresponding to the methods denoted above by (i), (ii), and (iii), respectively.
To obtain the dependence on the electric field Ez applied along the molecule of the HOMO energy (Fig. 6c), calculations at the OVGF/6-311++g(d,p) level of theory have been performed. Such quantum chemical calculations are known to be accurate not only for medium size molecules like the presently considered alkanethiol molecule but also for larger molecules (like C6067). As expected,14 differences between the OVGF HOMO energies and the Kohn–Sham “energies” (also shown in Fig. 6c) are very large. Differences between the OVGF energies and the Hartree–Fock (HF) values and those obtained within the second-order pole approximation (2P) are also significant, while the third-order (3P) pole approximation appears to be accurate in this case.
We applied the OVGF method because this is the most accurate approach to compute ionization (and electron attachment relevant for LUMO-mediated conduction) energies in the presence of an external electric field implemented in the existing (or, at least, to our disposal) quantum chemical packages. However, the example presented below suggests that there is no practical need to resort to even more elaborate many-body approaches to compute the lowest ionization energy (which would be the HOMO energy with reversed sign if the one-particle description applied).
CCSD (coupled-cluster (CC) singles (S) and doubles (D))68,69 is such an approach; it represents the state of the art of quantum chemistry to treat many-electron systems of medium size molecules. The CC technique constructs multi-electron wavefunctions by applying exponential cluster operators on the Hartree–Fock (HF) (molecular orbital) wavefunction. In the specific case of CCSD, the cluster operator is truncated to single and double excitations (in short, “singles” and “doubles”). Within the CCSD framework, the lowest ionization energy can be computed either by applying the equation of motion method (EOM-IP-CCSD)68 or by subtracting the total CCSD ground state energies of the cationic and neutral molecular species (Δ-CCSD14). As a further check of the OVGF approach, we mention that the OVGF-value (9.089 eV) agrees well with the values thus obtained (8.996 eV using EOM-IP-CCSD and 8.945 eV using Δ-CCSD) without an applied electric field.
CCSD calculations of this work have been performed using CFOUR,70 a package also utilized to compute the spatial distribution of the HOMO (see ref. 14 for details). Again, to avoid issues related to KS orbitals, we have calculated the natural orbital expansion of the reduced density matrix at the EOM-IP-CCSD level as the most reliable approach to characterize the spatial distribution of the extra hole (or electron in cases of LUMO-mediated conduction). By inspecting the natural orbital expansion, we found that the extra hole is almost entirely (∼97%) concentrated in a single natural orbital (“HOMO”). It is this spatial distribution that is shown in Fig. 6a and b.
The most important finding of this subsection emerges from the comparison of panels b and c of Fig. 6: the OVGF method (as well as the other methods related to it discussed above) predicts HOMO energies clearly exhibiting a trend opposite to the “lever rule” expectation. In view of this fact, namely, that cases exist, where the “lever rule” may fail, rather than the voltage division factor or potential profile asymmetry, Stark effect strength71 may be a possible more appropriate term when referring to the parameter γ.
Although a linear dependence of ε0 on the applied bias is often assumed in transport studies (also in the electrochemical context53,72), we are not aware of any quantum chemical study reporting such a result for molecules often used to fabricate molecular junctions. Therefore, we believe that the strict linearity of the dependence of the HOMO energy on the applied field/bias represents an important result of the present paper. Noteworthy, the results of the OVGF-computations (depicted by points in Fig. 6c), which perfectly lie on a straight line, correspond to electric field values of up to 2 V nm−1. These values safely cover the typical experimental range for molecular devices, which is in most cases up to about 1 V nm−1, since beyond this value field ionization may become significant.
3 Conclusion
An important finding of the present paper is the demonstration that current transport data processing based on cubic expansions of the current as a function of voltage is inappropriate. First, this typically underestimates the energy offset of the dominant molecular orbital by a factor of about two. Because DFT calculations typically underestimate the HOMO–LUMO gap by a similar factor, in the light of the present finding, “agreement” between experiments and theories using Kohn–Sham orbital energies uncorrected by employing more accurate quantum chemical methods and/or image charge effects could/should be reconsidered. Second, the application of the cubic expansion for bias ranges of experimental interest (almost inherently) yields parameter values depending on how broad is the bias range employed for fitting; this may easily be interpreted as an unphysical result, creating the impression that the single level description is invalid. In reality, more plausible is that the cubic expansion rather than the single-level description is inadequate. A third drawback of the cubic expansion is its inability to quantitatively describe asymmetric I(V) ≠ −I(−V) curves. This is revealed by the fact that, contrary to experiments,43 it yields transition (peak) voltages of equal magnitude for both bias polarities (cf.Fig. 2); this is an aspect on which a theoretical simulation presented in ref. 15 already drew attention.Another important finding reported in this paper is the fact that the bias-driven shifts of molecular orbital energies are necessarily determined neither by the asymmetry of the molecule–electrode couplings nor by the asymmetric location of the “center of gravity” of the molecular orbitals relative to the two electrodes. The latter aspect is also important because it emphasizes that even if a single orbital dominates the charge transport through a certain molecular junction, other molecular orbitals can have indirect contributions via subtle screening effects that may yield counterintuitive effects of the kind presented above. We chose to present a single (counter-)example, namely, the case of an isolated benchmark molecule (octanethiol) in an external field. We could present more (counter-)examples (e.g., a fuller class of alkanethiols), but this would not add any further evidence; we do by no means claim that the “lever rule” fails in all cases. To avoid ambiguity, we considered an isolated molecule. If we presented a molecule linked to electrodes, never ending questions might arise, e.g. on the contacts' geometry (atop, bridge, hollow) or nature (chemisorption vs. physisorption). What is important for the present purpose is to show that the (upward or downward) MO shift due to an applied electric field is not necessarily directly related to the MO location.
Acknowledgements
The author thanks Pramod Reddy for providing him the raw data utilized in Fig. 1 and 2. Financial support provided by the Deutsche Forschungsgemeinschaft (grant BA 1799/2-1) is gratefully acknowledged.References
- N. J. Tao, Phys. Rev. Lett., 1996, 76, 4066–4069 CrossRef CAS PubMed.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
- A. Nitzan and M. A. Ratner, Science, 2003, 300, 1384–1389 CrossRef CAS PubMed.
- L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907 CrossRef CAS PubMed.
- N. J. Tao, Nat. Nano, 2006, 1, 173–181 CrossRef CAS PubMed.
- S. M. Lindsay and M. A. Ratner, Adv. Mater., 2007, 19, 23–31 CrossRef CAS.
- S. H. Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486 CrossRef CAS PubMed.
- O. Tal, M. Krieger, B. Leerink and J. M. van Ruitenbeek, Phys. Rev. Lett., 2008, 100, 196804 CrossRef CAS PubMed.
- R. L. McCreery and A. J. Bergren, Adv. Mater., 2009, 21, 4303–4322 CrossRef CAS PubMed.
- C. A. Nijhuis, W. F. Reus, J. R. Barber, M. D. Dickey and G. M. Whitesides, Nano Lett., 2010, 10, 3611–3619 CrossRef CAS PubMed.
- H. Song, M. A. Reed and T. Lee, Adv. Mater., 2011, 23, 1583–1608 CrossRef CAS PubMed.
- W. Hong, H. Valkenier, G. Meszaros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. Garcia, C. J. Lambert, J. C. Hummelen and T. Wandlowski, Beilstein J. Nanotechnol., 2011, 2, 699–713 CrossRef PubMed.
- R. M. Metzger, Chem. Rev., 2015, 115, 5056–5115 CrossRef CAS PubMed.
- I. Bâldea, Faraday Discuss., 2014, 174, 37–56 Search PubMed.
- I. Bâldea, Phys. Chem. Chem. Phys., 2015, 17, 20217–20230 RSC.
- P. W. Anderson, Phys. Rev., 1961, 124, 41–53 CrossRef CAS.
- D. M. Newns, Phys. Rev., 1969, 178, 1123–1135 CrossRef CAS.
- W. Schmickler, J. Electroanal. Chem., 1986, 204, 31–43 CrossRef CAS.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge Univ. Press, Cambridge, 1997 Search PubMed.
- I. R. Peterson, D. Vuillaume and R. M. Metzger, J. Phys. Chem. A, 2001, 105, 4702–4707 CrossRef CAS.
- F. Zahid, M. Paulsson and S. Datta, in Advanced Semiconductors and Organic Nano-Techniques, ed. H. Morkoç, Academic Press, 2003, vol. 3, ch. Electrical Conduction through Molecules Search PubMed.
- S. Datta, Quantum Transport: Atom to Transistor, Cambridge Univ. Press, Cambridge, 2005 Search PubMed.
- H. Haug and A.-P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors, Springer Berlin Heidelberg, 2008, vol. 123, pp. 63–73 Search PubMed.
- B. M. Briechle, Y. Kim, P. Ehrenreich, A. Erbe, D. Sysoiev, T. Huhn, U. Groth and E. Scheer, Beilstein J. Nanotechnol., 2012, 3, 798–808 CrossRef PubMed.
- I. Bâldea, Nanoscale, 2013, 5, 9222–9230 RSC.
- L. Buimaga-Iarinca and C. Morari, RSC Adv., 2013, 3, 5036–5044 RSC.
- Z. Xie, I. Bâldea, C. Smith, Y. Wu and C. D. Frisbie, ACS Nano, 2015, 9, 8022–8036 CrossRef CAS PubMed.
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific Publishers, 2010 Search PubMed.
- I. Bâldea, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035442 CrossRef.
- I. Bâldea, Chem. Phys., 2012, 400, 65–71 CrossRef.
- I. Bâldea, J. Am. Chem. Soc., 2012, 134, 7958–7962 CrossRef PubMed.
- I. Bâldea, Nanotechnology, 2014, 25, 455202 CrossRef PubMed.
- R. M. Metzger, T. Xu and I. R. Peterson, J. Phys. Chem. B, 2001, 105, 7280–7290 CrossRef CAS.
- I. Bâldea and H. Köppel, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 193401 CrossRef.
- J. G. Simmons, J. Appl. Phys., 1963, 34, 1793–1803 CrossRef.
- J. G. Simmons, J. Appl. Phys., 1963, 34, 238–239 CrossRef.
- J. Rowell, in Tunneling Phenomena in Solids, ed. E. Burstein and S. Lundqvist, Springer, USA, 1969, pp. 385–404 Search PubMed.
- C. B. Duke, in Tunneling Phenomena in Solids, ed. E. Burstein and S. Lundqvist, Springer, USA, 1969, ch. 28, pp. 31–46 Search PubMed.
- C. B. Duke, Tunneling in Solids, Academic Press, N. Y., 1969 Search PubMed.
- W. F. Brinkman, R. C. Dynes and J. M. Rowell, J. Appl. Phys., 1970, 41, 1915–1921 CrossRef CAS.
- I. Bâldea, Z. Xie and C. D. Frisbie, Nanoscale, 2015, 7, 10465–10471 RSC.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. D. Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801 CrossRef PubMed.
- A. Tan, S. Sadat and P. Reddy, Appl. Phys. Lett., 2010, 96, 013110 CrossRef.
- J. M. Beebe, B. Kim, C. D. Frisbie and J. G. Kushmerick, ACS Nano, 2008, 2, 827–832 CrossRef CAS PubMed.
- H. Song, Y. Kim, Y. H. Jang, H. Jeong, M. A. Reed and T. Lee, Nature, 2009, 462, 1039–1043 CrossRef CAS PubMed.
- I. Bâldea, Chem. Phys., 2010, 377, 15–20 CrossRef.
- B. Kim, S. H. Choi, X.-Y. Zhu and C. D. Frisbie, J. Am. Chem. Soc., 2011, 133, 19864–19877 CrossRef CAS PubMed.
- S. Guo, J. Hihath, I. Diez-Pérez and N. Tao, J. Am. Chem. Soc., 2011, 133, 19189–19197 CrossRef CAS PubMed.
- W. Lee and P. Reddy, Nanotechnology, 2011, 22, 485703 CrossRef PubMed.
- K. Smaali, N. Clément, G. Patriarche and D. Vuillaume, ACS Nano, 2012, 6, 4639–4647 CrossRef CAS PubMed.
- I. Bâldea, J. Phys. Chem. Solids, 2012, 73, 1151–1153 CrossRef.
- G. Wang, Y. Kim, S.-I. Na, Y. H. Kahng, J. Ku, S. Park, Y. H. Jang, D.-Y. Kim and T. Lee, J. Phys. Chem. C, 2011, 115, 17979–17985 CAS.
- I. Bâldea, J. Phys. Chem. C, 2013, 117, 25798–25804 Search PubMed.
- I. Baldea, Phys. Chem. Chem. Phys., 2015, 17, 15756–15763 RSC.
- F. Zahid, A. W. Ghosh, M. Paulsson, E. Polizzi and S. Datta, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245317 CrossRef.
- I. Bâldea, Phys. Chem. Chem. Phys., 2014, 16, 25942–25949 RSC.
- G. Zhang, M. A. Ratner and M. G. Reuter, J. Phys. Chem. C, 2015, 119, 6254–6260 CAS.
- Notice the slightly different definitions used for the parameter denoted by δ in ref. 53, 54 and 56.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Clarendon, Oxford, 1989 Search PubMed.
- W. Kohn, A. D. Becke and R. G. Parr, J. Chem. Phys., 1996, 100, 12974–12980 CrossRef CAS.
- C.-O. Almbladh and U. von Barth, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3231–3244 CrossRef CAS.
- L. S. Cederbaum and W. Domcke, in Adv. Chem. Phys., ed. I. Prigogine and S. A. Rice, Wiley, New York, 1977, vol. 36, pp. 205–344 Search PubMed.
- W. von Niessen, J. Schirmer and L. S. Cederbaum, Comput. Phys. Rep., 1984, 1, 57–125 CrossRef CAS.
- A. L. Fetter and J. D. Walecka, Quantum Theory of Many Particle Systems, Dover Publication Inc., Mineola, N. Y., 3rd edn, 2003 Search PubMed.
- Notice that via the Dyson equation each term included in the self-energy amounts to include an infinite sub-series of terms in the perturbation expansion.65.
- V. G. Zakrzewski, O. Dolgounitcheva and J. V. Ortiz, J. Phys. Chem. A, 2014, 118, 7424–7429 CrossRef CAS PubMed.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1994, 101, 8938–8944 CrossRef CAS.
- J. Schirmer and F. Mertins, Theor. Chem. Acc., 2010, 125, 145–172 CrossRef CAS.
- CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package by J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- Y. Xue and M. A. Ratner, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 115406 CrossRef.
- A. Alessandrini, S. Corni and P. Facci, Phys. Chem. Chem. Phys., 2006, 8, 4383–4397 RSC.
Footnote |
| † Also at National Institute for Lasers, Plasmas, and Radiation Physics, Institute of Space Sciences, Bucharest-Mggurele, Romania. |
| This journal is © the Owner Societies 2015 |