Open Access Article
Open Access ArticleInterplay of experiment and theory: high resolution infrared spectrum and accurate equilibrium structure of BF2OH†
Natalja
Vogt
*ab,
Jean
Demaison
a,
Heinz Dieter
Rudolph
a and
Agnès
Perrin
c
aSection of Chemical Information Systems, University of Ulm, D-89069 Ulm, Germany. E-mail: natalja.vogt@uni-ulm.de
bDepartment of Chemistry, Lomonosov Moscow State University, 119991 Moscow, Russia
cLaboratoire Inter-Universitaire des Systèmes Atmosphériques (LISA), UMR 7583 CNRS et Universités Paris-Est Créteil et Paris Diderot-Paris 7, Institut Pierre-Simon Laplace, 61 Avenue du Général de Gaulle, 94010 Créteil Cedex, France
First published on 28th October 2015
Abstract
The high-resolution Fourier transform infrared (FTIR) spectrum of 11BF2OH (difluoroboric acid) is analyzed taking into account numerous interactions. The ν1, ν2 and ν3 infrared bands are analyzed for the first time, whereas the parameters of the 61, 71, 81 and 91 states and for the 41 and 92 interacting states are redetermined. These results are used to check the quality of the ab initio force field. It is found that the ab initio rovibrational corrections are more accurate than the experimental ones. An earlier attempt to determine a semiexperimental structure did not allow us to obtain an accurate equilibrium structure. The reasons of this failure are investigated. This failure was mainly due to the lack of useful experimental information. Indeed, there is no isotopic substitution available for the fluorine atoms, and the boron atom is extremely close to the center of mass. Furthermore, the available isotopic substitutions (H → D and 16O → 18O) induce a large rotation of the principal axis system which amplifies the errors. However, the mixed estimation method has allowed us to determine a complete and reliable equilibrium structure. Thanks to this method, it is possible to determine an accurate structure, even in extremely difficult cases. An extensive analysis of the quality of structure calculations at the CCSD(T) level is also performed using basis sets up to five ζ quality. It was found that, at the convergence limit, the effects of the diffuse functions are practically disappearing, whereas the core–core and core–valence electron correlation effects are quite important for the bond lengths.
1. Introduction
The spectra and structure of difluorohydroxyborane molecule or difluoroboric acid, BF2OH, were studied several times by experimental and theoretical methods. Nevertheless, there are still several problems that could not be solved until now. The molecule was first detected by mass spectrometry.1 The microwave spectrum of this planar asymmetric rotor was measured several times.2–5 The matrix infrared (IR) spectra of eight isotopologues were first observed by Jacox et al.6 Some of these data for the 11B isotopic species of BF2OH are also summarized in Table 1, which otherwise quotes the available high resolution infrared data. The first high resolution gas phase IR spectrum of BF2OH was observed by Collet et al.7 using a Fourier transform spectrometer, and this study led to the first investigation of the ν8 and ν9 fundamental bands of 11B (for the 11BF2OH and 10BF2OH isotopic species we will use henceforth in the text the abbreviated notation 11B and 10B, respectively). Subsequently, the high-resolution infrared spectrum was recorded by Fourier transform spectroscopy in the range 400–4000 cm−1.8 At that time no significant resonances were observed during the investigation of the ν5, ν8, ν9 and ν8 + ν9 bands. On the other hand the ν7 band was found to be affected by a C-type Coriolis resonance coupling together the 71 energy levels with those from the dark 61 state. Finally, the ν4 and 2ν9 bands,9 which correspond to the OH in-plane bending mode and to the first overtone of ν9 (OH torsion relative to the F2BO moiety), respectively, are strongly perturbed. Indeed, the energy levels of the 92 state are involved in B-type Coriolis resonances with those of the 6191 dark state. Moreover, the 41 levels are perturbed by B-type Coriolis resonances with 7191 levels and by C-type Coriolis and anharmonic resonances with the 6171 levels. In addition to these rather “classical” perturbations, large amplitude effects were evidenced during the analysis of the 2ν9 and ν4 bands8 and of the 3ν9–ν9 hot band.10 To give an order of magnitude, for low Ka values, tunnelling splittings of about 0.0051, 0.0038 and 0.031 cm−1 were observed for the energy levels of the 92, 41 and 93 states, respectively. There is a slow decrease of these splittings for high Ka values that are difficult to observe in the infrared region. These large amplitude effects for BF2OH were confirmed by a careful reinvestigation of the rotational spectrum by millimeterwave spectroscopy.5 In this study, torsional splittings were found for most of the rotational transitions within the ground state and could be satisfactorily reproduced using the IAM (internal axis method) formalism. Using this approach, reasonable agreement between the ab initio (0.0061 and 0.0043 cm−1) and experimental (0.0038 and 0.0051 cm−1) tunnelling splittings for the 41 and 92 states could be achieved. These results were later confirmed by another ab initio study.11| Statea | Description | ν (exp.) | Δωb | Interaction parameterb |
|---|---|---|---|---|
| a A′ and A′′ are the symmetry species in the Cs point group. b CCSD(T)_AE/TZ2Pf value, see text; Δω is the harmonic frequency. c Gas phase band centers from ref. 8. d Gas phase band centers from ref. 9. e Experimental value, this work. f Experimental value for 2ν9 = 1042.87 cm−1.9 g This work. | ||||
| ν9, A′′ | δ(BOH) o.p. | 522.87c | ω 9 − ω7 = 101 | ζ a 79 = 0.33; ζb79 = −0.11 |
| ω 9 − ω6 = 72 | ζ a 69 = −0.15; ζb69 = −0.01 | |||
| ν8, A′′ | δ(F2BO) o.p. | 684.16c | ω 6 − ω8 = 211 | ζ a 68 = −0.26; ζb68 = 0.16 |
| ν7, A′ | δ(F2BO) i.p. | 446.54c | ω 6 − ω7 = 30 | ζ c 67 = 0.75 |
| ω 9 − ω7 = 101 | ζ a 79 = 0.33; ζb79 = −0.11 | |||
| ν6, A′ | ν(F2BO) i.p. | 479.17c | ω 9 − ω6 = 72 | ζ a 69 = −0.15; ζb69 = −0.01 |
| ω 6 − ω7 = 30 | ζ c 67 = 0.75 | |||
| ω 6 − ω8 = 211 | ζ a 68 = −0.26; ζb68 = 0.16 | |||
| ν5, A′ | δ(BF2) i.p. | 880.74c | ω 5 − 2ω7 = 9 | ϕ 577 = −0.8 |
| ω 5 − ω6 − ω7 = −21 | ϕ 567 = −0.4 | |||
| ν4, A′ | δ(BOH) i.p. | 961.49d | ω 4 − ω7 − ω9 = 17 | 79,4 B x = −0.167274e |
| ω 4 − ω6 − ω7 = 89 | ϕ 467 = 2.2 | |||
| ω 4 − 2ω9 = −84f | ϕ 499 = 108 | |||
| ν3, A′ | ν s(BF) i.p. | 1419.2126g | ω 2 − ω3 = 52 | ζ c 23 = 0.798 |
| ν2, A′ | ν as(BF) i.p. | 1468.2762g | ω 2 − ω3 = 52 | ζ c 23 = 0.798 |
| ω 2 − ω4 − ω6 = 7 | ϕ 246 = −6 | |||
| ω 2 − ω4 − ω7 = 36 | ϕ 247 = 2 | |||
| ν1, A′ | ν(OH) i.p. | 3714.12g | 2ω2 + ω5 − ω1 = 9 | — |
| 2ω3 + ω4 − ω1 = 16 | — | |||
| 2ω3 + ω5− ω1 = −94 | — | |||
Ab initio calculations predict the existence of many vibrational–rotational resonances perturbing the rotational structure of most vibrational states of BF2OH.4 These additional resonances which were not accounted for during our previous energy level calculations7–9 will be considered here for the 61, 71, 81 and 91 states and for the 41 and 92 interacting states.
The equilibrium geometry and anharmonic force field up to semidiagonal quartic terms have been calculated at the coupled cluster level of theory including a perturbational estimate of the effects of connected triple excitations [CCSD(T)].4 The semiexperimental structure (SE) was also determined using a force field of CCSD(T) quality, but the result was not satisfactory. One of the main goals of this paper is to try to explain the reason for this failure and to propose solutions. There are two obvious explanations: there is no isotopic substitution available for the fluorine atom. Furthermore, the boron atom is extremely close to the center of mass; in other words, the substitution 11B → 10B does not bring useful information. In conclusion, there are not enough data (i.e. rotational constants) available. There is one more reason: BF2OH is an oblate molecule and isotopic substitutions may induce large rotations of the principal axis system (PAS) that may amplify the errors.12 This point will be confirmed here. Finally, it is also possible that the large amplitude motion of the OH group hinders an accurate determination of the semiexperimental structure. This last point will be investigated here.
The semiexperimental (SE) structures of several molecules with a large amplitude motion have already been determined. In the case of molecules with a methyl group (propene,13 methyl formate,14 dimethyl ether,15 dimethyl sulfide16), the internal rotation does not seem to affect negatively the accuracy of the SE structure. For molecules with an OH group, the situation is more complicated.17 It was possible to obtain accurate SE structures for nitrous acid (syn and anti conformers),18,19 formic acid (syn and anti conformers)20 as well as glycolaldehyde.17 On the other hand, for proline21 and glycidol,17 the SE rotational constants of the OD species were found to be incompatible with the best structure. Finally, although accurate SE structures could be determined for ethanol (anti conformer)17 and nitric acid,22 there was obviously a problem: the rotation–vibration interaction constants (α-constants) of the lowest fundamental vibration could not be reproduced accurately by the ab initio force field. It might lead us to think that it is due to the large amplitude vibration. However, the same problem is encountered in some rigid molecules such as HCOCl23 and vinyl fluoride.24 An alternative explanation is that the structure used to calculate the ab initio force field is not accurate and might therefore lead to inaccuracies in some α-constants. BF2OH is a favourable case to check this hypothesis because it is a rather small molecule; furthermore, it is planar.
In the present paper, after a short description of the experimental details, the spectra for the ν1, ν2 and ν3 bands are analyzed. The energy levels for the 11, 21 and 31 vibrational states as well as the {61,71,81,91} and {41,7191,6171,92,6191} resonating states are computed, and the molecular parameters are subsequently determined. Then, the accuracy of the Born–Oppenheimer ab initio structure is confirmed. Next, the quality of the ab initio anharmonic force field is evaluated followed by a discussion of the accuracy of the rovibrational corrections. Finally, the difficulties inherent in the determination of the semiexperimental structure are examined, and the SE structure is determined using the method of mixed estimation.
2. Experimental details
The details of the synthesis of the enriched isotopologues 10B (92.4%) and 11B (99%) of BF2OH and the recording of the high resolution FTIR spectra are given in ref. 8. The resolution (1/maximum optical path difference) was adjusted to 2.4 × 10−3 cm−1, and the precision and wavenumber accuracy are better than 0.5 × 10−3 and better than 1 × 10−3 cm−1.8As usual, water lines25 were observed as impurities in both spectral regions. In addition, the analysis was complicated in the 1430–1470 cm−1 region by the presence of lines from the strong ν3 perpendicular band of the 11BF3 impurity centered at 1453.98 cm−1.26
3. Analysis
In the present infrared study it was possible to perform the first high resolution analysis of the ν2 and ν3 bands together with the first identification of the ν1 band of 11B.During this study, the ground state energy levels were computed using the accurate ground state constants derived in ref. 4 and, as a model, a Watson A-type Hamiltonian written in Ir representation.27 For symmetry reasons, ν1, ν2 and ν3 are, in principle, hybrid bands with both A- and B-type transitions. Fig. 1 and 2 give overviews of the ν1 band and of the ν2 and ν3 bands, respectively. In fact, the ν1 and ν2 are mainly pure A-type bands while both A- and B-type transitions were observed for the ν3 band. For these three bands the Q branches are rather narrow, while in the P and R branches, lines are grouped into clusters, and each “s” cluster gathers together transitions [J, Ka, Kc] − [J ± 1, Ka, Kc ± 1], involving the same value of “s” with
| s = 2J − Kc | (1) |
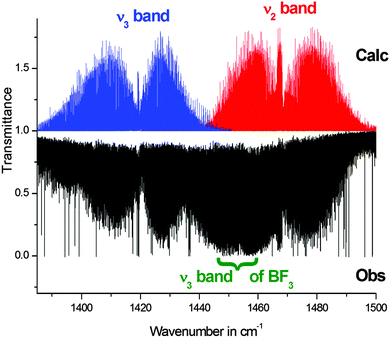 | ||
| Fig. 2 Overview of the ν2 and ν3 bands of BF2OH. In this spectral region, impurity lines from the ν3 band of BF3 are also clearly observable. | ||
For these unresolved doublet transitions,8J is the rotational quantum number and Ka, Kc are pseudo quantum numbers that correlate with the K = |k| quantum number about the a and c axes in the prolate and oblate symmetric top limits, respectively.
The first identifications were initiated by taking advantage of line regularities from one cluster to another one in the P and R branches. Once a few lines were assigned, the energy levels of the various upper vibrational states were computed by adding to the observed line positions the computed ground state energies. These first sets of energy levels were included in a least squares fit, and a first set of vibrational energies and upper state rotational constants were determined for the 11, 21 and 31 vibrational states. With these first sets of constants it was possible to make better predictions and hence to assign new lines. The process was repeated until it was no longer possible to perform new assignments.
For the ν2 band, the assignment is rather complete, because the band is only weakly perturbed. On the other hand, the ν3 band is highly perturbed, and this is why the analysis concerns only several series involving low Ka values.
For the ν1 band, the assignments are restricted to the identification of the “s” clusters in the P and R branches (see eqn (1)), with s ≤ 33, and no detailed and faithful information can be obtained on the rotational structure within each cluster in the 3600–3800 cm−1 region. This limitation is because the Doppler line width of each individual line (∼0.028 cm−1 at 296 K) in each cluster is already of the order of magnitude of the separation between two adjacent lines belonging to the same cluster. Furthermore, we presume that the ν1 band is perturbed, and this complicated further the analysis.
4. Energy level calculations
4.1. Theoretical model
Several vibration–rotation resonances were accounted for, depending on the resonating states considered. A brief description of the Hamiltonian models that we had to use to perform these calculations is given in the Appendix. As in ref. 9 the Euler angle θ, which could not be determined, was set at zero.4.2. The 11, 21 and 31 states
For the 21 state and 31 vibrational states we present two calculations. The first one was done assuming that these states are isolated, while the second one accounts for the C-type Coriolis resonance which couples together the 21 and 31 energy levels. Among the set of 21 and 31 measured energy levels, only those which can be considered as “less perturbed” by resonances involving dark states were considered in the least squares fit calculations. The parameters (vibrational energies, rotational constants and C-type interacting parameter) resulting from these computations are quoted together with their associated uncertainties in Table 2. The A rotational constants proved to be non-determinable and were maintained fixed at the value proposed by Breidung et al.4 Table S1 of the ESI† gathers details of the energy level calculations in terms of standard deviations and statistical analyses. It appeared that these two calculations (coupled and uncoupled) differ only marginally in terms of the quality of the fit. This outcome is expected because the resonances involving 21 and 31 energy levels with those of unidentified dark states were not considered during these two calculations.| E v | A | B | C | 2,3 C y | |
|---|---|---|---|---|---|
| a All centrifugal distortion constants are fixed to the ground state values. b Fixed to the ground state values.4 c For 31 the A rotational constant is maintained at the value predicted by Breidung et al.4 d C-type Coriolis constant. | |||||
| 0b | 0.3442527640 | 0.3368801590 | 0.1699552140 | ||
| 11 | 3714.1143(8) | 0.3437337(170) | 0.3359471(285) | 0.16984120(148) | 0 |
| 21 | 1468.2741(48) | 0.3427690(200) | 0.3357875(320) | 0.17047311(780) | 0 |
| 31 | 1419.1696(34) | 0.343047867c | 0.3365527(520) | 0.16787843(700) | 0 |
| 21 | 1468.2733(22) | 0.34277878(790) | 0.3357541(130) | 0.168557(240) | 0.3087(190) |
| 31 | 1419.1758(47) | 0.343047867c | 0.3365758(670) | 0.169788(240) | |
Finally, we performed an energy calculation for the 11 state. As input for the least squares fit calculation, we used the “pseudo” 11 energy levels obtained from the identification of the “s” clusters in the P and R branches (see eqn (1)). Among the resulting parameters generated during this fit (see Table 2) only the vibrational energy (E1 = 3714.1142 cm−1) has a physical meaning. Indeed, the A, B and C rotational constants which have clearly unrealistic values are quoted because these parameters were used to model the ν1 band presented in Fig. 1.
4.3. The {61,71,81,91} and {41,7191,6171,92,6191} resonating states
The experimental energy levels of 71, 81 and 91 (resp. of those 41,7191 and 92) resulting from the analysis performed in ref. 8 (resp. ref. 9) were introduced in a least squares fit calculation to determine the parameters (band centers, rotational and interacting constants, together with, eventually, torsional constants) for the {61,71,81,91} (resp. {41,7191,6171,92,6191}) resonating states.The goal of these new calculations was to account explicitly for the Fermi, or A-type, B-type and C-type Coriolis resonances predicted by the ab initio calculations.
The parameters (vibrational energies, rotational constants and interacting parameters) resulting from this computation are quoted together with their associated uncertainties in Tables 3–5.
| 61 | 71 | 81 | 91 | |
|---|---|---|---|---|
| a All other centrifugal distortion constants are fixed to the ground state values.4 b Fixed to the infrared observed broad structure (see text in ref. 8). | ||||
| E v | 479.17a | 446.55171(7) | 684.15840(7) | 522.86815(5) |
| A | 0.3459420(900) | 0.344720533(186) | 0.343991965(110) | 0.343258360(600) |
| B | 0.335897(141) | 0.337393954(636) | 0.336966965(240) | 0.336529392(380) |
| C | 0.1690340(173) | 0.170573446(520) | 0.170199092(58) | 0.169986115(190) |
| Δ K × 106 | 0.354948(940) | 0.361381(230) | 0.351405(710) | |
| Δ JK × 106 | −0.123463(220) | −0.1049458(280) | ||
| Δ J × 106 | 0.204124(910) | 0.208940(420) | 0.2004195(110) | |
| Δ K × 106 | 0.19104(370) | 0.172065(150) | 0.174388(230) | |
| Δ J × 107 | 0.96250(540) | 0.898740(630) | ||
| ν′ | ν′′ | Interaction | Operator | Parametera | |
|---|---|---|---|---|---|
| a For definitions, see Appendix. b Fixed to the ab initio value. | |||||
| 81 | 61 | Coriolis | Ĵ z | 8,6 A z | −0.216284(120) |
| 81 | 61 | Ĵ x | 8,6 B x | 6.3943(460) × 10−2 | |
| 91 | 71 | Ĵ z | 9,7 A z | 0.226997(780) | |
| 91 | 71 | Ĵ x | 9,7 B x | −7.4093(140) × 10−2 | |
| 61 | 71 | iĴ y | 6,7 C y | 0.284975(340) | |
| 91 | 61 | Ĵ z | 9,6 A z | −0.104092(960) | |
| 92 | 41 | Fermi | 99,4 F 0 | 27.1b | |
| 7191 | 41 | Coriolis | Ĵ x | 79,4 B x | −0.16727377(550) |
| {Ĵ2z, Ĵx} | 79,4 B xzz | 1.05205(180) × 10−5 | |||
| Ĵ x Ĵ 2 | 79,4 B xJ | −5.5892(110) × 10−6 | |||
| (Ĵ3+ + Ĵ3−) | 79,4 B x3 | −1.5266(180) × 10−7 | |||
| 6191 | 92 | Coriolis | 69,99 B yz | 1.67146(130) × 10−3 | |
| 6171 | 41 | Anharmonic | Ĵ 2 xy | 67,4 Anh xy | 3.96636(240) × 10−4 |
| {Ĵ2z, Ĵxy} | 67,4 Anh xyzz | −9.72824(590) × 10−8 | |||
| 92 | 6191 | 41 | 7191 | 6171 | |
|---|---|---|---|---|---|
| a The angles φTORS and θTORS in degree were maintained at the values determined in ref. 8. b Fixed to the 92 value. c Fixed to the 41 value. d All other centrifugal distortion constants are fixed to the ground state value.4 | |||||
| φ TORS (in degree) | 1.208a | 1.208a | |||
| θ TORS (in degree) | 0a | 0a | |||
| h TORS × 103 | 2.60833(250) | 1.82179(270) | |||
| E v | 1032.53828(1) | 1000.82(1) | 971.83087(1) | 970.99658(3) | 929.139(3) |
| h v xz × 103 | −4.05497(110) | −4.05497b | −1.36327(420) | 1.36327c | 1.36327c |
| A | 0.34190504(170) | 0.3408277(140) | 0.34300764(210) | 0.34311909(250) | 0.3756801(120) |
| B | 0.33889632(170) | 0.3378665(170) | 0.33816039(210) | 0.33807857(260) | 0.32184572(520) |
| C | 0.1700720766(21) | 0.17037573(980) | 0.1697909588(100) | 0.1680388324(57) | 0.17247533(120) |
| Δ K × 106 | 0.292585(280) | 0.537199(460) | 0.303302(720) | −4.0435(150) | |
| Δ JK × 106 | 0.052391(260) | −0.415120(290) | −0.106694(760) | 5.0582(100) | |
| Δ J × 106 | 0.17240131(160) | −0.00863(150) | 0.260944291(770) | 0.181817(210) | 0.10280(270) |
| δ K × 106 | 0.135086(130) | 0.151381(150) | |||
| δ J × 107 | 0.7359108(170) | 1.1828284(230) | 1.34300(110) | −5.7426(130) | |
Let us mention that the 61 band center was fixed at 479.17 cm−1 which corresponds to the infrared broad Q branch structure observed in the FTIR spectra recorded at Wuppertal.8 Also, the zero order term involved in the expansion of the Fermi operator coupling the 41 ⇔ 92 interacting states was maintained fixed at the value predicted by the ab initio calculation:
| 99,4F0 = 27.1 cm−1 | (2) |
The values achieved during this work for the hTORS (torsional) and hBend (bending) splitting parameters (hTORS = 2.60833(250) × 10−3 cm−1 and hBEND = 1.82179(270) × 10−3 cm−1, see Table 5) do not differ significantly from those obtained in ref. 9, when neglecting the Fermi resonance coupling 41 ⇔ 92 (hTORS = 2.54516(1000) × 10−3 cm−1 and hBEND = 1.78523(100) × 10−3 cm−1; see Table 8 in ref. 9). Clearly, the torsional splitting in the 41 state is not due to the existence of the weak Fermi resonance coupling the 41 and 92 states.
The assigned lines are given in Table S2 of the ESI.†
5. Ab initio equilibrium structure‡
The ab initio equilibrium structure has been previously optimized with the coupled cluster method with single and double excitations28 and a perturbative treatment of connected triples,29 CCSD(T), along with the correlation-consistent polarized valence n-tuple-ζ basis sets (cc-pVnZ with n = 3, 4).30 The inner-shell correlation was estimated with the second-order Møller–Plesset perturbation theory, MP2,31 and the Martin–Taylor (MT) basis set.32 To account for the electronegative character of the F and O atoms, the augmented cc-pVQZ33 basis set was used at the MP2 level. To investigate the structural effects of further basis set improvement (cc-pVQZ → cc-pV5Z), the cc-pV5Z basis set was employed at the MP2 level. The derived structure is expected to be accurate. However, to estimate its precision, we repeated the optimization using different schemes.First, the augmented correlation-consistent polarized weighted core–valence n-tuple-ζ, aug-cc-pwCVnZ, basis sets34 with n = D, T, Q, 5 were used, and all electrons were correlated (AE); consequently,
| rBOe(I) = re[CCSD(T)_AE/aug-cc-pwCV5Z]. | (3) |
| rBOe(II) = re[CCSD(T)_AE/cc-pwCV5Z]. | (4) |
| r BOe(I)a | r BOe(II)a | r BOe(III)a | r BOe(IV)a | r BOe(V)a |
r
SEe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
||||
|---|---|---|---|---|---|---|---|---|---|
| a For definitions, see eqn (3)–(6). b For the definition of the predicates, see text. The best structure is given in the last column. c F atom is in synperiplanar or antiperiplanar position with respect to the OH bond. d Condition number of the fit. | |||||||||
| BFsync | 1.3231 | 1.3226 | 1.3229 | 1.3229 | 1.3230 | 1.3248(12) | 1.3238(3) | 1.3238(1) | 1.3239(2) |
| BFantic | 1.3131 | 1.3127 | 1.3130 | 1.3130 | 1.3131 | 1.3128(11) | 1.3138(3) | 1.3138(1) | 1.3139(2) |
| BO | 1.3449 | 1.3446 | 1.3449 | 1.3449 | 1.3453 | 1.3428(2) | 1.3428(4) | 1.3428(2) | 1.3426(3) |
| OH | 0.9575 | 0.9573 | 0.9573 | 0.9573 | 0.9576 | 0.9583(4) | 0.9574(11) | 0.9585(4) | 0.9581(6) |
| ∠(OBFsyn) | 122.24 | 122.24 | 122.24 | 122.24 | 122.28 | 122.23(9) | 122.30(2) | 122.31(1) | 122.31(2) |
| ∠(BOH) | 113.14 | 113.12 | 113.11 | 113.11 | 112.98 | 113.12(4) | 113.14(7) | 113.06(3) | 113.09(4) |
| ∠(OBFanti) | 119.39 | 119.39 | 119.39 | 119.39 | 119.34 | 119.54(9) | 119.46(2) | 119.46(1) | 119.47(2) |
| ∠(FBF) | 118.37 | 118.37 | 118.37 | 118.37 | 118.38 | 118.23(2) | 118.23(3) | 118.23(2) | 118.22(3) |
| κd | 3480 | 478 | 424 | 402 | |||||
| predicates | |||||||||
| OH | 0.9585(20) | 0.9585(20) | 0.9585(20) | ||||||
| BFsyn–BFanti | 0.010(1) | 0.010(1) | 0.010(1) | ||||||
| ∠(BOH) | 113.14(20) | 113.14(20) | 113.14(20) | ||||||
The rBOe structure was also estimated in the frozen core, FC, approximation using the cc-pV5Z and aug-cc-pV5Z basis sets and the CCSD(T) method. The core–core and core–valence correlation is missing from this treatment. Therefore, the correlation corrections were estimated as differences between the values from AE and FC results at the CCSD(T) level using the cc-pwCVTZ, cc-pwCVQZ and cc-pwCV5Z basis sets, as well as at the MP2 level with cc-pwCVQZ and MT basis sets (see Table S4 of the ESI†). Consequently, the rBOe structures could be estimated by the following alternative schemes:
| rBOe(III) = re[CCSD(T)_FC/aug-cc-pV5Z] + re[CCSD(T)_AE/cc-pwCV5Z] − re[CCSD(T)_FC/cc-pwCV5Z] | (5) |
| rBOe(IV) = re[CCSD(T)_FC/cc-pV5Z] + re[CCSD(T)_AE/aug-cc-pwCV5Z] − re[CCSD(T)_FC/cc-pwCV5Z]. | (6) |
A further, cheaper scheme was also utilized. The structure was computed with the smaller cc-pwCVTZ basis set and the CCSD(T)_AE method, and the effect of further basis set enlargement, cc-pwCVTZ → cc-pwCVQZ, was estimated at the MP2 level. In other words, the rBOe parameters are obtained using the following equation:
| rBOe(V) = re[CCSD(T)_AE/cc-pwCVTZ] + re[MP2(AE)/cc-pwCVQZ] − re[MP2(AE)/cc-pwCVTZ]. | (7) |
In conclusion, when the basis set used is large enough, there is no need to use the augmented functions, and the MT basis set seems to be accurate enough to estimate the core correlation. In other words, an accurate structure may be obtained.
6. Semiexperimental structure
6.1. Anharmonic force field
The anharmonic force field has been previously calculated at the CCSD(T)_AE/TZ2Pf level of theory.4 The theoretical fundamental wavenumbers of the different isotopologues were found to be in good agreement with their experimental counterparts. Furthermore, the ab initio quartic centrifugal distortion constants are also in good agreement with the experimental ones. This agreement is an indication that the ab initio force field is likely to be accurate. Generally, it is more difficult to compute an accurate ab initio harmonic force field than a cubic one.39 We have tried to improve the ab initio harmonic force field by fitting at the best equilibrium structure, rBOe(I), the experimental quartic centrifugal distortion constants and the harmonic frequencies derived from the experimental fundamental frequencies and the anharmonicity corrections ωi−νi. No significant improvement was found. This fact confirms that the ab initio harmonic force field is probably indeed accurate.6.2. Rovibrational corrections‡
There is little difficulty obtaining accurate ground state rotational constants. Therefore, the accuracy of the derived SE structure depends on the accuracy of the rovibrational corrections. They were calculated at the CCSD(T)_AE/TZ2Pf level of theory.4 As a first check, they were also calculated with the Kohn−Sham density functional theory (DFT)40 using the B2PLYPD double hybrid exchange–correlation functional with long range dispersion correction,41 along with the 6-311+G(3df,2pd) basis set. The results of this lower-level calculation give a first indication that the rovibrational correction is indeed reliable. Indeed, for the unperturbed state 51, the values at the B2PLYPD/6-311+G(3df,2pd) level of theory are (in MHz) αA5 = 20.9, αB5 = 19.8 and αC5 = 10.6. These values are close to the CCSD(T)_AE/TZ2Pf ones; see Table 7.| Mode | Interactiona | α A i | α B i | α C i | |||
|---|---|---|---|---|---|---|---|
| Exp.b | Cal.c | Exp.b | Cal.c | Exp.b | Cal.c | ||
| a See text and Table 1. b This work and ref. 8 and 9. c CCSD(T)_AE/TZ2Pf value. d See text and Table 4. e Note that there is a good agreement for αA6 + αB6. f See text and Tables 3 and 4. | |||||||
| 1 | No | 15.6 | 3.9 | 28.0 | 12.8 | 3.4 | 4.1 |
| 2 | No | 44.5 | 46.3 | 32.8 | 33.1 | −15.5 | −20.6 |
| ζ 23 | 44.2 | 46.3 | 33.8 | 33.1 | 41.9 | 23.0 | |
| 3 | No | — | 36.1 | 9.8 | 44.2 | 62.3 | 67.3 |
| ζ 23 | — | 36.1 | 9.1 | 44.2 | 5.0 | 23.7 | |
| 4 | No | 38.1 | −8.6 | −37.4 | −8.3 | 3.8 | 3.7 |
| 37.3 | — | −38.4 | — | 4.9 | — | ||
| 5 | No | 19.7 | 19.4 | 19.1 | 19.3 | 10.2 | 10.0 |
| 6 | Noe | −10.0 | −15.1 | −9.2 | −6.9 | −49.7 | −50.0 |
| ζ 67 | −9.8 | −15.1 | −9.1 | −6.9 | 22.7 | 3.9 | |
| 7 | No | 6.2 | 4.8 | −12.8 | −18.8 | 56.1 | 55.8 |
| ζ 67 | 6.0 | 4.8 | −12.9 | −18.8 | −16.3 | 1.9 | |
| 8 | No | 1.0 | −0.1 | −3.2 | −4.0 | −7.3 | −7.5 |
| 9 | No | 2.0 | 13.3 | 8.6 | 3.7 | −0.9 | −0.8 |
| 29.8 | — | 10.5 | — | −0.9 | — | ||
| α A 9 | α B 9 | α C 9 | |
|---|---|---|---|
| a The statistical uncertainty is only a few kHz. b Coriolis interactions with 61 and 71. c Coriolis interactions with 61, 71 and 81. | |||
| From the CCSD(T)_AE/TZ2Pf force field | 13.292 | 3.681 | −0.808 |
| From 91 without interaction | 1.997 | 8.649 | −0.932 |
| From 81 + 91 and 81 | 4.857 | 10.033 | −0.314 |
| From 91 with interactionsb | 29.885 | 10.446 | −0.926 |
| From 91 with interactionsc | 29.805 | 10.527 | −0.924 |
As a further check, it is tempting to compare the experimental α-constants to the ones computed from the ab initio cubic force field. However, even when the rotational constants of all fundamental states have been determined, which is often an extremely difficult task, the experimental α-constants are different from the ab initio ones. The main cause is that a vibrational state is rarely isolated and, therefore, the derived rotational constants depend on the interactions that have been taken into account; see Section 4. There are numerous interactions between the fundamental states of 11BF2OH. As shown in Table 1, there is no isolated state. However, although the harmonic frequencies ω5 and 2ω7 are almost degenerate, the Fermi interaction ν5/2ν7 seems to be negligible due to the almost vanishing cubic constant φ577 = −0.8 cm−1. As a consequence, there is a very good agreement between the experimental and computed α's for the 51 state. There is a very strong c-type interaction between the states 61 and 71. However, it is still possible to determine the rotational constants from the low-J transitions neglecting this interaction. The corresponding experimental αC-constants are in good agreement with the computed ones; the same holds for the states 31, 41, 51, 81 and 91 for which there is no significant interaction affecting the C rotational constant (see Table 7). On the other hand, when the Coriolis interaction is taken into account, the agreement is much worse. The state 91, which is in weak Coriolis interaction with the states 61 and 71, allows us to see the effect of the interactions on the α-constants. They may be determined from the state 91 neglecting the interactions or taking them into account. It is also possible to obtain them from the states 81 + 91 and 81. The results are given in Table 8 and confirm that the α-constants may vary considerably.
Another way to check the accuracy of the rovibrational corrections is to compare the experimental ground state rotational constants with those derived from the best ab initio structure, rBOe(I), and the ab initio rovibrational corrections. A still simpler and more powerful test is to look at the equilibrium inertial defects calculated from the semiexperimental equilibrium rotational constants. Ideally, they should be zero because the molecule is planar but, in most cases, they slightly differ from zero because of a systematic error in the rovibrational corrections. The results are shown in Table 9. It is obvious that there is a problem with the A and B rotational constants of the deuterated species because their residual, which is expected to be mainly systematic, is significantly different from that of the other isotopologues. Likewise, the semiexperimental inertial defect of the deuterated species has a sign opposite to that of the other species. Such a problem was expected and easy to explain.12 The errors of the semiexperimental constants A and B of the deuterated species are of similar magnitude but of opposite sign, whereas their sum is almost the same for all species. It is due to a large rotation of the principal axis system (PAS) upon isotopic substitution that amplifies the errors of the rovibrational corrections, a typical difficulty of oblate tops. Fig. 3 clearly shows that there is an axis switching when going from BF2OH to BF2OD. It is also important to notice that the equilibrium inertial defect is much worse when any computed α-constants are replaced by their experimental values.
| 11BF2OH | 10BF2OH | 11BF2OD | 10BF2OD | 11BF218OH | 10BF218OH | |
|---|---|---|---|---|---|---|
| a Semiexperimental equilibrium rotational constants. b Difference between the semiexperimental value and the value calculated from the rBOe(I) structure from Table 6. c Semiexperimental equilibrium inertial defect. d Residuals of the fit, last column of Table 6. | ||||||
A
SEe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370.30 370.30 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370.53 370.53 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334.05 334.05 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334.11 334.11 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241.76 241.76 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241.75 241.75 |
B
SEe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136.86 136.86 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136.96 136.96 |
9446.32 | 9446.31 | 9543.99 | 9544.00 |
C
SEe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
5126.15 | 5126.26 | 4935.06 | 4935.07 | 4940.37 | 4940.37 |
| ΔAb | 4.04 | 4.05 | 2.03 | 1.99 | 3.23 | 3.21 |
| ΔBb | 3.14 | 3.18 | 5.15 | 5.14 | 3.97 | 3.97 |
| ΔCb | 1.82 | 1.85 | 1.80 | 1.79 | 1.90 | 1.90 |
| ΔA + ΔB | 7.18 | 7.23 | 7.18 | 7.13 | 7.19 | 7.19 |
| Δec | −0.0006 | −0.0009 | 0.0014 | 0.0014 | −0.0017 | −0.0018 |
| δAd | −0.003 | −0.015 | −1.762 | −1.808 | −0.010 | −0.025 |
| δBd | −0.028 | 0.009 | 1.757 | 1.745 | −0.026 | −0.016 |
| δCd | 0.022 | 0.048 | 0.010 | −0.005 | 0.072 | 0.078 |
6.3. Determination of the structure
There is no isotopic substitution available for fluorine. The boron atom is close to the center of mass, a(11B) = 0.019 Å and b(11B) = −0.034 Å; thus, the substitution 11B → 10B does not bring any new information. Furthermore, we have seen in the previous section that the A and B rotational constants of the deuterated species are affected by a rather large systematic error. Therefore, the available rotational constants do not allow us to determine a complete structure. To overcome this difficulty, the method of mixed regression may be used.42–44 This method, also called the predicate method, uses simultaneously equilibrium moments of inertia and bond lengths and bond angles from high-level quantum chemical calculations in the structure fitting. However, it is useful for large molecules only if reliable predicates may be estimated without using the expensive CCSD(T) method. Actually, it is known that the OH bond length can be estimated at the MP2 level using either the cc-pVTZ or the cc-pVQZ basis sets with an uncertainty less than 0.002 Å.45 On the other hand, the prediction of an accurate CF bond length is difficult. Nevertheless, it is easy to obtain an accurate value of the difference r(CFsyn) − r(CFanti) at the MP2/cc-pVQZ level; see Table S1 of the ESI.† Finally, the bond angles may be estimated at the MP2/6-311+G(3df,2pd) level of theory with an uncertainty of about 0.2°.46 Different combinations of predicates were tried. A fit with three predicate values, [r(OH), r(BFsyn) − r(BFanti) and ∠(BOH)], gives extremely good results; see Table 8. However, it is also possible to obtain a very satisfactory fit with only two predicate values as shown in Table 6. Yet, it has to be noted that, when r(BFsyn) − r(BFanti) is not used as a predicate, the fit is ill-conditioned with a large condition number, high correlation between the parameters and larger standard errors for the parameters. This result is simply due to the fact that there is not enough information to accurately determine the position of the fluorine atoms. On the other hand, the information given by the two predicates r(OH) and ∠(BOH) is somewhat redundant.Obviously, the predicates play a leading role in increasing the accuracy of the parameters, but it is possible to check their influence by reducing their weight. In the particular case of BF2OH, it does not significantly modify the parameters, but it increases their standard deviation as well as the condition number. Actually, the best guaranty of the compatibility of the predicates with the semiexperimental moments of inertia is an analysis of the residuals. The best semiexperimental structure is given in the last column of Table 6.
7. Conclusions
The ab initio calculation of the anharmonic force field and the analysis of the high-resolution infrared spectrum shows that almost all fundamental states are perturbed, even the lowest one. The only exception is the 51 state which does not appear to be perturbed although it is in Fermi resonance with the extremely close 72 state. This lack of mixing is due to the fact that the cubic force constant φ577 is vanishingly small. When the perturbation is small and can thus be neglected, there is a satisfactory agreement between the experimental rotation–vibration interaction constants and the values calculated from the force field. On the other hand, when the perturbations are taken into account in the analysis of the experimental spectra, the agreement becomes disappointing. This difficulty is rather frequent, HCOOH being another well studied example.20 In particular, for planar molecules, the equilibrium inertial defect, Δe, is closer to zero when calculated from the semiexperimental constants. For instance, in the case of HNO3,22Δe = 0.0002 uÅ2 with the semiexperimental rotational constants and Δe = 0.0069 uÅ2 when the available experimental α's replace the ab initio ones. It might be tempting to think that, in the presence of interactions, the system of normal equations becomes ill-conditioned and, therefore, the derived parameters are not accurate. However, fixing the non-diagonal interaction parameters to the ab initio values does not significantly improve the situation. Another possible explanation is that the levels may be affected by anharmonic resonances, even if they are far away as was shown by Saito in the particular case of SO2.47 However, the provisional conclusion is that there is no obvious explanation.Another interesting result of this study is that the large amplitude motion of the OH group does not hinder an accurate determination of the semiexperimental structure. In the particular case of BF2OH, there are two problems: there is not enough experimental data because there is no isotopic substitution available for the fluorine atoms and the boron atom is extremely close to the center of mass; therefore, its substitution does not bring any useful information. Furthermore, BF2OH is an oblate top with the moment of inertia Ic much larger than the other two moments of inertia, Ia and Ib. Molecules of this shape experience a large rotation of the principal axis system upon certain isotopic substitutions. For such isotopologues it is difficult to obtain a good structural fit to the semiexperimental moments of inertia, Ia and Ib. To achieve an accurate structure, the mixed estimation method is used. In this method, internal coordinates of good quality quantum chemical calculations (with appropriate uncertainties) are fitted simultaneously with the semiexperimental moments of inertia of all isotopologues.
A very accurate ab initio structure can be obtained either by direct optimization at the convergence limit, CCSD(T)_AE/cc-pwCVQZ, or by the less expensive additive method based on the CCSD(T)_AE/cc-pwCVTZ structure improved by small corrections to the convergence limit calculated at the MP2 level. In any case, the core–core and core–valence correlation effects have to be taken into account in the accurate structure calculations because they are very large (≈0.003 Å for BF and BO bond lengths).
Appendix: Hamiltonian
The v-diagonal block is a standard Watson Hamiltonian in A-reduction and representation Ir. However, for BF2OH, the ν4 mode (OH in plane bending) and the ν9 mode (OH-torsion relative to the BF2 moiety) are large amplitude motions.9 As a consequence, for each of the {41,7191,6171,92,6191} interacting states the v-diagonal blocks also include an XZv, non-orthorhombic operator| XZv = hvxz{Ĵx,Ĵz} + ⋯ | (A1) |
{Â,![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) } = Â } = Â![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) + + ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) Â Â | (A2) |
 | (A3) |
A-type Coriolis:
 | (A4) |
 | (A5) |
| Ĵ± = Ĵx ∓ iĴy | (A6) |
 | (A7) |
 | (A8) |
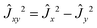 | (A9) |
Acknowledgements
We thank Prof H. Bürger (Wuppertal) for his essential help at the beginning of this investigation. We also thank Dr J. Breidung (Mülheim) for providing us the details of the force field of 11BF2OD and the reviewers for their careful reading of the manuscript. This work was supported by the Dr B. Mez-Starck Foundation (Germany).Notes and references
- R. F. Porter, D. R. Bidinosti and K. F. Watterson, J. Chem. Phys., 1962, 36, 2104–2108 CrossRef CAS.
- H. Takeo and R. F. Curl, J. Chem. Phys., 1972, 56, 4314–4317 CrossRef CAS.
- K. Vormann and H. Dreizler, Z. Naturforsch., 1989, 44a, 1191–1195 Search PubMed.
- J. Breidung, J. Demaison, J. F. D'Eu, L. Margulès, D. Collet, E. B. Mkadmi, A. Perrin and W. Thiel, J. Mol. Spectrosc., 2004, 228, 7–22 CrossRef CAS.
- L. H. Coudert, P. Garcia-Fernandez, H. Mäder, J. Demaison and J. E. Boggs, J. Phys. Chem. A, 2008, 112, 1536–1544 CrossRef CAS PubMed.
- M. E. Jacox, K. K. Irikura and W. E. Thompson, J. Chem. Phys., 2000, 113, 5705–5715 CrossRef CAS.
- D. Collet, A. Perrin, H. Bürger and J.-M. Flaud, J. Mol. Spectrosc., 2002, 212, 118–124 CrossRef CAS.
- A. Perrin, M. Cavajal-Zaera, Z. Dutkiewicz, J.-M. Flaud, D. Collet, H. Bürger, J. Demaison, F. Willaert, H. Mäder and N. W. Larsen, Mol. Phys., 2004, 102, 1641–1652 CrossRef CAS.
- A. Perrin, E. Bertseva, J.-M. Flaud, D. Collet, H. Bürger, T. Masiello and T. A. Blake, Mol. Phys., 2007, 105, 1833–1848 CrossRef CAS.
- A. Perrin, J. Demaison and H. Bürger, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 1226–1232 CrossRef CAS.
- F. J. Melendez, C. Muñoz-Caro, A. Niño, J. Sandoval-Lira and A. Rangel-Huerta, Int. J. Quantum Chem., 2011, 111, 4389–4399 CrossRef CAS.
- J. Demaison, A. G. Császár, L. Margulès and H. D. Rudolph, J. Phys. Chem. A, 2011, 115, 14078–14091 CrossRef CAS PubMed.
- J. Demaison and H. D. Rudolph, J. Mol. Spectrosc., 2008, 248, 66–76 CrossRef CAS.
- J. Demaison, L. Margulès, I. Kleiner and A. G. Császár, J. Mol. Spectrosc., 2010, 259, 70–79 CrossRef CAS.
- J. Demaison, A. G. Császár, I. Kleiner and H. Møllendal, J. Phys. Chem. A, 2007, 111, 2574–2586 CrossRef CAS PubMed.
- J. Demaison, L. Margulès and H. D. Rudolph, J. Mol. Struct., 2010, 978, 229–233 CrossRef CAS.
- N. Vogt, J. Demaison, J. Vogt and H. D. Rudolph, J. Comput. Chem., 2014, 35, 2333–2342 CrossRef CAS PubMed.
- J. Demaison, A. G. Császár and A. Dehayem-Kamadjeu, J. Phys. Chem. A, 2006, 110, 13609–13617 CrossRef CAS PubMed.
- V. Sironneau, J. Orphal, J. Demaison and P. Chelin, J. Phys. Chem. A, 2008, 112, 10697–10702 CrossRef CAS PubMed.
- J. Demaison, M. Herman and J. Liévin, J. Chem. Phys., 2007, 126, 164305 CrossRef CAS PubMed.
- W. D. Allen, E. Czinki and A. G. Császár, Chem. – Eur. J., 2004, 10, 4512–4517 CrossRef CAS PubMed.
- C. Gutle, J. Demaison and H. D. Rudolph, J. Mol. Spectrosc., 2009, 254, 99–107 CrossRef CAS.
- J. Demaison, J. E. Boggs and H. D. Rudolph, J. Mol. Struct., 2004, 695–696, 145–153 CrossRef CAS.
- J. Demaison, J. Mol. Spectrosc., 2006, 239, 201–207 CrossRef CAS.
- L. S. Rothman, I. E. Gordon, Y. Babikov, A. Barbe, D. C. Benner, P. F. Bernath, M. Birk, L. Bizzocchi, V. Boudon, L. R. Brown, A. Campargue, K. Chance, E. A. Cohen, L. Coudert, V. M. Devi, B. J. Drouin, A. Fayt, J. M. Flaud, R. R. Gamache, J. Harrison, J. M. Hartmann, C. Hill, J. T. Hodges, D. Jacquemart, A. Jolly, J. Lamouroux, R. J. LeRoy, G. Li, D. A. Long, C. J. Mackie, S. T. Massie, S. Mikhailenko, H. S. P. Müller, O. V. Naumenko, A. V. Nikitin, J. Orphal, V. Perevalov, A. Perrin, E. R. Polovtseva, C. Richard, M. A. H. Smith, E. Starikova, K. Sung, S. Tashkun, J. Tennyson, G. C. Toon, V. G. Tyuterev and G. Wagner, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 4–50 CrossRef CAS.
- T. Masiello, A. Maki and T. A. Blake, J. Mol. Spectrosc., 2005, 234, 122–136 CrossRef CAS.
- J. K. G. Watson, in Vibrational spectra and structure, ed. J. R. Durig, Elsevier, Amsterdam, 1977, vol. 6, pp. 1-89 Search PubMed.
- G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- J. M. L. Martin and P. R. Taylor, Chem. Phys. Lett., 1994, 225, 473–479 CrossRef CAS.
- R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- N. Vogt, L. S. Khaikin, O. E. Grikina and A. N. Rykov, J. Mol. Struct., 2013, 1050, 114–121 CrossRef CAS.
- N. Vogt, J. Demaison, D. N. Ksenafontov and H. D. Rudolph, J. Mol. Struct., 2014, 1076, 483–489 CrossRef CAS.
- N. Vogt, I. I. Marochkin, A. N. Rykov and O. V. Dorofeeva, J. Phys. Chem. A, 2013, 117, 11374–11381 CrossRef CAS PubMed.
- N. Vogt, I. I. Marochkin and A. N. Rykov, J. Phys. Chem. A, 2015, 119, 152–159 CrossRef CAS PubMed.
- W. D. Allen and A. G. Császár, J. Chem. Phys., 1993, 98, 2983–3015 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, 1133–1138 CrossRef.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- L. S. Bartell, D. J. Romanesko and T. C. Wong, in Chemical Society Specialist Periodical Report N20: Molecular Structure by Diffraction Methods, ed. G. A. Sims and L. E. Sutton, The Chemical Society, London, 1975, vol. 3, pp. 72–79 Search PubMed.
- J. Demaison, in Equilibrium Molecular Structures; ed. J. Demaison, J. E. Boggs and A. G. Császár, CRC Press, Boca Raton, 2011, pp. 29–52 Search PubMed.
- D. A. Belsley, Conditioning Diagnostics, Wiley, New York, 1991 Search PubMed.
- J. Demaison, M. Herman and J. Liévin, Int. Rev. Phys. Chem., 2007, 26, 391–420 Search PubMed.
- L. Margulès, J. Demaison and J. E. Boggs, THEOCHEM, 2000, 500, 245–258 CrossRef.
- S. Saito, J. Mol. Spectrosc., 1969, 30, 1–16 CrossRef CAS.
- A. Perrin, J. Orphal, J.-M. Flaud, S. Klee, G. Mellau, H. Mäder, D. Walbrodt and M. Winnewisser, J. Mol. Spectrosc., 2004, 228, 375–391 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Tables S1–S4. See DOI: 10.1039/c5cp05444c |
| ‡ In the present study, the CCSD(T) calculations were performed with the MOLPRO program package developed by H.-J. Werner, P. J. Knowles, F. R. Manby, M. Schütz, P. Celani, G. Knizia, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, MOLPRO, 2009. See also: H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253. The MP2 and B2PLYPD calculations were carried out by means of the GAUSSIAN09 program: M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN09, Rev.C.01, 2010, Wallingford, CT. |
| This journal is © the Owner Societies 2015 |