The addition of CO₂ to four superbase ionic liquids: a DFT study

Abstract

The addition of carbon dioxide to four superbase ionic liquids, [P₃₃₃₃][Benzim], [P₃₃₃₃][124Triz], [P₃₃₃₃][123Triz] and [P₃₃₃₃][Bentriz] was studied using a molecular DFT approach involving anions alone and individual ion pairs. Intermolecular bonding within the individual ion pairs is characterised by a number of weak hydrogen bonds, with the superbase anion geometrically arranged so as to maximize interactions between the heterocyclic N atoms and the cation. The pairing energies show no correlation to the observed CO₂ adsorption capacity. Addition of CO₂ to the anion alone clearly resulted in the formation of a covalently-bound carbamate function with the strength of binding correlated to experimental capacity. In the ion pair however the cation significantly alters the nature of the bonding such that the overall cohesive energy is reduced. Formation of a strong carbamate function occurs at the expense of weakening the interaction between anion and cation. In the more weakly absorbing ion pairs which contain [123Triz]⁻ and [Bentriz]⁻, the carbamate-functionalised systems are very close in energy to adducts in which CO₂ is more weakly bound, suggesting an equilibrium between the chemi- and physisorbed CO₂.

---

A. Introduction

The limitation of anthropogenic CO₂ emissions is an issue of global importance. In particular there have been significant advances in the utilization of CO₂ as a chemical reagent to synthesize products with high added value. To be attractive, these processes depend on the economic sustainability of CO₂ capture. Thus an important field of research focuses on the capture of CO₂ from different sources of gas originating, for instance, from a power plant, an incinerator or a digester. Possibilities exist for CO₂ capture: e.g. amine based sorbents^1–3 and microporous oxide and metal–organic frameworks.^2,4 However, these methods have drawbacks in terms of sustainability and selectivity. Since the observation of CO₂ solubility in 1-butyl-3-methylimidazolium hexafluorophosphate [C₄mIm][PF₆] by Brennecke and co-workers,⁵ many ionic liquids (ILs) have been shown to have promising CO₂ absorption and release capacities via physisorption. Subsequently in 2002 Davis and co-workers first proposed ILs with amino functional groups as selective adsorbents of CO₂via chemisorption.⁶ They were able to reach a 1 : 2 molar absorption capacity (1 mole of CO₂ for 2 moles of IL) at ambient conditions. Since then, there has been growing interest in functionalized ionic liquids, which offer chemisorption of CO₂. However, although ILs that absorb CO₂ chemically have much higher capacities compared to those that physically absorb CO₂, recovery of the CO₂ and regeneration of the IL will require more energy. Thus, ILs with which CO₂ forms a weak chemical bond should ideally be targeted for capture applications. In a situation where CO₂ is activated and converted in situ (perhaps in the presence of an additional catalyst), chemisorption would be desirable and the cost of recovering CO₂ not relevant.

1 : 1 molar absorption of CO₂ at atmospheric pressure by an IL containing an aprotic heterocyclic anion (AHA) was first reported in 2010 by Wang et al.⁷ The following year, Wang et al. explored some AHAs based on N-heterocyclic organic compounds, with one or more nitrogen atoms in a five-membered ring, to produce what have been termed superbase ionic liquids (SBILs) due to their high pK_a values. A wide range of absorption capacities was reported, up to a molar capacity of 1 : 1,⁸ with a link found between the pK_a of the corresponding superbase and the absorption capacity. Calculated estimates of the absorption enthalpies were made using density functional theory (DFT), showing a link between the absorption capacity and the value of the enthalpy. In a perspective paper in 2012, the effect of different substitutions (–CH₃, –F, –CF₃, OCH₃, etc.) on four AHAs on their CO₂ capture capacity was calculated.⁹ A wide range of absorption enthalpies between CO₂ and these AHAs from −10 kJ mol⁻¹ up to −100 kJ mol⁻¹ was demonstrated. In this work the enthalpy was calculated according to Scheme 1. The cation was neglected as it is often assumed that the cation does not make a major contribution to the CO₂ absorption.^10,11 In 2014, this tuning of SBILs was the subject of further experimental studies in which their high industrial potential was confirmed.¹² Indeed the absorption of CO₂ by AHAs is fast and exothermic at atmospheric pressure and room temperature. The wide range of CO₂ absorption capacities possible in these systems make them tuneable. It was also shown that viscosity is low and is not significantly affected by absorption, in contrast to other task-specific ionic liquids such as the amino-acid based ionic liquids.^6,13

Scheme 1 Representation of the adduct, x⁻_Ny*, and carbamate product, x⁻_Ny, from CO₂ addition on a nitrogen Ny of an N-heteroaromatic anion (AHA), x⁻.

In the same year, Taylor et al. determined the absorption capacities for four superbase ionic liquids (SBILs) (Table 1).¹⁴ Absorption capacity was determined under both dry and wet conditions. Molar absorption capacities from 30% to 120% were observed using a gravimetric saturation technique for four SBILs in which the cation trihexyl-tetradecylphosphonium ([P_666,14]⁺) was paired with the anions benzotriazolide ([Bentriz]⁻), benzimidazolide ([Benzim]⁻), 1,2,3-triazolide ([123Triz]⁻), and 1,2,4-triazolide ([124Triz]⁻) (Scheme 2). ¹³C-NMR spectroscopy confirmed that the addition of CO₂ to the SBILs resulted in the formation of carbamates. The current paper serves to augment this previous work by adding a theoretical dimension. The interaction between CO₂ and the AHAs is described from an electronic point of view within the approximation of DFT. In previous studies^8,9,12 DFT was used to evaluate the absorption enthalpy but no description of the bonding situation was given. Some of the AHAs have inequivalent nitrogen atoms but this was not always taken into account. For example, for the anion [124Triz]⁻, CO₂ addition is presented on nitrogen N₄ in one paper⁸ and on nitrogen N₁ in another.¹² In addition, in these previous studies, the effect of the cation was neglected when evaluating the CO₂ addition enthalpy. However, recent work has demonstrated the influence of the cation on the electronic properties of the ionic pair,^15,16 highlighting the importance of H-bonding in the pairing¹⁷ and the direct effect of the cation on CO₂ absorption properties.¹⁸

Table 1 Experimental CO₂ uptake (mole ratio nCO₂ : nIL) for the four ionic liquids at 22 °C and atmospheric pressure from ref. 14

Ionic pair	[P666,14][Benzim]	[P666,14][124Triz]	[P666,14][123Triz]	[P666,14][Bentriz]
CO2 capacity	1.20	1.01	0.69	0.39

---

Scheme 2 The four anions considered in this work with their respective atomic numeration.

The first section of this paper describes the methods and tools employed in this work along with results and discussion of the charge and electron density analyses for the four SBILs. In the second part, addition of CO₂ to the four anions will be presented both with and without inclusion of an explicit cation; enthalpies of addition, geometrical and electronic properties of the anion–CO₂ bonding will be compared for both models and among the four anions. The different results are compared with observed absorption capacities.

B. Simulation details – methodology

Density functional theory calculations were carried out using the Minnesota density functional M06.¹⁹ This hybrid meta-exchange correlation functional is versatile and included in its construction is a non-local interaction term that makes it well-suited to the treatment of ionic and hydrogen bonding.²⁰ Its predecessor M05 has been tested successfully for ILs.²¹ A Pople basis²² set 6-311+G(d,p) was used for all atoms. All cations, anions and ionic pairs were optimised using the software Gaussian 09²³ without symmetry constraints and, for each geometry, the nature of minima were checked with a frequency calculation. Energies were corrected for the zero-point energy and relative enthalpies were calculated at 298.15 K. Various tools were used to analyse the electronic density. Natural bond analysis (NBO) was carried out with NBO 3.1²⁴ as implemented in Gaussian 09. Atoms in molecules²⁵ (AIM) analysis was done with multiwfn.²⁶

There are multiple possibilities to arrange the cation and the anion to form each ionic pair. Two methods of building ionic pairs were followed in order to obtain local minima near to the global minimum on the potential energy surface. In the first, a molecular dynamics trajectory of five ns was generated at high temperature in the NVT ensemble using the AMBER software with the GAFF force field.²⁷ A large cell with one ionic pair was used. From the resulting trajectory, ten to twenty steps were extracted. These structures were optimized at DFT level with a small basis set, and the five most stable structure were then optimized at the M06/6-311+G(d,p) level. In parallel, the tetraalkylphosphonium cation and the anion were positioned in different configurations by human chemical intuition and optimized. For each ion pair, multiple minima were found which were very close in energy to the most favourable structure. This can be attributed to the configurational flexibility of the cation's alkyl chains. In the following analysis of the ionic pairing, only the most favourable structures are described. The geometries were created and monitored with Molden²⁸ and VMD²⁹ and the pictures were prepared with CYLview³⁰ and VMD.

C. Results and discussion

C.1. The ionic pair

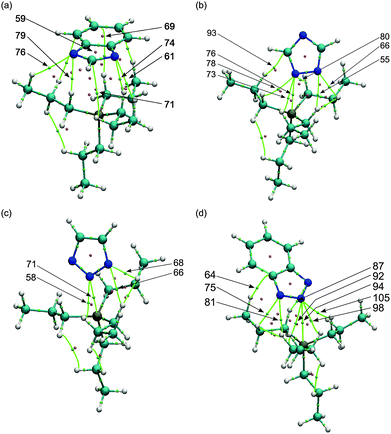
In order to avoid unnecessarily resource-intensive calculations and to decrease any error attributed to the alkyl chain configuration, we chose to use the tetrapropylphosphonium cation [P₃₃₃₃]⁺ as a model for the experimental cation trihexyl-tetradecylphosphonium [P_666,14]⁺. We note here that the balance of forces would be expected to differ slightly between the two cations, with the cohesive energy of the ionic liquid being influenced more strongly by van der Waals interactions in the case of [P_666,14]⁺. In contrast, electrostatic forces would be more dominant for [P₃₃₃₃]⁺. The four most stable ionic pairs are shown in Fig. 1. For all the ionic pairs, distances between anion nitrogen and hydrogen atoms of the cation are shown where they are less than, or close to, 2.75 Å, taken as the sum of the respective van der Waals radii.³¹ These invariably include the shortest cation–anion distance, given as r_SN in Table 2. For the ionic pairs [P₃₃₃₃][Benzim] (Fig. 1a), [P₃₃₃₃][123Triz] (Fig. 1c) and [P₃₃₃₃][Bentriz] (Fig. 1d), the anion is positioned in order to minimize the distance for both nitrogen atoms. All the nitrogen atoms exhibit short N–H_C1 distances, with H_C1 defined as a hydrogen bonded to a carbon adjacent to the phosphorus in the cation. For [P₃₃₃₃][124Triz] (Fig. 1b), the anion position allows nitrogen atoms N₁ and N₂ to be close to the cation whereas the nitrogen N₄ faces away from the phosphorus. The cations of a and d share an indenyl-type structure with a phenyl ring fused with a 5-membered ring. Despite this similarity only a seems to show a phenyl–H_C1 interaction, with a distance of 2.24 Å between H_C1 and the centre of the C₆ ring.

Fig. 1 Ionic pairs comprising a tetrapropylphosphonium cation, [P₃₃₃₃]⁺, with the four anions: (a) [P₃₃₃₃][Benzim], (b) [P₃₃₃₃][124Triz], (c) [P₃₃₃₃][123Triz] and (d) [P₃₃₃₃][Bentriz]. Dashed lines indicate intermolecular N–H distances less than or close to the sum of the vdW radii (2.75 Å) Colour code: blue – nitrogen; yellow – phosphorus; grey – carbon; white – hydrogen.

Table 2 Selected properties of the ionic pair. ΔE_IP pairing energy of the ionic pair as the energy difference between the monomer express in kJ mol⁻¹. δ_AHA is the sum of the NAO charges of the AHA anion moiety. CT = 1 − |δ| corresponds to the charge transfer from the anion to the cation. r_SN is the shortest distance between the closest nitrogen and the phosphorus

	Ionic pair	ΔEIP/kJ mol^−1	δ AHA	CT	r SN/Å
a	[P3333][Benzim]	−363.25	−0.94	0.06	2.19
b	[P3333][124Triz]	−374.50	−0.92	0.08	2.16
c	[P3333][123Triz]	−396.59	−0.88	0.12	2.26
d	[P3333][Bentriz]	−371.74	−0.93	0.07	2.25

---

The binding energy of the ionic pair ΔE_IP is defined as the difference between the ionic pair energy and the sum of energies of the separate ions (optimised individually), ΔE_IP = E_IP − (E_anion + E_cation). These are given in Table 2. All the pairing energies are weaker than 400 kJ mol⁻¹; our four cation/anion ion-pair binding energies are thus low compared to typical ionic liquids. The ascending order of pairing strength is [P₃₃₃₃][Benzim] (a) < [P₃₃₃₃][Bentriz] (d) < [P₃₃₃₃][124Triz] (b)< [P₃₃₃₃][123Triz] (c). This order does not correlate with the CO₂ absorption capacity (Table 1). To obtain an electronic description of the interaction properties, an NBO analysis was carried on the different ionic pairs as well as on the anions treated alone. Natural atomic charge analysis indicates a small charge transfer (CT) from the cation to the anion of between 0.06 and 0.12 units (Table 2) when comparing the atomic charges in the ionic pairs with those in the separate moieties (the full NAO charges are shown in Table S1 in ESI†). These are typical values for CT in ionic pairs as calculated accurately using a QM/MM approach for a variety of ILs in the liquid phase.³²

The influence of the cation may be seen in the adjustment of the anion natural charges in the ionic pair, compared to the monomer. Although on average the hydrogen charges become slightly more positive, there is a noticeable rearrangement of the atomic charges for each anion. For b, c, d, at least one nitrogen becomes more negative as a result of interaction with the cation (|Δδ| > 0.08). These correspond to those interacting most closely with the cation and can be identified as one of the equivalent nitrogen atoms for b and c, and the central nitrogen of d. This behaviour is not observed for a. The sum of the donor–acceptor interaction from second order perturbation analysis never exceeds 100 kJ mol⁻¹ and this interaction is shared among multiple contributions. NBO analysis draws the interaction as a sum of numerous weak interactions, of which the most important can be identified as a nitrogen lone pair LP(N) of the anion pointing towards an empty σ bond orbital σ_BD* (C–H) or σ_BD* (P–C). The corresponding interaction energy E_LP→σ* never exceeds 41 kJ mol⁻¹ (Table S2, ESI†). Indeed, the short distance between the nitrogen and the cationic hydrogen as well as the various LP(N) → σ_BD* (C–H) interactions, notably with hydrogen H_C1, are a good indication of multiple H-bonding interaction between the ions. The H-bond can be described as a bifurcated/chelated H-bond. According to the 2015 review of Hunt et al.¹⁷ on H-bonds in ionic liquids, the E_LP→σ* NBO parameters indicate that H-bonding between AHAs and the tetraalkylphosphonium cation is very weak.

To gain more insight into these interactions, the electronic density was analysed within Bader's theory of atoms in molecules (AIM). Properties of the intermolecular bond critical points (BCP) between the anion and the cation and ring critical points on the anion (RCP) are compiled in Table 3 and illustrated in Fig. 2. It is important to keep in mind that the critical point is dependent on the geometry and thus the results are specific to the interaction at this geometry. For all anions, multiple bond critical points are found between nitrogen of the anion and hydrogen atoms of the cation. Most of these BCPs are sited towards the hydrogen H_C1. At the BCPs, the density ρ(r) is low and the Laplacian ∇²ρ(r) is positive as expected for non-covalent interactions in closed-shell systems. According to Hunt et al.,¹⁷ where density ρ(r) < 0.02 a.u. at the BCP, intermolecular interactions between cation and anion can be described as weak H-bonds. In the ion pairs discussed here we can therefore characterise the interionic bonding in terms of an array of such weak hydrogen bonds. From the topology analysis of the density, the H-bond energy E_HB can be estimated as half of the potential energy density V(r)³³: E_HB = V(r)/2. Thus since E_HB is less than 16 kJ mol⁻¹ for all anion–cation H-bonds, we can confirm the weak strength of the H-bonding.

Table 3 Intermolecular critical points properties from atoms in molecules (AIM) analysis: electron density ρ(r), Laplacian of the electron density ∇²ρ(r) ellipticity ε and E_HB at ring and bond critical points. The critical points are numbered (Nb) as in Fig. 2

	Critical point	Nb	ρ(r)/a.u.	∇^2ρ(r)/a.u.	ε	V(r)/a.u.	E HB/kJ mol^−1
a	rcp – 5m	59	0.06110	0.39703	−1.32167	−0.09437
	rcp – 6m	69	0.02203	0.15674	−1.20857	−0.02508
	bcp N⋯HC1	79	0.01855	0.05806	0.03552	−0.01019	−13.38
	bcp N⋯HC1	74	0.01791	0.05757	0.13547	−0.00993	−13.03
	bcp N⋯HC3	76	0.00686	0.01830	0.25957	−0.00352	−4.62
	bcp N⋯HC3	61	0.00633	0.01713	0.25461	−0.00330	−4.33
	bcp C⋯HC2	71	0.00488	0.01472	0.81609	−0.00243	−3.19
b	rcp	61	0.06485	0.46430	−1.30564	−0.10595
	bcp N⋯HC1	55	0.01948	0.06892	0.08606	−0.01214	−15.94
	bcp N⋯HC2	66	0.00999	0.02811	0.16357	−0.00538	−7.07
	bcp N⋯HC1	78	0.01633	0.05679	2.16664	−0.01033	−13.56
	bcp N⋯HC1	80	0.01535	0.05373	1.54821	−0.00987	−12.96
	bcp N⋯HC2	63	0.01003	0.03073	0.86129	−0.00588	−7.72
	bcp N⋯P	76	0.02063	0.04807	0.16130	−0.01246
	bcp C1⋯HC1	93	0.00441	0.01404	3.40938	−0.00226	−2.97
c	rcp	54	0.06052	0.47120	−1.27012	−0.10086
	bcp N⋯HC2	58	0.01156	0.03759	1.19595	−0.00705	−9.26
	bcp N⋯P	71	0.02996	0.06078	0.14459	−0.01874
	bcp N⋯HC1	66	0.01410	0.05188	0.53841	−0.00874	−11.47
	bcp N⋯HC2	68	0.01086	0.03156	0.11228	−0.00583	−7.65
d	rcp – 5m	75	0.05877	0.45732	−1.28475	−0.09718
	rcp – 6m	62	0.02219	0.15867	−1.21916	−0.02524
	bcp N⋯HC1	87	0.01406	0.04792	1.57250	−0.00840	−11.02
	bcp N⋯HC1	105	0.01681	0.06099	0.25600	−0.01073	−14.09
	bcp N⋯HC2	98	0.00958	0.02897	0.69152	−0.00550	−7.21
	bcp N⋯P	94	0.01543	0.04098	0.36560	−0.00957	−12.56
	bcp N⋯C1	92	0.01406	0.05317	8.14350	−0.00956	−12.55
	bcp N⋯HC1	81	0.01634	0.05665	0.23375	−0.00969	−12.72
	bcp N⋯HC2	73	0.00968	0.02718	0.11019	−0.00526	−6.90
	bcp C4⋯HC1	64	0.00428	0.01186	1.72898	−0.00209	−2.74

---

Fig. 2 AIM analysis of the ionic pairs x. Atoms are coloured N = blue, C = cyan, P = brown, H = white. Small dots are critical point with bcp (−3,+1) = green, rcp (+3,+1) = pink. Green lines are the paths connecting atoms to bcp. Numbers are the cp labels.

C.2. Interaction with CO₂

The addition of CO₂ was explored according to Scheme 1. Addition to the individual anion monomers was first characterised, taking into account all non-equivalent nitrogen atoms. Subsequently CO₂ was added to ion pairs of each of the anions with tetrapropylphosphonium [P₃₃₃₃]⁺. For each anion, the carbamate formation enthalpy ΔH_r was calculated as well as the corresponding adduct formation enthalpy ΔH_a. We define an adduct as the combination of the anion and CO₂ in such a way that no bond is created but CO₂ loses its linearity and the distance between anion nitrogen and CO₂ carbon is less than 3 Å. These occur as separate minima on the potential energy surface. ΔH_r and ΔH_a are defined as the enthalpy difference between the carbamate or adduct respectively and the separate CO₂ and superbase (either as monomer or taking the whole ionic pair, depending on the model).

C.3. Anion + CO₂

Addition of CO₂ was simulated at all non-equivalent nitrogen atoms for the four anions. The enthalpy of carbamate formation is exothermic for both nitrogen and all anions (Table 4). It varies from ΔH_r = −13.54 kJ mol⁻¹ for the weakest to −55.99 kJ mol⁻¹ for the strongest. Adducts were also obtained for all anions except for [124Triz]⁻ (b). The enthalpy values obtained from this work for the anion alone are close to those previously published^8,12 and show a correlation between measured absorption capacity¹⁴ and enthalpy of carbamate variation (Fig. 3). The more negative the reaction enthalpy, the better the absorption capacity is. For the anion [124Triz]⁻, as in the work of Seo et al.,¹² we found a small difference between addition on N₁ and N₄ (|ΔΔH_r| < 4 kJ mol⁻¹) making the two configurations effectively isoenergetic. Also in agreement with the same authors, CO₂ was found to be more favourably coordinated at N₁ of [123Triz]⁻.

Table 4 Selected properties for (a) the carbamate formation for the anion alone x_Ny and (b) the respective adduct formation x_Ny* with a⁻ = [Benzim]⁻, b⁻ = [124Triz]⁻, c⁻ = [123Triz]⁻ and d⁻ = [Bentriz]⁻. Enthalpy ΔH in kJ mol⁻¹. Length of the carbamate bond d(N_x–C) in Å. CO₂ bending α(OCO) and torsion of the dihedral around the carbamate |θ| in °. nl = not located on the PES

(a)
	ΔHr	d(Nx–C)	α(OCO)	|θ|
a^−N1	−55.99	1.55	136.1	179.8
b^−N1	−55.24	1.59	137.9	179.9
b^−N4	−54.29	1.57	137.1	180.0
c^−N1	−47.60	1.61	138.6	179.9
c^−N2	−38.44	1.67	140.5	179.7
d^−N1	−30.80	1.62	138.8	179.9
d^−N2	−13.54	1.82	146.3	179.5

---

(b)
	ΔHa	d(Nx–C)	α(OCO)
a^−N1*	−30.81	2.39	165.4
b^−N1*	nl
b^−N4*	nl
c^−N1*	nl
d^−N1*	−26.03	2.47	168.1
d^−N2*	−23.71	2.52	169.1

---

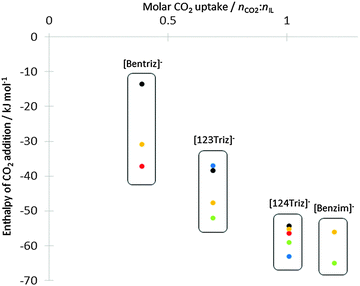Fig. 3 Comparison of CO₂ addition enthalpies (kJ mol⁻¹) for the four anions from the anion-only model, plotted against experimental CO₂ uptake from ref. 14. Key to data points: red circles from ref. 8 for b⁻_N4 and d⁻_N4, green from ref. 12 for x⁻_N1, blue from ref. 12 for b⁻_N4 and c⁻_N2, yellow and black from this work for x⁻_N1 and x⁻_N2 respectively.

The bonding strength can be correlated to the carbamate bond length between the relevant nitrogen N_x of the SB and the carbon C* of the coordinated CO₂ moiety, d(N_x–C*), and the angle of the CO₂α(OCO) as illustrated in Fig. 4. From the natural atomic charge analysis, coordination of the CO₂ leads to the transfer of half the negative charge from the AHA moieties to the COO functions (Table 5). The stronger the carbamate bond, the more negative charge is transferred. The adduct formation enthalpies are less favourable than for carbamate formation, although for [Bentriz]⁻ the difference is less than 5 kJ mol⁻¹ suggesting a possible equilibrium between the two products. For the four anions, a scan of the d(N_x–C*) distance was conducted to identify the presence of any energetic barrier to CO₂ coordination (see Fig. S1 in ESI†). A barrier was found only for [Bentriz]⁻, in that case having a height of 4.5 kJ mol⁻¹. In these systems, we therefore consider CO₂ coordination to be an effectively barrierless process at ambient temperatures.

Fig. 4 Carbamate bond length (red/left axis) and angle of the coordinated CO₂ (blue/right axis) plotted as functions of the anion-only carbamate formation enthalpy.

Table 5 Selected properties of the carbamate anion. Charges δ from NAO analysis of the carbamate with δ′_AHA and δ′_CO2 the NAO charges split between the superbase and the CO₂ moieties respectively

	Anion	δ′AHA	δ′CO2
a^−N1	[Benzim]^−	−0.46	−0.54
b^−N1	[124Triz]^−	−0.46	−0.54
c^−N1	[123Triz]^−	−0.51	−0.49
d^−N1	[Bentriz]^−	−0.53	−0.47

---

C.4. Ionic pair + CO₂

The carbamate product and CO₂ adducts were also optimized including a [P₃₃₃₃]⁺ cation explicitly (Fig. 5–7). Calculated enthalpies and geometric parameters for the carbamates and CO₂ adducts are reported in Table 6. The enthalpies ΔH are expressed taking the optimised ionic pair as reference (i.e. not including the pairing energy). For the four IPs, the carbamate formation enthalpy is weaker in all cases compared to the anion alone, and is even endothermic for c_N2 and d_N2. The ionic pair model also loses the trend between capacity and enthalpy of addition. For [P₃₃₃₃][Benzim], a, carbamate and adduct formation are 20 kJ mol⁻¹ less favourable. For [P₃₃₃₃][124Triz] b, the equivalence between N₁ and N₄ is lost as the carbamate formed on nitrogen N1, b_N1, is 24 kJ mol⁻¹ more stable than b_N4. Moreover b_N4 is also less stable than the two adducts b_N1* and b_N4*: the adduct b_N1* is only 10 kJ mol⁻¹ above b_N1. For [P₃₃₃₃][123Triz], c, the carbamate pair c_N1 and the CO₂ adduct c_N1* are isoenergetic with a formation enthalpy around ΔH = −13 kJ mol⁻¹ and carbamate formation on N2 is slightly exothermic. Finally, for [P₃₃₃₃][Bentriz] d, the most favourable product is the adduct on nitrogen N₂d_N2* with ΔH_a(d_N2*) = −15.66 kJ mol⁻¹. However, the formation enthalpies of the carbamate on N1 d_N1 and of the CO₂ adduct d_N1* are still exothermic and within 5 kJ mol⁻¹ of the d_N2* adduct. The inclusion of the cation makes the formation of N₂–carbamate d_N2 clearly endothermic ΔH_r(d_N2) = +14.47 kJ mol⁻¹.

Fig. 5 Carbamate ionic pairs resulting from N₁ CO₂ addition on the four ionic pairs: (a) [P₃₃₃₃][Benzim], (b) [P₃₃₃₃][124Triz], (c) [P₃₃₃₃][123Triz] and (d) [P₃₃₃₃][Bentriz]. Dashed lines indicate intermolecular N⋯H or O⋯H distances less than or close to the sum of the vdW radii (2.75 Å) colour code: blue – nitrogen; yellow – phosphorus; grey – carbon; white – hydrogen, red – oxygen.

Fig. 6 Carbamate ionic pairs for the alternative N–CO₂ addition comprising tetrapropyl-phosphonium and three anions: (b) [P₃₃₃₃][124Triz], (c) [P₃₃₃₃][123Triz] and (d) [P₃₃₃₃][Bentriz]. Dashed lines indicate intermolecular N⋯H or O⋯H distances less than or close to the sum of the vdW radii (2.75 Å) colour code: blue – nitrogen; yellow – phosphorus; grey – carbon; white – hydrogen, red – oxygen.

Fig. 7 CO₂ – ionic pair adducts comprising tetrapropylphosphonium and the four anions: (a) [P₃₃₃₃][Benzim], (b) [P₃₃₃₃][124Triz], (c) [P₃₃₃₃][123Triz] and (d) [P₃₃₃₃][Bentriz]. Dashed lines indicate intermolecular N⋯H or O⋯H distances less than or close to the sum of the vdW radii (2.75 Å) colour code: blue – nitrogen; yellow – phosphorus; grey – carbon; white – hydrogen, red – oxygen.

Table 6 Selected properties for (a) carbamate formation on the ionic pair for each nitrogen Ny of each anion x (x_Ny) and (b) the respective adduct formation x_Ny* with a = [P₃₃₃₃][Benzim], b = [P₃₃₃₃][124Triz], c = [P₃₃₃₃][123Triz] and d = [P₃₃₃₃][Bentriz]: enthalpies ΔH, length of the carbamate bond d(N_x–C), carbamate bond angle α(OCO), and torsion of the dihedral around the carbamate |θ|(CNCO). nl = adduct not located on the PES

(a)
	ΔHr/kJ mol^−1	d(Nx–C)/Å	α(OCO)/°	|θ|(CNCO)/°
aN1	−35.82	1.49	131.5	3.7
bN1	−32.62	1.51	133.6	8.4
bN4	−9.06	1.49	131.9	6.4
cN1	−13.50	1.57	137.0	3.5
cN2	+1.91	1.52	132.9	7.8
dN1	−13.03	1.55	136.0	4.0
dN2	+14.47	1.62	138.0	17.2

---

(b)
	ΔHa/kJ mol^−1	d(Nx–C)/Å	α(OCO)/°
aN1*	−8.29	2.61	172.2
bN1*	−21.92	2.79	175.3
bN4*	−17.93	2.77	175.1
cN1*	−12.46	2.70	174.2
cN2*	nl
dN1*	−10.63	2.74	174.5
dN2*	−15.66	2.79	176.0

---

To get an energetic explanation of this important modification caused by the cation, the ionic pairing energy, ΔE_IPCO2, was calculated for the ionic pair-carbamate products (Table 7). This energy is defined with respect to the corresponding optimised anion – only carbamate product and optimised cation. For each separate anion, the most favourable carbamate is the one with the strongest resulting ionic pair. Elsewhere the difference between the carbamate formation enthalpy on the four anions in the ionic pair model (x_Ny) and in the anion-only model (x⁻_Ny) is substantially similar to the energy difference between the ionic pairing energy after and before carbamate formation:

ΔH_r(x_Ny) − ΔH_r(x⁻_Ny) = ∼(ΔE_IPCO2 − ΔE_IP)

Table 7 Selected properties of the most stable ionic pair-carbamates: charges δ from NAO analysis of the carbamate with δ′_AHA and δ′_CO2 the NAO charges split between the superbase and the CO₂ moieties respectively. r_SN and r_SO are respectively the shortest distances between N(anion) and H(cation) and between O(carbamate) and H(cation)

	ΔEIPCO2/kJ mol^−1	δ′AHA	δ′CO2	CT	r SN/Å	r SO/Å
aN1	−344.18	−0.35	−0.59	0.06	2.62	2.25
bN1	−351.68	−0.38	−0.55	0.08	2.29	2.18
bN4	−328.37	−0.37	−0.55	0.07
cN1	−363.09	−0.45	−0.50	0.05	2.43	2.15
cN2	−356.22	−0.38	−0.55	0.07
dN1	−354.17	−0.43	−0.52	0.05	2.44	2.14
dN2	−340.58	−0.50	−0.46	0.04

---

It can thus be seen that the formation of carbamate has a destabilizing effect on the ion pair, resulting in a close relationship between the carbamate formation enthalpy and the ionic pair strength. In the ionic pair model, the carbamate formation enthalpy does not correlate as well with the CO₂ capacity as in the anion model. However, it is still consistent with the experimentally observed molar absorption capacities.¹⁴ Indeed for [P₃₃₃₃][Benzim] and [P₃₃₃₃][124Triz], N₁-carbamate formation is strongly preferred suggesting a total conversion of CO₂ to the carbamate. For [P₃₃₃₃][Bentriz] and [P₃₃₃₃][123Triz], carbamate formation is as favourable as the CO₂ adduct formation and they are both relatively weakly bound. This is consistent with an equilibrium between coordinated and non-coordinated CO₂. The explicit inclusion of the cation in the calculation results in a change in the geometry of the carbamate part. The superbase moiety shifts away somewhat from its optimal position in the ion pair, while the carbamate functions interact with the cation centre (Fig. 5 and 6). For example, on [P₃₃₃₃][Benzim], addition of CO₂ on N1 increases the distance r_SN from 2.19 Å to 2.62 Å whereas the shortest interionic oxygen–H(C1) distance, r_SO, is 2.25 Å (Table 7). As a general feature, the N–H distances become longer and multiple O–H interactions are formed. In the adducts, the anion is less affected by the presence of CO₂ (Fig. 7). The CO₂ tends to be oriented with one oxygen pointing toward the cation and the carbon C* close to a nitrogen (d(N–C*) < 2.79 Å).

As already mentioned, the bonding strength of the carbamate can be characterised by its geometric properties. In the ionic pair model, the length of the carbamate N_x–C* bond is shorter than for the anion alone (e.g. for b, δd = −0.08 Å) and the bond angle of the CO₂ moiety is lower (e.g. for b, δα = −5°) (Table 6). This means that, despite considerably more positive enthalpies ΔH_r in the ionic pair, the CO₂ forms a stronger carbamate bond. However, as pointed out in Section C.3, explicit inclusion of the cation increases the negative charge of one nitrogen atom in the ionic pair for b, c and d. This nitrogen corresponds to the most favourable CO₂ coordination position. NBO analysis was carried for the carbamate ionic pair and selected electronic properties are summarized in Table 7 (detailed NAO charges are given in ESI,† Table S1). Overall charge transfer between anion and cation is similar or slightly lower for the carbamate ionic pairs compared to the ion pairs by themselves. However, the partition of the charge on anions between the original AHA moiety and CO₂ reveals that half a negative charge is carried by the CO₂ function, similar to the anion-only clusters, whereas the charge transfer to cation derives exclusively from the AHA moieties. A comparison of the NAO charges for the carbamate in the ionic pair and the anionic monomer shows a very similar distribution of charges, where the negative charge is concentrated around the nitrogen and the carbamate function. This demonstrates that the charge transfer is mainly borne by the nitrogen. The presence of the cation thus increases the nucleophilicity of the nitrogen resulting in a stronger carbamate, though at the expense of weaker ion paring strength. Finally, AIM analysis was carried out on the carbamate ionic pairs. Similar to the topology of the ionic pair before addition of CO₂, we can identify a certain number of weak intermolecular H-bonds between the cation and the anion defined by BCPs with low values of ρ(r) and ∇²ρ(r) (see Tables S3–S5 and Fig. S2–S4 in ESI†). However, the addition of CO₂ results in the decrease of the number of N–H BCPs and creation of new O⋯H BCPs, especially with H_C1. At the carbamate function, the strong ρ(r) density and the negative value of its Laplacian ∇²ρ(r) at the BCP between the nitrogen and the carbamate carbon (bcp N–C*) suggest the presence of a strong covalent bond (Table 8). Moreover, the NC* bond is the strongest for [P₃₃₃₃][Benzim] followed by [P₃₃₃₃][124Triz]. Values for [P₃₃₃₃][123Triz] and [P₃₃₃₃][Bentriz] are the lowest and equivalent. This order corresponds to the CO₂ absorption capacity and confirms the previous experimental observations.¹⁴

Table 8 Critical points of the carbamate function from atoms in molecules (AIM) analysis for each ionic pair and each nitrogen: electron density ρ(r), Laplacian of the electron density ∇²ρ(r) and ellipticity ε

	Critical point	Nb	ρ(r)/a.u.	∇^2ρ(r)/a.u.	ε
aN1	bcp N–C*	66	0.24250	−0.54516	0.05187
	bcp C*–O1	62	0.39645	−0.42425	0.09079
	bcp C*–O2	67	0.38965	−0.44054	0.08572
bN1	bcp N–C*	84	0.22812	−0.46434	0.04150
	bcp C*–O1	80	0.39336	−0.40364	0.07997
	bcp C*–O2	69	0.40336	−0.38277	0.09625
bN4	bcp N–C*	60	0.24230	−0.55045	0.03796
	bcp C*–O1	61	0.38819	−0.45014	0.08248
	bcp C*–O2	64	0.39980	−0.40875	0.09485
cN1	bcp N–C*	114	0.20019	−0.30684	0.02202
	bcp C*–O1	115	0.39381	−0.39553	0.07888
	bcp C*–O2	120	0.41542	−0.29504	0.09992
cN2	bcp N–C*	74	0.22660	−0.45844	0.05555
	bcp C*–O1	72	0.39161	−0.41122	0.07624
	bcp C*–O2	82	0.40494	−0.35987	0.08956
dN1	bcp N–C*	122	0.20835	−0.34983	0.03255
	bcp C*–O1	121	0.39181	−0.40796	0.07879
	bcp C*–O2	127	0.41317	−0.31567	0.10354
dN2	bcp N–C*	126	0.18127	−0.21042	0.04014
	bcp C*–O1	120	0.40630	−0.33081	0.08463
	bcp C*–O2	130	0.41243	−0.30150	0.08766

---

D. Conclusions

CO₂ addition to four superbase tetraalkylphosphonium ionic liquids was studied using a molecular DFT approach. This has enabled us to explore in detail the nature of bonding in these complexes, and in particular to describe the carbamate function which results from the chemical bonding of CO₂ to these aprotic heterocyclic anions. The influence of the cation was found to be significant in determining the overall strength of binding.

The electronic properties of the ionic pairs were described both before and after the addition of CO₂. No direct relation between the pairing energy and the observed absorption capacity was evident and, in terms of the chemisorption energy, the models of CO₂ addition on the ion pairs do not reproduce the experimental trend as well as when the anion alone is considered. However, from the geometric and AIM topology analyses, it is possible to estimate the relative strength of the carbamate function. Thus it is evident that a more strongly bound carbamate, characterised by shorter N–C* bond and more acute O–C–O angle correlates with a higher CO₂ capture capacity. However, the global enthalpy of reaction is less favourable, which is due to a weakening of the ion pairing energy as a result of CO₂ addition. From this result [P₃₃₃₃][Benzim] is predicted to be the best absorbent followed by [P₃₃₃₃][124Triz]. For both these IPs a strong enthalpy of reaction is in agreement with the 1 : 1 experimental molar capacity. [P₃₃₃₃][123Triz] and [P₃₃₃₃][Bentriz] possess the same weak enthalpy of reaction in agreement with a sub-maximal absorption capacity. For [P₃₃₃₃][Bentriz], the adduct formation is even slightly more favourable as the CO₂ chemisorption competes strongly with ion pair binding. Overall it is clear that the experimental order of increasing CO₂ capacity [P_666,14][Bentriz] < [P_666,14][123Triz] < [P_666,14][124Triz] < [P_666,14][Benzim] may be directly related to the enthalpy of formation of the most favoured carbamate product in each case. This is in turn correlated to the strength of the carbamate bond itself, characterised by the degree to which the nitrogen is able to donate charge into the CO₂ unit. The anions with three neighbouring aromatic nitrogen atoms are seen to show less basicity towards CO₂ than the other anions.

Finally, the influence of the cation was highlighted. The most notable effect is the reaction site on the anion [124Triz]⁻. In the ionic pair, the cation causes an increase in negative charge on one nitrogen, thus enhancing the reactivity on N₁ whereas for the anion-only model the enthalpy of reaction is virtually identical on both nitrogen atoms. Also, as noted above, including the cation in our calculation results in an overall destabilization of the carbamate (though the carbamate function itself is not necessarily more weakly bound) due to a reduction of the ionic pairing energy. Further investigation is needed to establish if the cation effect is moderated by including more ionic pairs in the calculation and/or simulating the equilibrium dynamics of the system. Considering alternative cations, such as those based on ammonium, will enable the influence of the cation to be probed more deeply.

Acknowledgements

This work was carried out as part of the “4CU” programme grant, aimed at sustainable conversion of carbon dioxide into fuels, led by the University of Sheffield and carried out in collaboration with the University of Manchester; Queen's University Belfast; and University College London. The authors therefore gratefully acknowledge the Engineering and Physical Sciences Research Council (EPSRC) for supporting this work financially (Grant No. EP/K001329/1). The authors acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL), and associated support services, in the completion of this work.

References

1. C. Gouedard, D. Picq, F. Launay and P. L. Carrette, Int. J. Greenhouse Gas Control, 2012, 10, 244–270.
2. C. H. Yu, C. H. Huang and C. S. Tan, Aerosol Air Qual. Res., 2012, 12, 745–769.
3. E. F. da Silva and H. F. Svendsen, Ind. Eng. Chem. Res., 2004, 43, 3413–3418.
4. K. Sumida, D. L. Rogow, J. a. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T. H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781.
5. L. A. Blanchard, D. Hancu, E. J. Beckman and J. F. Brennecke, Nature, 1999, 399, 28–29.
6. E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis, J. Am. Chem. Soc., 2002, 124, 926–927.
7. C. Wang, H. Luo, D. Jiang, H. Li and S. Dai, Angew. Chem., 2010, 122, 6114–6117.
8. C. Wang, X. Luo, H. Luo, D. Jiang, H. Li and S. Dai, Angew. Chem., Int. Ed. Engl., 2011, 50, 4918–4922.
9. C. Wu, T. P. Senftle and W. F. Schneider, Phys. Chem. Chem. Phys., 2012, 14, 13163–13170.
10. E. J. Maginn, Acc. Chem. Res., 2007, 40, 1200–1207.
11. C. Cadena, J. L. Anthony, J. K. Shah, T. I. Morrow, J. F. Brennecke and E. J. Maginn, J. Am. Chem. Soc., 2004, 126, 5300–5308.
12. S. Seo, M. Quiroz-Guzman, M. A. DeSilva, T. B. Lee, Y. Huang, B. F. Goodrich, W. F. Schneider and J. F. Brennecke, J. Phys. Chem. B, 2014, 118, 5740–5751.
13. J. Zhang, S. Zhang, K. Dong, Y. Zhang, Y. Shen and X. Lv, Chem. – Eur. J., 2006, 12, 4021–4026.
14. S. F. R. Taylor, C. McCrellis, C. McStay, J. Jacquemin, C. Hardacre, M. Mercy, R. G. Bell and N. H. de Leeuw, J. Solution Chem., 2015, 44, 511–527.
15. L. Zhang, H. Li, Y. Wang and X. Hu, J. Phys. Chem. B, 2007, 111, 11016–11020.
16. P. A. Hunt, B. Kirchner and T. Welton, Chem. – Eur. J., 2006, 12, 6762–6775.
17. P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288.
18. O. Hollóczki, Z. Kelemen, L. Könczöl, D. Szieberth, L. Nyulászi, A. Stark and B. Kirchner, ChemPhysChem, 2013, 14, 315–320.
19. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
20. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600.
21. E. I. Izgorodina, U. L. Bernard and D. R. MacFarlane, J. Phys. Chem. A, 2009, 113, 7064–7072.
22. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
24. A. E. Reed, J. E. Carpenter and F. Weinhold, NBO version 3.1, 1998.
25. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990.
26. T. Lu and F. Chen, J. Chem. Phys., 2012, 33, 280–592.
27. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
28. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
29. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
30. C. Y. Legault, CYLview v1, Université de Sherbrooke, Québec, Canada, 2009.
31. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
32. M. Klähn and A. Seduraman, J. Phys. Chem. B, 2015, 119, 10066–10078.
33. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05153c

---