Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A method to calculate redox potentials relative to the normal hydrogen electrode in nonaqueous solution by using density functional theory-based molecular dynamics
Ryota
Jono
*ab,
Yoshitaka
Tateyama
bcd and
Koichi
Yamashita
*ab
aDepartment of Chemical System Engineering, School of Engineering, The University of Tokyo 7-3-1, Hongo, Bunkyo-ku, Tokyo 113-8656, Japan. E-mail: jono.ryota@gmail.com; yamasita@chemsys.t.u-tokyo.ac.jp
bCREST, Japan Science and Technology Agency (JST), 4-1-8 Honcho, Kawaguchi, Saitama 333-0012, Japan
cInternational Center for Materials Nanoarchitectonics (WPI-MANA), National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan
dPRESTO, Japan Science and Technology Agency (JST), 4-1-8 Honcho, Kawaguchi, Saitama 333-0012, Japan
First published on 16th September 2015
Abstract
We demonstrate the redox potential calculation relative to the normal hydrogen electrode (NHE) in nonaqueous solution using a density functional theory-based molecular dynamics (DFT-MD) simulation. The calculation of the NHE in nonaqueous solution consists of two processes: the first step is the equilibrated simulation for a proton in nonaqueous solution to determine the space for inserting a proton in solution, and the second step is the thermodynamic integration method to calculate the solvation energy of the proton in the nonaqueous solution. In this work, we apply the method for a cation and an anion, i.e., copper(II)/copper(I) and iodine/iodide in acetonitrile solution, and show that the errors in the calculated redox potential from experiments are within 0.21 V.
1 Introduction
The electron-transfer reaction is one of the most elementary and important reactions in chemistry and has been widely used in the field of technology. The degree of electron transfer is usually discussed by using a half reaction, Ox + e− ⇌ Red, and its redox potential, E(Ox/Red), where Ox is the oxidant and Red is the reductant. Calculating the redox potential of chemicals is important to understand and predict the electrochemistry of the chemical reactions. A thermodynamic cycle is applicable for calculating the redox potentials without considering bulk solvent molecules explicitly. This cycle has been used with many methods to describe bulk solvent molecules, such as the conductor-like screening model (COSMO),1–3 solvation models (SMx),4,5 the self-consistent reaction field based on the Poisson–Boltzmann equation,6,7 and the polarized continuum model (PCM).8 It succeeded in reproducing the experimentally observed redox potentials even with the assumption of there being no large changes of the solvation structures during electron transfer. However, it is not adequate if knowledge of the solvent coordination is not available. For example, it had been believed that the coordination number of water around Cu2+ is six, but it is actually five,9 and will fluctuate at nonzero temperatures. These differences may cause an error in the calculation because the changes in coordination numbers during the electron-transfer reaction Cu2+ + e− ⇌ Cu+ cause deviations from Marcus theory.10The redox potential calculation using a density functional theory-based molecular dynamics (DFT-MD) simulation has been applied, and showed the changes of solvent coordination of the redox reaction in aqueous solution.10–15 This method is now applicable directly to compare experimentally observed redox potentials with the help of a reference electrode calculation.16–18 The normal hydrogen electrode (NHE) is a reference electrode and includes the solvation process of the proton. The solvation energy is calculated by the free energy difference between the bulk solution and the solution including a proton. A particle insertion method is not an efficient method because of the impact between a randomly inserted proton and solvent molecules. To avoid this impact, a dummy atom is introduced to make a space for inserting the proton. In the aqueous solution case, it is easy to imagine that the inserted proton forms a covalent bond and hydrogen bonds with solvent water molecules. However, the position of the space, i.e., the definition of a dummy atom, in general solutions is not obvious. Therefore, it is necessary to establish the calculation method for redox potentials in nonaqueous solution, especially aprotic solvents, to understand and predict efficient organic synthesis and devices related to electrochemistry. We demonstrate the method for the case of an anion and a cation immersed in acetonitrile (AN) solution.
The iodine/iodide redox couple is a famous mediator in textbooks for redox reactions in nonaqueous solution because its redox potential is considered to be independent of the solvent as a result of its large ionic radius and point symmetrical structure.19 It is used in dye-sensitized solar cells to reduce oxidized dyes.8,20 The coordination structure of the iodide ion in an AN solution is well studied in the field of charge transfer to solvents. The neutral halogen–solvent distances are reported to be identical to the anion–solvent distances in the vertical photodetachment process.21 On the other hand, it is reported that the aqueous solvation structure of copper is drastically changed in a redox reaction. The copper(I) ion in AN is also important because the π back-donation mechanism stabilizes the copper(I) ion in an AN solution, although the copper(I) ion in aqueous solution is not stable. This difference in solution stability was used in the electrowinning/electrorefining of copper metal with low electrical power.19,22
In this work, we treat the redox half reaction of the iodine/iodide redox couple (I0/−) and copper(II)/copper(I) redox couple (Cu2+/+) in an AN solution to show that the method using density functional theory-based molecular dynamics (DFT-MD) is applicable to calculate the redox potentials in nonaqueous solvent with the elucidation of these solvent coordinations. We describe the procedure to calculate the redox potential with a calculation of the NHE as a reference.
2 Method
2.1 Thermodynamic integration method
The redox potential E(Ox/Red) is defined as the difference in Gibbs free energies of formation between oxidized (ΔfGOx) and reduced (ΔfGRed) states. It is equivalent to the free energy difference between oxidized (GOx) and reduced (GRed) states because the standard conditions for the oxidized and reduced states are the same. Suppose the changes in volume during one electron-transfer half reaction are negligible.23 Then, the Gibbs free energy can be replaced by the Helmholtz free energy (A), which is described by the NVT ensemble. Then the redox potential E(Ox/Red) is expressed as follows: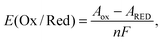 | (1) |
Aη = kBT ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zη, Zη, | (2) |
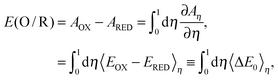 | (3) |
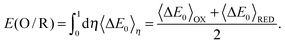 | (4) |
2.2 NHE as a reference
The redox potential is generally expressed as a value relative to some reference electrode, such as the NHE in aqueous solution. To compare the calculated redox potential with the experimentally reported value, here we extend the method described for the calculation of the NHE in aqueous solution16–18 to the NHE in a nonaqueous solution such as an AN solution. The NHE in an AN solution (NHEAN) is expressed by the summation of the dissociation energy of the H2 molecule in the gas phase (ΔAD,gas), ionization potential of hydrogen (IP), and solvation free energy of the proton ΔAsol,AN(H+) as follows:| NHFAN ≡ EAN(H+/½H2), |
| = ΔAD,gas(½H2 → H) + IP(H → H+ + e−) + ΔAsol,AN(H+). | (5) |
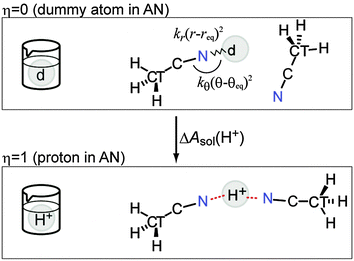
The dummy atom (d) is introduced for the cavity that gradually changes into a proton and does not interact with any other molecules.16 The position of the dummy atom should be constrained to avoid conflicting with neighboring AN molecules during proton insertion (Fig. 1). These constraints are introduced by an external potential of classical springs.
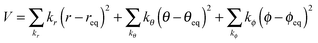 | (6) |
2.3 Computational details
All calculations were performed using the CP2K software package.26 A Nose–Hoover thermostat is used for generating the NVT ensembles. The temperature of the system is 300 K and the time step of the simulation is 0.5 fs. The dummy/proton atom, I0/−, or Cu2+/+ was immersed in 44 explicit AN molecules under periodic boundary conditions. The side length of the cubic unit cell is 15.74 Å and is determined to reproduce the experimentally observed density of AN solution (0.786 g cm−3) for the 45-molecule system. All quantum chemical calculations were performed with the PBE functional, DZVP-MOLOPT-GTH basis set, Goedecker–Teter–Hutter-type potential, and 280 Ry for the cutoff energy of the finest grid level using the Gaussian and plane wave mixed basis method (QUICKSTEP). The MD simulations were performed for 6 ps after 10 ps equilibration to determine the constraint parameters of the dummy atom and for 2.0 ps for each electronic state η used in the TI method. To compare the calculations with the experimentally reported redox potential, we used the experimentally reported 0.48 V for the conversion constant from the NHE in an AN solution (NHEAN) and that in aqueous solution (NHEaq).273 Results
3.1 NHE in the AN solution
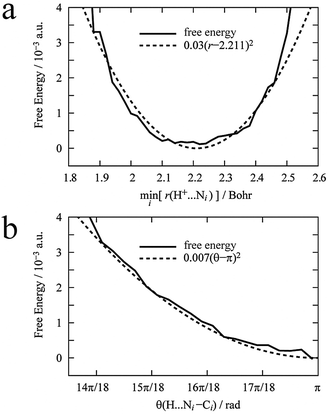
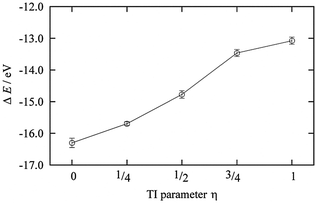
First, to define the constraints described in eqn (6) for the dummy atom, a DFT-MD simulation of the proton immersed in 44 AN molecules was performed for 6 ps. The proton was bonded to the nitrogen of an AN molecule by a hydrogen bond and moved back and forth between two AN molecules. Fig. 2 shows the free energy profiles along the distance between the proton and the nearest nitrogen of an AN molecule r(H+–N) and the angle formed by the proton and the AN molecule θ(H+–N–C). The free energy profiles were fitted by a quadratic polynomial, and their minima for distance req(H+–N) and angle θeq (H+–N–C) were 1.17 Å and π rad, with force constants kr and kθ, i.e., the curvature of the free energy profiles of 3.0 × 10−2 a.u. and 7 × 10−3 a.u., respectively. There are two constraints, which are sufficient because the solvation number of AN molecules for the proton is only two and the solvated structure is almost linear.The DFT-MD simulations for the TI method were performed under these constraints for the dummy atom for 2.0 ps for each η = 0, 1/4, 1/2, 3/4, and 1 (Fig. 3). The third term of eqn (5), i.e., the solvation free energy of a proton in AN, ΔAsol,AN(H+), was calculated to be −14.65 eV. The summation of the first and second terms of eqn (5) is half the energy of a hydrogen molecule with a minus sign. The energy of a hydrogen molecule with zero-point energy correction was −31.322 eV in the unit cell used in this work. Therefore, the NHEAN value was calculated to be 1.01 V.
3.2 Redox potential of the I0/− half reaction in the AN solution
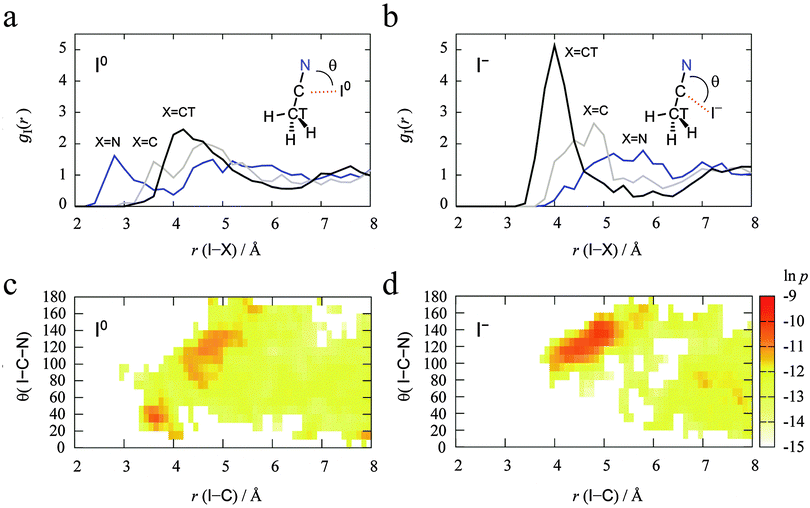
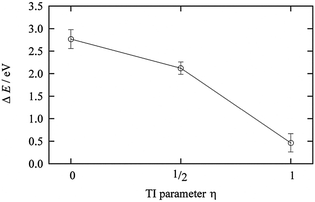
The MD simulations were performed for each I0/− in the 44 AN system. We first investigated the solvation structures of the redox couple I0/− in AN. The radial distribution functions (RDFs) from the DFT-MD trajectories of I0 and I− in AN are shown in Fig. 4(a) and (b). The peak heights of all the RDFs from both I0 and I−gI(r) for nitrogen (N), carbon (C), and terminal methyl carbon (CT) of AN were weak (see those for Cu2+/+ below). The CT side of AN molecules was directed to the I0 atom while the N side of AN molecules was directed to the I− ion. Fig. 4(c) and (d) show the distribution of the direction of AN molecules defined by the angle θ(I–C–N) along with the distance between I0/− and C of AN, r(I–C). These common coordinates for the distributions of both I0 and I− in AN systems reveal their differences. The I0 atom interacts with the nitrogen of an AN molecule if r(I–C) < 4 Å, while there are no AN molecules with r(I–C) < 4 Å for the I− anion. The distributions are almost the same in the range r(I–C) > 4 Å. The distribution of θ(I–C–N) is delocalized in the range from 90° to 150° at r(I–C) = 4–6 Å. In particular, the θ(I–C–N) of both I0 and I− fluctuated around 120° at r(I–C) = 4–4.5 Å because of a weak interaction between I0/− and a hydrogen of the AN molecules. The AN molecules in the r(I–C) > 7 Å region are seen to be bulk. The accumulated number of AN molecules in the range r(I–C) < 6.4 Å is 13.8 for I0 and 12.5 for I−. This is consistent with the results from experimental and classical molecular dynamics simulations.21The TI method was applied. The TI parameter η expresses the degree of electron transfer, and three points were selected as η = 0 (I0 in 44 AN), 1/2, and 1 (I− in 44 AN). The results of the TI are shown in Fig. 5 and the TI value is 1.87 V. The calculated redox potential of I0/− in AN is 0.86 V vs. NHEAN and is in good agreement with the experimental value of 0.75 V vs. NHEAN (1.23 V vs. NHEaq).20 The redox potential under a linear response regime was 0.60 vs. NHEAN and is different from the three-point TI value because of the solvation differences for r(I–C)<4 Å.
3.3 Redox potential of the Cu2+/+ half reaction in the AN solution
MD simulations were performed for each Cu2+/+ in the 44 AN system. The RDFs from the Cu atom (Fig. 6) show that AN molecules strongly solvate both Cu2+/+ ions. The coordination numbers of the AN molecule for Cu2+ and Cu+ are five (trigonal bipyramidal) and four (tetrahedral) in DFT-based MD simulations, while those for Cu2+ and Cu+ in the experimentally observed crystals are six (octahedral)28 and four (tetrahedral),29 respectively. The distances between Cu2+ and the nitrogen of AN molecules in the crystal are reported to be 1.999(2), 1.987(2), and 2.386(2) Å.28 The axial AN molecules of the tetragonal bipyramidal structure of Cu2+ are more weakly attached than the others because the d orbitals of Cu2+ in AN are split due to the Jahn–Teller effect. Therefore, one of the AN molecules solvated to Cu2+ in the crystal structure may be released in solution. This fivefold coordination is also observed in aqueous solution experimentally9 and theoretically.11 The fourfold AN-coordinated Cu+ ion is stable because the back-donation of the d10 electrons of Cu+ to the CN group enhances the σ bond character between copper and nitrogen . In fact, the CN distance of the AN molecules directly coordinated with the copper ion, r(CN), and the distance between nitrogen and the copper ion r(CuN) for Cu+ were longer and shorter, respectively, than those for Cu2+ in our DFT-MD simulation (Fig. 7).
. In fact, the CN distance of the AN molecules directly coordinated with the copper ion, r(CN), and the distance between nitrogen and the copper ion r(CuN) for Cu+ were longer and shorter, respectively, than those for Cu2+ in our DFT-MD simulation (Fig. 7).
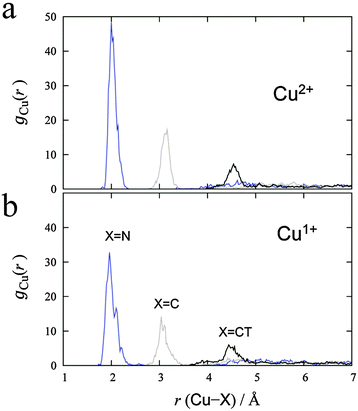 | ||
| Fig. 6 RDFs calculated from (a) Cu2+ and (b) Cu+ in 44 AN molecules. Blue, gray, and black lines denote the RDF for nitrogen, carbon, and carbon in the methyl group of AN, respectively. | ||
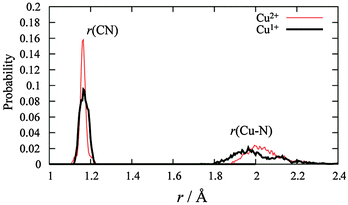 | ||
| Fig. 7 The distribution of the distance between carbon and nitrogen and that between the copper ion and nitrogen of directly connected AN molecules with a copper ion. | ||
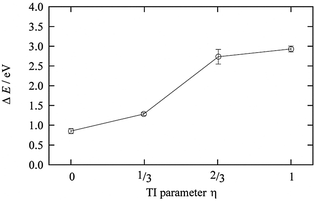
The TI method was performed for η = 0 (Cu2+ in AN solution), 1/3, 2/3, and 1 (Cu+ in AN solution). Fig. 8 shows the results of the TI method, and the 〈ΔE0〉η behavior along with η is clearly a nonlinear response profile. The coordination number of AN molecules changed from five to four in the range between 1/3 and 2/3, as reported in the case of Cu2+/+ in aqueous solution. This change in the coordination number of the AN molecule is smaller than that of aqueous solution but is enough to cause 〈ΔE0〉η to stray from the linear response regime. The TI value is 1.97 eV and the calculated redox potential of Cu2+/+ in AN relative to NHEAN is 0.96 V. This is in good agreement with the experimental 0.75 V vs. NHEAN,30 within 0.21 V.
4 Conclusions
The TI method achieves simulations of gradual particle generation in the environment system. The redox half reaction is the electron case for the particle in the TI method. We demonstrated the calculation of the redox reaction of an anion and a cation, i.e., I0/− and Cu2+/+ in a nonaqueous AN solution. The solvation structures of I0 and I− are almost the same except for the region r(I–N) < 4 Å. On the other hand, copper was strongly solvated by AN molecules. Back-donation of the d10 electrons of Cu+ to the CN group of the AN molecule was observed. The difference in solvent coordination in the oxidized and reduced states causes deviations from Marcus theory.Furthermore, the solvation free energy of the proton in AN solution was calculated using the TI method to obtain the NHE in an AN solution. It is composed of two processes: the first step is the equilibrium simulation for a proton in an AN solution to define the space for inserting the proton, and the second step is the TI method to calculate the solvation energy of the proton in an AN solution.
As a consequence of these, the redox potentials of I0/− and Cu2+/+ in an AN solution were obtained. It is an example of a redox potential calculation with respect to the NHE in nonaqueous solution using DFT-MD simulation. This method is an extended version of the previously reported method for the calculation in aqueous solution and is applicable for use in all solvents. From the view point of accuracy, it should be noted that there are problems related to the delocalization error in GGA functionals31,32 and/or the semi-core electron polarization.33 These problems may be solved by the improvement of DFT functionals or pseudopotential. Especially it is reported that the calculated redox potentials in aqueous solution is sensitive to the relative position from the VBM/CBM of the solvent. In the case of the copper ion in AN solution, the d orbital strongly interacts with the π orbitals of the AN and these problems may not be appeared. The development of the accurate method to describe the energy levels is needed for the further calculations of the redox potentials for the general case.
Acknowledgements
The authors thank Dr Jun Cheng and Professor Michiel Sprik of the University of Cambridge for valuable discussions. This work was partly supported by KAKENHI 20540384 and 23340089 as well as by the Strategic Programs for Innovative Research (SPIRE), MEXT, and the Computational Materials Science Initiative (CMSI), Japan. The calculations in this work were carried out at the supercomputer center in the NIMS, ISSP, at the University of Tokyo and IMS. This research also used the computational resources of the K computer and FX10 of the HPCI system provided by the RIKEN AICS and ITC at the University of Tokyo through the HPCI System Research Project (Project IDs: hp120078 and hp140075).Notes and references
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- M. Uudsemaa and T. Tamm, J. Phys. Chem. A, 2003, 107, 9997–10003 CrossRef CAS.
- M. Srnec, J. Chalupský, M. Fojta, L. Zendlová, L. Havran, M. Hocek, M. Kývala and L. Rulíšek, J. Am. Chem. Soc., 2008, 130, 10947–10954 CrossRef CAS PubMed.
- J. Li, T. Zhu, G. D. Hawkins, P. Winget, D. Liotard, C. J. Cramer and D. G. Truhlar, Theor. Chem. Acc., 1999, 103, 9–63 CrossRef CAS.
- P. Winget, E. J. Weber, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2000, 2, 1231–1239 RSC.
- M. Friedrichs, R. Zhou, S. R. Edinger and R. A. Friesner, J. Phys. Chem. B, 1999, 103, 3057–3061 CrossRef CAS.
- M.-H. Baik and R. A. Friesner, J. Phys. Chem. A, 2002, 106, 7407–7412 CrossRef CAS.
- R. Jono, M. Sumita, Y. Tateyama and K. Yamashita, J. Phys. Chem. Lett., 2012, 3, 3581–3584 CrossRef CAS PubMed.
- P. Frank, M. Benfatto, R. K. Szilagyi, P. D’Angelo, S. D. Longa and K. O. Hodgson, Inorg. Chem., 2005, 44, 1922–1933 CrossRef CAS PubMed.
- J. Blumberger, J. Am. Chem. Soc., 2008, 130, 16065–16068 CrossRef CAS PubMed.
- I. Tavernelli, R. Vuilleumier and M. Sprik, Phys. Rev. Lett., 2002, 88, 213002 CrossRef.
- J. Blumberger, L. Bernasconi, I. Tavernelli, R. Vuilleumier and M. Sprik, J. Am. Chem. Soc., 2004, 126, 3928–3938 CrossRef CAS PubMed.
- J. Blumberger and M. Sprik, J. Phys. Chem. B, 2005, 109, 6793–6804 CrossRef CAS PubMed.
- Y. Tateyama, J. Blumberger, M. Sprik and I. Tavernelli, J. Chem. Phys., 2005, 122, 234505 CrossRef PubMed.
- J. Blumberger, I. Tavernelli, M. L. Klein and M. Sprik, J. Chem. Phys., 2006, 124, 064507 CrossRef PubMed.
- M. Sulpizi and M. Sprik, Phys. Chem. Chem. Phys., 2008, 10, 5238–5249 RSC.
- J. Cheng, M. Sulpizi and M. Sprik, J. Chem. Phys., 2009, 131, 154504 CrossRef PubMed.
- F. Costanzo, M. Sulpizi, R. G. D. Valle and M. Sprik, J. Chem. Phys., 2011, 134, 244508 CrossRef PubMed.
- K. Izutsu, Electrochemistry in Nonaqueous Solutions, Wiley-vch, Weinheim, 2nd edn, 2009, p. 41, p. 349 Search PubMed.
- X. Wang and D. M. Stanbury, Inorg. Chem., 2006, 45, 3415–3423 CrossRef CAS PubMed.
- G. Markovich, L. Perera, M. L. Berkowitz and O. Cheshnovsky, J. Chem. Phys., 1996, 105, 2675–2685 CrossRef CAS PubMed.
- A. J. Parker, Electrochim. Acta, 1976, 21, 671–679 CrossRef CAS.
- M.-H. Baik and R. A. Friesner, J. Phys. Chem. A, 2002, 106, 7407–7412 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS PubMed.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- The CP2K developers group, http://www.cp2k.org/ (accessed December 2014).
- Y. Marcus, Pure Appl. Chem., 1985, 57, 1129–1132 CAS.
- A. K. Hijazi, H. Y. Yeong, Y. Zhang, E. Herdtweck, O. Nuyken and F. E. Kühn, Macromol. Rapid Commun., 2007, 28, 670–675 CrossRef CAS PubMed.
- I. Csöregh, P. Kierkegaard and R. Norrestam, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 314–317 CrossRef; J. R. Black, W. Levason and M. Webster, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1995, 51, 623–625 CrossRef.
- J. K. Senne and B. Kratochvil, Anal. Chem., 1972, 44, 585–588 CrossRef CAS.
- C. Adriaanse, J. Cheng, V. Chau, M. Sulpizi, J. VandeVondele and M. Sprik, J. Phys. Chem. Lett., 2012, 3, 3411–3415 CrossRef CAS PubMed.
- J. Cheng, X. Liu, J. VandeVondele, M. Sulpizi and M. Sprik, Acc. Chem. Res., 2014, 47, 3522–3529 CrossRef CAS PubMed.
- X. Liu, J. Cheng and M. Sprik, J. Phys. Chem. B, 2015, 119, 1152–1163 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |