Chemical trends in the optical properties of rocksalt nanoparticles

Abstract

The nature and magnitude of the optical gaps of rocksalt alkaline earth (MgO, CaO, SrO, MgS, MgSe) and transition metal chalcogenide (CdO, PbS) nanoparticles are studied using time-dependent density functional theory (TD-DFT) calculations on (MX)₃₂ nanoparticles. We demonstrate, just as we previously showed for MgO, that TD-DFT calculations on rocksalt nanoparticles require the use of hybrid exchange–correlation (XC-)functionals with a high percentage of Hartree–Fock like exchange (e.g. BHLYP) or range-separated XC-functionals to circumvent problems related to the description of charge-transfer excitations. Concentrating on the results obtained with TD-BHLYP we show that the optical gap in rocksalt nanoparticles displays a wide range of behavior; ranging from large optical gaps stemming from a localized excitation involving corner atoms in alkaline earth oxides to a delocalized excitation and small optical gaps in the transition metal chalcogenides. Finally, we rationalize this wide range of behaviour in terms of differences in the degree to which the Coulombic interaction between the excited electron and hole is screened in the different nanoparticles, and relate it to the optical dielectric constants of the bulk materials the nanoparticles are made from.

---

Introduction

The absorption spectra of nanoparticles of semiconducting materials are generally blue-shifted with respect to that of the infinite bulk due to the quantum confinement.^1–5 The excited state, the exciton, is delocalised over the whole particle and the finite size of the particle means that the exciton is spatially constrained, resulting in an upward shift of the excitation energy, the magnitude of which is inversely proportional to the particle size.

Nanoparticles, however, do not always have blue-shifted absorption spectra. Surface states, or more specifically the pinning of the excited state on corners or edges of a particle, might result in a particle with a red-shifted rather than a blue-shifted optical gap (onset of light absorption). A very clear illustration of the latter is the case of nanoparticles of magnesium oxide (MgO) studied experimentally by the group of Diwald,^6,7 and discussed from a theoretical perspective in our previous paper,⁸ as well as in computational work of Shluger and co-workers.^9–13 Small MgO nanoparticles of 3 nm experimentally absorb light at 220 and 270 nm (5.6 and 4.6 eV) compared to 160 nm (7.8 eV) for the bulk.¹⁴ Calculations using Time-Dependent Density Functional Theory (TD-DFT) reproduce this red-shift, both between MgO nanoparticles and the bulk and between MgO nanoparticles of different sizes, and show that these excitations involve a combination of 3-coordinated (3C) corner and 4-coordinated (4C) edge atoms.^8,11

On a more technical note, we also observed in our work on MgO nanoparticles that the use of the commonly employed B3LYP^15–17 exchange–correlation (XC-)functional, as well as other XC-functionals with no (i.e. GGA) or a low fraction of Hartree–Fock like exchange (HFLE), in TD-DFT calculations on these systems is problematic. Charge transfer (CT) excitations, where there is no or limited overlap between the place from where an electron gets excited from and where it gets excited to, are spuriously stabilised by such XC-functionals resulting in them erroneously being predicted as the low(est) energy excitations by TD-DFT.^18,19 The solution to this problem, in line with experience for inorganic^8,20,21 and organic^18,19,22 systems, was the use of XC-functionals with an increased percentage of HFLE (e.g. BHLYP²³) or range-separated XC-functionals (e.g. CAM-B3LYP²⁴).

Having successfully studied the effect of the particle size, here we extend our work by focussing on nanoparticles of other materials than MgO that crystallize experimentally in the rocksalt structure; calcium oxide (CaO), strontium oxide (SrO); magnesium sulfide (MgS); magnesium selenide (MgSe), cadmium oxide (CdO) and lead sulphide (PbS). We study nanoparticles of these materials by a series of calculations on cubic (MX)₃₂ structures of approximately 0.7 × 0.7 × 0.7 nm in size. For these nanoparticle structures we do not only consider the localisation of the excitons and to what extent their optical properties are related to surface pinning but in the case of CaO and SrO also discuss the ability of theory to reproduce the experimentally measured absorption spectrum for well-defined nanoparticles of those compositions.²⁵

Methodology

First, we optimise the (MX)₃₂ nanoparticles (MX = CaO, CdO, SrO, MgO, MgS, MgSe and PbS) using ground state Density Functional Theory (DFT). The lowest singlet vertical excitation energies of each nanoparticle and the UV-vis absorption spectra are then subsequently calculated using TD-DFT on the ground state geometries. Throughout we approximate the (XC-)functional by the hybrid-GGA B3LYP and BHLYP XC-functionals. The main difference between these XC-functionals is the percentage of Hartree–Fock like exchange (HFLE) included: 20% in B3LYP and 50% in BHLYP. Finally, The basis set used in all calculations is the triple-ζ quality def2-TZVP basis set,²⁶ which in the cases of Strontium²⁷ and Lead²⁸ includes an Effective Core Potential (ECP).

The computed absorption spectra reported in the paper have been created using a custom script which represents each excitation as a Gaussian function centred on the TD-DFT calculated excitation energy and with a standard deviation (broadening) of 0.1 eV. The latter value has been chosen so as to approximate the peak shape observed experimentally. The character of the excitations is analysed by considering the contributing Kohn–Sham orbitals and the differences between the natural bond order (NBO)²⁹ charges of the atoms in the particle in the ground and excited states. We further employed the Λ diagnostic of Peach et al.,¹⁹ to identify potentially problematic charge-transfer excitations.

The calculations using the BHLYP and B3LYP XC-functionals were performed using the TURBOMOLE 6.4³⁰ code, whereas the TD-B3LYP Λ diagnostic calculations used the GAMESS-US³¹ (1 OCT 2010 – R1) code. Visualisation of the highest occupied and the lowest unoccupied Kohn–Sham orbitals (i.e. the HOMO and the LUMO of each particle), finally, is performed using VMD.³²

Results and discussion

Having outlined the methodology used, we will now discuss the calculated optical properties of (MO)₃₂ (MgO, CaO and SrO) and (MgX)₃₂ (MgO, MgS and MgSe) particles. We will also analyse the optical properties of the (CdO)₃₂ and (PbS)₃₂ particles. First, however, we will start with a brief examination of the general features of the (MX)₃₂ particle structures.

Nanoparticle structures

As seen from Fig. 1, the (MX)₃₂ nanoparticles are cubic, highly symmetric and have T_d symmetry. The edges and faces of the (MX)₃₂ particles consist of four and sixteen ions, respectively. As can be seen in Tables S1 and S2 in the ESI,† the particle size, in terms of the M–X edge length and M–M and X–X body diagonals, increases when replacing magnesium and/or oxygen with heavier analogues. All in line with what would be expected based on the trend in ionic radii.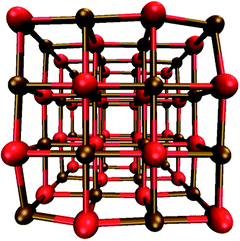

Fig. 1 DFT optimised structure of the (MgO)₃₂ nanoparticle as an example; all other (MX)₃₂ particles studied have the same structure and morphology.

Optical gap

Table 1 shows the lowest vertical t₂ excitation energies for the different particles predicted by TD-BHLYP and TD-B3LYP, as well as the Λ diagnostic values for the case of TD-B3LYP. This excitation corresponds to the optical gap (Δ_o) of the respective particles because excitations belonging to all other irreducible representations are optically disallowed (dark) in the electric dipole approximation. It can be seen that Δ_o is always smaller when the B3LYP rather than the BHLYP XC-functional is used. The Δ_o and Λ values obtained also vary considerably for nanoparticles of the different materials under consideration.

Table 1 Optical gap (Δ_o) of the (MX)₃₂ particles of the different compositions calculated using TD-BHLYP and TD-B3LYP, as well as the TD-B3LYP Λ values for the lowest t₂ excitation corresponding to the optical gap (in the case of PbS calculated with the small def2-SVP basis-set, see the text)

	MgO	CaO	SrO	MgS	MgSe	CdO	PbS
Δ o,B3LYP	3.55	3.30	2.89	3.62	3.21	1.48	2.71
Δ o,BHLYP	5.08	4.35	3.91	4.82	4.37	3.01	3.39
Λ	0.130	0.168	0.174	0.240	0.373	0.429	0.476

---

In the case of the (MO)₃₂ particles, Δ_o also corresponds to the overall lowest vertical excitation for each of the particles. All dark excitations have higher excitation energies. From Table 1 it is clear that both XC-functionals predict that as magnesium is replaced by heavier alkaline earth metals, Δ_o decreases, similar to what is experimentally observed for the bulk^33,34 and nanoparticles.²⁵ However, the overall change in Δ_o when going from MgO to SrO is more pronounced when using the XC-functionals that includes the greater percentage of HFLE (BHLYP). The largest variation in the TD-BHLYP data set is between MgO and CaO, (0.73 eV) whereas TD-B3LYP predicts the largest difference to be between CaO and SrO (0.41 eV). Finally, there is not only a consistent trend within each XC-functionals series, but from the data in Table 1 it is also clear that the TD-BHLYP excitation energies are always significantly larger than their TD-B3LYP counterparts, in line with what was previously observed by us for MgO.⁸ The difference between the predictions of the two XC-functionals, finally, decreases as the cation becomes heavier. MgO TD-BHLYP Δ_o is 1.53 eV larger than its TD-B3LYP counterpart, for CaO by 1.05 eV and for SrO by 1.02 eV.

In the case of the (MgX)₃₂ series Table 1 shows that TD-BHLYP predicts that Δ_o smoothly decreases as the anion becomes heavier, similar to what was found when varying the cation above, with the largest change in Δ_o between MgS and MgSe. The values predicted with TD-B3LYP display a slightly different trend however; Δ_o is predicted by TD-B3LYP to first increase when going from MgS to MgO and then decreases again to MgSe. Although, in line with the TD-BHYLP results, the largest change in Δ_o is predicted by TD-B3LYP again to be between MgS and MgSe. Different from (MO)₃₂, the lowest t₂ excitation is not always the lowest vertical excitation of the (MgX)₃₂ particles. In both TD-B3LYP and TD-BHLYP calculations the lowest dark a₂ excitation comes down in energy relative to where it sits for MgO and becomes the lowest vertical excitation for MgSe in the case of TD-B3LYP (at 3.16 eV) and for MgS and MgSe in the case of TD-BHLYP (at 4.57 and 4.05 eV respectively). We are not aware of any internally consistent study of MgX nanoparticles or optical absorption spectra of bulk MgX materials, but the TD-BHLYP trend for the (MgX)₃₂ nanoparticles appears in line with the experimentally measured band gap (Δ_o + exciton binding energy) values of bulk MgX.^35–37

The CdO Δ_o is predicted by both TD-BHLYP and TD-B3LYP to be the smallest and thus most red-shifted of the (MO)₃₂ oxide series, as well as of all the (MX)₃₂ particles considered, while the 1.53 eV difference in the predicted Δ_o between TD-BHLYP and TD-B3LYP is similar to that in the case of (MgO)₃₂. We are again not aware of any internally consistent study of MgO and CdO nanoparticles, but the red-shift in the Δ_o for CdO is similar to the red-shift in the experimental onset of absorption between bulk MgO and CdO.³⁸

The PbS Δ_o, finally, is predicted by both XC-functionals to be the second lowest of all the (MX)₃₂ particles studied, with a 0.68 eV difference between the TD-BHLYP and TD-B3LYP results. Our calculations did not include, however, the effect of spin–orbit coupling, which might be significant in the case of PbS. So while consistent within the set of particles studied, the experimental Δ_o for (PbS)₃₂ is likely to be significantly lower than that predicted here, because of a mixing of triplet and singlet excitations mediated by spin–orbit coupling.

The Λ diagnostic developed by Peach et al. is a gauge of the spatial overlap between the occupied and unoccupied Kohn–Sham orbitals contributing to a TD-DFT excitation. A Λ value of 0 corresponds to no overlap and 1 to complete overlap between the orbitals involved. Peach et al. proposed the Λ diagnostic as a quantitative indicator of excitations that have charge transfer (CT) character and hence might be problematic to describe using XC-functionals with no or a low percentage of HFLE, such as TD-B3LYP. Specifically, a low Λ value signals a problematic CT excitation, and Peach et al. propose a cut-off of 0.3 in the case of TD-B3LYP, below which the description of this CT excitation is likely to be challenging. However, this numerical cut-off was determined for organic systems and might be system dependent. Indeed, from our work on TiO₂ and MgO nanoparticles^8,20,21 we believe that this cut-off might be lower in the case of inorganic materials, because even local (i.e. non CT) excitations by definition involve the transfer of an electron from one sub-lattice or sub-systems to another.

From the Λ values shown in Table 1 it can be seen that for all (MO)₃₂ particles the Λ values of the lowest t₂ excitation corresponding to the optical gap fall below the cut-off value proposed by Peach et al. The exact Λ values increase slightly down the series MgO < CaO < SrO but this variation in Λ values between particles with different chemical compositions is much smaller than the change with particle size previously observed by us for MgO.⁸ In the case of the (MgX)₃₂ particles Table 1 shows that there is a stronger trend between the Λ value and chemical composition, they increases steadily down the series MgO < MgS < MgSe and becomes larger than the 0.3 cut-off for MgSe. The (CdO)₃₂ and (PbS)₃₂Λ values, finally, clearly lie above the cut-off. As an aside, the latter Λ value for (PbS)₃₂ was calculated using the smaller def2-SVP basis-set²⁶ because of convergence issues in GAMESS-US for this particle when using the def2-TZVP basis-set, but we believe this not to be a severe approximation as the def2-SVP and def2-TZVP TD-B3LYP predicted Δ_o values are very similar (2.64 vs. 2.71 eV). Overall, the above discussed Λ values thus suggest that for the (CaO)₃₂, (SrO)₃₂, and (MgS)₃₂ particles, as well as their larger analogues, the lowest energy t₂ excitation predicted by TD-B3LYP is likely to be a spuriously stabilised CT excitation rather than a local excitation, which would have been the lowest energy excitation in the absence of this stabilisation, similar to what we previously observed for MgO nanoparticles.⁸ The Δ_o values predicted by TD-B3LYP for these systems are thus also likely to be (severely) underestimated. In contrast for (MgSe)₃₂, (CdO)₃₂ and (PbS)₃₂, the Λ values suggest that the CT character of the lowest energy excitations and their description by TD-B3LYP should not be a problem.

Spectra

Before discussing the localisation associated with the optical gap data discussed above, we first present the vertical excitation spectra for the (CaO)₃₂ and (SrO)₃₂ particles and compare these with absorption spectra for well-defined CaO and SrO nanoparticles obtained experimentally.²⁵ This comparison builds upon our previous work on the absorption spectra of MgO nanoparticles, where we found that use of the BHLYP XC-functional and a rigid downwards (red-)shift of 0.5 eV on top of the computed spectra yielded a good agreement with the experimental obtained spectra.²⁵ The origin for the need of this empirical red-shift can be understood from the fact that increasing the percentage of HFLE in an XC-functional not only corrects problems with the description of CT-states but also shifts non-problematic local excitations up in energy. Amongst other things, we will test here whether this rigid shift applied to MgO TD-BHLYP spectra is also suitable for CaO and SrO nanoparticles.

The rigidly red-shifted TD-BHLYP spectra of the (MgO)₃₂, (CaO)₃₂ and (SrO)₃₂ are shown in Fig. 2 (for the unshifted spectra see Fig. S1 in the ESI†). When comparing these rigid-shifted BHLYP spectra in the range of 200–400 nm, there is an obvious trend: the longest wavelength peaks are predicted to lie at 270 nm (4.59 eV), 320 nm (3.87 eV), and 360 (3.44 eV) for (MgO)₃₂, (CaO)₃₂ and (SrO)₃₂ respectively. This trend is similar to that of the optical gap values discussed above, although here we focus by definition on excitations with significant oscillator strength and not necessarily the lowest possible bright excitation. The same relative trend can also be observed in the experimental spectra where the SrO nanoparticles have the lowest absorption onset, followed by CaO, and then MgO nanoparticles.

Fig. 2 TD-BHLYP rigidly red-shifted spectra of (MgO)₃₂ (green line, most blue-shifted spectra), (CaO)₃₂ (blue line), (SrO)₃₂ (red line, most red-shifted spectra) nanoparticles.

The rigidly red-shifted TD-BHLYP spectrum of (MgO)₃₂, as expected, matches the experimental spectrum of MgO nanoparticles in terms of absolute values very well. For the other materials the fit in terms of absolute values to the experimental spectra, however, is also good. The predicted peak maximum for the longest wavelength peak of (CaO)₃₂ at 320 nm is in good agreement with the first edge in the experimental absorption spectrum of CaO nanoparticles at ∼325 nm (3.81 eV). Similarly, for (SrO)₃₂, the predicted peak maximum of the longest wavelength peak at ∼360 nm (3.44 eV) agrees well with the experimental value of ∼350 nm (3.54 eV) for the first absorption edge. The same holds for CaO and SrO nanoparticles in terms of shorter wavelength features; the experimental shoulders at ∼270 and ∼220 nm (CaO) and ∼320 and ∼270 nm (SrO) appear to be mirrored in the calculated spectra for (CaO)₃₂ and (MgO)₃₂ in Fig. 2. Overall the combination of TD-BHLYP and an empirical red shift of 0.5 eV thus appears to also yield decent results when predicting the spectra of CaO and SrO nanoparticles. Although one should be slightly careful with overinterpreting the good fit between the prediction and the experiment, as experimentally the spectra were measured for nanoparticles that were (considerably) larger than (MX)₃₂ and differed from system to system (average particle size for MgO ∼3 nm, for CaO ∼27 nm and SrO 20–200 nm).

The vertical spectra predicted using the B3LYP XC-functional can be found in Fig. S2 of the ESI.† In line with the TD-B3LYP optical gap values discussed above, the use of B3LYP results in a significant overestimation of the wavelength (and underestimation of the excitation energy) of the first peak in the absorption peak relative to the experiment; for MgO 350 nm (3.55 eV) instead of ∼265 nm (∼4.68 eV), for CaO 381 nm (3.25 eV) instead of ∼325 nm (3.81 eV), and for SrO 425 nm (2.91 eV) instead of ∼350 nm (3.54 eV). Moreover, no single rigid-shift value can be used to bring the TD-B3LYP values consistently close to their experimental counterparts.

Excited state localisation

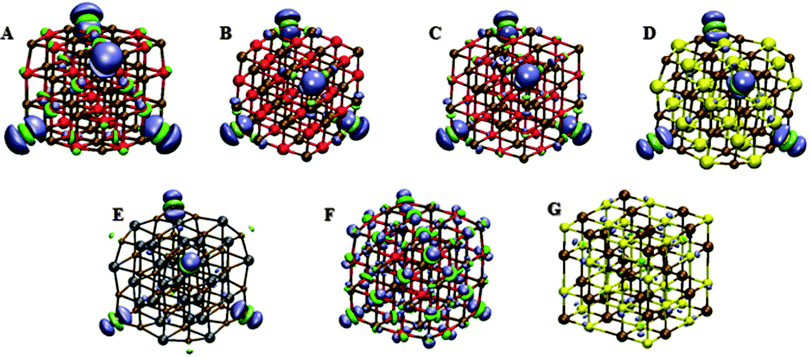
We now, finally, consider the spatial character of the lowest energy t₂ excitation responsible for the optical gap. Following our work on MgO we analyse the character of an excitation in terms of the difference in NBO charges between the ground and relevant excited state for every atom in the particle. All atoms in the different particles can be labelled as ‘corner’ (3-coordinated), ‘edge’ (4-coordinated), ‘face’ (5-coordinated) or ‘bulk’ (6-coordinated) and when contributions are discussed in the section below, what is meant is the percentage of the excited electron localised on a metal atom or a hole localised on the chalcogen atom, and where the contributions are summed up per atom types (e.g. metal corner or chalcogen edge).

Tables 2–4 show the contributions of each of the different atom types to the localisation of the lowest t₂ excitation in the alkaline earth oxide (MO)₃₂ nanoparticles, the magnesium chalcogenide (MgX)₃₂ nanoparticles, and the post-transition metal chalcogenide (CdO)₃₂ and (PbS)₃₂ nanoparticles respectively. Fig. 3 and Fig. S3 in the ESI† show the same information for TD-BHLYP and TD-B3LYP respectively but then in the form of plots of the excited-state ground-state density differences.

Table 2 Percentage contribution of different types of sites in the particle to the localisation of the lowest energy t₂ TD-BHLYP/TD-B3LYP excitation, corresponding to the optical gap, for the different (MO)₃₂ particles. See Section ESI-4 of the ESI for the underlying data

	M = Mg	M = Ca	M = Sr
O corner (%)	89.52/83.51	77.63/65.85	71.47/59.03
O edge (%)	0.96/4.28	4.24/1.37	3.49/1.46
O face (%)	3.10/3.62	9.84/16.49	14.34/19.05
O bulk (%)	6.42/8.59	8.28/16.29	10.70/20.47
M corner (%)	17.68/75.65	7.75/76.85	4.19/70.12
M edge (%)	72.24/7.37	81.25/0.29	80.57/4.00
M face (%)	5.36/9.07	0.52/0.37	6.66/12.86
M bulk (%)	4.72/7.90	10.48/22.49	8.58/13.02

---

Table 3 Percentage contribution of the different types of sites in the particle to the localisation of the lowest energy t₂ TD-BHLYP/TD-B3LYP excitation, corresponding to the optical gap, for the different (MgX)₃₂ particles. See Section ESI-4 of the ESI for the underlying data

	X = O	X = S	X = Se
X corner (%)	89.52/83.51	72.09/64.26	56.51/52.27
X edge (%)	0.96/4.28	1.99/1.12	6.01/2.07
X face (%)	3.10/3.62	25.73/33.96	35.67/42.08
X bulk (%)	6.42/8.59	0.19/0.66	1.81/3.58
Mg corner (%)	17.68/75.65	26.22/64.96	36.36/58.18
Mg edge (%)	72.24/7.37	65.97/24.77	56.17/32.34
Mg face (%)	5.36/9.07	3.57/9.52	4.70/9.22
Mg bulk (%)	4.72/7.90	4.24/0.75	2.78/0.26

---

Table 4 Percentage contribution of the different types of sites in the particle to the localisation of the lowest energy t₂ TD-BHLYP/TD-B3LYP excitation, corresponding to the optical gap, for the (CdO)₃₂ and (PbS)₃₂ particles. See Section ESI-4 of the ESI for the underlying data

	CdO	PbS
X corner (%)	22.97/24.56	8.73/14.40
X edge (%)	35.35/23.20	40.24/35.38
X face (%)	40.40/50.62	36.69/42.70
X bulk (%)	1.28/1.61	14.33/7.52
M corner (%)	49.24/53.00	2.87/2.56
M edge (%)	29.61/27.04	25.55/19.32
M face (%)	19.24/17.84	54.30/55.04
M bulk (%)	1.91/2.13	17.28/23.08

---

Fig. 3 TD-BHLYP electron density differences between the ground and lowest t₂ excited state for (A) MgO, (B) CaO, (C) SrO, (D) MgS, (E) MgSe, (F) CdO, and (G) PbS. Red spheres are oxygen atoms, brown are magnesium (or calcium/strontium/cadmium/lead) atoms, yellow spheres are sulphur atoms, black spheres are selenium atoms. Green signifies gain in electron density (excited electron), blue signifies loss in electron density (hole). Same contour value (0.001) used in all figures.

Focussing initially on Table 2 we see that, just as we previously observed for MgO,⁸ the use of BHLYP or B3LYP for the alkaline earth oxide nanoparticles leads to two rather different predictions. With TD-B3LYP the lowest energy t₂ excitation for every alkaline earth (MO)₃₂ particles has clear CT character, where the hole is predominantly localised on the oxygen corner atoms of the particle and the excited electron on the metal corner atoms. The use of TD-BHLYP, in contrast, yields a different picture, where the hole still is localised on the oxygen corner atoms but the excited electron now resides on the metal edge atoms adjacent to the oxygen corner atoms. For both TD-BHLYP and TD-B3LYP, the main change in the excited state localisation when replacing magnesium with its heavier analogues is an increased delocalisation of the hole over the particle, with significant contributions in the case of (SrO)₃₂ of edge and face oxygen atoms.

Switching our focus to the magnesium chalcogenide nanoparticles, we find, just as for the alkaline earth oxide nanoparticles, that TD-B3LYP predicts that the lowest t₂ excitation for the (MgX)₃₂ nanoparticles is a CT excitation that predominantly involves the metal and chalcogen corner atoms, while TD-BHLYP predicts an excitation dominated by the corner chalcogen atoms and the adjacent magnesium edge atoms. Different to the alkaline earth oxide nanoparticles, the effect of replacing oxygen with the heavier chalcogens is an increased delocalisation of not only the hole but also the excited electron. Both for TD-B3LYP and TD-BHLYP, the hole in the case of the heavier chalcogenides is delocalised over the corner and face chalcogen atoms, while the excited electron delocalises over the edge and corner magnesium atoms. As a result the excited state localisation predicted by TD-BHLYP and TD-B3LYP becomes more similar when going from MgO to MgSe, something that does not occur in the MgO to SrO series.

The post-transition metal chalcogenide nanoparticles in Table 4, finally, show a dramatically different behaviour than any of the other nanoparticles studied here. Firstly, TD-B3LYP and TD-BHLYP predict essentially the same localisation of the lowest energy t₂ excited state for (PbS)₃₂ and (CdO)₃₂. Secondly, in contrast of the very localised excited states found for the alkaline earth chalcogenide nanoparticles, the excited state in the post-transition metal oxides is predicted to be essentially delocalised. Specifically, in the case of (CdO)₃₂ the excited state is predicted to be delocalised over the surface of the nanoparticles, with large contributions of face and edge atoms, while in (PbS)₃₂ it is predicted to be delocalised over the whole particle, including a significant contribution of the bulk atoms in the centre of the particle.

The electron density differences between the ground and lowest t₂ excited state visualised in Fig. 3 and Fig. S3 (ESI†), finally, paint a similar picture to the charge differences in Tables 2–4. There appears to be a minor discrepancy, the fact that the excited electron localised on the corner metal atoms shows up less clearly than the hole in the TD-BHLYP calculation on the alkaline earth nanoparticles, but this simply arises from the fact there are four oxygen corner atoms and twelve adjacent metal edge atoms, and the density difference per unit volume, which is essentially visualised in a contour plot, at the metal edge atoms is ∼4/12^th of that at the corner oxygen atoms.

Discussion

As discussed above, our calculations show that rocksalt nanoparticles with different chemical composition can have distinctly different optical properties. The dramatic change in predicted excited state (de)localisation between MgO on the one side and CdO and PbS on the other side is probably the clearest illustration of this effect of chemical composition. This change in localisation is paralleled by a nearly 2 eV change of the optical gap in the series of particles studied, although that change is similar to that observed for the bulk, so not necessarily directly connected with nanostructuring.

Before discussing the possible physical origin of these large changes, we reflect first on the more technical question of which set of TD-DFT results to trust the most. For MgO in our previous work the case was very clear. The optical gap and the overall absorption spectrum predicted by TD-B3LYP for MgO are severely red-shifted relative to that measured experimentally for particles that were roughly similar in size. Also, while one can argue about the exact Λ value below which an excitation is likely to be problematic to describe using TD-B3LYP because of CT related issues, the Λ values we found for MgO particles with the rocksalt structure are really rather low and, moreover, decreased with increasing particle size; 0.15 for (MgO)₂₄ and 0.13 for (MgO)₃₂. This all, together with the fact that the excited state localisation predicted by TD-B3LYP had all the hallmarks of a CT-state and that predicted by the TD-BHLYP not, made us feel confident that the TD-B3LYP optical gap was a spuriously stabilised CT-state and that hence TD-B3LYP cannot be properly used to study MgO nanoparticles in the size range relevant to experiment. Considering the evidence, discussed above for the materials studied here, we feel that the same reasoning suggests that also in the case of the other alkaline earth oxide nanoparticles, (CaO)₃₂ and (SrO)₃₂, the use of TD-B3LYP is clearly problematic and use of TD-BHLYP or other XC-functionals with a large percentage of HFLE or range-separated XC-functionals (e.g. CAM-B3LYP) is advisable. A conclusion that is further supported by the success of the ad hoc recipe developed by us to reproduce the experimental absorption spectra of MgO nanoparticles, in reproducing the experimental spectra of CaO and SrO nanoparticles. A similar argument can be probably made for the case of MgS. The TD-B3LYP Λ value calculated for the lowest t₂ excitation of (MgS)₃₂ is slightly larger than that of the same excitation for the alkaline earth oxide nanoparticles, but the excited state localisation picture for the t₂ excitation is still very similar to that class of particles. MgSe, in contrast, appears as a material on the edge between two domains; a TD-B3LYP Λ value larger than 0.3 and similar but not the same excited localisation patterns predicted by TD-B3LYP and TD-BHLYP. The odd trend for the optical gap in the (MgO)₃₂–(MgS)₃₂–(MgSe)₃₂ series of particles, where the optical gap increases when going from (MgO)₃₂ to (MgS)₃₂ and then decreases again from (MgS)₃₂ to (MgSe)₃₂, in this context could arise from two competing trends down this series of structures. Those two trends would be the “true” physical trend of decreasing optical gap values when going from MgO to MgSe, as seen in the TD-BHLYP results, and at the same time a decrease in the spurious energetic stabilisation of CT-states down the series (indicated by the increasing Λ values) and a better approximation of the physical optical gap values by those calculated with TD-B3LYP. For (CdO)₃₂ and (PbS)₃₂ TD-B3LYP and TD-BHLYP, finally, predict a very similar localisation of the lowest t₂ excited state, as well as large TD-B3LYP Λ values (Λ > 0.4) for this excitation. While this suggests that, at least in terms of potential issues with CT-states, both XC-functionals should in principle work equally well in describing CdO and PbS nanoparticles, in the remainder of this discussion we focus on the TD-BHLYP results, as to treat the different nanoparticles in an as consistent as possible fashion.

We believe that the trend in exited state (de)localisation amongst the nanoparticles studied stems from differences in the extent the excited electron and hole are screened from one another, and that this to first approximation can be understood in terms of the optical dielectric constants of the bulk materials the nanoparticles are made from. The alkaline earth oxide nanoparticles, in which the excited state is very localised and the excited electron and hole are clearly separated in space, are all made of materials with low optical dielectric constant values (MgO 3.0; CaO 3.3; SrO 3.2–3.5).^39,40 The post-transition metal chalcogenide nanoparticles, in which in contrast to the alkaline earth oxide nanoparticles the excited state is delocalised, are made of materials with much higher optical dielectric constant values (CdO 5.4–6.2; PbS 17.2)^39,41 While the (MgS)₃₂ and (MgSe)₃₂ nanoparticles, which display intermediate (de)localisation, are made from materials that also have optical dielectric constant values that lie in between those of the alkaline earth oxides and post-transition metal chalcogenide materials (MgS 5.1; MgSe 5.9).³⁹ The observed (de)localisation here can, in analogy with the situation for polarons,⁴² be interpreted as the result of competition between a potential energy term arising from the electrostatic interaction between the excited electron and hole, favouring a localised excited state with the excited electron and hole in close proximity, and a kinetic energy term, favouring a delocalised excited state. In such a model the degree of screening and thus the optical dielectric constant then is a key parameter as it controls the relative magnitude of the potential energy term, the larger the optical dielectric constant the more the charges are screened and the smaller the potential energy, and thus the balance between delocalisation and localisation.

The optical dielectric constant values of the underlying bulk materials are, as demonstrated by the work of Penn,⁴³ Phillips^44–47 and van Vechten,³⁹ inherently connected to their electronic band structure and the degree to what the bonding is ionic or covalent.^47,48 Hence it is not surprising that the trend between the bulk optical dielectric constant and excited state (de)localisation in the nanoparticle also maps on trends between the bulk band gap and excited state (de)localisation in the nanoparticle (nanoparticles of materials with a smaller band gap have a more delocalised excited state) and the degree of ionic bonding in the bulk material and excited state (de)localisation in the nanoparticle (nanoparticles of more ionic materials have a more localised excited state). Quantum dots, in which quantum confinement is exploited to tune the optical properties by changing the particle size and which thus need a delocalised excited state, are not surprising typically made from small band gap materials such as CdSe and PbS. On a more methodological note, as problems with describing CT-excitations by TD-B3LYP are only likely to occur for particles with localised excited states, this issue is likely to only be relevant for nanoparticles of ionic materials with a large band gap. Finally, taking into account the apparent role played by the optical dielectric constant, it may be interesting to explore in the future what hybrid XC-functionals where the fraction of HFLE is treated as an explicit function of the optical dielectric constant^49–51 rather than an empirical constant predict for the optical properties of these systems.

Finally, if we trust the rigidly-red-shifted TD-BHLYP recipe that we developed for MgO nanoparticles, and which seems to also work well in reproducing the experimental spectra of CaO and SrO nanoparticles, as a good approximation to the optical gap for all materials studied then we can make some further interesting observations (see Table 5). Firstly, for the alkaline earth oxide nanoparticles the as such predicted Δ_o,rs values, that include the 0.5 eV redshift, consistently lie far below the band gap values⁴⁰ and lowest excitation energies^33,34 of the corresponding bulk materials. In line with their localised excited state, the Δ_o,rs values predicted for these particles are thus also clearly that of a material that shows a red shift rather than a blue shift upon reducing the particle size. For the magnesium chalcogenide particles it is more difficult to make a comparison due to the quality of the experimental data available,^35–37 especially for MgSe, but similarly the predicted Δ_o,rs values appear to lie below where the bulk starts absorbing light. For CdO and PbS, however, the predicted Δ_o,rs values lie clearly above the experimental onset of absorption,^38,52 and while this in the case of PbS can be partly due to the lack of spin–orbit coupling in our calculations, we feel that this, especially in the case of CdO, is evidence of the sort of blue-shift one would expect to see as a result of quantum confinement.

Table 5 Rigidly-red-shifted optical gap (Δ_o,rs) values for the (MX)₃₂ particles of the different compositions calculated using TD-BHLYP and a rigid redshift of 0.5 eV (see the text, all values in eV)

	MgO	CaO	SrO	MgS	MgSe	CdO	PbS
Δ o,rs	4.58	3.85	3.41	4.32	3.87	2.51	2.89

---

Conclusion

In this paper we have studied, using TD-DFT calculations on (MX)₃₂ particles, the magnitude and nature of the optical gap of rocksalt nanoparticles of CaO, SrO, MgS, MgSe, CdO and PbS. Firstly, on a technical note we observed that the lowest (t₂) excitations calculated with TD-B3LYP for all rocksalt nanoparticles considered, bar those of CdO and PbS, are, just as we previously found for MgO nanoparticles, charge-transfer excitations that are spuriously energetically stabilized relative to local excitations. As hybrid XC-functionals with a high percentage of Hartree–Fock like exchange, e.g. BHLYP, or range-separated XC-functionals, e.g. CAM-B3LYP, are known to correct for these charge-transfer artefacts, we therefore suggest that their use is essential when studying rocksalt nanoparticles. Concentrating on the TD-BHLYP results, we found that the magnitude and nature of the optical gap varies widely in between the different rocksalt nanoparticles. The alkaline earth oxide nanoparticles are all predicted to have large optical gaps, where the corresponding excited state has a very localised character and involves the oxygen corner atoms and the metal edge atoms nearby. The transition metal chalcogenide nanoparticles, in contrast, are predicted to have delocalised lowest excited states and much smaller optical gaps, while the magnesium chalcogenides, finally, display an intermediate behaviour. We propose that these differences can be understood in terms of the dielectric screening of the Coulomb interaction between the excited electron and hole, where the larger optical dielectric constant of materials such as CdO and PbS means that the potential energy term favouring localisation is much reduced.

Acknowledgements

We kindly acknowledge Dr Karol Kowalski, Dr Alexey Sokol, Dr Slavica Stankic and Dr Peter Sushko for stimulating discussions. Dr Enrico Berardo is thanked for the def2-SVP results on (PbS)₃₂. M.A.Z. acknowledges the UK Engineering and Physical Sciences Research Council (EPSRC) for a Career Acceleration Fellowship (Grant EP/I004424/1). Computational time on the IRIDIS regional high-performance computing service provided by the e-Infrastructure South Centre for Innovation (EPSRC Grants EP/K000144/1 and EP/K000136/1) and on Archer the UK's national high-performance computing service (via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC grant EP/L000202/1) is gratefully acknowledged.

References

1. A. P. Alivisatos, Semiconductor Clusters, Nanocrystals and Quantum Dots, Science, 1996, 271, 933–937.
2. A. P. Alivisatos, Perspectives on the Physical Chemistry of Semiconductor Nanocrystals, J. Phys. Chem., 1996, 100, 13226–13239.
3. W. Chen, Z. Wang, Z. Lin and L. Lin, Absorption and luminescence of the surface states in ZnS nanoparticles, J. Appl. Phys., 1997, 82, 3111–3115.
4. B. Brena and L. Ojama, Surface Effects and Quantum Confinement in Nanosized GaN Clusters: Theoretical Predictions, J. Phys. Chem. C, 2008, 112, 13516–13523.
5. S. N. Inamdar, P. P. Ingole and S. K. Haram, Determination of band structure parameters and the quasi-particle gap of CdSe quantum dots by cyclic voltammetry, ChemPhysChem, 2008, 9, 2574–2579.
6. O. Diwald, M. Sterrer and E. Knözinger, Site selective hydroxylation of the MgO surface, Phys. Chem. Chem. Phys., 2002, 4, 2811–2817.
7. A. Sternig, S. Stankic, M. Müller, N. Siedl and O. Diwald, Surface exciton separation in photoexcited MgO nanocube powders, Nanoscale, 2012, 4, 7494–7500.
8. M. Wobbe, A. Kerridge and M. A. Zwijnenburg, Optical excitation of MgO nanoparticles; a computational perspective, Phys. Chem. Chem. Phys., 2014, 16, 22052–22061.
9. A. L. Shluger, P. V. Sushko and L. N. Kantorovich, Spectroscopy of low-coordinated surface sites: theoretical study of MgO, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 2417–2430.
10. P. E. Trevisanutto, P. V. Sushko, A. L. Shluger, K. M. Beck, M. Henyk, A. G. Joly and W. P. Hess, A mechanism of photo-induced desorption of oxygen atoms from MgO nano-crystals, Surf. Sci., 2005, 593, 210–220.
11. M. Müller, S. Stankic, O. Diwald, E. Knözinger, P. V. Sushko, P. E. Trevisanutto and A. L. Shluger, Effect of protons on the optical properties of oxide nanostructures, J. Am. Chem. Soc., 2007, 129, 12491–12496.
12. K. P. McKenna, D. Koller, A. Sternig, N. Siedl, N. Govind, P. V. Sushko and O. Diwald, Optical properties of nanocrystal interfaces in compressed MgO nanopowders, ACS Nano, 2011, 5, 3003–3009.
13. A. Sternig, D. Koller, N. Siedl, O. Diwald and K. McKenna, Exciton Formation at Solid–Solid Interfaces: A Systematic Experimental and ab Initio Study on Compressed MgO Nanopowders, J. Phys. Chem. C, 2012, 116, 10103–10112.
14. R. C. Whited, C. J. Flaten and W. C. Walker, Exciton thermoreflectance of MgO and CaO, Solid State Commun., 1973, 13, 1903–1905.
15. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
16. A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
17. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, ab initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627.
18. M. J. G. Peach, C. R. Le Sueur, K. Ruud, M. Guillaume and D. J. Tozer, TDDFT diagnostic testing and functional assessment for triazene chromophored, Phys. Chem. Chem. Phys., 2009, 11, 4465–4470.
19. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: an evaluation and a diagnostic test, J. Chem. Phys., 2008, 128, 044118.
20. E. Berardo, H.-S. Hu, S. A. Shevlin, S. M. Woodley, K. Kowalski and M. A. Zwijnenburg, Modeling Excited States in TiO₂ Nanoparticles: On the Accuracy of a TD-DFT Based Description, J. Chem. Theory Comput., 2014, 10, 1189–1199.
21. E. Berardo, H.-S. Hu, H. J. J. van Dam, S. A Shevlin, S. M. Woodley, K. Kowalski and M. A. Zwijnenburg, Describing Excited State Relaxation and Localization in TiO₂ Nanoparticles Using TD-DFT, J. Chem. Theory Comput., 2014, 10, 5538–5548.
22. M. J. G. Peach and D. J. Tozer, Overcoming low orbital overlap and triplet instability problems in TDDFT, J. Phys. Chem. A, 2012, 116, 9783–9789.
23. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648.
24. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
25. A. Sternig, S. Stankic, M. Müller, J. Bernardi, E. Knözinger and O. Diwald, Photoluminescent Nanoparticle Surfaces: The Potential of Alkaline Earth Oxides for Optical Applications, Adv. Mater., 2008, 20, 4840–4844.
26. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
27. M. Kaupp, P. V. R. Schleyer, H. Stoll and H. Preuss, Pseudopotential approaches to Ca, Sr, and Ba hydrides. Why are some alkaline earth MX2 compounds bent?, J. Chem. Phys., 1991, 94, 1360–1366.
28. B. Metz, H. Stoll and M. Dolg, Small-core multiconfiguration-Dirac–Hartree–Fock-adjusted pseudopotentials for post-d main group elements: application to PbH and PbO, J. Chem. Phys., 2000, 113, 2563–2569.
29. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735.
30. R. Ahlrichs, M. Bär, H. Marco, H. Horn and C. Kölmel, Electronic Structure Calculations on Workstation Computers: The Program System TURBOMOLE, Chem. Phys. Lett., 1989, 162, 165–169.
31. M. S. Gordon and M. W. Schmidt, in Theory Appl. Comput. Chem. First Forty Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier Ltd, 2005, pp. 1167–1189.
32. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
33. R. C. Whited and W. C. Walker, Exciton spectra of CaO and MgO, Phys. Rev. Lett., 1969, 22, 1428–1430.
34. A. Rao and R. Kearney, Logarithmic derivative reflectance spectra of BaO and SrO, Phys. Status Solidi, 1979, 95, 243–250.
35. H. Mittendorf, Roentgenographische und optische Untersuchungen aufgedampfter Schichten aus Erdalkalichalkogeniden, Z. Phys., 1965, 183, 113–129.
36. G. A. Saum and B. Hensley, Fundamental Optical Absorption in the IIA–VIB Compounds, Phys. Rev., 1959, 113, 1019–1022.
37. I. A. Davidson, R. T. Moug, F. Izdebski, C. Bradford and K. A. Prior, Determination of the band-gap of MgS and MgS-rich Zn1-xMgxSySe1-y alloys from optical transmission measurements, Phys. Status Solidi B, 2010, 247, 1396–1398.
38. J. L. Freeouf, Far-ultraviolet reflectance of II–VI compounds and correlation with the Penn Phillips gap, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 7, 3810–3830.
39. J. A. Van Vechten, Quantum dielectric theory of electronegativity in covalent systems. I. Electronic dielectric constant, Phys. Rev., 1969, 182, 891–905.
40. A. E. Henderson and B. Hughes, in Point Defects Solids, Gen. Ion. Cryst., ed. J. H. Crawford and L. M. Slifkin, Plenum Press, 1972, pp. 381–490.
41. P. B. Littlewood, The dielectric constant of cubic IV–VI compounds, J. Phys. C: Solid State Phys., 1979, 12, 4459–4468.
42. A. M. Stoneham, J. Gavartin, A. L. Shluger, A. V. Kimmel, D. M. Ramo, H. M. Ronnow, G. Aeppli and C. Renner, Trapping, self-trapping and the polaron family, J. Phys.: Condens. Matter, 2007, 19, 255208.
43. D. R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev., 1962, 128, 2093–2097.
44. J. C. Phillips, Covalent bond in crystals. I. Elements of a structural theory, Phys. Rev., 1968, 166, 832–838.
45. J. C. Phillips, Covalent bond in crystals. II. Partially ionic binding, Phys. Rev., 1968, 168, 905–911.
46. J. C. Phillips, Dielectric definition of electronegativity, Phys. Rev. Lett., 1968, 20, 550–553.
47. J. C. Phillips, Ionicity of the chemical bond in crystals, Rev. Mod. Phys., 1970, 42, 317–356.
48. C. Catlow and A. Stoneham, Ionicity in Solids, J. Phys. C: Solid State Phys., 1983, 4321, 4321–4338.
49. A. Alkauskas, P. Broqvist and A. Pasquarello, Defect levels through hybrid density functionals: insights and applications, Phys. Status Solidi B, 2011, 248, 775–789.
50. M. Gerosa, C. E. Bottani, L. Caramella, G. Onida, C. Di Valentin and G. Pacchioni, Electronic structure and phase stability of oxide semiconductors: performance of dielectric-dependent hybrid functional DFT, benchmarked against G W band structure calculations and experiments, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 1–15.
51. Z. Yang, F. Sottile and C. A. Ullrich, Simple screened exact-exchange approach for excitonic properties in solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035202.
52. R. Dalven, A review of the semiconductor properties of PbTe, PbSe, PbS and PbO, Infrared Phys., 1969, 9, 141–184.

---

Footnote

† Electronic supplementary information (ESI) available: Structural information, unshifted TD-BHLYP spectra, TD-B3LYP spectra, ground and excited state charges, and Cartesian coordinates of all particles. See DOI: 10.1039/c5cp04851f

---