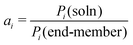Determination of the thermodynamic activities of LiF and ThF4 in the LixTh1−xF4−3x liquid solution by Knudsen effusion mass spectrometry
Received
11th August 2015
, Accepted 19th October 2015
First published on 26th October 2015
Abstract
Knudsen effusion mass spectrometry (KEMS) has been used to investigate the vapour pressure over the molten LiF–ThF4 salt and determine the thermodynamic activity of LiF and ThF4 in the liquid solution. As part of the study, the vaporization of pure LiF and pure ThF4 was examined and the results were compared with the literature values finding a good agreement. Next, the vapour pressure of the LixTh1−xF4−3x liquid solution was investigated by measuring four samples having different compositions (XLiF ∼ 0.2, 0.4, 0.6, 0.8 mol%). In order to determine the thermodynamic activities, the vapour pressure of LiF and ThF4 species over the liquid solution, as calculated from our results, were compared with the vapour pressure over the pure LiF(l) and pure ThF4(l) systems. A strong deviation from the Raoult's law was observed, more evident in case of LiF species, in agreement with the predictions by our thermodynamic model.
1 Introduction
The binary system LiF–ThF4 is a key system for various designs of the molten salt reactor (MSR). The MSR is one of the most promising future fission reactor technologies, selected by the Generation IV Forum, in which the fissile and fertile materials are dissolved into a molten salt mixture. Recent designs1,2 are based on a fast neutron spectrum reactor and on the thorium fuel cycle, therefore a crucial component is ThF4 which is dissolved mainly in the 7LiF solvent. In view of this fact, an extensive study is being conducted on the physico-chemical properties of the binary mixture LiF–ThF4 in order to determine the operation parameters and the safety limit of this technology. With respect to the reactor safety, one of the key parameter to be assessed is the vapour pressure of the salt mixture. A low pressure system offers the advantage of reducing the main driving force of radioactivity release during accidents and it is a beneficial parameter with regard to engineering issues. Furthermore, in a multi-component salt higher evaporation of one component in comparison with the others causes a change in the final composition of the mixture leading to a change in its thermodynamic properties. Since the salt composition is usually optimized to have the lowest liquidus temperature, a change in the concentrations would lead to an increase of the melting temperature and could approach the safety limit.
Vapour pressure measurements can be used to determine the activity of a species (such as LiF or ThF4) in a mixture, which is a measure of the thermodynamic stability of a system. These thermodynamic functions are extremely important in the development of thermodynamic models and they are particularly important in the context of the electrochemistry of the fuel salt. In fact, MSRs design includes a reprocessing of the fuel salt, mainly for separation of fissile material, actinides and fission products. Some of the steps of the global reprocessing scheme are based on the redox processes3 and thus on the electrochemical properties and the activities of the different elements and the solvent (LiF–ThF4).
The aim of the present work is to evaluate the vapour pressure over the molten LiF–ThF4 salt and determine the thermodynamic activities of the end-member species in the liquid solution. The system was investigated using Knudsen effusion mass spectrometry, which is a very well suited technique to measure high-temperature thermodynamic properties of condensed and gaseous phases. As first step, we have studied the vaporization of pure LiF and pure ThF4 focusing on the liquid phase. Rather good agreement was found between our results and the literature value. Next, the vapour pressure of the LixTh1−xF4−3x liquid solution was investigated by measuring four samples with different compositions (XLiF ∼ 0.2, 0.4, 0.6, 0.8 mol%). The vapour pressure of LiF and ThF4 species over the liquid solutions were compared with the vapour pressure over the pure LiF(l) and pure ThF4(l). From the observed difference with the ideal behaviour, the thermodynamic activity of LiF and ThF4 in the LixTh1−xF4−3x liquid solution were determined.
2 Experiment
2.1 Sample preparation
All the samples measured in this work were prepared from pure lithium fluoride LiF, obtained from Alfa Aesar, and pure thorium fluoride ThF4, obtained from Rhodia. Since fluorides are very sensitive to water molecules, the materials were stored in a protective atmosphere and the preparation of the samples was done completely inside an argon glove box, where a low level of oxygen and water is ensured (typically below 5 ppm). Moreover, both compounds have been subjected to pre-treatments to ensure the high purity of the starting materials. In case of LiF compound, it consists of a heating cycle at 623 K for several hours under inert argon flow in order to remove the residual moisture, if present. Different treatment is required for ThF4 that shows an additional tendency to oxidize and form oxyfluorides. A purification technique was applied using NH4HF2 as fluorinating agent as described in detail elsewhere.4 The purity of both compounds was then checked by identification of the melting point using the differential scanning calorimeter(DSC), as described in our previous works.4,5 The samples were encapsulated to prevent possible reactions with water/oxygen and protect the instrument from corrosive fluoride vapours. The results were in close agreement with the literature value, within ±5 K.
In total six samples have been prepared as listed in Table 1, in which the exact composition and the liquidus temperature of each sample, as measured by DSC, are reported. Typically, an amount of salt about 30–50 mg was loaded into a nickel crucible and placed in the Knudsen cell for the measurement.
Table 1 Composition and liquidus temperature of the samples measured in this work
| Sample |
Molar fraction ThF4 |
Molar fraction LiF |
Liquidus temperature (K) |
| LiF |
0 |
1 |
1121.2 |
| Li0.8Th0.2F1.6 |
0.200 |
0.800 |
893.8 |
| Li0.6Th0.4F2.2 |
0.391 |
0.609 |
1044.6 |
| Li0.4Th0.6F2.8 |
0.598 |
0.402 |
1200.0 |
| Li0.2Th0.8F3.4 |
0.796 |
0.204 |
1303.0 |
| ThF4 |
1 |
0 |
1383.2 |
2.2 Setup and measurements
The experimental setup used in this work consists of a Knudsen effusion cell coupled to a quadrupole mass spectrometer, as shown in Fig. 1. The facility is specifically designed for radioactive materials and irradiated fuel samples and it is described in details elsewhere.6 The Knudsen cell (cell dimensions: h = 21 mm, ∅ = 11 m, orifice dimensions: d = 0.25 mm, ∅ = 0.5 mm) is made of tungsten with an inserted internal liner made of pure nickel in order to avoid possible corrosion by the fluoride vapours. Prior the measurement, the chamber is evacuated to high vacuum (10−8 to 10−9 kPa) so that no interference between atmosphere and sample gas molecules occurs. The cell is heated to high temperature using a tungsten-coil heating element and seven cylindrical shields, both in tungsten and tantalum, are placed around the cell to provide the required thermal isolation. The molecular beam emerging from the effusion orifice on the top of the cell is ionized by a cross electron beam and then analyzed by a quadrupole mass spectrometer.
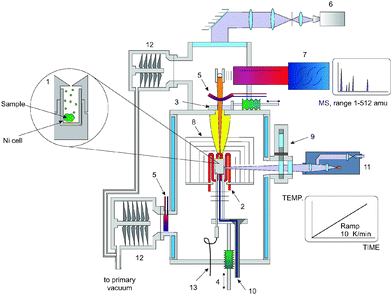 |
| | Fig. 1 The KEMS experimental setup used in this work. Main components: (1) Knudsen cell with Ni liner; (2) tungsten resistant coil; (3) molecular beam chopper; (4) facilities to lift the cell for fast heating/cooling; (5) liquid nitrogen trap to reduce background signal; (6) CCD camera to align the cell orifice and the chopper diaphragm; (7) quadrupole mass spectrometer; (8) thermal shield; (9) revolving protection windows; (10) inlet gas capillary; (11) linear pyrometer; (12) turbo molecular pump; (13) removable W/Re thermocouple. | |
Two main signals are measured during an investigation by the KEMS technique: the intensities of ion currents originating from the ionization of the evaporated gaseous species and the Knudsen cell temperature. The latter is measured using a pyrometer, which had been calibrated by determining the melting points (visible on the MS signal) of several standard materials (Zn, Cu, Fe, Pt, Al2O3). Furthermore, a calibration of the electron energy was performed prior the measurements by identifying the ionization potential of different gaseous and metal species (Ar, Kr, Xe, Zn, In, Ag).
A standard procedure was used for all the measurements performed, applying an electron ionization energy of 33.5 eV and a temperature ramp of 10 K min−1. The use of a continuous temperature increase, instead of isothermal steps, allows a good description over the widest possible temperature range in a relative short time. Nevertheless, equilibrium conditions are reached during the measurements as suggested by the reproducibility of the literature values for Ag, LiF and ThF4. The temperature was increased until both sample and standard material were quantitatively vaporized. Moreover, the possible reaction products between fluorine and tungsten were monitored but none of these masses were detected indicating that no corrosion occurred during the measurements. For the pure substances, appearance potentials measurements were also performed to identify dissociation processes. The intensity of each species was measured during two consecutive runs performed at constant temperature (1250 K for LiF and 1293 K for ThF4) and increasing the electron energy from 0.9 to 63.4 eV with step of 0.5 eV. The complete available energy range was scanned in order to have more information on the ionization process.
2.3 Mass spectral analysis
Under quasi equilibrium conditions (small ratio between the orifice cross section and the vaporising surface) and low pressure conditions, the partial pressure pA of the species A at the temperature T results from the following relation:| |  | (1) |
where K is the calibration factor, σA is the electron impact ionization cross section of the species A, 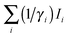 is the sum of intensities of the ion currents i originating from the molecule A considering the efficiency (γi) of the secondary electron multiplier (SEM) for each ion mass.
is the sum of intensities of the ion currents i originating from the molecule A considering the efficiency (γi) of the secondary electron multiplier (SEM) for each ion mass.
The calibration factor K is determined based on the quantitative evaporation of a known amount of a standard material, in our case silver, placed in the Knudsen cell during the measurements. The mass loss rate of silver dm/dt is given by the Hertz–Knudsen equation as follows:
| | 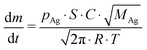 | (2) |
where
pAg is the vapour pressure of silver,
T is the temperature,
MAg is the molar mass of silver,
R is the universal gas constant,
S is the effusion orifice surface and
C is the Clausing factor. The latter term is the correction for an orifice with short but finite channel as reported by Santeler.
7 By integration over the measurement time of the Hertz–Knudsen equation combined with
eqn (1) for
pAg, it is possible to determine the calibration factor K.
| | 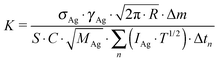 | (3) |
where
σAg is the electron impact ionization cross section of silver,
γAg is the efficiency of secondary electron multiplier for silver, Δ
m is the total mass evaporated and the term
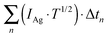
is the integrated product between the intensity of silver ion current and the temperature along the time of the experiments. In addition to this method, the calibration factor can be determined using the well-known vapour pressure of silver.
8
2.3.1 Ionization cross sections and efficiencies of SEM.
As described in the previous section, the determination of the absolute vapour pressure requires the knowledge of the efficiency of the SEM for each recorded ion and the electron impact ionization cross section of the molecular species. A detailed explanation on the estimation of these properties as applied in this work is given in this section.
The efficiency of the secondary electron multiplier depends on the mass of the species detected and is usually approximed, as suggested by Grimley,9 to:
where
δ is a constant and
Mi is the molar mass of the species
i. Using
eqn (4) the normalized SEM gains
γi/
γAg for the species Th
+, ThF
+, ThF
2+, ThF
3+ were determined as 0.68, 0.66, 0.63, 0.61 respectively. However, this approximation is good only for mass numbers greater than 50 amu and in case of the lighter species (Li
+, LiF
+, Li
2F
+) could not be applied. For that reason, the normalized SEM gains
γi/
γAg for the species Li
+, LiF
+, Li
2F
+ and Li
3F
2+ (0.87, 1.47, 1.66 and 2.48) were taken from Yamawaki
et al.10 and for more details of obtaining these values we refer to that study.
The second important term is the electron impact ionization cross section, which depends on the electron energy. For single atoms, the ionization cross sections have been computed by Mann11,12 and are available for a large range of energy. In this work, the SIGMA software,13 which is based on Mann's values, has been used for the calculation of the atomic cross sections. The case of molecules is more complex and the additivity rule postulated by Otvos and Stevenson14 is generally used. Following this rule, the cross section of a molecule is calculated as sum of the cross sections of the single components. However, this “simple” approach is not giving good estimations in case of complex molecules, such as ThF4 in the present case. If we consider as an example the similar SiF4 molecule, a clear contradiction of the additivity rule has been observed. In fact, for the series SiF, SiF2, SiF3 and SiF4, the ionization cross section decreases with increasing number of fluorine atoms (σSiF4 < σSiF3 < σSiF2 < σSiF). This discrepancy was explained by Deutsch et al.15 as an effect of the molecular bonding and weighting factors have to be introduced to take this effect into account. A modified additivity rule16 has been proposed for the calculation of total electron impact cross sections of molecules of the form ABn, as given by the following equation:
| | | σ+(ABn) = [rA2/rB2]α[ξA/(ξA + nξB)]σA+ + [nrB2/rA2]β[nξB/(ξA + nξB)]nσB+ | (5) |
where
rA and
rB are the atomic radii, taken from the table of Desclaux,
17ξA and
ξB are the effective number of atomic electrons and
σA and
σB are the atomic ionization cross sections calculated at the correct ionization energy. The exponents
α and
β are explicitly dependent on
rA,
rB,
ξA and
ξB and they are determined empirically (see details in
ref. 16).
Since no experimental data on the electron impact ionization cross section of ThF4 have been found in literature, the value was calculated based on eqn (5) and using parameters reported in Table 2. In this case the dependency of the cross section on energy is expressed solely by the energy dependence of the individual atomic ionization cross section, as follows:
| | | σ+(ThF4) = 0.44σTh+ + 2.08σF+. | (6) |
Table 2 Effective number of electrons, atomic radii from the tables of Desclaux17 and ionization cross-section at 33.5 eV (used in this study) calculated from SIGMA software13
| Atom |
Effective number of electron |
Atomic radius (cm) |
Ionization cross-section (cm2) |
| Th |
22 |
19.37 × 10−9 |
16.6974 × 10−16 |
| F |
7 |
3.81 × 10−9 |
0.7329 × 10−16 |
This relation gives, for the ionization energy used in our measurement, a total ionization cross section for ThF4 of σThF4 = 8.9184 × 10−16 cm2. In case of the LiF related species, the ionization cross section normalized to silver σi/σAg for the monomer, dimer and trimer was estimated to be 0.61, 0.71 and 0.85 as reported by Yamawaki et al.10 for a similar ionization energy as used in this study.
2.3.2 Thermodynamic calculations.
Calculations of thermochemical data for pure LiF and pure ThF4 were performed using both second law and third law approaches. Second law enthalpies of reaction (vaporization or sublimation) ΔrH0T are obtained based on the equilibrium constant measurement in a certain range of temperature, as given by the equation:| | 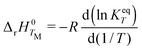 | (7) |
where R is universal gas constant, KeqT is the equilibrium constant of the vaporization reaction and TM is the mean temperature of the measurement. For a simple vaporization process, such as A(s) = A(g) or A(l) = A(g), the equilibrium constant is given by the following equation:| |  | (8) |
in which a(g), a(s) and a(l) are activities of the gas phase, the solid phase and the liquid phase respectively. Since activities of solids and liquids in equilibrium are equal to unity, KeqT becomes:| |  | (9) |
where P(g) is the equilibrium pressure and P0 is the standard pressure (105 Pa). Thus, a plot of ln(P(g)/P0) versus 1/T gives a linear relation with a slope 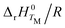 . The reaction enthalpy refers to the average temperature (1/T) of the measurements and it is converted to the reaction enthalpy at the standard temperature ΔrH0298 by using the reported Cp function for the different phases. The enthalpy of fusion was also considered to calculate the sublimation enthalpy from the liquid state data.
. The reaction enthalpy refers to the average temperature (1/T) of the measurements and it is converted to the reaction enthalpy at the standard temperature ΔrH0298 by using the reported Cp function for the different phases. The enthalpy of fusion was also considered to calculate the sublimation enthalpy from the liquid state data.
The third law approach is based on similar equations but requires in addition the knowledge of the standard entropy function S0T for all the phases. The enthalpy of the reaction at the standard temperature is given by the following equation:
| | ΔrH0298 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KeqT + TΔfefT KeqT + TΔfefT | (10) |
where fef
T is the free energy function which is defined for each phase as:
| | 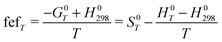 | (11) |
This results in an enthalpy of reaction for each data point and the average is taken from all the data. The thermodynamic functions for the third law calculation were taken from
ref. 18 for the LiF and from
ref. 19 and 20 for ThF
4 solid and gas phases. In case of the ThF
4 liquid phase, the data have been taken from our previous work
21 where they have been revised.
3 Results
3.1 Vapour pressure of pure LiF
The lithium fluoride vaporization has been studied by different authors during the past years using different techniques, such as the Miller and Kusch method22 (re-plotted by Scheefee et al.23), the KEMS technique,10,24–26 a double-oven apparatus27 and the torsion-effusion method.28 As established by all the authors, the LiF vapour system contains monomer, dimer and trimer species but some discrepancies on their relative amounts have been found owing to assumptions concerning the electron-impact ionization cross section and the ion–neutral precursor assignment.
In this work, four main ions were observed in the mass spectrum, namely Li+, LiF+, Li2F+, Li3F2+, in accordance with the literature works. The attribution of the measured molar mass to the respective ion was confirmed by the identification of the correct isotopic ratio (natural abundance: 7Li 92.41% and 6Li 7.59%). For each ion species, the ionization efficiency curve at fixed temperature was also recorded as illustrated in Fig. 2. Based on these results, the appearance energies of the ions were determined and they are listed in Table 3 in which the measured values are compared with literature. As mentioned before, although the LiF vapour system has been the subject of numerous investigations, there is disagreement in literature on the identity of the neutral precursors of each ions. In particular, the ions Li+ and LiF+ could be produced by different mechanisms from monomer, dimer or from both species. Since our measurements showed no clear inflection in the linear portion of the ionization efficiency curves, thus indicating no dissociation of molecules, as first attempt we considered that both ions (Li+ and LiF+) are generated only from the monomer. Using this approach, the resulting dimer pressure was found to be considerable lower than the literature value. Therefore, a different fragmentation path was tested, as given in one of the most recent work on LiF compound performed by Bonnell et al.26 Using a phase-sensitive mass spectral analysis, they report for similar ionization energy the following ion–precursor combinations: Li+ [90.4% LiF–9.6% Li2F2], LiF+ [18% LiF–71% Li2F2–11% Li3F3], Li2F+ [99.5% Li2F2–0.5% Li3F3] Li3F2+ [100% Li3F3]. This fragmentation path is not in disagreement with our experimental results when considering that most of the processes (i.e. for LiF+: simple ionization LiF + e− → LiF+ + 2e− and fragmentation Li2F2 + e− → LiF+ + LiF + 2e−) are probably within few eV (ref. 29) and a better energy resolution is needed to identify the slope changes. Applying the precursor partition as reported by Bonnell et al.,26 the best agreement with literature was observed for both monomer and dimer pressure, thus it was considered in all the calculations in this work. It is important to notice that although there are some uncertainties in the assignment of the neutral precursors to the ions, the different assumptions do not strongly influence neither the total vapor pressure of the salt (mainly given by the monomer) nor the activities (providing a consistent analysis for all the measurements).
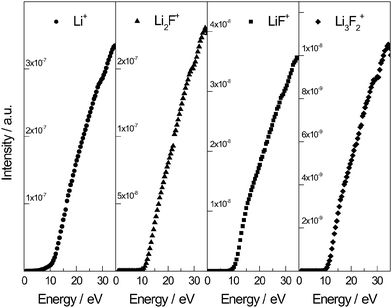 |
| | Fig. 2 Ionization efficiency curves measured for the ions Li+, LiF+, Li2F+, Li3F2+. The intensity of the signal is reported as function of the calibrated energy in the range between 0 and 35 eV. | |
Table 3 Appearance energy of the ion species detected by the mass spectrometer
| Reaction |
Appearance energy (eV) |
| Measured |
Literature |
| LiF + e− → Li+ + F + 2e− |
11.5 ± 0.5 |
11.5,27 11.825 and 11.410 |
| LiF + e− → LiF+ + 2e− |
11.8 ± 0.5 |
11.3,27 11.825 and 11.110 |
| Li2F2 + e− → Li2F+ + F + 2e− |
11.3 ± 0.5 |
11.5,27 13.025 and 11.710 |
| Li3F3 + e− → Li3F2+ + F + 2e− |
12.3 ± 0.5 |
12.325 and 11.410 |
| ThF4 + e− → Th+ + 4F + 2e− |
33.0 ± 0.5 |
3930 |
| ThF4 + e− → ThF+ + 3F + 2e− |
29.1 ± 0.5 |
3030 |
| ThF4 + e− → ThF2+ + 2F + 2e− |
21.1 ± 0.5 |
23.230 and 21.031 |
| ThF4 + e− → ThF3+ + F + 2e− |
13.4 ± 0.5 |
14.530 and 13.531 |
The experimental data measured in this work are shown in Fig. 3, where the vapour pressure of all the gaseous species LiF, Li2F2, Li3F3 are reported. Two LiF samples were measured under the same experimental conditions and the comparison confirms the reproducibility of the measurement. The results have been compared with the data calculated from the FactSage software32 based on the JANAF tables18 and the agreement is very good except for the trimer species. Such a discrepancy may arise from the low ion currents of the trimer, but we must note that our result is in line with the results obtained by other authors. The vapour pressure data of liquid phase of LiF (from 1121 K to 1352 K) were fitted using a least-square method and the following equations were found to represent the monomer, dimer and trimer pressure:
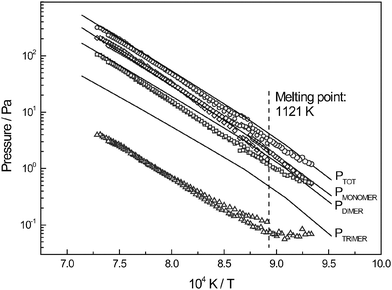 |
| | Fig. 3 Vapour pressure of lithium fluoride LiF. (○) Total pressure over LiF measured in this work. (◇) Data measured in this work for the monomer species. (□) Data measured in this work for the dimer species. (△) Data measured in this work for the trimer species. (—) Data calculated using FactSage software based on JANAF table.18 | |
Monomer:
| | ln(P/Pa) = (25.893 ± 0.124) − (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 ± 159)(T/K)−1 064 ± 159)(T/K)−1 | (12) |
Dimer:
| | ln(P/Pa) = (24.886 ± 0.055) − (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 ± 69)(T/K)−1 707 ± 69)(T/K)−1 | (13) |
Trimer:
| | ln(P/Pa) = (19.305 ± 0.161) − (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 ± 203)(T/K)−1. 566 ± 203)(T/K)−1. | (14) |
In addition, the enthalpy of sublimation have been calculated for all the LiF gaseous species using the second and third law methods, as described in Section 2.3.2. The results are summarized in
Table 4. A very good agreement between second and third law calculations was observed for the monomer while a slightly higher discrepancy was observed for dimer and trimer. Moreover, the results fit very well within the literature values.
Table 4 Enthalpy of sublimation ΔsH0298 (kJ mol−1) of LiF(s) at 298.15 K for the three found gaseous species
| Researchers |
ΔsH0298 (LiF) |
ΔsH0298 (Li2F2) |
ΔsH0298 (Li3F3) |
|
Second law calculation.
Third law calculation.
|
| Yamawaki et al.10 (1982)a |
284.5 ± 6.7 |
309.6 ± 7.1 |
326.7 ± 18.4 |
| Yamawaki et al.10 (1982)b |
283.3 ± 7.1 |
301.2 ± 7.1 |
349.9 |
| Grimley et al.25 (1978)a |
272.2 ± 2.1 |
308.1 ± 1.7 |
337.4 ± 1.3 |
| Snelson et al.33 (1969)a |
285.2 ± 4.6 |
337.2 ± 5.4 |
428.4 ± 6.7 |
| JANAF tables18 (1968) |
276.1 |
291.1 |
333.6 |
| Glushko tables34 (1982) |
277.4 ± 3 |
|
|
|
|
| Present worka |
277.9 ± 1.5 |
316.6 ± 1 |
333.5 ± 1.5 |
| Present workb |
277.48 ± 2 |
301.6 ± 8.2 |
360.3 ± 18.4 |
3.2 Vapour pressure of pure ThF4
There are three studies on the vapour pressure of ThF4(s) and ThF4(l), performed by Darnell et al.,35 Lau et al.31 and Nagarajan et al.36 The composition of the vapour phase is very simple, consisting of only ThF4(g) in the monomeric form. The observed ions in the mass spectrum of the vapour effusing from the cell were Th+, ThF+, ThF2+ and ThF3+ and the appearance potentials of these ions, as measured in this work (Fig. 4), are listed in Table 3. No evidences were found during the measurement for the presence of ThO2 or ThOF2 impurities in the salt.
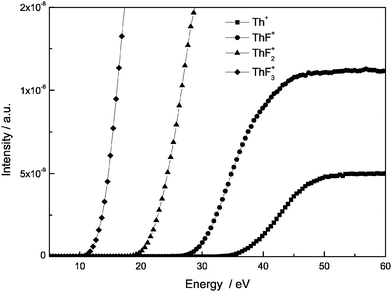 |
| | Fig. 4 Ionization efficiency curves measured for the ions Th+, ThF+, ThF2+, ThF3+. The intensity of the signal is reported as function of the calibrated energy in the range between 0 and 60 eV. | |
The measurements were performed from 1000 K to 1457 K when the complete evaporation of the sample was reached. Fig. 5 shows the results obtained, which are in good agreement with the literature. The total vapor pressure of solid and liquid ThF4 can be represented by the following equations:
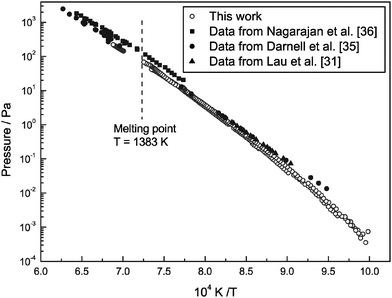 |
| | Fig. 5 Vapour pressure of thorium tetrafluoride ThF4. (○) Data measured in this work. (■) Data from Nagarajan et al.36 (●) Data from Darnell et al.35 (▲) Data from Lau et al.31 | |
Solid
ln(P/Pa) = (36.045 ± 0.101) − (43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 493 ± 124)(T/K)−1 493 ± 124)(T/K)−1 |
Liquid
| | ln(P/Pa) = (29.386 ± 0.124) − (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 ± 180)(T/K)−1. 858 ± 180)(T/K)−1. | (15) |
Also in the case of ThF
4 compound, the enthalpy of sublimation was determined by second and third law. The calculations gave Δ
sH0298 = 359.25 ± 2.6 kJ mol
−1 from second law method and Δ
sH0298 = 353.8 ± 2.5 kJ mol
−1 from third law method, similar to the selected literature value
37 of Δ
sH0298 = 349.3 ± 2 kJ mol
−1.
3.3 Vapour pressure of the LixTh1−xF4−3x liquid solution
The vapour pressure of the LixTh1−xF4−3x liquid solution was studied in this work for the first time. In order to understand the behaviour in the whole composition range, four binary mixtures were prepared with concentration step of 0.2 mol% and they were measured under the same experimental conditions as the end-members. The mass spectrum of all the samples showed the presence of the same ions, Li+, LiF+, Li2F+, Th+, ThF+, ThF2+, ThF3+ in addition to the reference signal Ag+, with different relative intensities. The Li3F2+ signal was too low to be detected in most of the cases and no evidences for formation of Li–Th molecules in the gaseous phase were found by scanning the complete range of molar masses. We note here that as reported in literature,38 the formation of an intermediate compound in the gas phase has been observed for several ionic halide systems and often the main ion formed after electron impact is Li+. In this case, it is not straightforward to separate the contribute to the ion signal from LixThyF4y+x(g) and from LiF(g), respectively. In absence of any experimental evidence on the formation of such compounds, none was consider in our analysis.
As an example, the temperature function of the mass spectrum of Li0.4Th0.6F2.8 is shown in Fig. 6, in which only the major isotopes are reported for clarity reasons. Since our method does not allow the determination of the background signal and the sample signal simultaneously, no background treatment has been performed. However, background intensities are very small in comparison to the overall signal in the temperature range considered for the analysis. It is important to notice that all the signals, except the reference, dropped after the complete vaporization at the same temperature/time giving a strong indication of the complete mixing between the end-members LiF and ThF4. The maximum temperature reached is around 1450 K, determined by complete vaporization of the salt in very low pressure conditions. In different conditions, for instance at ambient pressure, the salts are far from their boiling points and the complete vaporization would occur at higher temperatures.
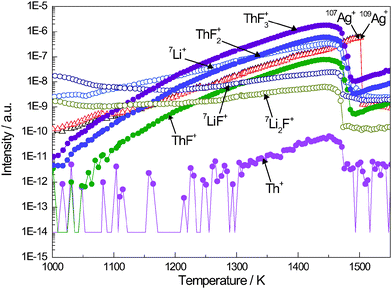 |
| | Fig. 6 The ion intensities versus temperature obtained for the intermediate composition Li0.4Th0.6F2.8. The main species recorded are: Li+, LiF+, Li2F+ (○), Th+, ThF+, ThF2+, ThF3+ (●) plus the reference signal Ag+ (△). Only the intensities of the most intensive isotope is given in each case. | |
The vapour pressure of the liquid mixtures was calculated in the range of temperature between the liquidus temperature of the binary mixture and the maximum temperature reached (complete vaporisation of the sample). All the data have been analysed using the same approach and the equations obtained for the partial pressure of the major species, LiF and ThF4, are summarized in Table 5. The plot of the vapour pressure measured as function of the composition of the liquid is shown in Fig. 7 for the LiF and ThF4 species.
Table 5 Vapor pressure equations for the LiF and ThF4 species over the LiF–ThF4 liquid solution
| Sample name |
Species |
Vapor pressure equation |
Measured temperature interval (K) |
| Li0.8Th0.2F1.6 |
LiF |
ln(P/Pa) = (21.428 ± 0.128) − (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 ± 161)(T/K) 940 ± 161)(T/K) |
1302–1443 |
| ThF4 |
ln(P/Pa) = (41.451 ± 0.140) − (53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 ± 180)(T/K) 818 ± 180)(T/K) |
|
|
| Li0.6Th0.4F2.2 |
LiF |
ln(P/Pa) = (22.916 ± 0.221) − (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439 ± 274)(T/K) 439 ± 274)(T/K) |
1202–1432 |
| ThF4 |
ln(P/Pa) = (33.046 ± 0.062) − (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 ± 127)(T/K) 905 ± 127)(T/K) |
|
|
| Li0.4Th0.6F2.8 |
LiF |
ln(P/Pa) = (19.742 ± 0.094) − (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 ± 122)(T/K) 783 ± 122)(T/K) |
1123–1441 |
| ThF4 |
ln(P/Pa) = (29.643 ± 0.128) − (35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 ± 168)(T/K) 886 ± 168)(T/K) |
|
|
| Li0.2Th0.8F3.4 |
LiF |
ln(P/Pa) = (17.755 ± 0.223) − (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 ± 32)(T/K) 455 ± 32)(T/K) |
1122–1443 |
| ThF4 |
ln(P/Pa) = (26.411 ± 0.322) − (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 ± 444)(T/K) 232 ± 444)(T/K) |
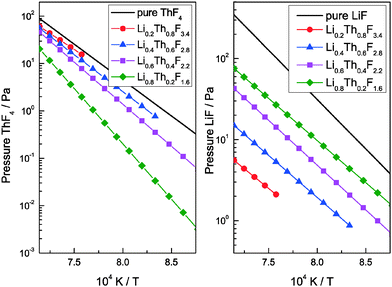 |
| | Fig. 7 Left graph: Comparison between the LiF vapour pressure (monomer) for the pure LiF liquid phase and for the LixTh1−xF4−3x liquid solution. Right graph: Comparison between the ThF4 vapour pressure for the pure ThF4 liquid phase and for the LixTh1−xF4−3x liquid solution. The vapour pressure of ThF4 has been extrapolated for temperature lower than the melting point from the equation of the liquid state. | |
Using the data obtained in this study for pure compounds and binary mixtures, the thermodynamic activities of both species in the liquid solution were determined. In general, the activity of one species is given by the relation:
| | 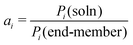 | (16) |
where
Pi(soln) is the vapour pressure of the species
i in the solution and
Pi(end-member) is the vapour pressure of the end-member species
i. Following this relation, the activities of LiF and ThF
4 have been calculated as function of the molar fraction and temperature. The reference state for pure ThF
4 is the supercooled liquid, as derived by extrapolation from the equation of the vapour pressure of the liquid phase (
eqn (15)). The results are plotted for three selected temperature 1200 K, 1300 K and 1400 K in
Fig. 8. In case of the LiF species, an alternative method to calculate the thermodynamic activity was also applied. In fact when both monomer and dimer are present in the salt vapor, the activity can be calculated directly from ion intensities,
39 as given by the following equation:
| |  | (17) |
where
ILi+ and
ILiF2+ are the intensities of the ion Li
+ and LiF
2+ for the pure component and for the mixed samples. This method, which is in principle applicable only when the ion intensities Li
+ and LiF
2+ result solely from the LiF and Li
2F
2 respectively, offers the advantage to give the value of the thermodynamic activities without necessity of pressure calibration. The results obtained with this method are in fair agreement with the activities calculated from absolute vapour pressure and the comparison between the two methods was used to estimate the uncertainty on the activity determination. For each measurement, the average deviation of the two methods was calculated and the maximum of those values (about 18%) was considered, in a first approximation, as the error of the thermodynamic activities of LiF and ThF
4.
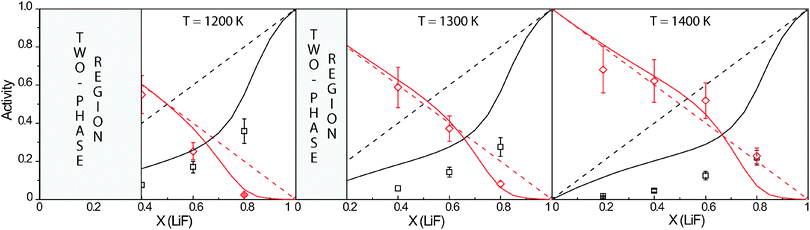 |
| | Fig. 8 Activities of LiF and ThF4 in the LixTh1−xF4−3x liquid solution as function of LiF molar fraction at T = 1200 K, 1300 K and 1400 K. The results are reported in red for the ThF4 species and in black for the LiF species. Dotted lines: Ideal behaviour of activity as calculated from Raoult's law. Solid lines: Activities calculated based on the thermodynamic model developed.4 (□) Measured activity of LiF. (◇) Measured activity of ThF4. | |
The results on the activity of the end members LiF and ThF4 in the LixTh1−xF4−3x liquid solution are shown in Fig. 8. The dashed lines in the figure represent the behaviour of the activities for an ideal solution which is given by the Raoult's law:
where
Xi is the molar fraction of the gaseous species
i. The results clearly show a strong deviation from the ideality of the Li
xTh
1−xF
4−3x liquid solution, more evident in case of LiF species. There is a strong connection between the microscopic structure and the deviation of the vapour pressure from the ideality. In ideal mixtures, the assumption is that at the microscopic level the intermolecular forces between two different molecules (LiF–ThF
4) are equal to those between similar molecules (LiF–LiF and ThF
4–ThF
4, respectively). The lesser the extent to which these criteria are true the greater the deviations of the partial pressures from their linear dependency on the mole fractions. The significant deviation from ideality of the studied system has been observed also for the enthalpy of mixing, as reported in our previous work.
4
For comparison, the solid lines in Fig. 8 represent predictions from the thermodynamic model developed for the LiF–ThF4 system.4 This assessment was performed considering the available experimental data on the binary system, that were the phase diagram temperatures, the enthalpy of fusion of the Li3ThF7 compound and the enthalpy of mixing of the liquid solution. Considering this fact, the agreement obtained between predictions and experiments is rather good. An higher discrepancy is observable in case of the LiF species, especially with increasing temperature, but the agreement is very good for the ThF4 species. It can thus be concluded that the model correctly predicts the general behaviour of the thermodynamic activities as function of composition and this confirms that the thermodynamic model predicts the mixture properties correctly.
4 Conclusions
This work presents the determination of the thermodynamic activities of LiF and ThF4 in the LixTh1−xF4−3x liquid solution. Knudsen effusion mass spectrometry has been successfully applied to measure fluoride samples at high temperatures. First the end-members LiF and ThF4 were investigated and next some selected intermediate compositions. The results for the end-members were found to be in very good agreement with the literature data for appearance potential, vapour pressure and enthalpy of sublimation. Afterwards, the same experimental procedure was applied to four different compositions of the LixTh1−xF4−3x liquid solution and its vapour pressure was determined for the first time. Based on these measurement the thermodynamic coefficients of LiF and ThF4 in the LixTh1−xF4−3x liquid solution were determined.
As mention in the introduction, these type of the data are of great interest to evaluate the safety and the performance of the MSR fuel as well as to evaluate the reprocessing scheme. The experimental results confirm that the LixTh1−xF4−3x liquid solution has low vapour pressure and it is therefore compatible with a low operating pressure of the reactor. Moreover, the experimental results fit well with the predictions based on the previously published thermodynamic model,4 confirming the reliability of the developed database.
Acknowledgements
E. C. acknowledge the European Commission for support given in the frame of the program “Training and Mobility of Researchers”. This work was supported by the EVOL project in the 7th Framework Programme of the European Commision (Grant agreement No. 249696).
References
- S. Delpech, E. Merle-Lucotte, D. Heuer, M. Allibert, V. Ghetta, C. Le-Brun, X. Doligez and G. Picard, J. Fluorine Chem., 2009, 130, 11–17 CrossRef CAS PubMed.
- A. Nuttin, D. Heuer, A. Billebaud, R. Brissot, C. L. Brun, E. Liatard, J.-M. Loiesaux, L. Mathieu, O. Meplan, E. Merle-Lucotte, H. Nifenecker and F. Perdu, Prog. Nucl. Energy, 2005, 46, 77–99 CrossRef CAS PubMed.
- S. Delpech, Pure Appl. Chem., 2013, 85, 71–87 CAS.
- E. Capelli, O. Beneš, M. Beilmann and R. J. M. Konings, J. Chem. Thermodyn., 2013, 58, 110–116 CrossRef CAS PubMed.
- O. Beneš, R. J. M. Konings, S. Wurzer, M. Sierig and A. Dockendorf, Thermochim. Acta, 2010, 509, 62–66 CrossRef PubMed.
- J.-P. Hiernaut, J.-Y. Colle, R. Pflieger-Cuvellier, J. Jonnet, J. Somers and C. Ronchi, J. Nucl. Mater., 2005, 344, 246–253 CrossRef CAS PubMed.
- D. Santeler, J. Vac. Sci. Technol., A, 1986, 4, 338–343 CAS.
-
R. Hultgren, R. Orr, P. Anderson and K. Kelley, Selected Value of Thermodynamic Properties of Metals and Alloys, John Wiley and Sons, Inc., 1963 Search PubMed.
-
R. Grimley, in The Characterization of High Temperature Vapors, ed. J. Margrave, John Wiley and Sons, 1967, ch. 8 Search PubMed.
- M. Yamawaki, M. Hirai, M. Yasumoto and M. Kanno, J. Nucl. Sci. Technol., 1982, 19, 563–570 CrossRef CAS PubMed.
-
J. Mann, Proc. Int. Conf on Mass Spectrometry, Baltimore, Tokyo and New York, 1970, pp. 814–819 Search PubMed.
- J. Mann, J. Chem. Phys., 1967, 46, 1646–1651 CrossRef CAS PubMed.
-
D. Bonnell and J. Hastie, Program SIGMA, a Fortran code for computing atomic ionization cross sections, NIST, Gaithersburg, MD, 1990–1997, unpublished work Search PubMed.
- J. Otvos and D. Stevenson, J. Am. Chem. Soc., 1956, 78, 546–551 CrossRef CAS.
- H. Deutsch, C. Cornelissen, L. Cespiva, V. Bonacic-Koutecky and D. Margreiter, Int. J. Mass Spectrom. Ion Processes, 1993, 129, 43–48 CrossRef CAS.
- H. Deutsch, K. Becker and T. Märk, Int. J. Mass Spectrom. Ion Processes, 1997, 167, 503–517 CrossRef.
- J. Desclaux, At. Data Nucl. Data Tables, 1973, 12, 311–406 CrossRef CAS.
-
M. W. Chase Jr, NIST-JANAF Thermochemical Tables Fourth Edition, J. Phys. Chem. Ref. Data, 1998, vol. 9 Search PubMed.
-
R. J. M. Konings, J. P. M. van der Meer and E. Walle, Chemical aspects of Molten Salt Reactor Fuel, European Commission Joint Research Centre, 2005 Search PubMed.
-
D. Wagman, R. Schumm and V. Parker, A computer assisted evaluation of the thermochemical data of the compounds of thorium, NBSIR-77-1300, 1977 Search PubMed.
- E. Capelli, O. Beneš and R. Konings, J. Nucl. Mater., 2014, 449, 111–121 CrossRef CAS PubMed.
- M. Eisenstadt, G. Rothberg and P. Kusch, J. Chem. Phys., 1958, 29, 797–804 CrossRef CAS PubMed.
- R. Scheffee and J. Margrave, J. Chem. Phys., 1959, 31, 1682–1683 CrossRef CAS PubMed.
- R. Porter and R. Schoonmaker, J. Chem. Phys., 1958, 29, 1070–1074 CrossRef CAS PubMed.
- R. Grimley, J. Forsman and Q. Grindstaff, J. Phys. Chem., 1978, 82, 632–638 CrossRef CAS.
- D. Bonnell, J. Hastie and K. Zmbov, High Temp. – High Pressures, 1988, 20, 251–262 CAS.
- J. Berkowitz, H. Tasman and W. Chupka, J. Chem. Phys., 1962, 36, 2170–2179 CrossRef CAS PubMed.
- D. Hildenbrand, W. Hall, F. Ju and N. Potter, J. Chem. Phys., 1964, 40, 2882–2890 CrossRef CAS PubMed.
- M. Veljkovic, O. Neskovic, M. Miletic and K. Zmbov, J. Serb. Chem. Soc., 1993, 58, 101–108 CAS.
- K. Zmbov, J. Inorg. Nucl. Chem., 1970, 32, 1378–1381 CrossRef CAS.
- K. Lau, R. Brittain and D. Hildenbrand, J. Chem. Phys., 1989, 90, 1158–1164 CrossRef CAS PubMed.
-
C. W. Bale, et al., FactSage Software, v.6.2 Search PubMed.
- A. Snelson, J. Chem. Phys., 1969, 73, 1919–1928 CrossRef CAS.
-
V. P. Glushko, L. V. Gurvich, G. A. Bergman, I. V. Veyts, V. A. Medvedev, G. A. Khachkuruzov and V. S. Yungman, Termodinamicheskie Svoistva Individual'nykh Veshchestv. Tom IV, Nauka, Moscow, 1982 Search PubMed.
- A. Darnell and F. Keneshea, J. Phys. Chem., 1958, 62, 1143–1145 CrossRef CAS.
- K. Nagarajan, M. Bhupathy, R. Prasad, Z. Singh, V. Venugopal and D. Sood, Thermochim. Acta, 1980, 36, 85–89 CrossRef CAS.
-
M. Rand, J. Fuger, I. Grenthe, V. Neck and D. Rai, Chemical Thermodynamics of Thorium, OECD Nuclear Energy Agency, Paris, 2008 Search PubMed.
-
K. Hilpert, Chemistry of inorganics vapors, in Structure and Bonding, Noble Gas and High Temperature Chemistry, ed. J. Clarke and J. B. Goodenough, Springer, Berlin, 1990, pp. 97–195 Search PubMed.
- J. Berkowitz and W. Chupka, Ann. N. Y. Acad. Sci., 1960, 79, 1073–1078 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
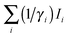 is the sum of intensities of the ion currents i originating from the molecule A considering the efficiency (γi) of the secondary electron multiplier (SEM) for each ion mass.
is the sum of intensities of the ion currents i originating from the molecule A considering the efficiency (γi) of the secondary electron multiplier (SEM) for each ion mass.
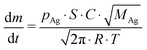
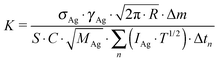
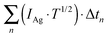 is the integrated product between the intensity of silver ion current and the temperature along the time of the experiments. In addition to this method, the calibration factor can be determined using the well-known vapour pressure of silver.8
is the integrated product between the intensity of silver ion current and the temperature along the time of the experiments. In addition to this method, the calibration factor can be determined using the well-known vapour pressure of silver.8
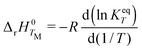


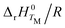 . The reaction enthalpy refers to the average temperature (1/T) of the measurements and it is converted to the reaction enthalpy at the standard temperature ΔrH0298 by using the reported Cp function for the different phases. The enthalpy of fusion was also considered to calculate the sublimation enthalpy from the liquid state data.
. The reaction enthalpy refers to the average temperature (1/T) of the measurements and it is converted to the reaction enthalpy at the standard temperature ΔrH0298 by using the reported Cp function for the different phases. The enthalpy of fusion was also considered to calculate the sublimation enthalpy from the liquid state data.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KeqT + TΔfefT
KeqT + TΔfefT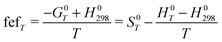


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 ± 159)(T/K)−1
064 ± 159)(T/K)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 ± 69)(T/K)−1
707 ± 69)(T/K)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 ± 203)(T/K)−1.
566 ± 203)(T/K)−1.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 493 ± 124)(T/K)−1
493 ± 124)(T/K)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 ± 180)(T/K)−1.
858 ± 180)(T/K)−1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 ± 161)(T/K)
940 ± 161)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 ± 180)(T/K)
818 ± 180)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439 ± 274)(T/K)
439 ± 274)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 ± 127)(T/K)
905 ± 127)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 ± 122)(T/K)
783 ± 122)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 ± 168)(T/K)
886 ± 168)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 ± 32)(T/K)
455 ± 32)(T/K)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 ± 444)(T/K)
232 ± 444)(T/K)