 Open Access Article
Open Access ArticleThermal instabilities and Rayleigh breakup of ultrathin silver nanowires grown in helium nanodroplets
Alexander
Volk
a,
Daniel
Knez
b,
Philipp
Thaler
a,
Andreas W.
Hauser
*a,
Werner
Grogger
b,
Ferdinand
Hofer
b and
Wolfgang E.
Ernst
*a
aInstitute of Experimental Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria. E-mail: andreas.w.hauser@gmail.com; wolfgang.ernst@tugraz.at; Fax: +43 (316) 873 108140; Tel: +43 (316) 873 8157 Tel: +43 (316) 873 8140
bInstitute for Electron Microscopy and Nanoanalysis & Graz Centre for Electron Microscopy, Graz University of Technology, Steyrergasse 17, A-8010 Graz, Austria
First published on 10th September 2015
Abstract
Ag nanowires with diameters below 6 nm are grown within vortex containing superfluid helium nanodroplets and deposited onto a heatable substrate at cryogenic temperatures. The experimental setup allows an unbiased investigation of the inherent stability of pristine silver nanowires, which is virtually impossible with other methods due to chemical processes or templates involved in standard production routes. We demonstrate by experiment and by adaption of a theoretical model that initially continuous wires disintegrate into chains of spheres. This phenomenon is well described by a Rayleigh-like breakup mechanism when the substrate is heated to room temperature. Our findings clarify the recent discussions on the cause of the observed segmented patterns, where a breakup during deposition [Gomez et al., Phys. Rev. Lett., 2012, 108, 155302] or mechanisms intrinsic to the helium droplet mediated growth process [Spence et al., Phys. Chem. Chem. Phys., 2014, 16, 6903] have been proposed. The experimental setup confirms the validity of previous suggestions derived from bulk superfluid helium experiments [Gordon et al., Phys. Chem. Chem. Phys., 2014, 16, 25229] for the helium droplet system, and further allows a much more accurate determination of the breakup temperature.
1 Introduction
One-dimensional nanostructures such as wires, rods and tubes, have attracted considerable attention due to their potential usage as building blocks in nanodevices,1,2 membranes,3 biosensors4–6 or waveguides.7 Ultrathin nanowires with diameters of less than 10 nm show a whole series of unusual properties such as ferromagnetism,8 negative magnetoresistance9 or quantum conductance,10 and have been suggested as components for miniature electronic circuits.11Superfluid helium nanodroplets (HeN) can be exploited as nanolabs for the production of 1D-structures without any chemical solvent, external field or template. Their applicability to studies of nanowire growth has been demonstrated recently.12,13 Doping of HeN with atoms, molecules or clusters is well established in spectroscopy,14–16 and has recently been adapted for the controlled production and structure preserving soft deposition of metal clusters.17–21 Helium droplets with diameters of about 1 μm, as used in this work, contain quantized vortices,22,23 a phenomenon attributed to superfluidity.24,25 As observed in bulk superfluid helium (He II),26–28 these vortices exhibit an attractive force on dopants immersed in the helium due to a pressure gradient around the vortex core,29,30 ultimately causing their agglomeration into nanowires.31–33
While continuous wires from Au, Ni, Cr and Si were formed with the HeN technique,12 only segmented chains of clusters were found in the case of Ag.23,34 Several attempts were made to explain this observation, including the breakup of wires during surface deposition or the existence of forces intrinsic to the HeN–vortex–Ag system hindering the agglomeration process.23,34 However, none of these suggestions could be either confirmed or falsified by experiment due to the complicated setup which is necessary to synthesise metal wires in HeN. The droplets, moving at ≈200 m s−1, do not allow a direct observation of cluster growth and wire formation. Theory, on the other hand, is only beginning to understand the nature of vortices in superfluid helium, and therefore not able to deliver quantitative answers yet. Fortunately, the solution to the phenomenon of wire breakup is much simpler than was assumed in the literature.
In this article, we show by experiment and computer simulations that the degradation of ‘ultrathin’, He droplet-grown silver wires with diameters below 6 nm appears only after deposition to a surface and is strongly dependent on the substrate temperature. Although similar problems are well documented in the literature on the miniaturisation of optical or electronic devices, the breakup of He-mediated nanowires due to thermal instabilities had not been taken into consideration. This might be due to the fact that the crucial temperatures for wire breakup in this size regime, as will be shown, are so surprisingly low that even standard conditions are sufficient to initiate the degradation process. Typically, such a breakup mechanism can be associated to thermally activated surface diffusion effects, and the final structures can be explained by adapting Rayleigh's model for the breakup of a fluid jet35as proposed by Nichols and Mullins.36–38 Experiments on larger structures were carried out on nanowires made from e.g. Ag,39 Cu,40,41 Au,42,43 Sn44 and Pt,45 all with diameters above 20 nm. Breakup temperatures well below the bulk melting temperature were reported in all cases, but still far above room temperature. Only for Ag nanofractals, with initial branch diameters of ≈16 nm structural changes near room temperature could be observed.46,47 We note that a breakup of the Ag nanowires synthesised in HeN on the surface had been suggested by Gordon et al. based on observations made in bulk He II. However, due to the nature of their experimental setup the direct observation of isolated ultrathin Ag nanowires and a temperature-dependent monitoring of the breakup process were not possible,48,49 which motivated us to conduct the present study. Due to the challenging nature of nanowire production in the sub 10 nm diameter range, Ag nanowires in this size range are typically stabilised by templates,50–52 which introduces a large bias in stability measurements at smallest diameters. Our study can therefore be taken as the first investigation of the thermal stability of ultrathin pristine Ag wires, thereby demonstrating the ability of the HeN technique to gain new insights into fundamental questions of material science.
2 Experimental
A detailed description of the used helium droplet apparatus will be given elsewhere.53 In brief, gaseous helium (99.9999% purity) is cooled to temperatures <10 K by a closed-cycle refrigerator (Sumitomo, RDK-408D2) and expanded into a high vacuum region through a 5 μm nozzle. For all experiments discussed in this work, the helium stagnation pressure is 20 bar, and the nozzle temperature is kept at 5.4 K. The resulting beam of helium droplets (mean droplet diameter D ≈ 1 μm) is collimated by a 0.4 mm skimmer and directed into a separate vacuum chamber with a base pressure ≈10−7 mbar. There the HeN incorporate multiple Ag atoms while crossing a region of silver vapor emanating from the evaporation of high purity (99.99%) silver, which leads to the formation of Ag clusters and ultimately to Ag nanowires inside the droplets. The Ag doping rate, and hence, the wire diameter, are controlled by the adjustment of the oven temperature while monitoring the attenuation of the total He flux into the adjacent deposition chamber (base pressure 10−10 mbar). Nanowire deposition is achieved by terminating the droplet beam on 3 nm amorphous carbon TEM grids (Ted Pella, Inc., Prod. No. 01824) cooled to LN2 temperature. After the deposition process the vacuum chamber is vented with N2 (99.999% purity), thereby preventing the substrate's exposure to ambient conditions. Before opening the vacuum chamber a glove bag is attached to the respective flange and filled with N2 as to prevent contact of the substrate with air. The substrate holder is removed from its LN2 cooled mount inside the vacuum chamber and totally immersed into LN2 within 5 s. All further substrate manipulations, such as the transfer from the substrate holder to a cryo-TEM holder (Gatan, Model 626) are performed in LN2, so that an inert environment is guaranteed at all times.For the nanowire stability investigations, TEM images are recorded with a 120 kV LaB6 FEI Tecnai 12 transmission electron microscope, equipped with a Bio Scan Camera (Gatan, Model 792). The substrate temperature can be controlled from 77 K to 363 K via the cryo-TEM holder. Temperature is increased from 243 K to 293 K in steps of 5 K every 15 min and finally set to the maximum of 363 K for 30 min. Multiple substrate spots are imaged for each temperature step.
3 Computational details
To verify that the Ag nanowire breakup originates from surface diffusion and not e.g. from an unexpected interaction with the substrate, we also performed model calculations, taking the initial nanowire contours as observed in the experiment as starting point. The gradient of the chemical potential for a surface atom can be related to the gradient of the surface curvature, and subsequently, to a force on the respective surface element.54 As with the cryo-TEM setup an accurate quantification of the wire thickness in three dimensions is impossible, we restrict ourselves to a 2D model.55 The contourlines of the nanowires are discretised and propagated in time based on the Mullins equation, originally introduced to describe the thermal grooving at metallic grain boundaries.54 Two mechanisms of mass transport along the surface can be distinguished: evaporation–condensation and surface diffusion. For silver, the latter is known to dominate the process. A partial differential equation can be derived, which relates J, the flux of surface atoms, to ∇K, the gradient of the local surface curvature, via55 | (1) |
[J(s) − J(s + ds)]Ωdt = dz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ds, ds, | (2) |
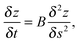 | (3) |
 | (4) |
Breakup events occur as soon as local constrictions of a wire lead to crossings of contour lines. In this case, the initial contour splits into two segments at the crossing point, and the contour lines of the new segments are propagated separately in the following timesteps. Numerical instabilities, which are intrinsic to this technique, evolve from inhomogeneous point distributions along a contour line after a breakup event. In contrast to ref. 55, where this problem is overcome by pruning the constricted parts of the corresponding contour line, we increase the point density after each breakup. Although computationally more costly, this approach reflects our experimental results in greater detail. The accuracy of the simulation can be judged by monitoring of the total surface area, which has to stay constant throughout propagation.55 For the initial contour lines taken from experiment, several million steps are necessary to obtain fully equilibrated structures (i.e., perfect circles in the 2D case). The surface is reduced by less than 4%.
4 Results and discussion
4.1 Nanowire growth, deposition and stability measurements
We use HeN to produce Ag nanowires with a mean length of 500 nm and mean diameter![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) nw = 5 nm. Fig. 1(a) shows a typical deposited Ag nanowire structure with some constrictions marked by arrows. No evidence of wire breakup could be found on the cooled substrate. During heatup of the sample, a smoothing of the wire surface as well as a further decrease of the diameter in the vicinity of initial constrictions can be observed already at 268 K (Fig. 1(b)), ultimately causing the breakup of the wire at temperatures below 293 K (Fig. 1(c)).
nw = 5 nm. Fig. 1(a) shows a typical deposited Ag nanowire structure with some constrictions marked by arrows. No evidence of wire breakup could be found on the cooled substrate. During heatup of the sample, a smoothing of the wire surface as well as a further decrease of the diameter in the vicinity of initial constrictions can be observed already at 268 K (Fig. 1(b)), ultimately causing the breakup of the wire at temperatures below 293 K (Fig. 1(c)).
Interestingly, for the investigated wires we are not able to observe a total relaxation into the equilibrium state, which corresponds to chains of spherical particles according to the Rayleigh model. An increase of the substrate temperature to 363 K leads to further segmentation (Fig. 1(d)), but the resulting segments stay well elongated. We can attribute this behaviour to a measurement artifact resulting from the deposition of a stabilising carbonaceous capping layer by ionisation and subsequent condensation of hydrocarbons present in the TEM vacuum. It is known that layers with a thickness of several nanometers can accumulate within minutes of specimen irradiation.56–58 We note that during the heating process the same substrate spots were repeatedly imaged in order to track any structural changes. Therefore, the imaged nanowires were exposed to the electron beam for times longer than 30 min. Comparative images taken from specimen areas which were not exposed to the electron beam at any stage of the prior investigation all show a complete decay of the nanowires into chains of spheres, as depicted in Fig. 2(a). Nanowires on a reference specimen, which was stored under ambient conditions for 1 week, show the same breakup patterns (Fig. 2(b)), indicating that at 293 K the equilibrium state is also reached.
 | ||
| Fig. 2 Undisturbed breakup patterns of Ag nanowires on substrate spots unimpaired by the electron beam. (a) shows sample from Fig. 1 heated to 363 K, (b) a reference substrate stored under ambient conditions for 1 week. Scale is the same for both images. | ||
We measured the distances λ between the centers of neighbouring spheres, as well as their diameters dsp for several chains of segments, using the image processing package FIJI.59 From the fits to the obtained histograms we can extract the ratios
![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) nw/2 and variances of ±20%.
nw/2 and variances of ±20%.
The observed behaviour is in good agreement with the model of a Rayleigh breakup, i.e. the growth of initial diameter perturbations caused by the diffusion of Ag atoms along the wire surface. This diffusion is driven by a gradient of the chemical potential which can be associated to the gradient of surface curvature.36,37,54
Nichols and Mullins predicted the ratio λ/R0 = 8.89 for surface diffusion dominated breakup of a cylindrical wire as result of harmonic surface perturbations.36 Assuming constant volume, one can estimate dsp/R0 = 3.76. The ratios observed in the present work exceed those obtained from theory. However, most investigated wires in literature are far from the ideal shape and isotropy which is assumed in this model calculation, thus the observed patterns deviate from the prediction.43,60,61 Additionally the presence of a substrate generally tends to stabilise the nanowires.62 The larger values of λ and dsp indeed reflect a slightly larger stability of the wires compared to the model and are in good agreement with other experimental findings.42,63
4.2 Simulation of the degradation process
The initial contourlines of nanowires after deposition are taken as starting point for a computational study, using the 2D model described in Section 3. Exemplary results of the simulation are presented in Fig. 3 for the contourline taken from the nanowire depicted in Fig. 1 after 9 × 105 and 9.6 × 105 simulation timesteps respectively. The points of wire breakup are in excellent agreement with the experimental data (compare Fig. 1(c) & (d) and 3). The reduced stability of the upper wire branch in the experiment compared to the simulation is related to a mass accumulation at the left upper end of the wire. While this is apparent from the higher contrast (i.e. a dark spot) in the TEM image, it is not accounted for in the 2D simulation. The model contours clearly propagate towards the spherical equilibrium state. The same tendency is seen in the experiment, but hindered due to the growth of carbon layers mentioned above. Nevertheless, the degradation process is very well captured by our simulations, which shows that thermally activated surface diffusion is the main reason for the breakup of the nanowires. According to the experiment, the onset of this process becomes noticeable at ≈260 K. | ||
| Fig. 3 Evolution of the nanowire contourline (red) as simulated using a 2D model. The upper part of the wire is still intact in (a) after 9 × 105 timesteps, although considerably constricted at some points. After 9.6 × 105 timesteps (b) most segments have reached their final circular shape. The initial contourline of the simulation (light grey) is taken from Fig. 1(a). The points of breakup coincide well with those observed in the experiment. | ||
In experiments on Ag nanofractals, a breakup of fractal arms (diameter ≈16 nm) was observed near room temperature.46 Relaxation into spherical particles has not been observed for fractals of pure Ag due to slow fragmentation kinetics. Interestingly, the doping of the fractals with oxygen impurities during the growth process led to a full decay into spheres. This behaviour was also confirmed in a follow-up study47 and was interpreted as a result of a strongly enhanced surface mobility near the oxygen atoms. Total spherodisation of the pure Ag nanofractal branches, on the other hand, was obtained only after annealing at 573 K.
In our study, the substrate is kept in an inert environment at all times. Therefore, a structure degeneration as a result of chemical processes can be fully excluded. This also rules out a possible Ag sulfidation by atmospheric gases as the origin of the degradation, which has been proposed in other cases.64–66 Breakup occurs within minutes after the sample was heated to ≈260 K. The observed timescale is in good agreement with the estimations derived for nanofractals.46 Furthermore, no alteration of the initial wire structures can be found for an identically prepared reference specimen which had been stored in LN2 for 48 h. This indicates a full suppression of the diffusion process at a temperature of 77 Kelvin. The advantage of our approach lies in the possibility to track structural changes in the TEM during the heatup. This also enables us to repeatedly image the same substrate spot and thereby track the structural changes of a single wire, which, in turn, facilitates a direct comparison to a simulation of exactly the same structure. The experimental approach allows a much more accurate determination of the decomposition temperature than in previous works.48,49
Our study confirms that the breakup of Ag nanowires synthesised in HeN occurs on the surface after deposition, as it had been proposed by Gordon et al. from results obtained in bulk He II.48,49 The authors of the respective studies exploited vortices to grow nanowires of different metals and also found instabilities in the case of Ag. While for Pt, In, and Au nanowires spanned across the holes of a porous carbon TEM grid were found to be stable at ambient conditions, no such wires could be observed in case of Ag. Only a Ag nanoweb consisting of considerably thicker wires was found to be stable long enough for recording TEM images. The breakup of the thin Ag wires was explained by a change in the surface tension at small wire diameters.49 In the framework of the Rayleigh breakup the surface tension γ enters the calculations as described in eqn (4). Therefore, an increase in γ influences the breakup of nanostructures. However, also the surface self-diffusion constant plays an important role, as it is not only strongly dependent on temperature, but also exhibits large values for Ag compared to Au, Cu or Ni.67 The suppression of the diffusion process at LN2 temperature as described in this work is in good agreement with this concept. It was found that a doping of the Ag nanowires with Cu atoms can increase their thermal stability by decreasing the surface atom mobility.48 This is a further indicator that Ds governs the differences between nanowires of the same diameter made from different metals, while a general onset of the breakup is only observable at small diameters in accordance to the suggestions made previously.49
5 Conclusions
Our results prove that the experimentally observed segmented lines or ‘chains’ of HeN-grown Ag clusters12,23,34 are neither an intrinsic feature of growth within the nanodroplets nor a consequence of the surface impact. Instead, the breakup is a consequence of diffusion processes caused by a ‘warm’ substrate. This confirms the suggestions of Gordon et al. of a nanowire breakup on the surface derived from bulk He II experiments.48,49 We further investigate the structural degradation of the nanowires as a function of temperature. Due to the possibility of directly tracking the breakup process of a single wire, our experiment delivers an accurate measure of the breakup temperature Tb ≈ 260 K of the nanowires. The large experimental effort of a wire synthesis within HeN is rewarded by the complete inertness of the production and measurement process. The total absence of any solvents or templates enables an unbiased view on the thermal stability of pristine ultrathin Ag nanowires. We believe these findings will be useful in the context of further miniaturisation attempts regarding electronic or optical devices.Acknowledgements
This research has been supported by the Austrian Science Fund (FWF) under Grant FWF-E-530 P19759 & FWF-E-P22962, by the European Commission and the Styrian Government within the ERDF program as well as by the European Union within the 7th Framework Programme (FP7/2007–2013) under Grant Agreement No. 312483 (ESTEEM2). The authors gratefully acknowledge support from NAWI Graz.References
- Z. K. Tang, L. Zhang, N. Wang, X. X. Zhang, G. H. Wen, G. D. Li, J. N. Wang, C. T. Chan and P. Sheng, Science, 2001, 292, 2462–2465 CrossRef CAS PubMed.
- Y. Huang, X. Duan, Y. Cui and C. M. Lieber, Nano Lett., 2002, 2, 101–104 CrossRef CAS.
- P. Kohli, C. C. Harrell, Z. Cao, R. Gasparac, W. Tan and C. R. Martin, Science, 2004, 305, 984–986 CrossRef CAS PubMed.
- J.-H. Ahn, S.-J. Choi, J.-W. Han, T. J. Park, S. Y. Lee and Y.-K. Choi, Nano Lett., 2010, 10, 2934–2938 CrossRef CAS PubMed.
- J. C. Claussen, A. D. Franklin, A. ul Haque, D. M. Porterfield and T. S. Fisher, ACS Nano, 2009, 3, 37–44 CrossRef CAS PubMed.
- Q. Wang, F. Min and J. Zhu, Mater. Lett., 2013, 91, 9–11 CrossRef CAS PubMed.
- Y. Yin, Y. Sun, M. Yu, X. Liu, T. Jiang, B. Yang, D. Liu, S. Liu and W. Cao, Sci. Rep., 2015, 5, 8152 CrossRef CAS PubMed.
- G. Zhu, S. Zhang, Z. Xu, J. Ma and X. Shen, J. Am. Chem. Soc., 2011, 133, 15605–15612 CrossRef CAS PubMed.
- K. Yu. Arutyunov, Physica C, 2008, 468, 272–275 CrossRef CAS PubMed.
- M. Dreher, F. Pauly, J. Heurich, J. C. Cuevas, E. Scheer and P. Nielaba, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075435 CrossRef.
- C. M. Lieber, MRS Bull., 2003, 28, 486–491 CrossRef CAS.
- E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Nano Lett., 2014, 14, 2902–2906 CrossRef CAS PubMed.
- P. Thaler, A. Volk, F. Lackner, J. Steurer, D. Knez, W. Grogger, F. Hofer and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155442 CrossRef.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- C. Callegari and W. E. Ernst, Handbook of High Resolution Spectroscopy, John Wiley & Sons, Chichester, 2011 Search PubMed.
- J. Tiggesbäumker and F. Stienkemeier, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC.
- V. Mozhayskiy, M. N. Slipchenko, V. K. Adamchuk and A. F. Vilesov, J. Chem. Phys., 2007, 127, 094701 CrossRef PubMed.
- E. Loginov, L. F. Gomez and A. F. Vilesov, J. Phys. Chem. A, 2011, 115, 7199–7204 CrossRef CAS PubMed.
- A. Volk, P. Thaler, M. Koch, E. Fisslthaler, W. Grogger and W. E. Ernst, J. Chem. Phys., 2013, 138, 214312 CrossRef PubMed.
- P. Thaler, A. Volk, M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2014, 140, 044326 CrossRef PubMed.
- M. P. de Lara-Castells, N. F. Aguirre, H. Stoll, A. O. Mitrushchenkov, D. Mateo and M. Pi, J. Chem. Phys., 2015, 142, 131101 Search PubMed.
- L. F. Gomez, K. R. Ferguson, J. P. Cryan, C. Bacellar, R. M. P. Tanyag, C. Jones, S. Schorb, D. Anielski, A. Belkacem, C. Bernando, R. Boll, J. Bozek, S. Carron, G. Chen, T. Delmas, L. Englert, S. W. Epp, B. Erk, L. Foucar, R. Hartmann, A. Hexemer, M. Huth, J. Kwok, S. R. Leone, J. H. S. Ma, F. R. N. C. Maia, E. Malmerberg, S. Marchesini, D. M. Neumark, B. Poon, J. Prell, D. Rolles, B. Rudek, A. Rudenko, M. Seifrid, K. R. Siefermann, F. P. Sturm, M. Swiggers, J. Ullrich, F. Weise, P. Zwart, C. Bostedt, O. Gessner and A. F. Vilesov, Science, 2014, 345, 906–909 CrossRef CAS PubMed.
- L. F. Gomez, E. Loginov and A. F. Vilesov, Phys. Rev. Lett., 2012, 108, 155302 CrossRef.
- R. P. Feynman, Progress in Low Temperature Physics, North-Holland, Amsterdam, 1955, pp. 17–53 Search PubMed.
- L. Onsager, Proc. Int. Conf. Theor. Phys., Science Council of Japan, Tokyo, 1953, pp. 877–880 Search PubMed.
- G. P. Bewley, D. P. Lathrop and K. R. Sreenivasan, Nature, 2006, 441, 588 CrossRef CAS PubMed.
- E. J. Yarmchuk, M. J. V. Gordon and R. E. Packard, Phys. Rev. Lett., 1979, 43, 214–217 CrossRef CAS.
- G. A. Williams and R. E. Packard, Phys. Rev. Lett., 1974, 33, 280–283 CrossRef CAS.
- R. J. Donelly, Quantized Vortices in Helium II, Cambridge University Press, Cambridge, 1991 Search PubMed.
- Y. A. Sergeev and C. F. Barenghi, J. Low Temp. Phys., 2009, 157, 429–475 CrossRef CAS.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko and I. I. Khodos, J. Exp. Theor. Phys., 2011, 112, 1061–1070 CrossRef CAS.
- P. Moroshkin, V. Lebedev, B. Grobety, C. Neururer, E. B. Gordon and A. Weis, EPL, 2010, 90, 34002 CrossRef.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, Low Temp. Phys., 2010, 36, 590–595 CrossRef CAS PubMed.
- D. Spence, E. Latimer, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Phys. Chem. Chem. Phys., 2014, 16, 6903–6906 RSC.
- J. W. S. Rayleigh, Proc. Lond. Math. Soc., 1878, 10, 4–13 CrossRef PubMed.
- F. A. Nichols and W. W. Mullins, Trans. Metall. Soc. AIME, 1965, 233, 1840–1848 CAS.
- F. A. Nichols and W. W. Mullins, J. Appl. Phys., 1965, 36, 1826–1835 CrossRef PubMed.
- F. A. Nichols, J. Mater. Sci., 1976, 11, 1077–1082 CrossRef.
- E. Marzbanrad, G. Rivers, P. Peng, B. Zhao and N. Y. Zhou, Phys. Chem. Chem. Phys., 2015, 17, 315–324 RSC.
- M. E. Toimil Molares, A. G. Balogh, T. W. Cornelius, R. Neumann and C. Trautmann, Appl. Phys. Lett., 2004, 85, 5337–5339 CrossRef CAS PubMed.
- H. Li, J. M. Biser, J. T. Perkins, S. Dutta, R. P. Vinci and H. M. Chan, J. Appl. Phys., 2008, 103, 024315 CrossRef PubMed.
- S. Karim, M. E. Toimil-Molares, A. G. Balogh, W. Ensinger, T. W. Cornelius, E. U. Khan and R. Neumann, Nanotechnology, 2006, 17, 5954–5959 CrossRef CAS.
- S. Karim, M. E. Toimil-Molares, W. Ensinger, A. G. Balogh, T. W. Cornelius, E. U. Khan and R. Neumann, J. Phys. D: Appl. Phys., 2007, 40, 3767–3770 CrossRef CAS.
- H. S. Shin, J. Yu and J. Y. Song, Appl. Phys. Lett., 2007, 91, 173106 CrossRef PubMed.
- M. Rauber, F. Muench, M. E. Toimil-Molares and W. Ensinger, Nanotechnology, 2012, 23, 475710 CrossRef CAS PubMed.
- C. Bréchignac, Ph. Cahuzac, F. Carlier, C. Colliex, J. Leroux, A. Masson, B. Yoon and U. Landman, Phys. Rev. Lett., 2002, 88, 196103 CrossRef.
- A. Lando, N. Kébaïli, Ph. Cahuzac, A. Masson and C. Bréchignac, Phys. Rev. Lett., 2006, 97, 133402 CrossRef CAS.
- E. Gordon, A. Karabulin, V. Matyushenko, V. Sizov and I. Khodos, Phys. Chem. Chem. Phys., 2014, 16, 25229–25233 RSC.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko and I. I. Khodos, J. Phys. Chem. A, 2015, 119, 2490–2501 CrossRef CAS PubMed.
- B. H. Hong, S. C. Bae, C.-W. Lee, S. Jeong and K. S. Kim, Science, 2001, 294, 348–351 CrossRef CAS PubMed.
- M. Malisauskas, R. Meskys and L. A. Morozova-Roche, Biotechnol. Prog., 2008, 24, 1166–1170 CrossRef CAS PubMed.
- D. M. Eisele, H. von Berlepsch, C. Böttcher, K. J. Stevenson, D. A. Vanden Bout, S. Kirstein and J. P. Rabe, J. Am. Chem. Soc., 2010, 132, 2104–2105 CrossRef CAS PubMed.
- P. Thaler, A. Volk, D. Knez, F. Lackner, G. Haberfehlner, J. Steurer, M. Schnedlitz and W. E. Ernst, J. Chem. Phys., 2015 Search PubMed , submitted.
- W. W. Mullins, J. Appl. Phys., 1957, 28, 333–339 CrossRef CAS PubMed.
- R. Thouy, N. Olivi-Tran and R. Jullien, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5321–5327 CrossRef CAS.
- L. Reimer and H. Kohl, Transmission Electron Microscopy, Springer-Verlag, New York, 2008, pp. 484–490 Search PubMed.
- S. Horiuchi, T. Hanada, M. Ebisawa, Y. Matsuda, M. Kobayashi and A. Takahara, ACS Nano, 2009, 3, 1297–1304 CrossRef CAS PubMed.
- A. Kumao, H. Hashimoto and K. Shiraishi, J. Electron Microsc., 1981, 30, 161–170 CAS.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- J. D. Powers and A. M. Glaeser, J. Am. Ceram. Soc., 2000, 83, 2297–2304 CrossRef CAS PubMed.
- K. F. Gurski and G. B. McFadden, Proc. R. Soc. London, Ser. A, 2003, 459, 2575–2598 CrossRef.
- K. F. Gurski, G. B. McFadden and M. J. Miksis, SIAM J. Appl. Math., 2006, 66, 1163–1187 CrossRef.
- D. Raabe and J. Ge, Scr. Mater., 2004, 51, 915–920 CrossRef CAS PubMed.
- H. H. Khaligh and I. A. Goldthorpe, Nanoscale Res. Lett., 2013, 8, 235 CrossRef PubMed.
- J. P. Franey, G. W. Kammlott and T. E. Graedel, Corros. Sci., 1985, 25, 133–143 CrossRef CAS.
- J. L. Elechiguerra, L. Larios-Lopez, C. Liu, D. Garcia-Gutierrez, A. Camacho-Bragado and M. J. Yacaman, Chem. Mater., 2005, 17, 6042–6052 CrossRef CAS.
- C. L. Liu, J. M. Cohen, J. B. Adams and A. F. Voter, Surf. Sci., 1991, 253, 334–344 CrossRef CAS.
| This journal is © the Owner Societies 2015 |


