 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transformation kinetics of vapor-deposited thin film organic glasses: the role of stability and molecular packing anisotropy
Cristian
Rodríguez-Tinoco
,
Marta
Gonzalez-Silveira
 *,
Joan
Ràfols-Ribé
,
Aitor F.
Lopeandía
and
Javier
Rodríguez-Viejo
*
*,
Joan
Ràfols-Ribé
,
Aitor F.
Lopeandía
and
Javier
Rodríguez-Viejo
*
Grup de Nanomaterials i Microsistemes, Physics Department, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain. E-mail: javier.rodriguez@uab.cat; marta.gonzalez@uab.cat
First published on 28th October 2015
Abstract
While ordinary glasses transform into supercooled liquid via a homogeneous bulk mechanism, thin film glasses of higher stability transform heterogeneously by a front propagating from the surface and/or the interfaces. In this work, we use quasi-adiabatic fast scanning nanocalorimetry to determine the heat capacity of thin glassy layers of indomethacin vapor-deposited in a broad temperature range of 110 K below the glass transition temperature. Their variation in fictive temperature amounts to 40 K. We show that a propagating front is the initial transformation mechanism in all cases. Using an ad hoc surface normalization procedure we determine the corresponding growth front velocity for the whole range of deposition temperatures. Although the transformation rate changes by a factor of 10 between the most and less stable samples, the relation between the mobility of the front and the thermodynamic stability of the glass is not uniquely defined. Glasses grown above 280 K, which are at equilibrium with the supercooled liquid, present a different dependence of the growth front velocity on fictive temperature compared to glasses grown out of equilibrium at Tdep < 250 K. These glasses transform faster with increasing Tf. Our data clarify previous reports and support the evidence that the fictive temperature alone is not an absolute indicator of the properties of the glass, at least when its structure is not completely isotropic. To interpret the data, we propose that the growth front velocity depends on three terms: the mobility of the liquid at a given temperature, the mobility of the glass and the arrangement of the molecules in the glass.
Introduction
Glasses are systems with great interest from the technological and scientific points of view.1 In chemical and pharmaceutical applications, for example, glasses are commonly used due to the increased bioavailability compared to their crystalline counterparts,2 reducing the dose of the product needed and, therefore, the toxicity of the treatment and the global cost. In the electronic industry, applications such as optical fibers or OLEDs take benefit from glasses due to the advantages of their preparation, with respect to conventional crystalline products.3 Glasses obtained by cooling the liquid are in general very unstable systems that easily undergo crystallization or physical aging, with the corresponding change in their properties. An important milestone in the research field of glasses was the achievement of ultrastability by means of physical vapor deposition by Ediger's group in 2007.4,5 By tuning the deposition conditions, it is possible to obtain glasses with an unprecedented thermal and kinetic stability in a few minutes, while millions of years would be required to attain similar stability levels by physical aging.6 These highly stable glasses present a series of striking properties that make them unique,7–16 and among them is the mechanism of transformation into the supercooled liquid.17–23 Experiments and glass theories have always led to conclude that conventional glasses transform into the supercooled liquid state by a homogeneous process that occurs throughout the volume of the sample. On the other hand, in the case of ultra-stable glasses, the increased density and tight molecular packing24–26 have been proposed as the cause for the transformation to start at regions where the mobility is higher, i.e., surfaces and interfaces. This observation has been predicted by random first order transition (RFOT) theory,27,28 by facilitated kinetic Ising model calculations,29 by vapor deposition simulation30 and by random particle pinning.31 Moreover, both experiments and theory agree that the propagation velocity is strongly related to the mobility of the molecules of the supercooled liquid layer.27 This behavior has been observed in several systems32 and for an extended temperature range.33One of the advantages of physical vapor deposition is the possibility to tailor the deposition conditions to prepare glasses of very different stabilities, spanning in limiting fictive temperature by more than 40 K, values not accessible for glasses prepared from the liquid. The glass transition of glasses of toluene grown at different deposition rates was measured by fast scanning calorimetry19 and glasses of TPD32 and IMC34 were deposited in a multi-temperature stage and measured by ellipsometry. In all cases the results were consistent with a transformation into the supercooled liquid via parallel growth fronts. Kinetic facilitation models predicted that the front propagation in highly stable glasses depends mainly on the relaxation time of the liquid phase. This is in agreement with the finding that glasses of different stabilities have the same temperature dependence at least in a limited temperature range, i.e. they share common activation energy. RFOT27 and pinning models31 also foresee a strong temperature dependence of the growth front velocity and a small influence of stability. Experimental evaluations of the growth front velocities for glasses of different stabilities grown at Tdep < 0.85Tg, where Tg is the glass transition temperature of a conventional glass, are consistent in general with this view, but the dependence on stability is much larger. Following the theoretical predictions, when Ediger et al. failed at trying to correlate density and the transformation rate,34 they concluded that density and glass mobility must be partly unrelated. In any case, the role that the glass plays in the transformation rate is not yet clear.
A remarkable feature of vapor-deposited organic glasses is the existence of molecular packing anisotropy.35 The degree and type of orientation strongly depend on the deposition conditions.11,12,36,37 For instance, IMC glasses grown at 0.8 < Tdep < 0.9Tg have a tendency to show a certain molecular orientation with the long axis oriented perpendicular to the substrate, while at Tdep < 0.8Tg, molecules are, on average, structured along the substrate plane. Above 0.9Tg the glass is nearly isotropic with molecules randomly distributed.26
In this work, we use fast scanning quasi-adiabatic nanocalorimetry to analyze the transformation kinetics of IMC glasses deposited over a wide temperature range. We identify the existence of parallel growth fronts starting at surfaces/interfaces and with variable penetration depths that depend on the stability of the glasses. Our data expand previous measurements by Dalal et al.34 and clearly show that the growth front velocity and the fictive temperature of the glass (i.e. density) are not correlated and, in fact, we identify two different regimes depending on the deposition temperature. The origin of this behavior is traced back to the presence of molecular anisotropy. Our work permits us to establish a clear link between the growth front velocity and the mobility of the adjacent supercooled liquid, and between the mobility of the glass and its molecular orientation.
Experimental method
IMC thin layers, with thicknesses ranging from 20 to 100 nm, were grown by thermal evaporation in a UHV chamber at a base pressure of 3 × 10−8 mbar, using an effusion cell (CREATEC) at a constant temperature of around 440 K. The evaporation rate was monitored with a quartz microbalance (Sycon) located close to the substrate and set to 0.1 nm s−1. A liquid nitrogen cold trap was used to reduce the vapor pressure of certain contaminants, especially water. Films with thicknesses above 20 nm have been shown to be continuous in a previous work.33The films were deposited onto a nanocalorimetric cell and measured in situ by quasi-adiabatic fast-scanning nanocalorimetry. This membrane-based technique allows the heat capacity measurement of samples with very low mass at fast heating rates (β = 3 × 104 K s−1 in this work), achieving very high sensitivity.38,39 The variation of the heating rate during the glass transition is always below 5%. A plate of 200 nm of aluminum was deposited onto the sensing area of the device in order to obtain a homogeneous thermal profile across the sample.
Samples of different stability were produced by changing the substrate temperature from 200 K to 310 K. The deposition temperature was controlled by supplying a fixed value of intensity to the nanocalorimeter during the deposition process. For certain thicknesses, multiple samples were deposited, measured and averaged in order to obtain more reliable data. Raw voltage data obtained during the measurement are treated in order to get heat capacity curves. The mass of each sample is determined by dividing heat capacity data above the glass transition by the specific heat of liquid IMC.40 We consider the resulting supercooled liquid to be equal in all cases, independently of the deposition conditions.
Results
We have measured the heat capacity of thin layers of IMC grown at substrate temperatures between 200 and 310 K. For each deposition temperature, films of at least 5 different thicknesses have been analyzed. We have previously shown that the normalization of the heat capacity in thin film stable glasses should account for the heterogeneous nature of the transformation into the supercooled liquid, since a standard normalization by the mass can yield incorrect conclusions. The detailed normalization procedure has been explained elsewhere.33 Briefly, the heat capacity as a function of temperature can be described by the contributions of heat capacity of glass and liquid and the transformation rate: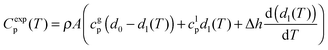 | (1) |
 | (2) |
 | (3) |
 | ||
| Fig. 1 Specific heat curves of IMC glassy films for three different thicknesses deposited at (a) 266 K and (b) 310 K and (c) fast cooled obtained by dividing the heat capacity curves by the mass. Panels (d–f) correspond respectively to heat capacity curves of samples deposited at 266 K, 310 K and fast cooled, normalized using eqn (2). | ||
In the case of the samples of lower stability (Tdep = 310 K, Fig. 1e) it can be seen that the curves only overlap along a limited temperature range. In this case, the glass transforms purely via parallel growth front only up to a few nanometers (∼5 nm). At a certain temperature, homogenous bulk transformation comes into play and dominates the transformation. The distance travelled by the growth front before the bulk interferes can be roughly estimated from the temperature region where all curves collapse. Growth front velocity can be calculated using eqn (3). In Fig. 2a we plot the logarithm of the front velocities as a function of temperature for glasses obtained in the range 0.63 < Tdep < 0.98Tg. A complementary representation of the data is presented in Fig. 2b, where the logarithm of the growth front velocity evaluated at T = 368 K is plotted as a function of substrate temperature. This temperature is chosen as a representative value; however, the trend of Fig. 2b is similar for other temperatures over the analyzed temperature range. The slowest transformation rate corresponds to the most stable glass, deposited at 0.85Tg (266 K). Glasses deposited at higher or lower temperatures have faster transformation fronts. The farther from 0.85Tg the deposition temperature, the faster the mobility of the front. We observe a 10-fold difference in the mobility of the front between the fastest and the slowest samples.
 | ||
| Fig. 2 (a) Logarithm of the growth front velocity as a function of temperature for IMC glasses. Continuous lines correspond to a fit of the data using the expression vgr = Cτ−γ where τ is the alpha relaxation time of the liquid and has been calculated using the VFT equation with values obtained by Paluch et al. for IMC.41 (b) Logarithm of the growth front velocity at T = 368 K as a function of deposition temperature. Values have been obtained by extrapolation (Tdep = 310 K) or interpolation (rest of deposition temperatures) of the experimental points presented in panel (a). The line is a guide to the eye. | ||
Discussion
Deposition temperature range
Our results demonstrate that IMC glasses deposited between 0.63 and 0.98Tg (with Tg = 315 K) transform, at least in a certain temperature range, uniquely via a propagating parallel front mechanism. In particular, glasses deposited at 310 K transform into the supercooled liquid exclusively via a parallel front up to a total thickness of the supercooled liquid layer of about 5 nm, moment at which the bulk transformation becomes perceptible. Because of the high sensitivity of the nanocalorimetric technique, we are able to extract transformation velocity values even in this reduced thickness range. We note that, in contrast to previous measurements by ellipsometry,34 where the value of the growth front velocity for samples deposited above 290 K could not be directly evaluated, we resolve the growth front velocity for the whole deposition temperature interval. This is of great importance since it permits us to draw new conclusions on the transformation mechanism as it will be discussed below. We note that the glass transition measured by fast-scanning nanocalorimetry has been obtained at higher temperatures compared to the ones determined by ellipsometry, that are carried out under isothermal or slow heating ramps at which the transition temperature is significantly reduced. We also remark that the calorimetric analysis cannot univocally distinguish if the transformation is due to one or two fronts starting at the free surface and/or interfaces. Sepúlveda et al.23 defined the crossover length as the distance reached by the transformation front before the homogeneous (bulk) transformation becomes the dominant mechanism. Our crossover length corresponds, therefore, to the total distance which has been transformed exclusively by the front.Dependence of growth front velocity on temperature
When we represent the logarithm of the front velocity as a function of temperature for samples that have been deposited at different substrate temperatures (see Fig. 2) we obtain a series of points that could be approximately fit by parallel lines. When representing the velocities as a function of the inverse of the temperature (not shown), the lines are even straighter and more parallel. From this representation, we could infer that there is an Arrhenius dependence between velocity and front, and from the slope we could derive an apparent activation energy, which would be constant for all samples. However, the range in temperature we are able to access by nanocalorimetry is small and to have a general picture it is important to extend this range. In a previous study we already showed that the relation:| vgr = Cτ−γ | (4) |
 | ||
| Fig. 3 (a) Log–log plot of growth front velocity for samples deposited at different substrate temperatures as a function of the alpha relaxation time of the liquid.41 The lines correspond to a fit of the data using eqn (4), where the exponent γ has been kept constant at a value of 0.79 ± 0.01 and the prefactor C depends on how the glass has been produced. (b) Extrapolation of the fit for two deposition temperatures to higher values of τ. In a previous study we already showed how it was possible to fit data from the ultrastable glass (Tdep = 266 K) for 12 orders of magnitude in τ. Here we show that the same function can fit the data obtained by nanocalorimetry (this work) and by ellipsometry (extracted from Dalal's work34) for a sample deposited at 220 K. The dashed line corresponds to a fit of the high temperature data (Tdep = 220 K) extended to the entire relaxation time range considering an Arrhenius dependence of the growth front velocity with temperature. | ||
The accessible temperature range using quasi-adiabatic nanocalorimetry is rather limited, covering a maximum of 15 K for each sample. In order to test if eqn (3) is still valid for an extended range of temperatures, we plot in Fig. 3b results obtained by Dalal and Ediger34 for an IMC sample deposited at 220 K and measured by ellipsometry at 320 and 325 K. Since they are able to distinguish between the front that starts at the surface and the front starting at the interface, and we are not, we have interpolated their data and we have taken the average velocity of the two fronts. Interestingly the same dependence is extended over the whole range of τ, i.e. temperature, which now covers 8 orders of magnitude in the alpha relaxation time, or equivalently, 55 K in temperature. In Fig. 3b we also present an alternative fit of the high temperature data using an Arrhenius dependence of growth front velocity on temperature, extended over the whole range of relaxation times. As can be clearly seen, it is not possible to fit the high and low temperature experimental points with the same function.
Dependence of growth front velocity on glass properties
Fig. 2b clearly highlights that the growth front velocity depends on the deposition temperature, and, in turn, the deposition temperature will determine the properties of the transforming glass. Generally it has been assumed that the mobility in the glass is directly related to its density or to its fictive temperature. We have calculated the enthalpic fictive temperature of all samples by integrating the specific heat curves, as explained in ref. 5, 33 and 42. As shown in Fig. 4a, glass density and fictive temperature display a good correlation in the case of IMC glasses deposited from the vapor. We are not aware that this correlation has been tested in other stable glasses; therefore we are cautious to draw generalities on this respect. One of the main outcomes of our heat capacity analysis is Fig. 4b, which represents the growth front velocity as a function of the fictive temperature of the glasses deposited between 0.63–0.98Tg. Interestingly, we observe two branches, i.e. two glasses that have the same limiting fictive temperature and have been grown at different deposition temperatures can have very different growth front velocities. In both of these branches, the transformation rate increases with Tf, which means that, generally speaking, the less stable the glass is, the faster the front is. Fig. 4b corroborates previous views that a unique fictive temperature cannot be taken as a signature of the structural state of the glass in equilibrium with the liquid.43 This explains why correlations between growth velocity and density cannot be accomplished simultaneously over the whole deposition interval, as shown in Fig. 5. In a previous work, Dalal and Ediger34 showed that it was possible to correlate growth front velocity and density for samples deposited below 0.85Tg, but it was not possible to extend this correlation to samples deposited above this temperature. In Fig. 5 we show how, by using appropriate scaling factors, it is possible to find a correlation also for deposition temperatures above 0.85Tg. Of course our results stand for thin films where the main transformation mechanism occurs through heterogeneous growth fronts. Whether a similar behavior occurs for a homogeneous transformation mechanism in bulk stable glasses is still not known. | ||
| Fig. 4 (a) Comparison between fictive temperature and density increment as a function of deposition temperature. (b) Front velocity as a function of fictive temperature. (c) Front velocity as a function of birefringence. The arrows indicate 4 samples with Tf = (287 ± 1) K. The star symbol has been obtained by interpolating the data in order to represent a sample with Tf = 287 K. Density and birefringence data have been extracted from ref. 26. In all panels, symbols correspond to different deposition conditions and the corresponding birefringence: red triangles correspond to samples deposited below 250 K (0.8Tg), which have negative birefringence; black squares correspond to samples obtained between 250 K and 300 K (0.8Tg and 0.95Tg respectively), which have positive birefringence; green circles correspond to samples deposited above 300 K, with no birefringence. The cartoons (adapted from ref. 36) represent schematically the distribution of the molecules for each type of birefringence. | ||
 | ||
| Fig. 5 Comparison between density change and the logarithm of the transformation front velocity. The scales have been adjusted to coincide in the region of deposition temperature below 0.85Tg (a) and above 0.85Tg (b). Density data have been extracted from ref. 26. | ||
Wisitsorasak and Wolynes performed numerical calculations on the growth front mobility using random first-order transition theory.27 In that study, they calculated the velocity of the front for TNB glasses (a similar glass to IMC) with Tf's differing 10 K and found that the impact of Tf variation was less important than the effect of temperature. The velocity of the front of stable glasses produced by random pinning by Hocky et al.31 also depends on stability (or density of fixed particles), although in this case there is not a direct estimation of fictive temperature for their pinned samples. It is worth noting that computer modeling was carried out with isotropic glasses.27,31
But then, what controls the growth front velocity? Our data clearly demonstrate that while the liquid mobility and the fictive temperature of the glass (density) play a relevant role in the mobility of the front, there is another, hidden, dependence not yet considered. To shed light on this issue we need to comment first on the birefringence measurements of Ediger and coworkers where they showed broadly three different regimes of molecular anisotropy depending on the deposition temperature.26
Glasses deposited at substrate temperatures lower than 250 K show a negative birefringence factor, while those deposited between 250 and 300 K display a positive value of this parameter. Above 300 K, the birefringence turns out to be zero. The existence of birefringence is linked to molecular orientation. Below 250 K, IMC molecules are on average with their long-axis oriented parallel to the substrate surface, whereas between 250 and 300 K the molecules tend to align perpendicular to the substrate. Above 300 K the glass is mostly isotropic.26 The existence of two branches in Fig. 4b could be understood from the packing anisotropy of the samples. Fig. 4c shows the growth front velocity as a function of the birefringence using Δn(Tdep) values from ref. 26. We disentangle the role of molecular anisotropy in the growth front velocity by comparing samples with identical fictive temperature, such as the ones marked with arrows in Fig. 4c, for which Tf = (287 ± 1) K. For a given Tf, the stronger the orientation of the molecules along the plane of the substrate, the faster the transformation rate. Low absolute values of birefringence give rise to slower fronts. The available data do not permit us to infer if a strong orientation of the molecules in the direction perpendicular to the surface would result in faster fronts. In spite of this shortcoming, the presented data suggest a clear dependence of the mobility of the front on the anisotropy of the glass. To our knowledge, this is the first report that clearly demonstrates this dependence and establishes the importance of the structure of the glass in the transformation dynamics into the supercooled liquid.
Conclusions
We present new experimental evidence on the heterogeneous transformation, via a parallel growth front, of glasses obtained from the vapor, spanning 40 K in fictive temperature. By using fast scanning nanocalorimetry, it is possible to determine the growth front velocity for glasses deposited at a wide range of deposition temperatures, from low temperature up to 0.98Tg. Moreover, the fast scanning rates achieved with this experimental technique shift the glass transition to higher temperatures. Thus, our velocities are measured at a temperature range which is not accessible by other techniques, several decades above the conventional glass transition temperature. Combining our measurements with previous results, we extract that the velocity of the front depends strongly on the mobility of the adjacent supercooled liquid layer, following the relation v = Cτ−γ. This result was previously demonstrated for ultrastable glasses, but we show now that glasses of lower stability follow the same dependence on τ and the different mobility of the glass is only reflected by a change in the prefactor C. We show that, at a certain temperature, the velocity of the front, and by extension the prefactor C, cannot be univocally described by the fictive temperature of the glass. While glasses grown at equilibrium with the supercooled liquid show a particular dependence on the thermal stability, the same dependence does not hold for the lower deposition temperature range. We consider that the orientation of the molecules, which depends on the deposition temperature as has been previously shown, plays an important role in the rate at which the molecules from the glass are incorporated into the growth front.Acknowledgements
This work was financially supported by the Spanish MINECO MAT2013-40896-P.References
- C. A. Angell, Science, 1995, 267, 1924 CAS.
- L. Yu, Adv. Drug Delivery Rev., 2001, 48, 27–42 CrossRef CAS PubMed.
- K. L. Kearns, H.-Y. Na, R. D. Froese, S. Mukhopadhyay, H. Woodward, D. Welsh, T. De Vries, D. Devore, P. Trefonas and L. Hong, Proc. SPIE, 2014, 9183, 91830F CrossRef.
- S. F. Swallen, K. L. Kearns, M. K. Mapes, Y. S. Kim, R. J. McMahon, M. D. Ediger, T. Wu, L. Yu and S. Satija, Science, 2007, 315, 353–356 CrossRef CAS PubMed.
- K. L. Kearns, S. F. Swallen, M. D. Ediger, T. Wu and L. Yu, J. Chem. Phys., 2007, 127, 154702 CrossRef PubMed.
- K. L. Kearns, S. F. Swallen, M. D. Ediger, T. Wu, Y. Sun and L. Yu, J. Phys. Chem. B, 2008, 112, 4934–4942 CrossRef CAS PubMed.
- E. Leon-Gutierrez, A. Sepúlveda, G. Garcia, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, Phys. Chem. Chem. Phys., 2010, 12, 14693–14698 RSC.
- K. J. Dawson, K. L. Kearns, M. D. Ediger, M. J. Sacchetti and G. D. Zografi, J. Phys. Chem. B, 2009, 113, 2422–2427 CrossRef CAS PubMed.
- S. L. L. M. Ramos, M. Oguni, K. Ishii and H. Nakayama, J. Phys. Chem. B, 2011, 115, 14327–14332 CrossRef CAS PubMed.
- K. Ishii and H. Nakayama, Phys. Chem. Chem. Phys., 2014, 16, 12073–12092 RSC.
- K. Dawson, L. A. Kopff, L. Zhu, R. J. McMahon, L. Yu, R. Richert and M. D. Ediger, J. Chem. Phys., 2012, 136, 094505 CrossRef PubMed.
- K. Dawson, L. Zhu, L. Yu and M. D. Ediger, J. Phys. Chem. B, 2011, 115, 455–463 CrossRef CAS PubMed.
- C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé, G. Garcia and J. Rodríguez-Viejo, J. Non-Cryst. Solids, 2015, 407, 256–261 CrossRef.
- L. Zhu and L. Yu, Chem. Phys. Lett., 2010, 499, 62–65 CrossRef CAS.
- Z. Fakhraai, T. Still, G. Fytas and M. D. Ediger, J. Phys. Chem. Lett., 2011, 2, 423–427 CrossRef CAS.
- T. Pérez-Castañeda, C. Rodríguez-Tinoco, J. Rodríguez-Viejo and M. A. Ramos, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11275–11280 CrossRef PubMed.
- S. F. Swallen, K. Traynor, R. J. McMahon and M. D. Ediger, Phys. Rev. Lett., 2009, 102, 065503 CrossRef PubMed.
- A. Sepúlveda, S. F. Swallen, L. A. Kopff, R. J. McMahon and M. D. Ediger, J. Chem. Phys., 2012, 137, 204508 CrossRef PubMed.
- D. Bhattacharya and V. Sadtchenko, J. Chem. Phys., 2014, 141, 094502 CrossRef PubMed.
- A. Sepúlveda, S. F. Swallen and M. D. Ediger, J. Chem. Phys., 2013, 138, 12A517 CrossRef PubMed.
- A. Sepúlveda, E. Leon-Gutierrez, M. Gonzalez-Silveira, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, J. Phys. Chem. Lett., 2012, 3, 919–923 CrossRef PubMed.
- Z. Chen, A. Sepúlveda, M. D. Ediger and R. Richert, J. Chem. Phys., 2013, 138, 12A519 CAS.
- A. Sepúlveda, M. Tylinski, A. Guiseppi-Elie, R. Richert and M. D. Ediger, Phys. Rev. Lett., 2014, 113, 045901 CrossRef PubMed.
- K. Ishii, H. Nakayama, S. Hirabayashi and R. Moriyama, Chem. Phys. Lett., 2008, 459, 109–112 CrossRef CAS.
- S. S. Dalal, A. Sepúlveda, G. K. Pribil, Z. Fakhraai and M. D. Ediger, J. Chem. Phys., 2012, 136, 204501 CrossRef PubMed.
- S. S. Dalal, Z. Fakhraai and M. D. Ediger, J. Phys. Chem. B, 2013, 117, 15415–15425 CrossRef CAS PubMed.
- A. Wisitsorasak and P. Wolynes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022308 CrossRef PubMed.
- P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1353–1358 CrossRef CAS PubMed.
- S. Léonard and P. Harrowell, J. Chem. Phys., 2010, 133, 244502 CrossRef PubMed.
- I. Lyubimov, M. D. Ediger and J. J. de Pablo, J. Chem. Phys., 2013, 139, 144505 CrossRef PubMed.
- G. M. Hocky, L. Berthier and D. R. Reichman, J. Chem. Phys., 2014, 141, 224503 CrossRef PubMed.
- D. M. Walters, R. Richert and M. D. Ediger, J. Chem. Phys., 2015, 142, 134504 CrossRef PubMed.
- C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé, A. F. Lopeandia, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, J. Phys. Chem. B, 2014, 118, 10795–10801 CrossRef PubMed.
- S. S. Dalal and M. D. Ediger, J. Phys. Chem. B, 2015, 119, 3875–3882 CrossRef CAS PubMed.
- D. Yokoyama, A. Sakaguchi, M. Suzuki and C. Adachi, Appl. Phys. Lett., 2008, 93, 173302 CrossRef.
- S. S. Dalal, D. M. Walters, I. Lyubimov, J. J. de Pablo and M. D. Ediger, Proc. Natl. Acad. Sci. U. S. A., 2015, 201421042 Search PubMed.
- A. Gujral, K. A. O’Hara, M. F. Toney, M. L. Chabinyc and M. D. Ediger, Chem. Mater., 2015, 27, 3341–3348 CrossRef CAS.
- E. León-Gutierrez, G. Garcia, A. F. Lopeandía, J. Fraxedas, M. T. Clavaguera-Mora and J. Rodríguez-Viejo, J. Chem. Phys., 2008, 129, 181101 CrossRef PubMed.
- A. F. Lopeandia, J. Rodríguez-Viejo, M. Chacon, M. T. Clavaguera-Mora and F. Munoz, J. Micromech. Microeng., 2006, 16, 965–971 CrossRef CAS.
- S. Shamblin and X. Tang, J. Phys. Chem. B, 1999, 103, 4113–4121 CrossRef CAS.
- Z. Wojnarowska, K. Adrjanowicz, P. Wlodarczyk, E. Kaminska, K. Kaminski, K. Grzybowska, R. Wrzalik, M. Paluch and K. L. Ngai, J. Phys. Chem. B, 2009, 113, 12536–12545 CrossRef CAS PubMed.
- C. T. Moynihan, A. J. Easteal, M. A. Debolt and J. Tucker, J. Am. Ceram. Soc., 1975, 8, 12–16 Search PubMed.
- H. N. Ritland, J. Am. Ceram. Soc., 1956, 39, 403–406 CrossRef CAS.
| This journal is © the Owner Societies 2015 |
