Cation–π interactions: computational analyses of the aromatic box motif and the fluorination strategy for experimental evaluation

Abstract

Cation–π interactions are common in biological systems, and many structural studies have revealed the aromatic box as a common motif. With the aim of understanding the nature of the aromatic box, several computational methods were evaluated for their ability to reproduce experimental cation–π binding energies. We find the DFT method M06 with the 6-31G(d,p) basis set performs best of several methods tested. The binding of benzene to a number of different cations (sodium, potassium, ammonium, tetramethylammonium, and guanidinium) was studied. In addition, the binding of the organic cations NH₄⁺ and NMe₄⁺ to ab initio generated aromatic boxes as well as examples of aromatic boxes from protein crystal structures were investigated. These data, along with a study of the distance dependence of the cation–π interaction, indicate that multiple aromatic residues can meaningfully contribute to cation binding, even with displacements of more than an angstrom from the optimal cation–π interaction. Progressive fluorination of benzene and indole was studied as well, and binding energies obtained were used to reaffirm the validity of the “fluorination strategy” to study cation–π interactions in vivo.

---

Introduction

The importance of noncovalent interactions in determining macromolecular structure and molecular associations in biology is well appreciated. Nevertheless, it remains a challenging task to confirm the importance of any particular noncovalent interaction, and even more difficult to quantify one. Different issues arise in attempting to evaluate hydrophobic effects, hydrogen bonds, or ion-pairing interactions, as each has its own unique characteristics. For some time we have been evaluating a particular noncovalent interaction – the cation–π interaction – in a range of proteins, most typically neuroreceptors and ion channels.^1–4 Only in recent years has structural information become available for such systems. Remarkably, the available structures point to a general structural motif for cation–π interactions, the so-called aromatic box.^2,5–7 This is formed by 3 to 5 aromatic side chains that can encapsulate the positive charge of a cationic molecule. This molecular cage has been seen in many receptors and in other binding sites for cationic guests. It is not known what the advantage of this motif is, nor is it clear to what extent 3–5 aromatics can simultaneously contribute to the binding of a cation.

Even if a structure is available and it shows a close contact between an ion and a π system, it cannot be assumed that a functionally significant noncovalent interaction exists. Over the past 20 years we have addressed this issue using non-canonical amino acid mutagenesis.^4,8 The aromatic of interest (the side chain of a phenylalanine (Phe), tyrosine (Tyr), or tryptophan (Trp)) is progressively fluorinated. Fluorine is well known to be deactivating in a cation–π interaction, and its effects are typically additive. One thus expects a correlation between protein function and/or ligand binding and degree of fluorination if a cation–π interaction is important. In a number of systems we have found a linear trend between the activation of a receptor by a cationic ligand and the calculated binding of a sodium ion to a series of fluorinated aromatic rings (indoles to mimic the side chain of Trp or benzenes to mimic Phe/Tyr). We considered this compelling evidence for a cation–π interaction.

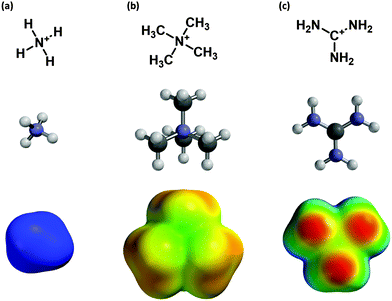
This “fluorination strategy” is surprisingly general. Linear plots have been seen in over 30 cases, spanning a range of proteins and ligand types. Drug-like molecules with widely differing structures have been studied, including quaternary ammonium ions (acetylcholine) and protonated amines, including primary (glycine, GABA, serotonin), secondary (epibatidine, cytidine, varenicline) and tertiary (nicotine). In addition, more complex cations such as granisetron, ondansetron,⁹ and the guanidinium toxin tetrodotoxin (TTX)¹⁰ have shown linear fluorination plots. In contrast, a study of another guanidinium compound, meta-chlorophenyl biguanide (mCPBG) binding to the 5-HT₃ (serotonin) receptor showed behavior that was difficult to interpret.¹¹ In all cases we compared experimental data to the binding of Na⁺ to the appropriate aromatics. While it may be reasonable to assume that a primary ammonium ion (RNH₃⁺) is well modeled by Na⁺, more complex ions such as a quaternary ammonium or a guanidinium show much different charge distributions (Fig. 1) and so may display different binding behaviors.

Fig. 1 Cations examined in this study. (a) The ammonium ion, (b) the tetramethylammonium ion, and (c) the guanidinium ion. Pictured are molecular structures and potential energy surfaces. (Geometry optimized M06/6-31G(d,p) ranging from +400 (red) to +700 (blue) kJ mol⁻¹.)

To address this issue we have computationally evaluated fluorination effects on cation–π interactions involving the more complex cations ammonium (NH₄⁺), tetramethylammonium (NMe₄⁺), and guanidinium (Fig. 1). Substituent effects on cation–π interactions and related noncovalent interactions involving benzene have been the subject of several recent investigations, including some with very high levels of theory.^12–14 These studies have revealed some unanticipated effects in such noncovalent interactions. The more modest goals of the present work involve the trends in cation–π binding energies in response to progressive fluorination for several combinations of cation and aromatic. When constrained to a cation–π binding geometry, these larger cations mimic the trends seen with Na⁺ as probe ion.

Methods

All calculations were performed using Spartan 14¹⁵ unless otherwise stated.

Calculating cation–π energies:

Cation–π interactions to benzene and derivatives were evaluated with full geometry optimization at M06/6-31G(d,p)¹⁶ with energies calculated using eqn (1):

BE = (E₊ + E_π) − E_TOT (1)

where E_TOT is the total complex energy, E₊ is the energy of the cation alone, and E_π is the energy of the aromatic system, whether it is a single aromatic or an aromatic box bereft of a cation. In this form, a positive BE signifies a favorable interaction.

Distance dependence

Distance dependence data were obtained by constraining the distance of the ion in question to benzene and performing a constrained geometry-optimized M06/6-31G(d,p) calculation. This distance constraint was increased iteratively from the starting (optimal) geometry, and the binding energy calculated using eqn 1. These data were fit using the KaleidaGraph™ software (Synergy Software).

Aromatic box calculations

Ab initio aromatic boxes with a complexed ion were generated using Spartan 14. Geometry-minimized (M06/6-31G(d,p) ≡ M06/6-31G**) structures were obtained for ammonium bound to 3 or 4 benzene molecules and for tetramethylammonium binding to 3, 4, or 5 benzene molecules. The binding energies were obtained using eqn (1), where E_π is the energy of the aromatic box without the tetramethylammonium ion.

Existing aromatic box motifs were imported from the Protein Data Bank using Gaussview 5,¹⁷ and protons were added to the structures. Cation–π binding energies were calculated using Gaussian09.¹⁸ Aromatic boxes were generated by deleting backbone and β atoms of the amino acids as well as the noncationic portion of acetylcholine or trimethyllysine (to generate NMe₄⁺ in both cases). The cation–π binding energy was computed by taking the single-point energy (M06/6-31G(d,p)) with and without the tetramethylammonium ion. Individual cation–π interactions between tetra-methylammonium and aromatic residues were found by deleting all but the cation and aromatic group of interest and computing a single point energy.

Fluorination series

In most cases, full geometry optimization was performed for complexes of cations to fluorinated aromatics. In some cases, however, this resulted in geometries that would not be considered cation–π interactions. In such cases, fluorines were appended to the benzene ring with C–F bond distances set to values determined by optimization of the isolated aromatic system. This allowed determination of a cation–π binding energy with the cation at the position appropriate to the benzene–ion complex. We will refer to this as the single-point binding energy. The structures were then allowed to relax to the lowest-energy geometry in the gas phase. The binding energy itself was calculated using eqn (1).

Several cation–π structures represented relatively shallow local minima, and were challenging to isolate. For the three separate orientations of the tetramethylammonium ion (one, two and three methyl groups facing the benzene), starting structures were the molecular mechanics-minimized structure. This enforced a symmetry on the structure that was maintained while optimizing at a higher level of theory. To achieve a stacked conformation for guanidinium–benzene, the distance from the center of the guanidinium molecule to three meta carbons of benzene was constrained to 3.4 Å and the (constrained) equilibrium geometry was calculated at M06/6-31G(d,p). The final stacked geometry was obtained using this restricted geometry as a starting point for full geometry optimization.

Results

Choice of computational method

We considered several different levels of theory to find which offers the best combination of accuracy and computational efficiency. Since one goal of the present work is to enable evaluation of larger systems related to protein crystal structures, we did not consider more computationally expensive correlational methods such as CCSD, nor did we consider overly large basis sets of the sort that have often been used to evaluate various methods. We considered four prototype cation–π interactions for which experimental gas phase data are available (Table 1).^19–22 Some time ago, we computed the binding of Na⁺ to a number of simple aromatic systems.²³ We found that a relatively simple level of theory – HF/6-31G(d,p) – performed remarkably well. As shown in Table 1, it remains the most accurate level of theory considered for both Na⁺ and K⁺ binding to benzene. HF does, however, perform poorly on the larger ions. MP2 performed inconsistently depending on the ion studied. Also, several years ago we evaluated the most popular DFT method at the time – B3LYP – and found the results to be disappointing. Subsequent studies have confirmed that B3LYP is not especially effective for noncovalent interactions without complex dispersion correcting potentials.^24–29

Table 1 Binding energies to benzene (kcal mol⁻¹)^a

Ion	HF 6-31G(d,p)	HF 6-311+G(d,p)	MP2 6-31G(d,p)	MP2 6-311+G(d,p)	B3LYP 6-31G(d,p)	B3LYP 6-311+G(d,p)	M06 6-316(d,p)	M06 6-311+G(d,p)	Expt.
a Computed values are ΔE; experimental values are ΔH. All data in the gas phase. b Mean absolute error of the four values.
Na^+	27.1	23.2	29.9	24.9	28.4	23.8	26.8	22.2	28.0
K^+	19.3	15.6	23.8	19.5	20.8	16.1	20.3	16.3	19.2
NH4^+	15.3	14.5	19.0	19.2	17.5	15.8	19.5	18.2	19.3
NMe4^+	6.6	5.6	11.3	11.7	7.7	6.0	10.8	10.0	9.4
Error^b	1.9	4.3	2.2	1.5	1.4	3.6	0.98	2.6	—

---

In recent years, a wide array of DFT methods has been developed, each targeting a specific computational challenge. Several methods have been specifically parameterized for noncovalent interactions, including M06-L, M06, M06-2X and others. A previous comparison of over a dozen DFT methods showed that M06 and M06-2X both performed well.¹⁶ For cation–π interactions, we find that M06 performs very well (Table 1), even with a modest basis set. The most significant effect is a substantial improvement in the binding to tetramethylammonium. Surprisingly, M06-2X overestimated the binding energies to benzene of Na⁺ and K⁺ by 2 and 4 kcal mol⁻¹, respectively, and so we did not consider it further. Clearly, when considering DFT methods one must make a choice on a case-by-case basis. Interestingly, for all the methods considered except MP2, the larger 6-311+G(d,p) basis set gave poorer results than 6-31G(d,p). This likely reflects a cancellation of effects to some extent, but the results are consistent across the various cations considered. Given the results of Table 1, we have settled on M06/6-31G(d,p) as the optimal level of theory. It gives quite good results for all the systems considered. We note that the simpler HF/6-31G(d,p) method reproduces all the trends seen with M06; the largest differences are seen in the quantitative results for tetramethylammonium and guanidinium ions.

Cation–π interactions with benzene

The cation–π binding energies and optimized geometries were calculated at M06/6-31G(d,p) for a number of different ions. For the simple metal ions Na⁺ and K⁺ as well as NH₄⁺, the cation binds to benzene in one conformation: directly centered in the middle of the benzene ring (en face). To evaluate the tetramethylammonium–benzene interaction, the complex was minimized in three separate cation–π geometries: with one, two, and three methyl groups en face (Fig. 2). Geometries with more methyl groups en face had higher binding energies, consistent with previously reported work.³⁰

Fig. 2 Examples of large cations binding to benzene. (a) Tetramethylammonium ions binding with one, two and three methyl groups towards the face of benzene. (b) Guanidinium ions binding in T-shaped and stacked conformations. (c) Tetramethylammonium binding to indole. Cation–π binding energies computed at M06/6-31G(d,p).

Cation–π energies of guanidinium ions to benzene were calculated in two separate conformations: T-shaped and stacked (see Fig. 2). As has been seen in other studies,^31,32 T-shaped interactions have a much stronger binding energy. Interestingly, according to M06/6-31G(d,p) the guanidinium ion adopts a propeller shape in the stacked conformation, with the amine groups adopting a 25 degree torsion angle from the plane of the cation. All cation–π binding energies are listed in Table 2.

Table 2 Cation–π binding energies (kcal mol⁻¹)^a

	Benzene	F-benzene	F2-benzene		F3-benzene
			1,3	1,4	1,2,3	1,3,5
a M06/6-31G(d,p) calculations; full geometry optimization unless otherwise noted. b Binding energy obtained via single point method.
Sodium	26.8	22.7	19.2	18.9	16.1	15.6
Potassium	20.3	17.7	14.6	14.4	12.0	11.7
Ammonium	19.5	16.2	12.8	12.9	10.1	10.1
Tetramethylammonium (1)	6.5	5.3^b	4.3^b	—	2.9^b	3.0
Tetramethylammonium (2)	8.7	7.2^b	5.5^b	5.7	4.0^b	—
Tetramethylammonium (3)	10.8	9.0^b	7.1^b	7.0	5.3^b	5.4
Guanidinium (T-shaped)	14.9	12.3	10.4	9.8	7.0^b	7.9
Guanidinium (stacked)	8.6	7.2^b	5.8^b	—	4.6^b	5.1

---

Distance dependence

In biological systems cations might bind to aromatic rings at non-optimal geometries (the optimum being essentially van der Waals contact), due to other constraints imposed by the protein and/or ligand. This might be especially true for the aromatic box motif, as discussed below. As such, it is important to probe non-optimal binding geometries. To evaluate this situation, we have determined the distance dependence of a cation–π interaction to benzene for Na⁺, K⁺, NH₄⁺, and tetramethylammonium (1-methyl down). As shown in Fig. 3, similar trends are seen, and the cation–π interaction distance dependence is not overly steep. For all three cations, displacement by a full Å from the optimal distance results in roughly a 40% drop in binding energy. When fit to a 1/rⁿ function, n values of 1.9, 2.0, 2.8, and 2.8 are obtained for Na⁺, K⁺, NH₄⁺, and tetramethylammonium, respectively. These results indicate that even a non-optimal cation–π interaction can contribute significantly to ligand binding or protein stability.

Fig. 3 Distance dependence of cation–π binding for sodium, potassium, ammonium, and NMe₄⁺ (one methyl down) ions. Binding energy is relative to the optimal binding, and distance is from the center of the benzene to Na⁺ or K⁺; N atom of ammonium; or methyl C of tetramethylammonium. Complexes with very short distances deviate from this electrostatic plot and were not included in the fitting.

The aromatic box

In recent years, it has become apparent that there is a common motif for a biological cation–π binding site – the so-called aromatic box.^2,5–7 This is formed by 3–5 aromatic side chains that encapsulate the positive charge of a cationic molecule (Fig. 4 and 5). An early and especially compelling example was seen in the ACh binding proteins (AChBP), which provide excellent models for the nicotinic acetylcholine receptor (nAChR) binding site.^33,34 Five aromatics form a box around the quaternary ammonium of ACh and around cationic sites of other ligands in this much discussed system (Fig. 5a). Another frequently seen box is found in proteins that bind a trimethyllysine (KMe₃⁺) side chain of a histone protein.^35–39 The KMe₃⁺ structure is a common and critical motif as part of the “histone code”. A number of crystal structures of transcriptional regulators bound to KMe₃⁺ have appeared, and all show an “aromatic box” that binds the quaternary ammonium ion through cation–π interactions (Fig. 5b).

We first probed the aromatic box by studying the simultaneous binding of 4 benzene rings to a tetramethylammonium.⁴⁰ As seen in Table 3 and Fig. 4a, a tetramethylammonium can easily bind to multiple benzenes simultaneously. The total binding energy is 39.2 kcal mol⁻¹ (Table 3). Each pairwise interaction has three methyl groups en face, and so four optimal interactions of this sort would produce a binding energy of 43.2 kcal mol⁻¹ (4 × 10.8; listed as “Theoretical” in Table 3). The individual binding energies are nearly optimal, as evidenced by the “Sum” column in Table 3. Similar results are seen for 2 or 3 or 5 benzenes (ESI†), although the 5th benzene binds less tightly than the others.

Table 3 Binding energies (kcal mol⁻¹) to a 4-benzene aromatic box

	Binding energy	Theoretical^a	Sum^b	Discrepancy^c
a Four times the binding energy for a single ion–benzene complex. b Four times the binding energy of a single cation-box aromatic. c The difference between the theoretical binding energy and the calculated binding energy.
NH4^+	59.6	78.0	71.1	18.4
NMe4^+	39.2	43.2	42.3	4.0

---

Fig. 4 Geometry-optimized complexes of four benzenes to (a) one tetramethylammonium and (b) one ammonium ion. Binding energies computed at M06/6-31G(d,p).

Receptors that bind primary ammonium ions (RNH₃⁺) such as GABA or serotonin also have a cluster of aromatic amino acids at the agonist binding site, so we considered the binding of ammonium to an aromatic box. Again, four benzenes can fit comfortably around an ammonium ion with no obvious steric conflicts (Fig. 4b). Experimental studies of K⁺, which is similar in size to ammonium, have shown that multiple benzenes can complex the ion.^21,41,42 The total binding energy of ammonium to four benzenes is 59.6 kcal mol⁻¹, but now the individual interactions are not optimal; the sum value (four times the binding energy of a single cation-box aromatic) differs considerably from the true binding energy. The even larger difference between the theoretical value and the binding energy could reflect a small negative cooperativity due to conflicts between induced dipoles generated by the binding.

Such induced dipoles are expected to be smaller when tetramethylammonium is the ion, consistent with the smaller deviation seen in Table 3.

The aromatic box motif found in biological systems uses Phe, Tyr, and Trp, although there is a general bias toward Tyr and Trp.³² Based on studies using Na⁺ as a probe ion,⁴⁴ Trp is expected to provide the strongest cation–π binding. Indeed, calculated binding energies for tetramethylammonium (3 methyls down) to benzene (Phe), phenol (Tyr), and indole (Trp) are 10.8, 12.5, and 15.1 kcal mol⁻¹, respectively. As in previous studies, the cation is significantly offset from the center of the phenol,⁴⁵ and it lies over the six-membered ring of the indole.³²

We replaced the ACh of AChBP with tetramethyl-ammonium and evaluated the total binding energy as well as the interaction to each individual ring (Fig. 5a and Table 4). We find a total binding energy of 28.9 kcal mol⁻¹, with four of the five aromatics contributing significantly. The largest contribution comes from TrpB, the residue that has been shown experimentally to make a functionally important cation–π interaction in most nAChRs.⁴

Table 4 Binding energies (kcal mol⁻¹) of tetramethylammonium to protein aromatic boxes^a

AChBP		Histone binding protein
a M06/6-31G(d,p) calculations; single-point energies. b Binding energy if all interactions were optimal and independent.
Aromatic box	28.9	Aromatic box	32.3
Predicted^b	67.7	Predicted^b	42.7
TrpB	8.3	Trp50	13.9
TyrC2	8.0	Trp47	12.0
TyrC1	7.5	Tyr26	9.0
TrpD	4.8
TyrA	2.3
Sum	30.9	Sum	34.9

---

We applied a similar analysis to the binding of KMe₃⁺ to a histone binding protein (Fig. 5b).⁴³ We find a total binding energy of 32.3 kcal mol⁻¹ for the tetramethylammonium. Trp47 and Trp50 contribute the bulk of the binding energy, but Tyr26 is still significant (Table 4). Based on the distance dependence of tetramethylammonium binding from Fig. 3, it is evident that all eight potential methyl⋯aromatic interactions of Fig. 5b contribute to the total binding energy. For both protein structures, the calculated total binding energy is slightly less than the sum of the individual interactions, as was seen in the model structures. Also for both systems, the total binding energy is much less than what would be expected if all cation–π interactions were optimal; deviations of 39 and 10 kcal mol⁻¹ are seen for AChBP and the histone binding protein, respectively.

Fig. 5 The aromatic box motif binding sites of (left) ACh binding to AChBP (PDB: 3WIP).³⁴ Residues are labeled according to their conventional designation in the nAChR. (right) Trimethyllysine binding to the polycomb chromodomain from Drosophila histone H3 protein (PDB: 1PFB).⁴³ Distances (Å) are from a carbon to the ring centroid; the calculated optimal distance for such an interaction is 3.6 Å.

Fluorination studies

In our experimental studies of a possible cation–π interaction to a Phe or a Tyr,⁴ we have used 4-F-Phe, 3,5-F₂-Phe, and 3,4,5-F₃-Phe as our cation–π interaction probes, while for Trp we use the 5-, 5,7-, 5,6,7-, and 4,5,6,7-fluorotryptophans. As such, we have focused on the analogous benzenes and indoles for our computational studies (Tables 2 and 5). For the most part these studies were straightforward: the ion remained roughly centered over the ring and the cation–π binding energy progressively decreased as fluorines were introduced.

Table 5 Cation–π binding energies (kcal mol⁻¹)^a

	Indole	F-indole	F2-indole	F3-indole	F4-indole
		5	5,7	5,6,7	4,5,6,7
a M06/6-31G(d,p) calculations; full geometry optimization unless otherwise noted. b Binding energy obtained via single point method.
Sodium	32.7	28.8	25.7	22.5	18.9
Tetramethylammonium (3)	15.2	13.5	11.9	10.1	9.1^b

---

The exceptions occurred with the larger ions tetramethylammonium and guanidinium binding to the fluorobenzenes and highly fluorinated indoles. In these cases full geometry optimization led to edge-on binding, with the cation attracted to the fluorine(s). Full details of these results are presented in the ESI.†

While these edge-on structures are interesting with regard to possible gas phase studies, the focus of the present work is the binding of cationic ligands to proteins, where structural constraints are likely to discourage edge-on geometries. We developed two strategies to determine the effect of fluorination on such constrained systems. First, we simply added fluorines to the ion–benzene complex (which is in an en face cation–π geometry) and performed single point calculations. Alternatively, we could use the symmetrical 1,4- and 1,3,5-fluorobenzenes, for which the ions stayed centered over the ring. The two strategies produced similar results, with the expected trends on progressive fluorination.

Comparison of fluorination calculations with in vivo data

As noted above, we previously compared experimental results for a fluorination study with binding energies for Na⁺ to the analogous aromatic.⁴ We can now perform more realistic comparisons. For primary amines, the previously described cation–π interaction between glycine and fluorinated phenylalanine residues in the glycine receptor⁴⁶ was re-evaluated using the results for the binding of an ammonium ion to fluorinated benzenes. As shown in Fig. 6, a linear trend between agonist potency and cation–π binding energy is still obtained.

Fig. 6 Cation–π binding plots for (a) glycine at the glycine receptor using computed cation–π binding energies for ammonium ions to fluorinated benzenes using in vivo data collected for activation of glycine receptor mutants⁴⁶ and (b) acetylcholine at the α4β2 nicotinic acetylcholine receptor (nAChR) using in vivo data collected for activation of α4β2 nAChR mutants⁴⁷ using cation–π energies for tetramethylammonium ions binding to fluorinated indoles.

We have several demonstrations of strong cation–π interactions between ACh and nicotinic ACh receptors.⁴⁷ The relevant calculation then is tetramethylammonium binding to fluorinated indoles. Fig. 6 shows such an analysis, considering tetramethylammonium binding to the indole ring with three methyl groups en face (Fig. 6). In each case, the calculated cation–π binding energies line up well with experimental results, confirming that the results of such an analysis of receptor binding are independent of the nature of the probe cation.

Discussion

The importance of the cation–π interaction in stabilizing protein structures and mediating protein–ligand interactions is well-established, and computational methods have always played an important role in evaluating cation–π interactions. Here we evaluated several modern computational protocols to find one that could be conveniently applied by experimentalists to evaluate potential cation–π interactions in biological structures. Gratifyingly, we find that a not overly complex method – M06/6-31G(d,p) – provides very good results on systems for which experimental data are available. For larger cations such as tetramethylammonium it provides a significant improvement over HF methods. Note that we did not employ counterpoise corrections or other methods to account for likely basis set superposition error (BSSE). It may well be that there is a compensation effect, where the relatively small basis set and the neglect of BSSE roughly compensate for each other. In the end, we feel the method espoused here is quite adequate for evaluating cation–π interactions.

The aromatic box motif is common in protein cation–π binding sites. This suggests that multiple aromatics can simultaneously have favorable interactions with a cation, although it seems likely that not all interactions would be optimal in a protein structure. This prompted us to revisit the issue of the distance dependence of the cation–π interaction. As in an earlier, preliminary study,¹ we find that the distance dependence is not steep (Fig. 3). For example, it could be argued that the cation–π interaction should be treated as an ion–quadrupole interaction. Ideally, an ion–quadrupole interaction should show a 1/r³ distance dependence for the binding energy. However, the cation–π interaction is better modeled by a 1/r² distance dependence for the prototype Na⁺ and K⁺ ions. For larger ions a roughly 1/r³ distance dependence is seen, likely reflecting the increased importance of polarizability for the larger ions. In any case, displacement of the ion by a full angstrom from van der Waals contact (the optimal binding arrangement) diminishes the interaction by less than half.

We have taken two approaches to evaluating the aromatic box motif. First, we evaluated the binding of multiple benzenes to both tetramethylammonium and ammonium ions under optimal conditions. We find that four aromatics can easily bind simultaneously to either ion. For tetramethylammonium, the total binding energy is close to what would be expected if all four individual benzene tetramethylammonium interactions were optimal and independent. For ammonium there is a significant deviation from expectation based on four optimal ammonium⋯benzene interactions. Mostly, this is because the individual interactions are not optimal; clearly the ammonium ion is a bit too small to perfectly bind four benzenes simultaneously. There is a second, non-additivity factor that we attribute to a clash between induced dipoles in the four benzenes. Nevertheless, the global conclusion is that multiple aromatics can readily contribute to the binding of a cation through cation–π interactions.

We next considered two exemplary aromatic boxes from protein structures: the acetylcholine binding protein (AChBP) and a polycomb chromodomain binding to a peptide model of trimethyllysine from the histone H3 protein. In each case we truncated the ligand (ACh or trimethyllysine) to a tetramethylammonium. We anticipated that all contacts between tetramethylammonium and an aromatic of the box would not be optimal, and indeed that is the case. As shown in Table 4, the “predicted” binding energy – that which would arise if each cation–π interaction was optimal – is substantially larger than the actual binding energy. Recalling that an optimal cation–π interaction for tetramethylammonium to Tyr or Trp would be 12.5 or 15.1 kcal mol⁻¹, it is clear that each interaction evaluated individually is weaker than optimal. The histone binding protein has three interactions approaching the ab initio-generated geometries and interaction energies, whereas some components of the AChBP box make only relatively minor contributions to the overall binding energy. Nevertheless, it is clear that a ligand can benefit simultaneously from multiple cation–π interactions to components of an aromatic box. Gratifyingly, the largest interaction in the AChBP is to TrpB, which is the residue most commonly involved in a functionally significant cation–π interaction in studies of nAChRs.

We also considered the extent to which the total binding energy deviates from the sum of the individual interactions. In each case, the deviation is not large, suggesting a relative lack of cooperativity (positive or negative) in the biological aromatic boxes.

We conclude that while the positioning of the aromatics in the biological structures is not optimal, a cation can still make energetically significant cation–π interactions to multiple amino acid side chains. The shallow distance dependence of the cation–π interaction presaged this observation.

While not as large as is theoretically possible, total binding energies for the two aromatic boxes are quite large. Like most noncovalent interactions, the cation–π interaction is attenuated on moving from the gas phase to a condensed medium, although the attenuation is not as large as is typically associated with a hydrogen bond or an ion pair, since the desolvation penalty is less severe.⁴⁸ Additionally, these calculations do not include any adjustments that the protein structure must make to adapt to the ligand; here we are considering perfectly preorganized binding sites.

It is also interesting that, despite the presence of 5 cation–π interactions, the AChBP shows a smaller binding energy than the histone binding protein with 3 cation–π interactions, because the cation–π interactions in the latter are individually much stronger. Experimentally, AChBP binds ACh with a ∼4 mM affinity,³³ while affinities on the order of 0.3 mM have been determined for the binding of KMe₃⁺ to a histone binding protein.⁴⁹

An additional goal of the present work was to determine whether previous experimental studies of complex biological receptors – in which cation–π binding to a receptor was correlated to the affinity of a Na⁺ to a substituted aromatic ring – would be altered if more realistic models of the biological ligand were used. The ligands studied included simple protonated amines, (RNH₃⁺), ACh and related compounds (RNMe₃⁺), and derivatives of guanidinium. As such, we have evaluated the binding of NH₄⁺, NMe₄⁺, and guanidinium to a series of fluorinated benzenes and indoles.

As noted above, several highly detailed analyses of noncovalent interactions involving aromatics have appeared in recent years.⁴⁹ These have emphasized direct interactions between the ion and the substituent, an interaction that might be expected to favor geometries in which the ion migrates away from the center of the ring toward the substituent(s). We find that for the simpler ions (Na⁺, K⁺, and ammonium) the ion stays over the center of the ring as fluorines are introduced. In contrast, for tetramethylammonium and guanidinium, edge-on geometries are competitive with and in some cases superior to the cation–π geometries for multiply fluorinated aromatics (ESI†). However, when in a cation–π binding geometry – achieved either through constraints or by using symmetrically substituted benzenes – tetramethylammonium and guanidinium follow the same patterns as the smaller ions.

Our results allow more reasonable modeling of the experimental studies. We find, perhaps not surprisingly, that the linear trends between receptor activation and cation–π binding energy arise regardless of the precise nature of the cation used in the calculations. These more realistic calculations do, however, allow some interesting quantitative comparisons to be made. We have several studies of ACh binding to a series of fluorinated Trp derivatives. The largest effect we have seen is a 540-fold drop in affinity on going from Trp to F₄-Trp, corresponding to 3.7 kcal mol⁻¹.⁴ Our calculations for tetramethylammonium show a corresponding drop of 6.1 kcal mol⁻¹. For a simple ammonium ion, our biggest effect has been seen for GABA binding to the GABA_A receptor, with a 16 500-fold drop in affinity on going from Phe to 3,4,5-F₃-Phe, corresponding to 5.75 kcal mol⁻¹.⁴ Our calculations on ammonium show a corresponding drop of 8.4 kcal mol⁻¹. We consider these results to be quite encouraging. As noted above, one might expect some attenuation of a cation–π interaction on going from the gas phase to a receptor binding site. The fact that the trend between the two studies is in the right direction, with the protein binding being roughly 60% of the gas phase binding in both cases, suggests that the present computational model may be able to provide semi-quantitative analyses of protein cation–π binding sites.

Conclusions

The cation–π interaction, common in protein structures, can be modeled well using the recently-developed density functional M06 and the modest 6-31G(d,p) basis set. Calculations at this level of theory show that in the gas phase, there is a relatively shallow distance dependence for the cation–π interaction. This allows multiple interactions to contribute to ligand binding, providing a rationale for the aromatic box motif commonly seen in protein cation–π interaction binding sites. In addition, we examined cation–π binding to the AChBP and histone binding protein aromatic boxes, and reproduce in vivo observations.

All the ions studied here show a linear fluorination trend when in a cation–π (en face) binding geometry, enforced either by computational constraints or symmetrical substitution patterns. This supports the use of fluorination plots as a means to evaluate potential cation–π interactions.

Acknowledgements

We thank the NIH (NS 34407) for support of this work.

Notes and references

1. D. A. Dougherty, Science, 1996, 271, 163–168.
2. D. A. Dougherty, Acc. Chem. Res., 2013, 46, 885–893.
3. J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324.
4. E. B. Van Arnam and D. A. Dougherty, J. Med. Chem., 2014, 57, 6289–6300.
5. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250.
6. L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed. Engl., 2011, 50, 4808–4842.
7. J. Cheng, R. Goldstein, A. Gershenson, B. Stec and M. F. Roberts, J. Biol. Chem., 2013, 288, 14863–14873.
8. D. A. Dougherty and E. B. Van Arnam, ChemBioChem, 2014, 15, 1710–1720.
9. N. H. Duffy, H. A. Lester and D. A. Dougherty, ACS Chem. Biol., 2012, 7, 1738–1745.
10. V. P. Santarelli, A. L. Eastwood, D. A. Dougherty, R. Horn and C. A. Ahern, J. Biol. Chem., 2007, 282, 8044–8051.
11. T. F. MIles, PhD thesis, California Institute of Technology, 2015.
12. R. M. Parrish and C. D. Sherrill, J. Am. Chem. Soc., 2014, 136, 17386–17389.
13. S. E. Wheeler and J. W. G. Bloom, J. Phys. Chem. A, 2014, 118, 6133–6147.
14. S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 3126–3127.
15. I. C. Wavefunction Inc.
16. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
17. T. K. Roy Dennington and J. Millam, Gaussview 5, Semichem, Inc, Shawnee Mission, KS, 2009.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc, Wallingford, CT, USA, 2009.
19. M. Meot-Ner (Mautner) and C. A. Deakyne, J. Am. Chem. Soc., 1985, 107, 469–474.
20. M. Meot-Ner and C. A. Deakyne, J. Am. Chem. Soc., 1985, 107, 474–479.
21. J. Sunner, K. Nishizawa and P. Kebarle, J. Phys. Chem., 1981, 85, 1814–1820.
22. B. C. Guo, J. W. Purnell and A. W. Castleman, Chem. Phys. Lett., 1990, 168, 155–160.
23. S. Mecozzi, A. P. West and D. A. Dougherty, J. Am. Chem. Soc., 1996, 118, 2307–2308.
24. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
25. E. R. Johnson and G. A. DiLabio, Chem. Phys. Lett., 2006, 419, 333–339.
26. E. R. Johnson, R. A. Wolkow and G. A. DiLabio, Chem. Phys. Lett., 2004, 394, 334–338.
27. S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175–180.
28. E. Torres and G. A. DiLabio, J. Phys. Chem. Lett., 2012, 3, 1738–1744.
29. S. Tsuzuki and H. P. Lüthi, J. Chem. Phys., 2001, 114, 3949–3957.
30. A. Pullman, G. Berthier and R. Savinelli, J. Comput. Chem., 1997, 18, 2012–2022.
31. E. M. Duffy, P. J. Kowalczyk and W. L. Jorgensen, J. Am. Chem. Soc., 1993, 115, 9271–9275.
32. J. P. Gallivan and D. A. Dougherty, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9459–9464.
33. T. K. Sixma and A. B. Smit, Annu. Rev. Biophys. Biomol. Struct., 2003, 32, 311–334.
34. J. A. Olsen, T. Balle, M. Gajhede, P. K. Ahring and J. S. Kastrup, PLoS One, 2014, 9, e91232.
35. R. M. Hughes, K. R. Wiggins, S. Khorasanizadeh and M. L. Waters, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11184–11188.
36. S. A. Jacobs and S. Khorasanizadeh, Science, 2002, 295, 2080–2083.
37. H. Li, S. Ilin, W. Wang, E. M. Duncan, J. Wysocka, C. D. Allis and D. J. Patel, Nature, 2006, 442, 91–95.
38. P. V. Peña, F. Davrazou, X. Shi, K. L. Walter, V. V. Verkhusha, O. Gozani, R. Zhao and T. G. Kutateladze, Nature, 2006, 442, 100–103.
39. S. D. Taverna, H. Li, A. J. Ruthenburg, C. D. Allis and D. J. Patel, Nat. Struct. Mol. Biol., 2007, 14, 1025–1040.
40. J. Cheng, Z. Gong, W. Zhu, Y. Tang, W. Li, Z. Li and H. Jiang, J. Phys. Org. Chem., 2007, 20, 448–453.
41. O. M. Cabarcos, C. J. Weinheimer and J. M. Lisy, J. Chem. Phys., 1998, 108, 5151–5154.
42. G. K. Koyanagi and D. K. Bohme, Int. J. Mass Spectrom., 2003, 227, 563–575.
43. J. Min, Y. Zhang and R. M. Xu, Genes Dev., 2003, 17, 1823–1828.
44. S. Mecozzi, A. P. West Jr. and D. A. Dougherty, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 10566–10571.
45. A. Campo-Cacharrón, E. M. Cabaleiro-Lago, J. A. Carrazana-García and J. Rodríguez-Otero, J. Comput. Chem., 2014, 35, 1290–1301.
46. S. A. Pless, A. P. Hanek, K. L. Price, J. W. Lynch, H. A. Lester, D. A. Dougherty and S. C. R. Lummis, Mol. Pharmacol., 2011, 79, 742–748.
47. X. Xiu, N. L. Puskar, J. A. Shanata, H. A. Lester and D. A. Dougherty, Nature, 2009, 458, 534–537.
48. J. P. Gallivan and D. A. Dougherty, J. Am. Chem. Soc., 2000, 122, 870–874.
49. H. van Ingen, F. M. A. van Schaik, H. Wienk, J. Ballering, H. Rehmann, A. C. Dechesne, J. A. W. Kruijzer, R. M. J. Liskamp, H. T. M. Timmers and R. Boelens, Structure, 2008, 16, 1245–1256.

---

Footnote

† Electronic supplementary information (ESI) available: Description of binding substituent effect: Fig. S1–S4 and Tables S1–S3. See DOI: 10.1039/c5cp04668h

---