Phonon anomalies predict superconducting T_c for AlB₂-type structures

Abstract

We show that the well-known Kohn anomaly predicts T_c for ordered AlB₂-type structures. We use ab initio density functional theory to calculate phonon dispersions for Mg_1−xAl_xB₂ compositions and identify a phonon anomaly with magnitude that predicts experimental values of T_c for all x. Key features of these anomalies correlate with the electronic structure of Mg_1−xAl_xB₂. This approach predicts T_c for other known AlB₂-type structures as well as new compositions. We predict that Mg_0.5Ba_0.5B₂ will show T_c = 63.6 ± 6.6 K. Other forms of the Mg_1−xBa_xB₂ series will also be superconductors when successfully synthesised. Our calculations predict that the end-member composition, BaB₂, is likely to show a T_c significantly higher than currently achieved by other diborides although an applied pressure ∼16 GPa may be required to stabilise the structure.

---

Introduction

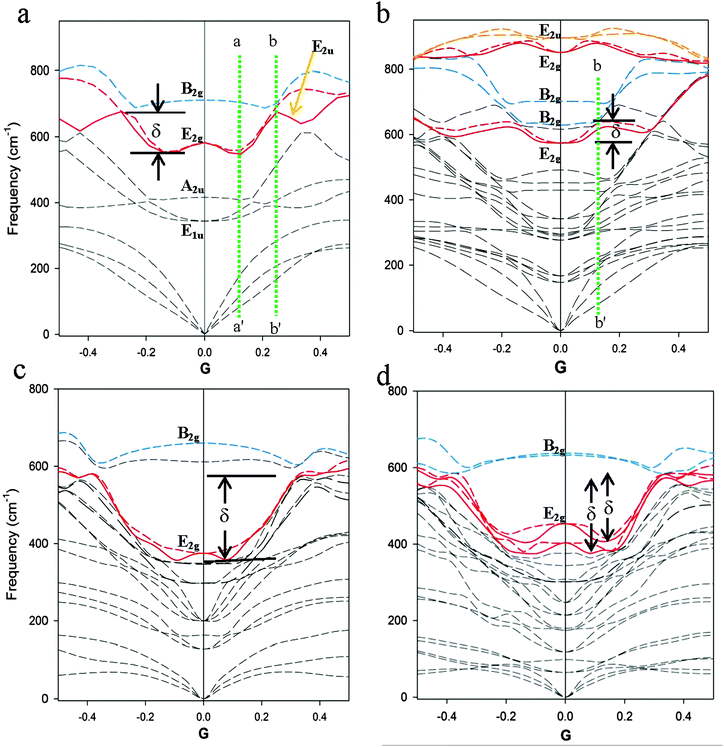
Magnesium diboride, with alternating layers of Mg and B atoms of hexagonal symmetry, is a superconductor below the transition temperature,¹T_c ∼ 39 K. Within the MgB₂ structure, shown in Fig. 1a and c, the boron layer is critical to the superconducting properties of MgB₂. Theory^2–4 and experiment^5,6 demonstrate close links, or coupling, between phonons and electrons.⁷ Phonons are collective excitations of atoms or molecules in a solid that oscillate at a single frequency and, by their nature, are temperature dependent. Boron vibration frequencies in MgB₂ vary with direction in real space. A dominant collective excitation of these atoms – a phonon mode – is designated the E_2g mode and is readily detected by Raman spectroscopy.^8,9 The wave vectors and the quantized energies of all atom vibrations are depicted in a phonon dispersion (PD) plot as shown in Fig. 1d. This plot identifies primary reciprocal space directions along the abscissa and, along the ordinate axis, the phonon frequency (or energy). The two in-plane orthogonal E_2g modes near the reciprocal space point G are also shown schematically in Fig. 1. These phonon modes are a key to understanding the superconducting properties of MgB₂ and metal-substituted forms^10–12 and, as we will show, provide a simple unambiguous method to calculate T_c.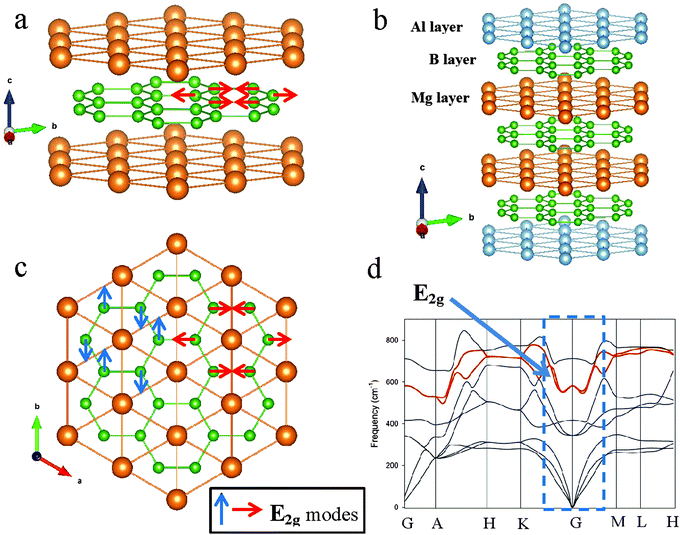

Fig. 1 Schematic of the AlB₂-type structure and relationship of key atom vibration modes to real and reciprocal space directions. (a) Alternating layers of Mg (gold spheres) and B (green spheres) for MgB₂ viewed at an angle to the a-axis direction. (b) Schematic of the Mg₂AlB₆ superlattice structure showing alternating layers of Mg, B and Al. For both (a) and (b) the c-axis is elongated by ∼30% and the a-axis tilted toward the viewer to highlight the hexagonal arrangements of atoms. (c) Projection of MgB₂ down the c* direction showing the two orthogonal E_2g phonon modes. (d) PD plot in reciprocal space of phonon modes in the MgB₂ structure showing the frequencies (or energies) of vibration with principal direction. The principal direction denoted G is at the origin of the unit cell (i.e. [0, 0, 0]). Phonon branches that contain the E_2g phonon modes are highlighted in red. The dotted rectangle along the G direction is the location of the phonon (or Kohn) anomaly and shown in detail in Fig. 2 for MgB₂, Mg₂AlB₆ and Mg_1−xBa_xB₂ compositions.

The density functional theory (DFT), which describes the electronic structure of solids in terms of an electron density distribution rather than a many-electron wave function^13,14 underpins our current understanding of many compounds and, in principle, allows prediction of bulk physical properties.¹⁴ Analysis and prediction is facilitated by major improvements in computational capacity and use of approximations to address the physics of electronic structure in order to describe electron density for specific crystal structures.^14,15 For superconductors, many computational methods have been used^2,3,16,17 to estimate physical properties such as T_c. However, predictions of T_c based on DFT band structure calculations alone typically involve estimates of adjustable parameters to ensure theory conforms with experiment.^2,7 Floris et al.¹⁶ have shown that superconducting DFT (SCDFT)¹³ can be employed, post facto, to estimate from the electronic band structure a calculated T_c that closely matches experimental data for MgB₂. However, this notionally ab initio method employs modifications to standard DFT models^13,16,18 including new approximations and additional parameterization to close the gap between theory and experiment.

We outline in this paper a method to determine phonon-mediated physical properties using ab initio DFT calculations and interpretation of PDs for AlB₂-type structures. We describe an approach to predict T_c that adds no new functionals to standard DFT models,¹⁹ does not invoke free or adjustable parameters^4,6,7 and accommodates metal atom substitutions. We use the Mg_1−xAl_xB₂ system to demonstrate that ab initio DFT calculation^19,20 predicts T_c across the compositional range 0.0 < x < 1.0 based on the magnitude of a phonon anomaly defined by PDs associated with the E_2g mode around the G-point in reciprocal space. This phonon anomaly is described as a Kohn anomaly along G–M based on inelastic X-ray scattering (IXS) experiments⁵ on MgB₂, which show a softening and broadening of the E_2g mode close to G.

Computational methods

DFT calculations were undertaken using the CASTEP^19,20 module of Materials Studio 7.0 and a more recent version, Materials Studio 8.0. This module provides the functionality to calculate vibrational properties for a wide range of materials. The linear response within the local density approximation (LDA) and generalized gradient approximations (GGA) with a dense k-grid mesh is used as detailed in our earlier work.^9,21

Calculations are undertaken with an ultra-fine cut-off typically >990 eV. Convergence criteria for most calculations are as follows: energy at 5 × 10⁻⁶ eV per atom; maximum force at 0.01 eV Å⁻¹; maximum stress at 0.02 GPa and maximum atom displacement at 5 × 10⁻⁴ Å. For BaB₂ calculations, the maximum stress value is varied.

Optimal calculation conditions using CASTEP for the AlB₂-type structure are given in earlier work.⁹ Ordered superlattice structures for non-end-member compositions within the Mg_1−xAl_xB₂ and Mg_1−xBa_xB₂ series are based on geometry optimization of unit cell parameters with P6/mmm symmetry. These optimized parameters correlate with experimentally determined values for Al substitutions.²² Experimentally determined values for Ba substitutions in the MgB₂ structure are not available. For end-member compositions, optimized unit cell parameters are based on literature values for MgB₂ and AlB₂ as shown in earlier work.^9,21 Schematic models of crystal structures shown in Fig. 1 are built using optimized cell parameters from CASTEP as input to the program VESTA.²³ Each schematic shows a unit cell in the c-axis direction only.

Calculations are undertaken with the High Performance Computing facility at QUT using <200 cores that are multiples of the k-grid mesh in a and b reciprocal space directions. Within these conditions, PD calculations for the more complex structures may require 7–10 days to achieve dispersion bands with positive values and convergence of the calculation. This requirement may force a compromise in the choice of k-grid mesh density, the accuracy of results and identification of the anomaly in PD plots.

Electronic band structure calculations for all compositions are consistent with earlier work, in particular, those that invoke a dense k-grid mesh.^2,4,16 Electronic structure calculations of substituted compositions also requires consideration of the k-grid mesh density² and, for MgB₂, influences resolution of the tubular sections of Fermi surfaces.

For each composition, calculations on a range of k-grid mesh densities are undertaken to determine the lowest k-value to achieve convergence. For extended superlattice models such as Mg₄AlB₁₀ or Mg₅AlB₁₂, computations for k = 0.02, 0.025, 0.027 and 0.03, respectively, are evaluated. The lowest k-value to achieve convergence is listed in Table 1 and, for all compositions, k ≤ 0.03 Å⁻¹ although the computational cost increases by a cube power as grid size is reduced.

Table 1 Calculated parameters for DFT models of Mg_1−xAl_xB₂

Al	Grid	Optimised unit cell parameters		DFT type	Fermi energy	DFT modelled values				Average values^a
						E2g at G	δ		T δ	δ av	T δ (av.)	σ T(error)
x	k	a (Å)	c (Å)		(eV)	(cm^−1)	(cm^−1)	(meV)	(K)	(meV)	(K)	(K)
a Average for both DFT models: LDA and GGA.
0.00	0.020	3.0391	3.4866	LDA	8.3976	582.3	127.0	15.7	40.6	16.3	42.0	3.3
0.00	0.020	3.0796	3.5538	GGA	8.1076	554.9	135.8	16.8	43.4
0.125	0.029	3.0297	27.6213	LDA	8.4968	579.4, 619.5, 652.4, 817.0	120.4	14.9	38.5	15.3	39.4	3.2
0.125	0.030	3.0682	28.1065	GGA	8.2262	543.0, 569.8, 594.6, 786.3	125.9	15.6	40.3
0.167	0.025	3.0287	20.6121	LDA	8.5908	563.1, 654.5, 853.7	104.1	12.9	33.3	14.3	35.5	3.9
0.167	0.024	3.0639	21.0239	GGA	8.3043	541.4, 581.9, 821.3	116.4	14.4	37.2
0.20	0.027	3.0253	17.1504	LDA	8.5786	549.2, 710.0, 810.7	91.7	11.4	29.3	12.2	31.3	3.4
0.20	0.027	3.0623	17.4416	GGA	8.3135	514.4, 646.0, 782.8	104.3	12.9	33.3
0.25	0.025	3.0233	13.6459	LDA	8.6535	607.7, 850.8	78.2	9.7	25.0	10.4	26.7	2.1
0.25	0.025	3.0593	13.8730	GGA	8.3911	569.5, 822.5	89.1	11.0	28.5
0.333	0.020	3.0169	10.1709	LDA	8.7013	574.0, 850.8	57.9	7.2	18.5	6.3	16.2	3.3
0.333	0.026	3.0514	10.3285	GGA	8.4612	570.1, 828.9	43.4	5.4	13.9
0.50	0.020	3.0241	6.5758	LDA	8.8714	893.6	12.1	1.5	3.9	1.8	4.6	2.5
0.50	0.030	3.0381	6.7710	GGA	8.6299	851.3	16.8	2.1	5.4
0.667	0.030	2.9978	9.9116	LDA	9.0831	935.4, 947.5	2.2	0.3	0.7	0.2	0.5	0.3
0.667	0.030	3.0273	10.0250	GGA	8.8601	914.3, 925.7	0.7	0.1	0.2
1.00	0.020	2.9795	3.2539	LDA	9.3125	963.9	na	na	0.0	0.0	0.0	0.0
1.00	0.020	3.0039	3.2806	GGA	9.0828	947.6	na	na	0.0

---

The values for the k-grid mesh density used in this work are comparable to, or higher than, that used for many PD calculations due to earlier studies^4,8,9,24 that identified key changes in PD characteristics with this parameter. These changes include shifts in E_2g frequency values at specific reciprocal lattice points^8,9,24 and the appearance of vibration mode branches in PD plots.⁹

Computational DFT methods are limited by fundamental assumptions on delocalisation and static correlation embedded in functional approximations²⁵ as well as the degree of complexity of material composition and structure,¹⁷ particularly structures containing transition metals.¹⁵ In this work, practical limits include the extent of superlattice models, extension of DFT calculations to include transition metal diborides with substituted compositions and, as noted above, the trade-off between k-grid mesh density, PD detail and convergence. Indications of computational limit for a particular composition in the Mg_1−xAl_xB₂ series are shown by (a) failure to converge, (b) inconsistent or irregular format of the anomaly in PD plots (e.g. multiple lows and highs of an E_2g mode within one branch) and (c) negative phonon frequency values.

Stoichiometry and superlattices

We use superlattices as a computational strategy to model compositions for which x is not an integer. CASTEP¹⁹ allows fractional occupancy of specific atoms in a structure for electronic band structure calculations. This structural description is an alternative method to represent intermediate compositions in the Mg_1−xAl_xB₂ series, but is not possible for PD calculations using CASTEP. Random fractional occupancy of atoms in a solid solution is an alternative approach for CASTEP calculations of band structure. However, this approach induces significant changes in electronic band structures that do not match experimental data. As noted by Kortus,² the approach is suited to low levels of metal doping (e.g. x < 0.1) but is expected to fail at higher doping concentrations.

Use of fractional occupancies may invoke inconsistent or uninterpretable shifts in the calculated electronic band structure, particularly in the proximity of the Fermi level. Hence, our PD calculations on ordered compositions do not utilise fractional site occupancies but invoke a superlattice along the c-axis. For superlattice unit cell calculations, appropriate multiples of the end member parameters are used and weighted combinations of these parameters are used as input for mixed compositions containing both Al and Mg or Ba and Mg. A schematic of the ordered composition for x = 0.33, in which an Al layer is sandwiched between two Mg layers, resulting in a 3x superlattice along the c axis, is shown in Fig. 1b. For x = 0.125, the cell size for a DFT calculation can increase to a ∼ 3.07 Å and c ∼ 28.0 Å. This size cell is the maximum we are able to optimise to then calculate a PD with convergence within a reasonable computation time when limited to <200 cores.

For each superlattice, the degrees of freedom per atom within the sub-lattice unit cell is nine although the number of phonon branches in calculated PDs will depend on the multiples of the sub-lattice used to form the P6/mmm unit cell for a specific composition. For structures used in these calculations, Z = 2, 3, 4 or 5 for the superlattice constructs while for the basic P6/mmm structure, such as MgB₂, Z = 1.²⁶ The Fermi energy corresponds to the average electron density of a structure and measures the highest energy (in the ground state) of valence electrons in the conduction band as free or nearly free electrons. Therefore, to compare phonon anomalies of end member and intermediate compositions, each superlattice is normalized to a single unit cell.

Error estimates

We have described intrinsic sources of error for PD calculations in earlier work.²¹ Estimates of error in the calculation of T_δ are obtained by measurement of δ for both branches of the E_2g mode in the G–M and G–K reciprocal directions for each calculation (i.e. for LDA and GGA). Our analysis and estimate of δ is dependent on measurement of calculated vibrational frequencies that show a mean relative error²⁷ of about ±5% for crystal structures of similar size and complexity to MgB₂. These values of δ are converted to T_δ using eqn (1) below. The error estimate is one standard deviation for the values of T_δ determined from all the measured values of δ. For some compositions, the value of T_δ is an average of up to eight separate estimates of δ obtained by measurement of the frequency difference on two branches of E_2g either side of G for both LDA and GGA models. The individual values for frequency measurements are not shown in Table 1.

Results

Phonon anomaly for Mg_1−xAl_xB₂

An example of the phonon anomaly for MgB₂ calculated using the LDA model with P6/mmm symmetry is given in Fig. 1d and, in closer detail, in Fig. 2a. Fig. 2a shows a portion of the total PD across the G–M (right-hand side of the diagram) and G–K (left-hand side of the diagram) reciprocal lattice directions. The phonon bands or branches that contain the degenerate E_2g modes at the G point and define the double parabolic phonon anomaly are shown in red. The upper limit of the anomaly is defined in this case by the B_2g mode at higher energy. For substituted compositions, the E_2u or the B_2g mode defines the upper extent of the phonon anomaly for E_2g bands in the G–M and G–K directions, as shown in Fig. 2b. For MgB₂, we show that these upper modes are important for energy conservation through conversion of phonon energies by coherent relaxation.^9,21

Fig. 2 Partial PD plots based on DFT models with k = 0.02 Å⁻¹ along the G–M and G–K directions of reciprocal space: (a) for MgB₂ and (b) for Mg₂AlB₆ using the LDA functional; for the predicted compositions (c) MgBaB₄ using the GGA functional and (d) for MgBa₂B₆ using the LDA functional. The phonon anomalies for the E_2g mode around the G-point are highlighted in red and the magnitude of the anomaly, δ, is shown. The dotted red lines show regions with non-degenerate E_2g modes. The green dotted line b–b′ corresponds to reciprocal lattice dimensions equivalent to the average diameter of the Fermi surface for the specific composition. The distance between a–a′ and b–b′ along the G–M direction is an indicator of coherence length in the a–b plane of an AlB₂-type structure.

In the vicinity of the G-point, the E_2g PD bands are degenerate and extend along the basal plane directions (i.e., G–K and G–M) with a characteristic inflection along these directions that is limited, or defined, by the B_2g mode. Note that outside the anomaly, along the G–K and G–M directions, the E_2g mode changes symmetry to E_2u for MgB₂. The magnitude of the anomaly, δ, is measured in frequency units (cm⁻¹), as shown in Fig. 2. This anomaly is evident in other publications^9,21,28 when there is sufficient resolution of the k-grid and is referred to as a Kohn anomaly in earlier work.^5,29

For high-Al compositions such as MgAl₂B₆, the frequency difference between E_2g and E_2u bands at the G-point is minimal or zero, and no anomaly occurs. In addition, for these high-Al compositions, the E_2g and E_2u bands do not show the inflection along the G–M and G–K directions as we show for MgB₂.⁹ For AlB₂, the E_2g mode is the highest frequency optical phonon and does not show a phonon anomaly.²¹ Similar PD plots for end-member compositions such as MgB₂ and AlB₂ are described in earlier work^9,21 and have been calculated for the compositions shown in Fig. 3 below (open symbols).

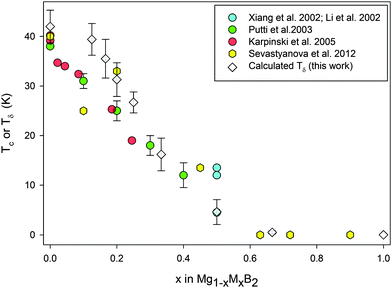Fig. 3 Plot of experimental T_c values for Mg_1−xAl_xB₂ (filled symbols) and calculated T_δ values (open symbols) determined by the method outlined in the text. Error bars (this work) represent one standard deviation and are as reported by Putti et al.³¹

Compositional trends

A summary of the modelled parameters for end-member and intermediate compositions of the Mg_1−xAl_xB₂ suite is shown in Table 1. The E_2g mode for non-end-member compositions in the Mg–Al series increases in energy with increase in Al content, as noted previously⁴ and, in each case, a higher phonon energy (e.g. B_2g or E_2u) occurs until x = 1 where E_2g is the highest frequency mode.²¹ These trends are evident with either the LDA or GGA model in the DFT calculation and are consistent with data calculated at sufficient k-grid mesh density.⁹ The calculated values for E_2g modes at G shown in Table 1 correspond with experimental values determined by spectroscopic techniques.^9,30 Calculated partial densities of phonon states (data not shown) show that Mg and Al contribute almost exclusively to modes below 350 cm⁻¹. As noted in earlier work,⁴ B atoms contribute to modes above 350 cm⁻¹ with minor contributions in a small overlap region at 100–350 cm⁻¹.

The E_2g band is doubly degenerate around the G-point along the basal plane directions for non-end-member compositions in the Mg_1−xAl_xB₂ series. Fig. 2b shows a portion of the PD around the G-point for x = 0.33 calculated using the LDA with a k-grid mesh value of 0.02 Å⁻¹. The two E_2g modes, which are degenerate at G, are consistent with ordered alternation of boron layers with a metal layer (e.g. either Mg or Al) in the AlB₂-type structure. In Fig. 2b, the E_2g modes at ∼570 cm⁻¹ and at ∼851 cm⁻¹ are highlighted in red, and the higher energy E_2u mode is indicated in orange. For this composition, measurement of the anomaly δ for the lower energy E_2g mode shows that it is significantly less (see Table 1) than the anomaly in Fig. 2a. This lower value of δ is consistent with a dampening of the dominant mode that influences superconductivity in Mg_1−xAl_xB₂.

Phonon thermal energy and T_c

We have calculated a thermal energy, T_δ, for each composition in Table 1 based on the equation:

δ = (nN/Z)·(k_BT_δ/2) (1)

where δ is the phonon anomaly (in cm⁻¹), n is the degrees of freedom per atom, N is the number of atoms per unit cell, Z is the number of formula units per unit cell, k_B is Boltzmann's constant, and k_BT_δ/2 is the well-known relationship between thermal energy and degrees of freedom.⁹ Values for the phonon anomaly, δ, when substituted in this equation determine the calculated temperature, T_δ, (in Kelvin) for each composition listed in Table 1.

Fig. 3 shows the calculated temperature (open symbols), T_δ, associated with the phonon anomaly compared with the experimentally determined T_c (solid symbols) for Al content in Mg_1−xAl_xB₂. Experimental data for Fig. 3 have been collated from studies that used structure refinements²² and/or microstructural and compositional analyses^26,31 to define stoichiometry and to account for the presence of second phases (e.g. MgB₄).^26,32 These experimental T_c values are for compositions determined on the as-synthesized product(s) made by an internally consistent method. The trend towards a lower T_δ with increased x value at intermediate compositions for 0.125 < x < 0.5 is consistent with experimental data^22,26,31 on well-characterized Mg_1−xAl_xB₂. For reference, experimental T_c values for x = 0.5 range from ∼4 K³³ to ∼13.5 K.^10,26,34

We have used this method to estimate T_c on other AlB₂-type structures. In these cases, the experimentally determined values for T_c are much lower (∼10 K) and thus, features ascribed to a phonon anomaly will be more difficult to detect. The base case for low T_c compounds is provided for the high-Al compositions listed in Table 1 (e.g. Mg_0.5Al_0.5B₂). However, compositions that do not contain boron atoms may also form in the AlB₂-type structure and, in some cases, show superconducting properties.^35–37 We use the approach outlined above to estimate the T_c of the disilicide compounds BaSi₂ and Ca(Al_0.5Si_0.5)₂. For these disilicides, our estimate for BaSi₂ of T_c = 9.3 ± 0.5 K compares with an experimental determination³⁶ of 8.9 K. An estimated T_c = 7.5 ± 0.5 K for Ca(Al_0.5Si_0.5)₂ is similar to the experimental value³⁵ of 7.8 K.

Phonon anomaly for Mg_1−xBa_xB₂

We show in Fig. 2c and d partial PD plots for MgBaB₄ and MgBa₂B₆. For these DFT calculations, both compositions are constructed as AlB₂-type structures with P6/mmm symmetry. The extent of the phonon anomaly, δ, is shown for MgBaB₄ in Fig. 2c and is similar in form to MgB₂ shown in Fig. 2a. Determinations of δ, as shown in Table 2 show that the magnitude of the anomaly for MgBaB₄ is significantly higher than for MgB₂. Table 2 summarises the calculated parameters for compositions of the Mg_1−xBa_xB₂ series similar to that shown in Table 1. We have calculated fewer compositions for this series compared with the Mg_1−xAl_xB₂ series because similar conclusions are evident from these calculations.

Table 2 Calculated parameters for DFT models of Mg_1−xBa_xB₂

Ba	Grid	Optimised unit cell parameters		DFT type	Fermi energy	DFT modelled values				Average values^b
						E2g at G	δ		T δ	δ av	T δ (av)	σ T(error)
x	k	a (Å)	c (Å)		(eV)	(cm^−1)	(cm^−1)	(meV)	(K)	(meV)	(K)	(K)
a DFT calculation undertaken at equivalent to 16 GPa hydrostatic pressure. b Average for DFT models: both LDA and GGA models.
0.333	0.020	3.0896	11.8631	LDA	8.0111	420.9	207.4	25.7	66.3	25.0	64.4	2.2
0.333	0.020	3.1390	12.1094	GGA	7.6371	431.7	195.2	24.2	62.4
0.500	0.020	3.1186	8.3362	LDA	7.8668	429.1	181.6	22.5	58.1	24.7	63.6	6.6
0.500	0.020	3.1727	8.5178	GGA	7.4234	374.6	216.3	26.8	69.2
0.666	0.020	3.1474	13.1914	LDA	7.6721	403.2, 453.6	179.3	22.2	57.3	24.1	62.1	5.8
0.666	0.020	3.2072	13.4716	GGA	7.1948	334.4, 364.8	208.9	25.9	66.8
1.00^a	0.015	3.0840	4.6612	LDA	8.4699	376.4	175.7	21.8	56.2	23.1	59.7	6.2
1.00^a	0.015	3.1424	4.7314	GGA	7.9646	415.8	197.5	24.5	63.1

---

Comparison of Tables 1 and 2 shows that the Fermi energies for Mg_1−xBa_xB₂ are lower than the Mg_1−xAl_xB₂ series by approximately 0.7 eV to 1.0 eV across the compositional range. In addition, the optical phonons for Mg_1−xBa_xB₂ compositions are typically at lower frequencies than Mg_1−xAl_xB₂ with the critical E_2g modes at lower frequencies at the G point for equivalent values of x.

Discussion

The Mg–Al diboride system is characterized by a sharp superconducting transition at x = 0 that decreases in value and gradually broadens with higher Al content.¹² Superconductivity in Mg_1−xAl_xB₂ is moderated, but not extinguished, by other influences such as order–disorder,³⁸ superlattice(s)^10–12 and the presence of other phases^32,33 for 0.0 < x < 0.5. Band structure calculations,^2,39,40 experimental data⁴¹ and phonon calculations⁸ have established that the vibrational properties of the E_2g mode for MgB₂ influence electron–phonon interactions and superconductivity.^4,7

Ordering and superlattice models

Superlattices are observed in Mg_1−xAl_xB₂ systems^10,11,26,34 with prominent diffraction spots at the reciprocal lattice dimension c*/2, which demonstrate a 2x c-axis superlattice³⁴ for Mg_0.5Al_0.5B₂. Superlattice structures are also predicted⁴² for vacancy-ordered MgB₂ but are not considered in this analysis. Detailed analysis of Al-substituted MgB₂ shows that superstructures occur for a range of compositions (x = 0.17;³⁴x = 0.25;¹⁰x = 0.45, 0.5 and 0.55¹¹) and microstructures.^10,11 Microstructural studies¹⁰ suggest that intimate mixtures of MgB₂ and Mg_0.5Al_0.5B₂ may also occur for 0.1 < x < 0.5. However, the dominant motif involves alternation of Mg and Al layers for x = 0.5.¹² Long range ordering of Al and Mg is observed in the a–b plane¹² with an extent ∼10 nm. Representation of this periodicity in the a–b plane is non-trivial for DFT calculations and is not considered here. Brutti and Gigli³⁸ used DFT calculations to show that for x > 0.31, the formation of an Al-rich phase leads to formation of thermodynamically stable Mg_0.5Al_0.5B₂ at 50% Al concentration in MgB₂.

Raman spectroscopy and inelastic neutron scattering studies⁴³ on Mg_1−xAl_xB₂ samples show evidence for alternate stacking of Mg and Al layers for x ∼ 0.5. In our earlier work, we note that additional Raman and IR peaks not predicted by P6/mmm symmetry for MgB₂ are due to super-lattice modes that approximate a dynamic, phonon-distorted lower-symmetry crystal.⁹ We show that a 2x super-lattice in the c-direction allows a simple correlation of the pair breaking energy and the superconducting gap.⁹

We have evaluated other c-axis ordered structures in which multiple adjacent Al-layers alternate with Mg-layers for key compositions (e.g. Mg–Mg–Al–Al for x = 0.5 or Mg–Mg–Mg–Mg–Al–Al for x = 0.33). In these cases, while there are differences of ∼0.15 eV in calculated enthalpies favouring the stability of single Al-layer stacking, ordered motifs with adjacent Al-layers also show a phonon anomaly similar to that in Fig. 2a and b. Thus, a superlattice repeat along the c-axis utilising a simple alternation of Mg and Al layers to minimise adjacent Al layers is an optimal configuration. For simplicity of computation, we follow a superlattice formalism confirmed by detailed experimental studies^11,43 and implied by DFT models³⁸

Phonon anomalies

The magnitude of the phonon anomaly varies with composition, as do experimentally determined T_c values. The average value of δ for MgB₂ shown in Table 1 is comparable to the gap energy,⁵ 2δ, of ∼15 meV. The variation in magnitude of the phonon anomaly reflects the predominant role of boron layer vibrations in many AlB₂-type structures^44,45 and, in this case, the influence of Al substitution on these vibrations. For the AlB₂-type structure, the D_6h point group symmetry results in two E_2g modes at the G-point and equivalent displacement modes, E_2u, at the A point of the hexagonal Brillouin zone.⁸

The doubly degenerate E_2g(G) band describes two distinct displacement patterns that are equivalent within the harmonic approximation.⁸ The E_2g and E_2u modes have the same movement pattern, albeit with different parity (gerade or ungerade), via a difference in relative phase.^8,46 One of the E_2g modes reflects in-plane B–B bond stretching modes that are strongly coupled to the sigma bonded Fermi surfaces related to the p_x and p_y in-plane orbitals.⁴⁶

Table 1 summarizes the difference in frequency, or the phonon anomaly, δ, between the low and high points of the E_2g mode inflection for both G–M and G–K directions for each calculated composition using both LDA and GGA in the Mg_1−xAl_xB₂ series. For both DFT calculation methods, the range of values for the phonon anomaly, δ, of each composition is similar, but not equal, because of different assumptions in the methods to calculate the charge distribution in the LDA and GGA methods,⁴ differences in optimized lattice parameters and the k-grid value required to attain convergence.

For each calculated composition in the Mg–Al series, the value of T_δ is slightly higher than the experimentally determined values for T_c as shown in Fig. 3. A difference of 1.0 K to 2.5 K is evident for models with x < 0.25 and probably relates to factors such as (a) a higher k-grid value (particularly for x = 0.125) that allows convergence of the PD calculation, (b) systematic errors associated with extended superlattice construction and (c) our DFT calculations are for absolute zero, ground state properties without correction for higher temperatures. Nevertheless, this ab initio determination of T_δ is internally consistent and in close agreement with the experimentally determined T_c trends^22,26,31 for Al-substituted MgB₂.

The phonon anomaly can be described in terms of interconnected hyperboloid surfaces in different proportions showing origins at different energies and inverse directions along a fixed axis that intercepts G. We can describe this hyperboloid for the E_2g mode(s) as follows. For the E_2g dispersion shown in Fig. 1 and 2, the phonon band is in the k_x − k_y plane for which k_z = 0. For one hyperboloid, the equation for k_z = 0 becomes

ω² = ω₀² + a²(k_x² + k_y²) (2)

which is symmetric in the k_x and k_y directions and can be extended to the k_x − k_y plane. Considering only the k_x direction,

ω² = ω₀² + a²k_x² or (ω/ω₀)² − (ak_x/ω₀)² = 1 (3)

The asymptote of the hyperbola described in eqn (3) is ω = ak_x. This hyperbola can be approximated to a parabolic dependence as below and as commonly encountered in descriptions of the Jahn–Teller effect:⁴⁷

ω = ω₀(1 + a²(k_x/ω₀)²)^1/2 ∼ ω₀(1 + (a²/2)(k_x/ω₀)²)

which equals

ω₀ + (a²/2ω₀)k_x². (4)

Taking the partial derivative of eqn (3), we obtain

2ω ∂ω/∂k_x = 2a²k_x. (5)

Since the group velocity, ν_g = ∂ω/∂k_x and the phase velocity, ν_p = ω/k_x, we obtain by substitution

ν_g = a²/ν_p. (6)

In the asymptotic region of the E_2g band, where the phonon dispersion changes abruptly from the lowest point of the anomaly towards the higher E_2u phonon band, the curve displays an approximate linear behaviour. This behaviour indicates that the group velocity, ν_g, is constant. From eqn (6), the phase velocity, ν_p, is also constant.

In the asymptotic region of the E_2g band, where the phonon dispersion changes abruptly from the lowest point of the anomaly towards the higher E_2u phonon band, the curve displays an approximate linear behaviour (in Fig. 2, the distance along the G–M direction between the green dotted lines a–a′ and b–b′). This behaviour indicates that the group velocity, ν_g, is constant and, as shown above, the phase velocity, ν_p, is also constant. Therefore, there is an interval of k-vectors, Δk, relating to phonon waves for which the wave is non-dispersive. That is, the group of waves moves at constant group velocity and each component of the interval also moves at constant phase velocity. In this instance, the wave packet retains shape and can be viewed as a coherent wave. The slope of the E_2g band in the linear section of the anomaly appears approximately parallel to the acoustic band of highest energy. This relationship suggests that the group velocity of the corresponding optical waves matches the sound velocity.

Phonons and Fermi surfaces

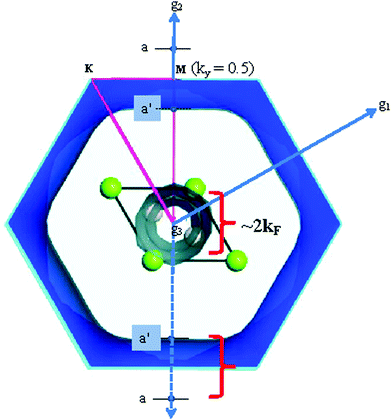
Comparison of electronic bands with PDs shows that the phonon anomalies in the Mg_1−xAl_xB₂ system originate from cusps of paraboloid bands across the Fermi level in the electronic band structure at the G-point. These anomalies are effected by a transfer of electronic charge from the vicinity of the cusps to and from adjacent unit cells and the flat bands in the G–A direction.^39,48 Our calculations show that cusp size is directly proportional to the PD anomaly. For example, the PD anomaly is deep when the cusp size in the electronic band is large. If the cusp dips below the Fermi level, for example as with AlB₂, the phonon anomaly does not occur; this is consistent with experimental data⁴⁹ that show no superconductivity for this composition. In addition, for superlattice constructs, multiple parallel cusps that intersect with the Fermi level occur. These intersections are reflected in a multiplicity of E_2g modes and of tubular sections in Fermi surface models.

Calculations of Fermi energies link electrons on or near the Fermi surface to strongly coupled phonons in MgB₂.³⁹ For example, Fig. 4 shows the Fermi surface for MgB₂ calculated with the GGA model for k = 0.02 Å⁻¹. For this model, the Fermi energy is 8.1087 eV. In a free electron approximation, the Fermi wave vector, k_F, is determined from the equation

E_F = ℏ²k_F²/2m (7)

where ℏ is Planck's constant, m is the electron mass, and E_F is the Fermi energy. For MgB₂, k_F = 1.458 Å⁻¹. Using reciprocal cell dimensions from our CASTEP calculations, and limiting this analysis to the k_y direction, the Fermi wave vector is ∼62% of the magnitude of the first reciprocal space vector |a₁*|. As shown in Fig. 4, the vector resides just outside the first Brillouin zone (point a in the extended zone). Re-plotting this vector to the reduced zone results in a point at position a′ on the Fermi surface, as shown in Fig. 4.

Fig. 4 Fermi surface projection along g₃ calculated for MgB₂ using the GGA model with k = 0.02 Å⁻¹. The projection shows the equivalent magnitude of the Fermi vector, 2k_F, along the k_y direction and tubular sections on the Fermi surface. Green spheres are Mg atoms; off-white spheres (partially obscured) are B atoms.

For two electrons to interact through a phonon, conservation of energy and momentum give the equation:

ℏ(k^e₁ − ℏk^e₂) = ℏ(K^ph + G) (8)

where k^e₁ and k^e₂ are electron wave vectors, K^ph is the phonon wave vector, and G is a reciprocal space point. For an interaction in the k_y direction, the magnitude of the electron wave vector will be +k_F or −k_F. For a pairing mechanism in which electrons with opposite momenta or wave vectors interact, 2k_F = K^ph + G for interaction along k_y. Substituting values for MgB₂ from CASTEP calculations, the ratio of 2k_F (after re-plotting to the reduced zone) to |a₁*| is 0.239. This ratio is equivalent to the point in reciprocal space along the G–M direction where the E_2g vibration mode meets the B_2g mode, as shown in Fig. 2a (green dotted vertical line denoted b–b′). Thus, a one-to-one correspondence between tubular elements of the Fermi surface and the phonon anomaly occurs for this composition. This reciprocal space point is similar for LDA and GGA models of MgB₂ with a value ∼0.24 along G–M (equivalent to 0.56 Å⁻¹). These values are approximately twice the experimentally estimated radii⁵ for cylindrical sigma surfaces parallel to G–A which show average values of 0.17 Å⁻¹ and 0.25 Å⁻¹ using IXS.

For Al-substituted compositions, this point shifts closer to the G-point in a PD plot, as shown in Fig. 2b (green dotted line denoted b–b′; ∼0.13 along G–M; equivalent to 0.31 Å⁻¹). This shift implies a reduction in size of the sigma sheets coupled to the E_2g phonon and is consistent with de Haas van Alfen effect measurements⁵⁰ of Al-substituted MgB₂. Our calculations for other compositions (data not shown) also show a size reduction of the cylindrical sigma sheets in Fermi surface projections with increased Al substitution. Al substitution in MgB₂ results in a commensurate change in the number of tubular sections in Fermi surface projections in proportion to the multiplicity of E_2g modes using superlattice models.

Predicted superconducting compositions

Extrapolation of the methods described above for Mg_1−xAl_xB₂ to other compositions^12,51 of MgB₂ and a consideration of diboride thermodynamics⁵² suggest particular atom substitutions to the type structure may also result in superconducting behaviour. For example, our LDA calculations on BaB₂ reveal an electronic band structure similar to MgB₂ but with a PD that shows unusual frequency variation and negative frequency values for modes in the A–H direction and around G. Subsequent calculations constrained to include hydrostatic pressure reduced the number and range of negative frequency values. At an applied hydrostatic pressure of 16 GPa convergence of the LDA and GGA models is achieved with phonon anomalies similar to that shown for MgB₂ in Fig. 2. The E_2g modes show a strong anisotropy in the PD plot particularly in the G–K direction. Nevertheless, these calculations indicate that a BaB₂ structure with an applied stress at 16 GPa is likely to show a phonon anomaly, and by inference, superconductivity.

BaB₂ is not a well-known compound and may be structurally unstable due to a larger Ba⁺² ionic radius compared with Mg⁺². Cava et al.¹² notes that a variation of approximately 50% of the metal atom size can be accommodated by the diboride structure. However, the existence of BaB₂ is not readily confirmed. Early literature⁵³ on the synthesis of BaB₂ reports cell dimensions that are inconsistent with an AlB₂-type structure and suggests that this compound is yet to be synthesised. In addition, the geometry optimised cell dimensions for BaB₂ shown in Table 2 are comparable to MgB₂ for the a axis. The c-axis dimension is ∼33% greater than the calculated values for MgB₂. These attributes, and the unstable nature of DFT models without a hydrostatic pressure constraint, suggest that BaB₂ may not be thermodynamically stable except at high pressure.

Our computational method utilises a linear response for both LDA and GGA models and is effective for structures with low anharmonicity. Outcomes from these linear calculations as well as structural considerations (e.g. Ba⁺² ionic radius), infer that anharmonicity is an important factor for BaB₂ PD calculations. An alternative calculation for BaB₂ using the Finite Displacement (FD) method at similar hydrostatic pressure shows a PD anomaly very similar to Fig. 2a. In this case, the extent of anomaly is significant (∼250 cm⁻¹) and, by similar analysis to that for DFPT calculations, suggests a T_c ∼ 79.1 ± 10.2 K.

The result from DFT calculations on BaB₂ under an applied stress indicates that substitution of an appropriate valence atom for Ba may also induce a similar shift in structural parameters or an improvement in the calculated PD. DFT calculations for compositions of Mg_1−xBa_xB₂, where 0 < x < 1, display phonon anomalies of varying magnitude as shown in Fig. 2c and d. Table 2 lists phonon anomalies for three compositions (x = 0.333; x = 0.5 and x = 0.666) and for the end-member BaB₂ at a hydrostatic pressure of 16 GPa. In all cases, calculated PDs for Mg_1−xBa_xB₂ show a phonon anomaly with an extent significantly greater than calculated for MgB₂. This analysis predicts that Mg_1−xBa_xB₂ will show superconductivity at T_c > 60 K over a wide compositional range. We infer from the smaller average c-axis cell dimensions shown in Table 2 that Mg_0.66Ba_0.33B₂ is more likely to be a stable phase in this compositional series. This T_c prediction for Mg_1−xBa_xB₂ is ∼20 K higher than that for MgB₂, currently the stand-out material in the diboride suite.⁵⁴

Coherence lengths

Using the width Δk in reciprocal space, we can derive a width Δx in real space that may be associated with the coherence length of the superconductor. Using the calculated PD for MgB₂ shown in Fig. 2a, we estimate the coherence length in the a–b plane as the distance along the G–M direction (i.e. the reciprocal a axis) between the approximately linear sections of the phonon anomaly manifest in the E_2g modes. This distance, measured in reciprocal lattice dimensions, can be converted to real space dimensions for the symmetry conditions of the unit cell. For MgB₂, our estimate of the coherence length is ∼50 Å ± 5 Å. This value compares favourably with experimentally determined values⁵⁴ between 61 Å and 65 Å for coherence length in the a–b plane for single crystals; noting that experimental determination of coherence length is dependent on the applied magnetic field⁵⁵ and temperature.⁵⁶ Similar estimates of coherence length for substituted MgB₂ can be inferred from these PD calculations. For Al-substituted MgB₂, these estimates of coherence length range from ∼70 Å to ∼80 Å with increasing Al content. For Mg_1−xBa_xB₂, estimates of coherence length range from ∼30 Å to ∼50 Å in the a–b plane.

Conclusions

We have utilised ab initio DFT calculations to show that PD plots of AlB₂-type structures including Mg_1−xM_xB₂ (where M = Al or Ba) and MSi₂ (where M = Ca, Al or Ba) are key indicators of physical properties. For known compositions, the phonon anomaly predicts physical properties such as the presence (or absence) of superconductivity in this structure type. The extent, or size (in frequency units), of the anomaly provides an estimate of T_c by the well-known relationship between thermal energy and degrees of freedom for a particular structure. Agreement between theory and experiment is strong even though DFT models ground state properties at absolute zero temperature. In addition, this approach does not use modified functionals or post facto corrections and is unable, at this time, to account for time dependent phenomena. The phonon anomaly for the AlB₂-type structure is also known as a Kohn anomaly. If present, the Kohn anomaly provides a means to predict T_c of unknown materials and to estimate other key parameters such as coherence length and Fermi surface structure that link electronic and magnetic properties of these materials. This work predicts that Mg–Ba compounds with the AlB₂-type structure and BaB₂ will show superconducting properties. The approach used in this work amplifies the value of DFT computations as a predictive tool.

Acknowledgements

We acknowledge financial assistance from QUT and assistance of Ashley Wright, Adam Siliato and Mark Barry with the High Performance Computing facilities.

References

1. J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, Nature, 2001, 410, 63–64.
2. J. Kortus, Phys. C, 2007, 456, 54–62.
3. I. I. Mazin and V. P. Antropov, Phys. C, 2003, 385, 49–65.
4. R. Heid, K.-P. Bohnen and B. Renker, Adv. Solid State Phys., 2002, 42, 293–305.
5. A. Q. R. Baron, H. Uchiyama, Y. Tanaka, S. Tsutsui, D. Ishikawa, S. Lee, R. Heid, K.-P. Bohnen, S. Tajima and T. Ishikawa, Phys. Rev. Lett., 2004, 92, 197004.
6. H. Kotegawa, K. Ishida, Y. Kitaoka, T. Muranaka, N. Nakagawa, H. Takagiwa and J. Akimitsu, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 064516.
7. A. Y. Liu, I. I. Mazin and J. Kortus, Phys. Rev. Lett., 2001, 87, 087005.
8. K. Kunc, I. Loa, K. Syassen, R. K. Kremer and K. Ahn, J. Phys.: Condens. Matter, 2001, 13, 9945–9962.
9. J. A. Alarco, A. Chou, P. C. Talbot and I. D. R. Mackinnon, Phys. Chem. Chem. Phys., 2014, 16, 24443–24456.
10. J. Y. Xiang, D. N. Zheng, J. Q. Li, L. Li, L. P. L. Lang, H. Chen, C. Dong, G. C. Che, Z. A. Ren, H. H. Qi, H. Y. Tian, Y. M. Ni and Z. X. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 214536.
11. H. W. Zandbergen, M. Y. Wu, H. Jiang, M. A. Hayward, M. K. Haas and R. J. Cava, Phys. C, 2002, 366, 221–228.
12. R. J. Cava, H. W. Zandbergen and K. Inumaru, Phys. C, 2003, 385, 8–15.
13. L. N. Oliveira, E. K. U. Gross and W. Kohn, Phys. Rev. Lett., 1988, 60, 2430–2433.
14. W. Kohn, Rev. Mod. Phys., 1999, 71, 1253–1266.
15. A. J. Cohen, P. Mori-Sanchez and W. Yang, Chem. Rev., 2012, 112, 289–320.
16. A. Floris, A. Sanna, M. Luders, G. Profeta, N. N. Lathiotakis, M. A. L. Marques, C. Franchini, E. K. U. Gross, A. Continenza and S. Massidda, Phys. C, 2007, 456, 45–53.
17. J. C. Phillips, Adv. Condens. Matter Phys., 2010, 2010, 1–13.
18. N. N. Lathiotakis, M. A. L. Marques, M. Luders, L. Fast and E. K. U. Gross, Int. J. Quantum Chem., 2004, 99, 790–797.
19. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
20. K. Refson, S. J. Clark and P. R. Tulip, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114.
21. J. A. Alarco, P. C. Talbot and I. D. R. Mackinnon, Phys. Chem. Chem. Phys., 2014, 16, 25386–25392.
22. J. Karpinski, N. D. Zhigadlo, S. Katrych, R. Puzniak, K. Rogacki and R. Gonnelli, Phys. C, 2007, 456, 3–13.
23. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
24. K.-P. Bohnen, R. Heid and B. Renker, Phys. Rev. Lett., 2001, 86, 5771–5774.
25. A. J. Cohen, P. Mori-Sanchez and W. Yang, Science, 2008, 321, 792–794.
26. L. G. Sevastyanova, O. K. Gulish, V. A. Stupnikov, V. K. Genchel, O. V. Kravchenko, B. M. Bulychev, R. A. Lunin and V. P. Tarasov, Cent. Eur. J. Phys., 2012, 10, 189–196.
27. L. He, F. Liu, G. Hautier, M. J. T. Oliveira, M. A. L. Marques, F. D. Vila, J. J. Rehr, G.-M. Rignanese and A. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 064305.
28. T. Morshedloo, M. R. Roknabadi and M. Behdani, Phys. C, 2015, 509, 1–4.
29. A. Q. R. Baron, H. Uchiyama, R. Heid, K. P. Bohnen, Y. Tanaka, S. Tsutsui, D. Ishikawa, S. Lee and S. Tajima, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 020505.
30. V. P. S. Awana, A. Vajpayee, M. Mudgel and H. Kishan, Supercond. Sci. Technol., 2009, 22, 034015.
31. M. Putti, M. Affronte, P. Manfrinetti and A. Palenzona, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–6.
32. R. A. Ribeiro, S. L. Bud'ko, C. Petrovic and P. C. Canfield, Phys. C, 2003, 385, 16–23.
33. S. Agrestini, A. Bianconi, S. De Negri, M. Giovannini and A. Saccone, Intermetallics, 2003, 11, 1339–1344.
34. J. Q. Li, L. Li, F. M. Liu, C. Dong, J. Y. Xiang and Z. X. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 132505.
35. M. Imai, K. Nishida, T. Kimura and H. Abe, Appl. Phys. Lett., 2002, 80, 1019–1021.
36. J. A. Flores-Livas, R. Debord, S. Botti, A. San Miguel, S. Pailhes and M. A. L. Marques, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184503.
37. M. Imai, E. H. S. Sadki, H. Abe, K. Nishida, T. Kimura, T. Sato, K. Hirata and H. Kitazawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064512.
38. S. Brutti and G. Gigli, J. Chem. Theory Comput., 2009, 5, 1858–1864.
39. J. M. An and W. E. Pickett, Phys. Rev. Lett., 2001, 86, 4366–4369.
40. O. de la Pena, A. Aguayo and R. de Coss, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 01251.
41. G. Campi, T. Proffen, X. Qiu, E. S. Bozin, S. J. L. Billinge, S. Agrestini, N. L. Saini and A. Bianconi, J. Supercond. Novel Magn., 2007, 20, 505–510.
42. Y. Zhao, C. Ban, Q. Xu, S.-H. Wei and A. C. Dillon, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–5.
43. B. Renker, K. B. Bohnen, R. Heid, D. Ernst, H. Schober, M. Koza, P. Adelmann, P. Schweiss and T. Wolf, Phys. Rev. Lett., 2002, 88, 067001.
44. X. K. Chen, M. J. Konstantinovic, J. C. Irwin, D. D. Lawrie and J. P. Franck, Phys. Rev. Lett., 2001, 87, 157002.
45. A. Pallas and K. Larsson, J. Phys. Chem. B, 2006, 110, 5367–5371.
46. A. Q. R. Baron, H. Uchiyama, S. Tsutsui, Y. Tanaka, D. Ishikawa, J. P. Sutter, S. Lee, S. Tajima, R. Heid and K.-P. Bohnen, Phys. C, 2007, 456, 83–91.
47. R. Englman, The Jahn-Teller Effect in Molecules and Crystals, Wiley-Interscience, 1972.
48. J. Kortus, I. I. Mazin, K. D. Belashchenko, V. P. Antropov and L. L. Boyer, Phys. Rev. Lett., 2001, 86, 4656–4659.
49. D. Sharma, J. Kumar, A. Vajpayee, R. Kumar, P. K. Ahluwalia and V. P. S. Awana, J. Supercond. Novel Magn., 2011, 24, 1925–1931.
50. A. Carrington, J. D. Fletcher, J. R. Cooper, O. J. Taylor, L. Balicas, N. D. Zhigadlo, S. M. Kazakov, J. Karpinski, J. P. H. Charmant and J. Kortus, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 060507(R).
51. D. G. Hinks, J. D. Jorgensen, H. Zheng and S. Short, Phys. C, 2002, 382, 166–176.
52. A. Saengdeejing, PhD dissertation, Pennsylvania State University, 2011.
53. K. Torkar, H. Krisehner and E. Hitsch, Monatsh. Chem., 1972, 103, 744–750.
54. C. Buzea and T. Yamashita, Supercond. Sci. Technol., 2001, 14, R115–R146.
55. T. Klein, L. Lyard, J. Marcus, Z. Holanova and C. Marcenat, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 184513.
56. J. D. Fletcher, A. Carrington, O. J. Taylor, S. M. Kazakov and J. Karpinski, Phys. Rev. Lett., 2005, 95, 079005.

---