The influence of large-amplitude librational motion on the hydrogen bond energy for alcohol–water complexes

Abstract

The far-infrared absorption spectra have been recorded for hydrogen-bonded complexes of water with methanol and t-butanol embedded in cryogenic neon matrices at 2.8 K. The partial isotopic substitution of individual subunits enabled by a dual inlet deposition procedure provides for the first time unambiguous assignments of the intermolecular high-frequency out-of-plane and low-frequency in-plane donor OH librational modes for mixed alcohol–water complexes. The vibrational assignments confirm directly that water acts as the hydrogen bond donor in the most stable mixed complexes and the tertiary alcohol is a superior hydrogen bond acceptor. The class of large-amplitude donor OH librational motion is shown to account for up to 5.1 kJ mol⁻¹ of the destabilizing change of vibrational zero-point energy upon intermolecular OH⋯O hydrogen bond formation. The experimental findings are supported by complementary electronic structure calculations at the CCSD(T)-F12/aug-cc-pVTZ level of theory.

---

1. Introduction

Intermolecular hydrogen bonding between alcohols and water is of general interest ranging from various fundamental microscopic aspects related to conformational isomerism, hydrogen bond donor/acceptor preferences and the large-amplitude and highly anharmonic hydrogen bond vibrational motion introduced upon complexation to more applied macroscopic aspects related to hydrophobic effects and the optimization of experimental separation technologies of bulk alcohol/water mixtures and bio-fuels. It has previously been demonstrated that the intermolecular interactions responsible for thermodynamic anomalies¹ such as negative heats of mixing^2,3 and negative excess volumes^4,5 of bulk alcohol/water mixtures can be addressed qualitatively by combined infrared and Raman spectroscopic investigations of hydrogen-bonded jet-cooled alcohol–water clusters.^6,7 These thermodynamic anomalies depend strongly on the relative hydrogen bond energies of mixed alcohol–water complexes versus the pure complexes of alcohols and water.⁸

The amount of experimental spectroscopic data reported in the literature for isolated mixed binary alcohol–water complexes is surprisingly limited. One explanation for this sparsity of spectroscopic data might be the absence of any suitable UV chromophores in these systems which would otherwise enable sensitive electronic double-resonance spectroscopy investigations.⁹ A series of pure rotational spectroscopic studies of adiabatically cooled mixed complexes of water with methanol¹⁰ and t-butanol¹¹ has unraveled the structure of the conformers where the water subunit acts as the hydrogen bond donor. The other conformations with the alcohol subunit acting as the hydrogen bond donor were not detected under the cold conditions of the seeded molecular beam studies. In terms of vibrational spectroscopy, a sensitive probe for intermolecular hydrogen bond formation is the OH-stretching manifold of the subunits¹² and recent combined infrared and Raman investigations have monitored bathochromic OH-stretching spectral shifts for vacuum-isolated mixed complexes of water with both methanol and ethanol.^6,7 The observed vibrational spectral signatures support the hydrogen bond donor/acceptor relationships found in the cited microwave studies. The ethanol–water complex furthermore represents one of the simplest mixed hydrogen-bonded molecular systems where internal conformational degrees of freedom influence the hydrogen bond formation. In the mixed ethanol–water complex, the ethanol subunit prefers the gauche conformation as the hydrogen bond acceptor although the trans conformation is the most stable for an isolated ethanol molecule. This is considered as one of the most elementary cases of adaptive aggregation, where a flexible molecule is forced into a less stable conformation upon non-covalent binding to a hydrogen bond donor molecule to optimize the mutual interaction energy.^6,7 A few other experimental studies of this vibrational OH-stretching manifold have been reported for mixed water complexes with methanol and ethanol embedded in cryogenic matrices of nitrogen and argon.^13,14 In the most perturbing matrix environment of nitrogen a reversed donor/acceptor relationship has been observed although severe site effects blurred the OH-stretching signatures of the alcohol donor subunits. This opposite donor/acceptor relationship observed in cryogenic nitrogen matrices has been explained by weak cooperative attractive interactions between the OH groups and the N₂ host molecules.¹⁵ In the mixed complexes where the alcohol molecule acts as the hydrogen bond donor both dangling OH groups of the water acceptor subunit might interact with N₂ host molecules and thereby increasing the acceptor character of the O nuclei on the water molecule. This effect could strengthen the intermolecular hydrogen bond to the alcohol molecule and overcome the energy barrier between the water–alcohol conformers.¹⁵

In the present work it is demonstrated how the strength, directionality and anharmonicity of these important intermolecular hydrogen bonding motifs can be probed directly via large-amplitude intermolecular OH librational modes of mixed isotopically substituted alcohol–water complexes. These direct spectroscopic observables detected in the challenging far-infrared region of the electromagnetic spectrum have been shown to enable an accurate characterization of the intermolecular potential energy landscape between identical hydrogen bond partners.^16–19 In a recent combined far-infrared supersonic jet and neon matrix isolation study of methanol dimer, the large-amplitude intermolecular donor OH librational transition was unambiguously assigned for the first time.¹⁸ This study demonstrated that this large-amplitude OH librational motion is basically unhindered in an inert neon matrix environment at 2.8 K and allowed for a rigorous benchmarking of theory. The present work shows the potential to detect these important spectroscopic observables in the far-infrared region for mixed alcohol–water complexes embedded in neon by a dual inlet deposition procedure. The mixed water complexes with the simplest primary alcohol, methanol, and the simplest tertiary alcohol, t-butanol, are the systems of choice since conformational isomerism of the t-butanol monomer is absent.

2. Experimental

Several millimeter thick matrices of pre-cooled neon (L'Air Liquide, 99.999%) doped with “freeze–pump–thaw” purified CH₃OH (Sigma Aldrich, 99.9%), C(CH₃)₃OH (Sigma Aldrich, 99.9%) and H₂O (Milli-Q) samples and isotopically substituted CH₃OH-d1 (Sigma Aldrich, 99.0% D), CH₃OH-d4 (Sigma Aldrich, 99.0% D), C(CH₃)₃OH-d1 (Sigma Aldrich, 99.0% D), C(CH₃)₃OH-d10 (Sigma Aldrich, 99.0% D) and D₂O (Sigma Aldrich, 99.5% D) samples with mixing ratios of ≃0.25 to 2.5 permille have been deposited with a flow rate of 0.02 mole on a gold-plated oxygen-free high thermal conductivity (OFHC) copper mirror at 3.6 K inside an immersion helium cryostat (IHC-3) modified for matrix isolation spectroscopy.^19,20 The pre-cooling of neon significantly reduces the heat load on the copper mirror and enables a total deposition time of less than 1 hour per experiment. A dual inlet deposition procedure enabled studies of individual deuterium-enriched samples without the risk of H/D exchange before deposition. The combination of resistive heaters and feedback electronics has been employed to maintain a stable mirror temperature at 2.8 ± 0.1 K before and after the depositions. The cold head was equipped with interchangeable CsI and polymethylpentene (TPX) windows and the combined mid- and far-infrared single-beam sample spectra have been collected by a Bruker IFS 120 FTIR spectrometer employing tungsten and globar lamps as radiation sources. Liquid nitrogen cooled HgCdTe and InSb detectors combined with Ge/KBr and CaF₂ beam splitters, respectively, were employed for the spectral region above 600 cm⁻¹. A Si-bolometer operating at 4.2 K combined with a 6 μm multilayer Mylar beam splitter was employed for the 30–650 cm⁻¹ spectral region. In most cases the doped neon matrices have been annealed up to 9 K and relaxed back to 3 K for the study of temperature effects. Single-beam background spectra were subsequently collected of the evacuated warm cryostat. A spectral resolution ranging from 0.1 to 1.0 cm⁻¹ was selected depending on observed band widths.

3. Vibrational assignments for the mixed methanol/water complex

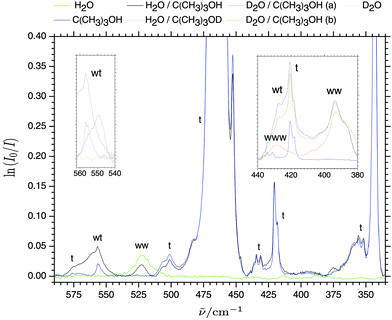
Fig. 1 shows a series of far-infrared absorption spectra (200–600 cm⁻¹) collected for several millimeter thick cryogenic neon matrices doped with pure water (H₂O : Ne) = (1 : 2000), pure methanol with traces of H₂O (CH₃OH : H₂O : Ne) = (3 : 1 : 13 000) and different isotopic water/methanol mixtures (CH₃OH : H₂O : Ne) = (3 : 2 : 6000) at 2.8 K. In previous studies of methanol embedded in solid matrices of para-H₂²¹ and neon,^18,22,23 the torsional-vibrational splittings into A and E sub-levels by torsional tunneling have been shown to persist although the standard A–A and E–E selection rules do not apply in the inert matrix environments. The torsional fundamental of methanol embedded in cryogenic neon matrices thus gives rise to four different sub-bands in the far-infrared region; the pair of “cold” A–E and A–A transitions observed at 212 and 269 cm⁻¹ and the pair of “hot” E–E and E–A transitions observed at 206 and 262 cm⁻¹.^18,22 The sub-bands observed at 447 and 507 cm⁻¹ have previously been assigned to components of the first torsional overtone transition for methanol monomer.²² In terms of pure methanol complexes, a combined far-infrared jet and neon matrix isolation study has recently revealed the donor OH librational transition at 557.7 cm⁻¹ as well as the acceptor OH torsional transition at 286 cm⁻¹ of the methanol dimer for the first time.¹⁸ In addition, the far-infrared absorption from pure complexes of water embedded in neon matrices have been explored previously.^19,24–27 In the spectral region above 200 cm⁻¹ the strong intermolecular high-frequency out-of-plane and low-frequency in-plane donor OH librational bands of the water dimer embedded in neon matrices have previously been assigned at 522.4 cm⁻¹ and 309.1 cm⁻¹, respectively.²⁴ The broad band observed around 226 cm⁻¹ has previously been attributed dimeric water absorption although the nature of this far-infrared transition is not yet understood in detail as the four other intermolecular fundamental modes have all been assigned at lower frequencies.²⁴ The in-plane donor OH librational band is slightly overlapped with the strong c-axis librational mode of cyclic water trimer previously assigned at 310.8 cm⁻¹. Five combination bands have previously been assigned the cyclic water trimer where the strongest are observed at 280.0, 386.8 and 414.1 cm⁻¹.²⁵

Fig. 1 The observed far-infrared absorption spectra of pure water (denoted w), pure methanol (denoted m) and different isotopic methanol/water mixtures embedded in neon matrices at 2.8 K with proposed vibrational assignments. The inserts show close-ups of the spectral regions belonging to the out-of-plane OH (left), out-of-plane OD (center) and in-plane OH (right) donor librational modes of the hydrogen-bonded complexes (ww: water dimer, wm: 1 : 1 methanol–water complex, mm: methanol dimer, etc.).

The assignment of the band observed at 527.3 cm⁻¹ (Fig. 1) was at first not possible even by dedicated methanol concentration series. In some annealing experiments at 9 K the intensity of this band increased significantly without any subsequent relaxation upon repeated cooling to 3 K. This observation pointed at an irreversible build-up of molecular complexes driven by diffusion in the soft matrix. The combined findings suggested the assignment to a mixed methanol–water complex as minor traces of water are always present in various amounts in the inlet system. The severe band overlap with the out-of-plane donor OH librational modes of water dimer assigned at 522.4 cm⁻¹ suggested that water takes the role as the hydrogen bond donor in the most stable mixed complex and possesses almost an identical donor OH librational motion as for the lass stable water dimer. An unambiguous identification of the hydrogen bond donor/acceptor relationship in the cryogenic neon environment could be settled by partial isotopic H/D substitution of the individual subunits enabled by the dual inlet deposition procedure. The three inserts of Fig. 1 show the spectral regions belonging to the donor OH (OD) librational modes. The H/D substitution on the water subunit introduces a significant red-shift from 527.3 cm⁻¹ to 397.6 cm⁻¹ confirming that water acts as hydrogen bond donor. The observed band origin ratio of 1.33 is close to the theoretical value of expected for a genuine harmonic hydrogen motion and supports an assignment to the out-of-plane donor OD librational mode for the complex of D₂O with methanol. The latter band origin is furthermore slightly larger than the corresponding out-of-plane donor OD librational band origin of (D₂O)₂ reported previously as expected.¹⁹ The H/D substitution on the OH group of methanol introduces only a minor red-shift of 4 cm⁻¹ for the out-of-plane donor OH librational mode confirming a hydrogen bond acceptor role of the methanol subunit. In terms of the in-plane donor OH librational bands, the isotopic H/D substitution on the OH group of methanol induces a more pronounced red-shift of around 13 cm⁻¹. A closer look at the normal mode pictures reveals that whereas the out-of-plane OH librational mode exhibits an almost localized genuine motion of the bound hydrogen atom not involving the dangling OH group on the water molecule, the in-plane OH librational mode can be pictured as a hindered overall c-axis rotation of the water subunit. The latter large-amplitude in-plane OH librational motion of the whole water molecule thus has a more significant effect on the center of mass and is more affected by isotopic substitution of the methanol subunit as summarized in Table 1.

Table 1 The observed high-frequency out-of-plane and low-frequency in-plane donor OH (OD) librational band origins (cm⁻¹) for isotopic water complexes and isotopic mixed complexes of water with methanol/t-butanol embedded in neon matrices at 2.8 K

Donor–acceptor	ν lib,out-of-plane	ν lib,in-plane	Donor–acceptor	ν lib,out-of-plane	ν lib,in-plane
a Ceponkus et al.^19 b Overlapped with (H2O)2. c Overlapped with (D2O)2. d Overlapped with C(CH3)3OH. e Overlapped with C(CH3)3OD. f Overlapped with C(CD3)3OD.
H2O–H2O	522.4^a	309.1^a	D2O–D2O	393.2^a	233.5^a
H2O–CH3OH	527.3		D2O–CH3OH	397.6
H2O–CH3OD	523.7	296.2	D2O–CH3OD	395.0
H2O–CD3OD	523.9	295.9	D2O–CD3OD
H2O–C(CH3)3OH	556.6	318.2	D2O–C(CH3)3OH	427.7
H2O–C(CH3)3OD	548.9	298.1	D2O–C(CH3)3OD		242.4
H2O–C(CD3)3OD	549.0

---

4. Vibrational assignments for the mixed t-butanol/water complex

Fig. 2 shows far-infrared absorption spectra (300–600 cm⁻¹) collected for several millimeter thick cryogenic neon matrices doped with pure water (H₂O : Ne) = (1 : 2000), t-butanol with small traces of H₂O (C(CH₃)₃OH : H₂O : Ne) = (4 : 1 : 4000) and different isotopic t-butanol/water mixtures (C(CH₃)₃OH : H₂O : Ne) = (5 : 2 : 3000) at 2.8 K. The spectral region below 300 cm⁻¹ (not shown) is dominated by complex torsional–vibrational coupling components of the monomer OH and methyl torsional motion which shall be considered in details elsewhere. In addition, the monomer of regular t-butanol in contrast to methanol exhibits several intramolecular skeletal fundamental transitions in the far-infrared spectral region.²⁸ In the cryogenic neon matrices doped solely with t-butanol the two overlapping CCC bending fundamental bands are assigned at 343.4 cm⁻¹ and 356.0 cm⁻¹, the symmetric CCO bending fundamental is assigned at 420.2 cm⁻¹ and the two stronger asymmetric CCO bending fundamentals are assigned between 450 and 475 cm⁻¹. A higher (Ne : C(CH₃)₃OH) mixing ratio relative to (Ne : CH₃OH) was employed to study the mixed t-butanol–water complexes but any formation of mixed t-butanol–water trimers could be excluded by the inspection of the corresponding mid-infrared absorption spectra recorded for all neon matrices.

Fig. 2 The observed far-infrared absorption spectra of water (denoted w), t-butyl alcohol (denoted t) with small traces of water and different isotopic t-butanol/water mixtures embedded in neon matrices at 2.8 K with proposed vibrational assignments. The inserts show close-ups of the spectral regions belonging to the out-of-plane OH (left) and OD (right) donor librational modes of the hydrogen-bonded complexes (ww: water dimer, www: water trimer, wt: 1 : 1 t-butanol–water complex, etc.). The latter insert shows the far-infrared spectra recorded for t-butanol/D₂O doped matrices before (b) and after (a) annealing to 9 K.

For the neon matrices doped simultaneously with small concentrations of water and t-butanol, two new bands appear in close vicinity to the donor OH librational modes of water dimer. This observation indicates that the water subunit also acts as the hydrogen bond donor in the mixed complex with t-butanol and supports the findings of the previous microwave molecular beam study where only this conformer was assigned.¹¹ A band observed at 556.6 cm⁻¹ is shifted by almost 35 cm⁻¹ relative to the water dimer transition and is assigned to the out-of-plane donor OH librational mode of the mixed complex. A lower band appears as a shoulder on the corresponding water dimer transition around 318.2 cm⁻¹ and is assigned to the in-plane OH librational band of the mixed complex. The unambiguous assignments could again be supported by partial isotopic H/D substitution of the individual subunits enabled by the dual inlet deposition procedure. Both the isotopic H/D substitution on the alcohol group alone and the full H/D substitution on t-butanol introduce a minor red-shift of around 7.5 cm⁻¹ for the 556.6 cm⁻¹ band indicating the hydrogen bond acceptor role of t-butanol. Unfortunately, the high-frequency donor OD librational band for the complex of D₂O with regular t-butanol accordingly is expected in the region of the symmetric CCO bending fundamental band around 420.2 cm⁻¹ assuming the band origin ratio of 1.33 observed for the methanol–water complex. In this spectral region the high-frequency out-of-plane OD libration of (D₂O)₂ is also located at 397.6 cm^−1 19 and the shear librational band of (D₂O)₃ is located around 428 cm⁻¹.²⁵ However, the far-infrared spectrum of t-butanol/D₂O doped matrices of neon nevertheless reveals a new distinct spectral feature at 427.7 cm⁻¹ on the high-frequency shoulder of the symmetric CCO bending fundamental band of t-butanol (see trace b) of Fig. 2. The intensity of this spectral feature at 427.7 cm⁻¹ clearly increases upon annealing of the matrix to 9 K without any subsequent relaxation upon repeated cooling to 3 K as witnessed by trace a of Fig. 2. The annealing is expected to enable the diffusion of the D₂O molecules in the neon matrix and trigger the formation of mixed complexes of D₂O with t-butanol more than the formation of (D₂O)₂ as the bulky t-butanol molecules are more likely collision partners in the matrices. The significant intensity increase of the 427.7 cm⁻¹ band relative to the (D₂O)₂ band at 397.6 cm⁻¹ upon annealing to 9 K thus supports an assignment to the high-frequency donor OD librational band for the mixed complex of D₂O with t-butanol. The observed band origin ratio of 1.3 for the proposed OH/OD librational bands is furthermore rather close to the theoretical value of expected for a genuine harmonic hydrogen motion. The two inserts of Fig. 2 show the spectral regions belonging to the donor OH (OD) librational modes of the mixed isotopic complexes of water with t-butanol. The proposed assignment of the low-frequency in-plane OH librational mode is furthermore supported by an isotopic red-shift of 20.1 cm⁻¹ upon O-deuteration of t-butanol. In addition, a tentatively assignment of the in-plane low-frequency OD librational transition at is 242.4 cm⁻¹ is proposed for the mixed complex of D₂O with t-butanol-d1 as summarized in Table 1. Whereas the high-frequency out-of-plane donor OH/OD librational modes are highly localized, the low-frequency in-plane OH/OD librational motion might couple slightly to the intramolecular skeletal motion of the t-butanol subunits.

The observed donor OH librational spectral signatures point at a stronger hydrogen bond interaction between water and t-butanol than between water and methanol. An inductive effect of the bulky alkyl groups of t-butanol improves the acceptor quality of the oxygen atom in the tertiary alcohol group. This inductive effect stiffens the intermolecular hydrogen bond and the more hindered internal rotational motion raises the band origins for the donor OH librational modes when the hydrogen bond acceptor changes from water to methanol and finally t-butanol. A far-infrared jet study has previously demonstrated that alkylation strengthens and stiffens the intermolecular hydrogen bonding between alcohol molecules.¹⁷ This was also reflected in increased average OH librational band origins for the clusters of t-butanol relative to methanol although these observations could not be captured by density functional methods lacking electron correlation available for such bulky alcohol clusters containing 30 to 60 atoms.¹⁷

5. Exploratory quantum chemical calculations

The smaller size of the water complexes with methanol and even t-butanol allows for rigorous ab initio computations including high degrees of electron-correlation of the electronic dissociation energy D_e which may be compared to results from both canonical and dispersion-corrected density functional theory. The quantum chemical software packages Gaussian09 (Rev. D.01)²⁹ and Turbomole (ver. 6.6)^30,31 have been employed for the present ab initio molecular orbital and DFT calculations. The geometries of the monomers and the mixed hydrogen-bonded complexes were all optimized and the resulting electronic energies calculated employing the canonical B3LYP level,³² the dispersion-corrected B3LYP-D3 approach³³ and the second-order Möller–Plesset MP2 methodology^34,35 coupled with Dunning's augmented correlation-consistent polarized triple-zeta (aug-cc-pVTZ) and quadruple-zeta (aug-cc-pVQZ) basis sets.³⁶ The root-mean-square force criterion has been set to 10⁻⁶ (atomic units) for all the geometry optimizations. The electronic energies for these optimized geometries were subsequently furthermore calculated employing both the coupled-cluster approach with single and double excitations and perturbative treatment of triple excitations CCSD(T)³⁷ and the explicitly-correlated CCSD(T)-F12 methodology³⁸ to optimize the level of electron correlation combined with the same basis sets. In the electronic energy calculations for the mixed alcohol–water complexes, the effects of the basis set superposition errors³⁹ have been accounted for by the counterpoise method.⁴⁰ The harmonic frequencies and overall ZPE contributions of the monomers and hydrogen-bonded complexes have been calculated in the doubly harmonic approximation whereas the anharmonic frequencies have been calculated employing the vibrational second-order perturbation theory (VPT2) approach⁴¹ as implemented in Gaussian09 (Rev. D.01).²⁹

6. Discussion

Table 2 shows the electronic dissociation energy D_e of the most stable methanol–water conformer and the energy difference ΔE_e between the two different conformers predicted from combined quantum chemical methodologies employed for geometry optimization and subsequent single-point electronic energy calculations. The potential energy minimum structures for the different conformers of the alcohol–water complexes are illustrated in Fig. 3. The benchmark level of theory available for both alcohol–water complexes employs the MP2/aug-cc-pVTZ^34–36 level for geometry optimization and the CCSD(T)-F12/aug-cc-pVTZ level^36,38 for the electronic dissociation energy D_e. The benchmark D_e-value of 24.62 kJ mol⁻¹ for the most stable methanol–water conformer and the energy difference of 2.65 kJ mol⁻¹ between the two conformers agree with the highest level of methodology employing a combined MP2/aug-cc-pVQZ/CCSD(T)-F12/aug-cc-pVQZ approach within 0.42 and 0.03 kJ mol⁻¹, respectively. The benchmark approach is thus expected to provide reliable dissociation energies for the two different conformers of the more bulky water complexes with t-butanol as listed in Table 3.

Table 2 The electronic dissociation energy D_e for the most stable hydrogen-bonded complex of water with methanol and the difference of electronic dissociation energy between the two different conformers ΔE_e predicted from several combined quantum chemical methodologies for geometry and electronic energy calculations

Geometry optimization^a	Electronic energy	D e/kJ mol^−1	ΔEe/kJ mol^−1
a RMS force criterion set to 10^−6 (atomic units) for all geometry optimizations. b CP = counterpoise correction applied.
B3LYP/aug-cc-pVTZ	B3LYP/aug-cc-pVTZ	20.58	2.18
B3LYP-CP/aug-cc-pVTZb	B3LYP/aug-cc-pVTZ	20.29	2.16
B3LYP-CP/aug-cc-pVTZb	CCSD(T)/aug-cc-pVTZ	24.64	2.53
B3LYP-D3/aug-cc-pVTZ	B3LYP-D3/aug-cc-pVTZ	25.18	3.03
B3LYP-D3-CP/aug-cc-pVTZ^b	B3LYP-D3/aug-cc-pVTZ	24.88	3.02
B3LYP-D3-CP/aug-cc-pVTZ^b	CCSD(T)/aug-cc-pVTZ	24.92	2.74
MP2/aug-cc-pVTZ	MP2/aug-cc-pVTZ	25.06	3.10
MP2-CP/aug-cc-pVTZ^b	MP2/aug-cc-pVTZ	22.71	2.88
MP2-CP/aug-cc-pVTZ^b	CCSD(T)/aug-cc-pVTZ	25.01	2.82
MP2-CP/aug-cc-pVTZ^b	CCSD(T)-F12/aug-cc-pVTZ	24.62	2.65
MP2/aug-cc-pVQZ	MP2/aug-cc-pVQZ	24.54	3.06
MP2-CP/aug-cc-pVQZ^b	MP2/aug-cc-pVQZ	23.36	2.91
MP2-CP/aug-cc-pVQZ^b	CCSD(T)/aug-cc-pVTZ	24.74	2.82
MP2-CP/aug-cc-pVQZ^b	CCSD(T)-F12/aug-cc-pVTZ	24.66	2.65
MP2-CP/aug-cc-pVQZ^b	CCSD(T)-F12/aug-cc-pVQZ	24.20	2.68

---

Fig. 3 Illustration of the predicted potential energy minima structures of the different alcohol–water conformers. The most stable conformers (b and d) have water as the hydrogen bond donor whereas the less stable conformers have the alcohol subunit as hydrogen bond donor (a and c).

Table 3 The electronic dissociation energy D_e of the most stable hydrogen-bonded complex of water with t-butanol and the difference of electronic dissociation energy between the two different conformers ΔE_e predicted from several combined quantum chemical methodologies for geometry and electronic energy calculations

Geometry optimization^a	Electronic energy	D e/kJ mol^−1	ΔEe/kJ mol^−1
a RMS force criterion set to 10^−6 (atomic units) for all geometry optimizations. b CP = counterpoise correction applied.
B3LYP/aug-cc-pVTZ	B3LYP/aug-cc-pVTZ	21.93	5.57
B3LYP-CP/aug-cc-pVTZ^b	B3LYP/aug-cc-pVTZ	21.54	5.52
B3LYP-CP/aug-cc-pVTZ^b	CCSD(T)/aug-cc-pVTZ	28.80	5.95
B3LYP-D3/aug-cc-pVTZ	B3LYP-D3/aug-cc-pVTZ	30.59	8.41
B3LYP-D3-CP/aug-cc-pVTZ^b	B3LYP-D3/aug-cc-pVTZ	30.15	8.34
B3LYP-D3-CP/aug-cc-pVTZ^b	CCSD(T)/aug-cc-pVTZ	30.03	6.64
MP2/aug-cc-pVTZ	MP2/aug-cc-pVTZ	30.09	6.90
MP2-CP/aug-cc-pVTZ^b	MP2/aug-cc-pVTZ	26.75	6.31
MP2-CP/aug-cc-pVTZ^b	CCSD(T)/aug-cc-pVTZ	30.06	6.65
MP2-CP/aug-cc-pVTZ^b	CCSD(T)-F12/aug-cc-pVTZ	29.29	6.52

---

The benchmark CCSD(T)-F12/aug-cc-pVTZ predictions confirm that t-butyl alcohol is a superior hydrogen bond acceptor than methanol. The electronic dissociation energy D_e of the most stable mixed water complex with t-butanol is predicted to be 4.67 kJ mol⁻¹ larger than for the corresponding mixed complex with methanol. The predictions listed in Table 2 show that the canonical B3LYP functional³² underestimate the binding energies for the mixed complexes of water with methanol by more than 15% whereas the B3LYP-D3 approach including Grimme and co-worker's dispersion corrections³³ reproduce the predictions by the highest level of methodology within 0.25 kJ mol⁻¹. However, the dissociation energies for the more electron-rich mixed complexes of water with t-butanol are strongly underestimated by 7.4 kJ mol⁻¹ (ca. 25%) by the B3LYP functional and slightly overestimated 1.3 kJ mol⁻¹ (ca. 5%) by the dispersion-corrected B3LYP-D3 predictions (Table 3). In the context of relative hydrogen bond donor/acceptor capabilities we note that the benchmark theoretical CCSD(T)-F12 predictions (in strong contrast to the canonical B3LYP predictions) indicate that t-butanol has a slightly higher interaction energy of 0.8 kJ mol⁻¹ with water than methanol when the alcohols act as the hydrogen bond donor. This increased interaction energy may be ascribed to the increased dispersion forces between the water molecule and the electron-rich t-butyl alcohol molecule. The effect of the zero-point energy (ZPE) contributions and in particular the influence of the donor OH librational motion on the electronic dissociation energy must be considered before reaching further conclusions.

The change of vibrational ZPE upon intermolecular hydrogen bond formation is notoriously difficult to predict computationally, in particular for the observed large-amplitude and highly anharmonic intermolecular hydrogen bond librational motion. In a recent combined jet and neon matrix isolation far-infrared study of methanol dimer, the donor OH librational band was observed and assigned for the first time at 560 cm⁻¹.¹⁸ This study predicted an overall sum of anharmonic contributions to the OH donor librational fundamental transition of 100 cm⁻¹ by vibrational second-order perturbation theory.⁴¹ In combination with a benchmark harmonic band origin of 660 cm⁻¹ predicted at the LCCSD(T)-F12 level, the anharmonic predicted band origin of 560 cm⁻¹ was in excellent agreement with the experimental findings. A similar detailed analysis of the mixed water complexes with methanol and t-butanol is beyond the scope of the present predominantly experimental work. However, standard vibrational frequency calculations at the MP2/aug-cc-pVTZ level in the doubly harmonic approximation provide harmonic band origins of 630, 647 and 669 cm⁻¹ for the high-frequency out-of-plane and 360, 375 and 388 cm⁻¹ for the low-frequency in-plane donor OH librational transitions for the pure water complex and the most stable mixed complexes of water with methanol and t-butanol, respectively. The ordering of these harmonic predictions is in qualitative agreement with the present experimental findings and the anharmonicity contributions seem to be in the order of 15–20% as found for the recent methanol dimer study.¹⁸ An anharmonic VPT2 analysis⁴¹ for the mixed complex of water with methanol at the MP2/aug-cc-pVTZ level predicts an overall anharmonicity of 18% for the high-frequency donor OH librational transition. This VPT2 calculation is not feasible for the multi-dimensional mixed complex of water and t-butanol. A similar analysis of the low-frequency in-plane donor OH librational transitions and the other intermolecular large-amplitude vibrational transitions for these non-rigid hydrogen-bonded complexes would be to stretch the reliability of the VPT2 approach. Table 4 thus provides the change of harmonic vibrational ZPE for the isotopic mixed complexes of water with methanol and t-butanol predicted at the common feasible MP2/aug-cc-pVTZ level.

Table 4 The electronic dissociation energy D_e (CCSD(T)-F12/aug-cc-pVTZ^a), the total change of harmonic vibrational zero-point energy upon complexation ΔZPE^calc_tot (MP2/aug-cc-pVTZ) and the resulting absolute dissociation energy D₀ for mixed isotopic hydrogen-bonded donor–acceptor complexes together with the observed (anharmonic) contribution to the zero-point energy from the class of donor OH librational modes ΔZPE^exp_lib (all values in units of kJ mol⁻¹)

	H2O–CH3OH	CH3OH–H2O	H2O–CD3OD	CD3OD–H2O	D2O–CH3OH	CH3OH–D2O
a Electronic dissociation energies De calculated at the CCSD(T)-F12/aug-cc-pVTZ level based on optimized geometries at the MP2/aug-cc-pVTZ level. b Includes the observed band origin of the high-frequency donor OD librational mode and an anharmonically predicted band origin for the low-frequency donor OD librational mode.
D e	24.62^a	21.98^a	24.62^a	21.98^a	24.62^a	21.98^a
ΔZPE^calctot	7.80	6.59	7.52	5.90	6.25	5.85
ΔZPE^explib	5.0		4.9		[3.8]^b
D 0	16.82	15.39	17.10	16.08	18.37	16.13

---

	H2O–C(CH3)3OH	C(CH3)3OH–H2O	H2O–C(CD3)3OD	C(CD3)3OD–H2O	D2O–C(CH3)3OH	C(CH3)3OH–D2O
D e	29.29^a	22.77^a	29.29^a	22.77^a	29.29^a	22.77^a
ΔZPE^calctot	8.40	6.34	8.06	5.74	6.77	5.57
ΔZPE^explib	5.2		5.1		[4.0]^b
D 0	20.89	16.43	21.23	17.04	22.52	17.20

---

The incorporation of the computed vibrational ZPE contributions has an enormous impact as evidenced by the resulting absolute ground-state dissociation energies D₀ of the mixed alcohol–water complexes listed in Table 4. The total vibrational ZPE account for between 5.6 and 8.4 kJ mol⁻¹ for the mixed water complexes with t-butanol in the harmonic approximation depending on the isotopic variant and the hydrogen donor/acceptor roles. The sum of the experimental anharmonic ZPE contributions from the donor OH librational motion alone accounts for up to 5.2 kJ mol⁻¹ or minimum 60% of the total anharmonic vibrational ZPE when water acts as hydrogen bond donor. This conformer has a significantly higher vibrational ZPE contribution owing to the two different donor OH librational modes. The conformer with the alcohol as hydrogen bond donor only has one single donor OH librational mode. The alcohol OH librational mode of this latter conformer is significantly blue-shifted relative to the free alcohol torsional mode but this blue-shift still introduces a smaller vibrational ZPE introduced upon intermolecular hydrogen bond formation. The benchmark energy difference prediction ΔE_e of 6.5 kJ mol⁻¹ for the two conformers of the water complex with t-butanol is accordingly translated into a significantly smaller 4.2 to 5.3 kJ mol⁻¹ difference between the resulting D₀-values depending on the isotopic variants when the ZPE contributions are incorporated. In terms of the more simple mixed complexes of water and methanol, the total harmonic vibrational ZPE account for between 5.9 and 7.8 kJ mol⁻¹ for the conformers of the mixed water complexes with methanol depending on the isotopic variant. For these simpler systems the sum of the experimental anharmonic ZPE contributions from the donor OH librational motion alone accounts for up to 5.0 kJ mol⁻¹i.e. minimum 65% of the total anharmonic vibrational ZPE for the conformer where water acts as hydrogen bond donor. The present benchmark energy difference prediction ΔE_e of 2.65 kJ mol⁻¹ between the methanol–water conformers also translates into a smaller 1.0 to 2.2 kJ mol⁻¹ difference between the resulting D₀-values depending on the isotopic substitutions. A diffusion quantum Monte Carlo study has previously predicted a difference of these D₀-values between 0.3 to 1.3 kJ mol⁻¹ for the regular isotopic methanol–water conformers depending on the exact theoretical treatment of the large-amplitude intermolecular vibrational motion.⁴² H/D isotopic substitutions on the methanol subunit further translated the resulting difference between D₀-values into the 0.04 to 1.2 kJ mol⁻¹ interval.

The effect of the large-amplitude intermolecular donor OH librational motion on the absolute intermolecular hydrogen bond energy D₀ for mixed alcohol–water complexes demonstrated by the present experimental findings has been explored previously for the pure complexes of water.^19,43 These far-infrared studies have shown that D-bonded water complexes are more stable than the H-bonded counterparts due to the difference in the total vibrational ZPEs. In particular, the distinct observation and vibrational assignments for the deuterium-bonded configuration of the mixed isotopic (HDO)₂ complex embedded at low temperatures have verified the strong preference for intermolecular deuterium bonds experimentally. Of the twelve possible H/D isotopologues of the water dimer only six of these have been detected in observable amounts in cryogenic neon matrices doped with H₂O/HDO/D₂O mixtures.¹⁹ The major explanation for these experimental findings could be found in the significant isotopic spectral red-shift of 129 m⁻¹ for the high-frequency out-of-plane donor OH librational mode of the pure water complex upon H/D substitution. This mode alone thus provide a stabilizing decrease of the vibrational ZPE upon complex formation by ca. 0.8 kJ mol⁻¹ for the D-bonded complexes.

7. Conclusions

To conclude is that the large-amplitude donor OH librational modes of partial isotopically substituted mixed complexes of water with aliphatic alcohols in the challenging far-infrared region have now been observed and assigned enabled by a dual inlet matrix deposition approach and supported by quantum chemical calculations. The far-infrared spectroscopic findings have demonstrated that water acts as the hydrogen bond donor upon complexation with aliphatic alcohols as methanol and t-butanol and the sum of the contributions from the class of donor OH librational motion alone has been quantified to be 5.0–5.2 kJ mol⁻¹. It's nature as a localized genuine motion of the bound hydrogen atom makes the high-frequency out-of-plane donor OH librational mode an excellent probe for the intermolecular hydrogen bond strength in a similar fashion as the often discussed Badger–Bauer relationship associated with the bathochromic shift of the hydrogen-bonded intramolecular OH stretching band origin.⁴⁴ A stronger intermolecular hydrogen bond results in a more hindered internal rotational motion and the increase of the band origin for this high-frequency hydrogen bond donor vibration. In the mixed complexes of water with aliphatic alcohols the donor OH librational spectral signatures thus act as a measure of the hydrogen bond acceptor strength of the alcohol molecule. The electron donating inductive effect of the alkyl groups of t-butanol transforms the oxygen atom into a significant better hydrogen bond acceptor than the oxygen atom on methanol which can be qualitatively read from the relative band origins of the donor OH librational modes. The isotopic H/D substitution furthermore allows for a manipulation of the overall vibrational ZPE due to significant spectral red-shift of these donor OH librational modes upon H/D substitution. Quantum chemical calculations predict that the full H/D isotopic substitution of the alcohol subunit introduces the largest difference of the vibrational ZPE between the two different alcohol–water conformers. The present experimental findings show that even this full H/D substitution of the methanol and t-butanol subunits cannot overcome the differences of the electronic dissociation energy D₀ between the alcohol–water conformers. It will be interesting to see how future anharmonic theoretical methodologies will perform in the predictions of these intermolecular force fields spanned by water and the studied prototypical alcohols of increasing structural complexity.

Acknowledgements

The authors appreciate discussions with D. W. Mahler, J. Ceponkus, B. Nelander, A. Engdahl and K. L. Feilberg. The authors acknowledge Centre for Scientific and Technical Computing (LUNARC) at Lund University for the generous allocation of computational resources for the Turbomole calculations. RWL acknowledges financial support from the Danish Council for Independent Research's Sapere Aude Programme (Grant Ref.: 12-125248).

References

1. F. Franks and D. J. G. Ives, Q. Rev., Chem. Soc., 1966, 20, 1–44.
2. G. L. Bertrand, F. J. Millero, C.-H. Wu and L. G. Hepler, J. Phys. Chem., 1966, 70, 699–705.
3. J. A. Larkin, J. Chem. Thermodyn., 1975, 7, 137–148.
4. J.-P. E. Grolier, Fluid Phase Equilib., 1981, 6, 283–287.
5. G. C. Benson and O. Kiyohara, J. Solution Chem., 1980, 9, 791–804.
6. M. Nedić, T. N. Wassermann, Z. Xue, P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2008, 10, 5953–5956.
7. M. Nedić, T. N. Wassermann, R. Wugt Larsen and M. A. Suhm, Phys. Chem. Chem. Phys., 2011, 13, 14050–14063.
8. G. Matisz, A.-M. Kelterer, W. M. F. Fabiand and S. Kunsagi-Mate, Phys. Chem. Chem. Phys., 2015, 17, 8467–8479.
9. C. J. Gruenloh, F. C. Hagemeister, J. R. Carney and T. S. Zwier, J. Chem. Phys., 1999, 103, 503–513.
10. P. A. Stockman, G. A. Blake, F. J. Lovas and R. D. Suenram, J. Chem. Phys., 1997, 107, 3782–3790.
11. L. Evangelisti and W. Caminati, Phys. Chem. Chem. Phys., 2010, 12, 14433–14441.
12. R. Wugt Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307.
13. N. Bakkas, Y. Bouteiller, A. Loutellier, J. P. Perchard and S. Racine, J. Chem. Phys., 1993, 99, 3335–3342.
14. N. Bakkas, Y. Bouteiller, A. Loutellier, J. P. Perchard and S. Racine, Chem. Phys. Lett., 1995, 232, 90–98.
15. S. Coussan, P. Roubin and J. P. Perchard, J. Phys. Chem. A, 2004, 108, 7331–7338.
16. R. Wugt Larsen and M. A. Suhm, J. Chem. Phys., 2006, 125, 154314.
17. R. Wugt Larsen and M. A. Suhm, Phys. Chem. Chem. Phys., 2010, 12, 8152–8157.
18. F. Kollipost, J. Andersen, D. W. Mahler, J. Heimdal, M. Heger, M. A. Suhm and R. Wugt Larsen, J. Chem. Phys., 2014, 141, 174314.
19. J. Ceponkus, P. Uvdal and B. Nelander, J. Chem. Phys., 2008, 129(19), 194306.
20. J. Andersen, J. Heimdal, D. W. Mahler, B. Nelander and R. Wugt Larsen, J. Chem. Phys., 2014, 140, 091103.
21. Y.-P. Lee, Y.-J. Wu, R. M. Lees, L.-H. Xu and J. T. Hougen, Science, 2006, 311, 365–368.
22. J. P. Perchard, Chem. Phys., 2007, 332, 86–94.
23. J. P. Perchard, F. Romain and Y. Bouteiller, Chem. Phys., 2008, 343, 35–46.
24. J. Ceponkus and B. Nelander, J. Phys. Chem. A, 2004, 108(31), 6499–6502.
25. J. Ceponkus, G. Karlstrom and B. Nelander, J. Phys. Chem. A, 2005, 109, 7859–7864.
26. J. Ceponkus, P. Uvdal and B. Nelander, J. Chem. Phys., 2010, 133(7), 074301.
27. J. Ceponkus, P. Uvdal and B. Nelander, J. Phys. Chem. A, 2010, 114(25), 6829–6831.
28. J. Korppi-Tommola, Spectrochim. Acta, 1978, 34, 1077–1085.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision D.01, 2009.
30. R. Ahlrichs, M. Baer, M. Haeser, H. Horn and C. Koelmel, Chem. Phys. Lett., 1989, 162, 165–169.
31. F. Furche, R. Ahlrichs, C. Haettig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2014, 4, 91–100.
32. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
33. S. E. S. Grimme, J. Antony and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
34. C. Møller and M. Plesset, Phys. Rev., 1934, 46, 618.
35. K. Raghavachari and J. A. Pople, Int. J. Quantum Chem., 1978, 14, 91.
36. R. A. Kendall, J. T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
37. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968.
38. T. B. Adler and H.-J. Werner, J. Chem. Phys., 2011, 135, 144117.
39. B. J. Ransil, J. Chem. Phys., 1961, 34, 2109.
40. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
41. V. Barone, J. Chem. Phys., 2005, 122, 14108.
42. J. W. Moskowitz, Z. Bacic, A. Sarsa and K. E. Schmidt, J. Chem. Phys., 2001, 114, 10294.
43. A. Engdahl and B. Nelander, J. Chem. Phys., 1987, 86, 1819.
44. S. H. Bauer and R. M. Badger, J. Chem. Phys., 1937, 5, 837.

---

Footnote

† Electronic supplementary information (ESI) available: The calculated absolute electronic energies employing the B3LYP, B3LYP-D3, MP2, CCSD(T) and CCSD(T)-F12 methodologies with the aug-cc-pVTZ and aug-cc-pVQZ basis sets and the calculated harmonic vibrational zero-point energy corrections employing the MP2/aug-cc-pVTZ method. See DOI: 10.1039/c5cp04321b

---