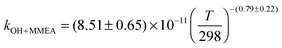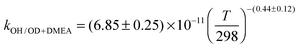Open Access Article
Open Access ArticleBranching ratios for the reactions of OH with ethanol amines used in carbon capture and the potential impact on carcinogen formation in the emission plume from a carbon capture plant†
L.
Onel
*a,
M. A.
Blitz
ab,
J.
Breen
a,
A. R.
Rickard
cd and
P. W.
Seakins
*ab
aSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK. E-mail: chmlo@leeds.ac.uk
bNational Centre for Atmospheric Science (NCAS), University of Leeds, Leeds, LS2 9JT, UK
cWolfson Atmospheric Chemistry Laboratories, Department of Chemistry, University of York, York, YO10 5DD, UK
dNational Centre for Atmospheric Science (NCAS), University of York, York, YO10 5DD, UK
First published on 2nd September 2015
Abstract
The OH initiated gas-phase chemistry of several amines that are potential candidates for use in post-combustion carbon capture (PCCC) plants have been studied by laser flash photolysis with OH monitored by laser induced fluorescence. The rate coefficients for the reaction of OH with N-methylethanolamine (MMEA) and N,N-dimethylethanolamine (DMEA) have been measured as a function of temperature (∼300–500 K): 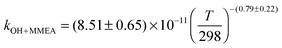 ,
, 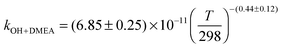 . The results for DMEA lie between previous values. This is the first kinetic study of the OH + MMEA reaction. At low pressures in the presence of oxygen, OH is recycled in the DMEA reaction as has been observed for other tertiary amines. Branching ratios for OH abstraction with MEA, DMEA and MMEA are dominated by abstraction from the αCH2 group. Abstraction from N–H is determined to be 0.38 ± 0.06 for MEA and 0.52 ± 0.06 for MMEA at 298 K. The impact of these studies has been assessed by using a modified chemical box model to calculate downwind concentrations of nitramines and nitrosamine formed in the photo-oxidation of MEA. Under clear sky conditions, the simulations suggest that current safe guidelines for nitramines may be significantly exceeded with predicted MEA emission rates.
. The results for DMEA lie between previous values. This is the first kinetic study of the OH + MMEA reaction. At low pressures in the presence of oxygen, OH is recycled in the DMEA reaction as has been observed for other tertiary amines. Branching ratios for OH abstraction with MEA, DMEA and MMEA are dominated by abstraction from the αCH2 group. Abstraction from N–H is determined to be 0.38 ± 0.06 for MEA and 0.52 ± 0.06 for MMEA at 298 K. The impact of these studies has been assessed by using a modified chemical box model to calculate downwind concentrations of nitramines and nitrosamine formed in the photo-oxidation of MEA. Under clear sky conditions, the simulations suggest that current safe guidelines for nitramines may be significantly exceeded with predicted MEA emission rates.
1. Introduction
One of the most feasible options for the mitigation of carbon dioxide emissions from fossil fuel power stations is post-combustion carbon capture (PCCC) using amines.1–4 Monoethanolamine (MEA) is considered as a benchmark solvent in terms of performance, and has been extensively investigated for use as a PCCC solvent although amines blends are most likely to be used in commercial applications.3,5–7 A range of amines are being investigated, including other primary amines such as 2-amino-2-methylpropan-1-ol, secondary amines such as piperazine (PZ) and diethanolamine, and tertiary amines such as N-methyldiethanolamine (MDEA) and triethanolamine.8 Other ethanolamines such as N-methylethanolamine (MMEA) and N,N-dimethylethanolamine (DMEA) have also been studied as PCCC potential solvents, and for our studies are useful model systems to help understand issues associated with the formation of toxic degradation products in the atmosphere.9,10 In addition, both MMEA and DMEA have been identified as potential products of the in situ degradation of MDEA during natural gas desulphurization and PCCC.8,11Given the substantial volumes of amines needed for efficient CO2 capture, large scale use of PCCC will potentially result in significant amine emissions to the atmosphere. A PCCC plant using MEA to remove ∼1 Mt CO2 per year is predicted to emit 40–160 tonnes of MEA per year.12 Previous studies of MEA, PZ and methylamines have shown that, once these amines are released into the atmosphere, their gas-phase processing, primarily initiated by OH radical reactions, will compete with heterogeneous uptake (lifetimes range from 15 min – 1 hour at peak OH concentrations, typically 5 × 106 molecule cm−3).13–18 The atmospheric removal of amines by reaction with Cl atoms in gas-phase has been found to be a minor sink for amines (lifetime of ∼20 days for typical peak Cl concentrations, around 2 × 103 atom cm−3).19,20 A major concern with PCCC is the impact of carcinogenic nitrosamines (R2N–NO) and nitramines (R2N–NO2), formed in the gas-phase processing of amines, on human health.19,21–24 The yield of these toxic products depends on the fraction of amine processed in the gas-phase (hence on the overall rate coefficient for the OH + amine reaction), and on the branching ratios in the initial OH abstraction reaction.
MEA has four potential sites for OH abstraction:
| HOCH2CH2NH2 + OH → HOCH2CHNH2 + H2O α abstraction | (R1a) |
| HOCH2CH2NH2 + OH → HOCH2CH2NH + H2O N–H abstraction | (R1b) |
| HOCH2CH2NH2 + OH → HOCHCH2NH2 + H2O β abstraction | (R1c) |
| HOCH2CH2NH2 + OH → OCH2CH2NH2 + H2O O–H abstraction | (R1d) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βC–H = 0.39
βC–H = 0.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.43,26 while calculations using the structure–activity relationships (SARs) predict that αC–H
0.43,26 while calculations using the structure–activity relationships (SARs) predict that αC–H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N–H = 0.45
N–H = 0.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.47 (Table S2, ESI†).19,27,28
0.47 (Table S2, ESI†).19,27,28
The N-centred radical generated by reaction (R1b) reacts with NO and NO2 to form 2-nitrosoaminoethanol, HOCH2CH2NHNO and 2-nitroaminoethanol, HOCH2CH2NHNO2 respectively (reactions (R2) and (R3)). Reactions (R2) and (R3) are potentially in competition with reaction (R4) forming 2-iminoethanol, HOCH2CHNH; little is known about (R4), but it is predicted to be slow (∼1 × 10−19 cm3 molecule−1 s−1).23,29
| HOCH2CH2NH + NO → HOCH2CH2NHNO | (R2) |
| HOCH2CH2NH + NO2 → HOCH2CH2NHNO2 | (R3) |
| HOCH2CH2NH + O2 → HOCH2CHNH + HO2 | (R4) |
The branching ratio for the abstraction at the N–H site, r1b, was reported to be <0.10 by Nielsen et al.,25 0.15 by Karl et al.23 and 0.17 by Xie et al.26 The SAR calculations lead to r1b = 0.47.19,27,28 Given the discrepancies between the reported branching ratios in reaction (R1), there is a clear need for the direct experimental determination of r1a − r1d.
The overall rate coefficient kOH+MMEA and the branching ratios in the reactions of OH with MMEA (HOCH2CH2NH(CH3)) and DMEA (HOCH2CH2N(CH3)2) have not previously been studied.
Here we report on the determination of the rate coefficients of OH + MMEA and DMEA reactions and their temperature dependence using laser flash photolysis (LFP) for OH generation and laser induced fluorescence (LIF) for time-resolved OH monitoring. We find OH regeneration in the OH + DMEA reaction in the presence of oxygen. The OH/OD signals obtained by 248 nm photolysis of (CH3)2N(CD2)2OH (d4-DMEA) in the presence of O2 are then used to determine the dominant H-abstraction site for DMEA.
On the millisecond scale of the OH + MEA/O2/NO and OH + MMEA/O2/NO LFP/LIF experiments, HO2 is generated through reaction (R5) and reacts further with NO (reaction (R6)) to give back OH.
| HOCH2CHNHR + O2 → HO2 + HOCH2CHNR | (R5) |
| HO2 + NO → OH + NO2 | (R6) |
| HOCH2CHNHR + O2 + M → HOCH2CH(O2)NHR + M | (R7) |
The impact of this work on the downwind formation of nitrosamines and nitramines following emission of MEA from a typical PCCC plant is assessed using an atmospheric chemistry box model. MEA and NOx emissions are based on the PCCC pilot plant located at Mongstad, on the west coast of Norway.24,34 The model also incorporates typical gas-phase chemistry of background compounds and MEA, heterogeneous uptake and reactions, and plume dispersion described by a time dependent Gaussian equation.
2. Experimental
This work has been carried out in a slow-flow pulsed LFP–LIF system that has been described in several previous publications.13,16,32 The flows of the OH/OD precursor, amine (MEA and DMEA: Sigma-Aldrich, ≥99.5%, MMEA and 2-methoxyethylamine (MeOEA): Alfa Aesar, 99%), O2 (if used, BOC 99.999%), nitrogen monoxide (if used, BOC >99.9%) and bath gas (N2, BOC oxygen free) were regulated through calibrated mass flow controllers, mixed in a manifold and introduced into a stainless steel reactor. The OH precursor was tertiary butylhydroperoxide (Sigma-Aldrich, 70% in water) and the OD precursor was deuterated acetone (acetone-d6) in the presence of O235 or (CH3)3COOD/N2 + D2O.32 The total pressure in the cell was controlled via a needle valve on the exhaust line and measured using a capacitance manometer. Temperatures were measured close to the observation region using a K-type thermocouple.DMEA was prepared as a diluted mixture in nitrogen in a glass bulb. Gaseous mixtures of MEA and MMEA could not be prepared because of the low vapour pressures of these amines at 298 K.36 Therefore, MEA and MMEA were introduced into the reactor from a glass bubbler by flowing N2 gas over liquid amine samples. The concentrations of MEA and MMEA were determined using the technique developed previously using in situ absorption measurements at 185 nm.16,18 Absorptions were converted into concentrations using the absorption cross sections of amines, σ185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm, MEA = (8.53 ± 0.24) × 10−18 cm2 molecule−1,16 and σ185
nm, MEA = (8.53 ± 0.24) × 10−18 cm2 molecule−1,16 and σ185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm, MMEA = (9.71 ± 0.37) × 10−18 cm2 molecule−1 (this work).
nm, MMEA = (9.71 ± 0.37) × 10−18 cm2 molecule−1 (this work).
Radicals were generated by excimer laser flash photolysis at 248 nm (Lambda Physik 210, typically 5–15 mJ cm−2, 5 Hz repetition rate). OH radicals were probed by off-resonance laser induced fluorescence at an excitation wavelength of ∼282 nm generated from a YAG pumped dye laser (Powerlite Precision II 8010, Sirah PRSC-DA-24, operating with Rhodamine 6G dye) introduced perpendicularly to the photolysis laser. OH fluorescence centred at 308 nm was observed with a photomultiplier tube (Thorn EMI model 9813 QKB) through an interference filter (Andover, 308 ± 10 nm). The time delay between the photolysis and the probe laser was varied using an in-house LabView program to build up an entire time-dependent OH profile. Depending on signal to noise ratios, 6–20 laser shots were averaged for each time point.
2.1. OH + amine reactions in the absence of NO
The reactions were carried out under pseudo-first-order conditions using amine concentrations in large excess over the initial OH concentration (∼1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Under these conditions, in the absence of NO, the fluorescence intensity, If, which is proportional to [OH], decayed according to the single exponential eqn (E1) (see the inset of Fig. 1 and Fig. S1 as examples, ESI†).
1). Under these conditions, in the absence of NO, the fluorescence intensity, If, which is proportional to [OH], decayed according to the single exponential eqn (E1) (see the inset of Fig. 1 and Fig. S1 as examples, ESI†).If(t) = If(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kOH′t) exp(−kOH′t) | (E1) |
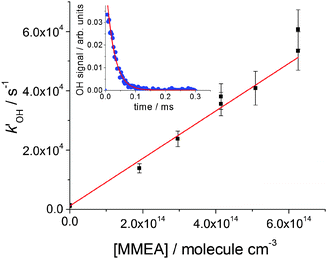 | ||
| Fig. 1 Bimolecular plot for MMEA, (8.01 ± 0.92) × 10−11 cm3 molecule−1 s−1, at 298 K and a total pressure of 17 Torr of N2. The error bars are at σ level. A typical OH fluorescence decay trace and fit to eqn (E1) is shown in the inset. | ||
For the reaction OH + DMEA in the presence of O2, the experiments were performed using sufficiently high O2 concentration (∼1016 molecule cm−3) to obtain single exponential OH decays. Examples of bimolecular plots for the DMEA + OH reaction in the absence/presence of O2 are shown in Fig. S1 (ESI†).
2.2. OH + MEA/MMEA and OD + deuterated MEA/MMEA reactions in the presence of O2/NO
Pseudo-first-order conditions were ensured by having amine (0.5–6.0 × 1014 molecule cm−3), O2 and NO concentrations in great excess over the initial radical concentration (0.5–2.0 × 1011 molecule cm−3). The O2 concentration was higher by a factor of ∼100 than the NO concentration and typically [NO] = 0.1–1.0 × 1015 molecule cm−3. Biexponential decays of OH were generated under these conditions due to reaction (R6) regenerating OH and were analysed as described previously.32In the reactions of OD with DOCH2CH2ND2 (d3-MEA) and DOCH2CH2ND(CH3) (d2-MMEA) (CH3)3COOD was used as OD precursor. The deuteration of amine and radical precursor were achieved by H/D exchange in the delivery tubing of the cell using D2O (99.9 atom% D), as described elsewhere.32
2.3. Synthesis of [1,1,2,2-2H4]-2-dimethylaminoethanol (d4-DMEA)
Ethyl 2-(dimethylamino)-2-oxoacetate (5.00 g, 34.4 mmol) was added slowly over 20 min to a stirred solution of LiAlD4 (3.47 g, 82.6 mmol) in dry THF (200 mL) at 0 °C. The mixture was heated under reflux for 6 h and the reaction cooled to 0 °C. The reaction was quenched by the drop-wise addition of saturated Na2SO4 solution until effervescence ceased and a white solid formed. After stirring for 30 min, the precipitate was collected by filtration and extracted into tetrahydrofuran (600 mL) by Soxhlet extraction for 18 hours to give a pale yellow solution. The solvent was removed in vacuo to give a yellow oil, which was purified by distillation (131–134 °C), to give d4-DMEA (1.98 g, 62%) as a colourless oil; 1H NMR (500 MHz, CDCl3): δ 2.04 (6H, s, CH3); 13C NMR (125 MHz, CDCl3): δ 45.2 (CH3), 57.9 (1JCD 21.7, CD2N), 60.0 (1JCD 20.2, CD2OH); m/z (EI+) 93.1.3. Results and discussion
3.1. Kinetics of OH + MMEA and DMEA
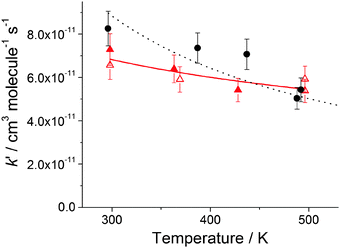
The averages of the measured room temperature rate coefficients, kOH+MMEA = (8.26 ± 0.82) × 10−11 cm3 molecule−1 s−1 and kOH+DMEA = (7.29 ± 0.72) × 10−11 cm3 molecule−1 s−1, are similar to kOH+MEA = (7.61 ± 0.76) × 10−11 cm3 molecule−1 s−1.16 The results are in good agreement with kOH/10−11 cm3 molecule−1 s−1 obtained using the SARs:19,27,28 8.45 for MMEA and 6.95 for DMEA (see Table S2, ESI†). This is the first determination of kOH+MMEA. The room temperature value for the OH + DMEA reaction is in between the measurement of Harris and Pitts, (4.7 ± 1.2) × 10−11 cm3 molecule−1 s−1,37 and the measurement of Anderson and Stephens, (10.3 ± 2.0) × 10−11 cm3 molecule−1 s−1.38 Both previous studies used the photolysis of water in the VUV (λ ≥ 105 nm37 and λ > 160 nm38) to generate OH, which was probed by resonance fluorescence using a microwave discharge lamp. The measurement of Anderson and Stephens almost overlaps with our measurement. The finding of OH recycling in the OH + DMEA/O2 system described in the next section offers a possible explanation for the lower rate coefficient found by Harris and Pitts if small amounts of oxygen were present in these experiments.Fig. 2 shows the temperature dependence of kOH+MMEA and kOH+DMEA. The negative temperature dependence observed for MMEA is similar to the temperature dependence found for MEA.16 The rate coefficient for OH + DMEA reaction decreases more slowly with temperature and at 500 K is about 85% relative to the value at 298 K. The result is consistent with the only other temperature dependent study for OH + DMEA reaction, which reports no evident temperature dependence over the range 234–364 K.38
In addition, the reaction between DMEA and OD was studied. As it can be observed in Fig. 2, the rate coefficients for OH + DMEA and OD + DMEA are similar, suggesting a minimal isotope effect. This result is in agreement with our previous finding that the rate coefficients for the reactions of methylamines with OH and OD are similar.13
3.2. Kinetics of OH + MEA, MMEA and DMEA reactions in the presence of oxygen
Fig. S1 (ESI†) shows examples of bimolecular plots for OH + DMEA reaction obtained using N2 (100%) and O2 (10%) + N2 (90%), respectively. It can be clearly seen that the bimolecular rate coefficient in the presence of excess O2, kO2, is lower than the bimolecular rate coefficient in the absence of O2, kN2, which is indicative of rapid OH regeneration. The OH yield, ΦOH, can be calculated from kN2 and kO2 (eqn (E2)), as shown in our previous work.13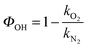 | (E2) |
Our observation of similar OH recycling for TMA (trimethylamine) + OH/O213 suggests that in the case of DMEA + OH/O2 the hydrogen abstraction occurs predominantly from a position next to the amine group of DMEA. Unlike TMA, not all the α-hydrogens are equivalent, however, the experiments using d4-DMEA/O2 described in ESI† show that the abstraction from the CH2 group next to the amine group largely dominates over the abstraction from CH3 groups. The OH recycling is the result of the reaction of O2 with HOCH2CHN(CH3)2 radical (reaction (R9) followed by reaction (R10)) generated by the initial abstraction (reaction (R8)).
| HOCH2CH2N(CH3)2 + OH → HOCH2CHN(CH3)2 + H2O | (R8) |
| HOCH2CHN(CH3)2 + O2 → HOCH2CH(O2)N(CH3)2* | (R9) |
| HOCH2CH(O2)N(CH3)2* → OH + CH3NCH2 + HOCH2CHO | (R10) |
DMEA photolysis at 248 nm in the presence of O2 generates the same radical as reaction (R8), HOCH2CHN(CH3)2, which explains the fast generation of OH observed in the absence of an OH precursor. By analogy with the recycling mechanistic scheme proposed for TMA/O2,13 we speculate that the by-products of OH regeneration route are N-methylimine, CH3NCH2, and glycolaldehyde, HOCH2CHO. The decomposition of the activated peroxy species, HOCH2CH(O2)N(CH3)2* (reaction (R10)) is in competition with collisional stabilization (reaction (R11)).
| HOCH2CH(O2)N(CH3)2* + M → HOCH2CH(O2)N(CH3)2 + M | (R11) |
 | (E3) |
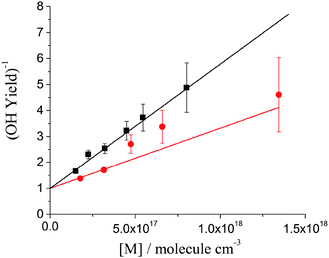 | ||
| Fig. 3 Stern–Volmer plots for OH yield from DMEA + OH/O2 system at 298 K, black squares and line and 363 K, red circles and line. The fits are constrained through unity intercept. | ||
Fig. 3 shows the Stern–Volmer plots, 1/ΦOHvs. [M], for the DMEA + OH/O2 system at 298 and 363 K. As expected, the Stern–Volmer gradient decreases with temperature showing that the activated peroxy radical, HOCH2CH(O2)N(CH3)2*, is generated with more energy at higher temperatures and hence dissociates in a greater fraction to eliminate OH.39 The Stern–Volmer plot at 298 K is similar to that obtained for OH + d4-DMEA/O2 at room temperature (Fig. S2, ESI†).
Table 1 shows the Stern–Volmer parameters and the calculated OH yields for DMEA at atmospheric pressure and 298 and 363 K. The results obtained for TMA at room temperature are also included for comparison.13 At both temperatures OH regeneration by DMEA/O2 is minor at atmospheric pressure. At 298 K and 1 atm ΦOH(DMEA) is about two times lower than ΦOH(TMA).13 The more efficient quenching of the OH + DMEA/O2 is to be expected given the larger size of the system.
| T (K) | Unconstrained intercept | Intercept constrained to unity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Intercepta | Gradienta/cm3 molecule−1/10−18 | OH yield at 760 Torra/% | Gradienta/cm3 molecule−1/10−18 | OH yield at 760 Torra/% | ||||||
| DMEA | TMA | DMEA | TMA | DMEA | TMA | DMEA | TMA | DMEA | TMA | |
a Obtained by weighting the linear fit by the error bars, 2σ, of reciprocal of OH yield, 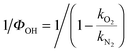 . Here σ are the standard errors calculated by the propagation of error equation using the statistical errors of kO2 and kN2. . Here σ are the standard errors calculated by the propagation of error equation using the statistical errors of kO2 and kN2.
|
||||||||||
| 298 | 0.88 ± 0.13 | 0.79 ± 0.02 | 5.31 ± 0.66 | 2.33 ± 0.11 | 0.77 ± 0.09 | 1.7 ± 0.1 | 4.79 ± 0.26 | 1.99 ± 0.07 | 0.84 ± 0.04 | 2.0 ± 0.1 |
The observation of OH regeneration in the OH + DMEA/O2 reaction, similar to that for the OH + TMA/O2 reaction,13 suggests that the direct OH recycling is a common feature of tertiary amines. No OH regeneration was observed in the OH + MEA/MMEA experiments with O2 over the temperature range 298–500 K. In addition, no OH signal was obtained following MEA and MMEA photolysis in the presence of oxygen. This result is in line with the lack of direct OH recycling in the case of other amines containing N–H bond(s), such as methylamine, DMA and PZ.13,18
3.3. OH + MEA/MMEA reactions in the presence of O2/NO
The observed generation of HO2 in the OH + MEA/MMEA reactions with O2 may occur through OH abstraction at either the α or β position, followed by abstraction at the N–H and O–H sites, respectively, by O2.23,32,40 Therefore, the HO2 yield for MEA, ΦHO2(MEA), is equal to the sum of the branching ratios for reactions (R1a) and (R1c), r1a + r1c. Experiments using the OH + 2-methoxyethylamine (MeOEA)/O2/NO system give a similar fraction of HO2 generation. In MeOEA, abstraction β to the N atom cannot lead to HO2 production, suggesting that r1a + r1c ≅ r1a (ESI†), in agreement with previous experimental studies reporting that the α position is the dominant abstraction site in the OH + MEA reaction.23,25 Therefore, ΦHO2(MEA) = r1a. The result is in disagreement with the theoretical calculations of Xie et al., which found that both C–H abstractions are significant for MEA.26Our result for MEA and the finding that the abstraction from DMEA by OH occurs predominantly from the α methylene group (vide supra) suggest that the abstraction from the α CH2 group dominates in the OH + MMEA reaction as well, hence ΦHO2(MMEA) ≅ rα(CH2).
The branching ratios, the HO2 yield for OH + MEA/MMEA and the DO2 yield for OD + d3-MEA/d2-MMEA were assigned by the method developed in previous work.32Table 2 shows the HO2/DO2 yields at room temperature and several total pressures. The values in Table 2 represent the means of a series of measurements where either [NO] or [O2] was varied (typically by one order of magnitude).
| p (Torr) | Φ HO2 = rαC–Ha | Φ DO2 = rαC–Ha | ||
|---|---|---|---|---|
| MEA | MMEA | d 3-MEA | d 2-MMEA | |
| a HO2/DO2 yields was determined as described previously32 and additionally presented in ESI. For MEA rαC–H = r1a. b Combination in quadrature of statistical errors at the 2σ level and an estimated 5% systematic error. | ||||
| 15 | — | — | 0.71 ± 0.05b | 0.57 ± 0.09b |
| 20 | 0.64 ± 0.04b | 0.48 ± 0.03b | ||
| 30 | — | — | 0.75 ± 0.07b | 0.54 ± 0.06b |
| 40 | — | 0.45 ± 0.06b | ||
| 60 | 0.61 ± 0.06b | 0.51 ± 0.04b | ||
| 150 | 0.62 ± 0.07b | — | ||
The slightly higher value of rαC–H for d3-MEA and d2-MMEA compared to rαC–H for MEA and MMEA suggests that the NH2 deuteration results in less abstraction from the amine group due to a small kinetic isotope effect (KIE) and is in agreement with the results for undeuterated and deuterated DMA and EA.32
Our result, r1a = 0.62 ± 0.06 for MEA, is in between of the value obtained by the EUPHORE studies of Karl et al., r1a = 0.8023 and the value predicted using the SARs (Table S2, ESI†), r1a = 0.45. Our work used a direct method for determination of branching ratios, while EUPHORE studies calculated the branching ratios by modelling the observed time profiles of end-products. The maximum branching ratio for N–H abstraction is rN–H = 1 − rαC–H and represents an upper limit for the carcinogenic compound production. For MMEA rN–H = 0.52 ± 0.06, which is 30% lower than the value obtained using the SARs, rN–H(MMEA) = 0.74, and is higher than the values found for the carbon capture amines MEA and PZ, rN–H(MEA) = 0.38 ± 0.06 and rN–H(PZ) = 0.09 ± 0.06.18 The result suggests that the PCCC emission of MMEA has a higher potential to form toxic compounds than the emission of MEA and PZ, although all secondary amines are of particular concern.
3.4. MESMER calculations for the pressure dependence of the HOCH2CHNH2 + O2 reaction
Reaction (R1a) generates an α carbon-centred radical, HOCH2CHNH2, known to react with O2 in the atmosphere. At low pressures the oxygen reaction occurs predominantly through O2 abstraction, producing HO2 and 2-iminoethanol (reaction (R5)), while at high pressures O2 addition, forming a collisionally stabilised peroxy species (reaction (R7)), dominates. EUPHORE chamber studies proposed that at atmospheric pressure the HOCH2CHNH2 + O2 reaction proceeds 100% through reaction (R7).23,25 In contrast with the EUPHORE studies, the theoretical calculations carried out by da Silva found that, at atmospheric pressure, the reaction largely bypasses the collisional stabilisation (R7) to proceed through reaction (R5).40In order to determine the branching ratios r5 and r7 at atmospheric pressure we performed master equation calculations using the MESMER package, details of which can be found elsewhere.32,33 MESMER solves the master equation and the subsequent eigenvalue–eigenvector analysis outputs the time profiles of species concentrations together with the phenomenological rate constants of the system.
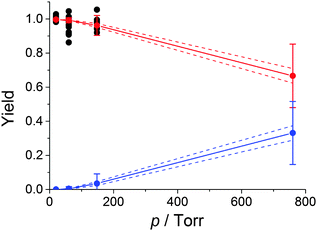
A negative pressure dependence of the HO2 yield and a corresponding positive dependence of the RO2 yield (ΓRO2) were obtained (Fig. 4), in agreement with previous studies of O2 reactions with RCHNHR radicals.32 At atmospheric pressure our result, ΓRO2 = 0.33 ± 0.18, is in agreement with the calculation of da Silva using the same value for ΔEdown as our work, 270 cm−1, ΓRO2 = 0.23, and disagrees with EUPHORE result, ΓRO2 = 1.23,25
4. Atmospheric modelling
4.1. Model description
Simulations were performed for the Mongstad PCCC plant emissions using two chemical box models. The first model contained typical gas-phase concentrations of volatile organic compounds (VOCs) observed at a European coastal background site – Mace Head, Ireland.41 The background concentrations of NO, NO2 and O3 were constrained to the hourly averaged diurnal cycles measured for the north-westerly wind sector at the Weybourne Atmospheric Observatory located on the Norfolk coast of England in September 2002 (Fig. S7–S9, ESI†).42,43 The Weybourne data are representative for summer conditions and have been chosen as their daily averages: [O3] = 39 ppbv, [NO] = 0.3 ppbv and [NO2] = 3 ppbv best describe the moderately polluted background conditions at Mongstad.34 The background model was based on detailed chemistry from the Master Chemical Mechanism (MCM v3.2), with the extracted model chemical mechanism containing 2255 species participating in 6920 gas-phase reactions.44,45 The model was run for four days re-initialising the background concentrations after each day, in order to generate model intermediate species in steady state. Fig. S10 (ESI†) shows the diurnal cycle of OH radical as an example. The concentrations at the end of four days were input in a second box model (the plume model), which contained both the background reactions and the OH initiated oxidation of the emitted MEA (vide infra), which was run for a further day. The time steps in the numerical simulations were 15 seconds in the clear day scenario and 1 second in the cloudy day scenario (vide infra). During these simulations the concentrations of NO2 and O3 were constrained to the one minute averages measured at Weybourne in September 2002 (ESI†).42,43 As the PCCC emits NO (133 tonnes per annum),34 the [NO] in the plume initially exceeds [NO] outside the plume and hence it is diluted to ambient values by the plume dispersion (vide infra).The amine chemistry scheme used in the plume model contained 20 species involved in 24 gas-phase reactions, reversible partitioning of MEA and the nitrosamine and nitramine products between the gas-phase and aqueous phase particles, and reactions of MEA, R2N–NO and R2N–NO2 with OH in the liquid phase (ESI†). Heterogeneous uptake was represented by a parameterization of a first-order loss process to the aerosol surface:46
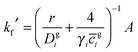 | (E4) |
![[c with combining overline]](https://www.rsc.org/images/entities/i_char_0063_0305.gif) gi is the mean molecular speed of i and A is the aerosol surface area per unit volume. More details on the parameters used in the calculation of kf′ are given in ESI.† The first-order rate coefficient describing the transfer from aerosol to gas-phase, kb′, was calculated using the Henry's law coefficient, Hi:34
gi is the mean molecular speed of i and A is the aerosol surface area per unit volume. More details on the parameters used in the calculation of kf′ are given in ESI.† The first-order rate coefficient describing the transfer from aerosol to gas-phase, kb′, was calculated using the Henry's law coefficient, Hi:34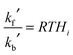 | (E5) |
 , where [i]aq is the molar concentration of compound i in the aqueous particles and pi is the partial pressure of gas i in the plume emitted by the PCCC plant.
, where [i]aq is the molar concentration of compound i in the aqueous particles and pi is the partial pressure of gas i in the plume emitted by the PCCC plant.
Two scenarios were studied: a clear day where r = 0.5 μm and atmospheric liquid water content, gw = 10−4 g m−3,47,48 and a cloudy day where r = 10 μm and gw = 0.5 g m−3.19,47 In the cloudy day scenario an attenuation of the actinic flux by a factor of 0.5 relative to the actinic flux under clear sky conditions was applied.49 Under the clear sky conditions emissions were set at 10:00, 14:00 and 24:00, while under the cloudy sky conditions the emissions were set at 10:00.
Emissions were set to 1.27 g s−1 of MEA (40 tonnes per year) and 4.22 g s−1 of NO34 in mid-July and T = 288.15 K. Species concentrations within the PCCC plume were modelled within a well-mixed box transported in downwind direction. Numerical simulations were started at 10 min after emission, when the plume was considered to have filled the boundary layer (set to 1000 m depth) by vertical mixing. Therefore, the box had a fixed height of 1000 m. The width of the plume, y(t), has been expanding via horizontal (cross-flow) mixing with the ambient air starting from y(0) = 3816 m at day time and from y(0) = 1658 m at night (ESI†):50,51
| y(t) = [y(0)2 + 8Kyt]1/2 | (E6) |
The emitted amine, NO and the targeted products nitrosamine (R2N–NO) and nitramine (R2N–NO2), were diluted with ambient air according to a Gaussian equation:
 | (E7) |
4.2. Results of the simulations
Fig. 7 and 8 show the concentrations of nitramine and nitrosamine in the PCCC plume vs. time and downwind distance from the emission point in the cloud free and cloudy sky scenarios, respectively. The time was converted into distance by using a wind speed of 3 m s−1. Fig. 7a shows the profile of nitramine concentration for emissions at 10:00 and 14:00. Emissions at 10:00 and 14:00 amplifies gas phase chemistry as at 10:00 NO and NO2 reach their maximum, while at 14:00 O3 peaks, maximising OH concentration (ESI†). The maximum of [R2N–NO2] is ∼30% higher for the 10:00 emission than in the 14:00 scenario and is three times above the current safe guideline level of 0.3 ng m−3 (annual average), as established by the Norwegian Institute for Public Health (NIPH).21 Owing to a lack of toxicity data on nitramines, the NIPH decided to use the cancer risk estimated for N-nitrosodimethylamine (DMA–NO) for the sum of the concentrations of nitramines and nitrosamines in air. The restriction of the air level of total nitrosamines and nitramines to 0.3 ng m−3 may be regarded as a conservative limit as DMA–NO was found to have ∼6 times higher cancer potency than N-nitrodimethylamine, DMA–NO2.21 However, recent studies reported that DMA–NO2 is less toxic than 2-nitroaminoethanol and emphasized the need for additional investigations of the cancer potency of nitramines.52
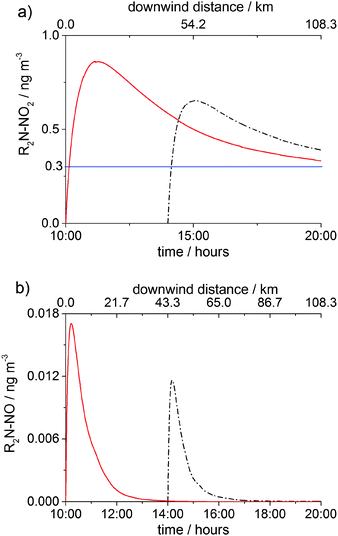 | ||
| Fig. 7 Gas-phase concentrations of (a) R2N–NO2 and (b) R2N–NO in the PCCC plume as a function of time (bottom axis) in the clear day scenario. Emission time: 10:00 (red solid line) and 14:00 (black dash dot line). The top axis shows the downwind distance from the source for the emission at 10:00. The horizontal blue line in (a) shows the safety limit of 0.3 ng m−3 for [R2N–NO2] + [R2N–NO] established by the NIPH.21 | ||
For both 10:00 and 14:00 cases the concentration of R2N–NO2 reaches its maximum after ca. 11 km (∼1 hour), where R2N–NO2 formation becomes less significant than R2N–NO2 loss (OH reaction and dispersion). [R2N–NO2] goes below the health limit after ∼130 km downwind of the emission. The concentration of nitrosamine peaks early (after ∼12 min or 2 km from source) at a value about 20 times lower than the safety limit (0.3 ng m−3), after which photolytic degradation and dispersion start to dominate.
Assuming that nitrosamine isomerises as soon as it is formed leading to an imine;23,25,30 for emission at 10:00 under clear sky conditions, the obtained concentration of R2N–NO2 is practically the same as [R2N–NO2] obtained considering that nitrosamine does not isomerise but photolyses to generate back R2N radical. Note that, assuming nitrosamine formation, the rate of nitramine formation is 10 times higher than the rate of nitrosamine formation.
Fig. 8 shows that, under cloudy conditions, the maximum value of [R2N–NO2] + [R2N–NO] is ∼75 times lower than the safety level. After a brief increase (over the first 12 s of the numerical simulation), both R2N–NO2 and R2N–NO are almost completely removed from the gas-phase within 90 s by heterogeneous uptake.
The rate coefficient of the reaction of MEA with NO3, kMEA+NO3, has not been determined experimentally. Karl et al. calculated kMEA+NO3 = 1.5 × 10−13 cm3 molecule−1 s−1 using a structure–property relationship,23 in good agreement with the SAR estimate kMEA+NO3 = 1.4 × 10−13 cm3 molecule−1 s−1 found by Carter.54 However, assuming that the linear correlation between the reactions of OH and NO3 with the same substrate19,53 is followed by amines, a value of 1 × 10−12 cm3 molecule−1 s−1 is obtained for kMEA+NO3. As shown below, using the higher estimates for the rate coefficient of NO3 with MEA leads to significant nitramine and nitrosamine formation. In addition, there are no data available for branching in the MEA + NO3 reaction. Here we consider the worst case scenario where 100% of the MEA + NO3 reaction proceeds to nitrogen-centred radical.
Fig. 9a and b show the time and the downwind distance dependences of [R2N–NO2] and [R2N–NO], respectively in three cases: the MEA + NO3 reaction is negligible and hence not considered in the model (the base case), kMEA+NO3 = 1.5 × 10−13 cm3 molecule−1 s−1 and kMEA+NO3 = 1 × 10−12 cm3 molecule−1 s−1. By using kMEA+NO3 = 1.5 × 10−13 cm3 molecule−1 s−1 an 8% increase over the base case in the total nitramine formed in the first 24 hours after emission is produced, while the value of 1 × 10−12 cm3 molecule−1 s−1 produces a 50% increase in the total nitramine formed in the first 24 hours. The change in the total nitrosamine generated over one day is more significant due to the lack of photolytic destruction at night: a 20% increase using 1.5 × 10−13 cm3 molecule−1 s−1 and a 100% increase using 1 × 10−12 cm3 molecule−1 s−1. In all three midnight scenarios the total amount of carcinogenic compounds formed over 24 hours is significant, several times larger than the one produced by the day time emissions (vide supra).
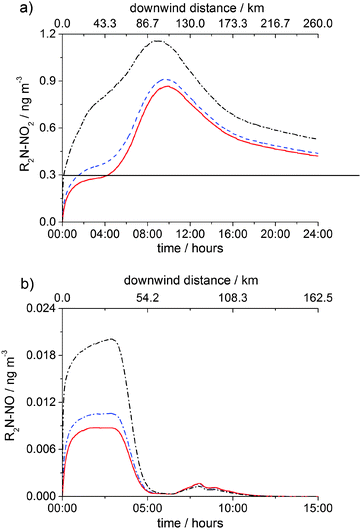 | ||
| Fig. 9 Gas-phase concentrations of (a) R2N–NO2 and (b) R2N–NO in the PCCC plume as a function of time (bottom axis) and downwind distance (top axis) from emission point under clear sky conditions and midnight emission scenario: no MEA + NO3 reaction (red solid line), kMEA+NO3 = 1.5 × 10−13 cm3 molecule−1 s−1 (blue dash line) and kMEA+NO3 = 1 × 10−12 cm3 molecule−1 s−1 (black dash dot line). The horizontal black line in (a) shows the safety limit of 0.3 ng m−3 for [R2N–NO2] + [R2N–NO] established by the NIPH.21 | ||
In all three midnight scenarios, dispersion is the main loss of MEA within the first five hours. As the dispersion rate decreases fast in time (eqn (E7)) and in the morning OH concentration starts to increase, between 05:00–10:00 the rate of the MEA + OH reaction increases, dominating over the dispersion rate (Fig. S13, ESI†) and leading to more nitramine formation. After reaching a maximum of about 3–4 times above the safety level at ∼10:00, nitramine is consumed by reaction with OH (Fig. 9a). Nitrosamine formed during the night is 15–30 times lower than the tolerance limit and photolyses rapidly upon sunrise (Fig. 9b). A small increase in R2N–NO occurs between 06:30–08:00 due to the increase in both OH and NO levels in the morning.
The previous investigations used a branching ratio for OH abstraction at NH2 group of 0.0834,55 while here we considered that the abstraction at N–H site to be ∼5 times greater (r1b = 0.38).31 Karl et al. identified that the branching ratios in the initial amine + OH reaction is one of the main uncertainties affecting their results.34 In line with these authors we have found that the sum of air concentrations of R2N–NO and R2N–NO2 increases linearly with the branching ratio for the OH abstraction at the N–H site. Koeijer et al.55 found that [R2N–NO2] + [R2N–NO] is 30–180 times lower than the defined safety level for emissions of MEA 10–60 times lower than in the present work and Karl et al.34
Our work treats the atmospheric chemistry in detail, while using a simple representation of the dispersion of amines and their toxic degradation products. The results show that, under cloud free conditions, for both day and night PCCC emissions, nitramine can reach levels significantly above the generally adopted tolerance limit of 0.3 ng m−3. The peak concentration for our scenario (horizontal wind speed of 3 m s−1) is at distance of ca. 10 km (∼1 hour) from the source for the daytime emissions and ca. 100 km (∼10 hours) from the emission point for the midnight scenario. For both day and night emissions the safety limit is still not met after 100 km away from the point of maximum health risk. The results obtained for the midnight scenario are more uncertain as kMEA+NO3 and the H atom abstraction branching ratios in the MEA + NO3 reaction are not well known. Results of numerical simulations using estimates of kMEA+NO3 are very sensitive to the value of this parameter. An order of magnitude increase of kMEA+NO3 generates an important increase in the total amount of gas-phase toxic products formed over 24 hours after emission, by 50% for nitramine and by 100% for nitrosamine. It is therefore important that more research is carried out in order to constrain the rate constants and H-abstraction branching ratios in the reaction of NO3 with ethanol amines.
5. Conclusions
The rate coefficients for the OH radical reactions with N-methylethanolamine (MMEA) and N,N-dimethylethanolamine (DMEA) have been determined as a function of temperature using the laser flash photolysis – laser induced fluorescence technique. The result for the OH + DMEA reaction is similar to previous results reported for a series of OH + amine reactions.13–15 This is the first kinetic study of the OH + MMEA reaction and shows that the room temperature rate coefficient kOH+MMEA and its temperature dependence are close to the results obtained for the OH + MEA reaction.16 The rate coefficients for both MMEA and DMEA at 298 K are in good agreement with the calculations using the structure–activity relationships (SARs).19,27,28Similarly to the OH + trimethylamine (TMA)/O2 reaction, the OH + DMEA/O2 reaction has been found to recycle OH. The result suggests that OH recycling through a chemical activated peroxy radical is a common signature for tertiary amines.
The dominant abstraction site in the OH reaction with monoethanolamine (MEA), MMEA and DMEA has been found to be the methylene group next to the amine group. The branching ratio for abstraction at the αC–H site of MEA is in between the value obtained by the EUPHORE atmospheric chamber study of Karl et al.23 and the value calculated using SARs (ESI†). Abstraction at the αC–H site generates a HOCH2CHNR radical, which reacts further with O2. Calculations using MESMER56 shows that at atmospheric pressure the HOCH2CHNR + O2 reaction occurs predominantly through the abstraction route, producing HO2 and 2-iminoethanol. The result is in agreement with previous findings for O2 reactions with RCHNHR (R = CH3 or H) radicals.19,32,57
The production of carcinogenic nitramines and nitrosamines depends on the branching ratio for abstraction at the N–H site, rN–H. As rN–H is higher for MMEA than for the standard postcombustion carbon capture (PCCC) solvent MEA, MMEA has a higher potential to form toxic compounds by atmospheric oxidation than MEA.
The health risks due to the formation of carcinogenic compounds following a typical MEA emission into the troposphere are assessed using a modified box model focusing on the detailed chemistry. Model plume emissions are based on the Mongstad PCCC pilot plant, located on the west coast of Norway. The results show that on clear, cloud free days concentrations of carcinogenic nitramine formed by the atmospheric photo-oxidation of the benchmark PCCC solvent MEA, exceed the recommended annual average value of 0.3 ng m−3. The studies also show that heterogeneous uptake significantly reduces atmospheric concentrations and so the annual average concentration will be very dependent on local meteorology.
Acknowledgements
This work was supported by grants from NERC (NE/1013474/1) and EPSRC (EP/J010871/1). The authors thank Prof. Chris Rayner for useful discussions on synthesis issues, Prof. Nielsen, University of Oslo, for on-going discussions and providing unpublished results from the Atmospheric Degradation of Amines (ADA) project supported by Masdar, Statoil, Vattenfall, Shell and the CLIMIT program under contracts 193438, 201604 and 208122, Dr Jenny Young for useful discussions regarding atmospheric modelling, Lucy Thonger for help with some of the experiments and Dr Zoe Fleming, NCAS, University of Leicester for supplying the Weybourne data.References
- M. E. Boot-Handford, J. C. Abanades, E. J. Anthony, M. J. Blunt, S. Brandani, N. Mac Dowell, J. R. Fernandez, M. C. Ferrari, R. Gross, J. P. Hallett, R. S. Haszeldine, P. Heptonstall, A. Lyngfelt, Z. Makuch, E. Mangano, R. T. J. Porter, M. Pourkashanian, G. T. Rochelle, N. Shah, J. G. Yao and P. S. Fennell, Energy Environ. Sci., 2014, 7, 130–189 CAS.
- L. Zhu, G. W. Schade and C. J. Nielsen, Environ. Sci. Technol., 2013, 47, 14306–14314 CrossRef CAS PubMed.
- E. F. da Silva and A. M. Booth, Environ. Sci. Technol., 2013, 47, 659–660 CrossRef PubMed.
- C. H. Yu, C. H. Huang and C. S. Tan, Aerosol Air Qual. Res., 2012, 12, 745–769 CAS.
- Y. Zhang, J. Xu, Y. Zhang, J. Zhang, Q. Li, H. Liu and M. Shang, Int. J. Greenhouse Gas Control, 2014, 20, 37–42 CrossRef CAS PubMed.
- E. S. Rubin, H. Mantripragada, A. Marks, P. Versteeg and J. Kitchin, Prog. Energy Combust. Sci., 2012, 38, 630–671 CrossRef CAS PubMed.
- G. T. Rochelle, Science, 2009, 325, 1652–1654 CrossRef CAS PubMed.
- C. Gouedard, D. Picq, F. Launay and P. L. Carrette, Int. J. Greenhouse Gas Control, 2012, 10, 244–270 CrossRef CAS PubMed.
- I. Eide-Haugmo, H. Lepaumier, A. Einbu, K. Vernstad, E. F. da Silva and H. F. Svendsen, Energy Procedia, 2011, 4, 1631–1636 CrossRef CAS PubMed.
- P. Bruder, K. G. Lauritsen, T. Mejdell and H. F. Svendsen, Chem. Eng. Sci., 2012, 75, 28–37 CrossRef CAS PubMed.
- A. Chakma and A. Meisen, J. Chromatogr., 1988, 457, 287–297 CrossRef CAS.
- K. Veltman, B. Singh and E. G. Hertwich, Environ. Sci. Technol., 2010, 44, 1496–1502 CrossRef CAS PubMed.
- L. Onel, L. Thonger, M. A. Blitz, P. W. Seakins, A. J. C. Bunkan, M. Solimannejad and C. J. Nielsen, J. Phys. Chem. A, 2013, 117, 10736–10745 CrossRef CAS PubMed.
- S. A. Carl and J. N. Crowley, J. Phys. Chem. A, 1998, 102, 8131–8141 CrossRef CAS.
- R. Atkinson, R. A. Perry and J. N. Pitts, Jr., J. Chem. Phys., 1978, 68, 1850–1853 CrossRef CAS PubMed.
- L. Onel, M. A. Blitz and P. W. Seakins, J. Phys. Chem. Lett., 2012, 3, 853–856 CrossRef CAS PubMed.
- N. Borduas, J. P. D. Abbatt and J. G. Murphy, Environ. Sci. Technol., 2013, 47, 6377–6383 CAS.
- L. Onel, M. Dryden, M. A. Blitz and P. W. Seakins, Environ. Sci. Technol. Lett., 2014, 1, 367–371 CrossRef CAS.
- C. J. Nielsen, H. Herrmann and C. Weller, Chem. Soc. Rev., 2012, 41, 6684–6704 RSC.
- J. M. Nicovich, S. Mazumder, P. L. Laine, P. H. Wine, Y. Tang, A. J. C. Bunkan and C. J. Nielsen, Phys. Chem. Chem. Phys., 2015, 17, 911–917 RSC.
- M. Låg, B. Lindeman, C. Instanes, G. Brunborg and P. Schwarze, Health Effects of Amines and Derivatives Associated with CO2 Capture, The Norwegian Institute of Public Health, 2011 Search PubMed.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS PubMed.
- M. Karl, C. Dye, N. Schmidbauer, A. Wisthaler, T. Mikoviny, B. D'Anna, M. Muller, E. Borras, E. Clemente, A. Munoz, R. Porras, M. Rodenas, M. Vazquez and T. Brauers, Atmos. Chem. Phys., 2012, 12, 1881–1901 CrossRef CAS.
- M. Karl, R. F. Wright, T. F. Berglen and B. Denby, Int. J. Greenhouse Gas Control, 2011, 5, 439–447 CrossRef CAS PubMed.
- C. J. Nielsen, B. D'Anna, C. Dye, M. Graus, M. Karl, S. King, M. M. Maguto, M. Mueller, N. Schmidbauer, Y. Stenstrom, A. Wisthaler and S. Pedersen, Energy Procedia, 2011, 4, 2245–2252 CrossRef CAS PubMed.
- H.-B. Xie, C. Li, N. He, C. Wang, S. Zhang and J. Chen, Environ. Sci. Technol., 2014, 48, 1700–1706 CrossRef CAS PubMed.
- P. J. Ziemann and R. Atkinson, Chem. Soc. Rev., 2012, 41, 6582–6605 RSC.
- E. S. C. Kwok and R. Atkinson, Atmos. Environ., 1995, 29, 1685–1695 CrossRef CAS.
- Y. Z. Tang and C. J. Nielsen, Atmos. Environ., 2012, 55, 185–189 CrossRef CAS PubMed.
- Y. Tang, M. Hanrath and C. J. Nielsen, Phys. Chem. Chem. Phys., 2012, 14, 16365–16370 RSC.
- G. da Silva, Environ. Sci. Technol., 2013, 47, 7766–7772 CrossRef CAS PubMed.
- L. Onel, M. Blitz, M. Dryden, L. Thonger and P. Seakins, Environ. Sci. Technol., 2014, 48, 9935–9942 CrossRef CAS PubMed.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- M. Karl, N. Castell, D. Simpson, S. Solberg, J. Starrfelt, T. Svendby, S. E. Walker and R. F. Wright, Atmos. Chem. Phys., 2014, 14, 8533–8557 CAS.
- S. A. Carr, M. T. Baeza-Romero, M. A. Blitz, B. J. S. Price and P. W. Seakins, Int. J. Chem. Kinet., 2008, 40, 504–514 CrossRef CAS PubMed.
- S. Kapteina, K. Slowik, S. P. Verevkin and A. Heintz, J. Chem. Eng. Data, 2005, 50, 398–402 CrossRef CAS.
- G. W. Harris and J. N. Pitts, Environ. Sci. Technol., 1983, 17, 50–51 CrossRef CAS PubMed.
- L. G. Anderson and R. D. Stephens, Int. J. Chem. Kinet., 1988, 20, 103–110 CrossRef CAS PubMed.
- S. A. Carr, D. R. Glowacki, C.-H. Liang, M. T. Baeza-Romero, M. A. Blitz, M. J. Pilling and P. W. Seakins, J. Phys. Chem. A, 2011, 115, 1069–1085 CrossRef CAS PubMed.
- G. da Silva, J. Phys. Chem. A, 2012, 116, 10980–10986 CrossRef CAS PubMed.
- A. C. Lewis, K. D. Bartle, D. E. Heard, J. B. McQuaid, M. J. Pilling and P. W. Seakins, J. Chem. Soc., Faraday Trans., 1997, 93, 2921–2927 RSC.
- Z.L. Fleming, Personal communication of diurnal cycles of O3, NO and NO2measured at Weybourne between 17 and 29 September 2002.
- Z. L. Fleming, P. S. Monks, A. R. Rickard, B. J. Bandy, N. Brough, T. J. Green, C. E. Reeves and S. A. Penkett, Atmos. Chem. Phys., 2006, 6, 5415–5433 CrossRef CAS.
- http://mcm.leeds.ac.uk/MCM .
- S. M. Saunders, M. E. Jenkin, R. G. Derwent and M. J. Pilling, Atmos. Chem. Phys., 2003, 3, 161–180 CrossRef CAS.
- S. E. Schwartz, in Chemistry of Multiphase Atmospheric Systems, ed. W. Jaeschke, Springer Berlin Heidelberg, 1986, vol. 6, pp. 415–471 Search PubMed.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 561–577 CrossRef CAS PubMed.
- Y. X. Bian, C. S. Zhao, N. Ma, J. Chen and W. Y. Xu, Atmos. Chem. Phys., 2014, 14, 6417–6426 CrossRef CAS.
- P. S. Monks, A. R. Rickard, S. L. Hall and N. A. D. Richards, J. Geophys. Res.: Atmos., 2004, 109, D17206 CrossRef.
- S. A. Mason, J. Trentmann, T. Winterrath, R. J. Yokelson, T. J. Christian, L. J. Carlson, T. R. Warner, L. C. Wolfe and M. O. Andreae, J. Atmos. Chem., 2006, 55, 273–297 CrossRef CAS.
- D. L. Mauzerall, J. A. Logan, D. J. Jacob, B. E. Anderson, D. R. Blake, J. D. Bradshaw, B. Heikes, G. W. Sachse, H. Singh and B. Talbot, J. Geophys. Res.: Atmos., 1998, 103, 8401–8423 CrossRef CAS.
- L. M. Fjellsbo, S. Verstraelen, A. Kazimirova, A. R. Van Rompay, Z. Magdolenova and M. Dusinska, Environ. Res., 2014, 134, 39–45 CrossRef PubMed.
- R. P. Wayne, I. Barnes, P. Biggs, J. P. Burrows, C. E. Canosamas, J. Hjorth, G. Lebras, G. K. Moortgat, D. Perner, G. Poulet, G. Restelli and H. Sidebottom, Atmos. Environ., Part A, 1991, 25, 1–203 CrossRef.
- W. P. L. Carter, Reactivity Estimates for Selected Consumer Product Compounds Contract No. 06-408, Center for Environmental Research and Technology, College of Engineering, University of California, Riverside, California, USA, 2008.
- G. de Koeijer, V. R. Talstad, S. Nepstad, D. Tønnessen, O. Falk-Pedersen, Y. Maree and C. Nielsen, Int. J. Greenhouse Gas Control, 2013, 18, 200–207 CrossRef CAS PubMed.
- http://sourceforge.net/projects/mesmer/ .
- M. M. Maguta, M. Aursnes, A. J. C. Bunkan, K. Edelen, T. Mikoviny, C. J. Nielsen, Y. Stenstrom, Y. Tang and A. Wisthaler, J. Phys. Chem. A, 2014, 118, 3450–3462 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details on OH + DMEA reaction in the absence/presence of O2, OH/OD + d4-DMEA reaction with O2, OH + MEA/MMEA/MeOEA reactions in the presence of O2/NO, SAR calculations, MESMER calculations and atmospheric modelling. See DOI: 10.1039/c5cp04083c |
| This journal is © the Owner Societies 2015 |