On the microscopic dynamics of the ‘Einstein solids’ AlV₂Al₂₀ and GaV₂Al₂₀, and of YV₂Al₂₀: a benchmark system for ‘rattling’ excitations

Abstract

The inelastic response of AV₂Al₂₀ (with A = Al, Ga and Y) was probed by high-resolution inelastic neutron scattering experiments and density functional theory (DFT) based lattice dynamics calculations (LDC). Features characteristic of the dynamics of Al, Ga and Y are established experimentally in the low-energy range of the compounds. In the stereotype ‘Einstein-solid’ compound AlV₂Al₂₀ we identify a unique spectral density extending up to 10 meV at 1.6 K. Its dominating feature is a peak centred at 2 meV at the base temperature. A very similar spectral distribution is established in GaV₂Al₂₀ albeit the strong peak is located at 1 meV at 1.6 K. In YV₂Al₂₀ signals characteristic of Y dynamics are located above 8 meV. The spectral distributions are reproduced by the DFT-based LDC and identified as a set of phonons. The response to temperature changes between 1.6 and ∼300 K is studied experimentally and the exceptionally vivid renormalization of the A characteristic modes in AlV₂Al₂₀ and GaV₂Al₂₀ is quantified by following the energy of the strong peak. At about 300 K it is shifted to higher energies by 300% for A = Al and 450% for A = Ga. The dynamics of A = Y in YV₂Al₂₀ show a minor temperature effect. This holds in general for modes located above 10 meV in any of the compounds. They are associated with vibrations of the V₂Al₂₀ matrix. Atomic potentials derived through DFT calculations indicate the propensity of A = Al and Ga to a strong positive energy shift upon temperature increase by a high quartic component. The effect of the strong phonon renormalization on thermodynamic observables is computed on grounds of the LDC results. It is shown that through the hybridization of A = Al and Ga with the V₂Al₂₀ dynamics the matrix vibrations in the low-energy range follow this renormalization.

---

I. Introduction

The ternary compound Al_xV₂Al₂₀ (space group Fd3̄m (227)^1–4) attracted attention by the conjecture of a low-energy peak at about 2 meV in its vibrational response.^5,6 This conjecture was based on thermodynamic experiments and the supposed peak was associated with a localized vibration of the excess Al_x in the V₂Al₂₀ matrix. Al_xV₂Al₂₀ was thus dubbed ‘Einstein solid’. Early microscopic experiments confirmed the presence of the peak, indicating a potential peak-shift to higher energies upon heating and suggesting the presence of another additional signal at the base temperature.⁷ These observations opened up a wide field for conjectures upon the true microscopic origin of the recorded features. For example, off-centre positions of Al at the 8a site were discussed provoking a complex dynamics of isolated harmonic oscillator excitations and rotator-like modes.^6,7

In recent years, the physical properties of Al_xV₂Al₂₀ were significantly refined in diffraction and thermodynamic experiments by Safarik et al.,⁸ Onosaka et al.⁹ and Hiroi et al.¹⁰ In particular Safarik and coworkers showed that anharmonicity driven by a sextic term in the potential of the Al occupying the 8a crystallographic site is required to explain the thermal displacement parameters of Al(8a), the heat capacity and thermal Grüneisen parameters and other macroscopic properties of Al_xV₂Al₂₀. A sextic term is supportive of the blue shift of modes upon heating deduced by Caplin and coworkers. Notably, the study elaborated as well a potential anharmonicity of the Al occupying the 16c site of the V₂Al₂₀ matrix. The results question the aforementioned microscopic scenario.

Onosaka et al. and Hiroi et al. expanded the study onto compounds with different occupation ratios x of the 8a site as well as to gallium and mixtures of Al and Ga as occupants. From heat capacity measurements they confirmed a very low characteristic energy of 0.6–0.7 meV of Ga(8a) and showed that the energies of Al(8a) and Ga(8a) vary weakly with the occupation ratio x as conjectured by Caplin et al. in ref. 7.

Very recently, some of us have started to probe the microscopic properties of A_xV₂Al₂₀ focusing particularly on the dynamics of different occupants A.¹¹ Our first approach was dedicated to establish the condition, i.e. to identify specific atoms A and their properties, at which the pronounced anharmonicity as reported by Caplin et al. and Safarik et al. is induced. We have followed this goal experimentally with specimens containing A = Sc, La and Ce which are supposed to have a fully occupied (x = 1) 8a site. The theoretical approximation of the experimental data is based on a model-free approach by density functional theory (DFT) and lattice dynamics calculations (LDC) of AV₂Al₂₀. Thus, intrinsic to our approach is the concept of ground-state properties being at the origin of the microscopic dynamics of the studied compounds. Having followed these two routes we showed that distinguished positive anharmonicity, i.e. a blue shift of vibrational modes upon heating dω/dT > 0, is exhibited by A = Sc in contrast to La and Ce containing AV₂Al₂₀ compounds. The ground state dynamics was characterized by normal modes with the DFT potentials of Sc being ruled by a strong quartic contribution in addition to the squared harmonic term.

In the present paper we expand our study and challenge the properties of the ‘Einstein solids’ AlV₂Al₂₀ and GaV₂Al₂₀. This work was carried out having followed closely the procedure described in detail in ref. 11. For this reason, we set aside the detailed description of the experimental and computational procedures and highlight, however, modifications applied to them. YV₂Al₂₀ was employed as a reference complementing results on the series of A containing compound.

II. Experiments and density functional calculations

A. Sample preparation and characterization

Polycrystalline samples of AlV₂Al₂₀, GaV₂Al₂₀ and YV₂Al₂₀ were prepared by a solid-state reaction.⁹ Uniform specimens were obtained by melting stoichiometric mixtures at a high temperature in an arc-melt furnace. The mixtures of AlV₂Al₂₀, GaV₂Al₂₀ and YV₂Al₂₀ were annealed in evacuated quartz ampoules at 650, 640 and 700 °C for 80 h, respectively.

The powdered specimens of AlV₂Al₂₀ and GaV₂Al₂₀ were characterized by neutron diffraction experiments carried out at the highest-resolution diffractometer D2b@ILL located at the European neutron source Institut Laue Langevin (ILL) in Grenoble, France. Both compounds were tested for their temperature response between about 5 and 300 K. The software package FullProf was engaged for data analysis.¹² We highlight the quality of the specimens and data in Fig. 1 by showing a diffractogram of AlV₂Al₂₀ recorded at 5 K. However, as we focus here on a limited set of inelastic data the diffraction results and their thorough interpretation will be reported in detail elsewhere.

Fig. 1 Diffraction signal of AlV₂Al₂₀ at 5 K measured using a highest-resolution diffractometer D2b@ILL with λ = 1.05 Å. Linestyle and color code are defined in the figure. Asterisks indicate regions contaminated by peaks from the low-temperature sample environment and excluded from the Rietveld refinement. Tick marks indicate Bragg reflections of the compound.

Within the Rietveld analysis all recorded peaks could be assigned by the symmetry and structural properties of the compounds. Having applied free fits of the occupation numbers x we have derived values of about 0.9 and 0.5 for the Al(8a) and Ga(8a) sites in the respective compounds. These numbers are varied by 3% for different T. Specifically, at T ≈ 5 K we obtain the following isotropic thermal displacement and occupation parameters for the compounds, U_iso(T) = 0.014(1) Ų and x = 0.93(2) for Al(8a) in AlV₂Al₂₀ (R_Bragg = 4.68, R_wp = 11.7) and U_iso(T) = 0.019(1) Ų and x = 0.52(1) for Ga(8a) in GaV₂Al₂₀ (R_Bragg = 5.59, R_wp = 11.0). Note that x = 0.5 for Ga(8a) in GaV₂Al₂₀ was obtained here without accounting for mixed occupations of the 8a site by Ga and Al such as discussed and elaborated in the literature.^7,10 The occupation number for Al(8a) approximates the values reported by Kontio and Stevens in ref. 13 and noted by Safarik et al. in ref. 8. For clarity reasons we refer to the compounds by their nominal stoichiometry as AlV₂Al₂₀ and GaV₂Al₂₀.

B. Inelastic neutron scattering experiments

The thermal neutron time-of-flight (ToF) spectrometer IN4@ILL was utilized for an extended coverage of the energy-momentum phase space and for monitoring the inelastic response down to the base temperature of 1.6 K at the Stokes line. The cold neutron ToF instrument IN6@ILL was exploited for its improved energy resolution to monitor the signal at high energies at the anti-Stokes line. Owing to the characteristic energies of the low-energy modes they could have been traced down to 20 K in AlV₂Al₂₀ and 10 K in GaV₂Al₂₀ at the anti-Stokes line. All measurements were carried out in cryostats in a helium atmosphere with a pressure of about 10 millibars at 100 K.

The response of AlV₂Al₂₀ and GaV₂Al₂₀ was sampled with λ_i = 1.8, 2.2, 2.6, 3.2 Å at IN4@ILL and 4.14, and 5.12 Å at IN6@ILL. See Fig. 7 of ref. 11 for sketches of the phase space coverage. To follow the anharmonicity in these compounds the characteristic T-raster corresponded approximately to 1.6, 10, 20, 50, 100, 150, 200, and 300 K. The exact T are presented here only with data reporting the T dependence of the characteristic frequencies of Al(8a) and Ga(8a) hereafter. Note that not all T were applied to each specimen at the different wavelengths. The experimental setups were optimized and adjusted to zoom for details in the inelastic responses. Thus, we have exploited the time-focusing option for best resolution at IN6@ILL only for the highest T = 300 K. The focus was set onto 7 meV. This cumbersome approach was made necessary as the contrast of the low-energy modes within the total signal is low and detailed features difficult to establish. The inelastic scattering power of the compounds' constituents is listed in Table 1.¹⁴ YV₂Al₂₀ was exclusively measured with 4.14 Å at IN6@ILL at T = 1.5, 50, 100, 200, and 300 K.

Table 1 Nuclear coherent σ_coh, incoherent σ_inc and total σ_tot neutron scattering cross sections in barns, masses in a.m.u., and total scattering power σ_tot/a.m.u. of the compounds' constituents

Element	σ coh	σ inc	σ tot	a.m.u.	σ tot/a.m.u. [×10^2]
Al	1.495	0.008	1.503	26.982	5.570
V	0.018	5.08	5.1	50.942	10.011
Ga	6.675	0.16	6.83	69.723	9.800
Y	7.55	0.15	7.7	88.906	8.661

---

Standard corrections were applied to the data.¹¹ The dynamic structure factor S(Q, ω, T) and the generalized density of states G(ω, T) were derived from the recorded signal through established mathematical relations.^15–18

C. Ab initio lattice dynamics calculation

The major part of the computation process comprising the density funtional theory (DFT) and lattice dynamics calculations (LDC) was carried out in full accordance with the procedure reported in ref. 11. However, due to the properties of the low-energy vibrational modes in AlV₂Al₂₀ and GaV₂Al₂₀ a denser sampling of the phase space is required for a sufficient accuracy in the range of acoustic phonons and properties determined and dominated by them, such as the velocity of sound, low-T specific heat C_V(T) and thermal displacement parameters U_iso(T). Thus, the phonon densities of states Z(ω) were computed on a mesh of 10⁷k points.

Powder averaged phonon form factors were evaluated for AlV₂Al₂₀. A mesh of 2.5 × 10⁵ randomly generated Q⃑-points with a maximum modulus of 5 Å⁻¹ was applied. For comparison the same procedure was applied to the lattice dynamics calculations of the binary V₂Al₂₀ compound. The Debye–Waller factors were taken into account with T = 1.0 K, only.

III. Results

A. Equation of state and structural properties

The equation of state (EoS) was evaluated from a series of DFT energy minimization runs for volume cells varied by ±5%. Bulk moduli B₀, their pressure derivatives B′ and equilibrium volumes V₀ were derived from a match of the Birch–Murnaghan equation to the total energy data.¹⁹ Corresponding properties are reported in Table 2. B₀ matches very well with experimental data at low T.⁸

Table 2 Physical properties from computer calculations and neutron diffraction experiments. Lattice parameters are derived from powder neutron diffraction at 5 K a′, by matching the volume dependent DFT calculations a₀ with the Birch–Murnaghan EoS, and from DFT optimized structures a. Bulk modulus B₀ and its pressure derivative B′ are obtained by matching the EoS. Compounds are characterized by the occupants of the 8a site

	Al	Ga	Y
a′ [Å]	14.4547(1)	14.4648(1)
a 0 [Å]	14.4603(3)	14.4852(3)	14.5013(2)
B 0 [GPa]	87.83(4)	86.94(5)	90.42(4)
B′ [GPa]	4.29(2)	4.35(2)	4.30(1)
a [Å]	14.4360	14.4622	14.4786

---

B. Lattice dynamics calculations

The computed Γ-point frequencies are listed in Table 3. Phonon dispersions ħω(Q) along high-symmetry directions are plotted in Fig. 2 with the focus on modes in the low-energy range. The total Z(ω) and partial Z_n(ω) phonon densities of states are reported in Fig. 3.

Table 3 Frequencies ω⁰_i in TeraHertz of the vibrational eigenstates at the Γ-point obtained for AV₂Al₂₀ (A = Al, Ga, and Y). They are grouped according to the symmetry of the eigenstates. Their multiplicity and their activity with respect to infrared (I) and Raman (R) scattering are indicated with their symmetries

	AlV2Al20	GaV2Al20	YV2Al20
T1u(I)	0.0	0.0	0.0
T1u(I)	0.848	0.522	2.752
T1u(I)	4.031	3.893	3.671
T1u(I)	4.239	4.142	5.056
T1u(I)	4.885	4.906	6.057
T1u(I)	5.937	5.834	6.598
T1u(I)	6.703	6.642	7.090
T1u(I)	7.424	7.419	7.336
T1u(I)	7.573	7.535	7.602
T1u(I)	8.475	8.409	8.445
T1u(I)	9.522	9.454	9.493
T1u(I)	11.174	11.016	10.550
T1u(I)	12.578	12.496	12.679
T2g(R)	1.719	1.111	2.943
T2g(R)	4.330	4.351	4.834
T2g(R)	5.273	5.283	5.570
T2g(R)	6.224	6.188	6.528
T2g(R)	7.106	7.026	7.400
T2g(R)	8.872	8.818	8.863
T2g(R)	9.168	9.081	9.156
T2g(R)	10.076	9.931	9.707
T2g(R)	12.047	11.949	11.940
Eg(R)	3.986	4.008	4.404
Eg(R)	6.001	5.957	5.999
Eg(R)	7.928	7.856	8.299
Eg(R)	10.238	10.119	9.659
A1g(R)	7.388	7.373	7.705
A1g(R)	9.281	9.152	9.006
A1g(R)	11.695	11.514	10.923
T2u	2.551	2.531	2.730
T2u	3.806	3.661	3.477
T2u	4.472	4.484	4.572
T2u	5.692	5.669	5.650
T2u	6.062	6.118	6.339
T2u	7.096	7.097	7.248
T2u	8.273	8.208	8.125
T2u	11.383	11.316	11.423
T1g	3.370	3.330	3.602
T1g	4.666	4.692	4.788
T1g	4.767	4.787	5.053
T1g	6.656	6.671	7.013
T1g	7.204	7.131	7.316
T1g	10.477	10.429	10.512
Eu	3.723	3.553	3.270
Eu	4.315	4.317	4.501
Eu	5.702	5.546	5.757
Eu	7.470	7.469	6.876
Eu	8.225	8.210	8.790
Eu	9.768	9.624	9.163
A2u	3.978	4.050	6.600
A2u	7.334	7.264	7.643
A2u	8.699	8.584	8.033
A2u	9.336	9.234	8.893
A2u	11.800	11.627	11.220
A2g	2.739	2.733	2.704
A1u	4.899	4.938	5.246

---

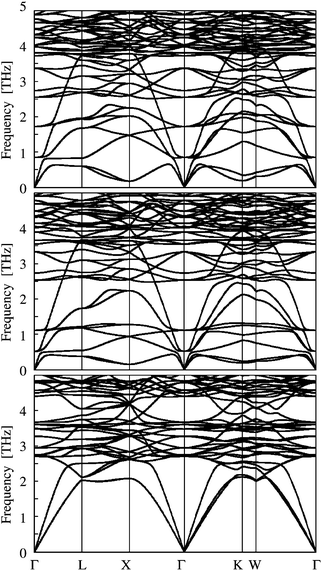Fig. 2 Phonon dispersion relations computed for the compounds AlV₂Al₂₀ (top figure), and GaV₂Al₂₀ (middle figure) and YV₂Al₂₀ (bottom figure).

Fig. 3 Total and partial densities of states of AV₂Al₂₀ with A = Al, Ga and Y. Linestyle and color scheme are indicated in the figures. Gray and black shaded areas highlight the total Z(ω) and the partial contribution Z_A(8a)(ω), respectively.

The vibrational eigenmodes of YV₂Al₂₀ show a dispersive behaviour in the energy range of up to about 8 meV (2 THz) in coincidence with the dynamics of LaV₂Al₂₀ and CeV₂Al₂₀.¹¹ The occupation of the 8a site by Al and Ga results in a substantial disruption of these dispersive acoustic phonons. Thereby, the formed Γ-point eigenstates of lowest energy are infrared [T_1u(I)] and Raman [T_2g(R)] active in contrast to the optically silent states (A_2g and T_2u) of the Y-containing compound. However, the dispersivity of the corresponding low-energy optic phonons in AlV₂Al₂₀ and GaV₂Al₂₀ conditions their energies to take on lower values in an extensive range of the phase-space as evidenced in Fig. 2. The higher mass of Ga sets the trend to lower eigenenergies in GaV₂Al₂₀ than Al in AlV₂Al₂₀.

These features are manifested in the phonon densities of states in Fig. 3. A stronger concentration of the partial contribution Z_Ga(8a)(ω) towards lower energies than for Z_Al(8a)(ω) is observed. The overall spectral shapes are very similar however in GaV₂Al₂₀ the prominent signal appears compressed to below 6 meV whereas in AlV₂Al₂₀ it expands up to about 9 meV. These trends are as well quantified by their mean energies (Ē_n) and variances (Ẽ_n) of the A(8a) partial densities in Table 4. The dispersivity of the formed low-energy modes is perceivable by the distinguished texture in Z_A(8a)(ω) featured by a number of peaks. For better visibility the low energy range is highlighted in Fig. 4. In both compounds the vibrations of A(8a) are most strongly coupled to the Al(16c) dynamics. The coupling is strongest for the mode bands at lowest energy. The mean energies of these bands are 1.7 and 1.2 meV in AlV₂Al₂₀ and GaV₂Al₂₀, respectively. The overall Ē_n and Ẽ_n of the Al(16c) are listed in Table 4.

Table 4 Mean energy Ē_n and the variance Ẽ_n of the partial spectral densities Z_n(ω) of Al(16c) and A(8a), and averaged sound velocities v_av and Debye temperaturesv Θ_D computed from Z(ω). Compounds are characterized by the occupants of the 8a site

	Al	Ga	Y
Ē Al(16c) [meV]	16.6	16.3	18.7
Ẽ Al(16c) [meV^2]	21.9	16.5	48.5
Ē A(8a) [meV]	7.3	4.2	12.8
Ẽ A(8a) [meV^2]	35.7	18.4	32.1
v av [m s^−1]	4500	4440	4660
Θ D [K]	528	520	545

---

Fig. 4 Low-energy range of the total and selected partial phonon densities of states of AlV₂Al₂₀ (a) and GaV₂Al₂₀ (b) compared with the signal of the binary compound VAl₁₀. The partial contributions of Al(8a), Ga(8a) and Al(16c) are highlighted. Horizontal arrows indicate two energy regions which have been engaged in a T-dependent renormalization of the partial densities. See the text for details.

The vibrational response of YV₂Al₂₀ is strongly reminiscent of the phonon dynamics of LaV₂Al₂₀ and CeV₂Al₂₀ established in ref. 11. A strong coupling of Y to the Al(16c) site leads to a split of Z_Al(16c)(ω) into two bands centred approximately at 14 and 28 meV. In YV₂Al₂₀ both partial densities are characterized by the highest mean energy and widest spread of eigenstates among the compounds studied here, see Table 4. A pronounced hybridization of the Al(16c) and Al(96g) dynamics within the first band leads to the formation of a strong peak at 14.5 meV and a characteristic mode gap between 15.5 and 17.5 meV. Within the second band, a localization of vibrational states with dominant contributions from Al(16c) and Al(48f) is observed at around 29 meV.

In AlV₂Al₂₀ and GaV₂Al₂₀ the acoustic regime characterized by ħω(q) ∝ q and Z(ω) ∝ ω² is limited by the low-energy optic modes to only 0.5 meV. In YV₂Al₂₀ a violation of these relations is indicative above 2 meV. We have computed the velocities of sound v_av and Debye temperatures Θ_D from Z(ω) of the compounds within the indicated limits accounting for the lattice parameters a reported in Table 2. The results are listed in Table 4. So far no measurements of the velocities of sound have been communicated in the literature and the reported Θ_D have been derived from basic models fitted to heat capacity data.^7,9,10 For AlV₂Al₂₀ characteristic Θ_D of 420–430 K are obtained, i.e. 20–25% lower than calculated here. However, for GaV₂Al₂₀ the same approach leads to non-physical values of about 90 K questioning the significance of the data analysis as outlined in ref. 10.

Safarik et al. measured the bulk B and shear G moduli of Al_0.2V₂Al₂₀ at T → 0 with values of 87.7 GPa and 49.5 GPa, respectively.⁸ We compute B = 92(1) GPa and B = 55(1) GPa from the linear dispersions of acoustic phonons of AlV₂Al₂₀ and GaV₂Al₂₀ in Fig. 2 and the DFT-derived a value in Table 2.

C. Atomic potentials and force constants

Fig. 5 depicts the atomic potentials U(Δx) of A(8a) and Al(16c) computed from a set of discrete displacements via DFT. The mesh of displacements is indicated with the data points of AlV₂Al₂₀. Since U(Δx) is proved to be strongly isotropic we limit the presentation to the x00 direction only with the exception of Al(16c) in YV₂Al₂₀. It is worthwhile noting that any probed U(Δx) is centred at Δx = 0. Table 5 reports parameters obtained from approximating the potentials as U(Δx) = AΔx² + BΔx⁴ within the displacement range of [−0.25, 0.25] Å. Results for both monitored directions x00 and xxx are reported. A cubic term along xxx of the A(8a) potentials proved to be of no significance unlike for the results approximated from experiments by Kontio and Stevens in ref. 13.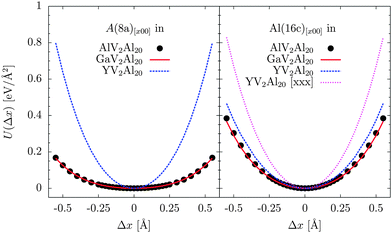

Fig. 5 Atomic potentials U(Δx) of A(8a) (left figure) and Al(16c) (right figure) computed from DFT in the direction x00. Potential of Y(8a) in xxx is shown to highlight its unique anisotropy.

Table 5 Fit parameters A in eV Å⁻² and B in eV Å⁻⁴ from approximating the atomic potentials as U(Δx) = AΔx² + BΔx⁴. Subscripts with A and B denote the approximated directions and superscripts the potentials

Compound	A ^Al(16c) x00	B ^Al(16c) x00	A ^Al(16c) xxx	B ^Al(16c) xxx	A ^A(8a) x00	B ^A(8a) x00	A ^A(8a) xxx	B ^A(8a) xxx
AlV2Al20	0.954(1)	1.01(1)	0.950(1)	0.43(1)	0.283(1)	0.86(4)	0.28(1)	0.8(2)
GaV2Al20	0.907(1)	1.00(1)	0.994(1)	0.37(4)	0.297(1)	0.833(9)	0.298(6)	0.8(1)
YV2Al20	1.301(1)	0.74(4)	2.409(5)	1.032(8)	2.107(1)	1.77(1)	2.10(4)	1.9(6)

---

The approximated parameters of the Al(16c) potentials follow the trend established in ref. 11. AlV₂Al₂₀ and GaV₂Al₂₀ match closely the values of the binary V₂Al₂₀ compound adding however by the occupation of the 8a site an anharmonic quartic component along xxx, i.e. the direct view between the 8a and 16c sites. Al(16c) in YV₂Al₂₀ experiences a potential reminiscence of the properties in LaV₂Al₂₀ and CeV₂Al₂₀.

The results are different for the properties of the A(8a) occupants. In AlV₂Al₂₀ and GaV₂Al₂₀ the harmonic and anharmonic parameters of A(8a) are approximately bisected in both directions in comparison to the properties of ScV₂Al₂₀. In YV₂Al₂₀ the harmonic contributions are reduced to about 2/3 of the values calculated for La and Ce in the respective compounds. Whereas the anharmonic contributions are augmented by about 3/2. Thus the potential of the 16c site in YV₂Al₂₀ appears to be prone to stronger anharmonicity than for La and Ce.

The force matrices as derived via the direct method of the LDC are listed in Table 6. The components follow closely the relations 2A_x00 = F_ii and 2A_xxx = F_ii + 2F_ij. A departure by only 3% is observed for the forces of Al(8a) and Ga(8a) as a result of the quartic component compensating slightly the harmonic force in this extended displacement range.

Table 6 Self force constants F_ij (i, j = x, y, z) in eV Å⁻² as calculated from the Hellmann–Feynman forces

Site	xx	yy	zz	xy	xz	yz
AlV2Al20
Al(8a)	0.577	xx	xx	0.0	xy	xy
Al(16c)	1.916	xx	xx	−0.003	xy	xy
Al(48g)	6.732	8.451	yy	0.0	xy	3.776
Al(96f)	5.300	xx	6.399	2.030	1.256	xz
V(16d)	13.358	xx	xx	2.223	xy	xy
GaV2Al20
Ga(8a)	0.605	xx	xx	0.0	xy	xy
Al(16c)	1.826	xx	xx	0.087	xy	xy
Al(48g)	6.666	8.384	yy	0.0	xy	3.716
Al(96f)	5.164	xx	6.361	1.957	1.168	xz
V(16d)	13.292	xx	xx	2.130	xy	xy
YV2Al20
Y(8a)	4.225	xx	xx	0.0	xy	xy
Al(16c)	2.607	xx	xx	1.106	xy	xy
Al(48g)	6.591	8.512	yy	0.0	xy	3.855
Al(96f)	5.024	xx	7.197	1.779	0.604	xz
V(16d)	12.587	xx	xx	2.273	xy	xy

---

Within the framework of the Debye model with Z(ω) = (ħω)²/(ħω_D)³ the second moment of energy corresponds to the Debye frequency as

We note that with the partial properties Z_n(ω), Ē_n, Ẽ_n, Fⁿ_xx and the elemental masses M_n of Al(8a) and Ga(8a) the following relation
expected for harmonic oscillators is obeyed with the same accuracy margin.

D. Inelastic neutron scattering

1. Generalized density of states. Fig. 6 depicts the generalized densities of states G(ω, 300 K) derived from data recorded at IN6@ILL with an incident neutron wavelength of 4.14 Å. All G(ω, 300 K) are normalized to match the number of modes in G(ω, 300 K) of LaV₂Al₂₀.¹¹ The spectral densities show identical features above 20 meV and match the responses of LaV₂Al₂₀ and CeV₂Al₂₀. This match holds for G(ω, 300 K) of YV₂Al₂₀ as well in the low-energy region which is marked by an intensity trough at around 18 meV followed by a double peak (12 and 15 meV) and two shoulders at around 9 and 11 meV. Differences in the scattering powers of Y, La and Ce result in the intensity variation in this energy range.

Fig. 6 Generalized density of states G(ω, 300 K) of AlV₂Al₂₀, GaV₂Al₂₀, and YV₂Al₂₀ derived from INS measurements on IN6@ILL. Inset depicts the difference spectrum ΔG(ω) derived by subtraction of the AlV₂Al₂₀ from the GaV₂Al₂₀ response.

In AlV₂Al₂₀ and GaV₂Al₂₀ the spectral density below 20 meV is redistributed in a way so the mode trough at around 18 meV in G(ω, 300 K) of YV₂Al₂₀ is filled up by a maximum opening up a trough at around 14 meV. A sharp peak remains at around 11 meV and a pronounced double shoulder spreads out the spectral weight towards lower energies. The low-energy shoulder is located approximately at 4.5 meV in GaV₂Al₂₀ and at 5.5 meV in AlV₂Al₂₀. We highlight this variation of the peak position in the inset of Fig. 6 by the difference signal ΔG(ω, 300 K). ΔG(ω, 300 K) deludes a higher spectral density of GaV₂Al₂₀ up to about 10 meV due to the different scattering powers of Al and Ga.

G(ω, 300 K) are reminiscent of the computed Z(ω) and indicative of features in the partial Z_n(ω) shown in Fig. 3. For example, the peak and mode trough at 15 meV and 18 meV in YV₂Al₂₀ on one hand and the maximum at 18 meV in AlV₂Al₂₀ and GaV₂Al₂₀ on the other can be conclusively explained by the renormalization of the Z_Al(16c)(ω) and Z_Al(96g)(ω) in this energy range. The sharp peak at 11 meV in AlV₂Al₂₀ and GaV₂Al₂₀ corresponds to the clear cut off of Z_Al(96g)(ω). It is only weakly modified by the hybridization with Y modes whose weight is oriented towards slightly higher energies both forming a shoulder and a maximum at 11 and 12 meV in Z(ω) of YV₂Al₂₀. The low-energy features in AlV₂Al₂₀ and GaV₂Al₂₀ find their correspondance in the Z_n(ω) of Al(8a) and Ga(8a). The mismatch of their characteristic energies in G(ω, 300 K) and Z(ω) is a result of temperature as we show next.

Fig. 7 depicts the dynamic structure factor S(Q, ω, T) of AlV₂Al₂₀ recorded at the temperatures T = 1.6, 100, and 300 K. The intensity of the signal is subject to the Bose thermal occupation number with no signal recorded at base temperature at the anti-Stokes line.^15,16 At T = 300 K the signal observed as an excess shoulder at 5.5 meV in G(ω, 300 K) appears condensed in S(Q, ω, 300 K) into distinguished regions of the energy-momentum phase space. Spots of high intensity are observed at around 5.5 meV at wave vectors with high contribution from Bragg reflections such as between 2.5–3 Å⁻¹ and 4–4.5 Å⁻¹. Strong acoustic phonons emanate from the strongest Bragg peaks at about 2.6, 2.9, and 4.3 Å⁻¹.

Fig. 7 Contrast plots of the dynamic structure factor S(Q, ω, T) of AlV₂Al₂₀ measured at IN4@ILL at T = 1.6, 100, and 300 K. Positive and negative energies correspond to the Stokes and anti-Stokes lines, respectively. The intensity is plotted on a linear scale with the maximum intensity at the elastic line limited to unity. Black arrows indicate peak positions derived from fits reported in the text. White arrows indicate acoustic phonons emanating from strong Bragg reflections. Black dashed lines with data at T = 1.6 K render the wave vector range exploited for fitting the T-dependent energy shift.

Upon temperature decrease the spots of high intensity are shifted towards lower energies conserving their wave vectors. At the base temperature the renormalization of the low-energy excitations results in an apparent merging of intensity with the intensity of the acoustic phonons.

A set of temperature dependent G(ω, T) is depicted in Fig. 8. We discriminate between three diferent regions in the spectral distribution G(ω, 1.6 K) of AlV₂Al₂₀. The first region being hampered by the strong elastic peak below 1 meV extends up to 10 meV. It is rendered by two sharp peaks at about 2 and 9 meV and a subtile texture in between. Some details of the intermediate texture could be consistently reproduced in different measurements such as the shoulder at around 7 meV. Others change for different wave vectors as a result of the coherent phonon form factor. This first region is separated from the second one by a mode trough between 9 and 10 meV. The second region is marked by three peaks of descending intensity located at about 10.5, 12, 13.5 meV best viewed in Fig. 8(a). The third region is separated from the second one by a shallow mode defficiency at 14 meV and is marked by a sharp peak at 16 meV and maxima at around 20 meV. In conclusion, the G(ω, 1.6 K) of AlV₂Al₂₀ imports all essential features established in Z(ω) shown in Fig. 3 and 4.

Fig. 8 Temperature dependence of the generalized density of states G(ω, T) of AlV₂Al₂₀, and GaV₂Al₂₀ derived from INS measurements. Temperatures and compounds are indicated in the figures. (a and b) Report the response of AlV₂Al₂₀ sampled at IN4@ILL with λ = 1.8 Å. The effect of the strong elastic line on G(ω, 1.6 K) has been estimated (black solid line) and the corrected data are highlighted as black open circles in (a). (c and d) Report the response sampled at IN4@ILL with λ = 2.2 Å.

Upon temperature increase the peak at lowest energy experiences a strong renormalization shifting from 2 meV at 1.6 K to about 4.5 meV at 150 K while loosing definition considerabely. A concomitant energy renormalization is observable for the shoulder at 7 meV and the peak at 9 meV. Here, the energy shift appears less extensive leading however in the present experiments to a merging of the peak at 9 meV and the mode gap at 10 meV above 50 K. At 300 K all characteristic features in the low energy region are modified beyond recognition as shown in Fig. 8(a) and (b) and 6.

In contrast to the low-energy response all characteristics at energies above 10 meV are preserved upon heating. A reduction of intensity is observed as a result of the Debye–Waller factor and a broadening of sharp features is detected at elevated T. We note that the reduction of intensity is more pronounced in regions which are dominated by the partial contributions of Al(8a) (0–9 meV) and Al(16c) (above 14 meV) than in the Al(96f)-weighted energy range (9–14 meV) in Z(ω) shown in Fig. 3.

The basic behaviour of G(ω, T) of GaV₂Al₂₀ is in line with the response of AlV₂Al₂₀. However, the first peak appears broader and at lower energies than in AlV₂Al₂₀ merging with the elastic line at 1.6 K. A worse definition applies as well to the second peak at 9 meV and the mode defficiency between 9 and 10 meV. The overall shape of G(ω, 1.6 K) of GaV₂Al₂₀ rather follows the response of AlV₂Al₂₀ and does not reflect the mode distribution concentrated to below 6 meV as evidenced by Z(ω) in Fig. 4.

2. Phonon renormalization. To quantify the energy shift of the low-energy peak we have approximated S(Q, ω, T) spectra with a set of Lorentzians L_i(Q, ω) asThe Lorentzians are weighted by the detailed balance factor and amplitude A_i(Q, T). Their number i is adapted to the complexity of the signal increasing with T. The elastic line I₀(Q, ω, T) shaped by the instrumental resolution function is matched by a sum of a Gaussian and a Lorentzian line both centred at ħω = 0. A flat background BG(Q, T) is taken into account.

S(Q, ω, T) has been chosen for this analysis as the G(ω, T) miss definition at highest T in general and at base T for GaV₂Al₂₀ as shown in Fig. 8. Nonetheless, to stay consistant throughout the entire fitting approach we had to compromise on two points. Firstly, fits were only possible at a few selected Q numbers omitting the overpowering elastic and acoustic phonon signals in the vicinity of strong bragg peaks. Secondly, only one side of the spectrum could be exploited. For IN4@ILL fits to the Stokes line were carried out as the anti-Stokes line missed resolution. For IN6@ILL data the anti-Stokes line was considered as the Stokes line was limited in energy.

Fig. 9 examplifies the quality of the data and significance of the performed fits. Data presented were extracted at Q = 2.1 ± 0.3 Å⁻¹, a range covered by both instruments. The sampled Q-range is indicated with the contrast plot of S(Q, ω, T = 1.6 K) in Fig. 7. The intensities have been arbitrarily scaled for best presentation.

Fig. 9 Selected constant wave vector S(Q, ω, T) of AlV₂Al₂₀ (top row) and GaV₂Al₂₀ (bottom row) recorded at different T reported with the data. The spectra have been collected at IN4@ILL and IN6@ILL and correspond to the Stokes (1.6 K) and anti-Stokes line (20, 100, 300 K) signals, respectively. Full lines represent the total fits to the data, black filled areas highlight the contribution of the low-energy peak approximated by a detailed balance weighted Lorentzian line. Energies of the applied Lorentzian lines are reported in the figures. The Arrow indicates an artificial signal due to the extreme experimental setup.

The energy parameters derived by this fitting procedure are shown in Fig. 10 on an absolute scale and compared with the prediction of the anharmonic isolated oscillator model by Dahm and Ueda (DUM) discussed in ref. 20. For the base T we derive energies, as average values over different Q ranges and experimental setups, of 1.97(4) meV for AlV₂Al₂₀ and 1.03(5) meV for GaV₂Al₂₀. Data from IN4@ILL and IN6@ILL show a consistant energy shift upon T increase with the only deviation for AlV₂Al₂₀ at 300 K. Note that the peaks characterized by the energies 5.6 and 7.6 meV in the IN6@ILL data shown in Fig. 9 were not resolved in the IN4@ILL experiment and fitted with a single Lorentzian. Within the framework of the DUM the derived T response of both compounds can be classified by the anharmonicity parameter β_DUM of 2–20. Both do not follow an exact β_DUM but cross to higher values for higher T consistant with the observations made with ScV₂Al₂₀.¹¹ AlV₂Al₂₀ displays a stronger cross-over behaviour. GaV₂Al₂₀ follows β_DUM ≈ 20 more closely and can be approximated by the high-T limit ħω(T) ∝ T^1/4 over a wider range of temperatures. This high-T limit is a result of DUM as well as the Yamakage and Kuramoto model (YKM) of an anharmonic cage-like structure elaborated in ref. 21.

Fig. 10 Temperature dependence of the characteristic low-energy peaks in the inelastic response of AlV₂Al₂₀ and GaV₂Al₂₀. Compounds and instruments utilized are characterized in the figure. Left, results on an absolute scale as derived from Lorentzian fits to S(Q, ω, T) data. Right, same data scaled by the characteristic frequencies at 1.6 K for comparison with the isolated oscillator model by Dahm and Ueda of ref. 20. The gray shaded area is given by the anharmonicity parameter 2.0 < β_DUM < 20.0.

To carry out a consistant parametrization of the energy shift in the entire T range we utilized the function E(T) = E* + A[1.0 − exp(−T/B)]. With the averaged energies E* at the base T of the compounds we derived the parameters A = 7.2(4) and B = 388(25) for AlV₂Al₂₀, and A = 3.72(4) and B = 134(3) for GaV₂Al₂₀. Fits are shown with the data in Fig. 10. This parametrization was exploited for a rescaling of thermal displacement parameters and thermodynamic observables discussed hereafter.

3. Phonon form factors. Selected constant energy spectra S(Q, ω, T) of AlV₂Al₂₀ derived from IN4@ILL experiments and PALD calculations are plotted in Fig. 11. The energy chosen for averaging the intensity within ±0.25 meV corresponds to the position of the strong low-energy peak and is adapted at each T for the experimental data. Stokes and anti-Stokes lines have been corrected for detailed balance. Different limits of the spectra are due to the phase space coverage by INS.

Fig. 11 Constant energy spectra S(Q, ω, T) as measured at IN4@ILL with λ = 2.2 Å (top figure) and derived from PALD calculations (bottom figure). The experimental data have been extracted at the peak energy of Al(8a) at the respective T. T and energies are reported in the figure. PALD data are calculated for different scattering strengths corresponding to full (x = 1.0), half (x = 0.5), and no (x = 0.0) scattering power from Al(8a). Data of VAl₁₀ highlight the signal of the empty structure at the respective energy. It is enlarged by a factor of two for clarity reasons. Gray shaded areas indicate the elastic structure factor S(Q, ω = 0,T) derived from experimental data at 1.6 K (top) and calculated from the DFT ground-state structural properties (bottom).

The three different experimental spectra shown follow a uniform texture marked by three strong peaks at 2.6, 4.3 and 4.9 Å⁻¹. A weaker peak can be conjectured at about 3.6 Å⁻¹. These features have been anticipated from the contrast plots of Fig. 7.

The PALD signal corresponds to the total intensity of the strong peak at around 1.7 meV. It has been calculated for T = 1 K. Calculations for different scattering powers of Al(8a) expressed by x in the figure highlight the contribution of Al(8a) to the orientationally averaged phonon form factor of the compound. Data with x = 0.0 and of VAl₁₀ accentuate the contribution of the hybridized V₂Al₂₀ matrix vibrations to the total signal. The form factor of VAl₁₀ corresponds to the signal of acoustic phonons whose fingerprints can be detected at some specific Q points in the signal of AlV₂Al₂₀, such as at about 1.7, 3.1 and 4.8 Å⁻¹.

The PALD data show a richer texture than the experimental S(Q, ω, T). Four strong peaks are observed at about 1.3, 2.4, 3.5 and 4.5 Å⁻¹ of ascending intensity. They are primarily due to the Al(8a) contribution as can be judged from x = 0.0 data which represents the form factor of the V₂Al₂₀ matrix and does not show any pronounced maxima at those positions. For x = 0.0 acoustic phonons become more accentuated as can be seen by comparison with the VAl₁₀ signal.

E. Thermal displacement parameters and heat capacity

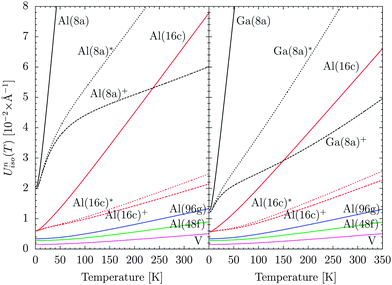
The thermal displacement parameters Uⁿ_iso(T) and heat capacities C_V(T) have been calculated from the partial Z_n(ω) and total phonon densities of states Z(ω) presented in Fig. 3. We show that it is essential to consider the renormalization of low-energy phonons to derive physically meaningful Uⁿ_iso(T) of A(8a) as well as of Al(16c) in AlV₂Al₂₀ and GaV₂Al₂₀. Two different rescaling procedures have been applied to the corresponding Z_n(ω). On one hand only the very first peak in Z_n(ω) has been renormalized according to the parametrized T-shift shown in Fig. 10. Observables derived this way are marked by (*). On the other hand the entire low-energy part of Z_n(ω) has been renormalized. Observables derived this way are marked by (+). The two different regions are sketched in Fig. 4 and marked by 1 and 2, respectively.

All computed Uⁿ_iso(T) of AlV₂Al₂₀ and GaV₂Al₂₀ are depicted in Fig. 12. Solid lines represent data derived from the pristine Z_n(ω), i.e. without renormalization. In both structures the Uⁿ_iso(T) of Al(48f), Al(96g) and V take on values comparable to data reported in the literature.^8,11,22,23Uⁿ_iso(T) of Al(16c) and in particular of A(8a) on the other hand exhibit an extreme rise which is in contrast to experimentally established results. However, for AlV₂Al₂₀ the zero point values U^Al(8a)_iso(T) and U^Al(16c)_iso(T) match well reported results such as by Safarik et al. in ref. 8 and 24. A renormalization of Z_Al(16c)(ω) following both aforementioned routines leads to and following closely the T-dependence established in ref. 8. A slightly better match is attested for 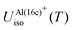. The rescale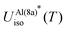d and show explicitely that a renormalization of the entire low-energy region of Z_Al(8a)(ω) is required to approximate the experimental data.

Fig. 12 Atomic thermal displacement parameters Uⁿ_iso(T) computed from partial Z_n(ω) of the compounds AlV₂Al₂₀ (left figure) and GaV₂Al₂₀ (right figure). Signals computed from renormalized spectral densities are marked by * and +. See text for details.

The properties of Ga(8a) and Al(16c) in GaV₂Al₂₀ are in line with these observations. The higher atomic mass of Ga leads to reduced values of any of the computed U^Ga(8a)_iso(T) compared to U^Al(8a)_iso(T). The amplified upturn of above 150 K is a result of the progressive suppression of the T-shift depicted in Fig. 10. It is apparent in at higher T.

Heat capacities of AV₂Al₂₀ (A = Al, Ga, and Y) and of the binary compound are depicted in Fig. 13(a). A weak excess of C_V(T) of AlV₂Al₂₀ and GaV₂Al₂₀ over YV₂Al₂₀ and V₂Al₂₀ is detected towards low T. The low-T properties are highlighted as C_V(T)/T in Fig. 13(b). An intense shoulder is present in the signals of AlV₂Al₂₀ and GaV₂Al₂₀ below 20 K. It is more pronounced in GaV₂Al₂₀ due to the higher spectral weight in the corresponding Z(ω). As is expected from the Z_n(ω) properties the partial signals of A(8a) are the main contributors to this excessive heat capacity. However, below 20 K a significant share is due to the residual signal as well, i.e. C_V(T) without the A(8a) contribution. It is examplified for AlV₂Al₂₀ in Fig. 13(b). It is weaker in GaV₂Al₂₀ due to the weaker hybridization of Ga(8a) dynamics with the matrix dynamics. Above 20 K the residual signal follows very closely the C_V(T) of the binary compound. A renormalization of the Z(ω) to account for the established T-shift has a minor effect on the C_V(T). The rescaling effect is examplified for the partial signal of Ga(8a) in GaV₂Al₂₀. It is weaker in the case of AlV₂Al₂₀.

Fig. 13 Heat capacities C_V(T) calculated from Z(ω). Compounds and signals are characterized in the figures. Total C_V(T) are displayed in (a). The corresponding low-T response is highlighted in (b) as C_V(T)/T. The contributions of the A(8a) sites (with A = Al and Ga) and of the residual signal (resid.) V₂Al₂₀ of AlV₂Al₂₀ are highlighted. Ga(8a)⁺denotes a signal derived from renormalized spectral density. See the text for details.

F. Grüneisen parameters and thermal expansion

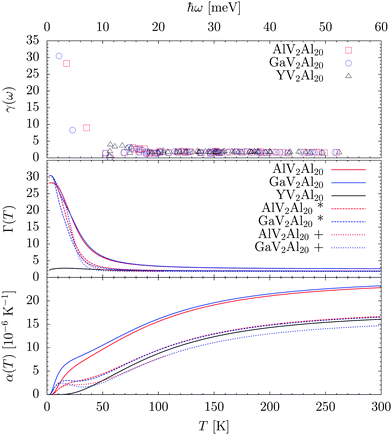
Fig. 14 shows the mode Grüneisen parameter γ(ω_i), thermodynamic Grüneisen parameter Γ(T) and the coefficient of linear expansion α(T). Their computetion followed the procedure discussed in ref. 11. Similarly, an additional set of α(T) has been rescaled by renormalizing the low-energy ω_i according to the established T-shift in AlV₂Al₂₀ and GaV₂Al₂₀.

Fig. 14 From top to bottom, the mode Grüneisen parameter γ(ω_i), the thermodynamic Grüneisen parameter Γ(T), and the coefficient of linear expansion α(T) of AlV₂Al₂₀, GaV₂Al₂₀, and YV₂Al₂₀. Linestyle and color scheme applicable to Γ(T) and α(T) data are indicated with Γ(T). Data computed from renormalized spectral densities are marked by * and +. See the text for details.

In general, the γ(ω_i), Γ(T) and α(T) follow the features and trends discussed in ref. 11. Thereby γ(ω_i) of Al(48f)-, Al(96g)- and V-dominated vibrational states take on values of 1.5–2. A strong participation of Al(16c) lifts the corresponding γ(ω_i) up to about 3. Values of up to 4 are calculated for eigenstates with high amplitudes of Y(8a) in YV₂Al₂₀ reminiscent of La(8a) in LaV₂Al₂₀. A significant difference is observed for the two eigenstates at lowest energies marked by γ(ω_i) of about 30 (T_1u(I)) and about 9 (T_2g(R)) in AlV₂Al₂₀ and GaV₂Al₂₀.

These high γ(ω_i) lift up the thermodynanic Γ(T) to about 30 at low T. From experiments Caplin et al. estimated an upper limit of 10² for Γ(T), Legg and Lanchester conjectured values of 81 and 87 for the Al and Ga doped compounds, respectively, and Safarik et al. derived a Γ(T = 5 K) of 43.^6–8 A value of 12 was computed for ScV₂Al₂₀.¹¹ At higher T all Γ(T) level out to about 2 which is in agreement with experimental data as well.

A renormalization of the low-energy eigenfrequencies upon increasing T suppresses the base T value more rapidly towards the high T limit which appears reduced to the value of YV₂Al₂₀. The renormalization proves as well here to be essential to derive realistic α(T) since calculations for AlV₂Al₂₀ and GaV₂Al₂₀ with the zero-point frequency distribution lift α(T) beyond the observed values. This effect is well compensated by the renormalization. Simultaneously the excess in α(T) below 50 K is properly accentuated and brought closer to the experimental results of Safarik et al. in ref. 8. It is interesting to note that a renormalization of both low-energy eigenstates, which corresponds to the rescaling scenario 2 sketched in Fig. 4, brings the α(T) even closer to the computed properties of the binary VAl₁₀ compound as reported in ref. 11.

IV. Discussion and conclusions

We focus the discussion primarily on the properties of AlV₂Al₂₀, summarize the most important results setting them into the closer context of literature data before commenting on the properies of GaV₂Al₂₀ and YV₂Al₂₀ and finishing with some remarks on the limitations of our study.

The characteristic distribution of vibrational modes in G(ω, T = 1.6 K) at ħω < 10 meV is unique among the AV₂Al₂₀ compounds studied here (Fig. 8) and in ref. 11. It is thus identified on purely experimental grounds as the genuine dynamic response of Al(8a). The intense peak pinpointed to 2 meV is in excellent agreement with early INS data reported by Caplin and coworkers in ref. 7 as well as characteristic energies conjectured from macroscopic exeriments by Caplin et al. in ref. 5 and 7, by Legg et al. in ref. 6, by Safarik et al. in ref. 8, and Onosaka et al. in ref. 9.

The most dominant features in G(ω, 1.6 K) are approximated with a Z(ω) derived from DFT-based lattice dynamics calculations (Fig. 3 and 4). The LDC reveals the low-energy signal as a set of phonons formed as hybride modes of Al(8a) with the V₂Al₂₀ matrix (Fig. 2). At the lowest energies, below about 3 meV, thus, in the range of the first intense peak in Z(ω) and G(ω, 1.6 K), the Al(8a) vibrations are dominantly hybridized with Al(16c) excitations.

Upon temperature increase the G(ω, T) at ħω < 10 meV is extensively altered with a blue-shift of the modes associated with the Al(8a) dynamics as observed by Caplin et al. and conjectured by Safarik and coworkers. The DUM anharmonicity parameter β_DUM of 2–20 by which we classified the degree of phonon renormalization is to our knowledge the highest β_DUM ever reported from INS (Fig. 10). For YbFe₄Sb₁₂ a β_DUM of 0.013(3) was approximated.²⁵ A β_DUM of 0.15–0.5 and about 0.5 was found for ScV₂Al₂₀ and the tetrahedrite compound Cu₁₂Sb₂Te₂S₁₃, respectively.^11,26 The series of AOs₂O₆ with A = K, Rb, Cs was characterized by a maximum β_DUM of 1 for A = K.²⁷

The required rescaling of the atomic thermal displacement parameters Uⁿ_iso(T) of Al(8a) as well as of Al(16c) for a reasonable match with experimental data demonstrates the significance of the phonon renormalization (Fig. 12). It highlights the hybridization of the Al(8a) and Al(16c) vibrational modes as well. The fact that the semi-empirical approach results in observables which are realistic on an absolute scale in the entire probed T range points out that the partial spectral densities Z_n(ω) approximate well the real distributions of vibrational states in AlV₂Al₂₀. The difference spectrum ΔG(ω, 300 K) shown in the inset of Fig. 6 indicates the extent of the A(8a) characteristic intensities to at least 9 meV. In line with this observation, Caplin et al. and Legg et al. conjectured inelastic intensities at higher energies than the primary strong peak at 2 meV in AlV₂Al₂₀ and 1 meV in GaV₂Al₂₀.^6,7 The confidence in the DFT and LDC results is further strengthened by the computed coefficient of thermal expansion α(T) which takes on realistic values when corrected by the same semi-empirical approach with the DFT and LDC derived mode Grüneisen paramaters γ(ω_i) (Fig. 14).

The renormalization does not apply uniformly to the low-energy range as modes above the dominant low-energy peak are apparently shifted at a lower rate. Due to the unspecific texture of the response we could not quantify this effect but carried out the renormalization of the entire low-energy assuming the rate established for the dominant low-energy peak (Fig. 9 and 10). Consequently, this coarse approach leads to the maximum possible rescaling of observables. The predominant effect is however due to the shift of the low-energy peak. Depending on the spectral distribution Z_n(ω) the renormalization of higher energy modes results in a variation within experimental uncertainties as shown with U_Al(16c)*(T) and U_Al(16c)⁺(T) in Fig. 12.

Beyond the match of quantified results presented here and discussed by Safarik et al. in ref. 8 there is a correspondance of implications that can be concluded from both studies as well. For example our DFT calculations uncover the local potential U(Δx) of the 8a site to be centred. This result supports the conclusions of Safarik et al. and contrasts the conjecture of off-centre positions by Caplin et al. in ref. 7. With the phonon calculations it indicates thus the dispensability of isolated-oscillator and rotator dynamics and of an associated Schottky scenario as speculated about in the literature.^6,7

From both studies the local potentials of Al(8a) and Al(16c) are disclosed anharmonic. Here, we have calculated the U(Δx) as a ground state property and matched the anharmonicity by a quartic term Δx⁴ in addition to the harmonic Δx². The strong Δx⁴ contribution is indicative of a renormalization of the Al(8a) and Al(16c) vibrations towards higher values for higher vibrational amplitudes Δx and thus upon T increase. On qualitative grounds it is in line with the observed renormalization in G(ω, T).

On quantitative grounds, the match and the derived parameters do not agree with the bulk sextic term applied by Safarik et al., neither with parameters computed with the DUM. However, we might not expect agreements with those cases as Safarik et al. elaborated their results on dynamic data and deployed a single mode to match the exerimental results. As far as the DUM is concerned, it is an isolated-oscillator model and therefore not strictly applicable to this case as discussed above. A dedicated phonon model such as the basic YKM of ref. 21 for cage-like structures might result in a better agreement. However, one can derive matching parameters with the DUM when following the semi-empirical approach taking into account the characteristic energies of the low-energy peak from G(ω, T = 1.6 K) or the LDC. As an additional alternative one can tune the mass of the isolated oscillator in the DUM to an efficient mass to find a better match for β_DUM computed from DFT parameters. This seems to be very reasonable for a phonon system.

This so far conclusive picture derived from the experiment and from the DFT and LDC study does not hold in two cases. Firstly, although G(ω, T = 1.6 K) is satisfactorily approximated by Z(ω) the phonon form factor is not reproduced correctly (Fig. 11). Consequently, bulk properties dependent on the spectral distribution such as Uⁿ_iso(T), C_V(T), and α(T) are adequately emulated. Properties dependent on the phonon dispersion, eigenvectors or form factors might not be well predicted by the LDC results. Secondly, the low-energy G(ω, T = 1.6 K) of GaV₂Al₂₀ does not follow the corresponding DFT- and LDC-computed Z(ω) (Fig. 8 and 4). It is reminiscent of the properties of AlV₂Al₂₀ albeit the first peak is unequivocally shifted to the lower energy of 1 meV and features at energies above are less well defined than in AlV₂Al₂₀.

Clearly, at this stage of the study we do not have an explanation at hand for these two discrepancies. We may however argue that for GaV₂Al₂₀ it is well established that not only Ga but also Al occupy the 8a sites.^6,7,10 The compound exhibits chemical disorder at least at these sites which should lead to a complex dynamics reminiscent of both, the Al- and Ga-characteristic frequency distributions. The most basic scenario should be a superposition of resonance modes of the V₂Al₂₀ matrix dynamics with Al(8a) and Ga(8a) local vibrations as demonstrated recently in the compounds Fe_1−xM_xSi (M = Ir, Os) and Mg₂Si_1−xSn_x.^28,29 Moreover, it is an A(8a)-deficient structure adding a component of structural disorder to its properties. Thus, strictly speaking the measured specimen is not the perfect crystal we have studied by DFT and LDC. Employing the analogy of the dynamics of glass-formers as disordered systems we expect the inelastic response to be blurred not only in energy as an effect of shortened phonon life time, but also in Q as a result of the random-phase component added by the disorder.^30–32 The later reasoning might be applied to the studied AlV₂Al₂₀ compound since the experimentally examined specimen is an Al-deficient structure. Whether this argumentation holds can and has to be studied in future with differently alloyed specimens.

The established form factor sets obvious limits to the present INS experiments. The low-energy features profitted from higher resolution data, however, with longer incident wavelengths, such as with the applied 5.12 Å at IN6@ILL, the wave vectors sampled at the Stokes line are reduced to a range in which the inelastic signal is too weak to be interpreted adequately. With higher Q the resolution mediated strong elastic signal disguises the low-energy spectral density such that for GaV₂Al₂₀ we can not exclude that spectral weight is significant below the 1 meV peak to leave finger prints at 0.6–0.7 meV as conjectured from thermal expansion by Legg and Lanchester and from heat capacity experiments by Hiroi and coworkers.^6,10

These arguments are ineffectual for the features established in YV₂Al₂₀ as the characteristic Y-dominated peaks are shifted to energies above 8 meV. The details of the inelastic response, its temperature dependence and the macroscopic properties derived are very similar to the properties of LaV₂Al₂₀ and CeV₂Al₂₀ studied in ref. 11.

Another complication for the data interpretation is raised by the complex structure of the compounds. It is tempting to interpret the intense maxima in the form factor centred around strong Bragg peaks as a signal from Brillouin zone centres. However, the signal is averaged over a high number of Brillouin zones even at this low Q. Contributions from any off-Γ point states must be expected. For the same reason a weak variation of the low-energy peak position observed at different Q values detracts from a meaningful interpretation.

Are AlV₂Al₂₀ and GaV₂Al₂₀ ‘rattling’ ‘Einstein solids’? If we understand the renormalization of eigenfrequencies towards higher values upon heating as ‘rattling’³³ then we may state that both are ‘rattling’ solids. GaV₂Al₂₀ sets the new benchmark for the ‘rattling’ phenomenon with a frequency shift of 450% up to 300 K and thus a β_DUM ≈ 20 derived from INS. A correct approximation of observables taking into account the effect of the ‘rattling’ phenomenon requires nonetheless the consideration of more than a single Einstein frequency. Like any other solid compound, AlV₂Al₂₀ and GaV₂Al₂₀ are rather ‘multi-Einstein solids’ however with an extraordinary temperature response.

The presented approximation of T effects on macroscopic observables from the microscopic dynamics by the semi-empirical approach is not only viable for other compounds but it is indispensable in some particular cases. We highlight the case of the Cu₁₂Sb₂Te₂S₁₃ tetrahedrite, a potential thermoelectric compound which shows a pronounced ‘rattling’ behaviour and a glass-like thermal conductivity, akin to ScV₂Al₂₀.^11,26 It is obvious that an approximation of thermodynamic response functions, such as the heat capacity, by a set of static Einstein modes as it has been performed for some closely related compounds could not lead to results of highest accuracy.³⁴ This statement should be expandable to any markedly ‘rattling’ solid.

V. Summary

We have identified by inelastic neutron scattering vibrational modes characteristic of the dynamics of A = Al, Ga, and Y in AV₂Al₂₀. The response of Al and Y containing compounds at base temperature has been satisfactorily approximated by density functional theory (DFT) based lattice dynamics calculations (LDC). The match is less convincing for GaV₂Al₂₀ as partial occupation of the A(8a) and admixtures of Al to the Ga sites are reckoned. An idiosyncratic renormalization of low-energy modes has been established in AlV₂Al₂₀ and GaV₂Al₂₀ whose counterpart explanation has been found in high quartic terms of the atomic potentials derived by DFT. The potentials of A(8a) as well as Al(16c) showed to be prone to a pronounced blue shift of characteristic frequencies upon increasing temperature. The significance of the anharmonicity and of the hybridizatin of the A(8a) dynamics with V₂Al₂₀ matrix modes have been demonstrated by a semi-empirical renormalization of low-energy phonons and its effect on atomic displacement parameters, heat capacities and thermal expansions of the compounds.

Acknowledgements

We are thankful for the excellent support during sample synthesis by Atsushi Onosaka and diffraction experiments by Clemens Ritter, and for fruitful discussions with Andreas Leithe-Jasper.

References

1. P. J. Brown, Acta Crystallogr., 1957, 10, 133.
2. A. E. Ray and J. F. Smith, Acta Crystallogr., 1957, 10, 604.
3. S. Samson, Acta Crystallogr., 1958, 11, 851.
4. P. I. Kripyakevich and O. S. Zarechnyuk, Dopov. Akad. Nauk Ukr. RSR, Ser. A: Fiz.-Tekh. Mat. Nauki, 1968, 30, 364.
5. A. D. Caplin, G. Grüner and J. B. Dunlop, Phys. Rev. Lett., 1973, 30, 1138.
6. G. J. Legg and P. C. Lanchester, J. Phys. F: Met. Phys., 1978, 8, 2125.
7. A. D. Caplin and L. K. Nicholson, J. Phys. F: Met. Phys., 1978, 8, 51.
8. D. J. Safarik, T. Klimczuk, A. Llobet, D. D. Byler, J. C. Lashley, J. R. O'Brien and N. R. Dilley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 014103.
9. A. Onosaka, Y. Okamoto, J.-I. Yamaura and Z. Hiroi, J. Phys. Soc. Jpn., 2012, 81, 023703.
10. Z. Hiroi, A. Onosaka, Y. Okamoto, J.-I. Yamaura and H. Harima, J. Phys. Soc. Jpn., 2012, 81, 124707.
11. M. M. Koza, A. Leithe-Jasper, E. Sischka, W. Schnelle, H. Borrmann, H. Mutka and Y. Grin, Phys. Chem. Chem. Phys., 2014, 16, 27119.
12. J. Rodriguez-Carvajal, Physica B, 1993, 192, 55.
13. A. Kontio and E. D. Stevens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1982, 38, 623.
14. V. F. Sears, Neutron News, 1992, 3, 26.
15. G. Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications, Inc., Mineola, New York, 1996.
16. S. Lovesey, Theory of Neutron Scattering from Condensed Matter, Oxford Science Publications, Oxford, UK, 1984.
17. M. M. Bredov, B. A. Kotov, N. M. Okuneva, V. S. Oskotskii and A. L. Shakh-Budagov, Phys. Solid State, 1967, 9, 214.
18. V. S. Oskotskii, Phys. Solid State, 1967, 9, 420.
19. F. Birch, Phys. Rev., 1947, 71, 809.
20. T. Dahm and K. Ueda, Phys. Rev. Lett., 2007, 99, 187003.
21. A. Yamakage and Y. Kuramoto, J. Phys. Soc. Jpn., 2009, 78, 064602.
22. M. J. Kangas, D. C. Schmitt, A. Sakai, S. Nakatsuji and J. Y. Chan, J. Solid State Chem., 2012, 196, 274.
23. O. Moze, L. Tung, J. Franse and K. Buschow, J. Alloys Compd., 1998, 268, 39.
24. D. J. Safarik, A. Llobet and J. C. Lashley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174105.
25. M. M. Koza, A. Leithe-Jasper, H. Rosner, W. Schnelle, H. Mutka, M. R. Johnson, M. Krisch, L. Capogna and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014306.
26. Y. Bouyrie, C. Candolfi, S. Pailhes, M. M. Koza, B. Malaman, A. Dauscher, T. Janusz, O. Boisron, L. Saviot and B. Lenoir, Phys. Chem. Chem. Phys., 2015, 17, 19751.
27. H. Mutka, M. M. Koza, M. R. Johnson, Z. Hiroi, J.-I. Yamaura and Y. Nagao, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104307.
28. O. Delaire, I. I. Al-Qasir, A. F. May, C. W. Li, B. C. Sales, J. L. Niedziela, J. Ma, M. Matsuda, D. L. Abernathy and T. Berlijn, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094307.
29. L. Chaput, J. Bourgeois, A. Prytuliak, M. M. Koza and H. Scherrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 064304.
30. J. M. Carpenter and C. A. Pelizzari, Phys. Rev. B: Solid State, 1975, 12, 2391.
31. J. M. Carpenter and C. A. Pelizzari, Phys. Rev. B: Solid State, 1975, 12, 2397.
32. U. Buchenau, Z. Phys. B: Condens. Matter, 1985, 58, 181.
33. L. E. Chadwick and H. Rahn, Science, 1954, 119, 442.
34. E. Lara-Curzio, A. F. May, O. Delaire, M. A. McGuire, X. Lu, C.-Y. Liu, E. D. Case and D. T. Morelli, J. Appl. Phys., 2014, 115, 193515.

---