 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterization of thin films of the solid electrolyte LixMg1−2xAl2+xO4 (x = 0, 0.05, 0.15, 0.25)†
Brecht
Put
*ab,
Philippe M.
Vereecken
ac,
Maarten J.
Mees
a,
Fabio
Rosciano
ad,
Iuliana P.
Radu
a and
Andre
Stesmans
b
aImec, Kapeldreef 75, 3001 Leuven, Belgium. E-mail: brecht.put@imec.be
bKU Leuven Department of Physics and Astronomy, Celestijnenlaan 200D, 3001 Leuven, Belgium
cKU Leuven Centre for surface Chemistry and Catalysis, Kasteelpark Arenberg 23, 3001 Leuven, Belgium
dToyota Europe – Hoge Wei 33 – Technical Centre B – 1930 Zaventem, Belgium
First published on 12th October 2015
Abstract
RF-sputtered thin films of spinel LixMg1−2xAl2+xO4 were investigated for use as solid electrolyte. The usage of this material can enable the fabrication of a lattice matched battery stack, which is predicted to lead to superior battery performance. Spinel LixMg1−2xAl2+xO4 thin films, with stoichiometry (x) ranging between 0 and 0.25, were formed after a crystallization anneal as shown by X-ray diffraction and transmission electron microscopy. The stoichiometry of the films was evaluated by elastic recoil detection and Rutherford backscattering and found to be slightly aluminum rich. The excellent electronic insulation properties were confirmed by both current–voltage measurements as well as by copper plating tests. The electrochemical stability window of the material was probed using cyclic voltammetry. Lithium plating and stripping was observed together with the formation of a Li–Pt alloy, indicating that Li-ions passed through the film. This observation contradicted with impedance measurements at open circuit potential, which showed no apparent Li-ion conductivity of the film. Impedance spectroscopy as a function of potential showed the occurrence of Li-ion intercalation into the LixMg1−2xAl2+xO4 layers. When incorporating Li-ions in the material the ionic conductivity can be increased by 3 orders of magnitude. Therefore it is anticipated that the response of LixMg1−2xAl2+xO4 is more adequate for a buffer layer than as the solid electrolyte.
Li-ion batteries currently dominate the battery market of consumer products, thanks to their higher energy and power density than other battery chemistries.1,2 Yet, to enable large scale use in new market segments, further improvement is needed.3,4 In domains where safety and miniaturization are of key importance, opportunities are present for implementation of solid state thin film batteries.5 Typical examples of these areas are medical implants, on chip storage, the Internet of things, body area networks, etc. The use of solid state thin-film batteries generally leads to an increased safety of operation and offers a wider temperature window,6,7 improvements originating directly from the replacement of the liquid electrolyte by a solid state one. This eliminates the risk of leaking and reduces the temperature dependence of the ionic conductivity. Currently, the lack of solid electrolytes with a sufficiently high ion conductivity and wide electrochemical window is one of the main obstacles for the implementation of these devices.4,8,9
Typically, a solid electrolyte provides electronic insulation between the two electrodes thereby preventing self-discharge. Moreover, it also facilitates efficient Li-ion transport between the electrodes. The solid electrolyte, however, does not contribute to the energy content of the battery, so downscaling the electrolyte will increase the system's energy density. Currently the liquid electrolyte and the separator make up 15% of the mass, and approximately 10% of the volume, of the battery stack,10,11 with a typical separator thickness of about 20 μm.11,12 By replacing this with a nanometer sized solid electrolyte, a significant increase in volumetric energy density can be obtained.13 Furthermore, the use of a solid electrolyte puts less stringent requirements on the packaging, so further gains might be obtained here by reducing packaging mass and cost.
Reducing the electrolyte's thickness also allows the use of materials with lower ionic conductivity. Indeed, the shorter diffusion length of the Li-ion between the battery electrodes, results in lower ionic resistance. For example, an electrolyte of 100 nm with a conductivity of 10−9 S cm−1 has the same ionic resistance as a 100 μm one with a conductivity of 10−6 S cm−1. This reasoning however only holds if a good contact can be ensured between the solid electrolyte and the electrode. It has been reported that the interfacial regions between the electrodes and the electrolyte can be over 50 nm in size.14 This undoubtedly introduces an extra resistance, thus lowering the battery power output.15
To prevent the formation of these interface regions, it has been suggested to lattice match the battery components.16 This should result in lithium conduction highways, giving rise to a high power output and therefore superior battery performance.8,17,18 The lattice matching can also lead to an increased stability upon cycling since it can provide anchoring points for the electrodes.
Electrode materials with the spinel crystal structure are among the most promising electrodes currently known for lithium ion batteries.19,20 As cathodes, a wide variety of doped LiMn2O4 forms have been described.21,22 As a typical example of an anode material, the spinel structured Li4Ti5O12 is often studied.23,24 Both of these materials have a small volume change (<3%25) upon lithium intercalation and a good capacity.20
However, good electrolytes with the spinel crystal structure are still lacking, although different spinels have already been studied in the past.26–28 These typically have a limited electrochemical window (e.g. Li2MgTi3O8 and LiCoTi3O8) and low ionic conductivity values, the highest reported value being 10−8 S cm−1 for Li2NiGe3O8.26 Recently, a new spinel electrolyte, LixMg1−2xAl2+xO4, has been suggested by Rosciano et al.8 It has a wide electrochemical window (0–10 V vs. Li+/Li)8 and powder nuclear magnetic resonance (NMR) measurements predict good ionic conductivity values. However, phase separation of the lithium rich compound into lithium blocking LiAl5O8 layers might occur for materials with high lithium content. These findings are confirmed by modeling where an increase in formation enthalpy with increasing lithium content has been inferred.25
In the present work, we describe the results on physical, electrical, and electrochemical characterization of RF-sputtered thin films of the spinel LixMg1−2xAl2+xO4. Different stoichiometries (x = 0, 0.05, 0.15, 0.25) have been investigated for potential use as solid electrolyte. Electrical and ionic conductivity was determined in an unambiguous way. Evaluation of ionic conductivity in thin films is more straightforward compared with powder samples, as thin films inherently ensure good electrical contact and do not require a critical sintering step. Our work further focuses on the electrochemical characterization of the material and the variation of the ionic conductivity upon altering the potential difference across the electrolyte.
Experimental
Depositions of spinel layers were performed on an 80 nm thick platinum current collector. This layer was deposited by DC sputtering on a 10 nm thick TiN adhesion layer fabricated by atomic layer deposition. Underneath the adhesion layer, 30 nm of thermally grown SiO2 was present as a barrier to prevent silicidation. Prior to the platinum deposition, the stack was subjected to a preannealing process at 800 °C in an atmosphere of 21% O2 and 79% N2, to prevent outgassing and recrystallization of the TiN layer in later stages of the experiment.The LixMg1−2xAl2+xO4 layers were deposited by RF sputtering (power 90 W, Ar flow 25 sccm, and pressure of 2.2 × 10−3 mBar) from a stoichiometric target. Four different stoichiometries have been investigated, namely MgAl2O4 (x = 0), Li0.05Mg0.9Al2.05O4 (x = 0.05), Li0.15Mg0.7Al2.15O4 (x = 0.15) and Li0.25Mg0.5Al2.25O4 (x = 0.25). Different film thicknesses were fabricated ranging from 20 nm to 600 nm. The layers were subjected to a crystallization anneal in an rapid thermal annealing oven (Annealsys) at 800 °C in an oxygen atmosphere. The morphology of the layers before and after annealing was checked by scanning electron microscopy (SEM, Nova). Transmission electron microscopy (TEM) was done using a Titan(FEI) operating at 120 kV.
| Target composition | Techn. | Li (%) | Mg (%) | Al (%) | O (%) |
|---|---|---|---|---|---|
| MgAl2O4 as-deposited | RBS | — | 29.4 (33) | 70 (66) | — |
| Li0.05Mg0.9Al2.05O4 ann. | ERD | 0.48 (0.7) | 9.5 (12.8) | 30 (29) | 60 (57.1) |
| Li0.15Mg0.7Al2.15O4 ann. | ERD | 1.4 (2.1) | 6.4 (10) | 35 (30.7) | 57.2 (57.1) |
| Li0.25Mg0.5Al2.25O4 ann. | ERD | 2.5 (3.6) | 4.7 (7.1) | 33.3 (32) | 59 (57.1) |
Crystallinity was determined by X-ray diffraction (XRD) in the grazing incidence configuration (X'pert pro, Panalytical) using Cu Kα radiation. Compositional analysis of the layers was done using elastic recoil detection (ERD) and Rutherford backscattering (RBS). In ERD experiments, a primary ion beam of Cl4+ is accelerated to 6 MeV by a 2 MV tandem accelerator. The forward, recoiled and scattered ions are detected using a Time-of-flight-Energy (ToFE) telescope.29 For these experiments, the LixMg1−2xAl2+xO4 layers were deposited on a Si3N4 substrate to prevent interference from the underlying Pt layer.
All electrochemical testing involving lithium was done in an Ar glove box (O2, H2O < 1 ppm). The testing was carried out in a three electrode cell using Li foil as counter and reference electrodes. A solution of 1 M of LiClO4 (battery grade, Sigma Aldrich) in propylene carbonate was used as the electrolyte. Electrochemical impedance spectroscopy (EIS) was performed at open circuit voltage (OCV) between 0.1 Hz and 1 MHz with an RMS amplitude of 10 mV using an autolab (Metrohm) potentiostat with a frequency response analyzer module operated using Nova software.
When performing EIS at different potentials, the potential is altered in steps of 100 mV starting from OCV. After every step the current is allowed to relax until a steady state is reached before an impedance measurement is performed. From the relaxation measurements the total charge flowing into the layer was calculated. The fitting of the impedance data was done using the MEISP software (Kumho Chemical Laboratories). The obtained fits have a χ2 in the range 10−3 to 10−4, indicating a reliable fit. The relative standard deviation of the fitted values is approximately 10−3 or lower.
To conduct electrical measurements, gold metal dots (blocking contacts) were evaporated on the layers through a shadow mask. Both current–voltage (I–V) and impedance characterization were performed: the I–V measurements were carried out using an Agilent 4156C precision semiconductor parameter analyzer.
Results and discussion
Physical characterization
Fig. 1 shows the results of XRD characterization of 100 nm thick LixMg1−2xAl2+xO4 (x between 0 and 0.25) layers, sputtered on a platinum current collector. It can be seen that all the layers exhibit the spinel structure (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The crystal planes are indicated according to JPDS entry 01-072-6950. Substrate contributions are also visible next to the LixMg1−2xAl2+xO4 peaks, that is, peaks due to the Pt current collector and the TiO2 (rutile) adhesion layer which are labeled on the XRD pattern. No impurity phases were detected in these patterns.
m). The crystal planes are indicated according to JPDS entry 01-072-6950. Substrate contributions are also visible next to the LixMg1−2xAl2+xO4 peaks, that is, peaks due to the Pt current collector and the TiO2 (rutile) adhesion layer which are labeled on the XRD pattern. No impurity phases were detected in these patterns.
 | ||
| Fig. 1 (a) XRD pattern of 100 nm thick layers of LixMg1−2xAl2+xO4 with different stoichiometries. All layers crystallize in the spinel phase after annealing at 800 °C for 1 h. An offset was applied to the different patterns for clarity. Clear peaks characterizing the spinel phase can be seen, the different crystal planes are indicated. (b) shows the variation of the lattice parameter as a function of the Li content of the layers. The trend fits well with results based on powder samples and modeling.8,18,25 | ||
From the width of the (111) peak in the XRD pattern, the lattice constant was calculated and is plotted versus the layer stoichiometry in Fig. 1b. The values obtained by modeling25 and powder diffraction8 are shown for comparison. Similar values and trends are found in all cases, thus confirming the formation of spinel structured LixMg1−2xAl2+xO4 thin films. The slight off-set of the simulated data points is within expectation as explained elsewhere.25 The linear relationship between the lattice parameters and lithium content indicates a solid solution behavior between MgAl2O4 (a = 8.08 Å30) and LiAl5O8 (a = 7.903 Å31), in accordance with Vegard's law.32
The stoichiometry of the layers was probed by RBS and ERD (see Table 1). The latter was used to determine the lithium content of the layers. The experiments show that the crystalline layers are slightly lithium and magnesium deficient, and aluminum enriched. The stoichiometry for the as-deposited and annealed samples was comparable (see also Table S1 in the ESI†), except for a slight decrease in the oxygen content after annealing. This is a known problem in materials requiring a high temperature annealing process.33
The excess aluminum and deficiency in Mg and Li in the studied layers is attributed to preferential sputtering of aluminum. This is a common problem when sputtering from a stoichiometric, multi-element target.34 Upon annealing in an oxygen atmosphere at a temperature of 900 °C, i.e. higher than the 800 °C applied here, for 12 h the formation of Al2O3 or LiAl5O8 has been discovered in powder systems.8 Both of these compounds have a higher atomic percentage of aluminum compared to LixMg1−2xAl2+xO4. In the current work, no peaks of Al2O3 or LiAl5O8 are detected by XRD (cf.Fig. 1); the spinel phase is obtained with the expected lattice parameters. However, the presence of some amorphous Al2O3 cannot be excluded, as the annealing temperature used here (800 °C) is too low to obtain crystalline Al2O3.35
LiAl5O8 is an inverse spinel with lattice constants very close to the MgAl2O4 spinel, therefore both have closely related XRD patterns. This makes identification of the different materials very difficult. Most likely no LiAl5O8 is present in the layers sputtered here, a conclusion based on the observed linear trend in the lattice parameter and the comparison of the intensity pattern of the different stoichiometries. Again, the existence of the amorphous phase cannot be excluded. If occurring, the presence of both Al2O3 or LiAl5O8 will obviously impact the ionic conductivity of the material.
The morphology of the LixMg1−2xAl2+xO4 layers was investigated using a combination of TEM and SEM. Fig. 2a shows an SEM image of an unannealed MgAl2O4 layer. A smooth layer can be seen on top of the platinum current collector. The lack of fine structure within the layer confirms its amorphous character as seen in the inset of Fig. 2a. Fig. 2b shows a Li0.05Mg0.9Al2.05O4 layer on top of a platinum current collector layer after crystallization annealing at 800 °C. The layer is closed and pinhole free. The polycrystalline nature of the layer can be ascertained from the granular morphology that can be clearly distinguished in the inset. An increased crystal size is also seen within the platinum layer after annealing. Note that the film forms a close contact with the underlying current collector, thus ensuring good electrical contact.
TEM characterization was performed on crystalline 150 nm films of Li0.25Mg0.5Al2.25O4. Fig. 3 shows the key results of this characterization, more detail is provided in the ESI† (Fig. S1 and S2). It is known that with increasing lithium content, phase separation into MgAl2O4 and amorphous LiAl5O8 is more likely, as concluded from first principles simulations.25 However, the Li0.25Mg0.5Al2.25O4 film, having the highest lithium stoichiometry investigated here, remains highly crystalline, as illustrated in Fig. 3a. The spinel crystal lattice can be seen in all regions of the image. From the high resolution TEM fast Fourier transform a lattice constant of 8 Å is found, in good agreement with the value inferred from the XRD data shown in Fig. 1.
Fig. 3b is an image taken at a different area of the sample than pictured in a, exposing differences in contrast. This dissimilarity can be due to the different grain orientation in the sample but could also be the result of the presence of amorphous material. Yet, we note that even in the areas where the contrast difference is present, the layer remains crystalline. Therefore if the change would be due to the presence of an amorphous region in the material it never spans the entire thickness of the TEM lamella (50 to 70 nm). Towards the bottom of the image typical twinning is observed; the twins also show distinct contrast in the image, reinforcing the idea that these contrast differences originate from different grain orientations.
To assess the possibility of phase separation into amorphous Al2O3 or LiAl5O8 constituents, TEM coupled energy-dispersive X-ray spectroscopy (EDS) was conducted. The aluminum and oxygen images are shown in Fig. 3c and d respectively. No local aluminum or oxygen enrichment could be detected. Also, no direct correlation was found between the observed contrast differences and the elemental distribution. All the investigated elements (Al, O) are found to be evenly distributed over the layer. Note that no magnesium map is shown since the Mg signal overlaps with the platinum of the current collector.
From the physical characterization data outlined above, it can be concluded that polycrystalline LixMg1−2xAl2+xO4 films were fabricated, hereafter referred to as crystalline films for the sake of brevity. These are slightly lithium and magnesium deficient, and aluminum rich. The material crystallizes in the spinel crystal structure after annealing at 800 °C for 1 h in an oxygen atmosphere.
Electrical and electrochemical characterization
The sputtered LixMg1−2xAl2+xO4 films were also evaluated for their solid electrolyte properties. Independent NMR measurements on LixMg1−2xAl2+xO4 powders indicated an activation energy for ionic conductivity as low as 0.35 eV for x = 0.05.8 For this reason good ionic conductivity is anticipated in similar layers. Furthermore, the material is known to have a wide electrochemical window (between 0 and 10 V vs. Li+/Li).8 The electronic conductivity of the material is expected to be low due to its wide bandgap.25The electronic leakage was investigated first using metal–insulator–metal (MIM) capacitors fabricated using thermally evaporated gold dots. Fig. 4 displays the I–V characteristics for 100 nm crystalline layers of LixMg1−2xAl2+xO4 with x between 0 and 0.25. The leakage current density remains below 45 nA cm−2 over the whole voltage range probed. This low leakage confirms the absence of cracks and pinholes, as assessed from the SEM images in Fig. 2. Because of the use of two blocking contacts (Pt and Au), only a limited contribution of the mobile lithium ions is expected.
At 2 V an average current density of 2 × 10−8 A cm−2 is measured for the different layers, corresponding to a resistivity of 1013 Ω cm. This is in the same range as what has been reported for Al2O3 elsewhere,36,37 indicating negligible contribution of the mobile ions in the layers. The obtained response is similar to typical good dielectrics such as SiO2 and Al2O3. It confirms the good dielectric properties of the LixMg1−2xAl2+xO4 layers.
The results of the I–V measurements on the amorphous LixMg1−2xAl2+xO4 layers are depicted in the ESI† (Fig. S3). Leakage current density of these layers is roughly an order of magnitude smaller than for the crystalline layers.
The high resistivity proves the insulating character of the material, an inherent advantage of a MgAl2O4-based electrolyte. Undoped MgAl2O4 has a bandgap of 7.8 eV and therefore a very low electronic conductivity.38,39 Furthermore, it was concluded from first principles calculations by Mees et al.25 that the bandgap remains unchanged by doping with Al and Li.
We have thus shown the electronic insulating properties of the LixMg1−2xAl2+xO4 layers which are indeed required for a solid electrolyte. However, also good ionic conductivity and high stability are needed. To assess these properties, electrochemical measurements were performed.
Fig. 5a shows the observed current–potential curves for the 100 nm thick crystalline LixMg1−2xAl2+xO4 layers (x = 0 and 0.25) on platinum as well as for a bare platinum electrode. The material was evaluated in a potential range from −0.1 V up to 4 V vs. Li+/Li. The bare platinum electrode shows clear lithium plating and stripping peaks around 0 V. Plating sets in from approximately 0.3 V on. This early onset is likely caused by underpotential deposition (UPD) on platinum; UPD deposition of lithium on platinum substrates is a known phenomenon.40 The charge under the UPD peaks is 2.1 mC cm−1 corresponding to 31 monolayers of lithium. This number is too high for UPD, typically 1 or 2 monolayers. However, due to the lithium–platinum alloy formation, UPD deposition can continue for a longer time.
In the reverse scan, lithium stripping is seen when the potential is increased above 0 V. When further raising the potential to 0.3 V another set of peaks is observed, corresponding to the dealloying from the lithium–platinum alloy.40,41 A charge of 5.6 mC cm−2 of lithium is plated, while only 2.2 mC cm−2 is stripped. This continues up to approximately 1.5 V vs. Li+/Li when the remaining 3 mC cm−2 is extracted.40 The peak at 1.8 V corresponds to intercalation and extraction of lithium into the TiO2 adhesion layer. The peak at approximately 3 V is not clearly attributable.
When comparing the current–potential curves of the bare platinum with those of the LixMg1−2xAl2+xO4 layers on platinum, the current of the latter is 2 to 3 orders of magnitude lower as evident from Fig. 5a. The inset illustrates that the current remains low in the potential range from 0.3 to 4 V vs. Li+/Li, the value remaining around 10−7 A cm−2. This confirms the stability of the electrolyte in this window.
Upon decreasing the potential below 0.3 V, an increase in current is seen. This increase in current is attributed to the onset of Li plating through the LixMg1−2xAl2+xO4 layer, a result of the onset of UPD on Pt as observed for the platinum reference. As for the bare platinum a steep increase in current is seen when the potential drops below 0 V, corresponding to the onset of Li-plating on the platinum substrate under the LixMg1−2xAl2+xO4 film and likely Li–Pt alloy formation.
Upon reversing the potential, the Li-ions are stripped again. The clear similarity between the platinum reference and the LixMg1−2xAl2+xO4 layers hints at the formation of similar alloys. Since the LixMg1−2xAl2+xO4 layers are electronically insulating, as was shown above, lithium ions must be transported through the layers. Only upon reaching the platinum current collector, reduction to metallic lithium and platinum–lithium alloy formation can occur.
Fig. 5b depicts the current–potential curves shown in Fig. 5a on a logarithmic scale. In the reverse scan, stripping of the lithium is seen from 0 V onward, with a distinct current peak in all cases. However, all cathodic charge is extracted again only when increasing the potential to 1.5 V. This is explained by the formation of lithium–platinum alloys also for the cases with LixMg1−2xAl2+xO4 layers. The distinct Li–Pt alloy peaks are clearly revealed in Fig. 5b. Peaks are present around 0.2, 0.5 and 1.2 V. These match with those seen for the bare platinum reference layer. The appearance of these (de)alloying peaks confirms the ability of lithium transport through the LixMg1−2xAl2+xO4 layers.
To determine the ionic conductivity, EIS was performed. First we will discuss the results obtained at OCV; in later paragraphs we will discuss the potential dependence of the impedance response.
EIS observations on 100 nm thick crystalline LixMg1−2xAl2+xO4 films, performed at OCV, are depicted in Fig. 6 on a complex plane or Nyquist plot. Ionic conductivity is typically characterized by the presence of a semi-circle. The first intercept of this circle with the real axis corresponds to the series resistance (generally attributed to cables, contacts and the liquid electrolyte), the second one to the ionic resistance of the solid electrolyte.42Fig. 6 shows the results measured on LixMg1−2xAl2+xO4 (x = 0 to 0.25) layers.
No clear semi-circle can be detected for the LixMg1−2xAl2+xO4 layers with x = 0, 0.05 and 0.15. Only the Li0.25Mg0.5Al2.25O4 layer shows a large semi-circle (intercepting the real axis at 2 MΩ), corresponding to an ionic conductivity of approximately 1 × 10−11 S cm−1. This low conductivity limits practical applicability and differs from the conductivities anticipated elsewhere.8,18
The conductivity behavior of the LixMg1−2xAl2+xO4 layers (with x = 0, 0.05 and 0.15) closely resembles an ionic blocking layer. This contrasts with the findings by NMR, where the layer with x = 0.05 showed the clearest signature of conductivity. The absence of ionic conductivity as reflected by the EIS data indicates that the NMR line width measurements likely determined Li hopping between the 8a and 16c spinel crystal positions.8 This hopping does not necessarily result in long range lithium ion conductivity as the Li-ion can go back and forth between 8a and 16c positions. Mees et al. concluded that the lowest energy path for Li-ion diffusion would be from 8a to 16c and then into the next neighboring 8a site. The 16c site thus emerges as an intermediate position in ionic motion.25
Potential dependent conductivity
The poor conductivity found from the impedance measurements seems contradictory to the fact that lithiation is observed in the cyclic voltammetry data. Indeed, the presence of lithium–platinum alloy formation and lithium plating illustrates the possibility of conductivity through the LixMg1−2xAl2+xO4 layers. Various reasons for this discrepancy can be thought of, e.g., lithium transport through grain boundaries on application of an electric field, liquid electrolyte penetrating into defects or lithiation of the LixMg1−2xAl2+xO4 layers in a mechanism similar to Al2O3.43 The mechanism of the lithium transport will be investigated in the following paragraphs.To assess the effect of grain boundaries, amorphous (i.e., not annealed) LixMg1−2xAl2+xO4 layers have been subjected to cyclic voltammetry experiments (data shown in ESI,† Fig. S4). For these amorphous layers, cyclic voltammetry still showed distinct lithium plating peaks and lithium–platinum alloy formation, confirming ionic movement through the layer. The currents are in the same order of magnitude as those of the crystalline MgAl2O4, leading to the conclusion that grain boundary transport is not the main facilitator of ionic conductivity through the layers.
To assess the possibility of pinholes in the films, copper plating and stripping experiments were conducted. SEM inspection showed no obvious presence of defects or pinholes in the films (cf.Fig. 2). Also electrical characterization (Fig. 4) did not reveal any shorting. However, SEM cannot detect the small pinholes and the evaporated metal dots might not contact them. In the wet copper plating and stripping experiments, the aqueous solution will be able to access even the smallest pinholes.44 On the other hand it is assumed that the doubly charged copper ion will not be transported through the LixMg1−2xAl2+xO4 layer.
Copper plating and stripping measurements using cyclic voltammetry on MgAl2O4 coated platinum substrates did show evidence of copper plating and stripping (see Fig. S5 in the ESI†). However, the measured plating currents are in the same order of magnitude as the electronic leakage through the dielectric films (see Fig. 4). Therefore, it is likely that copper is initially plated due to the electronic leakage. This plated copper can introduce further defects in the MgAl2O4 layers.
Coincidently, the plating currents observed on amorphous MgAl2O4 are 100 times smaller than for the crystalline films, as is approximately also the case for the leakage currents. Additionally, a large IR drop is found for the copper plating and stripping in both annealed and unannealed MgAl2O4 layers, indicating their good electronically insulating quality. However, we cannot fully exclude that there is some contribution of grain boundaries and defects in the annealed layers. The effect of these should however remain limited as similar lithium plating and stripping currents are seen in the amorphous and crystalline LixMg1−2xAl2+xO4 layers.
To further investigate the transport of lithium through the LixMg1−2xAl2+xO4 layers, EIS measurements were performed at various potentials. The potential was lowered from OCV (around 3 V vs. Li+/Li) down to 0.1 V in steps of 100 mV. The lower cutoff potential was limited to 0.1 V to prevent delamination of the LixMg1−2xAl2+xO4 layer from the platinum current collector. This due to lithium plating at the interface between the latter two layers during the long measurement times.
After every potential step, the current was allowed to relax until a steady state was reached, which was then followed by an impedance spectroscopy measurement (see ESI,† Fig. S6). The frequency spectrum obtained this way was fitted using the circuit shown in Fig. 7. A detailed element assignment is given at a later stage. Fig. 8 shows an overview of the impedance behavior for a 100 nm thick amorphous MgAl2O4 layer. Fig. 8a presents a logarithmically scaled complex plane plot of the data obtained at different potentials (starting at OCV) – this for easy comparison of values and features as the response profoundly changes with decreasing potential. The full line is the fit through the data points based on the model of Fig. 7, indicating that the model used fits the changing impedance response well.42
 | ||
| Fig. 7 Equivalent circuit model used to fit the impedance data obtained by performing impedance spectroscopy at varying potential values. | ||
 | ||
| Fig. 8 (a) Logarithmically scaled complex plane plot of the variation in impedance characteristics of a 100 nm thick unannealed MgAl2O4 layer at different potentials. The solid line represents the fit to the data based on the equivalent circuit model depicted in Fig. 7. (b) Complex plane plot showing the high frequency region of the data. Also in this case the model is found to fit the data well. (c and d) Overview of the variation in model parameters of a 100 nm amorphous MgAl2O4 layer upon lowering (c) and increasing the potential (d). A drop in resistance of over 3 orders of magnitude is seen upon lowering of the potential. Upon increasing the potential a hysteresis is visible, attributable to the platinum current collector acting as a source of lithium. | ||
Fig. 8b shows a complex plane plot zoomed-in on the high frequency region. A good fit of the model to the data can be seen over the entire potential range. Generally, the χ2 square values range between 10−3 and 10−4, indicating a reliable fit.45 This confirms the suitability of the model to analyze the acquired impedance data. The layer response changes from that characteristic for a capacitor at high potentials, which is seen almost as a vertical line, to a semi-circle. The semi circle seen at lower potentials is commonly modeled by a resistor in parallel with a capacitor. When measuring solid electrolytes, such response is commonly attributed to the electrostatic capacitance of the layer and the resistance of Li-ion transport through the layer.
Fig. 8c and d show the variation of the resistance values as extracted from the impedance data. These resistances, R1 and R2, correspond to the components shown in Fig. 7. Fig. 8c shows the changes in resistances and the charge that flows when decreasing the potential from OCV to 0.1 V vs. Li+/Li. This charge is calculated by integrating the current that flows during the 1 h relaxation time (see the figure in the ESI†) after every discrete potential step. All the data shown here are calculated for steps of 0.1 V. Fig. 8d depicts the behavior of these elements (R1, R1 and the charge that flowed during every discrete step) upon increasing the potential back to OCV. The left axis on the figures corresponds to the resistance values, and the right axis shows the absolute charge that flowed during every potential step. From these figures a complete picture of the variation in resistance of the layer with changing potential is obtained.
Upon lowering the potential, a plateau is visible in the resistance values (see Fig. 8c). This persists from 3 V to approximately 0.6 V vs. Li+/Li. When the potential drops below 0.6 V a reduction in resistance is measured, coinciding with an increased charge flow. Eventually, a drop in resistance (R2) of over 3 orders of magnitude from the plateau value is achieved at a potential of 0.1 V. This is also reflected in the abrupt change of the impedance response in Fig. 8a and b. Upon increasing the potential again, the resistances evolve back to their original state, but only when a potential of approximately 2 V is reached. Hence a hysteresis of ∼1 V is present when comparing the down and up traces, cf.Fig. 8c and d, respectively.
A similar trend is observed in the measured charge associated with each discrete potential step. From 3 V up to 0.6 V versus Li+/Li negligible charge flows, following the plateau trend seen in the resistance. Starting from 0.6 V, an increased (negative) charge flow is seen in Fig. 8c, which increases steeply. During the reverse cycle (cf.Fig. 8d), increasing the potential again, a large (positive) charge flow now exists up to approximately 1.5 V, after which it reduces to the background level. A clear charge peak is seen around 0.6 V vs. Li+/Li. In the cyclic voltammogram of Fig. 5 a peak was found at this potential as well which was attributed to a lithium–platinum dealloying peak. Thereby the behavior of the charge closely resembles the current–potential curves of Fig. 5.
A clear hysteresis is present when comparing the measured evolution of the resistance and charge for decreasing or increasing potential (cf. comparing panels c and d in Fig. 8). The original resistance values are only recovered upon reaching a potential of 1.5 V, coinciding with the final lithium–platinum dealloying peak. Both the charge shown in Fig. 8c and d and the cyclic voltammogram of Fig. 5 show peaks at 0.5 V and 1.5 V vs. Li+/Li attributed to the (de)alloying from platinum.
The influence of the platinum current collector is confirmed by performing similar experiments on a TiN current collector. When amorphous Li0.25Mg0.5Al2.25O4 is deposited hereon, the initial resistance values are regained in reverse trace at 1 V vs. Li+/Li (1 V faster than on Pt) (see Fig. S8 in the ESI†), reflecting a more symmetric behavior. The lithium–platinum alloy formation as a cause for the hysteresis in these experiments is hereby established. From this it can be concluded that the charging current, seen in Fig. 8, is due to the movement of lithium ions through or into the LixMg1−2xAl2+xO4 layer and subsequently in the platinum current collector.
As the charge that flows upon a potential step is due to a Li-ion current, the entry of Li-ions into the layer causes the reduction in resistance. Such a decrease only occurs provided the inserted lithium ions are mobile. Note that we started from a lithium free MgAl2O4, so the introduction of lithium ions, thus an increase in Li+ concentration, would indeed lower the resistance. At its optimum, the total conductivity of the MgAl2O4 layer shown here reaches 10−10 S cm−1. Upon increasing the potential again, the lithium ions move out of the layer and the resistance returns to its original value. Since lithium dealloys from the platinum current collector up to 1.5 V, it acts as a source of lithium.40,41 The platinum–lithium alloy supplies Li-ions into the layer which keeps the resistance low. Once the platinum has completely dealloyed, the lithium is removed from the layer and the resistances evolve to their initial value.
From Fig. 8, one might feel tempted that the resistance reduction is linked to the change in DC current. However this is not the case. The resistance is measured at the end of the 1 h current relaxation or equilibration step and the current after such a step shows minor dependence on the potential (see ESI,† Fig. S7). The limited change in current can therefore not account for the observed change of over 3 orders of magnitude in the impedance response.
The behavior described above regarding the impedance characteristics was found in MgAl2O4 and Li0.25Mg0.5Al2.25O4 layers with various thicknesses, both in the amorphous and crystalline state. All of these layers showed a behavior similar to the one depicted in Fig. 8.
Conductivity mechanism
The entry of positively charged lithium ions into the LixMg1−2xAl2+xO4 layer leads to a charging of the material. A fraction of this charge can be of a capacitive nature, e.g., formation of the double layer. However the magnitude of the charge measured here cannot solely be explained by the formation of a double layer. The accumulated charge at 0.1 V is approximately 0.3 mC cm−2 and corresponds to approximately 4–5 nm plated lithium; such charge is too large to be accounted for by the formation of a double layer (typically in the μC range).46 Furthermore, the growth of an electrochemical double layer can also not explain the drop with a factor of 103 in the resistance.It is thus more likely that a reaction occurs involving the LixMg1−2xAl2+xO4 layer and the lithium ions, similar to electrode intercalation. Lithiation of Al2O3 has been shown before.43,47 It was reported that metallic lithium reacts with the Al2O3 until a composition of Li3.4Al2O3 is formed. This composition is thermodynamically the most favorable and has a Li-ion conductivity 3 orders of magnitude larger than LixAl2O3 with compositions between x = 0.2 and 0.4.43 Note that in this compound the oxidation state of Al has changed from (+III) to (+II).
A similar mechanism seems to be operating in the layers studied in this work. Gradual lithiation of the LixMg1−2xAl2+xO4 leads to an increased lithium ion conductivity, the lithiation proceeds until a stable composition is formed that shows a significantly higher conductivity (roughly an increase of 3 orders of magnitude). The Li+-ion intercalation reaction may then be described by the equation:
| MgAl2O4 + xe− + xLi+ ↔ LixMgAl2O4 | (1) |
Reaction (1) shows that the insertion of lithium ions in the layer coincides with a reduction of the aluminum's oxidation state from (+III) to (+II) thus ensuring charge neutrality as for Li+-ion intercalation electrodes. The reaction will proceed until the thermodynamically most favorable composition is obtained as reported for Al2O3.43 Once this composition is formed, which has a higher Li-ion conductivity, the material functions as an ionic conductor and facilitates lithiation of the platinum current collector. The indifference of the mechanism proposed here to the starting stoichiometry and annealing condition of the studied layers matches well with the observations.
Note that LixMgAl2+xO4 which forms in reaction (1) differs from the original material. In the sputtered LixMg1−2xAl2+xO4 the oxidation state of the aluminum remains fixed at (+III), independent of the lithium content. However, when lithium is electrochemically intercalated the aluminum has to change the oxidation state to preserve charge neutrality.
Different reasons can now be suggested for the reduction of the resistance. First, the lowering of the resistance seen in the LixMg1−2xAl2+xO4 layers could be due to the lithiation of Al2O3 present in the layers. However, similar reductions in resistance are seen in crystalline and amorphous LixMg1−2xAl2+xO4 while no Al2O3 is present in the amorphous material. Furthermore, from Fig. S9 in the ESI,† it is seen that the lithiation of Al2O3 is an irreversible process. Once the low resistance state is reached, the original layer resistance cannot be recovered, whereas by contrast, the variations in resistance of LixMg1−2xAl2+xO4 are shown to be reversible.
The results reported here (cf.Fig. 9 and ESI,† Fig. S9) are in good agreement with the modeling results reported elsewhere.43 They also constitute the first experimental investigation of the changing ionic conductivity of buffer layers both LixMg1−2xAl2+xO4 as well as for Al2O3.
 | ||
| Fig. 9 (a) depicts the changes of R1, determined from the plateau (3–1 V vs. Li+/Li) data (cf.Fig. 8c and d), versus the layer thickness. Little variation is seen with varying layer thickness. (b) shows the variation of R2versus layer thickness. A linear relationship between the two quantities is seen. (c) shows the capacity extracted from CPE1, (cf.Fig. 7), versus layer thickness. Only a limited variation is seen in the C1 value when changing the layer thickness. (d) depicts the variation of C2 (extracted from CPE2). As the layer thickness decreases C2 increases, as is expected for a capacitor. | ||
Another explanation for the drop of resistance might originate from the change in electronic conductivity on intercalating Li in the LixMg1−2xAl2+xO4. The oxidation state of aluminum changes during reaction (1), and the mixed valence state will lead to a higher electronic conductivity. However, in this case no influence would be expected from the platinum current collector. No difference would be present between the measurement on a TiN or Pt substrate, while clear differences are shown here. The platinum substrate leads to a hysteresis, delaying the recovery of the original resistance values. This phenomenon was explained by the platinum–lithium alloy acting as a source of lithium for the LixMg1−2xAl2+xO4 layer. The changing resistance can thus be attributed to the presence of lithium in the LixMg1−2xAl2+xO4 layer, and hence the observed changes in resistance are concluded to correspond to a change in the ionic conductivity of the material.
From the above it is thus concluded that LixMg1−2xAl2+xO4 does not function as a solid electrolyte. Instead it intercalates lithium at low potentials and thus operates as an electrode with low electronic conductivity. For this reason LixMg1−2xAl2+xO4 could be used as a buffer layer similar to Al2O3 for lithium ion electrodes.48,49 The recovery of the original resistance state after the experiment hints at good reversibility of the process, however more detailed cycling experiments are needed to confirm these findings.
Model interpretation
As was mentioned before, all impedance data were fitted based on the circuit shown in Fig. 7. In this section the components of the model are discussed in more detail. Some of these have a straightforward meaning, others require a more in depth analysis.The simplest element in the circuit is the series resistance Rs, commonly attributed to contact resistances, cabling etc. In this work its value is consistently found to be ∼150 Ω. The CPEW element is attributed to the low frequency diffusion component in the electrolyte. Its n value (see eqn (2)) is commonly found around 0.5 corresponding to a Warburg impedance element.
To gain insight into the meaning of the remaining elements, an overview of their plateau (3–1 V vs. Li+/Li) values (cf.Fig. 8c and d) is presented in Fig. 9 for the different LixMg1−2xAl2+xO4 layers studied.
Fig. 9a and b show the variation of, respectively, R1 and R2versus the layer thickness. Resistance R1 remains approximately constant upon varying the film thickness; with the exception of the 40 nm crystalline MgAl2O4 layer. R2 on the contrary shows a linear increase with film thickness, as expected for a resistor. As shown before, R2 is roughly two orders of magnitude larger than R1. Both resistances do not show a clear dependence on the material stoichiometry, yet, the magnitude of R2 for the crystalline films is consistently lower than for the amorphous ones.
Fig. 9c and d depict the variation of the capacitances associated with the constant phase elements versus layer thicknesses. The constant phase elements are modeled according to:50
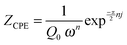 | (2) |
The obtained capacitance values are situated in the microfarad range for C1 and around ten to one hundred nF for C2. C2 clearly depends on the layer thickness, showing an inverse relation to the layer thickness, as one would expect for a capacitance. The value of C2, in the range of 100 of nF, fits well with typical electrostatic capacitors of, e.g., Al2O3 (dielectric constant εr ∼ 7).
C 1 on the other hand shows little dependence on the layer thickness. It shows only minor variations when changing the layer thickness. The response does not match the behavior expected for a ‘classical’ capacitor (C ∝ 1/d). Its magnitude, around 10−6 F, matches well with typical values of an electrochemical double layer, which is expected to be independent of the layer thickness.
The behavior of the circuit elements displayed in Fig. 9 leads to the conclusion that the first RC branch (composed of C1 (CPE1) & R1), represents a double layer or possibly a solid electrolyte interface. This is supported by the independence of the elements on the layer thickness and the magnitude of C1 which matches with typical values of the electrochemical double layer.
The second RC branch corresponds to the bulk response of the material. The capacitor can be matched with the electrostatic capacitance of the layer as was shown above. The resistance values found here are attributed to the ionic conductivity of the material, which is very small in the MgAl2O4 and the unannealed Li0.25Mg0.5Al2.25O4 layer, as shown in Fig. 6. The value shown for annealed Li0.25Mg0.5Al2.25O4 in Fig. 9d matches with what was extracted from for the ionic conductivity before, namely a value of 10−11 S cm−1 (cf.Fig. 6).
Conclusion
The behavior of different stoichiometries of thin films of LixMg1−2xAl2+xO4 (x = 0, 0.05, 0.15, 0.25) was evaluated as solid electrolyte. The material crystallized into the spinel structure as shown by both XRD and TEM investigations, although being aluminum rich. The layers showed low electronic conductivity, down to the thinnest layer probed here, namely 100 nm thick. This was confirmed by both dry current–voltage measurements and copper plating tests. Li-ion transport through the layers was shown by the formation of a lithium–platinum alloy in cyclic voltammetry. However, no signature of ionic conductivity was found in EIS measurements at OCV. This seeming discrepancy between the EIS investigation and cyclic voltammetry was resolved by performing potential dependent impedance spectroscopy. Such measurements showed a change of over 3 orders of magnitude in ionic conductivity upon lithium insertion into the LixMg1−2xAl2+xO4 layer.It was argued that the LixMg1−2xAl2+xO4 layers incorporate lithium through an intercalation like mechanism. The inserted Li-ions are mobile in the layer, causing a reduction in resistance. When the thermodynamically most favorable stoichiometry is reached, Li-ions are able to cross the electrolyte and alloy with the platinum current collector. Upon increasing the potential, lithium ions are repelled from the layer. A similar mechanism has recently been demonstrated for Li-ion conductivity through Al2O3 which also resulted in an increase in conductivity of over 3 orders of magnitude. We have thus shown that LixMg1−2xAl2+xO4 does not function as a solid electrolyte, however it might still find use as a buffer layer. In this case lattice matching can still occur between the interface of the spinel electrode (e.g. LiMn2O4, Li4Ti5O12,…) and the buffer layer. This might lead to better performance of a lattice matched buffer layer compared to e.g. amorphous Al2O3. An additional benefit of using spinel structured buffer layers, might be an increased cyclability of the electrodes. When using spinel LixMg1−2xAl2+xO4 buffer layers, the latter might provide anchoring points at the electrode interface which might help to maintain the structural integrity when these electrodes undergo volume changes or detrimental phase changes.
Acknowledgements
The authors thank Marcel Lux for providing the SEM, and Johan Meersschaut for the ERD and RBS characterization.References
- R. V. Noorden, Nature, 2014, 507, 26–28 CrossRef PubMed.
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- F. T. Wagner, B. Lakshmanan and M. F. Mathias, J. Phys. Chem., 2010, 1, 2204–2219 CAS.
- A. Arico, P. Bruce, B. Scrosati, J.-M. Tarascon and W. V. Schalkwijk, Nat. Mater., 2005, 4, 366–377 CrossRef CAS PubMed.
- M. Donders, J. Oudenhoven, L. Baggetto, H. Knoops, M. V. de Sanden, W. Kessels and P. Notten, ECS Trans., 2010, 32, 213–222 Search PubMed.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- P. Vereecken, 2014, http://electroiq.com/blog/2014/05/towards-all-solid-state-3d-thin-film-batteries-for-durable-and-fast-storage/.
- F. Rosciano, P. P. Pescarmona, K. Houthoofd, A. Persoons, P. Bottke and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 6107–6112 RSC.
- M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195, 7904–7929 CrossRef CAS PubMed.
- A. N. Lab, Materials and energy flows in the materials production, assembly and end-of-life stages of the automotive lithium ion battery life cycle, 2010.
- A. N. Lab, Modeling the Performance and Cost of Lithium-Ion Batteries for Electric-Drive Vehicles, 2011.
- P. Arora and Z. Zhang, Chem. Rev., 2004, 104, 4419–4462, DOI:10.1021/cr020738u.
- D. Ruzmetov, V. P. Oleshko, P. M. Haney, H. J. Lezec, K. Karki, K. H. Baloch, A. K. Agrawal, A. V. Davydov, S. Krylyuk, Y. Liu, J. Y. Huang, M. Tanase, J. Cumings and A. A. Talin, Nano Lett., 2012, 12, 505–511 CrossRef CAS PubMed.
- D. Santhanagopalan, D. Qian, T. McGilvray, Z. Wang, F. Wang, F. Camino, J. Graetz, N. Dudney and Y. S. Meng, J. Phys. Chem. Lett., 2014, 5, 298–303 CrossRef CAS PubMed.
- Y. Liu, X. H. Liu, B.-M. Nguyen, J. Yoo, J. P. S. S. T. Picraux, J. Y. Huang and S. A. Dayeh, Nano Lett., 2013, 13, 4876–4883 CrossRef CAS PubMed.
- M. M. Thackery and J. B. Goodenough, Solid state cell wherein an anode solid electrolyte and cathode each comprise a cubic-close-packed framework structure, US Pat., 4507371, 1985 Search PubMed.
- F. Rosciano, P. P. Pescarmona and A. Persoons, Ion conductor and solid state battery, US Pat., Application 20130045426 A1, 2013 Search PubMed.
- F. Rosciano, P. P. Pescarmona and A. Persoons, 218th ECS Meeting, 2010, vol. 127.
- M. Thackeray, L. de Picciotto, A. de Kock, P. Johnson, V. Nicholas and K. Adendorff, J. Power Sources, 1987, 21, 1–8 CrossRef CAS.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- M. Thackeray, P. Johnson, L. A. de Picciotto, P. Bruce and J. Goodenough, Mater. Res. Bull., 1984, 19, 174–187 CrossRef.
- R. Gummow, A. Kock and M. Thackery, Solid State Ionics, 1994, 69, 59–67 CrossRef CAS.
- T. Aaltonen, V. Miikkulainen, K. B. Gandrud, A. Pettersen, O. Nilsen and H. Fjellvg, 220th ECS Meeting, 2011.
- K. M. Colbow, J. R. Dahn and R. R. Haering, J. Power Sources, 1989, 26, 397–402 CrossRef CAS.
- M. J. Mees, G. Pourtois, F. Rosciano, B. Put, P. M. Vereecken and A. Stesmans, Phys. Chem. Chem. Phys., 2013, 16, 5399–5406 RSC.
- H. Kawai, M. Tabuchi, M. Nagata, H. Tukamoto and A. R. West, J. Mater. Chem., 1998, 8, 1273–1280 RSC.
- H. Lutz, W. Schmidt and H. Haeuseler, J. Phys. Chem. Solids, 1981, 42, 287–289 CrossRef CAS.
- R. Kanno and Y. T. O. Yamamoto, Mater. Res. Bull., 1981, 16, 999–1005, DOI:10.1016/0025-5408(81)90142-2.
- S. Giangrandi, T. Sajavaara, B. Brijs, K. Arstila, A. Vantomme and W. Vandervorst, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 5144–5150 CrossRef CAS PubMed.
- J. Shou-Yong, L. Li-Bin, H. Ning-Kang, Z. Jin and L. Yong, Phys. Chem. Chem. Phys., 2000, 19, 225–227 Search PubMed.
- M. Lejus and R. Collongues, C.R. Chim., 1962, 2005–2007 Search PubMed.
- L. Vegards, Z. Phys., 1921, 5, 17–26 CrossRef.
- F. Ayguavivesa, B. Agius, B. Ea-Kim and I. Vickridge, J. Mater. Res., 2001, 16, 3005–3008 CrossRef.
- S. Berg and I. Katardjiev, J. Vac. Sci. Technol., A, 1999, 17, 1916–1925 CAS.
- S. Jakschik, U. Schroeder, T. Hecht, M. Gutsche, H. Seid and J. W. Bartha, Thin Solid Films, 2003, 425, 216–220 CrossRef CAS.
- A. Rahman and M. S. Raven, Thin Solid Films, 1980, 71, 7–13, DOI:10.1016/0040-6090(80)90177-7.
- M. Voigt and M. Sokolowski, Mater. Sci. Eng., B, 2004, 109, 99–103 CrossRef PubMed.
- M. Bortz, R. French, D. Jones, R. Kasowski and F. Ohuchi, Phys. Scr., 1990, 41, 537–541 CrossRef CAS.
- M. Ihara, Y. Arimoto, M. Jifuku, T. Kimura, S. Kodama, H. Yamawaki and T. Yamaoka, J. Electrochem. Soc., 1982, 129, 2569–2573, DOI:10.1149/1.2123611.
- H. Honbo and H. Momose, J. Electroanal. Chem., 2010, 638, 269–274 CrossRef CAS PubMed.
- R. Wibowo, S. E. Jones and R. G. Compton, J. Phys. Chem. B, 2009, 113, 12293–12298 CrossRef CAS PubMed.
- R. Huggins, Ionics, 2002, 8, 300–313 CrossRef CAS.
- S. C. Jung and Y. Han, J. Phys. Chem. Lett., 2013, 4, 2681–2685 CrossRef CAS.
- G. Song, X. Li, Y. Wang, Z. Peng, Y. Yu and P. Li, Mater. Charact., 2010, 61, 371–375 CrossRef CAS PubMed.
- J. Macdonald, LEVM Manual, 2015, http://jrossmacdonald.com/jrm/wp-content/uploads/LEVMMANUAL.pdf.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods Fundamentals and Applications, John Wiley and Sons, 2001 Search PubMed.
- A. C. Kozen, C.-F. Lin, A. J. Pearse, M. A. Schroeder, X. Han, L. Hu, S.-B. Lee, G. W. Rubloff and M. Noked, ACS Nano, 2015, 9, 5884–5892 CrossRef CAS PubMed.
- Y. S. Jung, A. S. Cavanagh, L. A. Riley, S.-H. Kang, A. C. Dillon, M. D. Groner, S. M. George and S.-H. Lee, Adv. Mater., 2010, 22, 2172–2176 CrossRef CAS PubMed.
- X. Xiao, P. Lu and D. Ahn, Adv. Mater., 2011, 23, 3911–3915 CrossRef CAS PubMed.
- M. E. Orazem, I. Frateur, B. Tribollet, V. Vivier, S. Marcelin, N. Pebere, A. L. Bunge, E. A. White, D. P. Riemer and M. Musiani, J. Electrochem. Soc., 2013, 160, C215–C225, DOI:10.1149/2.033306jes.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp03916a |
| This journal is © the Owner Societies 2015 |





