Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Two-photon absorption of fluorescent protein chromophores incorporating non-canonical amino acids: TD-DFT screening and classical dynamics†
M.
Alaraby Salem
and
Alex
Brown
*
Department of Chemistry, University of Alberta, Edmonton, Alberta T6G 2G2, Canada. E-mail: alex.brown@ualberta.ca; Fax: +780-492-8231; Tel: +780-492-1854
First published on 4th September 2015
Abstract
Two-photon spectroscopy of fluorescent proteins is a powerful bio-imaging tool characterized by deep tissue penetration and little damage. However, two-photon spectroscopy has lower sensitivity than one-photon microscopy alternatives and hence a protein with a large two-photon absorption cross-section is needed. We use time-dependent density functional theory (TD-DFT) at the B3LYP/6-31+G(d,p) level of theory to screen twenty-two possible chromophores that can be formed upon replacing the amino-acid Tyr66 that forms the green fluorescent protein (GFP) chromophore with a non-canonical amino acid. A proposed chromophore with a nitro substituent was found to have a large two-photon absorption cross-section (29 GM) compared to other fluorescent protein chromophores as determined at the same level of theory. Classical molecular dynamics are then performed on a nitro-modified fluorescent protein to test its stability and study the effect of the conformational flexibility of the chromophore on its two-photon absorption cross-section. The theoretical results show that the large cross-section is primarily due to the difference between the permanent dipole moments of the excited and ground states of the nitro-modified chromophore. This large difference is maintained through the various conformations assumed by the chromophore in the protein cavity. The nitro-derived protein appears to be very promising as a two-photon absorption probe.
1 Introduction
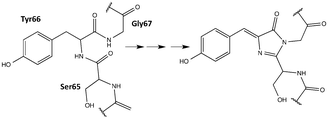
Fluorescent proteins (FPs) are the family of homologues of the green fluorescent protein (GFP) of Aequorea victoria initially discovered in the 1960s.1 FPs found great utility as spectroscopic tools after the cloning of the GFP gene2 and the demonstration that they can be expressed in other organisms while maintaining their fluorescent properties.3,4 The unique light-absorbing and fluorescence ability for FPs is due to the formation of a chromophore by a post-translational modification of three precursory amino acids within the protein shell (Fig. 1).5,6 The coarse tuning of the colour of fluorescence is generally mediated by the alteration of the precursory amino acids which lead to different chromophores upon maturation. Changes in the micro-environment of the chromophore can also strongly affect the colour of the fluorescence, as seen in some yellow variants of the GFP.7 In addition to fluorescence wavelength, the protein environment generally offers fine tuning for all photophysical properties of the FP. A full palette spanning red to blue fluorescent proteins has been synthesized8,9 with the red-shifted chromophores being of great interest due to their lower cell-toxicity.10Two-photon microscopy of FPs offers many advantages over its conventional one-photon counterpart. It is less phototoxic, as photons of longer wavelength (and less energy) are absorbed and provides better focus and less out-of-focus bleaching enabling it to have deeper penetration into thick tissues.11,12 These advantages arise because the two-photon absorption (TPA) probability, the so-called TPA cross-section, is directly proportional to the square of incident light intensity. This property, however, causes TPA to have less sensitivity compared to its one-photon counterpart. Thus, fluorophores with large TPA cross-sections are preferred – a major motivation for this work. TPA is governed by different quantum mechanical selection rules as compared to one-photon absorption (OPA) and so structural modifications in the protein environment can significantly affect the TPA of a FP with minimal effect on its OPA. For example, in the series of red FPs, their measured TPA cross-sections range from 15 GM (for mTangerine13) to 119 GM (for tdTomato13) for the lowest-energy excitation although they all share the same chromophore.14
In addition to the known general difficulty of measuring absolute TPA cross-sections,15 measurements in biological systems like FPs are more challenging due to the need for additional calibration. Drobizhev et al. comprehensively explained and cited the discrepancies in the reported absolute TPA cross-sections of FPs.14 Generally, the TPA spectrum of a FP has two regions of strong absorption: one is at (approximately) double the wavelength of the OPA peak and an additional (strong) band of absorption corresponds to a shorter wavelength. In the FPs with anionic chromophores, the TPA peak is blue-shifted with respect to the corresponding OPA peak (at half the wavelength). This has been rationalized by the enhancement of a vibronic transition in the two-photon process.16–19 The additional band that is absent from the corresponding OPA spectrum was first theoretically predicted20 to be present in the TPA spectra of all FPs and later confirmed through experimental measurements.14 Theoretical investigations showed that the peak at longer wavelength is caused by the excitation to the first excited state (S0 to S1), while the other short-wavelength peak is due to a transition to a higher electronic state (S0 to Sn). TPA corresponding to the higher-energy transitions has been shown to be amplified due to a resonance enhancement effect.20–22 Being in the near-IR region, the S0 to S1 absorptions are of more practical relevance and thus are the focus of the present work.
Some theoretical studies of the TPA properties of FPs include the whole protein via combined quantum mechanics/molecular mechanics (QM/MM) approaches. List et al. studied the steric factors and chromophore protein-interactions that result in the enhancement of the TPA peak corresponding to the S0–S1 transition in DsRED,23 a red FP.19 They attributed the TPA enhancement to the increase in the difference between the permanent dipole moments of the excited and ground states. Another study on GFP succeeded in qualitatively reproducing most of the experimental features of the TPA spectrum.24 Although the TPA cross-section of a chromophore can be largely altered by the protein environment, studying the isolated chromophore can be a good starting point to predict or understand the TPA properties of the protein.20 A study of the chromophore and close-by residues of a yellow variant of GFP employed RICC2 and TD-DFT with CAM-B3LYP to discern the effect of π–π stacking on TPA.25 Although there was good qualitative agreement between the two methods, the values of the TPA cross-sections had to be scaled for comparison. In a benchmark study, Salem and Brown evaluated the use of several functionals by comparing the TPA of isolated FP chromophores as computed via TD-DFT to averaged experimental data and higher-level CC2 computations.22 Results showed that the B3LYP functional can provide a semi-quantitative description of the major TPA peaks. Recently, equation-of-motion coupled-cluster with single and double substitutions (EOM-CCSD)26,27 was formulated for TPA and applied to chromophores of GFP and photoactive yellow protein.28 TPA transition moment values computed with this method are comparable to TD-DFT values for similar model chromophores. These studies support the use of computation to design rationally new chromophores.
While many FPs have been engineered and a subset scrutinized computationally, they have, in general, been built from the canonical 20 amino acids. However, the protein engineering toolbox has been rapidly expanding as protein chemists have developed methods for incorporating non-canonical amino acids (ncAAs) into proteins.29–33 Incorporating ncAAs can generate proteins with novel properties. A number of FPs containing ncAAs, which have been incorporated into the chromophore, have been engineered and experimentally characterized for their OPA and fluorescence properties;34–42 to the best of our knowledge, TPA has not been explored for FPs containing ncAAs. A notable example for OPA is the Gold FP (GdFP),36 which is represented by model 20 in Fig. 2 where Trp57 and Trp56 in enhanced cyan FP (ECFP) have been replaced by 4-amino-Trp. These substitutions lead to a strongly red-shifted emission compared to ECFP. Site-specific substitutions of ncAAs for Tyr66 in GFP have also lead to novel chromophore structures with spectral properties notably different from the wild-type GFP.35,38 As examples for residue-specific mutations, two tyrosine analogues (3-amino-L-tyrosine and 3-fluoro-L-tyrosine) have been incorporated into the DsRed-Monomer FP, leading to shifts in fluorescence wavelengths but, more importantly, increases in quantum yield.39 While incorporation of ncAAs can directly influence the chromophore structure, ncAAs inserted outside the central chromophore can indirectly change its excitation and/or emission behavior.43 Although using ncAAs in FP design clearly opens up new possibilities, the use of ncAAs is difficult. Thus, any newly designed FP must function better or differently than one that can be engineered using the 20 canonical amino acids. In this work, we use TD-DFT to screen a variety of possible chromophores that can result from the replacement of the Tyr residue of the tripeptide precursor with one of the ncAAs previously used in protein synthesis. The property at focus is the TPA of the chromophore. The most promising candidate is further simulated in a proposed protein environment using molecular dynamics (MD) to study the protein stability and the steric effects of the protein on the TPA of the chromophore.
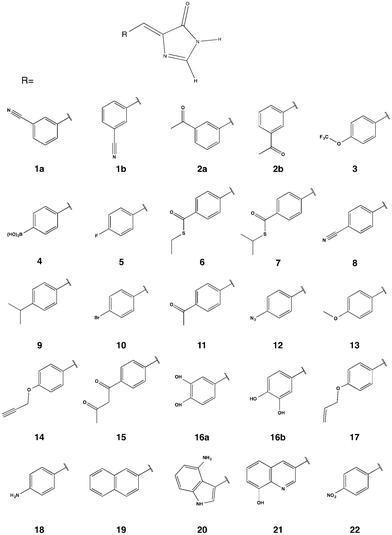 | ||
| Fig. 2 Chromophore models built from the parent GFP chromophore by replacing the phenol of Tyr-66 with the corresponding moiety in a ncAA. | ||
2 Computational methods
2.1 Chromophores
A template chromophore model was obtained from GFP by breaking the chromophore connections to the rest of the protein and capping with H-atoms. The π-conjugated system necessary for TPA is preserved. Our previous work showed that methyl capping is only crucial when the chromophore has an extended conjugation beyond that in the GFP chromophore.22 Since we only include chromophores derived from a GFP-chromophore template, capping with hydrogen atoms in this present study yields nearly the same TPA values as with methyl groups. We selected candidate amino acids from those compiled by Liu et al.30 based on the following two criteria: (1) having an aromatic ring that is necessary for extended conjugation and (2) excluding bulkier systems that are less likely to fit in the chromophore cavity (without engineering the protein to accommodate the larger sized moiety). For comparison, however, we considered 2 models (19 and 21) with two-cyclic rings that are comparable to that in the GdFP (model 20). The protein with the 2-naphthyl moiety (model 19) was previously shown to be non-fluorescent probably because the cavity needed to be further manipulated to accommodate the chromophore, as suggested by the authors.35 Assuming a point mutation at Tyr 66, the phenol ring of the chromopohore is replaced with the corresponding moiety in the given ncAA yielding the chromophore models in Fig. 2. For chromophores 1, 2 and 16, both the E and the Z isomers were considered and labelled a and b, respectively.2.2 Ab initio computations
Following a previous protocol,22 the chromophore models were optimized in the gas phase using the PBE0 functional44,45 (optimized coordinates are given in Table S1, ESI†). Excited-state properties were computed with TD-DFT46 within the response theory framework using the B3LYP functional47 and the conductor-like polarizable continuum model (commonly referred to as PCM)48–51 with parameters for water – except where noted. The basis set 6-31+G(d,p)52–56 in cartesian form, i.e., 6 d-functions, was used in all computations. OPA oscillator strengths (and similarly the transition dipole moments from ground to excited states) were computed via linear response57 while the two-photon transition matrix elements and the transition dipole moments between excited states were evaluated from the single and double residues of the quadratic response function,58–61 respectively. Dipole moment elements not involving the ground state (〈n|μ|n〉 and 〈n|μ|m〉, where n, m ≠ 0) were computed via the DALTON62 software package in the gas phase. All other computations were done with GAMESS-US63 (the May-2013 version). For computations with PCM, default parameters in the GAMESS code were utilized.For linearly polarized light, the transition moment for TPA is
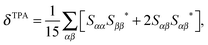 | (1) |
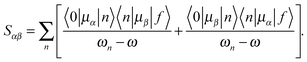 | (2) |
From the TPA transition moment and excitation energies (ωf) produced by GAMESS, the TPA cross-section is calculated in macroscopic units by:
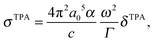 | (3) |
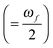 and Γ is the broadening factor derived from a Lorentzian function and chosen to be 0.1 eV, as previously employed20,22,64 for comparison with experiment. The choice of the conversion equation (eqn (3)) and the broadening factor, Γ, affect the resulting values of the TPA cross-sections. In a recent study, Beerepoot et al.65 discussed the various forms of eqn (3) and gave recommendations on presenting TPA data for computational studies.
and Γ is the broadening factor derived from a Lorentzian function and chosen to be 0.1 eV, as previously employed20,22,64 for comparison with experiment. The choice of the conversion equation (eqn (3)) and the broadening factor, Γ, affect the resulting values of the TPA cross-sections. In a recent study, Beerepoot et al.65 discussed the various forms of eqn (3) and gave recommendations on presenting TPA data for computational studies.
2.3 Molecular dynamics simulation
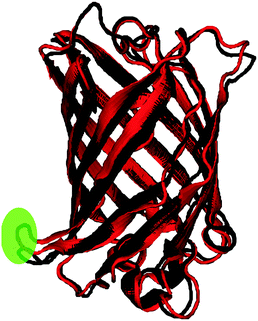
To test the stability of a protein upon the introduction of a selected ncAA, MD trajectories were generated following the same protocol for two FPs: (1) a reference EGFP (PDB ID: 2Y0G) with the corresponding anionic chromophore which we refer to as control and (2) the same protein after replacing the chromophore with model 22 (see Fig. 2) that is assumed to be formed by replacing Tyr 66 with a Tyrosine-derived ncAA. We refer to this modified protein as nitro.The crystal structure for the control and its modified nitro version were prepared using the pdb4amber and reduce programs66 in Ambertools 14. The 2Y0G crystal structure is missing 12 residues from the protein termini and hence these are unlikely to affect the dynamics of the β-barrel or the chromophore environment. The missing residues are not considered and the protein is renumbered, so that the chromophore is formed by residue 63. The all-atom forcefield AMBER ff12SB67,68 was used to parameterize both protein models except for the chromophore residue. The chromophore in both cases includes all atoms between the LEU 62 and the VAL 64 so that more linker atoms are considered than in the attenuated models used for DFT screening (see Tables S2 and S3, ESI†). Although previously validated parameters are available for the control chromophore,69 we adopted a general procedure to parameterize both nitro and control chromophores and it can be easily extended to test other residues of interest. The parameters generated here serve the purpose of determining the protein stability and conformational freedom of the chromophore. We used ANTECHAMBER70 to generate parameters for the nitro chromophore that are consistent with the General Amber Force Field (GAFF).71 We assigned similar parameters to the control chromophore. Charges were derived using the online R.E.D. server development tool72 following the default scheme for amino acid fragments. All parameters are given in the ESI† (see Tables S2 and S3 for atom types and charges). All crystallographic water molecules were removed, including those in the vicinity of the chromophore to enable extra conformational freedom. Each protein model was solvated with approximately 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TIP3P water molecules in a cuboid solvation box with an edge length of 20 Å. To neutralize the negatively charged protein, 7 Na+ ions were added to each model followed by 64 Na+ and Cl− ions to reach a salt concentration of 0.15 M.
000 TIP3P water molecules in a cuboid solvation box with an edge length of 20 Å. To neutralize the negatively charged protein, 7 Na+ ions were added to each model followed by 64 Na+ and Cl− ions to reach a salt concentration of 0.15 M.
The MD simulations were done with the AMBER Molecular Dynamics package73 following a standard protocol that consists of minimization, heating, density equilibration and production. Minimization was done first with restraints on the protein atoms and then repeated without restraints. Heating was applied gradually for 20 ps with restraints on the protein atoms. Density equilibration was achieved in four 50 ps runs while gradually relieving the restraint. This was followed by a production run at constant pressure for 99 ns. Langevin dynamics were employed globally throughout the simulations. Details of the simulations are provided in terms of Amber input files in the ESI.† Trajectories were analyzed via CPPTRAJ.74
3 Results and discussion
Computing the TPA of FPs involves several levels of complexity. In addition to the intrinsic nature of the chromophore, there are other factors that affect the TPA of a FP. One factor is that the protein shell can change the conformation of the chromophore to enhance or diminish its two-photon absorption cross-section.19,22 This factor can be accounted for via TD-DFT which can capture the change in TPA associated with various conformers in a semi-quantitative fashion.22 Another level of complexity is added by the protein–chromophore interactions, or the electric field due to the protein around the chromophore, which can greatly influence the TPA cross-section.14,19 In the present work, we compute TPA cross-sections for isolated chromophores ignoring the protein shell (Section 3.1). We then account for part of the influence of the protein shell by running a classical MD simulation for an EGFP-based protein with the chromophore predicted to have the largest cross-section (nitro) and compare it to an analogous simulation for its native form (control). The motivation is to obtain insight into the relative stability of the protein after introducing the new moiety (Section 3.2) and to account for part of the influence of the protein shell on the chromophore, through studying its flexibility over the trajectory and computing TPA for different conformations of the isolated chromophore (Section 3.3).3.1 TPA cross-sections
The TPA cross-sections for the lowest-energy transition (S0–S1) of all the GFP-derived chromophores with natural amino acids have been previously computed.22 Their TPA cross-sections at the B3LYP/6-31G+(d,p) level of theory in PCM H2O range from 1 GM (for the BFP75,76 chromophore) to 7 GM (for the CFP76 chromophore) when scaled according to eqn (3) in the present study. As discussed by Beerepoot et al.,65 the TPA values reported previously22 are too large by a factor of 4. An equivalent range of TPA cross sections is determined for molecules 5 through 18 in this study. TPA cross-sections, as computed from eqn (3), are given in Table 1 while δTPA values are given in Table S4 in the ESI.† Proteins with bromo, methoxy and amino substituted chromophores (models 10, 13 and 18, respectively) have been previously synthesized and shown to be fluorescent.35 Their measured OPA energies are: 3.31 eV, 3.15 eV and 2.85 eV, respectively.35 Compared to the values 3.37 eV, 3.29 eV and 3.14 eV in Table 1, TD-DFT using B3LYP/6-31+G(d,p) captures the proper trend within the expected error range. For model 20, the computed energy of 2.69 eV is very close to the measured absorption peak at 2.66 eV for the corresponding GdFP.36 The trend in Table 1 looks very promising because, in general, the chromophores with the largest computed TPA cross-sections are the most red-shifted ones.| Model | Energy (eV) | OS | TPA (GM) |
|---|---|---|---|
| 1a | 3.455 | 0.640 | 0 |
| 2a | 3.468 | 0.679 | 0 |
| 1b | 3.473 | 0.652 | 0 |
| 2b | 3.452 | 0.557 | 0 |
| 3 | 3.463 | 0.705 | 0 |
| 4 | 3.387 | 0.787 | 0 |
| 5 | 3.467 | 0.704 | 1 |
| 6 | 3.197 | 0.912 | 1 |
| 7 | 3.200 | 0.927 | 1 |
| 8 | 3.304 | 0.796 | 2 |
| 9 | 3.403 | 0.841 | 3 |
| 10 | 3.369 | 0.848 | 3 |
| 11 | 3.256 | 0.812 | 4 |
| 12 | 3.210 | 0.984 | 5 |
| 13 | 3.289 | 0.853 | 7 |
| 14 | 3.310 | 0.894 | 7 |
| 15 | 3.222 | 0.837 | 7 |
| 16a | 3.218 | 0.577 | 8 |
| 16b | 3.260 | 0.711 | 7 |
| 17 | 3.284 | 0.901 | 8 |
| 18 | 3.137 | 0.927 | 9 |
| 19 | 3.138 | 0.553 | 11 |
| 20 | 2.689 | 0.363 | 15 |
| 21 | 2.985 | 0.298 | 17 |
| 22 | 2.965 | 0.638 | 29 |
Although the computation was done in the response theory framework, comparison to a truncated sum-over-states expression gives insight into the factors contributing to the TPA cross section. In a 2-level model (2LM) approximation, the TPA cross-section is proportional to the square of the difference between the permanent dipole moments of the excited and ground states (〈1|μ|1〉 − 〈0|μ|0〉)2 and that of the transition dipole moment from the ground to the excited state (〈0|μ|1〉2). The dipole elements for the chromophore models were determined in the gas phase, as the corresponding PCM computations were difficult to converge in DALTON. This change in medium does not affect the analysis, as the trend of TPA cross-sections for the first bright transition is the same whether computed with PCM or in the gas phase (Table S7, ESI†). The dipole elements and the corresponding cross-sections (σ2LM) calculated directly using eqn (1)–(3) are given in Table 2 for the models where the first gas-phase excitation corresponds to the first PCM one. There is a significant discrepancy between the absolute σ values computed via response theory (see Table S7, ESI†) and the corresponding 2LM ones (Table 2). However, the trend is the same (with the exchange of order for models 16a and 18). Since all studied molecules are nearly planar (symmetry was not enforced during geometry optimization), there is no contribution from dipole elements along the z-axis. Most of the contribution comes from the dipole moments along the x-axis which runs through the π-conjugated system. The nitro-derivative, molecule 22, has both large dipole difference and transition dipole moment which explains the large cross-section obtained via response theory computation.
| Model | (Δμx)2 | (Δμy)2 | μ x01 2 | μ y01 2 | σ 2LM |
|---|---|---|---|---|---|
| 6 | 0.0 | 0.1 | 9.8 | 0.1 | 1 |
| 7 | 0.1 | 0.1 | 9.9 | 0.1 | 1 |
| 12 | 0.6 | 0.0 | 10.5 | 0.0 | 5 |
| 13 | 0.8 | 0.0 | 8.7 | 0.0 | 6 |
| 14 | 0.8 | 0.0 | 9.3 | 0.1 | 6 |
| 16a | 5.2 | 0.0 | 5.0 | 0.2 | 22 |
| 18 | 1.2 | 0.0 | 9.6 | 0.0 | 10 |
| 19 | 8.8 | 0.1 | 4.0 | 0.1 | 31 |
| 20 | 10.6 | 0.7 | 3.8 | 0.1 | 34 |
| 22 | 7.0 | 0.0 | 7.6 | 0.0 | 46 |
3.2 Protein stability
The root-mean-square deviation (RMSD) for the backbone atoms and the root-mean-square fluctuation (RMSF) for the protein residues are shown for the two trajectories in Fig. 3. As expected due to the modification introduced to the nitro model, its RMSD is larger than the control. The RMSD deviation, however, is still within range of the crystal-structure resolution of 1.5 Å. A comparison of the average bond lengths in the chromophores from the MD simulations with the DFT-optimized values, and, for the control, those from X-ray crystallography show no significant deviations (see Tables S5 and S6 in ESI†). Fig. 4 shows a superposition of an average structure for each model generated from the trajectory between 60 and 99 ns. Residue 153 with the largest RMSF is a loop residue outside the β-barrel structure and thus is more flexible than the residues composing the β-sheets (see Fig. 4). In addition to the duly conserved 3D structure in the modified model of the protein, the unique neutral form of the nitro chromophore should make it, in principal, less sensitive to changes in the surrounding micro-environment.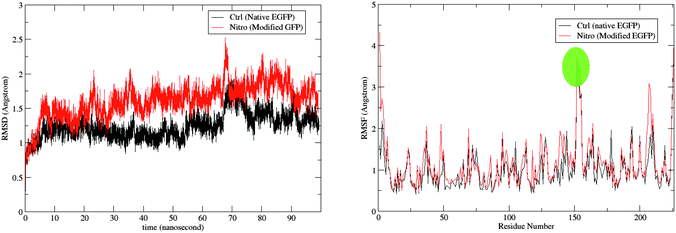 | ||
| Fig. 3 The RMSD of the protein in reference to the original minimized structure (left) and the RMSF of the protein residues (right) over the simulation period of 99 ns. Fluctuation for residue 153 is highlighted (see Fig. 4). | ||
3.3 Conformational analysis of the chromophore
We monitored the conformational flexibility of the chromophore using three characteristic angles: the angle corresponding to the methine bridge, as well as the tilting and the twisting angles of the nitro-benzylidine moiety with respect to the imidazolinone ring (see Fig. 5). The three angles were recorded for 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 snapshots over the course of 99 ns. The minimum, maximum and average values for these angles are shown in Table 3. The methine bridge shows the least flexibility with more than 14% of the snapshots having the average angle of 134° and 95% of the snapshots having an angle within 129° and 139°. The twisting and tilting angles show more flexibility where 6.5% and less than 3.5% snapshots have the average angles for each, respectively. In 95% of the snapshots, the twist angle ranges from 160° to 200° and the tilt angle ranges from −30° to 30°. Hence, we generated 117 conformers by varying the twist and tilt angles by 5° within these ranges and fixing the methine bridge at the average angle of 134°. For each conformer, we computed the first excitation energy, OPA and TPA at the same level of theory used in screening the chromophore models, that is, TD-B3LYP/6-31+(d,p) in PCM with parameters for H2O. The trends for the TPA cross-section and OPA oscillator strength are illustrated in Fig. 6.
511 snapshots over the course of 99 ns. The minimum, maximum and average values for these angles are shown in Table 3. The methine bridge shows the least flexibility with more than 14% of the snapshots having the average angle of 134° and 95% of the snapshots having an angle within 129° and 139°. The twisting and tilting angles show more flexibility where 6.5% and less than 3.5% snapshots have the average angles for each, respectively. In 95% of the snapshots, the twist angle ranges from 160° to 200° and the tilt angle ranges from −30° to 30°. Hence, we generated 117 conformers by varying the twist and tilt angles by 5° within these ranges and fixing the methine bridge at the average angle of 134°. For each conformer, we computed the first excitation energy, OPA and TPA at the same level of theory used in screening the chromophore models, that is, TD-B3LYP/6-31+(d,p) in PCM with parameters for H2O. The trends for the TPA cross-section and OPA oscillator strength are illustrated in Fig. 6.
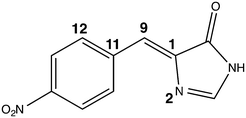 | ||
| Fig. 5 The nitro chromophore model showing the three angles monitored in the conformational study: the methine bridge is the angle between atoms 11 - 9 - 1, the tilt angle is the dihedral between atoms 11 - 9 - 1 - 2 and the twist is the dihedral between atoms 12 - 11 - 9 - 1. The full z-matrix is given in Table S8 in the ESI.† | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 snapshots of the full simulation trajectory
511 snapshots of the full simulation trajectory
| Methine bridge | Tilt | Twist | |
|---|---|---|---|
| Minimum | 123° | −49° | 152° |
| Maximum | 145° | 60° | 207° |
| Average | 134° | −6° | 178° |
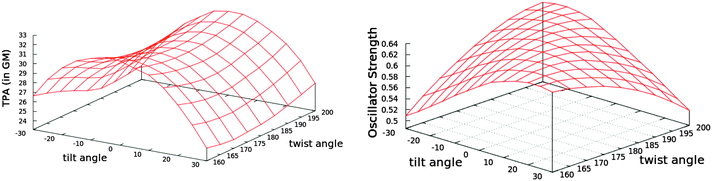 | ||
| Fig. 6 The variation of TPA cross-section (left) and OPA oscillator strength (right) with the tilt and twist angles while fixing the methine bridge at 134° (see Fig. 5 for the definition of the angles). The tabulated values are given in Table S9 in the ESI.† | ||
The trend in the excitation energy is similar to that for the TPA cross-section. Nevertheless, the TPA trend is not driven by the change in energy, as the largest energy difference in the set of conformers is less than 0.1 eV (Fig. S1, ESI†). Further, the same TPA trend is generated even if the same excitation energy is used to calculate the TPA cross-section for all conformers. For the OPA oscillator strength, a uniform parabola can be noticed when the tilt angle is fixed to the planar value, 0°, and the twist is varied, or the twist is fixed to 180° and the tilt is varied. In such cases, the oscillator strength decreases upon deviation from planarity. The decrease is the same whether the tilt or the twist is varied. As the fixed angle deviates from the planar value, the curve is skewed. On the other hand, the TPA cross-section increases when the twist angle deviates from 180° and decreases when the tilt angle deviates from a planar or near-planar value. The TPA value is significantly more sensitive to the tilt angle than it is to the twist angle. To further investigate the reason for such trends in the TPA cross-sections, we computed the difference between the first excited state permanent dipole moment and the ground state dipole moment for each conformer (〈1|μ|1〉 − 〈0|μ|0〉) at the TD-B3LYP/6-31G+(d,p) level of theory in the gas phase. The square of the x-components of the dipole difference are plotted in Fig. 7. The resemblance in trend and the magnitude of the difference as the tilt and twist angles change strongly confirms that the TPA cross-section variation is driven by the difference between permanent dipoles. These results could further guide the protein engineering of the chromophore cavity to optimize its TPA, where a (near) planar value is needed for the tilt angle and deviation of the twist angle from planarity is desirable.
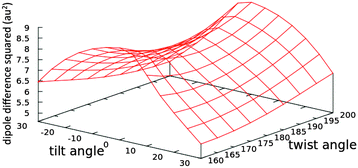 | ||
| Fig. 7 The effect of changing the tilt and twist angles while fixing the methine bridge at 134° (see Fig. 5) on the square of the difference between the x-components of the permanent dipoles of the first excited and the ground states (〈1|μx|1〉 − 〈0|μx|0〉) of the nitro chromophore (model 20) computed at the TD-B3LYP/6-31G+(d,p) level of theory in the gas phase. The tabulated values are given in Table S9 in the ESI.† | ||
4 Conclusion
A group of 22 proposed FP chromophore models derived from ncAAs are screened for their TPA cross-sections. TD-DFT employing the B3LYP functional was used in the screening. Most of the studied molecules exhibited poor intrinsic TPA cross-sections similar to the naturally occurring GFP-derived chromophore models. Molecules with multiple rings, as expected due to the extended conjugation, showed relatively large TPA cross-sections. The chromophore with the largest cross-section, however, was the one derived from a nitro-based ncAA. Two-state model analysis suggests that the increase in TPA is due to both its large transition dipole moment (〈0|μ|1〉) and the significant difference between the permanent dipole moments of its first excited and ground state (〈1|μ|1〉 − 〈0|μ|0〉).To investigate this model further, MD simulations were run on both a native EGFP (control) and a nitro-derived EGFP (nitro). Comparison with the control showed that the protein was stable after the replacement of the hydroxyl group with the nitro substituent. A conformational analysis was then performed to study the change of TPA with a range of the conformations visited by the chromophore in the protein cavity. Results show that a large TPA cross-section (24–32 GM) is maintained through the various conformations and that the TPA fluctuation is, again, driven by the change in the difference between the permanent dipole moments of its first excited state and its ground state (〈1|μ|1〉 − 〈0|μ|0〉).
In this proposed model, we accounted for two degrees of complexity, that is, the nature of the chromophore and the effect of the protein environment on the chromophore conformation. There still remains the consideration of the chromophore-protein interactions and the electric field due to the protein shell as both can affect the TPA cross-section. The sensitivity to the surrounding electrostatic environment of the chromophore is due to the dependence of the TPA cross-section on 〈1|μ|1〉 − 〈0|μ|0〉. The red FPs share the same chromophore that has an intrinsic TPA cross-section of about 5 GM, as computed previously at the same level of theory used in the present work (TD-B3LYP/6-31+G(d,p)).22 However, due to the protein shell, some red FP proteins reach an experimental TPA cross-section of 139 GM;14 a 27-fold amplification. This amplification has been attributed to the sensitivity of the difference between permanent dipoles (〈1|μ|1〉 − 〈0|μ|0〉) to the electric field of the protein.14 The nitro model, having most of its TPA driven by a large difference between permanent dipoles, seems to be a promising FP target especially if properly engineered to amplify its large intrinsic cross-section.
Acknowledgements
This work was supported by the Natural Sciences and Engineering Council of Canada (NSERC Discovery Grant to A.B.). This research was enabled in part by support provided by Westgrid (http://www.westgrid.ca) and Compute/Calcul Canada (http://www.computecanada.ca).References
- O. Shimomura, F. H. Johnson and Y. Saiga, J. Cell. Comp. Physiol., 1962, 59, 223–229 CrossRef CAS PubMed.
- D. C. Prasher, V. K. Eckenrode, W. W. Ward, F. G. Prendergast and M. J. Cormier, Gene, 1992, 111, 229–233 CrossRef CAS PubMed.
- M. Chalfie, Y. Tu, G. Euskirchen, W. W. Ward and D. Prasher, Science, 1994, 263, 802–805 CrossRef CAS PubMed.
- S. Inouye and F. I. Tsuji, FEBS Lett., 1994, 341, 277–280 CrossRef CAS PubMed.
- M. Ormo, A. B. Cubitt, K. Kallio, L. A. Gross, R. Y. Tsien and S. Remington, Science, 1996, 273, 1392–1395 CrossRef CAS PubMed.
- F. Yang, L. G. Moss and G. Phillips, Nat. Biotechnol., 1996, 14, 1246–1251 CrossRef CAS PubMed.
- R. M. Wachter, M. A. Elsliger, K. Kallio, G. T. Hanson and S. J. Remington, Structure, 1998, 6, 1267–1277 CrossRef CAS PubMed.
- R. Nifosì and V. Tozzini, Fluorescent Proteins I, Springer, Berlin, Heidelberg, 2012, vol. 11, pp. 3–40 Search PubMed.
- N. C. Shaner, P. A. Steinbach and R. Y. Tsien, Nat. Methods, 2005, 2, 905–909 CrossRef CAS PubMed.
- R. Weissleder, Nat. Biotechnol., 2001, 19, 316–317 CrossRef CAS PubMed.
- C. Xu, W. Zipfel, J. B. Shear, R. M. Williams and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 10763–10768 CrossRef CAS.
- W. R. Zipfel, R. M. Williams and W. W. Webb, Nat. Biotechnol., 2003, 21, 1369–1377 CrossRef CAS PubMed.
- N. C. Shaner, R. E. Campbell, P. A. Steinbach, B. N. G. Giepmans, A. E. Palmer and R. Y. Tsien, Nat. Biotechnol., 2004, 22, 1567–1572 CrossRef CAS PubMed.
- M. Drobizhev, N. S. Makarov, S. E. Tillo, T. E. Hughes and A. Rebane, Nat. Methods, 2011, 8, 393–399 CrossRef CAS PubMed.
- D. Oulianov, I. Tomov, A. Dvornikov and P. Rentzepis, Opt. Commun., 2001, 191, 235–243 CrossRef CAS.
- Y. Ai, G. Tian and Y. Luo, Mol. Phys., 2013, 111, 1316–1321 CrossRef CAS.
- E. Kamarchik and A. I. Krylov, J. Phys. Chem. Lett., 2011, 2, 488–492 CrossRef CAS.
- M. Drobizhev, N. S. Makarov, S. E. Tillo, T. E. Hughes and A. Rebane, J. Phys. Chem. B, 2012, 116, 1736–1744 CrossRef CAS PubMed.
- N. H. List, J. M. H. Olsen, H. J. A. Jensen, A. H. Steindal and J. Kongsted, J. Phys. Chem. Lett., 2012, 3, 3513–3521 CrossRef CAS PubMed.
- R. Nifosì and Y. Luo, J. Phys. Chem. B, 2007, 111, 14043–14050 CrossRef PubMed.
- M. Drobizhev, N. S. Makarov, T. Hughes and A. Rebane, J. Phys. Chem. B, 2007, 111, 14051–14054 CrossRef CAS PubMed.
- M. A. Salem and A. Brown, J. Chem. Theory Comput., 2014, 10, 3260–3269 CrossRef CAS PubMed.
- L. A. Gross, G. S. Baird, R. C. Hoffman, K. K. Baldridge and R. Y. Tsien, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 11990–11995 CrossRef CAS PubMed.
- A. H. Steindal, J. M. H. Olsen, K. Ruud, L. Frediani and J. Kongsted, Phys. Chem. Chem. Phys., 2012, 14, 5440–5451 RSC.
- M. T. P. Beerepoot, D. H. Friese and K. Ruud, Phys. Chem. Chem. Phys., 2014, 16, 5958–5964 RSC.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- R. J. Bartlett, Mol. Phys., 2010, 108, 2905–2920 CrossRef CAS.
- K. D. Nanda and A. I. Krylov, J. Chem. Phys., 2015, 142, 064118 CrossRef PubMed.
- N. Budisa, Angew. Chem., Int. Ed., 2004, 43, 6426–6463 CrossRef CAS PubMed.
- C. C. Liu and P. G. Schultz, Annu. Rev. Biochem., 2010, 79, 413–444 CrossRef CAS PubMed.
- J. A. Johnson, Y. Y. Lu, J. A. V. Deventer and D. A. Tirrell, Curr. Opin. Chem. Biol., 2010, 14, 774–780 CrossRef CAS PubMed.
- M. G. Hoesl and N. Budisa, Curr. Opin. Biotechnol., 2012, 23, 751–757 CrossRef CAS PubMed.
- R. B. Quast, D. Mrusek, C. Hoffmeister, A. Sonnabend and S. Kubick, FEBS Lett., 2015, 589, 1703–1712 CrossRef CAS PubMed.
- M. Taki, T. Hohsaka, H. Murakami, K. Taira and M. Sisido, FEBS Lett., 2001, 507, 35–38 CrossRef CAS PubMed.
- L. Wang, J. Xie, A. A. Deniz and P. G. Schultz, J. Org. Chem., 2003, 68, 174–176 CrossRef CAS PubMed.
- J. H. Bae, M. Rubini, G. Jung, G. Wiegand, M. H. Seifert, M. Azim, J.-S. Kim, A. Zumbusch, T. A. Holak, L. Moroder, R. Huber and N. Budisa, J. Mol. Biol., 2003, 328, 1071–1081 CrossRef CAS PubMed.
- P. P. Pal, J. H. Bae, M. K. Azim, P. Hess, R. Friedrich, R. Huber, L. Moroder and N. Budisa, Biochem., 2005, 44, 3663–3672 CrossRef CAS PubMed.
- D. Kajihara, T. Hohsaka and M. Sisido, Protein Eng., Des. Sel., 2005, 18, 273–278 CrossRef CAS PubMed.
- A. Goulding, S. Shrestha, K. Dria, E. Hunt and S. K. Deo, Protein Eng., Des. Sel., 2008, 21, 101–106 CrossRef CAS PubMed.
- F. Wang, W. Niu, J. Guo and P. G. Schultz, Angew. Chem., Int. Ed., 2012, 51, 10132–10135 CrossRef CAS PubMed.
- M. S. Padilla and D. D. Young, Bioorg. Med. Chem. Lett., 2015, 25, 470–473 CrossRef CAS PubMed.
- S. Chen, Z.-J. Chen, W. Ren and H.-W. Ai, J. Am. Chem. Soc., 2012, 134, 9589–9592 CrossRef CAS PubMed.
- S. M. Kuhn, M. Rubini, M. A. Müller and A. Skerra, J. Am. Chem. Soc., 2011, 133, 3708–3711 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhoff, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed [Erratum] Phys. Rev. Lett. 1996, 78, 1396.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708–4717 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- P. Hariharan and J. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. E. Casida, Recent Advances in Density Functional Methods, Part I, World Scientific, Singapore, 1995, ch. 5, pp. 155–192 Search PubMed.
- P. Sałek, O. Vahtras, J. Guo, Y. Luo, T. Helgaker and H. Ågren, Chem. Phys. Lett., 2003, 374, 446–452 CrossRef.
- L. Frediani, Z. Rinkevicius and H. Ågren, J. Chem. Phys., 2005, 122, 244104 CrossRef PubMed.
- S. Tretiak and V. Chernyak, J. Chem. Phys., 2003, 119, 8809–8823 CrossRef CAS.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
- “Dalton, a molecular electronic structure program, Release DALTON2013.2, see “http://www.daltonprogram.org”.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- P. Cronstrand, Y. Luo and H. Ågren, Adv. Quantum Chem., 2005, 50, 1 CrossRef CAS.
- M. T. P. Beerepoot, D. H. Friese, N. H. List, J. Kongsted and K. Ruud, Phys. Chem. Chem. Phys., 2015, 17, 19306–19314 RSC.
- J. Word, S. C. Lovell, J. S. Richardson and D. C. Richardson, J. Mol. Biol., 1999, 285, 1735–1747 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- N. Reuter, H. Lin and W. Thiel, J. Phys. Chem. B, 2002, 106, 6310–6321 CrossRef CAS.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, Nucleic Acids Res., 2011, 39, W511–W517 CrossRef CAS PubMed.
- D. Case, T. Darden, T. Cheatham III, C. Simmerling, J. Wang, R. Duke, R. Luo, R. Walker, W. Zhang, K. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. Goetz, I. Kolossváry, K. Wong, F. Paesani, J. Vanicek, R. Wolf, J. Liu, X. Wu, S. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M. Hsieh, G. Cui, D. Roe, D. Mathews, M. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. Kollman, AMBER 12, University of California, San Francisco, 2012 Search PubMed.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- R. M. Wachter, B. a. King, R. Heim, K. Kallio, R. Y. Tsien, S. G. Boxer and S. J. Remington, Biochemistry, 1997, 36, 9759–9765 CrossRef CAS PubMed.
- R. Heim, D. C. Prasher and R. Y. Tsien, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12501–12504 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Coordinates of optimized chromophore structures (Table S1), parameters used for the chromophores in the MD simulation (Tables S2 and S3 and following text), input files for the MD simulation, δTPA values (Table S4), comparison of bond lengths from MD simulations, DFT, and, for EGFP, crystal structure (Tables S5 and S6), comparison of PCM and gas-phase TD-DFT results for selected chromophores (Table S7), 3D plot for the variation of energy with the studied angles in the conformational analysis (Fig. S1), z-matrix used to generate various conformers in the conformational analysis (Table S8), TD-DFT results for the conformational analysis (Table S9). See DOI: 10.1039/c5cp03875h |
| This journal is © the Owner Societies 2015 |