 Open Access Article
Open Access ArticlePeptides in the presence of aqueous ionic liquids: tunable co-solutes as denaturants or protectants?†
Volker
Lesch
a,
Andreas
Heuer
a,
Vasileios A.
Tatsis
a,
Christian
Holm
b and
Jens
Smiatek
*b
aInstitut für Physikalische Chemie, Westfälische Wilhelms-Universität Münster, Corrensstrasse 28/30, D-48149 Münster, Germany
bInstitut für Computerphysik, Universität Stuttgart, Allmandring 3, D-70569 Stuttgart, Germany. E-mail: smiatek@icp.uni-stuttgart.de
First published on 9th September 2015
Abstract
We studied the stability of a small β-hairpin peptide under the influence of an aqueous 1-ethyl-3-methylimidazolium acetate ([EMIM]+[ACE]−) solution via all-atom molecular dynamics simulations in combination with metadynamics. Our free energy results indicate a denaturation of the peptide structure in the presence of the ionic liquid which is validated by a significant broadening of the end-to-end distance. The radial distribution functions between the ions and the peptide were used for the calculation of the preferential binding coefficients in terms of the Kirkwood–Buff theory. A significant structure dependent binding behavior of acetate to the peptide was found which can be interpreted as the main reason for the denaturation of the native conformation. The outcomes of our simulations allow us to propose a simple mechanism to explain the unfolding of the peptide with regard to the specific properties of ionic liquids. Our results are in good agreement with experimental findings and demonstrate the benefits of ionic liquids as tunable co-solutes with regard to their influence on protein structural properties.
The influence of chaotropic (protein structure denaturants) and kosmotropic (protein structure protectants) co-solutes on the stability of proteins was often studied by experimental and computational approaches.1–8 It was found that molecules like urea and guanidinium lead to a destabilization of protein structures (denaturants) whereas trimethylamine-N-oxide (TMAO) and hydroxyectoine are known as protein protectants.9–11 A well established framework to qualitatively discuss the underlying mechanisms for denaturants and protectants was introduced by Collins et al.5–7 In this context, it was proposed that denaturants directly interact with protein surfaces whereas protectants are located in the second or the third hydration shell. Thus, the resulting behavior can be either described by a preferential binding mechanism for denaturants or a preferential exclusion mechanism for protectants. Indeed, this description has been often revealed as being too general. A recent publication12 has demonstrated that the chemical properties of the protein or the surface also impose a significant contribution to the resulting preferential binding or preferential exclusion behavior.
In recent years, a class of molten salts, so-called room-temperature ionic liquids (ILs), in addition to usual co-solutes, has been discussed as potential candidates to modify the structural properties of proteins.13,14 In fact, room-temperature ionic liquids have also attracted a lot of interest as ‘designer solvents’.13,15–21 Notably, there exist a large number of ionic liquids that differ in their anion and cation composition and also in their functionalities.22,23 With regard to their influence on enzymes and proteins, ILs have been proven to have a strong impact on biocatalytic reactivity and structural stability.14,24–28 It was discussed that either denaturant or protectant behavior can be observed for differently combined ILs and proteins. Computer simulations validated that the stabilization of the enzyme cutinase significantly depends on the ionic liquid concentration of the aqueous solution.14 Pronounced stabilization effects were also observed in the presence of protic ionic liquids. It was assumed that intermolecular hydrogen bonds between the protein and the ILs are able to maintain the secondary structure even above critical temperatures.29,30 In contrast to these studies, aprotic ionic liquids with alkyl imidazolium cations have been shown to impose a denaturation effect on ribonuclease A.31,32 In three recent reviews,28,32,33 the results of several studies have been summarized which discuss Hofmeister effects34 as being one of the main reasons for IL anion- and cation related specific stabilizing and destabilizing effects.
In this communication, we study the influence of 1-ethyl-3-methylimidazolium acetate ([EMIM]+[ACE]−, in the following denoted as EMIM and ACE) on the stability of a small β-hairpin peptide (the C-terminal from the B1 domain of the protein G with residues 41–56, denoted by its PDB identifier 2GB1) by atomistic molecular dynamics simulations. In addition to the computation of the Kirkwood–Buff integrals for the study of the ionic binding behavior, we have also conducted metadynamics simulations to evaluate the resulting free energy landscapes for the peptide in pure water and in an aqueous EMIM ACE solution. Our results evidence a denaturation effect in the presence of the ionic liquid which is mostly driven by a structure-dependent binding behavior of the acetate anions and an attraction of EMIM cations to the peptide due to short-ranged Lennard-Jones interactions. Our results are in good agreement with experimental findings for alkyl-imidazolium based ionic liquids.31 Additionally, the outcomes of our study provide detailed insights into the underlying binding mechanism with regard to a ‘tunable co-solute’ IL approach.
The molecular dynamics simulations were performed using the software package GROMACS (version 4.6.7)35,36 utilizing the non-polarizable CL&P force field for EMIM and ACE,37–40 the OPLS/AA force field for proteins,41 which is compatible with the CL&P force field37 and the TIP3P water model for the aqueous solution.42 The number of EMIM ACE pairs was Npairs = 250 which resulted in a concentration of c = 0.57 mol L−1. We used the original metadynamics method for the evaluation of the free energy landscapes at 298 K43–45 and chose the end-to-end distance Re between the center-of-mass of the first and the last residue and the root-mean-square deviation (RMSD) with regard to the atomic positions of the energy-minimized initial PDB structure as collective variables. In order to analyze the binding behavior, we have evaluated the corresponding Kirkwood–Buff integrals46–48 to study the preferential binding coefficients.12,48 As a prerequisite, chain conformation effects have to be diminished which has been achieved by fixing the positions of the heavy Cα atoms for the native folded peptide structure and a fully unfolded conformation. The unfolded structure has been obtained by high temperature simulations at 500 K which gave us also the chance to find appropriate collective variables for the metadynamics simulations to clearly distinguish between the folded and the unfolded conformation.49,50 Each production run of the restrained simulations had a length of 100 ns and was performed in an NpT ensemble at 298 K and 1 bar. More details on the simulation protocol can be found in the ESI.†
We studied the binding behavior of the ionic liquid in terms of the radial distribution function and the preferential binding coefficient. The Kirkwood–Buff integral for computational purposes is given by
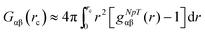 | (1) |
| ν23 = ρ3(G23 − G21) | (2) |
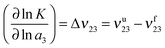 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K with respect to the logarithmic chemical activity ln
K with respect to the logarithmic chemical activity ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a3 of the ionic liquid with the preferential binding coefficients of the unfolded νu23 and the folded conformations νf23. The usage of the chemical activity a3 instead of the IL concentration takes into account all deviations from an ideal solution and is a common approach. A positive value for Δν23 indicates the shift of the chemical equilibrium towards the unfolded state whereas a negative value implies the stabilization of the folded state.
a3 of the ionic liquid with the preferential binding coefficients of the unfolded νu23 and the folded conformations νf23. The usage of the chemical activity a3 instead of the IL concentration takes into account all deviations from an ideal solution and is a common approach. A positive value for Δν23 indicates the shift of the chemical equilibrium towards the unfolded state whereas a negative value implies the stabilization of the folded state.
The results for the radial distribution functions between the center-of-masses of the Cα atoms of 2GB1 and the EMIM, respectively, ACE ions (center-of-mass) are presented in Fig. 1. It can be clearly seen that the unfolded conformation of 2GB1 attracts more acetate ions than the folded state whereas the values for EMIM are nearly identical for both conformations. Moreover, the position of the highest EMIM peak at 1 nm in the radial distribution functions is roughly identical for the folded and the unfolded structure. Only slight deviations like the occurrence of a small EMIM peak at 0.7 nm around the unfolded conformation can be observed.
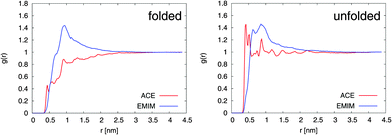 | ||
| Fig. 1 Radial distribution function g(r) between EMIM, respectively ACE (center-of-mass) and the Cα-atoms (center-of-mass) of 2GB1 for the folded (left side) and the unfolded conformation (right side). | ||
A significantly different behavior can be found for ACE. With regard to the folded structure, it can be observed that ACE is more or less excluded from the first hydration shells around the peptide at distances between 0.3 and 2.5 nm. In contrast, the occurrence of a well pronounced acetate ion shell around the unfolded conformation within distances of 0.3 to 0.7 nm is obvious. Interestingly, a slight tendency to form EMIM ACE ion pairs around the unfolded structure at distances of 0.9 nm is evident. Noteworthily, a shell-like accumulation behavior of EMIM ACE around differently charged solutes has been also discussed in a recent publication.21 The formation of distinct ion shells is also revealed by the individual radial distribution functions between the peptide residues and the ionic liquid. A more detailed analysis with regard to the properties of the interactions validates that acetate ions strongly interact via electrostatic interactions with the peptide whereas the more bulky EMIM cations induce stronger Lennard-Jones interactions. The corresponding analysis can be found in the ESI.†
With regard to the Kirkwood–Buff integrals, the results for the preferential binding coefficient ν23 between the Cα-atoms and EMIM, respectively ACE ions for the folded and the unfolded peptide conformation are presented in Fig. 2. It becomes evident that EMIM ions strongly bind to both conformations of the peptide as it was discussed above due to positive and converged values for ν23 at large distances. Indeed, the preferential binding coefficients for EMIM are nearly identical for both structures which emphasizes the fact that the transfer free energies of EMIM with ΔF = −RTν23, where RT denotes the thermal energy with the molar gas constant R, are also comparable.12 Thus, it can be assumed that a conformation dependent binding is absent and it can be concluded that the chemical equilibrium constant K according to eqn (3) remains unchanged under the influence of EMIM. With regard to these findings, EMIM can be neither regarded as a denaturant nor a protectant of 2GB1 although it can be definitely considered as a chaotropic co-solute in terms of its binding behavior.6,34
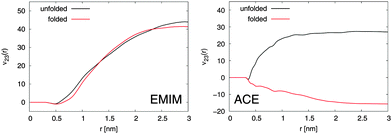 | ||
| Fig. 2 Left: Preferential binding coefficient ν23(r) between Cα-atoms of 2GB1 and EMIM cations for the folded (red line) and the unfolded peptide conformation (black line). Right: Preferential binding coefficient between Cα-atoms of 2GB1 and ACE anions for the folded (red line) and the unfolded (black line) peptide conformation. | ||
In contrast to EMIM, acetate ions show a more pronounced preferential binding behavior to the unfolded conformation (νu23 > 0 and νf23 < 0). Thus, a preferential exclusion mechanism can be observed for the folded conformation in contrast to a preferential binding behavior to the unfolded state. Indeed, the positive charge of the first EMIM layer attracts ACE anions that form a second layer around the native hairpin structure of the peptide. An increase of the solvent-accessible surface area due to unfolding promotes the formation of EMIM-ACE ion pairs at short distances around 2GB1 in addition to stronger electrostatic interactions with the peptide. More details on this mechanism which closely resembles the accumulation behavior of EMIM and ACE around differently charged and neutral spheres21 can be found in the ESI.† With regard to the corresponding influence on the chemical equilibrium constant according to eqn (3), it can be concluded that the presence of acetate ions induces the unfolding of the native peptide conformation. Indeed, these results are in good agreement with experimental findings,28,31 where it has been discussed that the choice of different anions in the presence of EMIM strongly influences the melting temperature of the protein ribonuclease A.
In addition to the preferential binding behavior, we have also performed metadynamics simulations to obtain the free energy landscapes for the two peptide conformations in the presence of pure water and a 0.57 molar aqueous EMIM ACE solution. The corresponding results in pure water and in aqueous ionic liquid solution are presented in Fig. 3 and 4. It can be clearly seen that the most stable free energy minimum conformation in the presence of pure water is given by a β-hairpin structure at Re = 0.5–0.8 nm and a RMSD of 0.4–0.6 nm. As a remark, a RMSD of zero corresponds to the reference structure of an energy minimized conformation without further equilibration which explains the occurrence of the large RMSD value for the local free energy minimum. The landscape clearly indicates the stability of a folded structure in a funnel-like global free energy minimum. Thus, the lowest free energy conformation is located in a very narrow region which is roughly 2 kcal mol−1 more stable than slightly distorted β-hairpin conformations. Moreover, it can be assumed that the relevant accessible phase space is restricted to free energy differences of ΔF ≈ 5–8 kcal mol−1. These findings are in good agreement with previous results for 2GB1 in pure water although different collective variables for the evaluation of the corresponding free energy landscapes were used.54,55
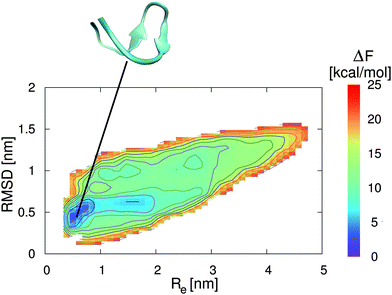 | ||
| Fig. 3 Free energy landscape for 2GB1 in pure water. The collective variables are given by the end-to-end distance Re between the first and the last residue of the strand (center-of-mass) and the root-mean square deviation (RMSD) to the energy minimized structure. The solid lines correspond to free energy differences of 2 kcal mol−1. The snapshot presented at the top corresponds to a native β-hairpin structure which represents the local free energy minimum conformation at the corresponding position as denoted by the black line. | ||
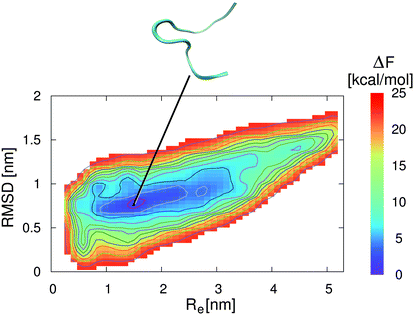 | ||
| Fig. 4 Free energy landscape for 2GB1 in an aqueous ionic liquid solution with a concentration of c = 0.57 mol L−1. The collective variables are given by the end-to-end distance Re between the first and the last residue of the strand (center-of-mass) and the root-mean square deviation (RMSD) to the energy minimized structure. The solid lines correspond to free energy differences of 2 kcal mol−1. The snapshot presented at the top corresponds to an unfolded peptide structure which represents the local free energy minimum conformation at the corresponding position as denoted by the black line. | ||
In contrast to these results, the lowest free energy conformation in the presence of the aqueous EMIM ACE solution is located at Re = 1.6 nm and a RMSD of 0.8 nm (Fig. 4). Thus, a significant broadening of the end-to-end distance compared with the stable folded conformation in pure water can be observed. Furthermore, it becomes obvious that the free energy basin in pure water which corresponds to the native β-hairpin structure in Fig. 3 vanishes in the presence of the ionic liquid. The resulting free energy landscapes verify that EMIM and ACE ions induce the denaturation of the native conformation in agreement with previous results.32 Moreover, it has to be noticed that the accessible phase space in the presence and absence of EMIM ACE for all values of ΔF ≤ 25 kcal mol−1 remains roughly unchanged. With regard to the results, it can be concluded that the ionic liquid induces a displacement of the global free energy minimum in terms of the native β-hairpin state to a new location as compared with the pure water results.
In summary, we have studied the influence of an ionic liquid, namely 1-ethyl-3-methylimidazolium acetate, in an aqueous solution on the stability of a peptide fragment from protein G by all-atom molecular dynamics simulations. With regard to the Kirkwood–Buff theory, we were able to study the ionic preferential binding behavior. Our results indicate large and nearly identical preferential binding parameters of EMIM to the folded and the unfolded peptide structure whereas ACE exclusively binds to the unfolded conformation. These results clearly indicate that the presence of acetate anions can be regarded as the main driving force for the denaturation of the hairpin structure. Indeed, the presence of large cations like EMIM, which form a first layer around the peptide due to strong Lennard-Jones interactions, is mandatory for the accumulation of the acetate ions. Hereby, EMIM cations of the first layer attract the oppositely charged ACE ions due to electrostatic interactions. The preferential binding of ACE at shorter distances is then facilitated by an unfolding of the native structure. The results of the presented metadynamics simulations finally validate the energetic destabilization of the native β-hairpin structure in the presence of an aqueous EMIM ACE solution. With regard to the previous discussion and the binding properties, we conclude that EMIM ACE behaves like a denaturant.
Indeed, it can be assumed that the presence of two ion species gives rise to new functionalities in terms of ‘tunable co-solutes’. With regard to this assumption, it has been found in ref. 32 and discussed in ref. 28 that the exchange of the imidazolium cation with protic cations like choline would result in a significant increase of the protein melting temperature. Therefore, ionic liquids might be regarded as potential candidates to overcome the limitations of common denaturants in terms of tunable functionalities.
We greatly acknowledge the helpful discussions with Anand Narayanan Krishnamoorthy, Ewa Anna Oprzeska-Zingrebe, Julian Michalowsky, Samantha Micciulla, Jan Heyda, Francisco Rodriguez-Ropero, Nico van der Vegt and Pavel Jungwirth. The authors thank the Deutsche Forschungsgemeinschaft through the cluster of excellence initiative ‘Simulation Technology’ (EXC 310), the collaborative research centers SFB 716 and TRR 61 and the federal ministry of research and education (Förderkennzeichen: 03X4631N) for financial support.
References
- P. H. Yancey, J. Exp. Biol., 2005, 208, 2819–2830 CrossRef CAS PubMed.
- D. R. Canchi and A. E. Garca, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- D. Harries and J. Rösgen, Methods Cell Biol., 2008, 84, 679–735 CAS.
- R. Politi and D. Harries, Chem. Commun., 2010, 46, 6449–6451 RSC.
- K. D. Collins, Biophys. J., 1997, 72, 65–76 CrossRef CAS.
- K. D. Collins, Methods, 2004, 34, 300–311 CrossRef CAS PubMed.
- K. D. Collins, G. W. Neilson and J. E. Enderby, Biophys. Chem., 2007, 128, 95–104 CrossRef CAS PubMed.
- Y. Zhang and P. S. Cremer, Annu. Rev. Phys. Chem., 2010, 61, 63–83 CrossRef CAS PubMed.
- J. Smiatek, R. K. Harishchandra, O. Rubner, H.-J. Galla and A. Heuer, Biophys. Chem., 2012, 160, 62–68 CrossRef CAS PubMed.
- J. Smiatek, R. K. Harishchandra, H.-J. Galla and A. Heuer, Biophys. Chem., 2013, 180, 102–109 CrossRef PubMed.
- A. Narayanan Krishnamoorthy, C. Holm and J. Smiatek, J. Phys. Chem. B, 2014, 118, 11613–11621 CrossRef CAS PubMed.
- J. Smiatek, J. Phys. Chem. B, 2014, 118, 771–782 CrossRef CAS PubMed.
- T. Yasuda and M. Watanabe, MRS Bull., 2013, 38, 560–566 CrossRef CAS.
- N. M. Micaêlo and C. M. Soares, J. Phys. Chem. B, 2008, 112, 2566–2572 CrossRef PubMed.
- P. Wasserscheid and W. Keim, Angew. Chem., 2000, 39, 3772–3789 CrossRef CAS.
- A. Matic and B. Scrosati, MRS Bull., 2013, 38, 533–537 CrossRef CAS.
- O. Borodin, G. D. Smith and W. Henderson, J. Phys. Chem. B, 2006, 110, 16879–16886 CrossRef CAS PubMed.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 12353–12357 CrossRef CAS PubMed.
- Z. Li, G. D. Smith and D. Bedrov, J. Phys. Chem. B, 2012, 116, 12801–12809 CrossRef CAS PubMed.
- V. Lesch, S. Jeremias, A. Moretti, S. Passerini, A. Heuer and O. Borodin, J. Phys. Chem. B, 2014, 118, 7367–7375 CrossRef CAS PubMed.
- V. Lesch, A. Heuer, C. Holm and J. Smiatek, Phys. Chem. Chem. Phys., 2015, 17, 8480–8490 RSC.
- K. R. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351–356 CrossRef CAS.
- D. Bedrov, O. Borodin, Z. Li and G. D. Smith, J. Phys. Chem. B, 2010, 114, 4984–4997 CrossRef CAS PubMed.
- M. Klähn, G. S. Lim, A. Seduraman and P. Wu, Phys. Chem. Chem. Phys., 2011, 13, 1649–1662 RSC.
- M. Haberler, C. Schröder and O. Steinhauser, Phys. Chem. Chem. Phys., 2011, 13, 6955–6969 RSC.
- M. Haberler, C. Schröder and O. Steinhauser, J. Chem. Theory Comput., 2012, 8, 3911–3928 CrossRef CAS.
- M. Haberler and O. Steinhauser, Phys. Chem. Chem. Phys., 2012, 13, 17994–18004 RSC.
- R. Patel, M. Kumari and A. B. Khan, Appl. Biochem. Biotechnol., 2014, 172, 3701–3720 CrossRef CAS PubMed.
- N. Byrne and C. A. Angell, J. Mol. Biol., 2008, 378, 707–714 CrossRef CAS PubMed.
- A. Kumar and P. Venkatesu, RSC Adv., 2013, 3, 362–367 RSC.
- D. Constantinescu, H. Weingärtner and C. Herrmann, Angew. Chem., Int. Ed., 2007, 46, 8887–8889 CrossRef CAS PubMed.
- H. Weingärtner, C. Cabrele and C. Herrmann, Phys. Chem. Chem. Phys., 2012, 14, 415–426 RSC.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- P. Lo Nostro and B. W. Ninham, Chem. Rev., 2012, 112, 2286–2322 CrossRef CAS PubMed.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- J. N. Canongia Lopes and A. A. H. Padua, J. Phys. Chem. B, 2006, 110, 19586–19592 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- J. N. Canongia Lopes, A. A. H. Padua and K. Shimizu, J. Phys. Chem. B, 2008, 112, 5039–5046 CrossRef CAS PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601 CrossRef.
- J. Smiatek and A. Heuer, J. Comput. Chem., 2011, 32, 2084–2096 CrossRef CAS PubMed.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS PubMed.
- P. E. Smith, Biophys. J., 2006, 91, 849–856 CrossRef CAS PubMed.
- V. Pierce, M. Kang, M. Aburi, S. Weerasinghe and P. E. Smith, Cell Biochem. Biophys., 2008, 50, 1–22 CrossRef CAS PubMed.
- J. Smiatek, D. Janssen-Müller, R. Friedrich and A. Heuer, Physica A, 2014, 394, 136–144 CrossRef CAS PubMed.
- J. Smiatek, D. Liu and A. Heuer, Curr. Phys. Chem., 2012, 2, 115–123 CrossRef CAS.
- P. E. Smith, J. Phys. Chem. B, 1999, 103, 525–534 CrossRef CAS.
- S. Weerasinghe and P. E. Smith, J. Phys. Chem. B, 2003, 107, 3891–3898 CrossRef CAS.
- J. Smiatek, A. Wohlfarth and C. Holm, New J. Phys., 2014, 16, 025001 CrossRef.
- R. Zhou, B. J. Berne and R. Germain, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14931–14936 CrossRef CAS PubMed.
- G. Bussi, F. L. Gervasio, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2006, 128, 13435–13441 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp03838c |
| This journal is © the Owner Societies 2015 |
