Identification of vibrational excitations and optical transitions of the organic electron donor tetraphenyldibenzoperiflanthene (DBP)

Abstract

Tetraphenyldibenzoperiflanthene (DBP) attracts interest as an organic electron donor for photovoltaic applications. In order to assist in the analysis of vibrational and optical spectra measured during the formation of thin films of DBP, we have studied the vibrational modes and the electronic states of this molecule. Information on the vibrational modes of the electronic ground state has been obtained by IR absorption spectroscopy of DBP grains embedded in polyethylene and CsI pellets and by calculations using density functional theory (DFT). Electronic transitions have been measured by UV/vis absorption spectroscopy applied to DBP molecules isolated in rare-gas matrices. These measurements are compared with the results of ab initio and semi-empirical calculations. Particularly, the vibrational pattern observed in the S₁ ← S₀ transition is interpreted using a theoretical vibronic spectrum computed with an ab initio model. The results of the previous experiments and calculations are employed to analyze the data obtained by high-resolution electron energy loss spectroscopy (HREELS) applied to DBP molecules deposited on a Au(111) surface. They are also used to examine the measurements performed by differential reflectance spectroscopy (DRS) on DBP molecules deposited on a muscovite mica(0001) surface. It is concluded that the DBP molecules in the first monolayer do not show any obvious degree of chemisorption on mica(0001). Regarding the first monolayer of DBP on Au(111), the HREELS data are consistent with a face-on anchoring and the absence of strong electronic coupling.

---

1 Introduction

Semiconductive organic materials have become an ingredient of light-emitting and photovoltaic devices. Ultimately they are expected to be less costly to use in production processes than inorganic semiconductor materials and to allow the development of thinner and lighter, even flexible, components. The production of organic semiconductor components may require the formation of thin layers of molecules by physical vapor deposition (PVD) onto a substrate. During the procedure, the molecules adsorb on the surface of the substrate or the topmost deposited material and arrange themselves. Optical spectroscopy can provide information on this arrangement by comparing the spectrum of the deposited molecules with the spectrum of the same molecules taken when they are free from the adsorption-induced interactions. Carried out for various stages of deposition, this comparison can reveal how the molecules interact individually with the substrate before showing how they interact with each other as the first monolayer approaches completion, then as the number of molecular monolayers increases.¹ For physisorbed species, accurate optical measurements can also reveal the possible deformation of the deposited molecules, especially when they have a high symmetry in their free state, for any loss of symmetry causes the rise of new spectral features as observed in the spectrum of 3,4,9,10-perylenetetracarboxylic dianhydride (PTCDA) molecules on a KCl(100) surface.² Cases of significant chemisorption can be revealed by considerably broadened optical spectra and/or noticeable spectral shifts, sometimes leading to a complete loss of any resemblance to the monomeric absorption behavior such as in the case of PTCDA on Ag(111).³

The polycyclic aromatic hydrocarbon tetraphenyldibenzoperiflanthene (5,10,15,20-tetraphenylbisbenz[5,6]indeno[1,2,3-cd:1′,2′,3′-lm]perylene, DBP, C₆₄H₃₆) was first reported for its properties of electrogenerated chemiluminescence.⁴ Since then it has been investigated as an electron donor for photovoltaic cells,^5–11 and it has been tested as an assistant dopant in organic light-emitting diodes.^12,13 It was used as the electron donor in the single-junction organic solar cell with a high fill factor that showed the highest open-circuit voltage reported at that time.¹¹ DBP is especially interesting because it has been found more efficient than frequently-used copper phthalocyanine as an electron donor in heterojunction photovoltaic structures.⁵ In particular, vapor-deposited DBP molecules can form films thin enough to enable exciton diffusion while retaining high absorption, because they arrange themselves with their transition moment parallel to the surface of the film.¹⁴

To date, a detailed description on the molecular level of the self-organization of DBP molecules during the formation of thin films by PVD is missing. Even though it was observed that the temperature of the substrate affects the structure of a DBP thin film formed by vapor deposition,¹⁵ better knowledge of mechanisms at work in the growth of such a film would be welcome.¹⁶ To contribute to this knowledge, we have measured absorption spectra of DBP molecules and carried out theoretical calculations to assist in the analysis of the measurements. The spectra were measured in the mid-infrared (MIR) wavelength domain on DBP grains embedded in pellets of polyethylene (PE) and of CsI. Measurements were also performed in the visible and near ultraviolet regions on DBP molecules isolated in Ne and Ar matrices. After the spectra were analyzed with the assistance of theoretical calculations, the usefulness of these experimental and theoretical data was demonstrated by using them in two examples. They were exploited to interpret high-resolution electron energy loss spectroscopy (HREELS) measurements performed on DBP molecules deposited on a Au(111) surface with submonolayer and few-monolayer coverages. They were also used to study differential reflectance spectroscopy (DRS) measurements carried out on DBP molecules deposited with a submonolayer coverage on a mica(0001) surface.

2 Methods

2.1 Experimental methods

The DBP powder used in the experiments was provided by Luminescence Technology Corp. (Lumtec) with a nominal purity of >99%. The powder was further purified by two cycles of temperature gradient sublimation using a setup detailed in the literature.¹⁷Fig. 1 shows the skeletal formula of DBP.

Fig. 1 Skeletal formula of 5,10,15,20-tetraphenylbisbenz[5,6]indeno[1,2,3-cd:1′,2′,3′-lm]perylene, also called tetraphenyldibenzoperiflanthene (DBP), C₆₄H₃₆, Chemical Abstracts Service (CAS) Registry No.: 175606-05-0.

2.1.1 Infrared absorption spectroscopy. The MIR absorption bands of DBP were measured at room temperature using grains embedded in two different solid pellets. Each pellet was produced by pressing the DBP and pellet material powders after they were finely ground and mixed in a mortar. The two pellet materials were CsI (Aldrich, purity 99.999%) and polyethylene (PE; Seishin Co., SK-PE-20L powder). The mass ratio of DBP to the pellet material was 1 : 700 with CsI for a total mass of 233.49 mg while it was 1 : 500 with PE for a total of 258.74 mg. Both pellets were prepared by pressing the mixed powders at 10 t for 10 min in a die 13 mm in diameter.

The IR spectrum was derived from transmission measurements performed using a Fourier transform IR spectrometer (Bruker 113v). Measurements were carried out on the DBP:CsI pellet over the 150–660 and 400–6000 cm⁻¹ ranges and on the DBP:PE pellet over the 50–220 and 150–660 cm⁻¹ ranges. An adequate beamsplitter was paired with a specific detector depending on the frequency range. Thus two mylar beamsplitters, 12 and 3.5 μm thick, were combined with a DTGS-type detector equipped with a PE window to scan the 50–220 and 150–660 cm⁻¹ ranges, respectively. The 400–6000 cm⁻¹ domain was explored by pairing a KBr beamsplitter with a DTGS-type detector equipped with a KBr window. Every spectrum was measured by averaging 32 scans carried out with a resolution of 2 cm⁻¹ and an interval of ≈1 cm⁻¹ between consecutive measurements. For each frequency range and sample pellet, a spectrum was recorded using a pellet of pure material, either CsI or PE, with a mass similar to that of the corresponding sample pellet. This spectrum served as reference for baseline correction.

2.1.2 Electron energy loss spectroscopy. High-resolution electron energy loss spectroscopy (HREELS) has been carried out at room temperature using an Ibach spectrometer.¹⁸ The sample consisted of a layer of DBP on a Au(111) surface. The Au(111) surface was cleaned by Ar⁺ bombardment and annealing. Cleanliness was checked by specular electron energy spectra, which, except for the signature of the acoustic surface plasmon,¹⁹ were featureless. Clean Au(111) was exposed to DBP at room temperature. The molecules were sublimated from a heated Ta crucible at ≈350 °C. Exposure times ranged from 0 to 3600 s so as to obtain submonolayer coverages and also deposits a few monolayers thick. Spectra were acquired in specular scattering geometry with an angle of impinging electrons of 64° with respect to the surface normal. The primary energy of the incident electrons was set to 5 eV with an energy resolution ranging from 3.5 to 4.5 meV.

2.1.3 Ultraviolet and visible absorption spectroscopy. Absorption spectra of DBP at UV/vis wavelengths were previously reported for solutions (DBP in benzene,⁴ and in dichloromethane^13,20) and comparatively thick films.^5,9,14,16,21 For this work, absorption spectroscopy was applied to DBP molecules isolated in rare-gas matrices at cryogenic temperatures.

As the matrix-isolation spectroscopy apparatus has been described elsewhere,²² only specific details are given here. The DBP-doped matrices were produced by depositing DBP molecules together with rare-gas atoms in excess onto a transparent substrate kept at ≈6 K when the rare gas was Ne, at ≈12 K when it was Ar. We used a CaF₂ substrate to form the DBP-doped Ne matrix while KBr was employed for the experiment with Ar. The DBP molecules were transferred into the gas phase by heating the sample powder at temperatures between 331 and 355 °C in an oven that was equipped with a nozzle directed toward the cold substrate. The DBP molecules exiting the oven through the nozzle were mixed with rare-gas atoms that were provided with a mass flow of 5 sccm (sccm: standard cubic centimers per minute) for Ne and Ar as well. The molecules and atoms were deposited for 20 min during the experiment with Ne and 15 min when using Ar. The UV/vis spectra were measured with a step of 0.2 nm and a linewidth of 0.2 nm at a rate of ≈55 points per minute. A spectrum of the clean, cold substrate was measured before the deposition of the rare-gas matrices to serve as a baseline reference.

2.1.4 Differential reflectance spectroscopy. Differential reflectance spectroscopy (DRS²³) was employed to monitor and characterize in situ the deposition of DBP molecules on muscovite mica (hereafter referred to as mica for simplicity) with a coverage increasing from 0.1 to 1 ML (ML: monolayer).

The DRS setup has been described elsewhere.¹ The mica surface was cleaved on the front and backside ex situ parallel to the (0001) planes and rinsed for ≈3 min in deionized water in order to remove minor traces of unbalanced potassium ions from the surface.²⁴ The sample was degassed for 30 min at ≈550 K in ultra-high vacuum and, after cooling down to room temperature, DBP molecules were deposited using a temperature of the effusion cell of ≈330 °C stable within 1 °C. The DRS measurements were carried out in situ during the deposition. Due to the integration times, the independently recorded spectra represent consecutive film thickness intervals whose mean values are given in the text. The DRS signal of an absorbing species is in good approximation proportional to its absorbance on a transparent substrate and should thus depend linearly on the film thickness provided that the latter is much smaller than the wavelengths used.

2.2 Computational methods

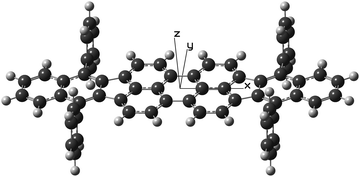
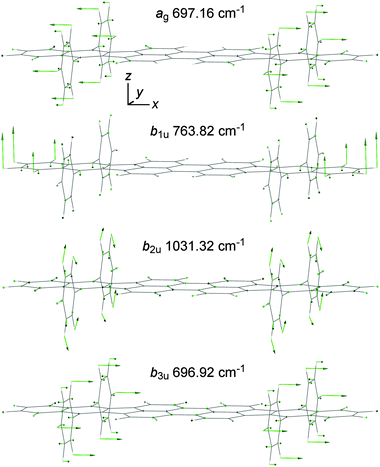
Theoretical calculations using both the ab initio and density functional theory (DFT) approaches and also a semi-empirical model were carried out with the GAUSSIAN 09 software.²⁵ Unless otherwise mentioned, the default parameters of the software were used. After tests, the molecule was forced to exhibit the symmetry elements of the D_2h point group in all calculations. As depicted in Fig. 2, its geometry was described using an x, y, and z frame of coordinates placed at the center of mass of the molecule so as to have the x-axis aligned with the long C₂ axis of the dibenzoperiflanthene plane and the z-axis aligned with the C₂ axis perpendicular to that plane. The D_2h-symmetrical geometry is the equilibrium geometry of the isolated molecule. A DBP molecule embedded in a dense phase such as a crystal may lose this high symmetry to be packed in an arrangement of lowest energy. For instance, its elongated body could be warped as the phenyl groups offer the possibility of internal rotation, although it is limited due to steric hindrance.

Fig. 2 Pseudo-three-dimensional representation of DBP with D_2h-type symmetry. The light- and dark-colored spheres represent H and C atoms, respectively. The frame of coordinates used in the theoretical calculations is indicated using axes labeled with x, y, and z.

2.2.1 Vibrational modes. Since DBP comprises 100 atoms, its structure yields 294 vibrational modes defined by the displacements of the atoms from their average position. In the presence of a molecular structure (mass and charge distributions) that exhibits symmetry elements, each mode transforms according to an irreducible representation of the corresponding point group and is labeled with the name of this representation. In the case of the D_2h point group, the irreducible representations are a_g, b_1g, b_2g, b_3g, a_u, b_1u, b_2u, and b_3u. In this work, the indexes 1, 2, and 3 relate to the C₂ axes oriented in the z, y, and x directions, respectively (see Fig. 2). As remarkable modes, those of the a_g type are conserved by all the symmetry operations that constitute the D_2h point group, meaning that the molecular symmetry is not modified during these vibrational motions. The g and u indexes indicate whether a mode is symmetric or antisymmetric with respect to the symmetry center of the structure. Thus only u-type modes can produce an instantaneous electric dipole moment and are therefore IR active. Of interest to this work, the b_1u-type modes are conserved by the C_2z, σ_xz, and σ_yz operations. As IR-active modes (u index), they generate an instantaneous dipole moment with the z direction (1 index). Fig. 3 shows some examples of atomic displacements associated with vibrational modes.

Fig. 3 Examples of vibrational modes in DBP with symmetry types and scaled theoretical frequencies given in units of wavenumbers (see Section 3.1). The molecular structure is rendered as a wireframe with green arrows indicating the displacement of the atoms. The frame of coordinates used in the theoretical calculations is indicated using axes labeled with x, y, and z.

2.2.2 Electronic ground state. The geometry of DBP in its electronic ground state was optimized in an application of DFT combining the B3LYP functional^26–29 with the 6-31+G(d,p) basis set.³⁰ The preset tight convergence criteria for optimization were applied as well as the predefined ultrafine grid for the calculation of integrals. The vibrational modes and the IR spectrum were calculated at the optimized geometry. The computed frequencies were positive, real numbers indicating that the optimization procedure yielded a geometry corresponding to a minimum in the potential energy surface. This molecular structure is given in the ESI.†

Even though the results of the DFT calculation at the B3LYP/6-31+G(d,p) level of theory would give a more accurate description, the geometry and vibrational modes of the electronic ground state of DBP were also derived in a Hartree–Fock (HF) calculation using the 6-31G(d,p) basis set.³¹ In this calculation, tight optimization criteria, the ultrafine grid, and frozen cores were applied. The HF description of the ground state was needed for a consistent calculation of the vibronic intensity pattern in the first allowed electronic transition of DBP considering the model employed to compute the excited state (see Section 2.2.3).

2.2.3 Electronic excited state. The first excited electronic state and its vertical excitation energy were obtained in a configuration-interaction calculation with single excitation (CIS).³² Because the excitation energies derived with the ab initio CIS approach are not accurate enough in the case of PAH molecules, they were also computed using the Zerner intermediate neglect of differential overlap (ZINDO/S) model,^33–36 which is more reliable in such occurrences.³⁷ The CIS and ZINDO/S calculations were carried out at the geometry derived with the B3LYP/6-31+G(d,p) model chemistry.

Furthermore, the geometry and the vibrational modes of DBP in its first excited state were determined with CIS calculations. As CIS electronic states are derived from the HF ground state, the vibrational modes computed with these two models were used for a consistent computation of the vibronic spectrum of the first electronic transition. Accordingly, the 6-31G(d,p) basis set and frozen cores were also applied when calculating the excited state and tight convergence criteria were used along with the ultrafine grid. The geometry of the first electronic excited state was also optimized so as to preserve a D_2h-type symmetry. The success of the optimization procedure was verified with the fact that the frequencies were positive, real numbers. Using the HF/6-31G(d,p) and CIS/6-31G(d,p) vibrational modes of the electronic ground and excited states, respectively, the relevant Franck–Condon factors were computed with the PGOPHER software.³⁸

3 Results and discussion

3.1 Infrared spectrum of grains

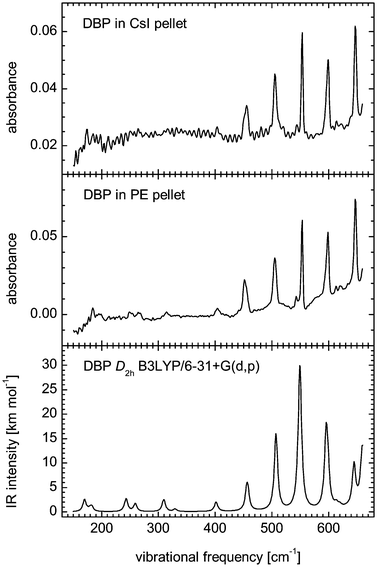
Fig. 4 shows the spectra of DBP in PE and CsI over the 150–660 cm⁻¹ range. At frequencies lower than 500 cm⁻¹, the spectrum of DBP grains in CsI is affected by an interference pattern that obscures weak bands possibly present below 400 cm⁻¹. Indeed, the measurements obtained with the pellet prepared with PE clearly show absorption peaks at frequencies down to 180 cm⁻¹. The measurements obtained between 50 and 220 cm⁻¹ with the DBP:PE pellet are not displayed because they did not reveal any clear feature. They showed, however, that there could be only weak absorptions in that frequency range. Absorptions in the 400–6000 cm⁻¹ domain were measured using the DBP:CsI pellet and the corresponding spectrum is shown in Fig. 5. All measured peak positions are given in Table 1.

Fig. 4 Observed MIR spectra of DBP embedded in PE and CsI pellets compared with the theoretical spectrum obtained at the B3LYP/6-31+G(d,p) level of theory while constraining the symmetry to D_2h type. In the latter spectrum, the frequencies have been scaled using a factor of 0.9799 and the bands have been given a Lorentzian profile with a FWHM of 7 cm⁻¹.

Fig. 5 MIR spectrum of DBP embedded in a CsI pellet compared with the theoretical spectrum obtained at the B3LYP/6-31+G(d,p) level of theory while constraining the symmetry to D_2h type. In the latter spectrum, the frequencies have been scaled using a factor of 0.9799 and the bands have been given a Lorentzian profile with a FWHM of 7 cm⁻¹.

Table 1 Experimental and theoretical vibrational energies of DBP in units of cm⁻¹

FTIR	DFT^a	Mode description^b	FTIR	DFT	Mode description
a Theoretical harmonic frequencies scaled by a factor of 0.9799. b The subscripts DP, Ph, and DP–Ph indicate deformations of the dibenzoperiflanthene plane, the phenyl groups, and the CC bond between them, respectively. Notation of modes: r(CH), CH stretching; R(CC), CC stretching; α(CCC), in-plane carbon ring angular deformation; β(CCH), in-plane CH bending; ε(CH), out-of-plane CH bending; τ(CCC), out-of-plane carbon ring angular deformation.
184.2	169.64	b1uτ(CCC)DP	1029.8	1031.17	b3uR(CC)Ph
194.8	182.31	b1uτ(CCC)DP	1029.8	1031.32	b2uR(CC)Ph
248.8	243.01	b3u phenyl wagging	1037.5	1041.69	b3uR(CC)DP
264.2	259.22	b1u phenyl rocking, τ(CCC)DP	1071.3	1077.41	b1uR(CC)Ph
314.3	309.41	b3uα(CCC)DP	1100.2	1105.02	b3uβ(CCH)DP
331.7	329.55	b2uα(CCC)DP	1133.9	1138.46	b3uβ(CCH)DP
404.0	401.60	b2uα(CCC)DP	1157.1	1159.31	b1uβ(CCH)Ph
451.3	455.57	b1uτ(CCC)DP	1165.8	1168.47	b3uβ(CCH)DP
451.3	457.38	b1uτ(CCC)DP	1174.4	1178.85	b2uβ(CCH)Ph
505.3	507.29	b3uα(CCC)DP, τ(CCC)Ph	1174.4	1179.02	b3uβ(CCH)Ph
542.9	545.21	b2uα(CCC)DP, τ(CCC)Ph	1229.4	1225.31	b3uR(CC)DP–Ph
553.5	549.46	b3uα(CCC)DP, τ(CCC)Ph	1245.8	1247.74	b3uR(CC)DP, β(CCH)DP
598.8	595.53	b2uα(CCC)DP	1297.9	1299.07	b3uR(CC)DP, β(CCH)DP
598.8	598.56	b3uα(CCC)DP, τ(CCC)Ph	1358.6	1361.89	b3uβ(CCH)DP
613.3	613.78	b1uε(CH)DP, α(CCC)Ph	1369.2	1366.59	b2uR(CC)DP–Ph
620.0	619.82	b3uα(CCC)DP, α(CCC)Ph	1369.2	1370.20	b3uR(CC)DP
647.0	644.85	b1uτ(CCC)DP	1423.2	1428.71	b3uR(CC)DP
663.4	659.22	b2uα(CCC)DP, τ(CCC)Ph	1441.5	1444.35	b1uR(CC)Ph
672.1	667.56	b3uα(CCC)DP	1466.6
684.6	679.45	b1uτ(CCC)DP, ε(CH)DP	1488.8	1486.78	b2uR(CC)DP
699.1	696.93	b3uτ(CCC)Ph	1488.8	1495.72	b3uR(CC)Ph
740.5	735.90	b3uα(CCC)DP, ε(CH)Ph	1488.8	1499.84	b2uR(CC)Ph
757.9			1511.9	1521.10	b3uR(CC)DP
762.7	763.82	b1uε(CH)DP	1574.6
776.2	773.45	b3uα(CCC)DP, ε(CH)Ph	1584.2	1587.03	b3uR(CC)DP, β(CCH)DP
810.0	806.30	b3uα(CCC)DP	1584.2	1588.20	b1uR(CC)Ph
832.1	830.22	b1uε(CH)DP	1584.2	1590.74	b2uR(CC)DP
846.6			1584.2	1592.92	b3uR(CC)DP
915.1	915.63	b3uε(CH)Ph	1593.9
937.2	934.54	b2uα(CCC)DP, ε(CH)Ph	3025.8		b1u, b2u, b3ur(CH)
976.8	975.55	b3uR(CC)DP, ε(CH)Ph	3063.4		b1u, b2u, b3ur(CH)
1000.9	989.10	b2uα(CCC)DP, R(CC)Ph
1000.9	994.35	b3uα(CCC)Ph
1000.9	994.41	b2uα(CCC)DP, α(CCC)Ph

---

The assignment of the IR absorption bands relies on the comparison of the laboratory measurements with the results of the quantum chemical calculations described in Section 2.2. Fig. 4 and 5 include the theoretical IR spectrum of DBP in its electronic ground state S₀(A_g) computed at the B3LYP/6-31+G(d,p) level of theory successfully assuming a D_2h-type symmetry. As already mentioned, only the vibrational modes of types a_u, b_1u, b_2u, and b_3u are IR active and can give rise to absorption bands. The harmonic frequencies of the vibrational modes have been scaled to fit the observed band positions. More precisely, the comparison of the experimental spectra with the theoretical B3LYP/6-31+G(d,p) spectrum allowed us to pair the clearest 27 vibrational bands with computed harmonic frequencies and to derive a scaling factor of 0.9799. The bands corresponding to CH stretching modes were not included in the derivation of the scaling factor as better results are obtained by treating them separately.³⁹ In Fig. 5, however, the scaling factor of 0.9799 has been applied to render them for simplicity. One may note that the value of 0.9799 is consistent with those obtained using the same chemistry model applied to 2- and 9-vinylanthracene,⁴⁰ as well as with the scaling factors derived from other models.³⁹ To plot the theoretical IR spectra in Fig. 4 and 5, the bands have been given a Lorentzian profile with a full width at half maximum (FWHM) of 7 cm⁻¹. In these plots, the IR intensity scale has not been corrected to take into account the area of the bands.

Several broad or composite peaks that appear in the measured spectrum between 1600 and 2000 cm⁻¹ are not present in the theoretical spectrum. Thus they do not correspond to fundamental vibrations. They must correspond to harmonic or combination vibrations, which can be strong enough to be detected when modes that give strong IR absorption bands are involved. Interestingly, the same features can be seen in the IR spectrum of rubrene,⁴¹ suggesting that they arise from combinations of vibrations in the phenyl side groups and terminal benzene rings of the tetracene backbone. At least one of the most strongly IR-active vibrations, i.e., the b_3u out-of-plane phenyl group deformation that gives the band at 699.1 cm⁻¹ or the b_1u out-of-plane CH bending of the terminal benzene rings that causes the absorption at 762.7 cm⁻¹, is likely involved.

It can be noted that the peak at 762.7 cm⁻¹ is the highest of the two that crown the feature arising at 760 cm⁻¹. This feature shows a secondary peak at 757.9 cm⁻¹ that does not correspond to any computed mode and is too strong to be caused by a combination of the vibrations that have a lower frequency. As the feature is broader than the other strong bands, it might be split. Because it is attributed to the b_1u out-of-plane CH bending of the terminal benzene rings, the splitting could indicate two different arrangements of the molecules in the grains that would especially affect this vibrational mode.

Beside those mentioned in the two previous paragraphs, the differences between the experimental and theoretical results consist of minor peaks in the measured spectrum that do not have a clear computed counterpart. These minor peaks (at 846.6, 1466.6, 1574.6, and 1593.9 cm⁻¹) could correspond to combination bands or to bands that are not accurately calculated. There are obvious discrepancies between the relative intensities in the observed and theoretical spectra. One cannot rule out an effect of the experimental conditions on the measured intensities. Indeed, the theoretical spectrum corresponds to a free molecule while the measurements were carried out on molecules in the solid phase. Still, differences can be inherent to the theoretical model employed. For instance, it was reported that IR intensities for aromatic CH stretching modes are overestimated by a factor of two when using the B3LYP functional.^39,42

The experimental MIR spectrum of DBP grains is nonetheless generally well reproduced by the theoretical spectrum of the isolated molecule computed while assuming it has a D_2h-type symmetry. All differences arising from the imperfection of the theoretical model could be attenuated a priori by employing a larger basis set, though the size of the molecule would make the calculation costly, and possibly another functional. Finally, within the limits of accuracy of the present IR study, we conclude that the structure of DBP exhibits the D_2h-type symmetry in the grains.

3.2 UV/vis spectrum in rare-gas matrices

3.2.1 Electronic transitions. Fig. 6 shows the UV/vis absorption spectra of DBP molecules isolated in Ar and Ne matrices. The two spectra are very similar and reveal the same absorptions. As expected, when using Ar instead of Ne as the matrix material, the absorption bands are found at slightly lower energy and their profile is broader. The energy shift is essentially due to the difference between the polarizabilities of the Ar and Ne atoms (see Section 3.2.2) while the variation of the bandwidth reflects the general dependence of the homogeneous broadening on the matrix material and temperature.

Fig. 6 UV/vis spectra of DBP molecules isolated in Ar and Ne matrices shown above a stick spectrum of the theoretical electronic transitions computed using the ZINDO/S semi-empirical model at the B3LYP/6-31+G(d,p) geometry of the S₀ state. A baseline attributed to scattering has been subtracted from each measured spectrum.

The allowed electronic transition of lowest energy gives a band at 2.2437 eV (18 097 cm⁻¹) when Ne is the matrix material. It marks the origin of the electronic transition and it is accompanied by several vibronic bands. At higher energy, between 3.7 and 4.8 eV, other bands suggest the presence of three electronic transitions, likely more. These bands are broader than the peaks marking the allowed electronic transition of lowest energy. At even higher energy, between 5 and 6 eV, the baseline variations may signal the presence of strong, though extremely broadened, absorptions.

The theoretical calculations using the CIS and ZINDO/S models predict the S₁ ← S₀ transition to be allowed and strong. Thus the band found at 2.2437 eV for DBP isolated in solid Ne can be attributed to this transition. The symmetry type of the first excited singlet state S₁ is B_3u, which means that the transition moment is oriented along the x direction, i.e., the long axis of the molecule. The theoretical transition energies and oscillator strengths computed for this electronic transition are given in Table 2.

Table 2 Theoretical and experimental first electronic excitation energies of DBP

Method	Geometry	Transition	Energy (cm^−1/eV)	Oscillator strength
a Peak position for a coverage of 0.2 ML. b Values derived from the absorption wavelength of 587 nm.^20 c Values derived from the absorption wavelength of 589 nm obtained by shifting the emission wavelength of 596 nm by 7 nm.^4
CIS/6-31+G(d,p)	S0 [B3LYP/6-31+G(d,p)]	S1(B3u) ← S0(Ag)	23 835/2.9551	2.1555
CIS/6-31G(d,p)	S1 [CIS/6-31G(d,p)]	S1(B3u) ← S0(Ag)	21 921/2.7178	2.1958
ZINDO/S	S0 [B3LYP/6-31+G(d,p)]	S1(B3u) ← S0(Ag)	19 172/2.3770	1.8108
Gas phase (extrapolated)			18 269/2.2651
MIS/Ne			18 097/2.2437
MIS/Ar			17 556/2.1767
DRS/mica(0001)			17 365/2.153^a
CH2Cl2 solution^20			17 036/2.1122^b
Benzene solution^4			16 978/2.1050^c

---

Beside the S₁ ← S₀ transition, about 50 transitions are allowed within the whole 2–6 eV range according to the results of the calculations using the ZINDO/S model. They are represented with a stick spectrum in Fig. 6. Four strong transitions arising between 4.2 and 5.0 eV in the ZINDO/S spectrum likely correspond to the bands observed between 3.7 and 4.8 eV for DBP isolated in solid Ne. An assignment is not straightforward, however, because of the difference between the computed and observed energy transitions. Moreover, the difficulty is increased because the observed features overlap and are broadened. Hence, we refrain from assigning them.

The three strong transitions predicted by the ZINDO/S calculation near 6 eV cannot be distinguished in the measured spectra. We propose that this apparent discrepancy is the consequence of a severe broadening, therefore a lowered peak intensity. It would be consistent with the baseline variations between 5 and 6 eV mentioned above.

Both the CIS and ZINDO/S models attributed a high oscillator strength, ≈2, to the S₁ ← S₀ transition, in agreement with the experimental data. As the oscillator strength is related to the number of electrons in the molecule and considering that we are discussing a π–π* transition, this high value is a priori an indication of the large number of electrons that constitute the extended π system of the dibenzoperiflanthene unit in DBP.

For comparison, we have computed the oscillator strength of the S₁ ← S₀ transition for the related molecules periflanthene (diindenoperylene, DIP, C₃₂H₁₆, CAS No. 188-94-3), tetraphenyldiindenoperylene (Ph4-DIP, C₅₆H₃₂, CAS No. 222849-28-7), and dibenzoperiflanthene (bisbenzindenoperylene, BIP, C₄₀H₂₀, CAS No. 176741-59-6). It was essential to apply the theoretical approach already used for DBP as calculated electronic transitions can vary significantly depending on the theoretical model. Care was taken to optimize the structure of these species at the same level of DFT used for DBP, i.e., B3LYP/6-31+G(d,p), with the same accuracy criteria. The atoms and their coordinates in the resulting structures are given in the ESI.† While a D_2h-type symmetry was successfully assumed for DIP and BIP, Ph4-DIP has been found to be twisted into a structure with a D₂-type symmetry. The deviation from a higher symmetry is caused by the steric interaction between the phenyl groups and the H atoms at the corners of the central perylene unit. In DBP, this interaction is balanced by the steric interaction between the phenyl groups and the lateral H atoms carried by the terminal benzene rings of the dibenzoperiflanthene body, leading to the higher D_2h-type symmetry.

The electronic transitions of DIP, Ph4-DIP, and BIP were calculated using the ZINDO/S model for consistency as mentioned above. In each case the moment of the S₁ ← S₀ transition was found to be parallel to the long axis of the molecule. The transition energies derived for DIP, Ph4-DIP, and BIP are 2.58, 2.47, and 2.47 eV, respectively, to be compared with 2.38 eV for DBP. While the oscillator strength computed for the S₁ ← S₀ transition of DBP is 1.81, we have obtained 1.32, 1.42, and 1.76 for DIP, Ph4-DIP, and BIP, respectively. As expected, the oscillator strength increases with the size of the π electronic system of the main body. One can note that the presence of the phenyl groups also coincides with an increase of the oscillator strength, though of lower magnitude. The mechanism of this effect is yet to be determined. Thus, at this level of theory, DBP exhibits the strongest S₁ ← S₀ transition, which gives rise to photon absorption at the longest visible wavelength.

Table 2 shows that the transition energies computed for DBP are larger than the energy measured on the molecules isolated in a Ne matrix, i.e., 2.2437 eV. This value would be slightly lower than the transition energy for a free molecule. Indeed, in Section 3.2.2, the latter is estimated to be 2.2651 eV. In comparison with the CIS model, ZINDO/S gives a vertical excitation energy closer to this value (see Table 2). This is consistent with what is generally observed in the calculation of the first excited electronic states of neutral PAHs, provided that the ZINDO/S calculation is carried out at a reasonably accurate geometry. Such a geometry was presently obtained with a calculation at the B3LYP/6-31+G(d,p) level of theory and the corresponding ZINDO/S S₁ ← S₀ excitation energy is 0.1119 eV (903 cm⁻¹) higher than the transition energy expected for the free DBP molecule (see Section 3.2.2).

While applying the ab initio CIS model, the energy of the S₁ ← S₀ transition was computed for two different geometries. It was computed for the geometry of the S₀ state obtained at the B3LYP/6-31+G(d,p) level of theory and also for the relaxed geometry of the S₁ state optimized at the CIS/6-31G(d,p) level. Both values are clearly larger than the transition energy expected for the free molecule. When applying the CIS model to PAH molecules, the difference observed between the theoretical and measured transition energies is quite common.

Thus the ZINDO/S calculation is relatively successful in reproducing the S₁ ← S₀ transition energy of the DBP molecules in the Ne matrix while considering the geometry optimized at the B3LYP/6-31+G(d,p) level of theory with a D_2h-type symmetry. This indicates that DBP molecules exhibit the symmetry elements of this point group when they are isolated in Ar and Ne matrices and, by extension, when they are in the gas phase.

3.2.2 Extrapolation to the gas phase. We are interested in the characteristics of free DBP molecules to use them as references in the study of the formation of DBP thin films. Although our experiments were not carried out with free molecules, the spectra we have measured provide useful information.

For instance, the energy of the S₁ ← S₀ transition in free DBP molecules can be extrapolated from the energies measured for the same transition with molecules isolated in Ne and Ar matrices.⁴³ This is achieved by considering that dispersion is the main interaction mechanism between PAH molecules and rare-gas atoms. Thus,

where [small nu, Greek, tilde]_gas phase, [small nu, Greek, tilde]_Ne matrix, and [small nu, Greek, tilde]_Ar matrix are the transition energies in the various media and R_α = 4.13 is the ratio of the polarizability of Ar to that of Ne.⁴⁴ Taking [small nu, Greek, tilde]_Ne matrix = 2.2437 eV and [small nu, Greek, tilde]_Ar matrix = 2.1767 eV, one finds [small nu, Greek, tilde]_gas phase = 2.2651 eV.

3.2.3 Vibronic spectrum. Details of the S₁(B_3u) ← S₀(A_g) absorption of DBP isolated in a Ne matrix can be examined in Fig. 7. The strongest peak, which is found at the lowest energy (18 097 cm⁻¹), is the origin band of the transition. The next peak (at 18 242 cm⁻¹) could be either a second origin band caused by a site effect or a vibronic band corresponding to the excitation of a low-frequency vibration in the S₁ state. Even though the vibronic structure is not clear enough to rule out a site-effect pattern, the assignment of the peak to a low-frequency vibration is supported by the comparison of the measured spectrum with the components of the theoretical vibronic spectrum that is also displayed in Fig. 7. This stick spectrum represents Franck–Condon factors derived from the vibrational modes computed at the HF/6-31G(d,p) and CIS/6-31G(d,p) levels of theory for the S₀ and S₁ states, respectively. Beside the origin band, the theoretical spectrum comprises vibronic bands that correspond to the excitation of vibrational modes with the a_g-type symmetry. All fundamental modes, all second harmonics, and all third harmonics have been taken into account. Moreover, the strongest bands arising from combinations of two different modes have also been included. According to the list of vibrational modes computed for S₁ at the CIS/6-31G(d,p) level of theory, the band measured at 18 242 cm⁻¹ can be attributed to the wagging motion of the phenyl groups that conforms to an a_g-type symmetry.

Fig. 7 The S₁ ← S₀ transition of DBP isolated in solid Ne compared with a decomposed theoretical stick spectrum (see the main text for details on its computation). The origin of the stick spectrum has been placed at the position of the observed origin band and the vibrational shifts correspond to unscaled harmonic frequencies. A synthetic spectrum resulting from the convolution of the stick spectrum with a Lorentzian profile having a FWHM of 100 cm⁻¹ is plotted for further comparison.

Fig. 7 also features a synthetic spectrum obtained by convoluting the CIS-HF/6-31G(d,p) vibronic stick spectrum with a Lorentzian profile to which was given a FWHM of 100 cm⁻¹. While the synthetic spectrum does not precisely reproduce the observed S₁ ← S₀ spectrum of DBP isolated in a Ne matrix, the intensity pattern up to 1000 cm⁻¹ from the origin band coincides well with the measurements. The discrepancies can be attributed to the use of two different methods, HF and CIS, to describe, respectively, the lower and upper states, both methods being moderately accurate. The synthetic spectrum does not contradict the conclusion previously drawn from the calculation of the electronic states, namely, that DBP molecules isolated in rare-gas matrices exhibit the D_2h-type symmetry.

3.3 DBP on mica(0001)

Fig. 8 shows the S₁ ← S₀ transition of DBP deposited on a mica(0001) surface as obtained by DRS for several values of coverage from 0.1 to 1 ML. The absorption spectrum of Ne-matrix-isolated DBP in the same energy region is displayed along for the purpose of comparison. A synthetic spectrum resulting from the convolution of the matrix-isolation spectrum with a Lorentzian profile characterized by a FWHM of 0.09 eV is also plotted to emphasize the relationship with the DRS data. While the spectrum of DBP on mica(0001) appears to comprise the same features as the spectrum of the Ne-matrix-isolated molecule, the features are broadened and shifted toward lower energies. The broadening and the shift can be attributed to the interaction of the DBP molecules with the mica(0001) surface and with neighboring DBP molecules in close-packed islands, which is expectedly stronger than the interaction between DBP molecules and surrounding Ne atoms in a matrix. It can be seen that the shift increases slightly from 0.0905 to 0.1162 eV (or 0.1119 to 0.1376 eV with respect to the band position extrapolated for the free molecule) as the coverage value increases from 0.2 to 1 ML. This effect can be interpreted as the result of the increasing occurrences of interaction between the DBP molecules, added to the interaction with the mica(0001) surface. Furthermore, these room-temperature differential reflectance spectra are subject to thermal and possibly also inhomogeneous broadening, the latter being caused by nonequivalent adsorption environments.

Fig. 8 S₁ ← S₀ transition of DBP on mica(0001) measured by DRS at different coverage values compared with the absorption spectrum of DBP isolated in Ne matrix of Fig. 6. For an easier comparison, a synthetic spectrum obtained by convoluting the matrix-isolation spectrum with a Lorentzian profile characterized by a FWHM of 0.09 eV is also displayed. Note the relative shift of 0.1 eV between the horizontal scales. The vertical arrow indicates the increase of the signal accompanying the increase of the coverage from 0.1 to 1 ML with increments of 0.1 ML.

One may compare the shift toward lower energies observed for the S₁ ← S₀ transition of DBP molecules deposited on a mica(0001) surface with the shift observed for DBP in rare gas matrices and in solutions (Table 2). The shift observed for non-polar solute molecules, such as DBP, surrounded by a non-polar host medium, like rare-gas atoms or benzene molecules, is essentially caused by the variation of the dispersion interaction energy between the solute molecule and the solvent or the host material when the former undergoes an electronic transition and its polarizability changes.^45–49 For a given molecule and electronic transition, the magnitude of the shift depends on the polarizability of the surrounding medium. This is the mechanism we have taken advantage of to extrapolate the energy of the S₁ ← S₀ transition in free molecules using the measurements on DBP molecules isolated in Ar and Ne matrices. The increasing shift observed for DBP surrounded by Ne and Ar atoms, by CH₂Cl₂ and benzene molecules, reflects the increasing polarizability of these species, respectively, 0.397,⁴⁴ 1.64,⁴⁴ ≈6.6,⁵⁰ and ≈10.4 × 10⁻³⁰ m³.⁵⁰ A quantitative prediction of the shift is complex as it should take into account the volume and topology of both the solute and host species.

In contrast to molecules dispersed in a solution or in a matrix, molecules adsorbed on a rigid surface are not completely surrounded by a polarizable medium. Consequently they interact with somewhat less than half the same amount of material – or even much less depending on their shape, i.e., flat like a regular PAH molecule or spherical like C₆₀, and also on the adsorption configuration with the surface, i.e., face-on, side-on, or head-on anchoring – resulting in a smaller shift of transition energies considering identical media. In the case of the DBP molecule, even if it is lying face-on on a rigid surface, most of its polarizable volume, which is constituted by the dibenzoperiflanthene body, is kept at an extra distance from this surface, standing on the phenyl groups. Since the dispersion interaction varies conversely with the sixth power of the distance, it is weaker and the transition energy shifts are expected to be smaller. This has to be taken into account to understand the energy shift of the S₁ ← S₀ transition of DBP on mica(0001) with respect to the transition energy of the free molecule. Note that while the shift induced by the mica surface is smaller than the shift observed in solution spectra, the broadening is larger for DBP on mica(0001) than for dissolved DBP.^4,13,20

When molecules are not isolated from each other and form aggregates, their transition energy can be affected significantly by an additional effect, which is the interaction between the individual transition moments of the deposited molecules. It is related to the coherently delocalized excitation and superradiance phenomena. Its magnitude depends on the relative distances and orientations of the aggregated molecules. The effect has been observed, for instance, with two-dimensional ordered aggregates of adsorbed PTCDA molecules.^51,52 It likely contributes to the coverage-dependent energy shift observed in the DRS measurements of Fig. 8 and mentioned in the first paragraph of this section.

The DRS measurements carried out on DBP molecules deposited on a muscovite mica(0001) surface with submonolayer coverages do not reveal a strong degree of chemisorption. The data have not allowed us to determine the anchoring configuration of the molecules onto this surface, although a face-on configuration is expected as it would likely maximize the interaction energy, thus lowering the energy of the system.

3.4 DBP on Au(111)

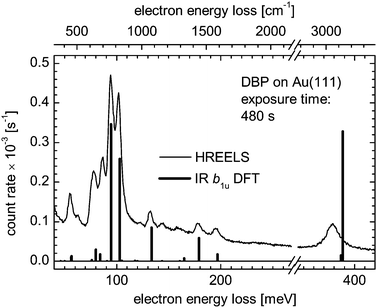
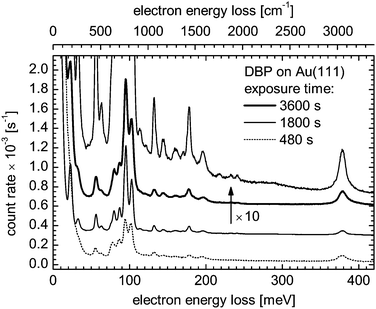
The FTIR spectra measured on grains embedded in PE and CsI pellets have allowed us to scale theoretical harmonic frequencies so as to reproduce the observed vibrational frequencies. We have used the scaled theoretical spectrum to analyze the HREEL spectrum obtained at low energies for DBP molecules deposited on a Au(111) surface. Fig. 9 shows the HREEL spectrum of a submonolayer deposit on a Au(111) surface and the theoretical b_1u-type IR absorption bands are superimposed as sticks for comparison. It is found that the two spectra are virtually identical. Since the selection rules for HREELS measurements in specular geometry allow only vibrational modes that produce a dynamical dipole moment with a component perpendicular to the substrate surface, the coincidence between the two spectra indicates that the DBP molecules are anchored face-on on the Au(111) surface. As in the case of terrylene, which also adsorbs face-on on the same surface,⁵³ the two strongest bands, at 94.2 and 101.7 meV in Fig. 9, are assigned to out-of-plane CH bending modes. In comparison to the spectrum of terrylene, the peak at 380 meV that corresponds to aromatic CH stretching modes is much stronger. It can be explained by the fact that, even though both molecules lie face-on on the Au(111) surface, the phenyl groups in DBP are perpendicular to this surface and their CH stretching motions can be excited by the impinging electrons whenever they contribute to a b_1u-type vibrational mode, yielding a HREELS signal. Two of the CH stretching modes actually involve the phenyl groups and transform according to the b_1u representation.

Fig. 9 HREEL spectrum of a DBP submonolayer deposit on a Au(111) surface. The IR activity of all the b_1u-type modes calculated at the B3LYP/6-31+G(d,p) level of theory is shown as a stick spectrum with an arbitrary vertical scale for comparison. The theoretical frequencies have been scaled using a factor of 0.9799.

Although the HREEL spectrum largely reflects the theoretical b_1u-type vibrational pattern, Fig. 9 presents at least two peaks at ≈63 and ≈87 meV that do not closely correspond to any of these modes. A third one at 113.5 meV is visible in Fig. 10, which presents spectra of three DBP coverages from the submonolayer range to at least the second molecular layer. Of course the pattern of the HREELS measurements may differ from the theoretical IR spectrum of an isolated molecule simply because the proximity of the Au substrate induces vibrational energy shifts through van der Waals and electrostatic interactions. Accordingly, the peak at ≈87 meV – a position slightly overestimated due to overlapping peaks – could be assigned to the b_1u-type mode found at 84.9 meV (684.6 cm⁻¹) in the FTIR spectrum of grains and computed at 84.2 meV (679.45 cm⁻¹) for a free molecule (see Table 1). On the other hand, one may attempt to attribute these bands to modes exhibiting another symmetry type than b_1u. Normally inactive in HREELS, these modes would have produced peaks due to a lowering of the molecular symmetry possibly caused by the deformation of the molecule upon adsorption on the Au surface.

Fig. 10 Low-energy range in the HREEL spectrum of DBP molecules deposited on a Au(111) surface as measured at different exposure times. At 480 s, the coverage is submonolayer. The thickness of the deposit is greater than 1 ML at 1800 and 3600 s. A vertical offset has been applied to the curves for clarity.

For instance, neglecting any major shift between the HREELS peak positions and the scaled theoretical vibrational frequencies, the peak observed near 63 meV could be assigned to an out-of-plane deformation of the phenyl groups, i.e., a b_3u-type vibration of D_2h-symmetric DBP. Similarly, four modes could be responsible for the HREELS peak at ≈87 meV according to their frequencies. All are out-of-plane vibrations of the phenyl groups, one of them being of the b_3u type while the others transform according to a_g, b_2u, and b_1g, still considering D_2h-symmetric DBP. Finally, the peak detected at 113.5 meV could be attributed to another b_3u-type out-of-plane vibration of the phenyl groups. While the involvement of out-of-plane vibrations of the phenyl groups in each of these instances does not seem to be possibly coincidental, a lowering of the symmetry would likely allow more than three modes to become active and would cause energy shifts in the vibrational spectrum.

An electronic coupling of specific vibrational modes of adsorbed DBP to electronic states of the substrate would be revealed by the activation of a_g-type modes and their excitation would give rise to peaks with a Fano profile.^54–57 This spectroscopic signature, however, is not observed in Fig. 9. In addition, the vibrational spectra of DBP on Au(111) do not exhibit qualitative changes with increasing exposure, apart from an increase of the signal strength as illustrated with the spectra presented in Fig. 10. As the upper molecular layer is likely decoupled from Au(111) and the spectra for different DBP coverages are similar, we conclude that the electronic coupling between DBP molecules and Au(111) at submonolayer coverages is rather weak.

Table 3 summarizes the peak positions obtained from the loss spectrum of DBP on Au(111) after exposure for 1800 s as this time gives the best resolved spectrum. The peaks have been attributed to b_1u-type vibrational modes in accordance with the previous discussion, in most cases in a straightforward comparison with IR bands of DBP grains. The peak arising at ≈87 meV is assigned to a b_1u-type mode assuming a shift that is somewhat larger than what is observed for the other peaks. Four peaks could not be assigned to b_1u-type modes, two of them apparently coinciding with bands of a different symmetry type that are present in the IR spectrum of DBP grains. Other vibrational modes that owing to their b_1u-type symmetry should be observed in specular spectra fall below the detection limit of the spectrometer. We assign the absence of the spectroscopic signature of symmetry-allowed vibrational modes to their low scattering cross section at the chosen scattering geometry. The scattering cross section depends on the angle of incidence of primary electrons and their energy.⁵⁸

Table 3 Assignment of HREELS vibrational bands of DBP adsorbed on Au(111)

HREELS^a/meV	HREELS^a/cm^−1	FTIR^b/cm^−1	Mode description^c
a Energies and frequencies from the measurements made after 1800 s exposure time. b Frequencies between parentheses are assigned to b3u-type modes. c See footnotes of Table 1 for the notation of modes. d Theoretical harmonic frequencies scaled by a factor of 0.9799.
22.5	181	184.2	b1uτ(CCC)DP
22.5	181	194.8	b1uτ(CCC)DP
32.5	262	264.2	b1u phenyl rocking, τ(CCC)DP
56.0	452	451.3	b1uτ(CCC)DP
63.3	511	(505.3)	(b3uα(CCC)DP, τ(CCC)Ph)
Shoulder	Shoulder	613.78	b1uε(CH)DP, α(CCC)Ph
79.7	643	647.0	b1uτ(CCC)DP
87.0	702	684.6	b1uτ(CCC)DP, ε(CH)DP
95.1	767	762.7	b1uε(CH)DP
103.1	832	832.1	b1uε(CH)DP
113.5	915	(915.1)	(b3uε(CH)Ph)
122.0	984
132.4	1068	1071.3	b1uR(CC)Ph
144.3	1164	1157.1	b1uβ(CCH)Ph
160.2	1292	1294.6^d	b1uR(CC)Ph
170.2	1373
178.1	1436	1441.5	b1uR(CC)Ph
196.0	1581	1584.2	b1uR(CC)Ph
378.5	3053	3063.4	b1ur(CH)Ph

---

4 Conclusions

We have characterized the DBP molecule with FTIR spectroscopy applied to grains embedded in PE and CsI pellets, and also with UV/vis spectroscopy on molecules isolated in Ne and Ar matrices. The IR and UV/vis measurements have been analyzed with the support of theoretical calculations employing semiempirical and ab initio models as well as density functional theory. The IR-active vibrational modes of DBP in its electronic ground state S₀ have been accurately measured and identified. With regard to the first excited singlet electronic state S₁, the S₁ ← S₀ transition energy of the free molecule has been extrapolated from the measurements carried out with DBP-doped rare-gas matrices. The vibronic pattern of the transition has been analyzed.

Using the results of the previous experiments, we have interpreted measurements carried out with DRS on DBP molecules deposited on a muscovite mica(0001) surface with low coverages and in particular submonolayer coverage. We have found that DBP molecules deposited on the mica(0001) surface do not show a significant degree of chemisorption and retain the behavior of single molecules for coverage values up to 1 ML. Even though it is expected that the molecules lie face-on on the surface, it could not be verified experimentally yet. Concerning DBP molecules deposited on a Au(111) surface, the interpretation of the HREEL spectra is consistent with a face-on anchoring and the absence of strong electronic coupling with the substrate.

It was previously found that DBP molecules vacuum-deposited on an indium tin oxide surface form a film with their S₁ ← S₀ transition moment parallel to the surface of the film.¹⁴ In the case of a Au(111) surface, the present work goes a step further by finding that the molecules in the first monolayer are adsorbed face-on. Future studies will focus on the arrangement of the molecules in the first monolayer and beyond.

Acknowledgements

This work was carried out within a cooperation between the Max-Planck-Institut für Astronomie and the Friedrich-Schiller-Universität Jena. We are thankful to Dr Harald Mutschke at the Astrophysikalisches Institut und Universitäts-Sternwarte for giving us access to the FTIR spectrometer and to Gabriele Born for preparing the DBP-containing pellets and measuring their MIR spectra. R. F., M. G., T. K., and T. F. acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) through grant No. FR 875/9-3. T. K. thanks the Evonik Stiftung for awarding a PhD scholarship. Finally, M. R. and J. K. acknowledge funding by the DFG through grant No. KR 2912/7-1.

References

1. R. Forker, M. Gruenewald and T. Fritz, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2012, 108, 34–68.
2. M. Müller, A. Paulheim, C. Marquardt and M. Sokolowski, J. Chem. Phys., 2013, 138, 064703.
3. M. Gruenewald, K. Wachter, M. Meissner, M. Kozlik, R. Forker and T. Fritz, Org. Electron., 2013, 14, 2177–2183.
4. J. D. Debad, J. C. Morris, V. Lynch, P. Magnus and A. J. Bard, J. Am. Chem. Soc., 1996, 118, 2374–2379.
5. D. Fujishima, H. Kanno, T. Kinoshita, E. Maruyama, M. Tanaka, M. Shirakawa and K. Shibata, Sol. Energy Mater. Sol. Cells, 2009, 93, 1029–1032.
6. M. Hirade and C. Adachi, Appl. Phys. Lett., 2011, 99, 153302.
7. X. Xiao, J. D. Zimmerman, B. E. Lassiter, K. J. Bergemann and S. R. Forrest, Appl. Phys. Lett., 2013, 102, 073302.
8. Y.-Q. Zheng, W. J. Potscavage, Jr., T. Komino, M. Hirade, J. Adachi and C. Adachi, Appl. Phys. Lett., 2013, 102, 143304.
9. C.-W. Chen, Z.-Y. Huang, Y.-M. Lin, W.-C. Huang, Y.-H. Chen, J. Strzalka, A. Y. Chang, R. D. Schaller, C.-K. Lee, C.-W. Pao and H.-W. Lin, Phys. Chem. Chem. Phys., 2014, 16, 8852–8864.
10. X. Che, X. Xiao and S. R. Forrest, Photovoltaic Specialist Conference (PVSC), 2014 IEEE 40th, 2014, pp. 0140–0142.
11. Y. Peng, L. Zhang and T. L. Andrew, Appl. Phys. Lett., 2014, 105, 083304.
12. H. Nakanotani, T. Higuchi, T. Furukawa, K. Masui, K. Morimoto, M. Numata, H. Tanaka, Y. Sagara, T. Yasuda and C. Adachi, Nat. Commun., 2014, 5, 4016.
13. T. Kasahara, S. Matsunami, T. Edura, R. Ishimatsu, J. Oshima, M. Tsuwaki, T. Imato, S. Shoji, C. Adachi and J. Mizuno, Sens. Actuators, B, 2015, 207(Part A), 481–489.
14. D. Yokoyama, Z. Q. Wang, Y.-J. Pu, K. Kobayashi, J. Kido and Z. Hong, Sol. Energy Mater. Sol. Cells, 2012, 98, 472–475.
15. Y. Zhou, T. Taima, Y. Shibata, T. Miyadera, T. Yamanari and Y. Yoshida, Sol. Energy Mater. Sol. Cells, 2011, 95, 2861–2866.
16. Y. Zhou, T. Taima, T. Kuwabara and K. Takahashi, Adv. Mater., 2013, 25, 6069–6075.
17. A. A. Levin, T. Leisegang, R. Forker, M. Koch, D. C. Meyer and T. Fritz, Cryst. Res. Technol., 2010, 45, 439–448.
18. H. Ibach, J. Electron Spectrosc. Relat. Phenom., 1993, 64–65, 819–823.
19. S. J. Park and R. E. Palmer, Phys. Rev. Lett., 2010, 105, 016801.
20. X. Chen, P. Lu and Y. Wang, Chem. – Eur. J., 2011, 17, 8105–8114.
21. Z. Wang, Z. Hong, T. Zhuang, G. Chen, H. Sasabe, D. Yokoyama and J. Kido, Appl. Phys. Lett., 2015, 106, 053305.
22. G. Rouillé, M. Steglich, F. Huisken, T. Henning and K. Müllen, J. Chem. Phys., 2009, 131, 204311.
23. J. D. E. McIntyre and D. E. Aspnes, Surf. Sci., 1971, 24, 417–434.
24. T. Dienel, A. Krause, R. Alle, R. Forker, K. Meerholz and T. Fritz, Adv. Mater., 2010, 22, 4064–4070.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision A.02), Gaussian, Inc., Wallingford CT, 2009.
26. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
27. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
28. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
29. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
30. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
31. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
32. J. B. Foresman, M. Head-Gordon, J. A. Pople and M. J. Frisch, J. Phys. Chem., 1992, 96, 135–149.
33. J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134.
34. M. C. Zerner, G. H. Loew, R. F. Kirchner and U. T. Mueller-Westerhoff, J. Am. Chem. Soc., 1980, 102, 589–599.
35. P. C. de Mello, M. Hehenberger and M. C. Zerner, Int. J. Quantum Chem., 1982, 21, 251–258.
36. M. C. Zerner, in Reviews in Computational Chemistry II, ed. K. B. Libkowitz and D. B. Boyd, VCS, New York, 1991.
37. A. Staicu, G. Rouillé, T. Henning, F. Huisken, D. Pouladsaz and R. Scholz, J. Chem. Phys., 2008, 129, 074302.
38. C. M. Western, P GOPHER version 8.0, University of Bristol Research Data Repository, 2014 DOI:10.5523/bris.huflggvpcuc1zvliqed497r2.
39. C. W. Bauschlicher and S. R. Langhoff, Spectrochim. Acta, Part A, 1997, 53, 1225–1240.
40. A. Maurya, S. Rastogi, G. Rouillé, F. Huisken and T. Henning, Astrophys. J., 2012, 755, 120.
41. P. Zhang, X. Zeng, J. Deng, K. Huang, F. Bao, Y. Qiu, K. Xu and J. Zhang, Jpn. J. Appl. Phys., 2010, 49, 095501.
42. D. M. Hudgins and S. A. Sandford, J. Phys. Chem. A, 1998, 102, 329–343.
43. R. Gredel, Y. Carpentier, G. Rouillé, M. Steglich, F. Huisken and T. Henning, Astron. Astrophys., 2011, 530, A26.
44. A. A. Radzig and B. M. Smirnov, in Reference Data on Atoms, Molecules, and Ions, ed. J. P. Toennies, Springer-Verlag, Heidelberg, 1985, vol. 31.
45. F. London, Trans. Faraday Soc., 1937, 33, 8–26.
46. Y. Ooshika, J. Phys. Soc. Jpn., 1954, 9, 594–602.
47. H. C. Longuet-Higgins and J. A. Pople, J. Chem. Phys., 1957, 27, 192–194.
48. E. G. McRae, J. Phys. Chem., 1957, 61, 562–572.
49. W. E. Henke, W. Yu, H. L. Selzle, E. W. Schlag, D. Wutz and S. H. Lin, J. Chem. Phys., 1985, 97, 205–215.
50. K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8533–8542.
51. M. Müller, A. Paulheim, A. Eisfeld and M. Sokolowski, J. Chem. Phys., 2013, 139, 044302.
52. M. Müller, E. Le Moal, R. Scholz and M. Sokolowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 241203(R),  DOI:10.1103/PhysRevB.83.241203.
53. P. Navarro, F. C. Bocquet, I. Deperasińska, G. Pirug, F. S. Tautz and M. Orrit, J. Phys. Chem. C, 2015, 119, 277–283.
54. J. Kröger, S. Lehwald and H. Ibach, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10895–10904.
55. J. Kröger, D. Bruchmann, S. Lehwald and H. Ibach, Surf. Sci., 2000, 449, 227–235.
56. F. S. Tautz, M. Eremtchenko, J. A. Schaefer, M. Sokolowski, V. Shklover and E. Umbach, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 125405.
57. W. Dou, S. Huang, R. Q. Zhang and C. S. Lee, J. Chem. Phys., 2011, 134, 094705.
58. H. Ibach and D. L. Mills, Electron energy loss spectroscopy and surface vibrations, Academic Press, New York, 1982.

---

Footnote

† Electronic supplementary information (ESI) available: Molecular structures. See DOI: 10.1039/c5cp03761a

---