Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
X-ray absorption resonances near L2,3-edges from real-time propagation of the Dirac–Kohn–Sham density matrix
Marius
Kadek
a,
Lukas
Konecny
b,
Bin
Gao
a,
Michal
Repisky
*a and
Kenneth
Ruud
*a
aCentre for Theoretical and Computational Chemistry, Department of Chemistry, University of Tromsø—The Arctic University of Norway, N-9037 Tromsø, Norway. E-mail: kenneth.ruud@uit.no; michal.repisky@uit.no; Tel: +47 77623101
bDepartment of Inorganic Chemistry, Faculty of Natural Sciences, Comenius University, Bratislava, Slovak Republic
First published on 7th August 2015
Abstract
The solution of the Liouville–von Neumann equation in the relativistic Dirac–Kohn–Sham density matrix formalism is presented and used to calculate X-ray absorption cross sections. Both dynamical relaxation effects and spin–orbit corrections are included, as demonstrated by calculations of the X-ray absorption of SF6 near the sulfur L2,3-edges. We also propose an analysis facilitating the interpretation of spectral transitions from real-time simulations, and a selective perturbation that eliminates nonphysical excitations that are artifacts of the finite basis representation.
X-ray absorption spectroscopy (XAS) is a powerful technique to determine the structural and electronic properties of matter at the atomic level, in which core electrons are excited to unoccupied or continuum states after absorbing photons in the X-ray energy range. The resulting absorption peaks, normally called edges in XAS, are conventionally labeled according to the originating core state, for instance K-edge for 1s, L1-edge for 2s, L2-edge for 2p1/2 and L3-edge for 2p3/2, and the spectrum near these edges is called X-ray absorption near-edge structure (XANES). The involvement of core electrons brings great challenges for theoretical studies of XAS because core–valence excitations have to be described. Methods for calculating XAS spectra have been developed for many decades, and several approaches have been proposed: the static exchange approximation,1 the multiple scattering methods,2,3 the Bethe–Salpeter equation,4–6 and different ab initio methods (such as the coupled cluster7 and second-order algebraic-diagrammatic construction model8), to name just a few. Time-dependent density functional theory9 (TDDFT) has proved to be economic for calculating electronic excitations,10 but its application to XAS is prohibitively expensive except for small molecules, as a large number of roots must be determined in order to access the high-energy excitations. Several solutions have been proposed to circumvent this difficulty, such as the restricted excitation window TDDFT (REW-TDDFT)11,12 or the complex polarization propagator approach.13–15
In this work we examine an alternative route to the simulation of X-ray absorption processes near the L2,3-edges. The essence of the approach is the combination of a rigorous relativistic formalism based on the Dirac–Coulomb Hamiltonian with the real-time formulation of TDDFT (RT-TDDFT). In contrast to previous methods based on linear-response TDDFT (LR-TDDFT), the present real-time approach also offers the possibility to simulate a wide range of spectroscopic techniques involving strong electromagnetic fields while at the same time variationally accounting for all indispensable relativistic corrections, of which the spin–orbit (SO) coupling is of significant importance, as manifested by the multiplet structure of the spectral lines near/at L2,3 absorption edges. Although the RT-TDDFT formalism has already been used for modeling core-level absorption spectroscopy of molecular systems,16–20 in this work we present the first application of the approach at the relativistic 4-component level of theory with the variational inclusion of SO corrections. The usefulness of such a method has been examined on hydrogen-like systems by Selstø et al.21 and in the perspective on relativistic quantum chemistry by Belpassi et al.22
Furthermore, in this Letter we address two shortcomings of current applications of RT-TDDFT to XAS. One problem is that the comparison of high-energy excitations with experiment can often be hampered by competing excitation processes, some of which are artifacts of treating the excitations in a finite basis set that cannot properly describe excitations to the continuum. By restricting the perturbation operator, we significantly reduce the intensity of such artificial transitions, thus identifying the genuine core excitations. The second difficulty is to classify and interpret the characters of the transitions, for which there is no unique and straightforward way in real-time simulations. To overcome this issue, we introduce the dipole-weighted transition analysis (DWTA). Finally, we assess the methodology on the XAS of the SF6 molecule near the sulfur L2,3-edges, and compare the theoretical spectrum with available high-resolution experimental data.23
The central equation of motion of (RT-)TDDFT in the formalism of the density matrix is the Liouville–von Neumann equation, which reads (in atomic units)
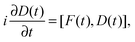 | (1) |
A numerically stable and robust solver of eqn (1) should preserve essential properties of the density matrix, such as trace (number of electrons) and idempotency.24,25 Our implementation consists of two main components: (1) the second-order mid-point Magnus solver, which is based on the truncation and approximation of the Magnus expansion of the evolution operator.26 (2) An extrapolation–interpolation scheme,27 required by the nonlinear [in terms of D(t)] character of eqn (1). The latter proved important for ensuring the stability of the time propagation.
To compute the X-ray absorption spectrum from an RT-TDDFT simulation, we first perform a time-independent DFT calculation to obtain the reference ground-state density matrix D0. The initial perturbed density matrix D(0+) is obtained from the ground-state density matrix using
D(0+) = exp(iκPn)D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iκPn), exp(−iκPn), | (2) |
During the time propagation of the perturbed state, we calculate the induced dipole moment on-the-fly, which is then Fourier transformed and used to calculate the field-dependent dynamical dipole polarizability tensor α(ω). The final absorption spectrum of a compound is the dipole strength function S(ω) obtained from the polarizability tensor as
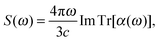 | (3) |
We have implemented the relativistic four-component RT-TDDFT method in the ReSpect program,28 and the implementation combines the Dirac–Coulomb Hamiltonian with the non-relativistic adiabatic DFT exchange–correlation functionals, of which the hybrid B3LYP functional was applied in the present work.29,30 The DFT contributions were evaluated numerically on an adaptive molecular grid and their rotational invariance was preserved by means of a non-collinear approach with the spin density described by the norm of the spin magnetization vector. The molecular geometry was optimized at the four-component level of theory (rS–F = 1.60753 Å; experimental value31 is 1.564 Å) using the ReSpect program package, employing for the large component uncontracted all-electron Gaussian-type basis sets of triple-zeta quality (cc-pVTZ).32 The small-component basis was generated on-the-fly imposing the restricted kinetically balanced relation.33 In the RT-TDDFT simulations, we used the calculated molecular geometry along with an augmented version of the correlation-consistent basis family; aug-cc-pV(T+d)Z for sulfur34 and a modified aug-cc-pVTZ for fluorine (all f and the most diffuse d functions were removed).35 For all nuclei, a finite-sized Gaussian model was used. The X-ray absorption spectrum of SF6 was obtained from RT-TDDFT such that the electronic ground state was perturbed using an analytic δ-function pulse with strength κ = 0.0005 au and evolved for 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps of length 0.025 au (≈0.6 attoseconds), this corresponds to a total simulation time of approximately 34 fs and leads to an energy (frequency) resolution of 122 meV in the calculated spectrum. An average wall-clock time per time step was 36.1 seconds, where each step requires two Fock matrix constructions and two matrix diagonalizations—the implementation details can be found in ref. 27. To account for the error caused by the finite-simulation length, we artificially damped the time signal with an exponential function exp(−γt), γ = 0.0038 au before its Fourier transformation, resulting in broadened Lorentzian-shaped peaks. This damping is not related to genuine lifetimes of excited states which remain infinite in the present theoretical model. The spectrum is normalized in accordance with experiment23—the intensity of the first peak equals one. The final figures were plotted using Python's matplotlib library.36
000 time steps of length 0.025 au (≈0.6 attoseconds), this corresponds to a total simulation time of approximately 34 fs and leads to an energy (frequency) resolution of 122 meV in the calculated spectrum. An average wall-clock time per time step was 36.1 seconds, where each step requires two Fock matrix constructions and two matrix diagonalizations—the implementation details can be found in ref. 27. To account for the error caused by the finite-simulation length, we artificially damped the time signal with an exponential function exp(−γt), γ = 0.0038 au before its Fourier transformation, resulting in broadened Lorentzian-shaped peaks. This damping is not related to genuine lifetimes of excited states which remain infinite in the present theoretical model. The spectrum is normalized in accordance with experiment23—the intensity of the first peak equals one. The final figures were plotted using Python's matplotlib library.36
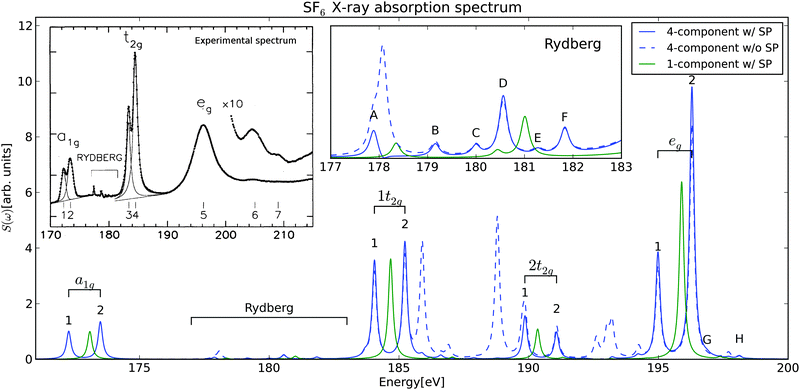
TDDFT calculations in a finite basis representation introduce the two following problems in order to correctly predict the XANES experiment: first, DFT exchange–correlation (XC) functionals tend to underestimate excitation energies due to the self-interaction error and the associated integer discontinuity in the derivative of the total energy with respect to the number of electrons.37 However, this problem manifests itself only in a global, frequency-independent offset of the excitation energies, which is then corrected by uniformly shifting the entire spectrum by a constant. In our case, we shifted the calculated spectrum by 7.89 eV to match the first experimental peak. We note, that this correction accounts for various deficiencies of the density functional theory, such as the incomplete description of dynamical relaxation or self-interaction errors. The second problem is the emergence of non-physical transitions from non-core occupied orbitals to high-laying virtual orbitals. These peaks often appear in the XANES region as artificial peaks and prevent the interpretation of simulated spectra. We observe on SF6 that restricting the perturbation electric dipole moment operator Pn only to excitations from sulfur 2p core spin–orbitals suppresses the intensities of the artificial peaks by several orders of magnitude. Furthermore, intensities of resonances in the energy region below 170 eV were also reduced, while leaving the genuine L-edge transitions unaltered. We will refer to the restriction of the perturbation operator as selective perturbation (SP), which is easily implemented by keeping nonzero only those Pn,ai matrix elements for which i denotes occupied core orbitals, and a spans all virtuals, thus formally making transitions between any other orbitals dipole forbidden. It is important to note that we do not reduce the dimensions of the matrices, preserving the orbital relaxation orbitals, as opposed to the alternative approach taken in REW-TDDFT. Moreover, the selective perturbation is not limited to real-time methods, and can also be applied in the LR-TDDFT approach. The contrast in calculated XANES spectra of SF6 with SP (continuous line) and without SP (dashed line) is depicted in Fig. 1.
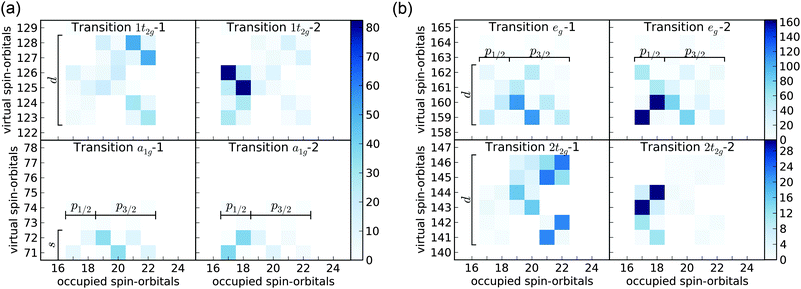
An additional known weakness of real-time simulations is any interpretation of resonances. In order to determine the nature of a particular electronic excitation in terms of transitions between molecular orbitals, and also to prove that the peaks suppressed due to the SP correspond to non-core excitations, we propose the dipole-weighted transition analysis (DWTA). This approach is based on a Fourier transform of the partial contributions of an occupied-virtual spin–orbital pair ia to the dynamic polarizability:
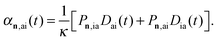 | (4) |
We used DWTA to analyze all X-ray absorption resonances of SF6 between 170 and 200 eV, and the result for the eight most intense transitions is shown in Fig. 2. The analysis revealed the following: (1) all nonphysical peaks observered in the simulations without SP arise from excitations of electrons from non-core occupied orbitals to high-laying virtual orbitals. This observation justifies the use of SP. (2) The doublet structure originates from the spin–orbit splitting of the sulfur 2p orbitals—the lower-energy resonances correspond to promotion from 2p3/2, whereas those at higher-energies are from 2p1/2. (3) All dipole-allowed transitions can be grouped according to irreducible representations of the octahedral point group: a1g, t2g and eg (Table 1).
| Peak | Assignmenta | Exc. energy [eV] | Intensity [arb.] | ||
|---|---|---|---|---|---|
| This workb | Exp. | This work | Exp. | ||
| a All holes correspond to sulfur 2p spin–orbitals. b The simulated spectrum was shifted by 7.89 eV to account for the self-interaction error. | |||||
| a1g−1 | a11g(2p3/2)−1 | 172.27 | 172.27 | 1.00 | 1.00 |
| a1g−2 | a11g(2p1/2)−1 | 173.49 | 173.44 | 1.35 | 1.62 |
| A | a11g(2p3/2)−1 | 177.89 | 177.42 | 0.07 | |
| B | a11g(2p1/2)−1 | 179.16 | 178.63 | 0.03 | |
| C | e1g(2p3/2)−1 | 180.00 | 178.80 | 0.03 | |
| D | t21g(2p3/2)−1 | 180.56 | 178.76 | 0.16 | |
| E | e1g(2p1/2)−1 | 181.28 | 180.00 | 0.01 | |
| F | t21g(2p1/2)−1 | 181.83 | 179.96 | 0.07 | |
| 1t2g−1 | t21g(2p3/2)−1 | 184.06 | 183.40 | 3.53 | 2.71 |
| 1t2g−2 | t21g(2p1/2)−1 | 185.23 | 184.57 | 4.21 | 5.53 |
| 2t2g−1 | t21g(2p3/2)−1 | 189.86 | 1.55 | ||
| 2t2g−2 | t21g(2p1/2)−1 | 191.07 | 0.97 | ||
| eg−1 | e1g(2p3/2)−1 | 194.98 | 196.2 | 3.80 | 15.7 |
| eg−2 | e1g(2p1/2)−1 | 196.29 | 9.80 | ||
| G | a11g(2p3/2)−1 | 196.87 | 0.05 | ||
| H | a11g(2p1/2)−1 | 198.12 | 0.09 | ||
The final calculated and experimental photoabsorption specta of SF6 near the sulfur L2,3-edges are depicted in Fig. 1. For clarity, the figure also provides comparison between the nonrelativistic (1-component) and the relativistic (4-component) theoretical spectra, clearly demonstrating the importance of a full spin–orbit treatment in reproducing the doublet structure of all spectral lines. The molecular resonances at 172–174 eV represent an excitation of a sulfur 2p electron to the lowest-unoccupied molecular orbital (LUMO). The LUMO is an antibonding σ* orbital of a1g symmetry, attributed primarily to the sulfur 4s1/2. The calculated spin–orbit splitting of 1.22 eV between the low-lying photoabsorption resonances, (S 2p1/2)−1a1g and (S 2p3/2)−1a1g, agrees very well with the experimental observation (1.17 eV). Notably, the present theoretical model predicts correctly the declination of intensity ratio between (S 2p3/2)−1 and (S 2p1/2)−1 from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3. This reversed intensity ratio is a phenomenon caused by a significant exchange interaction between an electron in an inner-well excited state and the remaining sulfur core electrons.38 The calculated ratio of 1
1.3. This reversed intensity ratio is a phenomenon caused by a significant exchange interaction between an electron in an inner-well excited state and the remaining sulfur core electrons.38 The calculated ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 is, however, slightly below the experimental XANES ratio of 1
1.3 is, however, slightly below the experimental XANES ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6. The second intense doublet (at 184–186 eV), just above the sulfur L2,3 thresholds, is a molecular shape resonance, assigned to the promotion of a single sulfur 2p electron to a quasi-bound orbital of t2g symmetry. The theoretical magnitude of the SO splitting (1.17 eV) matches the XANES experiment exactly. The intensity ratio of 1
1.6. The second intense doublet (at 184–186 eV), just above the sulfur L2,3 thresholds, is a molecular shape resonance, assigned to the promotion of a single sulfur 2p electron to a quasi-bound orbital of t2g symmetry. The theoretical magnitude of the SO splitting (1.17 eV) matches the XANES experiment exactly. The intensity ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.19 is slightly below the experimental value 1
1.19 is slightly below the experimental value 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.04. The next shape resonance is of eg symmetry, and consists of a single wide peak in the experiment, spanning the energy range between 190–200 eV. Due to the absence of mechanisms capturing the finite lifetime of such states, we can probe by present calculation the structure of this peak in more detail. In particular, the spin–orbit splitting of the 2p orbitals is again responsible for the doublet structure of the transition (1.31 eV). Moreover, we observe an additional weaker doublet of t2g symmetry (labeled 2t2g in the figures and the table) and a very weak doublet of a1g symmetry in close proximity to the eg transition. Ferrett et al.39 found that the resonance also exhibits strong multielectron effects in its decay, but study of such effects is beyond the scope of this Letter. In the Rydberg region we identified three pairs of resonances with a1g,eg and t2g symmetries, matching the states with excitations to lower outer-well orbitals observed experimentally. For each pair, the calculated value of the spin–orbit splitting was 1.27–1.28 eV, which is in very good agreement with the experimental observation of 1.20–1.21 eV, in particular if we consider the character of the final states—Rydberg states.
2.04. The next shape resonance is of eg symmetry, and consists of a single wide peak in the experiment, spanning the energy range between 190–200 eV. Due to the absence of mechanisms capturing the finite lifetime of such states, we can probe by present calculation the structure of this peak in more detail. In particular, the spin–orbit splitting of the 2p orbitals is again responsible for the doublet structure of the transition (1.31 eV). Moreover, we observe an additional weaker doublet of t2g symmetry (labeled 2t2g in the figures and the table) and a very weak doublet of a1g symmetry in close proximity to the eg transition. Ferrett et al.39 found that the resonance also exhibits strong multielectron effects in its decay, but study of such effects is beyond the scope of this Letter. In the Rydberg region we identified three pairs of resonances with a1g,eg and t2g symmetries, matching the states with excitations to lower outer-well orbitals observed experimentally. For each pair, the calculated value of the spin–orbit splitting was 1.27–1.28 eV, which is in very good agreement with the experimental observation of 1.20–1.21 eV, in particular if we consider the character of the final states—Rydberg states.
Finally, there are several factors that affect the accuracy of the simulations. Apart from the choice of the DFT functional, there are two notable sources of error responsible for the differences between the calculation and the experiment. First, intensities of Rydberg states and high-energy shape resonances were much more susceptible to changes of basis set. The poorer description of the Rydberg states is mostly due to the delocalized character of outer-well orbitals. On the other hand, the inner-well state (first a1g) was perfectly described even with smaller basis sets. Second, the finite simulation time resulted in the finite resolution. The error was sufficiently small for stronger resonances, but affected the weak transitions. The intensities of the Rydberg transitions were more prone to both errors, therefore we omitted them from the comparison with the experiment.
In conclusion, we have reported the first implementation and application of relativistic four-component real-time TDDFT to the simulation of core-level near-edge X-ray absorption spectroscopy. The proposed formalism accounts variationally for relativistic corrections arising from the Dirac–Coulomb Hamiltonian, of which the spin–orbit coupling is of significant importance for reproducing the multiplet structure of the spectral lines near L2,3 absorption edges. The computed XANES spectrum of SF6 agrees very well with experimental results, in particular when reducing the intesity of nonphysical excitations by the developed selective perturbation. The character of the eight most intense excitations was analyzed in terms of molecular orbitals by means of a proposed DWTA technique, and both the assignments and fine-structure splittings were found to be in good agreement with high-resolution experimental data.
Acknowledgements
This work was supported by the Research Council of Norway (Grants 179568 and 214095), European Research Council through a Starting Grant (Grant No. 279619), and from the Slovak Research and Development Agency (APVV-0510-12). Computational time has been provided through a grant from the Norwegian supercomputing program NOTUR (Grant No. NN4654K). We thank Angela K. Wilson and Kenneth G. Dyall for helpful comments on choice of basis set.References
- H. Ågren, V. Carravetta, O. Vahtras and L. G. Pettersson, Chem. Phys. Lett., 1994, 222, 75–81 CrossRef.
- P. Lee and J. Pendry, Phys. Rev. B: Solid State, 1975, 11, 2795 CrossRef CAS.
- A. Ankudinov, B. Ravel, J. Rehr and S. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565 CrossRef CAS.
- E. E. Salpeter and H. A. Bethe, Phys. Rev., 1951, 84, 1232–1242 CrossRef.
- E. L. Shirley, Phys. Rev. Lett., 1998, 80, 794 CrossRef CAS.
- A. Ankudinov, Y. Takimoto and J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165110 CrossRef.
- T. Fransson, S. Coriani, O. Christiansen and P. Norman, J. Chem. Phys., 2013, 138, 124311 CrossRef PubMed.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. Prince, A. Trofimov, E. Gromov, I. Zaytseva and J. Schirmer, Chem. Phys., 2008, 347, 360–375 CrossRef CAS PubMed.
- E. Runge and E. K. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- M. Stener, G. Fronzoni and M. De Simone, Chem. Phys. Lett., 2003, 373, 115–123 CrossRef CAS.
- Y. Zhang, J. D. Biggs, D. Healion, N. Govind and S. Mukamel, J. Chem. Phys., 2012, 137, 194306 CrossRef PubMed.
- U. Ekström, P. Norman, V. Carravetta and H. Ågren, Phys. Rev. Lett., 2006, 97, 143001 CrossRef.
- P. Norman, D. M. Bishop, H. J. A. Jensen and J. Oddershede, J. Chem. Phys., 2001, 115, 10323–10334 CrossRef CAS PubMed.
- U. Ekström and P. Norman, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 042722 CrossRef.
- T. Akama, Y. Imamura and H. Nakai, Chem. Lett., 2010, 39, 407–409 CrossRef CAS.
- T. Akama and H. Nakai, J. Chem. Phys., 2010, 132, 054104 CrossRef PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS.
- A. J. Lee, F. D. Vila and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115107 CrossRef.
- B. Gao, K. Ruud and Y. Luo, J. Chem. Phys., 2012, 137, 194307 CrossRef PubMed.
- S. Selstø, E. Lindroth and J. Bengtsson, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 043418 CrossRef.
- L. Belpassi, L. Storchi, H. M. Quiney and F. Tarantelli, Phys. Chem. Chem. Phys., 2011, 13, 12368–12394 RSC.
- E. Hudson, D. A. Shirley, M. Domke, G. Remmers, A. Puschmann, T. Mandel, C. Xue and G. Kaindl, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 361–372 CrossRef CAS.
- R. Kosloff, J. Phys. Chem., 1988, 92, 2087–2100 CrossRef CAS.
- A. Castro, M. a. L. Marques and A. Rubio, J. Chem. Phys., 2004, 121, 3425–3433 CrossRef CAS PubMed.
- W. Magnus, Commun. Pure Appl. Math., 1954, 7, 649–673 CrossRef PubMed.
- M. Repisky, L. Konecny, M. Kadek, S. Komorovsky, O. L. Malkin, V. G. Malkin and K. Ruud, J. Chem. Theory Comput., 2015, 11, 980–991 CrossRef CAS.
- ReSpect, version 3.4.2, 2015 – Relativistic Spectroscopy DFT Program of Authors: M. Repisky, S. Komorovsky, V. G. Malkin, O. L. Malkina, M. Kaupp, K. Ruud, with contributions from R. Bast, U. Ekstrom, M. Kadek, S. Knecht, L. Konecny, I. Malkin Ondik and E. Malkin, see http://www.respectprogram.org.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- G. Herzberg, Molecular spectra and molecular structure. Vol. 3: Electronic spectra and electronic structure of polyatomic molecules, Van Nostrand Reinhold, New York, 1966 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS PubMed.
- R. E. Stanton and S. Havriliak, J. Chem. Phys., 1984, 81, 1910–1918 CrossRef CAS PubMed.
- T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 CrossRef.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz Jr, Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS.
- J. L. Dehmer, J. Chem. Phys., 1972, 56, 4496–4504 CrossRef CAS PubMed.
- T. Ferrett, D. Lindle, P. Heimann, M. Piancastelli, P. Kobrin, H. Kerkhoff, U. Becker, W. Brewer and D. Shirley, J. Chem. Phys., 1988, 89, 4726–4736 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |